2017至2018年北京高三模拟分类汇编之立体几何大题
2017-2018年高考数学立体几何汇编及答案解析

2017—2018年高考数学试题立体几何汇编及答案解析类型一 空间几何体的结构特征与三视图1.【2017浙江,3】某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:cm 3)是A .12+πB .32+πC .123+πD .323+π【答案】A 【解析】2π1211π3(21)1322V ⨯=⨯⨯+⨯⨯=+,选A. 2.【2017北京,理7】某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为(A ) (B )(C ) (D )2 【答案】B 【解析】几何体是四棱锥,如图红色线为三视图还原后的几何体,最长的棱长为正方体的对角线,l == B.3.【2017山东,理13】由一个长方体和两个14圆柱体构成的几何体的三视图如右图,则该几何体的体积为 .【答案】22π+【解析】该几何体的体积为21112211242V π=π⨯⨯⨯+⨯⨯=+. 4.(2018年高考北京卷理科)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为( )A.1 B.2 C.3 D.4【解答】解:四棱锥的三视图对应的直观图为:PA⊥底面ABCD,AC=,CD=,PC=3,PD=2,可得三角形PCD不是直角三角形.所以侧面中有3个直角三角形,分别为:△PAB,△PBC,△PAD.故选:C.5.(2018年高考数学全国卷1理科)某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为()A.2B.2C.3 D.2【解答】解:由题意可知几何体是圆柱,底面周长16,高为:2,直观图以及侧面展开图如图:圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度:=2.故选:B.6.(2018年高考数学全国卷3理科)中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是()A. B . C . D .【解答】解:由题意可知,如图摆放的木构件与某一带卯眼的木构件咬合成长方体,小的长方体,是榫头,从图形看出,轮廓是长方形,内含一个长方形,并且一条边重合,另外3边是虚线,所以木构件的俯视图是A .故选:A .7.(2018年高考浙江卷)某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:cm 3)是( ) A .2B .4C .6D .8【解答】解:根据三视图:该几何体为底面为直角梯形的四棱柱.如图所示:故该几何体的体积为:V=.故选:C .8.某多面体的三视图如图所示,则该几何体的体积与其 外接球的体积之比为( )A .π186B .π96 C .π36 D .π26选A类型二 空间几何体与空间旋转体的面积、体积问题1、如图,半径为4的球O中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是______.解:如图,2、设球的一条半径与圆柱相应的母线的夹角为α,圆柱侧面积S =2π×4sin α×2×4cos α=32πsin2α,当α=π4时,S 取最大值32π,此时球的表面积与该圆柱的侧面积之差为32π.3、(2018年高考数学天津卷理科)已知正方体ABCD ﹣A 1B 1C 1D 1的棱长为1,除面ABCD 外,该正方体其余各面的中心分别为点E ,F ,G ,H ,M (如图),则四棱锥M ﹣EFGH 的体积为 .【解答】解:正方体的棱长为1,M ﹣EFGH 的底面是正方形的边长为:,四棱锥是正四棱锥,棱锥的高为, 四棱锥M ﹣EFGH 的体积:=.故答案为:.4、(2014·课标Ⅱ)如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm ,高为6cm 的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )A.1727B.59C.1027D.13解:原来毛坯体积为:π·32·6=54π(cm 3),由三视图知该零件由左侧底面半径为2cm ,高为4cm 的圆柱和右侧底面半径为3cm ,高为2cm 的圆柱构成,故该零件的体积为:π·22·4+π·32·2=34π(cm 3),切削掉部分的体积为54π-34π=20π(cm 3),故切削掉部分的体积与原来毛坯体积的比值为20π54π=1027 .故选C.6.【2017课标3,理8】已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为A .πB .3π4C .π2D .π4【答案】B【解析】由题可知球心在圆柱体中心,圆柱体上下底面圆半径r =则圆柱体体积23ππ4V r h ==,故选B.7.【2017天津,理10】已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为 . 【答案】92π 【解析】设正方体边长为a ,则226183a a =⇒= ,外接球直径为34427923,πππ3382R V R ====⨯=. 8.【2017江苏,6】 如图,在圆柱12,O O 内有一个球O ,该球与圆柱的上、下面及母线均相切.记圆柱12,O O 的体积为1V ,球O 的体积为2V ,则12V V 的值是 ▲ .【答案】32 【解析】设球半径为r ,则2132π2342π3V r r V r ⨯==.故答案为32. 9、(2018年高考数学全国卷3理科)10.(5分)设A ,B ,C ,D 是同一个半径为4的球的球面上四点,△ABC 为等边三角形且面积为9,则三棱锥D ﹣ABC 体积的最大值为( ) A .12B .18C .24D .54【解答】解:△ABC 为等边三角形且面积为9,可得,解得AB=6,球心为O ,三角形ABC 的外心为O′,显然D 在O′O 的延长线与球的交点如图:O′C==,OO′==2,则三棱锥D ﹣ABC 高的最大值为:6, 则三棱锥D ﹣ABC 体积的最大值为:=18.故选:B .10、(2018年高考数学全国卷2理科)16.(5分)已知圆锥的顶点为S ,母线SA ,SB 所成角的余弦值为,SA 与圆锥底面所成角为45°,若△SAB 的面积为5,则该圆锥的侧面积为40π .【解答】解:圆锥的顶点为S ,母线SA ,SB 所成角的余弦值为,可得sin ∠AMB==.△SAB 的面积为5,可得sin ∠AMB=5,即×=5,即SA=4.SA 与圆锥底面所成角为45°,可得圆锥的底面半径为:=2.则该圆锥的侧面积:π=40π.故答案为:40π.11、(2018年高考数学全国卷1理科)12.(5分)已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为( )A .B .C .D .【解答】解:正方体的所有棱中,实际上是3组平行的棱,每条棱所在直线与平面α所成的角都相等,如图:所示的正六边形平行的平面,并且正六边形时,α截此正方体所得截面面积的最大,此时正六边形的边长明明就的最大值为:6×=.故选:A.12、(2018年江苏省高考数学试卷)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为.【解答】解:正方体的棱长为2,中间四边形的边长为:,八面体看做两个正四棱锥,棱锥的高为1,多面体的中心为顶点的多面体的体积为:2×=.故答案为:.类型三点共线、线共点问题1、如图,E,F,G,H分别是空间四边形内AB,BC,CD,DA上的点,且EH与FG交于点O.求证:B,D,O三点共线.证明:∵点E∈平面ABD,点H∈平面ABD,∴EH⊂平面AB D.∵EH∩FG=O,∴点O∈平面AB D.同理可证点O∈平面BC D.∴点O∈平面ABD∩平面BCD=B D.即B,D,O三点共线.类型四共面问题1、下列如图所示的正方体和正四面体,P、Q、R、S分别是所在棱的中点,则四个点共面的图形是____________.(填所有满足条件图形的序号)解:易知①③中PS ∥Q R ,∴四点共面.在②中构造如图所示的含点P ,S ,R ,Q 的正六边形,易知四点共面.在④中,由点P ,R ,Q 确定平面α,由图象观察知点S 在平面α外,因此四点不共面.综上知,故填①②③.类型五 异面直线问题1.【2017课标II ,理10】已知直三棱柱111C C AB -A B 中,C 120∠AB =,2AB =,1C CC 1B ==,则异面直线1AB 与1C B 所成角的余弦值为( )A ..5 C .5D 【答案】C【解析】如图所示,补成四棱柱1111ABCD A B C D - ,则所求角为1111,BC D BC BD C D AB ∠=====因此1cos 5BC D ∠== ,故选C 。
北京高考真题之立体几何

一.1. 已知正三棱锥P ABC−的六条棱长均为6,S是ABC△及其内部的点构成的集合,设集合{5}T Q S PQ=∈,则T表示的区域的面积为(A)34π(B)π(C)2π(D)3π2. 某四面体的三视图如图所示,该四面体的表面积为()A. B. 4 C. 3+ D. 23. 某三棱柱的底面为正三角形,其三视图如图所示,该三棱柱的表面积为().A. 6+B. 6+C. 12+D. 12+4. 某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为()A.1B.2C.3D.45. 某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为()A.3B.2C.2D.26. 某三棱锥的三视图如图所示,则该三棱锥的体积为()A.60 B.30 C.20 D.107. 某三棱锥的三视图如图所示,则该三棱锥的体积为()A.B.C.D.18. (5分)已知l,m是平面α外的两条不同直线.给出下列三个论断:①l⊥m;②m∥α;③l⊥α.以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:.二.1. (2019文)如图,在四棱锥P﹣ABCD中,P A⊥平面ABCD,底面ABCD为菱形,E为CD的中点.(Ⅰ)求证:BD⊥平面P AC;(Ⅱ)若∠ABC=60°,求证:平面P AB⊥平面P AE;(Ⅲ)棱PB上是否存在点F,使得CF∥平面P AE?说明理由.2. 如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD∥平面MAC,PA=PD=,AB=4.(1)求证:M为PB的中点;(2)求二面角B﹣PD﹣A的大小;(3)求直线MC与平面BDP所成角的正弦值.3. (2020) 如图,在正方体1111ABCD A B C D −中,E 为1BB 的中点.(Ⅰ)求证:1//BC 平面1AD E ;(Ⅱ)求直线1AA 与平面1AD E 所成角的正弦值.5. (2022·)如图,在三棱柱111ABC A B C 中,侧面11BCC B 为正方形,平面11BCC B ⊥平面11ABB A ,2AB BC ==,M ,N分别为11A B ,AC 的中点.(1)求证:MN ∥平面11BCC B ;(2)再从条件①、条件②这两个条件中选择一个作为已知,求直线AB 与平面BMN 所成角的正弦值. 条件①:AB MN ⊥; 条件②:BM MN =.注:如果选择条件①和条件②分别解答,按第一个解答计分.7. (2019理)如图,在四棱锥P﹣ABCD中,P A⊥平面ABCD,AD⊥CD,AD∥BC,P A=AD=CD=2,BC=3.E为PD的中点,点F在PC上,且=.(Ⅰ)求证:CD⊥平面P AD;(Ⅱ)求二面角F﹣AE﹣P的余弦值;(Ⅲ)设点G在PB上,且=.判断直线AG是否在平面AEF内,说明理由.8. (14分)如图,在三棱柱ABC﹣A1B1C1中,CC1⊥平面ABC,D,E,F,G分别为AA1,AC,A1C1,BB1的中点,AB=BC=,AC=AA1=2.(Ⅰ)求证:AC⊥平面BEF;(Ⅱ)求二面角B﹣CD﹣C1的余弦值;(Ⅲ)证明:直线FG与平面BCD相交.9. 如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=.(Ⅰ)求证:PD⊥平面PAB;(Ⅱ)求直线PB与平面PCD所成角的正弦值;(Ⅲ)在棱PA上是否存在点M,使得BM∥平面PCD?若存在,求的值,若不存在,说明理由.答案2. 二面角B﹣PD﹣A的大小为60°;直线MC与平面BDP所成角的正弦值为|cos<>|=||=||=3. (Ⅰ)证明见解析;(Ⅱ)2 3.所以PAB为直角三角形,又因为PB=2PB BC+,则PBC为直角三角形,故又因为BC PA⊥PA PB P=,平面PAB,又x轴,过A所以(0,0,1),(1,1,0),(0,1,0),(1,1,AP AC BC PC ====−设平面PAC 的法向量为()111,,m x y z =,则00m AP m AC ⎧⋅=⎪⎨⋅=⎪⎩,即1=,则11y =−,所以(1,1,0)m =−,的法向量为(22,,x n y =00BC PC ⎧⋅=⋅=,即,所以(1,0,1)n =,11,222m n m n m n⋅===⨯,又因为二面角A PC B −−为锐二面角,所以二面角A PC B −−的大小为π系,利用空间向量可求线面角的正弦值. 【详解】(1)取AB 的中点为K ,连接,MK NK , 由三棱柱111ABC A B C 可得四边形11ABB A 为平行四边形, 而11,B M MA BK KA ==,则1//MK BB ,而MK ⊄平面11BCC B ,1BB ⊂平面11BCC B ,故//MK 平面11BCC B , 而,CN NA BK KA ==,则//NK BC ,同理可得//NK 平面11BCC B , 而,,NK MK K NK MK =⊂平面MKN ,故平面//MKN 平面11BCC B ,而MN ⊂平面MKN ,故//MN 平面11BCC B , (2)因为侧面11BCC B 为正方形,故1CB BB ⊥, 而CB ⊂平面11BCC B ,平面11CBB C ⊥平面11ABB A , 平面11CBB C ⋂平面111ABB A BB =,故CB ⊥平面11ABB A , 因为//NK BC ,故NK ⊥平面11ABB A , 因为AB ⊂平面11ABB A ,故NK AB ⊥,若选①,则AB MN ⊥,而NK AB ⊥,NK MN N =, 故AB ⊥平面MNK ,而MK ⊂平面MNK ,故AB MK ⊥, 所以1AB BB ⊥,而1CB BB ⊥,CB AB B ⋂=,故1BB ⊥平面ABC ,故可建立如所示的空间直角坐标系,则()()()()0,0,0,0,2,0,1,1,0,0,1,2B A N M , 故()()()0,2,0,1,1,0,0,1,2BA BN BM ===, 设平面BNM 的法向量为(),,n x y z =, 则00n BN n BM ⎧⋅=⎨⋅=⎩,从而020x y y z +=⎧⎨+=⎩,取1z =−,则()2,2,1n =−−,设直线AB 与平面BNM 所成的角为θ,则4,2n AB =⨯,故1BB M MKN ≅, 111A B BB ⊥, 1BB ⊥平面ABC ,故可建立如所示的空间直角坐标系,则()0,0,0,B 故()()(0,2,0,1,1,0,0,1,2BA BN BM ===设平面BNM 的法向量为(),,n x y z =,00n BN n BM ⎧⋅=⎨⋅=⎩,从而020x y y z +=⎧⎨+=⎩,取,则(2,2,n =−−设直线AB 与平面所成的角为42cos ,233n AB ==⨯6.7. 证明:(Ⅰ)∵P A ⊥平面ABCD ,∴P A ⊥CD , ∵AD ⊥CD ,P A ∩AD =A , ∴CD ⊥平面P AD .解:(Ⅱ)以A 为原点,在平面ABCD 内过A 作CD 的平行线为x 轴, AD 为y 轴,AP 为z 轴,建立空间直角坐标系, A (0,0,0),E (0,1,1),F (,,),P(0,0,2),B(2,﹣1,0),=(0,1,1),=(),平面AEP的法向量=(1,0,0),设平面AEF的法向量=(x,y,z),则,取x=1,得=(1,1,﹣1),设二面角F﹣AE﹣P的平面角为θ,则cosθ===.∴二面角F﹣AE﹣P的余弦值为.(Ⅲ)直线AG在平面AEF内,理由如下:∵点G在PB上,且=.∴G(,﹣,),∴=(,﹣,),∵平面AEF的法向量=(1,1,﹣1),=﹣=0,故直线AG在平面AEF内.8.二面角B﹣CD﹣C1的余弦值为﹣.(III)证明:F(0,0,2),(2,0,1),∴=(2,0,﹣1),∴•=2+0﹣4=﹣2≠0, ∴与不垂直,∴FG 与平面BCD 不平行,又FG ⊄平面BCD , ∴FG 与平面BCD 相交.9. ;.。
2017十区一模分类汇编-立体几何文 试题版

2017年北京各区一模文科立体几何汇编1.(2017海淀一模文18)已知四棱锥P ABCD -中,底面ABCD 为正方形,PA ABCD ⊥平面,2PA AB ==,,E F 分别是,PB PD 的中点.(Ⅰ)求证:PB平面FAC ;(Ⅱ)求三棱锥P EAD -的体积; (Ⅲ)求证:平面EAD ⊥平面FAC .2.(2017西城一模文18)如图,在四棱锥P ABCD -中,底面ABCD 为正方形,PA ⊥底面ABCD ,PA AC =.过点A 的平面与棱,,PB PC PD 分别交于点,,E F G (,,E F G 三点均不在棱的端点处).(Ⅰ)求证:平面PAB ⊥平面PBC ; (Ⅱ)若PC ⊥平面AEFG ,求PFPC的值; (Ⅲ)直线AE 是否可能与平面PCD 平行?证明你的结论.FEABDCP3.(2017东城一模文17)如图,在四棱锥P ABCD -中,四边形ABCD 是平行四边形,AD BD ⊥且=AD BD ,AC BD O =,PO ⊥平面ABCD .(Ⅰ)E 为棱PC 的中点,求证://OE 平面PAB ; (Ⅱ)求证:平面PAD ⊥平面PBD ;(Ⅲ)若PD PB ⊥,=2AD ,求四棱锥P ABCD -的体积.4.(2017朝阳一模文18)如图,在四棱锥P ABCD -中,平面PAB ⊥平面ABCD ,AD BC ,PA AB ⊥,CD AD ⊥,12BC CD AD ==,E 为AD 的中点. (Ⅰ)求证:PA CD ⊥;(Ⅱ)求证:平面⊥PBD 平面PAB ; (Ⅲ)在平面..PAB 内是否存在M ,使得直线CM平面PBE ,请说明理由.PAB C DE5.(2017丰台一模文17)如图1,平行四边形ABCD 中,AC BC ⊥,1BC AC ==,现将△DAC 沿AC 折起,得到三棱锥D ABC -(如图2),且DA BC ,点E 为侧棱DC 的中点.(Ⅰ)求证:平面ABE ⊥平面DBC ; (Ⅱ)求三棱锥E ABC -的体积;(Ⅲ)在ACB ∠的角平分线上是否存在点F ,使得DF ∥平面ABE ?若存在,求DF 的长;若不存在,请说明理由.6.(2017石景山一模文18)如图,在△ABC 中,C ∠为直角,4AC BC ==.沿△ABC 的中位线DE ,将△ADE 折起到△A DE '的位置,使得90A DC '∠=︒,得到四棱锥A BCDE '-.(Ⅰ)求证:BC ⊥平面A CD '; (Ⅱ)求三棱锥E A BC '-的体积;(Ⅲ)M 是棱CD 的中点,过M 做平面α与平面A BC '平行,设平面α截四棱锥A BCDE '-所得截面面积为S ,试求S 的值.图1图 27.(2017房山一模文18)如图1,在直角梯形ABCD 中,AB CD ,AB BC ⊥,2AB CD =,DE AB ⊥. 沿DE 将1A BD 折起到1A ED 的位置,连接11,A B AC ,,M N 分别为1,AC BE 的中点,如图2.(Ⅰ)求证:1DE A B ⊥; (Ⅱ)求证:1MNA ED 平面;(Ⅲ)在棱1A B 上是否存在一点G ,使得1EG A BC ⊥平面?若存在,求出1AG GB的值;若不存在,说明理由.8.(2017平谷一模文18)如图,在四棱锥P ﹣ABCD 中,底面ABCD 是菱形,∠DAB=60°,PD ⊥平面ABCD ,PD=AD=3,PM=2MD ,AN=2NB ,(Ⅰ)求证:直线AM ∥平面PNC ;(Ⅱ)在AB 上是否存在一点E ,使CD ⊥平面PDE ,若存在,确定E 的位置,并证明,若不存在,说明理由;(Ⅲ)求三棱锥C ﹣PDA 的体积.9.(2017大兴一模文18)如图,在四棱锥P ABCD -中,平面PAD ⊥平面ABCD ,90DAB ABC ︒∠=∠=,2,AD BC =四棱锥P ABCD -的体积为10,点P 在PD 上.(Ⅰ)求证:BC //平面PAD ;(Ⅱ)若AM PD ⊥,求证:PD ⊥平面ABM ;(Ⅲ)若点M 是棱PD 的中点,求三棱锥B ACM -的体积.10.(2017通州一模文18)如图1,直角梯形ABCD 中,AB AD ⊥,,//AD BC ,,6AD =,4BC =,1AB =,点E F ,分别在BC AD ,上,2BE AF ==,现将四边形ABEF 沿EF 折起到''A B EF 的位置,使得'3A C =,如图2所示.(Ⅰ)若P 为线段'A D 的中点,求证://CP 平面''A B EF ; (Ⅱ)求证:平面''A B EF ⊥平面EFDC ; (Ⅲ)求几何体''A B EFDC 的体积.。
2017至2018年北京高三模拟分类汇编之集合

2017至2018年北京高三模拟分类汇编之集合精心校对版题号一二三总分得分△注意事项:1.本系列试题包含2017年-2018年北京高考一模和二模真题的分类汇编。
2.本系列文档有相关的试题分类汇编,具体见封面。
3.本系列文档为北京双高教育精心校对版本4.本系列试题涵盖北京历年(2011年-2020年)高考所有学科一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.(2017北京西城区高三一模数学(文))已知全集{1,2,3,4,5,6}U ,集合{1,3,5}A ,{1,4}B ,那么U A B e (A ){3,5}(B ){2,4,6}(C ){1,2,4,6}(D ){1,2,3,5,6}二、选择题(本大题共21小题,每小题0分,共0分。
在每小题给出的四个选项中,只有一个选项是符合题目要求的)2.(2017北京东城区高三一模数学(文))如果|0R A x x ,0,1,2,3B ,那么集合B A A.空集 B.0C.0,1 D.1,2,33.(2017北京丰台区高三一模数学(文))如果集合21A x x Z ,101B ,,,那么A B = (A )2101,,,(B )101,,(C )01,(D )10,4.(2017北京丰台区高三二模数学(文))已知集合142,A x x B x x ,那么A B U (A )(24),(B )(24,](C )[1+),(D )(2),+5.(2017北京东城区高三二模数学(文))已知全集U 是实数集R .右边的韦恩图表示集合{|2}M x x 与{|13}N x x 关系,那么阴影部分所表示的集合可能为姓名:__________班级:__________考号:__________●-------------------------密--------------封--------------线--------------内--------------请--------------不--------------要--------------答--------------题-------------------------●。
2017十区一模分类汇编-立体几何文 答案版

2017年北京各区一模文科立体几何汇编1.(2017海淀一模文18)已知四棱锥P ABCD -中,底面ABCD 为正方形,PA ABCD ⊥平面,2PA AB ==,,E F 分别是,PB PD 的中点.(Ⅰ)求证:PB平面FAC ;(Ⅱ)求三棱锥P EAD -的体积; (Ⅲ)求证:平面EAD ⊥平面FAC .解:(Ⅰ)连接BD ,与AC 交于点O ,连接OF , 在PBD ∆中,O ,F 分别是BD ,PD 中点, 所以OFPB ,又因为OF ⊂平面FAC ,---1分 PB ⊄平面FAC , 所以PB平面FAC .{说明:本题下面过程中的标灰部分不写不扣分}(Ⅱ)法1:因为PA ⊥平面ABCD ,,AB AD ⊂平面ABCD , 所以PA AB ⊥,PA AD ⊥, 又因为AB AD ⊥,PA AB A =,,PA AB ⊂平面PAB ,所以AD ⊥平面PAB ,在直角PAB ∆中,2PA AB ==,E 为PB 中点, 所以1PAE S ∆=,法2:因为PA ⊥平面ABCD ,所以PA 为棱锥P ABD -的高. 因为2PA AB ==,底面ABCD 是正方形,FEABDCP(Ⅲ)证明:因为AD ⊥平面PAB ,PB ⊂平面PAB , 所以AD PB ⊥,在等腰直角PAB ∆中,AE PB ⊥, 又AEAD A =,,AE AD ⊂平面EAD ,所以PB ⊥平面EAD , 又OFPB ,所以OF ⊥平面EAD , 又OF ⊂平面FAC , 所以平面EAD ⊥平面FAC .2.(2017西城一模文18)如图,在四棱锥P ABCD -中,底面ABCD 为正方形,PA ⊥底面ABCD ,PA AC =.过点A 的平面与棱,,PB PC PD 分别交于点,,E F G (,,E F G 三点均不在棱的端点处).(Ⅰ)求证:平面PAB ⊥平面PBC ; (Ⅱ)若PC ⊥平面AEFG ,求PFPC的值; (Ⅲ)直线AE 是否可能与平面PCD 平行?证明你的结论.解:(Ⅰ)因为PA ⊥平面ABCD , 所以PA BC ⊥. 因为ABCD 为正方形, 所以AB BC ⊥, 所以BC ⊥平面PAB . 所以平面PAB ⊥平面PBC .(Ⅱ)连接AF . 因为PC ⊥平面AEFG , 所以PC AF ⊥. 又因为PA AC =, 所以F 是PC 的中点.(Ⅲ)AE 与平面PCD 不可能平行.证明如下: 假设//AE 平面PCD ,因为//AB CD ,AB ⊄平面PCD . 所以//AB 平面PCD . 而AE AB ⊂,平面PAB ,所以平面//PAB 平面PCD ,这显然矛盾 所以假设不成立,即AE 与平面PCD 不可能平行.3.(2017东城一模文17)如图,在四棱锥P ABCD -中,四边形ABCD 是平行四边形,AD BD ⊥且=AD BD ,AC BD O =,PO ⊥平面ABCD .(Ⅰ)E 为棱PC 的中点,求证://OE 平面PAB ; (Ⅱ)求证:平面PAD ⊥平面PBD ;(Ⅲ)若PD PB ⊥,=2AD ,求四棱锥P ABCD -的体积.解:(I )因为O 是平行四边形ABCD 对角线交点,所以O 为AC 中点 又E 为棱PC 中点,所以//OE PA 因为OE ⊄平面PAB ,PA ⊂平面PAB , 所以//OE 平面PAB(II )因为PO ABCD ⊥面, 所以PO AD ⊥又BD AD ⊥,BD PO O ⋂=, 所以AD PBD ⊥面 因为AD PAD ⊂面, 所以PAD PBD ⊥面面(III )因为O 是平行四边形ABCD 对角线交点,所以O 为BD 中点 又PD PB ⊥,2AD BD ==,可求得112PO BD == 因为PO ABCD ⊥面,所以13P ABCD ABCD V S PO -=1222242ABCD ABD S S ∆==⨯⨯⨯=所以11441333P ABCD ABCD V S PO -==⨯⨯=四边形4.(2017朝阳一模文18)如图,在四棱锥P ABCD -中,平面PAB ⊥平面ABCD ,ADBC ,PA AB ⊥,CD AD ⊥,12BC CD AD ==,E 为AD 的中点. (Ⅰ)求证:PA CD ⊥;(Ⅱ)求证:平面⊥PBD 平面PAB ;(Ⅲ)在平面..PAB 内是否存在M ,使得直线CM平面PBE ,请说明理由.证明:(Ⅰ)因为平面PAB ⊥平面ABCD , 平面PAB平面ABCD AB =,又因为PA AB ⊥, 所以PA ⊥平面ABCD . 则PA CD ⊥.(Ⅱ)由已知,BCED ,且BC =ED ,所以四边形BCDE 是平行四边形,又CD AD ⊥,=BC CD ,所以四边形BCDE 是正方形, 连接CE ,所以⊥BD CE , 又因为,=BCAE BC AE ,所以四边形ABCE 是平行四边形, 所以CEAB ,则⊥BD AB .由(Ⅰ)知PA ⊥平面ABCD ,所以⊥PA BD , 又因为PAAB A =,则⊥BD 平面PAB , 且⊂BD 平面PBD , 所以平面⊥PBD 平面PAB .(Ⅲ)在梯形ABCD 中,AB 与CD 不平行.延长AB ,DC ,相交于点M (M ∈平面P AB ),点M 即为所求的一个点. 理由如下: 由已知,BCED ,且BC =ED .所以四边形BCDE 是平行四边形,所以CD EB ,即CM EB ,又EB ⊂平面PBE ,CM ⊄平面PBE , 所以CM 平面PBE .PABC DE5.(2017丰台一模文17)如图1,平行四边形ABCD 中,AC BC ⊥,1BC AC ==,现将△DAC 沿AC 折起,得到三棱锥D ABC -(如图2),且DA BC ,点E 为侧棱DC 的中点.(Ⅰ)求证:平面ABE ⊥平面DBC ; (Ⅱ)求三棱锥E ABC -的体积;(Ⅲ)在ACB ∠的角平分线上是否存在点F ,使得DF ∥平面ABE ?若存在,求DF 的长;若不存在,请说明理由.解:(Ⅰ)证明:在平行四边形ABCD 中,AD BC AC ==, 又因为E 为侧棱DC 的中点, 所以AE CD ⊥;因为AC BC ⊥,AD BC ⊥,且AC AD A =,所以BC ⊥平面ACD . 因为AE ⊂平面ACD , 所以AE BC ⊥; 因为BCCD C =,所以AE ⊥平面BCD , 又因为AE ⊂平面ABE , 所以平面ABE ⊥平面BCD .(Ⅱ)解:因为E ABC B ACE V V --=,BC ⊥平面ACD , 所以BC 是三棱锥的高, 故13B ACE ACE V BC S -∆=⨯⨯,又因为=1BC ,=2CD ,22AE =, 所以111211=2=222224ACE S AE CD ∆=⨯⨯⨯⨯⨯, 所以有 11=312B ACE ACE V BC S -∆=⨯⨯图1图2(Ⅲ)解:取AB中点O,连接CO并延长至点F,使CO OF=,连接AF,DF,BF.因为BC AC=,所以射线CO是角ACB∠的角分线.又因为点E是的CD中点,所以OE∥DF,因为OE⊂平面ABE,DF⊄平面ABE,所以DF∥平面ABE.因为AB、FC互相平分,故四边形ACBF为平行四边形,有BC∥AF.因为DA BC⊥,⊥,所以有AF AD6.(2017石景山一模文18)如图,在△ABC 中,C ∠为直角,4AC BC ==.沿△ABC 的中位线DE ,将△ADE 折起到△A DE '的位置,使得90A DC '∠=︒,得到四棱锥A BCDE '-.(Ⅰ)求证:BC ⊥平面A CD '; (Ⅱ)求三棱锥E A BC '-的体积;(Ⅲ)M 是棱CD 的中点,过M 做平面α与平面A BC '平行,设平面α截四棱锥A BCDE '-所得截面面积为S ,试求S 的值.(Ⅰ)证明:因为//DE BC ,且90C ∠=︒, 所以DE A D '⊥,同时DE DC ⊥, 又A D DC D '⋂=, 所以DE ⊥面.A CD ' 又因为//DE BC , 所以BC ⊥平面A CD '.(Ⅱ)由(Ⅰ)可知:BC ⊥平面A CD ',又A D '⊂平面A DC ', 所以A D BC '⊥,又因为90A DC '∠=︒,所以A D DC '⊥.又因为BC DC C ⋂=,所以A D '⊥平面BCDE . 所以,13E A BCA EBC EBC V V S A D ''--∆'==⨯. 依题意,11=42422EBC S BC CD ∆⨯=⨯⨯=.所以,184233E A BC V '-=⨯⨯=.(Ⅲ)分别取A D ',EA ',A B '的中点N ,P ,Q ,并连接MN ,NP ,PQ ,QM . 因为平面α//平面A CD ',所以平面α与平面A CD '的交线平行于A C ', 因为M 是中点,所以平面α与平面A CD '的交线是A CD '∆的中位线MN . 同理可证,四边形MNPQ 是平面α截四棱锥A BCDE '-的截面. 即:=MNPQ S S .由(I )可知:BC ⊥平面A CD ',所以BC A C '⊥, 又//,//QM A C MN BC QM MN '∴⊥.∴四边形MNPQ 是直角梯形.7.(2017房山一模文18)如图1,在直角梯形ABCD 中,AB CD ,AB BC ⊥,2AB CD =,DE AB ⊥. 沿DE 将1A BD 折起到1A ED 的位置,连接11,A B AC ,,M N 分别为1,AC BE 的中点,如图2.(Ⅰ)求证:1DE A B ⊥; (Ⅱ)求证:1MNA ED 平面;(Ⅲ)在棱1A B 上是否存在一点G ,使得1EG A BC ⊥平面?若存在,求出1AG GB的值;若不存在,说明理由.(Ⅰ)证明:DE ABDE AE DE EB⊥∴⊥⊥、 即1DE A E DE EB ⊥⊥、 又1A E ⊂平面1A EB 、EB ⊂平面1A EB 且1EB A E E ⋂=DE ∴⊥平面1A EB1A B ⊂平面1A EB 1DE A B ∴⊥(Ⅱ)找出1A D 中点F ,连接点M 与点F 、点E 与点F .F M 、分别为. 1A D 、1AC 中点 12MF DC ∴∥在直角梯形ABCD 中:CB AB AB DF ⊥⊥、且AB CD ∥则四边形EBCD 为矩形DC EB ∴∥N 为EB 中点 1122EN EB DC ∴== MF EN ∴∥则四边形ENMF 为平行四边形MN EF ∴∥ 又EF ⊂平面1A ED , MN ⊄平面1A EDMN ∴∥平面1A ED(Ⅲ)满足题意的G 存在. ED AB ⊥1ED EB ED A E ∴⊥⊥、 又EB ⊂平面1A EB 、1A E ⊂平面1A EB且1A E EB E =ED ∴⊥平面1A EB则ED EG ⊥要使EG ⊥平面1A BC ,即1EG A B ⊥ 在矩形ABCD 中: 2AB CD DC EB AE EB==∴=、 即1A E EB =则三角形1A EB 为等腰三角形要使1EG A B ⊥,点G 应为1A B 中点8.(2017平谷一模文18)如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=3,PM=2MD,AN=2NB,(Ⅰ)求证:直线AM∥平面PNC;(Ⅱ)在AB上是否存在一点E,使CD⊥平面PDE,若存在,确定E的位置,并证明,若不存在,说明理由;(Ⅲ)求三棱锥C﹣PDA的体积.证明:(Ⅰ)在PC上去一点F,使PF=2FC,连接MF,NF,因为PM=2MD,AN=2NB,所以FM∥DC,,AN∥DC,AN=,所以.所以MFNA为平行四边形即AM∥NA又AM⊄平面PNC所以直线AM∥平面PNC(Ⅱ)因为E是AB中点,底面ABCD是菱形,∠DAB=60°,所以∠AED=90°因为AB∥CD,所以,∠EDC=90°,即CD⊥DE.又PD⊥平面ABCD,所以CD⊥PD又DE∩PD=D所以直线CD⊥平面PDE(Ⅲ)直线AB∥DC,且由(Ⅱ)可知,DE为点A到平面PDC的距离,,,.9.(2017大兴一模文18)如图,在四棱锥P ABCD -中,平面PAD ⊥平面ABCD ,90DAB ABC ︒∠=∠=,2,AD BC =四棱锥P ABCD -的体积为10,点P 在PD 上.(Ⅰ)求证:BC //平面PAD ;(Ⅱ)若AM PD ⊥,求证:PD ⊥平面ABM ;(Ⅲ)若点M 是棱PD 的中点,求三棱锥B ACM -的体积.()I 证明:因为90DAB ABC ︒∠=∠=,所以//BC AD ,又因为BC ⊄平面PAD ,AD ⊂平面PAD ,所以//BC 平面PAD .()II 证明:因为90DAB ︒∠=,所以BA AD ⊥,又因为面PAD ⊥平面ABCD ,PAD ABCD AD =, 所以BA ⊥面PAD ,所以BA PD ⊥,又因为AM PD ⊥,BA AM A =,所以PD ⊥平面ABM .10.(2017通州一模文18)如图1,直角梯形ABCD 中,AB AD ⊥,,//AD BC ,,6AD =,4BC =,1AB =,点E F ,分别在BC AD ,上,2BE AF ==,现将四边形ABEF 沿EF 折起到''A B EF 的位置,使得'3A C =,如图2所示.(Ⅰ)若P 为线段'A D 的中点,求证://CP 平面''A B EF ;(Ⅱ)求证:平面''A B EF ⊥平面EFDC ;(Ⅲ)求几何体''A B EFDC 的体积.。
2017-2018立体几何高考真题分类汇编(文科)

2017-2018立体几何高考真题分类汇编(文科)2017新课标1卷6.如图,在下列四个正方体中,A ,B 为正方体的两个顶点,M ,N ,Q 为所在棱的中点,则在这四个正方体中,直接AB 与平面MNQ 不平行的是答案:A16.已知三棱锥S-ABC 的所有顶点都在球O 的球面上,SC 是球O 的直径。
若平面SCA ⊥平面SCB ,SA =AC ,SB =BC ,三棱锥S-ABC 的体积为9,则球O 的表面积为________。
答案:36π 18.(12分)如图,在四棱锥P-ABCD 中,AB//CD ,且90BAP CDP ∠=∠=(1)证明:平面PAB ⊥平面PAD ; 90APD ∠=,且四棱锥P-ABCD 的体积为83,求该四(2)若PA =PD =AB =DC ,棱锥的侧面积.2017新课标2卷6.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为 A.90π B.63π C.42π D.36π答案:B15.长方体的长、宽、高分别为3,2,1,其顶点都在球O 的球面上,则球O 的表面积为答案:14π18.(12分)如图,四棱锥P-ABCD 中,侧面PAD 为等边三角形且垂直于底面ABCD ,AB=BC=12AD, ∠BAD=∠ABC=90°。
(1) 证明:直线BC ∥平面PAD;(2) 若△PAD 面积为,求四棱锥P-ABCD 的体积。
2017新课标3卷9.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为 A .πB .3π4C .π2D .π4答案:B10.在正方体1111ABCD A B C D 中,E 为棱CD 的中点,则A .11A E DC ⊥B .1A E BD ⊥C .11A E BC ⊥D .1AE AC ⊥答案:C19.(12分)如图,四面体ABCD中,△ABC是正三角形,AD=CD.(1)证明:AC⊥BD;(2)已知△ACD是直角三角形,AB=BD.若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.2018新课标1卷5. 已知圆柱的上、下底面的中心分别为,,过直线的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为A. B. C. D.【答案】B9. 某圆柱的高为2,底面周长为16,其三视图如右图,圆柱表面上的点在正视图上的对应点为,圆柱表面上的点在左视图上的对应点为,则在此圆柱侧面上,从到的路径中,最短路径的长度为A. B.C. D. 2【答案】B10. 在长方体中,,与平面所成的角为,则该长方体的体积为 A. B. C.D.【答案】C18. 如图,在平行四边形中,,,以为折痕将△折起,使点到达点的位置,且, (1)证明:平面平面,(2)为线段上一点,为线段上一点,且,求三棱锥的体积.2018新课标2卷9.在正方体中,为棱的中点,则异面直线与所成角的正切值为 A .BCD答案:C16.已知圆锥的顶点为,母线,互相垂直,与圆锥底面所成角为,若的面积为,则该圆锥的体积为__________.答案:8π19.(12分)如图,在三棱锥中,,,为的中1111ABCD A B C D -E 1CC AE CD 2S SA SB SA 30︒SAB△8P ABC -AB BC ==4PA PB PC AC ====O AC点.(1)证明:平面;(2)若点在棱上,且,求点到平面的距离.2018新课标3卷3.中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫棒头,凹进部分叫卯眼,图中木构件右边的小长方体是棒头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是答案:A12.设A ,B ,C ,D 是同一个半径为4的球的球面上四点,ABC △为等边三角形且其PO ⊥ABC M BC 2MC MB =CPOM体积的最大值为面积为D ABCA.B.C.D.答案:B19.(12分)如图,矩形ABCD所在平面与半圆弧CD所在平面垂直,M是CD上异于C,D的点.(1)证明:平面AMD⊥平面BMC;(2)在线段AM上是否存在点P,使得MC∥平面PBD?说明理由.。
2018北京各区数学一模试题分类汇编——立体几何 精品
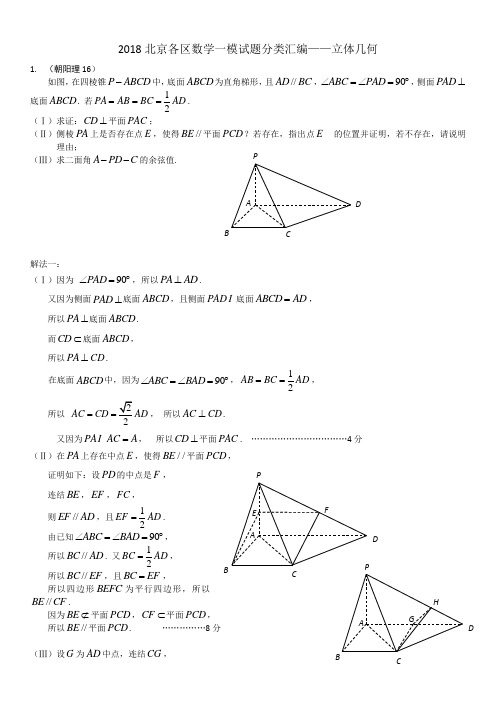
2018北京各区数学一模试题分类汇编——立体几何1. (朝阳理16)如图,在四棱锥P ABCD -中,底面ABCD 为直角梯形,且//AD BC ,90ABC PAD ∠=∠=︒,侧面PAD ⊥底面ABCD . 若12PA AB BC AD ===. (Ⅰ)求证:CD ⊥平面PAC ;(Ⅱ)侧棱PA 上是否存在点E ,使得//BE 平面PCD ?若存在,指出点E 的位置并证明,若不存在,请说明理由;(Ⅲ)求二面角A PD C --的余弦值.解法一:(Ⅰ)因为 90PAD ∠=︒,所以PA AD ⊥.又因为侧面PAD ⊥底面ABCD ,且侧面PAD 底面ABCD AD =, 所以PA ⊥底面ABCD . 而CD ⊂底面ABCD , 所以PA ⊥CD .在底面ABCD 中,因为90ABC BAD ∠=∠=︒,12AB BC AD ==, 所以2AC CD AD ==, 所以AC ⊥CD . 又因为PA AC A = , 所以CD ⊥平面PAC . ……………………………4分 (Ⅱ)在PA 上存在中点E ,使得//BE 平面PCD ,证明如下:设PD 的中点是F , 连结BE ,EF ,FC ,则//EF AD ,且12EF AD =.由已知90ABC BAD ∠=∠=︒,所以//BC AD . 又12BC AD =,所以//BC EF ,且BC EF =,所以四边形BEFC 为平行四边形,所以//BE CF .因为BE ⊄平面PCD ,CF ⊂平面PCD所以//BE 平面PCD . (8)(Ⅲ)设G 为AD 中点,连结CG ,则 CG ⊥AD .又因为平面ABCD ⊥平面PAD , 所以 CG ⊥平面PAD . 过G 作GH PD ⊥于H ,连结CH ,由三垂线定理可知CH PD ⊥. 所以GHC ∠是二面角A PD C --的平面角.设2AD =,则1PA AB CG DG ====, DP =. 在PAD ∆中,GH DG PA DP =,所以GH =. 所以tan CG GHC GH ∠==,cos GHC ∠=. 即二面角A PD C --………………………………13分解法二:因为 90PAD ∠=︒, 所以PA AD ⊥.又因为侧面PAD ⊥底面ABCD , 且侧面PAD 底面ABCD AD =, 所以 PA ⊥底面ABCD . 又因为90BAD ∠=︒,所以AB ,AD ,AP 两两垂直. 分别以AB ,AD ,AP 为x 轴, y 轴,z 轴建立空间直角坐标系,如图.设2AD =,则(0,0,0)A ,(1,0,0)B ,(1,1,0)C ,(0,2,0)D ,(0,0,1)P .(Ⅰ)(0,0,1)AP = ,(1,1,0)AC = ,(1,1,0)CD =-,所以 0AP CD ⋅= ,0AC CD ⋅=,所以AP ⊥CD ,AC ⊥CD .又因为AP AC A = , 所以CD ⊥平面PAC . ………………………………4分(Ⅱ)设侧棱PA 的中点是E , 则1(0, 0, )2E ,1(1, 0, )2BE =- .设平面PCD 的一个法向量是(,,)x y z =n ,则0,0.CD PD ⎧⋅=⎪⎨⋅=⎪⎩n n 因为(1, 1, 0)CD =- ,(0, 2,1)PD =-,所以0,20.x y y z -+=⎧⎨-=⎩ 取1x =,则(1, 1, 2)=n .所以1(1, 1, 2)(1, 0, )02BE ⋅=⋅-= n , 所以BE ⊥ n .因为BE ⊄平面PCD ,所以BE 平面PCD . ………………………………8分(Ⅲ)由已知,AB ⊥平面PAD ,所以(1, 0, 0)AB =为平面PAD 的一个法向量.由(Ⅱ)知,(1, 1, 2)=n 为平面PCD 的一个法向量. 设二面角A PD C --的大小为θ,由图可知,θ为锐角,所以cos AB ABθ⋅===n n . 即二面角A PD C --的余弦值为6………………………………13分2. (朝阳文17)如图,在四棱锥P ABCD -中,底面ABCD 为直角梯形,且//AD BC ,90ABC ∠=︒,侧面PAD ⊥底面ABCD ,90PAD ∠=︒. 若12AB BC AD ==. (Ⅰ)求证:CD ⊥平面PAC ;(Ⅱ)设侧棱PA 的中点是E ,求证:BE 平面PCD .解:(Ⅰ)因为 90PAD ∠=︒, 所以PA AD ⊥.又因为侧面PAD ⊥底面ABCD , 且侧面PAD 底面ABCD AD =, 所以PA ⊥底面ABCD . 而CD ⊂底面ABCD , 所以PA ⊥CD . 在底面ABCD 中,因为90ABC BAD ∠=∠=︒,12AB BC AD ==, 所以AC CD AD ==, 所以AC ⊥CD . 又因为PA AC A = , 所以CD ⊥平面PAC . ……………………………6分PA B CD QM(Ⅱ)设侧棱PD 的中点为F ,连结BE ,EF ,FC ,则EF AD ,且12EF AD =. 由已知90ABC BAD ∠=∠=︒,所以BC AD . 又12BC AD =,所以BC EF . 且BC EF =.所以四边形BEFC 为平行四边形,所以BE CF . 因为BE ⊄平面PCD ,CF ⊂平面PCD ,所以BE 平面PCD . ………………………………………………………13分3. (丰台理16)如图,在四棱锥P -ABCD 中,底面ABCD 为直角梯形,AD //BC ,∠ADC =90°,平面PAD ⊥底面ABCD ,Q 为AD 的中点,M 是棱PC 上的点,PA =PD =2,BC =12AD =1,CD (Ⅰ)若点M 是棱PC 的中点,求证:PA // 平面BMQ ; (Ⅱ)求证:平面PQB ⊥平面PAD ;(Ⅲ)若二面角M -BQ -C 为30°,设PM =tMC ,试确定t 的值 .证明:(Ⅰ)连接AC ,交BQ 于N ,连接MN .∵BC ∥AD 且BC =12AD ,∴四边形BCQA 为平行四边形,且N 为AC 中点, 又∵点M 在是棱PC 的中点,∴ MN // PA ∵ MN ⊂平面MQB ,PA ⊄平面MQB , ∴ PA // 平面MBQ . (Ⅱ)∵AD // BC ,BC =12AD ,Q 为AD 的中点, ∴四边形BCDQ 为平行四边形,∴CD // BQ . ∵∠ADC =90° ∴∠AQB =90° 即QB ⊥AD . 又∵平面PAD ⊥平面ABCD 且平面PAD ∩平面ABCD=AD , ∴BQ ⊥平面PAD .∵BQ ⊂平面PQB ,∴平面PQB ⊥平面PAD . …………………9分 另证:AD // BC ,BC =12AD ,Q 为AD 的中点, ∴ 四边形BCDQ 为平行四边形,∴CD //∵ ∠ADC =90° ∴∠AQB =90°. ∵ PA =PD , ∴PQ ⊥AD .∵ PQ ∩BQ =Q , ∴AD ⊥平面PBQ . ∵ AD ⊂平面PAD ,∴平面PQB PAD .……9分(Ⅲ)∵PA =PD ,Q 为AD 的中点, ∴PQ ⊥AD .∵平面PAD ⊥平面ABCD ,且平面PAD ∩平面ABCD=AD , PA BCDQM∴PQ ⊥平面ABCD .如图,以Q 为原点建立空间直角坐标系.则平面BQC 的法向量为(0,0,1)n =;(0,0,0)Q,P ,B,(1C -.设(,,)M x y z,则(,,PM x y z =,(1,)MC x y z =---, ∵PM tMC = ,∴(1))(x t x y t y z t z =--⎧⎪=⎨⎪=-⎩), ∴11t x t y t z ⎧=-⎪+⎪⎪=⎨+⎪⎪=⎪⎩ …………………12分在平面MBQ中,QB =,(1t QM t =-+ ,∴ 平面MBQ法向量为)m t =.∵二面角M -BQ -C 为30°,c o s 30n m n m ︒⋅===∴ 3t =. ……………………14分4. (丰台文16)如图,在四棱锥P ABCD -中,底面ABCD 为直角梯形,AD //BC ,∠ADC =90°,BC =12AD ,PA =PD ,Q 为AD 的中点.(Ⅰ)求证:AD ⊥平面PBQ ;(Ⅱ)若点M 在棱PC 上,设PM =tMC ,试确定t 的值,使得PA //平面BMQ .证明:(Ⅰ)AD // BC ,BC =12AD ,Q 为AD 的中点, ∴ 四边形BCDQ 为平行四边形, ∴CD // BQ . ∵ ∠ADC =90° ∴∠AQB =90° 即QB ⊥AD . ∵ PA =PD ,Q 为AD 的中点, ∴PQ ⊥AD . ∵ PQ ∩BQ =Q ,∴AD ⊥平面PBQ . ……………………6分C(Ⅱ)当1t =时,PA //平面BMQ .连接AC ,交BQ 于N ,连接MN . ∵BC //12DQ , ∴四边形BCQA 为平行四边形,且N 为AC 中点, ∵点M 是线段PC 的中点, ∴ MN // PA .∵ MN ⊂平面BMQ ,PA ⊄平面BMQ ,∴ PA // 平面BMQ . ……………………13分5. (门头沟理16)已知四棱锥P ABCD -的底面ABCD 为菱形,且060,ABC ∠=2PB PD AB ===,PA PC =,AC 与BD 相交于点O .(Ⅰ)求证:⊥PO 底面ABCD ;(Ⅱ)求直线PB 与平面PCD 所成角的正弦值; (Ⅲ)若M 是PB 上的一点,且PB CM ⊥,求PM MB的值.(Ⅰ)证明:因为ABCD 为菱形,所以O 为,AC BD 的中点……………………………1分 因为,PB PD PA PC ==,所以,PO BD PO AC ⊥⊥所以⊥PO 底面 ABCD …………3分 (Ⅱ)因为ABCD 为菱形,所以AC BD ⊥建立如图所示空间直角坐标系 又060,2ABC PB AB ∠===得1,1OA OB OP === ……………………………4分所以(0,0,1),(0,(1,0,0),P B C D(0,1)PB =- ,(1,0,1)PC =-,1)PD =-……………………5分 设平面PCD 的法向量(,,)m x y z =APDCOB有00m PC m PD ⎧=⎪⎨=⎪⎩所以00x z z -=⎧⎪-=解得x z y z =⎧⎪⎨=⎪⎩所以m =……………………………8分cos ,m PB m PB m PB =cos ,7m PB ==- ……………………………9分 PB 与平面PCD…………………10分 (Ⅲ)因为点M 在PB 上,所以(0,1)PM PB λλ==-所以(0,,1)M λ-+, (1,,1)CM λ=--+因为PB CM ⊥所以 0CM PB = , 得310λλ+-= 解得14λ=所以13PMMB = ……………………………14分6. (门头沟文16)如图所示,PA 垂直矩形ABCD 所在的平面, F E 、分别为PC AB 、的中点。
北京各区2018年高中高三一模解析几何汇编

.【海淀一模】(19) (本小题14分)x 2 y 2 1 (ab 0)的离心率为 3 ,且点T(2,1)在椭圆C 上,设 已知椭圆C :2 b 2 2 a与OT 平行的直线l 与椭圆C 订交于P ,Q 两点,直线TP ,TQ 分别与x 轴正半轴交于M ,两点.求椭圆C 的标准方程; (Ⅱ)判断OM ON 的值能否为定值,并证明你的结论. (19)(本小题 14分) 4 11 a2b 2(Ⅰ)由题意a 2b 2c 2,c 3e2a解得:a 22,b2,c6 故椭圆C 的标准方程为 x 2 y 21·······························5分8 2(Ⅱ)假定直线 TP 或TQ 的斜率不存在,则P 点或Q 点的坐标为(2,-1),直线l 的方程为112(x2),即y 2x2.y1x 2 y 218 2联立方程,得x 2 4x40,y1 2x2此时,直线 l 与椭圆C 相切,不合题意 .故直线TP 和TQ 的斜率存在.方法1:设P(x 1,y 1),Q(x 2,y 2),则直线TP:y1y 1 1(x2),x 1 2直线TQ:y1y 2 1(x2)x 2 2x 12x 2 2故|OM|2,|ON|21y 11 y 2;...由直线OT:y1x ,设直线PQ:y1x t (t 0)22x 2 y 2 182x 22tx 2t 24 0联立方程,1xy t2当0时,x 1 x 22t ,x 1x 22t 24|OM||ON|4(x12x 2 2)y 11 y2 14 (x 1 2x 2 21x)1xt1 t12 12 24x 1x 2 (t 2)(x 1 x 2) 4(t1)1124 x 1x 2 2 (t1)(x 1x 2)(t1)42t 2 4 (t2)(2t) 4(t1)1(t1)(1(2t 24)2t)(t1)242···································14分方法2:设P(x 1,y 1),Q(x 2,y 2),直线 TP 和TQ的斜率分别为k1和k2由OT:y1x ,设直线PQ:y1x t (t 0)22x 2 y 218222联立方程,x 2tx 2t 401xy t2当0时,x 1 x 22t ,x 1x 22t 24k 1 k 2y 1 1 y 2 1x 1 2x 2 21x 1 t 1 1x 2 t 12 2 x 1 2x 2 2x 1x 2 (t2)(x 1 x 2) 4(t 1)(x 1 2)(x 22);...2t 24 (t 2)(2t) 4(t 1)(x 1 2)(x 2 2)故直线TP 和直线TQ 的斜率和为零故 TMN TNM故TMTN故T 在线段MN 的中垂线上,即MN 的中点横坐标为2故|OM| |ON| 4···································14分【东城一模】(18)(本小题13分)已知椭圆C :x 2y 21(ab0)的离心率为3,且过点A(2,0).a 2b 22(Ⅰ)求椭圆C 的方程;(II )设M,N 是椭圆C 上不一样于点A 的两点,且直线AM ,AN 斜率之积等于1 ,试问直4线MN 能否过定点?假如,求出该点的坐标;若不是,请说明原因.(19)(本小题14分)411a 2b 2(Ⅰ)由题意a 2b 2c 2 ,ec 3a2解得:a2 2,b2,c6故椭圆C 的标准方程为x 2 y 2 1·······························5分8 2(Ⅱ)假定直线 TP 或TQ 的斜率不存在,则 P 点或Q 点的坐标为(2,-1),直线l 的方程为y11(x2),即y1x2 .22x 2 y 218 2联立方程,得x 24x40,y 1x 22此时,直线 l 与椭圆C 相切,不合题意 .故直线TP 和TQ 的斜率存在.;...方法1:设P(x1,y1),Q(x2,y2),则直线TP:y1y11(x2),x12直线TQ:y1y21 (x2)x22故|OM|2x12,|ON|2x22 y11y21由直线OT:y 1x,设直线PQ:y1x t(t0)22x2y218222联立方程,x2tx2t401xy t2当0时,x1x22t,x1x22t24|OM||ON|4(x12x22)y11y214(x12x221x2) 1x1t1t1 224x1x2(t2)(x1x2)4(t1) 1xx1(t1)(x x)(t1)2 41221242t24(t2)(2t)4(t1) 1(2t24)1(t1)(2t)(t1)2 42···································14分方法2:设P(x1,y1),Q(x2,y2),直线TP和TQ的斜率分别为k1和k2由OT:y 1x,设直线PQ:y1x t(t0)22x2y218222联立方程,x2tx2t401xy t2;..当0时,x1x22t,x1x22t24k1k2y11y21x12x221x1t11x2t122x12x22x1x2(t2)(x1x2)4(t1)(x12)(x22)2t24(t2)(2t)4(t1)(x12)(x22)故直线TP和直线TQ的斜率和为零故TMN TNM故TMTN故T在线段MN的中垂线上,即MN的中点横坐标为2故|OM| |ON|4···································14分【西城一模】19.(本小题满分14分)已知圆O:x2y24和椭圆C:x22y24,F是椭圆C的左焦点.(Ⅰ)求椭圆C的离心率和点F的坐标;(Ⅱ)点P在椭圆C上,过P作x轴的垂线,交圆O于点Q(P,Q不重合),l是过点Q的圆O的切线.圆F的圆心为点F,半径长为|PF|.试判断直线l与圆F的地点关系,并证明你的结论.解:(Ⅰ)由题意,椭圆C的标准方程为x2y21.[1分] 42所以a24,b22,进而c2a2b22.所以a2,c2.故椭圆C的离心率e c2.[3分]a2椭圆C的左焦点F的坐标为(2,0).[4分](Ⅱ)直线l与圆F相切.证明以下:[5分]设P(x0,y0),此中2x02,则x022y024,[6分] ;..依题意可设Q(x 0,y 1),则x 02y 124.[7 分]直线l的方程为y y 1x 0(x x 0),y 1整理为 x 0xy 1y 4 0.[ 9分]所以圆F 的圆心F 到直线l的距离d| 2x 04| | 2x 2|.[11分]x 02 y 122由于|PF|2(x2)2y2(x2)21(4x2) 1x 2 22x4.[13分]0 022所以|PF|2 d 2,即|PF|d ,所以 直线l 与圆F 相切.[14分]【旭日一模】19.(本小题满分 14分)222,且过点(1,已知椭圆C:x2y 2 1(a b 0)的离心率为2 ).ab22(Ⅰ)求椭圆C 的方程;(Ⅱ)过椭圆C 的左焦点的直线l 1 与椭圆C 交于A,B 两点,直线l 2 过坐标原点且与直线l 1的斜率互为相反数.若直线l 2 与椭圆交于E,F 两点且均不与点A,B 重合,设直线AE 与x 轴所成的锐角为 1,直线BF 与x 轴所成的锐角为2,判断1与2大小关系并加以证明.19.(本小题满分 14分)c2,a2解:(Ⅰ)由题意得a 2b 2 2 ,解得a 2, b1 ,c.c 11 1 1.a22b22故椭圆C 的方程为xy 2 1...5分2(Ⅱ)1=2.证明以下:由题意可设直线 l 1的方程为yk(x 1),直线l 2 的方程为y kx ,设点A(x 1,y 1),;..B(x 2,y 2) ,E(x 3,y 3), F(x 3, y 3).要证1=2,即证直线 AE 与直线BF 的斜率之和为零,即k AE k BF 0.由于k AEkBFy 1 y 3 y 2 y 3x 1 x 3 x 2x 3k(x 1 1)kx 3k(x 2 1)kx 3x 1 x 3 x 2 x 3k[2xx(xx) 2x 2]12 12x 3)3.(x 1 x 3)(x 2yk(x1),由x 2y2得(1 2k 2 )x 24k 2 x 2k 22 0 ,1,222所以x 1x 21 4k ,x 1x 22k2 .2k 2 1 2k 2ykx,2由 x 2得(1 2k 2)x 22,所以 22.y2 1,x 31 2k2所以2x 1x 2(x 1 2 4k 244k 24.x 2)2x 3 121 2k 21202k2kkAEkBFk[2x 1x 2 (x 1 x 2) 2x 32]0 .(x 1 x 3)(x 2 x 3)所以1=2...14分【丰台一模】(19)(本小题共 14分)3x 2 y 21(ab0)上,F(1,0)是椭圆的一个焦点.已知点P(1,)在椭圆C :b 2 2a 2(Ⅰ)求椭圆C 的方程;(Ⅱ)椭圆C 上不与P 点重合的两点D ,E 对于原点O 对称,直线PD ,PE 分别交y 轴于M ,N 两点.求证:以MN 为直径的圆被直线 y3 截得的弦长是定值.2(19)(本小题共14分)解:(Ⅰ)依题意,椭圆的另一个焦点为F(1,0),且c1.1分由于2a22(3)22(3)24,22;..所以a 2,ba 2 c 23,⋯⋯⋯⋯⋯⋯⋯⋯3分所以C 的方程x 2y 2 1.⋯⋯⋯⋯⋯⋯⋯⋯4分4 3(Ⅱ)明:由意可知D ,E 两点与点P 不重合.因D ,E 两点对于原点称,所以D(m,n),E( m, n),(m1).⋯⋯⋯⋯⋯⋯⋯⋯5分以MN 直径的与直y3 交于G(t,3),H(t,3)(t0)两点,所以GM GN .222⋯⋯⋯⋯⋯⋯⋯⋯6分3n直PD :y32(x1).2m1当x 0,y3 直PE :y2n33 n 32 ,所以M(0, 2 m 1 2 m 1n 32 (x1). m13).⋯⋯⋯⋯⋯⋯7分2 n 33n当x0,y2 m 13,所以N(0,22m13).⋯⋯⋯⋯⋯⋯⋯⋯8分2n33n所以GM (t,2),m1GN(t,2),m 1⋯⋯⋯⋯⋯⋯⋯⋯ 9分因GMGN ,所以GMGN0,⋯⋯⋯⋯⋯⋯⋯⋯10分2所以GM GNt 24n 2 9 0. ⋯⋯⋯⋯⋯⋯⋯⋯11分4(m 1)因m 2n 2 1,即3m 2 4n 212,4n 2 93 3m 2,⋯⋯⋯⋯⋯⋯12分43所以t23 0,所以t3⋯⋯⋯⋯⋯⋯⋯⋯13分4.2所以G(3,3),H(3,3),所以GH3.2 2 2 2所以以MN 直径的被直y3 3.⋯⋯⋯⋯14分截得的弦是定2【石景山一模】18.(本小共 13分);...在平面直角坐标系xOy中,动点E到定点(1,0)的距离与它到直线x1的距离相等.(Ⅰ)求动点E的轨迹C的方程;(Ⅱ)设动直线 l:y kx b与曲线C相切于点P,与直线x1订交于点Q.证明:以PQ为直径的圆恒过x轴上某定点.18.(本小题共13分)(Ⅰ)解:设动点E的坐标为(x,y),由抛物线定义知,动点E的轨迹是以(1,0)为焦点,x1为准线的抛物线,所以动点E的轨迹C的方程为y24x.5分y kxb4y4b0.(Ⅱ)证明:由,消去x得:ky2y24x由于直线l与抛物线相切,所以16-16kb0,即b 1.8分k所以直线l的方程为y kx 1.k令x1,得y k1.k所以Q1,k1.10分k设切点坐标P(x0,y0),则ky024y0+40,k12解得:P( , ),11分设M(m,0),MQMP 1m(1m)21)2m1 k2k(k=m m2k2k所以当m2m2=0,即m1时,MQMP0m-10所以MQ MP所以以PQ为直径的圆恒过x轴上定点M(1,0).13分;..。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017至2018年北京高三模拟分类汇编之立体几何大题精心校对版题号一二三总分得分△注意事项:1.本系列试题包含2017年-2018年北京高考一模和二模真题的分类汇编。
2.本系列文档有相关的试题分类汇编,具体见封面。
3.本系列文档为北京双高教育精心校对版本4.本系列试题涵盖北京历年(2011年-2020年)高考所有学科一、解答题(本大题共23小题,共0分)1.(2017北京东城区高三一模数学(文))如图,在四棱锥P ABCD 中,四边形ABCD 是平行四边形,AD BD 且=AD BD ,AC BD O , PO 平面ABCD . (I )E 为棱PC 的中点,求证://OE 平面PAB ;(II )求证:平面PAD 平面PBD ;(III) 若PD PB ,=2AD ,求四棱锥P ABCD 的体积. 2.(2017北京丰台区高三一模数学(文))如图1,平行四边形ABCD 中,AC BC ,1BC AC ,现将△DAC 沿AC 折起,得到三棱锥D ABC (如图2),且DA BC ^,点E 为侧棱DC 的中点. (Ⅰ)求证:平面ABE 平面DBC ;(Ⅱ)求三棱锥E ABC 的体积;(Ⅲ)在ACB 的角平分线上是否存在点F ,使得DF ∥平面ABE ?若存在,求DF 的长;若不存在,请说明理由. 姓名:__________班级:__________考号:__________●-------------------------密--------------封-
-------------线--------------内--------------请--------------不--------------要--------------答--------------题-------------------------● A B C D P O。
