图形推理中的“一笔画成”的规律
2018河南公务员考试行测:快速判定图形推理之一笔画考点(一)
2018河南公务员考试行测:快速判定图形推理之一笔画考点(一)在2018河南公务员考试中,行测是公务员考试笔试阶段的必考科目之一。
一笔画问题,一直是行测考试中的高频考点和难点题型,虽然大家在复习的时候都会重点的复习这部分内容,但是在考试的时候很多考生面对的问题是,知道如何判断一个图形至少一笔完成,或者至少几笔完成,但是却不知道如何识别一道题是考查一笔画的题目。
本篇文章就为大家介绍一下,如何根据题干的特点来判定一道题是考查一笔画问题的。
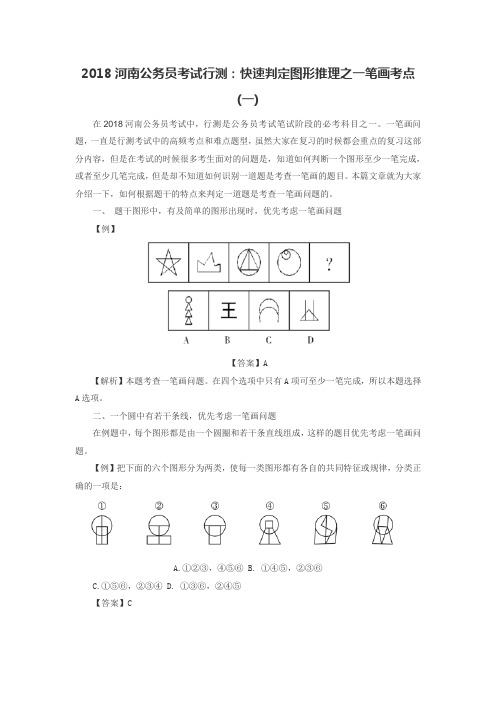
一、题干图形中,有及简单的图形出现时,优先考虑一笔画问题【例】【答案】A【解析】本题考查一笔画问题。
在四个选项中只有A项可至少一笔完成,所以本题选择A选项。
二、一个圆中有若干条线,优先考虑一笔画问题在例题中,每个图形都是由一个圆圈和若干条直线组成,这样的题目优先考虑一笔画问题。
【例】把下面的六个图形分为两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是:A.①②③,④⑤⑥B. ①④⑤,②③⑥C.①⑤⑥,②③④D. ①③⑥,②④⑤【答案】C【解析】数量类。
考查一笔画的规律,其中,①⑤⑥都是一笔画成,而②③④均两笔画成。
三、一个图形中包含两个或者三个相同的图形,优先考虑一笔画在例题中的⑤图中出现了两个相同的五角星,这样的题目优先考虑一笔画问题。
【例】把下面的六个图形分为两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是:A.①④⑥,②③⑤B.①②⑤,③④⑥C.①②⑥,③④⑤D.①②④,③⑤⑥本文由华图小编整理,想要了解更多信息请关注河南华图官网()或官方微信公众号“河南华图”。
浅谈一笔画问题

浅谈一笔画问题公司内部档案编码:[OPPTR-OPPT28-OPPTL98-OPPNN08]浅谈一笔画问题摘要:一笔画问题是一个几何问题,传统意义上的几何学是研究图形的形状大小等性质,而存在一些几何问题,它们所研究的对象与图形的形状和线段的长短没关系,而只和线段的数目和它们之间的连接关系有关,比如一笔画问题就是如此。
一笔画问题是一个简单的数学游戏,即平面上由曲线段构成的一个图形能不能一笔画成,使得在每条线段上都不重复例如汉字‘日’和‘中’字都可以一笔画的,而‘田’和‘目’则不能。
关键词:一笔画规律原理早在18世纪,瑞士的着名数学家欧拉就找到了一笔画的规律。
欧拉认为,能一笔画的图形必须是连通图。
连通图就是指一个图形各部分总是有边相连的.但是,不是所有的连通图都可以一笔画的。
能否一笔画是由图的奇、偶点的数目来决定的。
一笔画问题是图论中一个着名的问题。
一笔画问题起源于柯尼斯堡七桥问题。
数学家欧拉在他1736年发表的论文《柯尼斯堡的七桥》中不仅解决了七桥问题,也提出了一笔画定理,顺带解决了一笔画问题。
一般认为,欧拉的研究是图论的开端。
与一笔画问题相对应的一个图论问题是哈密顿问题。
一、一笔画规律数学家欧拉找到一笔画的规律是:(一)凡是由偶点组成的连通图,一定可以一笔画成。
画时可以把任一偶点为起点,最后一定能以这个点为终点画完此图。
(二)凡是只有两个奇点的连通图(其余都为偶点),一定可以一笔画成。
画时必须把一个奇点为起,,另一个奇点终点。
(三)其他情况的图都不能一笔画出。
(有偶数个奇点除以二便可算出此图需几笔画成)比如附图:(a)为(1)情况,因此可以一笔画成;(b)(c)(d)则没有符合以上两种情况,所以不能一笔画成。
补充:相关名词的含义◎顶点与指数:设一个平面图形是由有限个点及有限条弧组成的,这些点称为图形的顶点,从任一顶点引出的该图形的弧的条数,称为这个顶点的指数。
◎奇顶点:指数为奇数的顶点。
◎偶顶点:指数为偶数的顶点。
图形推理中的“一笔画成”的规律
图形推理中的“一笔画成”的规律京佳教育在公务员考试之行测试卷的判断推理模块,其中图形推理试题常考规律中,有一类较为典型的规律被称之为“一笔画成”规律。
下面,京佳的老师们将结合公考真题为大家详细解读一下。
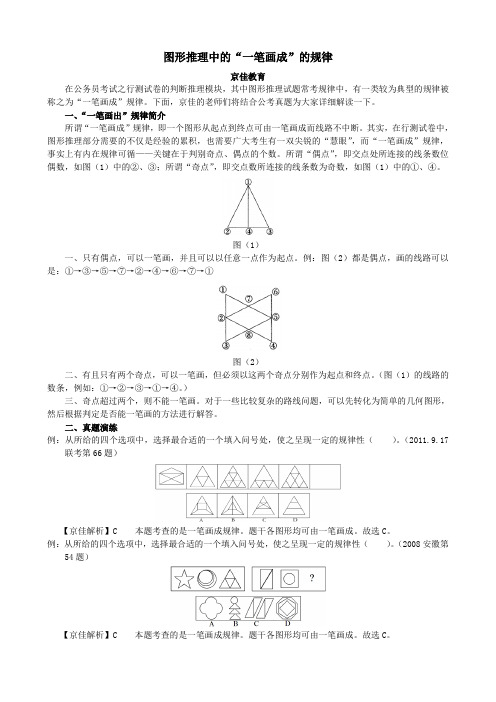
一、“一笔画出”规律简介所谓“一笔画成”规律,即一个图形从起点到终点可由一笔画成而线路不中断。
其实,在行测试卷中,图形推理部分需要的不仅是经验的累积,也需要广大考生有一双尖锐的“慧眼”,而“一笔画成”规律,事实上有内在规律可循——关键在于判别奇点、偶点的个数。
所谓“偶点”,即交点处所连接的线条数位偶数,如图(1)中的②、③;所谓“奇点”,即交点数所连接的线条数为奇数,如图(1)中的①、④。
图(1)一、只有偶点,可以一笔画,并且可以以任意一点作为起点。
例:图(2)都是偶点,画的线路可以是:①→③→⑤→⑦→②→④→⑥→⑦→①图(2)二、有且只有两个奇点,可以一笔画,但必须以这两个奇点分别作为起点和终点。
(图(1)的线路的数条,例如:①→②→③→①→④。
)三、奇点超过两个,则不能一笔画。
对于一些比较复杂的路线问题,可以先转化为简单的几何图形,然后根据判定是否能一笔画的方法进行解答。
二、真题演练例:从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性()。
(2011.9.17联考第66题)【京佳解析】C 本题考查的是一笔画成规律。
题干各图形均可由一笔画成。
故选C。
例:从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性()。
(2008安徽第54题)【京佳解析】C 本题考查的是一笔画成规律。
题干各图形均可由一笔画成。
故选C。
浅谈一笔画问题

浅谈一笔画问题摘要:一笔画问题是一个几何问题,传统意义上的几何学是研究图形的形状大小等性质,而存在一些几何问题,它们所研究的对象与图形的形状和线段的长短没关系,而只和线段的数目和它们之间的连接关系有关,比如一笔画问题就是如此。
一笔画问题是一个简单的数学游戏,即平面上由曲线段构成的一个图形能不能一笔画成,使得在每条线段上都不重复?例如汉字‘日’和‘中’字都可以一笔画的,而‘田’和‘目’则不能。
关键词:一笔画规律原理早在18世纪,瑞士的著名数学家欧拉就找到了一笔画的规律。
欧拉认为,能一笔画的图形必须是连通图。
连通图就是指一个图形各部分总是有边相连的.但是,不是所有的连通图都可以一笔画的。
能否一笔画是由图的奇、偶点的数目来决定的。
一笔画问题是图论中一个著名的问题。
一笔画问题起源于柯尼斯堡七桥问题。
数学家欧拉在他1736年发表的论文《柯尼斯堡的七桥》中不仅解决了七桥问题,也提出了一笔画定理,顺带解决了一笔画问题。
一般认为,欧拉的研究是图论的开端。
与一笔画问题相对应的一个图论问题是哈密顿问题。
一、一笔画规律数学家欧拉找到一笔画的规律是:(一)凡是由偶点组成的连通图,一定可以一笔画成。
画时可以把任一偶点为起点,最后一定能以这个点为终点画完此图。
(二)凡是只有两个奇点的连通图(其余都为偶点),一定可以一笔画成。
画时必须把一个奇点为起,,另一个奇点终点。
(三)其他情况的图都不能一笔画出。
(有偶数个奇点除以二便可算出此图需几笔画成)比如附图:(a)为(1)情况,因此可以一笔画成;(b)(c)(d)则没有符合以上两种情况,所以不能一笔画成。
补充:相关名词的含义◎顶点与指数:设一个平面图形是由有限个点及有限条弧组成的,这些点称为图形的顶点,从任一顶点引出的该图形的弧的条数,称为这个顶点的指数。
◎奇顶点:指数为奇数的顶点。
◎偶顶点:指数为偶数的顶点。
二、一笔画原理(一)一笔画必须是连通的(图形的各部分之间连接在一起);(二)没有奇点的连通图形是一笔画,画时可以以任一偶点为起点,最后仍回到这点;(三)只有两个奇点的连通图形是一笔画,画时必须以一个奇点为起点,以另一个奇点为终点;(四)奇点个数超过两个的图形不是一笔画利用一笔画原理,七桥问题很容易解决。
2014浙江省公务员考试:图形推理规律总结之“一笔画”

2014年浙江公务员行测之图形推理规律总结之“一笔画”2014年国家(浙江)公务员考试即将拉开帷幕,又一轮的独木桥争夺大赛再次开始,王侯将相宁有种乎,2013年公考失利我们将在2014年重头再来,浙江华图根据历年浙江公务员考试笔试的特点,总结出一套备考方法,为广大考生公务员考试提供备考服务!!作为判断推理部分常见四大题型之一的图形推理往往成为许多考生的痛,几个图形看来看去一头雾水,不知从何做起。
正所谓,难者不会,会者不难。
图形推理部分没有所谓的难题,只要将找规律的方法和规律告诉你,那便是秒杀的题。
因此,要想在考试中拿下图形推理这部分的分值,考生就需要熟练把握找规律的常见路线和常考要素。
在图形推理中笔画是个不容忽视的考点,对它的考察经常会以汉字,图形,字母等形式出现。
一笔画又是笔画考察中的一个特殊考点,下面给大家做一个详细的介绍。
【例】A B C D【解析】答案为C选项。
这是道九宫格类的图形推理题,通过观察不难发现题干所给几个图形组成比较凌乱,故而可以锁定此题是在考察数量类的图形规律。
横着看第一组三个图形,有的为直线图形有的为曲线图形,从属性上并不能找出共同规律。
但三个图有一个共同特征,那就是图形组成较为简单,均可由一笔画成。
带着这一规律,在第二行中进行验证。
通过验证发现这一规律同样在第二行中出现,在第三行进行规律运用,由此可以得出问号处应该选择一个一笔画的图形。
【知识拓展】一笔画在考试中往往作为一个重要的考点被考察,但在考场上,在紧张的气氛中,考生通过简单的手画往往会判断错误。
因此,我们要掌握一笔画的判断方法。
要判断一个图形是否为一笔画,必须满足两个条件:第一,图形必须为连通图;第二,图形中包含的奇点数为0或者2。
所谓奇点数是指,从某一点发出的线条数目为奇数个的点。
总之,当一个连通的图形中没有包含奇点或者有两个奇点时,这个图形就能一笔画出。
此外,在一笔画的基础上也会考察多笔画问题。
那么一个图形至少需要几笔画出,它的判断方法与奇点数息息相关。
一笔画问题

在行测考试中,图形推理中的一笔画问题,一直都是考生在考试中容易失分的题目。
其实主要问题存在于几个方面。
一、考生无法判断,什么样的图形考查的是一笔画;二、对一笔画图形的判断方法不了解。
接下来,中公教育专家卢志喜会从这两个方面给大家揭开一笔画的神秘面纱。
一、什么样的图形是一笔画图形定义:一笔画图形是一个图形从起点到终点可由一笔画成而中间没有间断,一笔画图形点可以重复,而线不可以重复。
一笔画图形具有两个比较明显的特点。
①图形相异;②图形简单;③图形一部分。
因此考生在复习图形推理时,除了要掌握相异图形常考的考点,点、线之外,还要掌握一笔画。
在复习备考的过程中首先要掌握一些简单的一笔画图形。
例如:长方形、正方形、三角形、五角星、圆。
当出现这些基本图形,或者在简单图形上增减了部分线条时,有一定的敏感性。
二、如何判断一个图形是否是一笔画图形方法一、奇偶点判断法奇点:从一个点引出的线条数为奇数;偶点:从一点引出的线条数为偶数。
规律:⒈凡是奇点数为2或者0的图形,一定可以一笔画成。
画时必须把一个奇点为起点,另一个奇点终点。
(利用奇点数判断,图形必须是一部分,比如“回”,奇点数为0,但是不能一笔画)2.其他情况的图都不能一笔画出。
(有偶数个奇点除以二便可算出此图需几笔画成。
)利用奇偶点法判断下列几个图形是否为一笔画图形,非一笔画图形需几笔画成分析:图形1.奇点数为2,偶点为2,可以一笔画成。
图2.奇点为0,偶点为3,可一笔画。
图3.奇点为6,偶点为0,三笔可画成。
图4.奇点为0,偶点为10,可一笔画。
图5.奇点为4,偶点为5,可2笔画。
图6.奇点为4,可2笔画。
奇偶点判断法规律适合一切一笔画图形。
方法二、区域连通法规律:1、平面内区域可以构成两两连通的区域(表示图形没有单独的出头的线条),且区域之间属于单连通,这样的图形可以一笔画。
(单连通表示从一个区域到另一个区域只有唯一的路径,且经过的区域不能重复)利用区域连通法,判断下列几个图形是否为一笔画图形分析:首先对图形进行区域划分,如下:图1.区域1到区域2是单连通,可以一笔画。
一笔画问题

在行测考试中,图形推理中的一笔画问题,一直都是考生在考试中容易失分的题目。
其实主要问题存在于几个方面。
一、考生无法判断,什么样的图形考查的是一笔画;二、对一笔画图形的判断方法不了解。
接下来,中公教育专家卢志喜会从这两个方面给大家揭开一笔画的神秘面纱。
一、什么样的图形是一笔画图形定义:一笔画图形是一个图形从起点到终点可由一笔画成而中间没有间断,一笔画图形点可以重复,而线不可以重复。
一笔画图形具有两个比较明显的特点。
①图形相异;②图形简单;③图形一部分。
因此考生在复习图形推理时,除了要掌握相异图形常考的考点,点、线之外,还要掌握一笔画。
在复习备考的过程中首先要掌握一些简单的一笔画图形。
例如:长方形、正方形、三角形、五角星、圆。
当出现这些基本图形,或者在简单图形上增减了部分线条时,有一定的敏感性。
二、如何判断一个图形是否是一笔画图形方法一、奇偶点判断法奇点:从一个点引出的线条数为奇数;偶点:从一点引出的线条数为偶数。
规律:⒈凡是奇点数为2或者0的图形,一定可以一笔画成。
画时必须把一个奇点为起点,另一个奇点终点。
(利用奇点数判断,图形必须是一部分,比如“回”,奇点数为0,但是不能一笔画)2.其他情况的图都不能一笔画出。
(有偶数个奇点除以二便可算出此图需几笔画成。
)利用奇偶点法判断下列几个图形是否为一笔画图形,非一笔画图形需几笔画成?分析:图形1.奇点数为2,偶点为2,可以一笔画成。
图2.奇点为0,偶点为3,可一笔画。
图3.奇点为6,偶点为0,三笔可画成。
图4.奇点为0,偶点为10,可一笔画。
图5.奇点为4,偶点为5,可2笔画。
图6.奇点为4,可2笔画。
奇偶点判断法规律适合一切一笔画图形。
方法二、区域连通法规律:1、平面内区域可以构成两两连通的区域(表示图形没有单独的出头的线条),且区域之间属于单连通,这样的图形可以一笔画。
(单连通表示从一个区域到另一个区域只有唯一的路径,且经过的区域不能重复)利用区域连通法,判断下列几个图形是否为一笔画图形?分析:首先对图形进行区域划分,如下:图1.区域1到区域2是单连通,可以一笔画。
2015选调生考试图形推理中的一笔画问题

2015选调生考试图形推理中的一笔画问题在近几年的公务员考试中,图形推理中总会出现这样一类问题,即一笔画问题,这类问题对于很多考生来说都是一个经常被遗忘的知识点,因此,在这里对一笔画问题进行一定的梳理和讲解,希望对考生有帮助。
众所周知,公务员考试中的图形推理中没有任何的文字提示,完全靠考生对于知识点的了解和对图形的感觉,因此,一笔画问题这个考点的题型特点以及解决特点就成为了解决一笔画问题的关键点。
那考试中,什么样的图形是一笔画呢?一个图形,只有同时满足两个条件的时候,才是一个一笔画。
第一个条件就是,这个图形是一个连通图,第二个条件是,这个图形中,奇点个数必须是0个或者2个。
那么什么事连通图呢,即一个图形中,任意的找到两个点,这两个点能够通过图形本身相遇,那就是一个连通图,例如“日”,在这个图形上任意找到两点,都能通过图形本身相遇,则为一个连通图,而“回”这个图形中,我任意找到两个点,不一定能够通过图形本身相遇,则其并非一个连通图;接下来,第二个要素,奇点个数为0个或者2个,什么是奇点呢,奇点的概念是这样的,从一个点引发出的线条数(可直线可曲线)为奇数个的时候,那么这个点就是一个奇点。
那只有当一个图形满足这两个条件的时候,才能成为一个一笔画,例如“﹫”“☆”“日”“8”等等,都是一笔画。
那我们来看一下一笔画这个考点的真题是怎样的。
【例】【解析】D 本题中,我们会发现,九宫格中第一行的第一个图形,第二行第一个图形,以及第三行第二个图形,有明显的变化,即,第一行第一个图形只有一个部分,第二行第一个图形明显是两个部分,第三行第二个图形有三个部分,因此我们考虑这是笔画的1、2、3这一规律,进而我们通过观察图形是否为连通图,数每个图形的奇点,来判断,问号国家公务员| 事业单位| 村官| 选调生| 教师招聘| 银行招聘| 信用社| 乡镇公务员| 各省公务员|处应该选择一个3笔画,A项是一个有四个几点的连通图,为两笔画;B项是一个有四个几点的连通图,为两笔画;C项中没有奇点,连通图,为一笔画;D项,首先并非连通图,因此一横需要单独的一笔,剩余的图形中有四个奇点,为两笔画,加上单独的一笔,共三笔,因此为正确答案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图形推理中的“一笔画成”的规律
京佳教育
在公务员考试之行测试卷的判断推理模块,其中图形推理试题常考规律中,有一类较为典型的规律被称之为“一笔画成”规律。
下面,京佳的老师们将结合公考真题为大家详细解读一下。
一、“一笔画出”规律简介
所谓“一笔画成”规律,即一个图形从起点到终点可由一笔画成而线路不中断。
其实,在行测试卷中,图形推理部分需要的不仅是经验的累积,也需要广大考生有一双尖锐的“慧眼”,而“一笔画成”规律,事实上有内在规律可循——关键在于判别奇点、偶点的个数。
所谓“偶点”,即交点处所连接的线条数位偶数,如图(1)中的②、③;所谓“奇点”,即交点数所连接的线条数为奇数,如图(1)中的①、④。
图(1)
一、只有偶点,可以一笔画,并且可以以任意一点作为起点。
例:图(2)都是偶点,画的线路可以是:①→③→⑤→⑦→②→④→⑥→⑦→①
图(2)
二、有且只有两个奇点,可以一笔画,但必须以这两个奇点分别作为起点和终点。
(图(1)的线路的数条,例如:①→②→③→①→④。
)
三、奇点超过两个,则不能一笔画。
对于一些比较复杂的路线问题,可以先转化为简单的几何图形,然后根据判定是否能一笔画的方法进行解答。
二、真题演练
例:从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性()。
(2011.9.17联考第66题)
【京佳解析】C 本题考查的是一笔画成规律。
题干各图形均可由一笔画成。
故选C。
例:从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性()。
(2008安徽第54题)
【京佳解析】C 本题考查的是一笔画成规律。
题干各图形均可由一笔画成。
故选C。
