第三讲数图形的规律
人教版九年级上册数学 讲义 二次函数的图像与性质
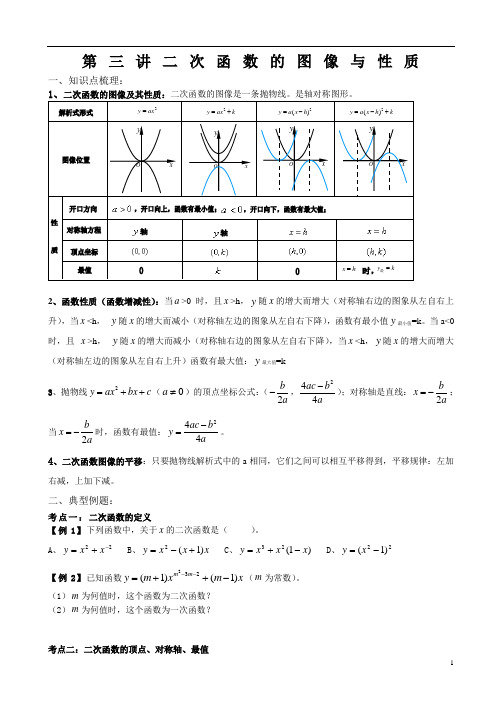
C. D.
【例2】已知二次函数y=ax2+bx+1的大致图象如图所示,则函数y=ax+b的图
象不经过( )
A.第一象限B.第二象限C.第三象限D.第四象限
【例3】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b<0;③a-b+c<0;④a+c>0,其中正确结论的个数为().
3、抛物线 ( )的顶点坐标公式:( , );对称轴是直线: ;当 时,函数有最值: 。
4、二次函数图像的平移:只要抛物线解析式中的a相同,它们之间可以相互平移得到,平移规律:左加右减,上加下减。
二、典型例题:
考点一:二次函数的定义
【例1】下列函数中,关于 的二次函数是( )。
A、 B、 C、 D、
A.y1<y2<y3B.y2<y1<y3
C.y3<y1<y2D.y1<y3<y2
【例2】已知二次函数 ,若自变量 分别取 , , ,且 ,则对应的函数值 的大小关系正确的是()
A. B. C. D.
三、强化训练:
【夯实基ห้องสมุดไป่ตู้】
1、二次函数 的图象上有两点(3,-8)和(-5,-8),则此拋物线的对称轴是()
【例2】已知函数 ( 为常数)。
(1) 为何值时,这个函数为二次函数?
(2) 为何值时,这个函数为一次函数?
考点二:二次函数的顶点、对称轴、最值
【例1】写出下列抛物线的对称轴方程、顶点坐标及最大或最小值;
(1) (2) (3)
考点三:抛物线的平移(上加下减,左加右减)
【例1】把抛物线 向左平移2个单位,再向下平移2个单位,则所得的抛物线的表达式是;
A、4个B、3个C、2个D、1个
考点五:直线与抛物线的位置关系
小学数学找规律画图

第三讲 找规律画图当你看到●○■□●○■□●○■□……你会有什么发现?其实很多时候图案之间也是有某种联系的,能够发现图案之间的联系,对我们小朋友来说也是一种思维的锻炼。
经典例题观察下面的卡片,想一想后面的卡片应该怎么画。
解题策略通过仔细观察,我们可以发现,第一张卡片全部是白圆点,有5个,到了第二张卡片,是4个白圆点,1个黑圆点,第三张、第四张卡片的白圆点分别是3个和2个,而黑圆点分别是2个和3个。
因此卡片的变化规律是,后一幅图与前一幅图相比,白圆点减少1个,黑圆点减1个。
按照这个规律,后两张卡片分别应该这样画。
举一反三1、下面的图形是有一定的排列规律的,请你画出所缺少的图形。
1、再在空格处画上合适的图形。
3、在下面的两行图形中,涂色部分是按一定方向转动的,请按规律在最后一个图形中涂上颜色。
融会贯通4、仔细观察方格里图形的排列规律,再在“?”的空格里画上合适的图形。
做一名好教师需要一颗爱孩子的心“心与心相连,手与手相牵”这就是我,幼儿教师的生活和梦想。
有人说,幼儿教师是个浪费青春年华的职业,而我却认为这是世间最灿烂,最有生命力的职业。
当我面对一张张幼稚可爱的小脸,当我面对世上最纯洁的心灵,我觉得我的选择是对的。
在与家长的交谈中,我意识到家长对我的信任,此时我感到肩上责任之重大。
虽说我是老教师,但我更要努力工作来回报家长对我的信任。
“可怜天下父母心”,道出了父母对子女无私的爱。
教师可以拥有几十个孩子,可孩子对父母而言却是唯一,对于从事幼教事业31年的我经过认真的反思认为,要想成为一名家长满意的好教师应做好以下几项工作:首先,要树立为家长服务的意识,解决家长的后顾之忧,服务于家长,为家长解决后顾之忧是幼儿园工作的目标之一。
若将教育作为一个产业而言,则教师是“生产者””,家长是“消费者””。
为了让消费者(家长)满意,作为教师的我们,则要全心全意为家长服务,想家长之所想,设身处地的为家长着想,不图回报的解决家长的后顾之忧。
北师大版数学五年级《图形中的规律》

图形中的规律
光武一小 杨玲
三角形个数 1 2 3 4
摆成的图形
小棒的根数 3 5 7 9
… …
10
每多摆1个三角形就增加2根小棒。
3 + 2 + 2 + 2 = 9(根) 3×4 – 3 = 9(根)
摆20个三角形需要多少根小棒呢?
笑笑接着摆下去,一共用了37根小棒,你知道 她摆了多少个三角形吗?
观察每个点阵中点ቤተ መጻሕፍቲ ባይዱ个数,你发现了什么?
说一说,画一画,下一个点阵有多少个点?是怎么排列的?
▪ 从不同的角度观察,你会发现一些新的规律
一张方桌可以坐4人。
两张方桌这样拼起来,可以坐6人。
照这样的方法拼下去,5张方桌可以坐多少人
照这样的方法拼下去,16人需要多少张方桌?
第三讲 找规律

第三讲找图形的规律找规律是解决数学问题的一种重要手段。
而发现规律既需要敏锐的观察力,又需要严密的逻辑推理能力。
这一讲将为你提供很多图形,它们在某一个方面,比如颜色、形状、大小、结构、位置或繁难等有些共同的特征或变化规律,我们要学会通过观察找规律,并根据规律来推断结果。
第一部分、旋转、轮换规律例题1:相传古时候一位老人留在人间很多宝盒,里面装着世界上最宝贵的财富,但是并不是拥有宝盒都可以得到这笔财富,在宝盒的上面设置了密码,只有写出密码的人才会真正拥有这笔财富,聪明的你你能找出密码吗?○□☆△○□☆△△○□☆△○□☆☆△○□☆△○□()()()()()()()()分析与解答我们仔细观察一下这个图形,可以看出来。
第一排第一个位置的图形,圆,现在在第二排的第二个位置;第一排的第二个图形,正方形,现在在第二排第三个位置;以此类推。
而第一排的最后一个图形,三角形,现在在第二排的第一个位置。
也就是说,我们把第一排的最后一个图形拿到第二排的第一个位置。
而第一排其余位置的图形,依次向后挪一个位置。
那么第三排的图形,就是第二排最后一个位置的图形放在第一个位置,第二排其余位置的图形依次往后挪一个位置得到的。
所以密码就是:□☆△○□☆△○练习1、下面的图形是按一定规律排列的,请仔细观察,并在“?”处填上适当的图形.(1)第2组(2)第2组(3)第2组(1)仔细观察可发现第1组和第2组中间的部分都是由三个小图形构成的.构成的规律是:当按照第1、第2、第3组的顺序观察时,6个小图形都在向左移动,而且移动的同时又在重新分组和组合,但排列顺序保持不变,当某一个小图形移动到了最左边时,下一步它就回到了最右边.按这个规律可知图中第3组中间“?”处是:□△0.(2)注意观察第1组和第2组,每组都是由三对小图形组成;而每对小图形都是由一个“空白”的和一个“黑色”的小图形组成;而且它俩的排列顺序都是“空白”的在左边,“黑色”的在右边.再按着第1、第2、第3组的顺序观察下去,可发现每对小图形在各组中的位置的变化规律:它们都在向左移动,当一对小图形移动到最左边后,下一步它就回到了最右边.按这个移动规律,可知第3组“?”处应填:○▲.(3)观察第1组与第2组,每组中有三种图形:★、□、■,我们把每组图形再分为三小组,将更明显的得出变化规律. “?”是:□、■、★。
【一升二】小学数学奥数第3讲:找规律-教案

练习一:根据前面几幅图的规律,接下去该怎么画?(课件出示练习一,教师可根据课件,让学生更直观地观察到每个规律之间的变化)分析:第一幅图比第二幅图多1朵花,第二幅图比第三幅图多1朵花,根据前一幅图比后一幅图多1朵花的规律,可知第三幅图比第四幅图多1朵花,即画2朵花。
板书:(二)例题二:根据前面几幅图的规律,请你接着画。
(课件出示例题二)师:这里有好多漂亮的图形,小朋友都认识么?生:认识。
师:哪位小朋友能告诉老师,你都看到了什么?生:我看到了外面有一个蓝色的大圆,大圆里面有黑色的小圆和白色的小圆,还有红色的正方形。
师:恩,很好。
有哪位小朋友可以告诉老师每幅图形的数量变化?生:第二幅图,第四幅图,第六幅图都是3个红色正方形,没有变化。
师:既然没有变化,那接下来3个红色正方形会出现在哪幅图里?生:第八幅图里。
师:这是为什么呢?生:每隔一幅图,就会出现3个红色正方形。
师:同学们很细心,那么根据规律我们就可以知道第七幅里是圆形,那到底是什么颜色圆形,又有几个呢?生:共8个圆,是一黑一白的排列。
师:小朋友们都那么聪明,那老师可要好好的测试测试,你们是不是都明白了。
板书:(课件出示练习二)练习二:请你接着画。
分析:第一幅图中12个三角形中只有1个,第三幅图中有2个,第五幅图中有3个,可以发现每隔一幅图依次增加1个并减少1个,即第七幅图中12个三角形有4个;第二幅图中有4个、4个,第四幅图中有3个、5个,第六幅图中有2个、4个,每隔一幅图在依次减少1个,同时增加1个,即第八幅图中有1个、7个。
板书:小结:对于图形找规律的题目,我们需要注意以下几点:1. 仔细观察每幅图里的图形以及图形数量的变化。
2. 找出每幅图之间图形变化的规律。
第二课时师:是的,单个数它是作为个体,两个及两个以上是作为整体,因此我们在做整体数的比较就要更加仔细并且把它们之间的规律都找出来。
让我们来练一练吧。
板书:(1)(10,1),(8,2),(6,3),(4,4)(2)(1,2,3),(2,4,6),(3,6,9),(4,8,12)(课件出示练习四)练习四:找出每组数的变化规律,并写出空格中的数。
北师大版小学数学六年级上册《数与形结合的规律》知识点讲解总结练习解析

数与形结合的规律知识精讲1.数与形结合的规律“数”:指数学中的数量和数量关系,如数字、等式等,表达的信息具有抽象性和精确性;“形”:指图形,表示量对应的图形意义等,表达的信息具有直观性和形象性。
数与形结合主要有两种方式:以数辅形、以形助数。
以数辅形:借助数的精确性说明形的特征,通过准确计算,把图形问题转化成数量问题,化难为易。
以形助数:利用图形更好地揭示实际问题中蕴含的数量关系,进而解决实际问题。
2.数与形结合的规律——以数辅形如可以借助数形结合的方法数线段、角、三角形等图形的数量。
数线段的方法:可以结合图形,按照基本线段的个数得出一共有几条线段。
注:基本线段是指一条线段被端点所分成的几条线段。
1条基本线段:线段数量=1(条)。
2条基本线段:线段数量=2+1=3(条)。
3条基本线段:线段数量=3+2+1=6(条)。
4条基本线段:线段数量=4+3+2+1=10(条)。
……n条基本线段:线段数量=n+(n-1)+…+2+1 (条)。
类似地,数角或三角形等图形的数量,也可以数形结合运用基本角和基本三角形的个数来求。
3.数与形结合的规律——以形助数如下图是公共汽车从解放路到游乐园之间行驶速度变化的情况。
从图中可以观察得出以下信息。
(1)公共汽车从解放路到游乐园共行驶了4分。
(2)在第1分内,汽车行驶速度从0提高到400米/分。
(3)从0分到1分,汽车行驶速度在增加;从3分到4分,汽车行驶速度在减少;从1分到3分,行驶速度保持不变,是400米/分。
除了可以之间观察得出的信息之外,还可以根据图像推断出一些实际情况。
如根据上图可知汽车在1分至3分之间匀速行驶,因此路程是在增加,共增加了800米。
易错易误点混淆基本图形的数量和所求图形的数量在数线段或其他图形的数量时,容易只数基本图形,即将所求图形的数量和基本图形的数量混淆,从而导致错误。
如下图中一共有多少个角?错解:4。
这里错在只数出了4个基本角,而要求的是一共有多少个角。
学而思三年级第三讲(数列图形规律)

兔子数列规律:第一项和第二项均是 1,从第三项开始,每一项是它的前两项的和。 该规律拓展运用(类兔子数列): 例:
2, 1, 3, 4, 7, 11, 18, 29……
2+1=3 1+3=4 3+4=7 4+7=11 7+11=18 11+18=29 1, 1, 1, 3, 5, 9, 17, 31…… 发现从第 4 项开始,每一项都是它的前 3 项之和
(2)号图:1+3=4 个 (3)号图:1+3+5=9 个 (4)号图:1+3+5+7=16 个 (5)号图:1+3+5+7+9=25 个
三年级秋季班(五级下) 3.2
三年级 2010 秋季 第三讲 数列数表图形规律
程雪
火柴根数:有些三角形共用一条边,不便计算,我们应尽量找独立的三角形。
灰色为对立三角形
个数出现一个5的倍数2除以3的余数每8个数为一周期循环3奇偶数每3个为一周期循环奇奇偶1第11项第10项345589个数出现一个5的倍数第20项正好是5的倍数所以被53409831366组周期的最后一个是偶数所以第4098项是偶数4
三年级 2010 秋季 第三讲 数列数表图形规律
程雪
第三讲 数列数表图形规律
程雪
1 11
121
1 3 31
14 6 41
1, 5, 10, 10, 5, 1
1, 6, 15, 20, 15, 6, 1
解析:本题是著名的杨辉三角,很多孩子在以前接触过,所以前两问都不算难。
(1) 杨辉三角的规律:a.三角的两边都由 1 组成;b.第几行就有几个数;c.除开两边的 1,每个
三上奥数练习题

第一讲:自然数的计数法12?其中最大的三位数和最小的三位数相差多少?3.在一个三位数的左面添上一个数字6,得到的四位数和原来三位数的和为6578,求原三位数是多少?4.去掉三位数左面最高位的数字6,得到的两位数与原三位数之和是706,求原三位数是多少? 5.小明写了一个三位数,小东划掉了它个位数字0,该数减少了378,那么小小明写的数是什么? 6.小红用数字卡片摆了一个两位数。
小淘气将两个数字交换了一下位置,说:“我的数比你的数大63。
”小红摆的数是什么呢?7.小巧写了一个两位数,小明在她写的数的末尾添上了一个0后说:“我写的数比你写的数大468。
”请你猜猜看,小红写的数是什么?8.老师在黑板上写了一个两位数,淘气在它的末尾添上一个数字4,使得该数增加了868,那么老师写的数是什么?9.做一道整数加法题时,小丁丁把一个加数个位上的7看成1,把另一个加数十位上的6看成了9,结果得出和为148,那么正确的答案应该是多少?第二讲:加减法的速算与巧算计算下列各题。
57+123+1732436+372+564+1628965-172-32847+(653+145)666-(266-357)568+1991536-547+164+1477243-803297+304+306+299+296 532-(336-268)-64第三讲:图形找规律一.填空题1.按照图形的变化规律接下去画。
2.仔细观察,在空白处应如何填?3.下图中最后一幅图的小圆点应该怎样画?4.按照前面图形的排列特点,在空白处画上合适的图。
二.选择题5.仔细观察,从右边图形中选出一个合适的图形,左图空白处应填( )。
6.下面图形的空白处应填( )A. B.C. D.三、解答题7.根据前三张图片的规律,画出第四张图的阴影部分。
8.说说下面图形的变化规律,接下去的图形怎样画?9.请在下图中按规律把图画完整。
第四讲:数列找规律1.找出下面数列的规律,并按照规律填数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三讲数图形的规律
【专题导引】
我们已经认识了线段、角、三角形、长方形等基本图形,当这些图形重重叠
叠地交错在一起时就构成了复杂的几何图形。
要正确数出图形的个数,就必须有次序、有条理地数,关键是要从基本图形入手。
首先要弄清图形中包含的基本图形是什么,有多少个,然后再数出由基本图形组成的新的图形,并求出它们的和。
【典型例题】
【例1】数出下面图中有多少条线段。
【思路导航】从图中可以看出,从A点出发的不同线段有3条:AB、AC、AD;从B点出发的不同线段有2条:BC、BD;从C点出发的不同线段有1条:CD。
简单来说,就是要数有几个间隔,有三个间隔。
因此,图中共有3+2+1=6条线段。
【试一试】
1.数出下图中有多少条线段
2.数出下图中有几个锐角
【例2】数一数下图中共有多少个三角形。
A
B C D E
E
A B C D
O
D
C
B
A
【思路导航】图中BE边上的每一条线段与顶点A构成一个三角形,也就是说,BE边上有几条线段,就构成了几个三角形,因为BE上有4个点,共有1+2+3=6条线段,所以图中有6个三角形。
【试一试】
1.数出下图中分别有多少个三角形
2. 数出图中共有多少个平行四边形
【例3】数出下图中有多少个长方形
【思路导航】数图形中有多少个长方形和数三角形的方法一样,长方形是由长宽两对线段围成,线段CD上有3+2+1=6条线段,其中每一条与AC中一条线段对应,分别作为长方形的长和宽,这里共有6×1=6个长方形;而AC上共2+1=3条线段也就有6×3=18个长方形。
它的计算公式为:
长方形的总数=长边线段的总数×宽边线段的总数
【试一试】数一数,下面各图中分别有几个长方形
【例4】数一数,下图中有多少个正方形(每个小方格是边长为1的正方形)
F
E
D
C
B
A
K
G
I
H
G
F
E
D
C
B
A
D
B
C
A
【思路导航】图中边长为1个长度单位的正方形有3×3=9个,边长为2个长度单位的正方形有2×2=4个,边长为3个长度单位的正方形有1×1=1个。
所以图中的正方形总数为:1+4+9=14个。
经进一步分析可以发现,由相同的n×n个小方格组成的几行几列的正方形其中所含的正方形总数为:1×1+2×2+…+n×n。
【试一试】数一数下列各图中分别有多少个正方形(每个小方格为边长是1的小正方形)
(1)
【例5】有5个同学,每两个人握手一次,一共要握手多少次
【思路导航】这道题可以用数线段的方法来解答。
根据题意,画出线段图,每一个端点代表一个同学。
从图上可以看出,第1个同学要与其余4个同学握手共握手4次;第2个同学还要与其余3个同学握手共握手3次,第3个同学要与其余2个同学握手共握手2次;第4个同学还要与最后1个同学握手共握手1次。
所以,一共要握手4+3+2+1=10(次)
【试一试】
1.银海学校三年级有9个班,每两个班要比赛拔河一次,这样一共要拔河几次
2.从上海到武汉的航运线上,有9个停靠码头,航运公司要为这段航运线准备多少种不同的船票
3.有1——6六个数字,能组成多少个不同的两位数
课外作业
家长签名:__________
1.下列各图中各有多少个锐角
_5
_4
_3
_2
_1
2. 下图中各有多少个三角形
3. 数出下图中有多少个长方形。
4. 有10个小朋友,每2个人照一张合影,一共要照多少张照片 我的学习收获:
.
.
我来编题:。
