学案 52山西大学附中高二年级椭圆及其简单几何性质(2)
高二数学高效课堂资料教案、学案 2.2.2椭圆的几何性质

高二数学高效课堂资料教案2.2.2椭圆的几何性质教学目标:(1)通过对椭圆标准方程的讨论,理解并掌握椭圆的几何性质;(2)能够根据椭圆的标准方程求焦点、顶点坐标、离心率并能根据其性质画图; (3)培养学生分析问题、解决问题的能力,并为学习其它圆锥曲线作方法上的准备.重点:椭圆的几何性质. 通过几何性质求椭圆方程并画图 难点:椭圆离心率的概念的理解. 教学方法:讲授法 教学过程: 一、导入新课:1.椭圆的定义,椭圆的焦点坐标,焦距.2.椭圆的标准方程. 二、形成概念:(一)通过提出问题、分析问题、解决问题激发学生的学习兴趣,在掌握新知识的同时培养能力.[在解析几何里,是利用曲线的方程来研究曲线的几何性质的,我们现在利用焦点在x 轴上的椭圆的标准方程来研究其几何性质.]已知椭圆的标准方程为:)0(12222>>=+b a b y a x三、概念深化: 1.范围[我们要研究椭圆在直角坐标系中的范围,就是研究椭圆在哪个区域里,只要讨论方程中x ,y 的范围就知道了.]问题1 方程中x 、y 的取值范围是什么?由椭圆的标准方程可知,椭圆上点的坐标(x,y)都适合不等式22a x ≤1, 22by ≤1即x2≤a2, y2≤b2所以|x|≤a,|y|≤b即-a≤x≤a, -b≤y≤b这说明椭圆位于直线x=±a, y=±b所围成的矩形里。
2.对称性复习关于x轴,y轴,原点对称的点的坐标之间的关系:点(x,y)关于x轴对称的点的坐标为(x,-y);点(x,y)关于y轴对称的点的坐标为(-x, y);点(x,y)关于原点对称的点的坐标为(-x,-y);问题2 在椭圆的标准方程中①以-y代y②以-x代x③同时以-x代x、以-y代y,你有什么发现?(1)在曲线的方程里,如果以-y代y方程不变,那么当点P(x,y)在曲线上时,它关于x的轴对称点P’(x,-y)也在曲线上,所以曲线关于x轴对称。
人教新课标版数学高二选修2-1导学案 椭圆的简单几何性质(二)学生版

2.2.2 椭圆的简单几何性质(二)【学习目标】1.进一步巩固椭圆的简单几何性质.2.掌握直线与椭圆位置关系的相关知识.【学习过程】一、自主学习知识点一 点与椭圆的位置关系设P (x 0,y 0),椭圆x 2a 2+y 2b 2=1(a >b >0),则点P 与椭圆的位置关系如下表所示:知识点二 (1)判断直线和椭圆位置关系的方法:将直线的方程和椭圆的方程联立,消去一个未知数,得到一个一元二次方程.若Δ>0,则直线和椭圆 ;若Δ=0,则直线和椭圆 ;若Δ<0,则直线和椭圆 .(2)根与系数的关系及弦长公式:设直线l :y =kx +b (k ≠0,b 为常数)与椭圆x 2a 2+y 2b2=1(a >b >0)相交,两个交点为A (x 1,y 1)、B (x 2,y 2),则线段AB 叫做直线l 截椭圆所得的弦,线段AB 的长度叫做 .下面我们推导弦长公式:由两点间的距离公式,得AB =(x 1-x 2)2+(y 1-y 2)2,将y 1=kx 1+b ,y 2=kx 2+b 代入上式,得AB =(x 1-x 2)2+(kx 1-kx 2)2=(x 1-x 2)2+k 2(x 1-x 2)2=1+k 2|x 1-x 2|,而|x 1-x 2|=(x 1+x 2)2-4x 1x 2,所以AB =1+k 2·(x 1+x 2)2-4x 1x 2,其中x 1+x 2与x 1·x 2均可由根与系数的关系得到.(3)直线和椭圆相交是三种位置关系中最重要的,判断直线和椭圆相交可利用Δ>0.例如,直线l :y =k (x -2)+1和椭圆x 216+y 29=1.无论k 取何值,直线l 恒过定点(2,1),而定点(2,1)在椭圆内部,所以直线l 必与椭圆相交.二、合作探究问题1 点P (x 0,y 0)与椭圆x 2a 2+y 2b 2=1(a >b >0)有几种位置关系?问题2 直线与椭圆有几种位置关系?问题3 如何判断y =kx +m 与椭圆x 2a 2+y 2b 2=1(a >b >0)的位置关系?探究点1 直线与椭圆的位置关系例1 (1)直线y =kx -k +1与椭圆x 22+y 23=1的位置关系是( ) A .相交 B .相切 C .相离 D .不确定(2)在平面直角坐标系xOy 中,经过点(0,2)且斜率为k 的直线l 与椭圆x 22+y 2=1有两个不同的交点P 和Q .求k 的取值范围.探究点2 直线与椭圆的相交弦问题例2 已知椭圆x 236+y 29=1和点P (4,2),直线l 经过点P 且与椭圆交于A 、B 两点. (1)当直线l 的斜率为12时,求线段AB 的长度; (2)当P 点恰好为线段AB 的中点时,求l 的方程.探究点3 椭圆中的最值(或范围)问题例3 已知椭圆4x 2+y 2=1及直线y =x +m .(1)当直线和椭圆有公共点时,求实数m 的取值范围;(2)求被椭圆截得的最长弦所在的直线方程.三、当堂测试1.点A (a,1)在椭圆x 24+y 22=1的内部,则a 的取值范围是( ) A .-2<a < 2B .a <-2或a > 2C .-2<a <2D .-1<a <12.已知直线l :x +y -3=0,椭圆x 24+y 2=1,则直线与椭圆的位置关系是( ) A .相交B .相切C .相离D .相切或相交3.椭圆x 24+y 23=1的右焦点到直线y =3x 的距离是( ) A.12 B.32C .1 D. 3 4.椭圆x 216+y 24=1上的点到直线x +2y -2=0的最大距离是( ) A .3B.11 C .2 2 D.105.若直线y =x +1与椭圆x 22+y 2=1相交于A ,B 两个不同的点,则|AB |=________. 四、课堂小结本节课我们学习过哪些知识内容?五、学后反思1、我的疑问:2、我的收获:。
编号90山西大学附中椭圆的标准方程与几何性质2

山西大学附中高三年级(上)数学导学设计 编号90椭圆的标准方程与几何性质(二)1.设1F 、2F 是椭圆2222:1(0)x y E a b a b+=>>的左、右焦点,P 为直线32a x =上一点,∆21F PF 是底角为30的等腰三角形,则E 的离心率为 A.12 B . 23 C. 34 D .452.已知椭圆22221(0)x y a b a b+=>>的左焦点为F ,右顶点为A ,点B 在椭圆上,且BF x ⊥轴,直线AB 交y 轴于点P .若2AP PB =,则椭圆的离心率是A B .2 C .13 D .123.从椭圆22221(0)x y a b a b+=>>上一点P 向x 轴作垂线,垂足恰为左焦点1F ,A 是椭圆与x 轴正半轴的交点,B 是椭圆与y 轴正半轴的交点,且//AB OP (O 是坐标原点),则该椭圆的离心率是A B .12 C D 4.设P 为椭圆12222=+by a x )0(>>b a 上一点,F 1、F 2为焦点,如果 7521=∠F PF , 1512=∠F PF ,则椭圆的离心率为A .22B .23C .32D .36 5.1F 、2F 为椭圆的两个焦点,以2F 为圆心作圆2F ,已知圆2F 经过椭圆的中心,且与椭圆交于M 点,若直线1MF 恰与圆2F 相切,则椭圆的离心率e 为 A.13- B.32- C.22 D.23 6.椭圆12222=+by a x )0(>>b a 与圆222)2(c b y x +=+(c 为椭圆半焦距)有四个不同交点,则椭圆离心率e 的取值范围是A .5355<<eB .153<<eC .155<<eD .530<<e 7.以椭圆上一点和两个焦点为顶点的三角形的最大面积为1,则长轴长的最小值为A .1B .2C .2D .228.已知点12,F F 是椭圆2222xy 的两个焦点,点P 是该椭圆上的一个动点,则12PF PF 的最小值是9.椭圆1522=+my x 的离心率为510,则实数m 的值为 . 10.椭圆2222:1(0)x y a b a bΓ+=>>的左.右焦点分别为12,F F ,焦距为c 2,若直线)y x c =+与椭圆Γ的一个交点M 满足12212MF F MF F ∠=∠,则该椭圆的离心率e = .11.在ABC △中,AB BC =,7cos 18B =-.若以A B ,为焦点的椭圆经过点C ,则该椭圆的离心率e = .12.已知椭圆2222:1(0)x y C a b a b+=>>的左焦点为,F C 与过原点的直线相交于,A B 两点,连接,AF BF ,若410,6,cos ABF 5AB AF ==∠=,则C 的离心率e = . 13.已知A ,B 为椭圆:C 1122=++my m x 的长轴的两个端点,P 是椭圆C 上的动点,且APB ∠的最大值是32π,则实数m 的值是___________. 14.椭圆14922=+y x 的两个焦点为1F 、2F ,点P 为其上的动点,当已知21PF F ∠为钝角,点P 的横坐标的取值范围为 .15. 已知21,F F 分别是椭圆)0(12222>>=+b a by a x 的左、右焦点,上顶点为M .若在椭圆上存在一点P ,分别连结21PF PF ,交y 轴于B A ,两点,且满足||||,2PF λ==,则实数λ的取值范围为 .16.若F 是椭圆1121622=+y x 的右焦点,M 是该椭圆上的点,)1,2( -A 是该椭圆内一点,则MF MA +的最小值是 .17.过点(1,1)M 作斜率为12-的直线与椭圆C :22221(0)x y a b a b +=>>相交于,A B ,若M 是线段AB 的中点,则椭圆C 的离心率为 .18.已知椭圆C :22194x y +=,点M 与C 的焦点不重合,若M 关于C 的焦点的对称点分别为B A ,,线段MN 的中点在C 上,则||||AN BN += .。
椭圆的简单几何性质教案

椭圆的简单几何性质教案椭圆是一个非常重要的几何图形,具有许多有趣的几何性质。
在这个简单的几何性质教案中,我将介绍一些关于椭圆的基本性质和定理。
一、椭圆的定义:椭圆是平面上到两个固定点F1、F2距离之和为常数2a的点P的集合。
F1、F2称为椭圆的焦点,而2a称为椭圆的长轴长度。
二、椭圆的性质:1. 椭圆的长轴与短轴:长轴是焦点F1、F2的中点连线的长度,短轴是焦点F1、F2与椭圆上点A的连线的长度。
2. 椭圆的对称轴:椭圆的长轴是对称轴,即沿长轴折叠椭圆的两边重合。
3. 椭圆的离心率:离心率e是一个确定椭圆形状的参数,表示焦点与椭圆上点A的距离与椭圆长轴长度之比。
离心率的计算公式:e = F1F2 / (2a)当离心率e=0时,椭圆退化为一个点;当0 < e < 1时,椭圆存在,且是一个闭合曲线;当e = 1时,椭圆退化为一条线段;当e > 1时,曲线退化为两个分离的直线。
4. 椭圆的焦半径:椭圆上任意一点P到两个焦点F1、F2的距离之和等于椭圆的长轴长度,即PF1 + PF2 = 2a。
三、椭圆的定理:1. 椭圆的反射性质:椭圆上的任意一条直线与椭圆的两个焦点的连线的夹角等于该直线与该椭圆上与焦点处的切线的夹角。
2. 椭圆的切线性质:椭圆上任意一点处的切线与该点到两个焦点的连线的交点与该点、两个焦点连线的垂线,共线。
3. 椭圆的切点性质:椭圆上任意一点处的切线与该点到两个焦点的连线的交点与该点、两个焦点连线的垂线以及该点三条线共线。
四、椭圆的应用:椭圆是地球等天体轨道的几何形状,也是经典力学、天体力学等领域的重要研究对象。
此外,椭圆还广泛应用于工程类问题中,例如天然气管道的优化布局、平面轮廓设计等。
五、课堂练习:1. 画出椭圆的长轴、短轴和焦点。
2. 若已知椭圆的长轴长度a=6cm,离心率e=2/3,求焦距;3. 若已知椭圆的离心率e=1/2,焦半径PF1=3cm,求椭圆的长轴长度。
学案 50山西大学附中高二年级椭圆及其标准方程(2)

山西大学附中高二年级(上) 导学设计 编号50椭圆及其标准方程(2)【学习目标】应用几种点的轨迹的方法求椭圆的标准方程.【学习重点】应用几种点的轨迹的方法求椭圆的标准方程【学习难点】应用几种点的轨迹的方法求椭圆的标准方程【学习过程】一、导读问题1:椭圆上221259x y +=一点P 到椭圆的左焦点1F 的距离为3,则P 到椭圆右焦点2F 的距离是 .问题2:在椭圆的标准方程中,6a =,b 则椭圆的标准方程是 .到点(3,0)-的距离等于2的所有点都在圆 上.二、导练例1在圆224x y +=上任取一点P ,过点P 作x 轴的垂线段PD ,D 为垂足.当点P 在圆上运动时,线段PD 的中点M 的轨迹是什么?变式: 若点M 在DP 的延长线上,且32DM DP =,则点M 的轨迹又是什么?小结1:椭圆与圆的关系:圆上每一点的横(纵)坐标不变,而纵(横)坐标伸长或缩短就可得到椭圆.例2设点,A B 的坐标分别为()()5,0,5,0-,.直线,AM BM 相交于点M ,且它们的斜率之积是49-,求点M 的轨迹方程 .变式:点,A B 的坐标是()()1,0,1,0-,直线,AM BM 相交于点M ,且直线AM 的斜率与直线BM 的斜率的商是2,点M 的轨迹是什么?练1.求到定点()2,0A 与到定直线8x =的动点的轨迹方程.练2.一动圆与圆22650x y x +++=外切,同时与圆226910x y x +--=内切,求动圆圆心的轨迹方程式,并说明它是什么曲线.三、目标检测1.若关于,x y 的方程22sin cos 1x y αα-=所表示的曲线是椭圆,则α在( ).A .第一象限B .第二象限C .第三象限D .第四象限2.若ABC ∆的个顶点坐标(4,0)A -、(4,0)B ,ABC ∆的周长为18,则顶点C 的轨迹方程为.A .221259x y +=B .221259y x += (0)y ≠C .221169x y +=(0)y ≠D .221259x y +=(0)y ≠ 3.设定点1(0,2)F - ,2(0,2)F ,动点P 满足条件124(0)PF PF m m m+=+>,则点P 的轨迹是( ).A .椭圆 B .线段 C .不存在 D .椭圆或线段4.与y 轴相切且和半圆224(02)x y x +=≤≤内切的动圆圆心的轨迹方程是 .5. 设12,F F 为定点,|12F F |=6,动点M 满足12||||6MF MF +=,则动点M 的轨迹是 .6.已知三角形ABC 的一边长为6,周长为16,求顶点A 的轨迹方程.7.点M 与定点(0,2)F 的距离和它到定直线8y =的距离的比是1:2,求点的轨迹方程式,并说明轨迹是什么图形.。
高二数学椭圆的简单几何性质2

a2=b2+c2
x2 b2
y2 a2
1(a
b
0)
|x|≤ b,|y|≤ a
同前
(b,0)、(-b,0)、 (0,a)、(0,-a) (0 , c)、(0, -c)
同前
同前
同前
复习练习:
1.椭圆的长短轴之和为18,焦距为6,则椭圆 的标准方程为( C )
A. x2 y2 1. 9 16
所示的直角坐标系,AB与地球交与C,D两点。
设所求的方程为 x2 a2
y2 b2
1
a b0 ,
Y
由题意知:AC=439, BD=2384,
F2C F2D 6371. 则 : a c OA OF2 F2 A
B
F1 F2
DO
CA X
6371 439 6810
y
2
=1的离心率为
0.5,则:k=__45_或__4
9
5、若某个椭圆的长轴、短轴、焦距依次成等差数列,
3 则其离心率e=___5_______
6、点P是椭圆
x2 a2
y2 b2
1上的动点,当P的坐标为(±a,0)时,
P到原点O的最大距离为
a
;当P的坐标为(0, ±b时) ,
a2=b2+c2
标准方程 范围 对称性 顶点坐标 焦点坐标 半轴长 离心率
a、b、c的关 系
x2 y2 1(a b 0) a2 b2
|x|≤ a,|y|≤ b
关于x轴、y轴成轴对称; 关于原点成中心对称
(a,0)、(-a,0)、 (0,b)、(0,-b) (c,0)、(-c,0)
椭圆的简单几何性质导学案

椭圆的简单几何性质导学案(复习课)教学目标:1.深入了解椭圆的范围、对称性、顶点、离心率等简单几何性质。
2.掌握a、b、c几何意义以及a、b、c、e 的相互关系。
3.能利用椭圆的有关知识解释实际问题。
4.贯彻数形结合思想,运用曲线方程研究几何性质。
教学重、难点:重点:椭圆的简单几何性质。
难点:运用椭圆的几何性质解决有关椭圆的综合问题。
椭圆的标准方程及其几何性质:常见题型一:椭圆几何性质的简单应用例1 已知椭圆方程为16x 2+25y 2=400,它的长轴长是: 。
短轴长是:焦距是 。
离心率等于: 。
焦点坐标是: 。
顶点坐标是: 。
例2 求适合下列条件的椭圆的标准方程(1)与椭圆4x 2+9y 2=36有相同的焦点,且离心率为 55 ;(2)长轴长是短轴长的2倍,且过点A (2,0);练习:(1) 在x 轴上的一个焦点与短轴两个端点的连线互相垂直,且焦距为6,求椭圆的标准方程;(2) 椭圆的一个焦点到长轴两端点的距离之比为1:4,短轴长为8,求椭圆的标准方程。
常见题型二:有关椭圆的离心率例3(1)已知椭圆C: 14222=+y a x 的一个焦点(2,0),求椭圆的离心率。
(2)若椭圆的焦距、短轴长、长轴长构成一个等比数列,求椭圆的离心率.练习:1、若椭圆长轴长、短轴长和焦距成等差数列,求该椭圆的离心率.2. (13四川)从椭圆 22221(0)x y a b a b +=>>上一点P向x轴作垂线,垂足恰为左焦点,A 是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且 //AB OP ,O是坐标原点,则该椭圆离心率是( )A.4 B. 12C.2 D.2目标测试:1. 椭圆以坐标轴为对称轴,离心率 e= 32,长轴长为6,则椭圆的方程为( )A. 1203622=+y xB.15922=+y xC.15922=+y x 或15922=+x yD.1203622=+x y 或1203622=+y x2.椭圆 12222=+b y a x 和 k b y a x =+2222 (k>0)具有( )A.相同的长轴B.相同的焦点C.相同的顶点D.相同的离心率思考: 设椭圆22221(0)x y a b a b +=>>的左、右焦点分别为21F F 、,如果椭圆上存在点P ,使︒=∠90PF F 21,求离心率e 的取值范围。
人教版高中数学高二数学《椭圆的几何性质》教案2
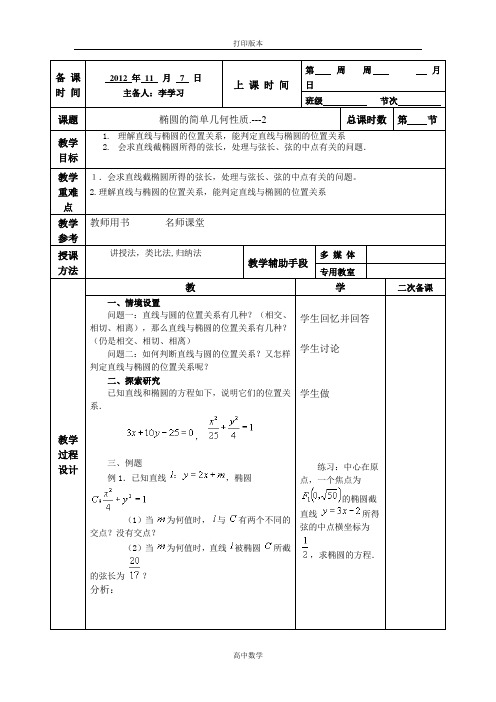
备课时间2012 年11 月7 日主备人:李学习上课时间第周周月日班级节次课题椭圆的简单几何性质.---2 总课时数第节教学目标1.理解直线与椭圆的位置关系,能判定直线与椭圆的位置关系2.会求直线截椭圆所得的弦长,处理与弦长、弦的中点有关的问题.教学重难点1.会求直线截椭圆所得的弦长,处理与弦长、弦的中点有关的问题。
2.理解直线与椭圆的位置关系,能判定直线与椭圆的位置关系教学参考教师用书名师课堂授课方法讲授法,类比法,归纳法教学辅助手段多媒体专用教室教学过程设计教学二次备课一、情境设置问题一:直线与圆的位置关系有几种?(相交、相切、相离),那么直线与椭圆的位置关系有几种?(仍是相交、相切、相离)问题二:如何判断直线与圆的位置关系?又怎样判定直线与椭圆的位置关系呢?二、探索研究已知直线和椭圆的方程如下,说明它们的位置关系.,三、例题例1.已知直线,椭圆(1)当为何值时,与有两个不同的交点?没有交点?(2)当为何值时,直线被椭圆所截的弦长为?分析:学生回忆并回答学生讨论学生做练习:中心在原点,一个焦点为的椭圆截直线所得弦的中点横坐标为,求椭圆的方程.教学过程设计教学二次备课例2 过椭圆内一点引一条弦,使弦被点平分,求这条弦所在直线的方程.解法一:设所求直线的方程为,代入椭圆方程并整理,得.设直线与椭圆的交点为、,则,是上述方程的两根,于是.又为的中点∴.解得.故所求直线的方程为.小结:1、直线与椭圆的位置关系,一般是通过方程组转化为一元二次方程,运用一元二次方程的知识(如求根、判别式、根与系数关系)求得.2、要注意二次曲线与二次方程,二次函数三个二次之间的关系.解法二:设直线与椭圆的交点为、.∵为的中点∴,.又、两点在椭圆上,则,两式相减得课外作业1.求与椭圆相交于、两点,的中点为的直线方程。
2.P66第16题教学小结。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
山西大学附中高二年级(上) 导学设计 编号52 椭圆及其简单几何性质(2)
【学习目标】 1.根据椭圆的方程研究曲线的几何性质;
2.椭圆与直线的关系.
【学习重点】椭圆与直线的关系
【学习难点】椭圆与直线的关系
【学习过程】
一、导学
复习1:椭圆22
11612
x y +=的焦点坐标是( )( );长轴长 、短轴长 ;离心率 . 复习2:直线与圆的位置关系有哪几种?如何判定?
探究:
问题1:想想生活中哪些地方会有椭圆的应用呢?
问题2:椭圆与直线有几种位置关系?又是如何确定?
反思:点与椭圆的位置如何判定?
二、导练
例1 一种电影放映灯泡的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分.过对称轴的截口BAC 是椭圆的一部分,灯丝位于椭圆的一个焦点1F 上,片门
位于另一个焦点2F 上,由椭圆一个焦点1F 发出的光线,经过旋转椭圆面反射后集中到另
一个焦点2F ,已知12BC F F ⊥,1 2.8F B cm =,12 4.5F F cm =,试建立适当的坐标系,求
截口BAC 所在椭圆的方程.
变式:若图形的开口向上,则方程是什么?
小结:①先化为标准方程,找出,a b ,求出c ; ②注意焦点所在
坐标轴.
例2 已知椭圆22
1259
x y +=,直线l :45400x y -+=。
椭圆上是否存在一点,它到直线l 的距离最小?最小距离是多少?
变式:最大距离是多少?
练1已知地球运行的轨道是长半轴长81.5010a km =⨯,离心率0.0192e =的椭圆,且太阳在这个椭圆的一个焦点上,求地球到太阳的最大和最小距离.
练2.经过椭圆2
212
x y +=的左焦点1F 作倾斜角为60的直线l ,直线l 与椭圆相交于,A B 两点,求AB 的长.
三、目标检测
1.设椭圆的两个焦点分别为F 1、、F 2,过F 2作椭圆长轴的垂线交椭圆于点P ,若△F 1PF 2为等腰直角三角形,则椭圆的离心率是( ).
C. 2-1 2.已知椭圆22
1169
x y +=的左、右焦点分别为12,F F ,点P 在椭圆上,若P 、F 1、F 2是一个直角三角形的三个顶点,则点P 到x 轴的距离为( ).
A. 95
B. 3
C. 94 3.椭圆的焦距、短轴长、长轴长组成一个等到比数列,则其离心率为 .
4.椭圆22
14520
x y +=的焦点分别是1F 和2F ,过原点O 作直线与椭圆相交于,A B 两点,若2ABF ∆的面积是20,则直线AB 的方程式是 .
5.求下列直线310250x y +-=与椭圆22
1254
x y +=的交点坐标.
6.若椭圆22149x y +=,一组平行直线的斜率是32
⑴这组直线何时与椭圆相交?
⑵当它们与椭圆相交时,这些直线被椭圆截得的线段的中点是否在一直线上?
课堂小结
1 .椭圆在生活中的运用;
2 .椭圆与直线的位置关系:相交、相切、相离(用∆判定).
直线与椭圆相交,得到弦,弦长12l x -= 其中k 为直线的斜率,1122(,),(,)x y x y 是两交点坐标.。
