双星模型---拉格朗日点
第七章专题“张角”类问题拉格朗日点问题讲义高一下学期物理人教版

张角类问题【试炼感悟】1.如下图,某一飞行器绕火星做匀速圆周运动,轨道半径为r,该飞行器观测火星的张角为β,以下说法正确的选项是〔〕A.绕火星匀速圆周运动的飞行器的轨道半径r越大,其周期越小B.绕火星匀速圆周运动的飞行器的轨道半径r越大,其速度越大C.假设测得该飞行器运动的周期T和张角β,可得到火星的平均密度D.假设测得该飞行器运动的周期T及角速度ω,可得到火星的质量【分析渐悟】【情景】假设物体绕中心天体做匀速圆周运动,过物体做中心天体的两条切线,两切线对着中心天体的夹角称为张角。
【必备学问】锐角三角函数的几何学问、万有引力表达式、向心力表达式、密度公式【关键力量】物体环绕中心天体时万有引力供应向心力的思路【策略】设张角为θ,R为中心天体半径,r为轨道半径,那么sinθ2=Rr1、加速度:G Mmr2=ma,得a=G Mr2=G Msin2θ2R2∝sin2θ22、速度:G Mmr2=m v2r,得v=√GMr=√GM sinθ2R∝√sinθ23、角速度:G Mmr2=mω2r,得ω=√GMr3=√GM sin3θ2R3∝√sin3θ24、周期:G Mmr2=m4π2T2,得T=2π√r3GM=√R3GM sin3θ2∝√1sin3θ25、中心天体质量:G Mmr2=m4π2T2,得M=4π2GT2r3=4π2GT2R3sin3θ26、中心天体密度:ρ=MV=M43πR3=3πGT2(Rr)3=3πGT21sin3θ2注解:很多求中心天体密度的选择题,ABCD四个选项的区分不在于3πGT2,就在Rr不同,关键就在于求出Rr即可,不必求出R、r详细是多少。
“张角〞类问题就是经典的告知该比值的题型,此外,还有通过小孔成像告知该比值的体系。
【练习顿悟】2.如下图,卫星P绕地球做匀速圆周运动,地球对卫星P的张角θ=60°,地球外表的重力加速度为g,地球半径为R,忽视地球自转的影响,以下说法正确的选项是〔〕A .卫星的线速度大小为12√2gRB .卫星的角速度大小为√g2R C .卫星的周期为2π√2Rg D .卫星的加速度大小为g 43.在地球赤道上空有一颗运动方向与地球自转方向相同的卫星A ,对地球赤道掩盖的最大张角α=60°,赤道上有一个卫星监测站B 〔图中末画出〕,近地卫星的周期约1.4h ,那么监测站B 能连续监测到卫星A 的最长时间约为〔 〕提示:A 和B 都在转动,这是圆周运动的追及问题。
2023届高三物理复习重难点突破33双星多星模型 卫星的变轨及能量问题 拉格朗日点(解析版)

专题33 双星多星模型卫星的变轨及能量问题拉格朗日点考点一双星模型双星系统:绕公共圆心转动的两个星体组成的系统,而且两颗星与该中心点总在同一直线上,如图,1.两个星体各自所需的向心力由彼此间的万有引力相互提供,即Gm1m2L2=m1ω21r1,Gm1m2L2=m2ω22r22.两颗星的周期及角速度都相同,即T1=T2,ω1=ω23.两颗星的半径与它们之间的距离关系为:r1+r2=L4.由m1ω21r1=m2ω22r2 得:两颗星到圆心的距离r1、r2与星体质量成反比,即m1m2=r2r15.双星的总质量公式m1+m2=4π2L3T2G推论:L3T2=kM总6.双星的运动周期T=2π)(213mmGL1.(多选)我国天文学家通过“天眼”(FAST,500米口径球面射电望远镜)在武仙座球状星团M13中发现一个脉冲双星系统,如图所示,由恒星A与恒星B组成的双星系统绕其连线上的O点做匀速圆周运动,若恒星A的质量为3m,恒星B的质量为5m,恒星A和恒星B之间的距离为L,引力常量为G。
下列说法正确的是()A.恒星A运行的角速度大于恒星B运行的角速度 B.恒星A与恒星B的线速度之比为5:3C.恒星A到O点的距离为35L D.恒星B的运行周期为π√L32Gm【答案】BD【解析】A.由于双星系统在相等时间内转过的圆心角相同,则双星的角速度一定相等,A错误;C.对恒星A有G5m×3mL2=3mω2rA对恒星B有G3m×5mL2=5mω2rB解得rArB=53又由于rA +rB=L解得rA=58L,rB=38L C错误;B.根据v=ωr解得vAvB=53B正确;D.恒星B的运行周期为T=2πω=π√L32GmD正确。
2.(2022·全国·高三课时练习)(多选)天文学家通过观测两个黑洞并合的事件,间接验证了引力波的存在。
该事件中甲、乙两个黑洞的质量分别为太阳质量的36倍和29倍,假设这两个黑洞绕它们连线上的某点做圆周运动,且两个黑洞的间距缓慢减小。
2023高考物理专题冲刺训练--万有引力、天体运动专题(四)

万有引力与天体运动(四)一、 双星或多星模型1. 冥王星与其附近的另一星体卡戎可视为双星系统,质量比约为7:1,同时绕它们连线上某点O 做匀速圆周运动,由此可知,冥王星绕O 点运动的( )A .轨道半径约为卡戎的71B .角速度大小约为卡戎的71 C .线速度大小约为卡戎的7倍 D .向心力大小约为卡戎的7倍2. 如图所示,两恒星A 、B 构成双星体,在万有引力的作用下绕连线上的O 点做匀速圆周运动,在观测站上观察该双星的运动,测得该双星的运动周期为T ,已知两颗恒星A 、B 间距为d ,引力常量为G ,则可推算出双星的总质量为( )A .π2d 3GT 2B .4π2d 3GT 2C .π2d 2GT 2D .4π2d 2GT 23. (多选)宇宙中,两颗靠得比较近的恒星,只受到彼此之间的万有引力作用互相绕转,称之为双星系统,在浩瀚的银河系中,多数恒星都是双星系统。
设某双星系统中两星A 、B 绕其连线上的O 点做匀速圆周运动,如图所示,若OB AO ,则( )A .星球A 的质量一定大于B 的质量B .星球A 的线速度一定大于B 的线速度C .双星间距离一定,双星的总质量越大,其转动周期越小D .双星的总质量一定,双星间的距离越大,其转动周期越小4. 宇宙中,两颗靠得比较近的恒星,只受到彼此的万有引力作用,分别围绕其连线上的某一点做周期相同的匀速圆周运动,称为双星系统.由恒星A 与恒星B 组成的双星系统绕其连线上的O 点做匀速圆周运动,如图8所示.已知它们的运行周期为T ,恒星A 的质量为M ,恒星B 的质量为3M ,引力常量为G ,则下列判断正确的是( )A .两颗恒星相距3GMT 2π2B .恒星A 与恒星B 的向心力大小之比为3∶1C .恒星A 与恒星B 的线速度大小之比为1∶3D .恒星A 与恒星B 的轨道半径之比为3∶15. 地球刚诞生时自转周期约为8小时,因为受到月球潮汐的影响,地球自转在持续减速,现在地球自转周期是24小时.与此同时,地月间的距离不断增加.若将地球和月球视为一个孤立的双星系统,两者绕其连线上的某一点O 做匀速圆周运动,地球和月球的质量与大小均保持不变,则在地球自转减速的过程中( )A .地球的第一宇宙速度不断减小B .地球赤道处的重力加速度不断增大C .地球、月球匀速圆周运动的周期不断减小D .地球的轨道半径与月球的轨道半径之比不断增大6. (多选)如图为某双星系统A 、B 绕其连线上的O 点做匀速圆周运动的示意图,若A 星的轨道半径大于B 星的轨道半径,双星的总质量为M ,双星间的距离为L ,其运动周期为T ,则( )A .A 的质量一定大于B 的质量 B .A 的线速度一定大于B 的线速度C .L 一定,M 越大,T 越大D .M 一定,L 越大,T 越大7. 双星系统由两颗恒星组成,两恒星在相互引力的作用下,分别围绕其连线上的某一点做周期相同的匀速圆周运动,研究发现,双星系统演化过程中,两星的总质量、距离和周期均可能发生变化,若某双星系统中两星做圆周运动的周期为T ,经过一段时间演化后,两星总质量变为原来的k 倍,两星之间的距离变为原来的n 倍,则此时圆周运动的周期为( )A .T k n ⋅23B .T k n ⋅3C .T k n ⋅2D .T k n ⋅8. 2017年8月28日,中科院南极天文中心的巡天望远镜观测到一个由双中子星构成的孤立双星系统产生的引力波.该双星系统以引力波的形式向外辐射能量,使得圆周运动的周期T 极其缓慢地减小,双中子星的质量m 1与m 2均不变,则下列关于该双星系统变化的说法正确的是( )A .双星间的距离逐渐增大B .双星间的万有引力逐渐增大C .双星的线速度逐渐减小D .双星系统的引力势能逐渐增大9. (多选)2017年,人类第一次直接探测到来自双中子星合并的引力波.根据科学家们复原的过程,在两颗中子星合并前约100 s 时,它们相距约400 km ,绕二者连线上的某点每秒转动12圈.将两颗中子星都看作是质量均匀分布的球体,由这些数据、万有引力常量并利用牛顿力学知识,可以估算出这一时刻两颗中子星( )A .质量之积B .质量之和C .速率之和D .各自的自转角速度10. (多选)在宇宙中,当一颗恒星靠近黑洞时,黑洞和恒星可以相互绕行,从而组成双星系统.在相互绕行的过程中,质量较大的恒星上的物质会逐渐被吸入到质量较小的黑洞中,从而被缓慢吞噬掉,黑洞吞噬恒星的过程也被称为“潮汐瓦解事件”,天鹅座1-X 就是这样一个由黑洞和恒星组成的双星系统,它们共同以两者连线上的某一点为圆心做匀速圆周运动,如图所示,在刚开始吞噬的较短时间内,恒星和黑洞的距离不变,则在这段时间内,下列说法正确的是( )A .它们间的万有引力变大B .它们间的万有引力大小不变C .恒星做圆周运动的线速度变大D .恒星做圆周运动的角速度变大11. 由三个星体构成的系统,叫作三星系统.有这样一种简单的三星系统,质量刚好都相同的三个星体甲、乙、丙在三者相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O 在三角形所在的平面内做相同周期的圆周运动.若三个星体的质量均为m ,三角形的边长为a ,万有引力常量为G ,则下列说法正确的是( )A .三个星体做圆周运动的半径均为aB .三个星体做圆周运动的周期均为2πa a 3GmC .三个星体做圆周运动的线速度大小均为 3Gm aD .三个星体做圆周运动的向心加速度大小均为3Gm a212. (多选)如图,天文观测中观测到有三颗星位于边长为l 的等边三角形三个顶点上,并沿等边三角形的外接圆做周期为T 的匀速圆周运动.已知引力常量为G ,不计其他星体对它们的影响,关于这个三星系统,下列说法正确的是( )A .三颗星的质量可能不相等B .某颗星的质量为4π2l 33GT 2C .它们的线速度大小均为23πl TD .它们两两之间的万有引力大小为16π4l 49GT 413. (多选)太空中存在一些离其他恒星较远的、由质量相等的三颗星组成的三星系统,通常可忽略其他星体对它们的引力作用.已观测到稳定的三星系统存在两种基本的构成形式(如图):一种是三颗星位于同一直线上,两颗星围绕中央星在同一半径为R 的圆轨道上运行;另一种形式是三颗星位于等边三角形的三个顶点上,并沿外接于等边三角形的圆形轨道运行.设这三颗星的质量均为M ,并且两种系统的运动周期相同,则( )A .直线三星系统中甲星和丙星的线速度相同B .直线三星系统的运动周期T =4πR R 5GMC .三角形三星系统中星体间的距离L =3125R D .三角形三星系统的线速度大小为125GM R14.(多选)如图,甲、乙、丙是位于同一直线上的离其他恒星较远的三颗恒星,甲、丙围绕乙在半径为R 的圆轨道上运行,若三颗星质量均为M ,引力常量为G ,则( )A .甲星所受合外力为2245R GMB .乙星所受合外力为22R GMC .甲星和丙星的线速度相同D .甲星和丙星的角速度相同15. (多选)如图为一种四颗星体组成的稳定系统,四颗质量均为m 的星体位于边长为L 的正方形四个顶点,四颗星体在同一平面内围绕同一点做匀速圆周运动,忽略其他星体对它们的作用,引力常量为G .下列说法中正确的是( )A .星体做匀速圆周运动的圆心不一定是正方形的中心B .每个星体做匀速圆周运动的角速度均为(4+2)Gm 2L 3C .若边长L 和星体质量m 均是原来的两倍,星体做匀速圆周运动的加速度大小是原来的两倍D .若边长L 和星体质量m 均是原来的两倍,星体做匀速圆周运动的线速度大小不变二、稳定自转临界问题,拉格朗日点问题,观测问题1. 一近地卫星的运行周期为T 0,地球的自转周期为T ,则地球的平均密度与地球不致因自转而瓦解的最小密度之比为( )A .T 0TB .T T 0C .T 02T 2D .T 2T 022. 2018年2月,我国500 m 口径射电望远镜(天眼)发现毫秒脉冲星“J0318+0253”,其自转周期T =5.19 ms.假设星体为质量均匀分布的球体,已知万有引力常量为6.67×10-11 N·m 2/kg 2.以周期T 稳定自转的星体的密度最小值约为( )A .5×109 kg/m 3B .5×1012 kg/m 3C .5×1015 kg/m 3D .5×1018 kg/m 33. (2020·全国卷)若一均匀球形星体的密度为ρ,引力常量为G ,则在该星体表面附近沿圆轨道绕其运动的卫星的周期是( )A .3πGρB .4πGρC .13πGρD .14πGρ4. (多选)2011年8月,“嫦娥二号”成功进入了环绕“日地拉格朗日点”的轨道,我国成为世界上第三个造访该点的国家,如图所示,该拉格朗日点位于太阳和地球连线的延长线上,一飞行器处于该点,在几乎不消耗燃料的情况下与地球同步绕太阳做圆周运动,则此飞行器的( )A .线速度大于地球的线速度B .向心加速度大于地球的向心加速度C .向心力仅由太阳的引力提供D .向心力仅由地球的引力提供5. 2018年5月21日,我国发射世界首颗月球中继卫星“鹊桥”,6月14日进入地月拉格朗日2L 点的环绕轨道,为在月球背面着陆的嫦娥四号与地球站之间提供通信链路.如图所示,“鹊桥”中继星处于2L 点上时,会和月、地两天体保持相对静止的状态.设地球的质量为月球的k 倍,地月间距为L ,拉格朗日2L 点与月球间距为d ,地球、月球和“鹊桥”均视为质点,忽略太阳对“鹊桥”中继星的引力.则“鹊桥”中继星处于2L 点上时,下列选项正确的是( )A .“鹊桥”与月球的线速度之比为鹊v :=月v L :d L +B .“鹊桥”与月球的向心加速度之比为鹊a :=月a L :d L +C .k 、L 、d 之间的关系为3221)(1L d L kd d L +=++D .k 、L 、d 之间的关系为3221)(1L d L d d L k +=++6. 某颗行星的同步卫星正下方的行星表面上有一观察者,他用天文望远镜观察被太阳光照射的此卫星,发现日落的T 21时间内有T 61的时间看不见此卫星.(已知该行星的自转周期为T ,该行星的半径为R ,不考虑大气对光的折射)则该同步卫星距该星球的高度是( )A .RB .R 2C .R 6.5D .R 6.67. 我国的“天链一号”卫星是地球同步轨道卫星,可为载人航天器及中低轨道卫星提供数据通信.如图为“天链一号”卫星a 、赤道平面内的低轨道卫星b 和地球的位置关系示意图,O 为地心,卫星a 、b 相对地球的张角分别为1θ和2θ,(2θ图中未标出),卫星a 的轨道半径是b 的4倍.已知卫星a 、b 绕地球同向运行,卫星a 的周期为T ,在运行过程中由于地球的遮挡,卫星b 会进入与卫星a 通信的盲区.卫星间的通信信号视为沿直线传播,信号传输时 间可忽略,下列分析正确的是( )A .张角1θ和2θ满足12sin 4sin θθ=B .卫星b 的周期为4TC .卫星b 每次在盲区运行的时间为πθθ14)(21T+D .卫星b 每次在盲区运行的时间为πθθ16)(21T +8. 某颗地球同步卫星正下方的地球表面上有一观察者,他用天文望远镜观察被太阳光照射的此卫星,春分那天(太阳光直射赤道)在日落12小时内,有1t 时间该观察者看不见此卫星.已知地球半径为R ,地球表面处的重力加速度为g ,地球自转周期为T ,卫星的运动方向与地球转动方向相同,不考虑大气对光的折射.下列说法正确的是( ).A .同步卫星离地高度为32224πT gR B .同步卫星的加速度小于赤道上物体的向心加速度 C .322214arcsinππTgR R Tt = D .同步卫星的加速度大于近地卫星的加速度答案一、1.A2.B3.BC4.A5.B6.BD7.B8.B9.BC 10.AC 11.B 12.BD 13.BC 14.AD 15.BD二、1.D2.C3.A4.AB5.C6.A7.C8.C。
宇宙航行(多星问题及拉格朗日点)导学案 高一下学期物理人教版(2019)必修第二册
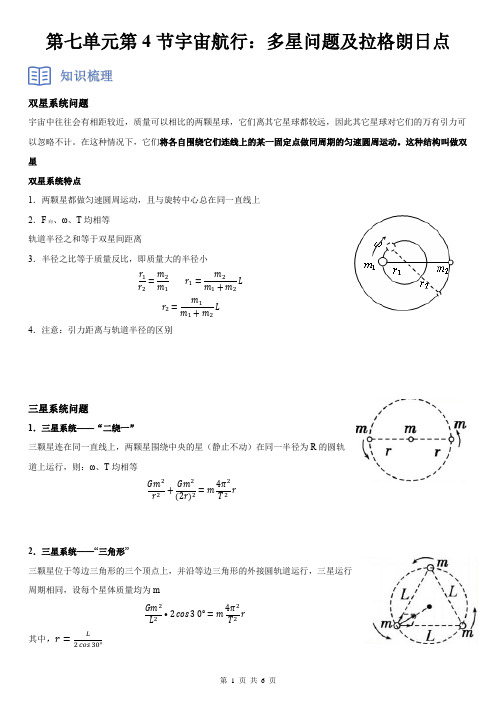
第七单元第4节宇宙航行:多星问题及拉格朗日点双星系统问题宇宙中往往会有相距较近,质量可以相比的两颗星球,它们离其它星球都较远,因此其它星球对它们的万有引力可以忽略不计。
在这种情况下,它们将各自围绕它们连线上的某一固定点做同周期的匀速圆周运动。
这种结构叫做双星双星系统特点1.两颗星都做匀速圆周运动,且与旋转中心总在同一直线上2.F向、ω、T均相等轨道半径之和等于双星间距离3.半径之比等于质量反比,即质量大的半径小r1 r2=m2m1r1=m2m1+m2L r2=m1m1+m2L4.注意:引力距离与轨道半径的区别三星系统问题1.三星系统——“二绕一”三颗星连在同一直线上,两颗星围绕中央的星(静止不动)在同一半径为R的圆轨道上运行,则:ω、T均相等Gm2 r2+Gm2(2r)2=m4π2T2r2.三星系统——“三角形”三颗星位于等边三角形的三个顶点上,并沿等边三角形的外接圆轨道运行,三星运行周期相同,设每个星体质量均为mGm2 L2•2cos30°=m4π2T2r其中,r=L2cos30°题型五:四星系统问题1.正方形:一种是四颗星稳定地分布在边长为a 的正方形的四个顶点上,均围绕正方形对角线的交点做匀速圆周运动2.三角形:有三颗星位于边长为a 的等边三角形的三个项点上,并沿外接于等边三角形的圆形轨道运行,而第四颗星刚好位于三角形的中心不动题型六:拉格朗日点一个小物体在两个大物体的引力作用下在空间中的一点,在该点处,小物体相对于两大物体基本保持静止【例1】两个星球组成双星,它们在相互之间的万有引力作用下,绕连线上某点做周期相同的匀速圆周运动。
现测得两星中心距离为R ,其运动周期为T ,求两星的总质量。
【例2】我们的银河系的恒星中大约四分之一是双星。
某双星由质量不等的星体S 1和S 2构成,两星在相互作用的万有引力作用下绕二者连线上某一定点C 做匀速圆周运动。
由天文观察测得其运动周期为T ,S 1到C 点的距离为r 1,S 1和S 2的距离为r ,已知引力常量为G ,由此可求出S 2的质量为( )A .4π2r 2(r−r 1)GT 2B .4π2r 13GT 2C .4π2r 3GT 2D .4π2r 2r 1GT 2【例3】神奇的黑洞是近代引力理论所预言的一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系麦哲伦云时,发现了LMCX3双星系统,它由可见星A和不可见的暗星B构成.两星视为质点,不考虑其他天体的影响,A、B围绕两者的连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图所示.引力常量为G,由观测能够得到可见星A的速率v和运行周期T.(1)可见星A所受暗星B的引力F A可等效为位于O点处质量为m′的星体(视为质点)对它的引力,设A和B的质量分别为m1、m2,试求m′(用m1、m2表示);(2)求暗星B的质量m2与可见星A的速率v、运行周期T和质量m1之间的关系式.【例4】如图所示,科学家设想在拉格朗日点L建立空间站,使其与月球同周期绕地球运动,拉格朗日点L位于地球和月球连线上,处在该点的空间站在地球和月亮引力的共同作用下,可与月球一起以相同的周期绕地球运动.以v1、ω1、a1分别表示近地卫星的线速度、角速度、向心加速度的大小,以v2、ω2,a2分别表示该空间站的线速度、角速度、向心加速度的大小,以v3、ω3、a3分别表示月亮的线速度、角速度、向心加速度的大小.则正确的是()A.v1>v3>v2B.ω1>ω2=ω3C.a1>a2>a3D.a1>a3>a21.2017年10月16日晚,全球天文学界联合发布一项重大发现:人类首次直接探测到了双中子星并合产生的引力波及其伴随的电磁信号。
(完整版)双星三星四星问题

双星模型、三星模型、四星模型一、双星问题1.模型构建:在天体运动中,将两颗彼此相距较近,且在相互之间万有引力作用下绕两者连线上的某点做角速度、周期相同的匀速圆周运动的恒星称为双星。
2.模型条件: (1)两颗星彼此相距较近。
(2)两颗星靠相互之间的万有引力提供向心力做匀速圆周运动。
(3)两颗星绕同一圆心做圆周运动。
3.模型特点: (1)“向心力等大反向”——两颗星做匀速圆周运动的向心力由它们之间的万有引力提供。
(2)“周期、角速度相同”——两颗恒星做匀速圆周运动的周期、角速度相等。
(3)三个反比关系:m1r1=m2r2;m1v1=m2v2;m1a1=m2a2推导:根据两球的向心力大小相等可得,m1ω2r1=m2ω2r2,即m1r1=m2r2;等式m1r1=m2r2两边同乘以角速度ω,得m1r1ω=m2r2ω,即m1v1=m2v2;由m1ω2r1=m2ω2r2直接可得,m1a1=m2a2。
(4)巧妙求质量和:Gm1m2L2=m1ω2r1①Gm1m2L2=m2ω2r2②由①+②得:G m1+m2L2=ω2L ∴m1+m2=ω2L3G4. 解答双星问题应注意“两等”“两不等”(1)“两等”: ①它们的角速度相等。
②双星做匀速圆周运动向心力由它们之间的万有引力提供,即它们受到的向心力大小总是相等。
(2)“两不等”:①双星做匀速圆周运动的圆心是它们连线上的一点,所以双星做匀速圆周运动的半径与双星间的距离是不相等的,它们的轨道半径之和才等于它们间的距离。
②由m1ω2r1=m2ω2r2知由于m1与m2一般不相等,故r1与r2一般也不相等。
二、多星模型(1)定义:所研究星体的万有引力的合力提供做圆周运动的向心力,除中央星体外,各星体的角速度或周期相同.(2)三星模型:①三颗星位于同一直线上,两颗环绕星围绕中央星在同一半径为R的圆形轨道上运行(如图甲所示).②三颗质量均为m的星体位于等边三角形的三个顶点上(如图乙所示).(3)四星模型:①其中一种是四颗质量相等的恒星位于正方形的四个顶点上,沿着外接于正方形的圆形轨道做匀速圆周运动(如图丙).②另一种是三颗恒星始终位于正三角形的三个顶点上,另一颗位于中心O,外围三颗星绕O做匀速圆周运动(如图丁所示).三、卫星的追及相遇问题1、某星体的两颗卫星从相距最近到再次相距最近遵从的规律:内轨道卫星所转过的圆心角与外轨道卫星所转过的圆心角之差为2π的整数倍。
2024届高考物理一轮复习:天体运动热点问题

第四章曲线运动天体运动热点问题【考点预测】1.卫星的变轨问题2. 星球稳定自转的临界问题3. 双星、多星模型4. 天体的“追及”问题5.万有引力定律与几何知识的结合【方法技巧与总结】卫星的变轨和对接问题1.变轨原理(1)为了节省能量,在赤道上顺着地球自转方向发射卫星到圆轨道Ⅰ上,如图所示.(2)在A点(近地点)点火加速,由于速度变大,万有引力不足以提供卫星在轨道Ⅰ上做圆周运动的向心力,卫星做离心运动进入椭圆轨道Ⅱ.(3)在B点(远地点)再次点火加速进入圆形轨道Ⅲ.2.变轨过程分析(1)速度:设卫星在圆轨道Ⅰ和Ⅲ上运行时的速率分别为v1、v3,在轨道Ⅱ上过A点和B 点时速率分别为v A、v B.在A点加速,则v A>v1,在B点加速,则v3>v B,又因v1>v3,故有v A>v1>v3>v B.(2)加速度:因为在A点,卫星只受到万有引力作用,故不论从轨道Ⅰ还是轨道Ⅱ上经过A点,卫星的加速度都相同,同理,卫星在轨道Ⅱ或轨道Ⅲ上经过B点的加速度也相同.(3)周期:设卫星在Ⅰ、Ⅱ、Ⅲ轨道上的运行周期分别为T1、T2、T3,轨道半径分别为r1、r2(半长轴)、r3,由开普勒第三定律r3T2=k可知T1<T2<T3.(4)机械能:在一个确定的圆(椭圆)轨道上机械能守恒.若卫星在Ⅰ、Ⅱ、Ⅲ轨道的机械能分别为E1、E2、E3,从轨道Ⅰ到轨道Ⅱ,从轨道Ⅱ到轨道Ⅲ,都需要点火加速,则E1<E2<E3. 【题型归纳目录】题型一:卫星的变轨问题题型二:星球稳定自转的临界问题题型三:双星模型题型四:天体的“追及”问题【题型一】卫星的变轨问题【典型例题】例1.(2023·安徽·校联考模拟预测)《天问》是中国战国时期诗人屈原创作的一首长诗,全诗问天问地问自然,表现了作者对传统的质疑和对真理的探索精神,我国探测飞船天问一号发射成功飞向火星,屈原的“天问”梦想成为现实,也标志着我国深空探测迈向一个新台阶,如图所示,轨道1是圆轨道,轨道2是椭圆轨道,轨道3是近火圆轨道,天问一号经过变轨成功进入近火圆轨道3,已知引力常量G,以下选项中正确的是()A.天问一号在B点需要点火加速才能从轨道2进入轨道3B.天问一号在轨道2上经过B点时的加速度大于在轨道3上经过B点时的加速度C.天问一号进入近火轨道3后,测出其近火环绕周期T,可计算出火星的平均密度D.天问一号进入近火轨道3后,测出其近火环绕周期T,可计算出火星的质量【方法技巧与总结】卫星的变轨问题卫星变轨的实质卫星速度突然增大卫星速度突然减小练1.(2023·广东·广州市第二中学校联考三模)天问一号火星探测器搭乘长征五号遥四运载火箭成功发射意味着中国航天开启了走向深空的新旅程。
高中物理教研论文双星模型、三星模型、四星模型

双星模型、三星模型、四星模型天体物理中的双星,三星,四星,多星系统是自然的天文现象,天体之间的相互作用遵循万有引力的规律,他们的运动规律也同样遵循开普勒行星运动的三条基本规律。
双星、三星系统的等效质量的计算,运行周期的计算等都是以万有引力提供向心力为出发点的。
双星系统的引力作用遵循牛顿第三定律:F F =',作用力的方向在双星间的连线上,角速度相等,ωωω==21。
【例题1】天文学家将相距较近、仅在彼此的引力作用下运行的两颗恒星称为双星。
双星系统在银河系中很普遍。
利用双星系统中两颗恒星的运动特征可推算出它们的总质量。
已知某双星系统中两颗恒星围绕它们连线上的某一固定点分别做匀速圆周运动,周期均为T ,两颗恒星之间的距离为r ,试推算这个双星系统的总质量。
(引力常量为G ) 【解析】:设两颗恒星的质量分别为m 1、m 2,做圆周运动的半径分别为r 1、r 2,角速度分别为ω1、ω2。
根据题意有21ωω=①rr r =+21②根据万有引力定律和牛顿定律,有G 1211221rw m rm m = ③G 1221221rw m r m m =④联立以上各式解得2121m m r m r +=⑤根据解速度与周期的关系知Tπωω221==⑥联立③⑤⑥式解得322214rGT m m π=+【例题2】神奇的黑洞是近代引力理论所预言的一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系大麦哲伦云时,发现了LMCX3双星系统,它由可见星A 和不可见的暗星B 构成,两星视为质点,不考虑其他天体的影响.A 、B 围绕两者连线上的O 点做匀速圆周运动,它们之间的距离保持不变,如图4-2所示.引力常量为G ,由观测能够得到可见星A 的速率v 和运行周期T.(1)可见星A 所受暗星B 的引力F a 可等效为位于O 点处质量为m′的星体(视为质点)对它的引力,设A 和B 的质量分别为m 1、m 2,试求m′(用m 1、m 2表示).(2)求暗星B 的质量m 2与可见星A 的速率v 、运行周期T 和质量m 1之间的关系式;(3)恒星演化到末期,如果其质量大于太阳质量m s 的2倍,它将有可能成为黑洞.若可见星A的速率v=2.7×105 m/s ,运行周期T=4.7π×104 s ,质量m 1=6m s ,试通过估算来判断暗星B 有可能是黑洞吗?(G=6.67×10-11 N·m 2/kg 2,m s =2.0×1030 kg )解析:设A 、B 的圆轨道半径分别为,由题意知,A 、B 做匀速圆周运动的角速度相同,设其为。
专题31 双星多星问题、张角问题、拉格朗日点和黑洞潮汐现象(解析版)

2023届高三物理一轮复习重点热点难点专题特训专题31 双星多星问题、张角问题、拉格朗日点和黑洞潮汐现象特训目标 特训内容目标1 双星多星问题(1T —4T ) 目标2 张角问题(5T —8T ) 目标3 拉格朗日点(9T —12T ) 目标4黑洞潮汐现象(13T —16T )一、双星多星问题1.宇宙中有很多恒星组成的双星运动系统,两颗恒星仅在彼此的万有引力作用下,绕共同点做匀速圆周运动,如图所示。
假设该双星1、2的质量分别为1m 、2m ,圆周运动的半径分别为1r 、2r ,且1r 小于2r ,共同圆周运动的周期为T ;引力常量为G 。
则下列说法正确的是( )A .恒星1做圆周运动的向心加速度为221m Gr B .恒星1表面的重力加速度一定大于恒星2表面的重力加速度 C .恒星1的动量一定大于恒星2的动量D .某些双星运动晚期,两者间距逐渐减小,一者不断吸食另一者的物质,则它们在未合并前,共同圆周运动的周期不断减小【答案】D【详解】A .对于恒星1m ,其圆周运动方程为()1211212=+n Gm m m a r r 则恒星1m 的向心加速度()21212=+n Gm a r r故A 错误; B .由2GMm mg R =解得2GMg R=由于不能确定两恒星半径R 的大小,故不能确定表面重力加速度的大小,故B 错误;C .对于双星运动有1122m r m r =又因为角速度相同,根据角速度与线速度关系有1122m r m r ωω=即1122m v m v =即动量大小相等,故C 错误;D .设两星球之间距离为L ,对星球1m ,有2121122⎛⎫= ⎪⎝⎭Gm m m r L T π对星球2m ,有2122222⎛⎫= ⎪⎝⎭Gm m m r L T π 上述两式相加得2221122222⎛⎫⎛⎫+=+ ⎪ ⎪⎝⎭⎝⎭Gm Gm r r L L T T ππ解得()3122L T G m m =+可以看到当两者间距逐渐减小,总质量不变时,双星运动的共同周期逐渐减小,故D 正确。
