背包问题课件
图解01背包问题
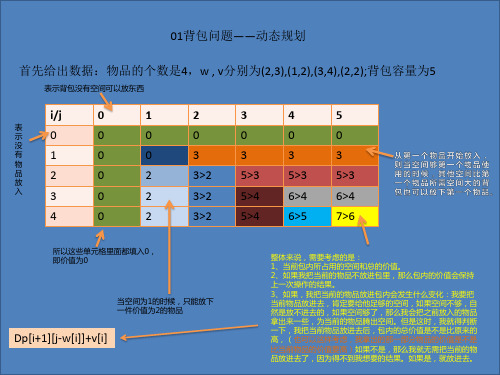
表示背包没有空间可以放东西
i/j
表 示 没 有 物 品 放 入
0 0 0 0 0 0
1 0 0 2 2 2
2 0 3 3>2 3>2 3>2
3 0 3 5>3 5>4 5>4
//该方法是使用的记忆搜索的方法,请自行简化。 Int rec( int I , int j){ int res; if(i==n){ res=0; //表明物品已经放完了。 }else if(j<w[i]){ res=rec(i+1,j);//此时包内的空间不够放下第I个物品。 }else{ res=max(rec(i+1,j),rec(i+1,j-w[i])+v[i]); // 进行比较,如果放入物品的价值比原来已经放入物品的总价 值高,则替换原来的 } dp[i][j]=res; return dp[i][j]; }
#include<iostream> using namespace std; #include<iostream> using namespace std; int n,W; int w[10],v[10]; int dp[10][10]; int max(int x,int y){ if(x>y)return x; else return y; } void slove(){ cout<<rec(0,W); } int main(){ cout<<"please enter n and W:"; cin>>n>>W; for(int i=0;i<n;i++){ cin>>w[i]>>v[i]; } slove(); return 0; }
背包九讲完整版

背包问题九讲 v1.0目录第一讲 01背包问题第二讲完全背包问题第三讲多重背包问题第四讲混合三种背包问题第五讲二维费用的背包问题第六讲分组的背包问题第七讲有依赖的背包问题第八讲泛化物品第九讲背包问题问法的变化附:USACO中的背包问题前言本篇文章是我(dd_engi)正在进行中的一个雄心勃勃的写作计划的一部分,这个计划的内容是写作一份较为完善的NOIP难度的动态规划总结,名为《解动态规划题的基本思考方式》。
现在你看到的是这个写作计划最先发布的一部分。
背包问题是一个经典的动态规划模型。
它既简单形象容易理解,又在某种程度上能够揭示动态规划的本质,故不少教材都把它作为动态规划部分的第一道例题,我也将它放在我的写作计划的第一部分。
读本文最重要的是思考。
因为我的语言和写作方式向来不以易于理解为长,思路也偶有跳跃的地方,后面更有需要大量思考才能理解的比较抽象的内容。
更重要的是:不大量思考,绝对不可能学好动态规划这一信息学奥赛中最精致的部分。
你现在看到的是本文的1.0正式版。
我会长期维护这份文本,把大家的意见和建议融入其中,也会不断加入我在OI学习以及将来可能的ACM-ICPC的征程中得到的新的心得。
但目前本文还没有一个固定的发布页面,想了解本文是否有更新版本发布,可以在OIBH论坛中以“背包问题九讲”为关键字搜索贴子,每次比较重大的版本更新都会在这里发贴公布。
目录第一讲 01背包问题这是最基本的背包问题,每个物品最多只能放一次。
第二讲完全背包问题第二个基本的背包问题模型,每种物品可以放无限多次。
第三讲多重背包问题每种物品有一个固定的次数上限。
第四讲混合三种背包问题将前面三种简单的问题叠加成较复杂的问题。
第五讲二维费用的背包问题一个简单的常见扩展。
第六讲分组的背包问题一种题目类型,也是一个有用的模型。
后两节的基础。
第七讲有依赖的背包问题另一种给物品的选取加上限制的方法。
第八讲泛化物品我自己关于背包问题的思考成果,有一点抽象。
数学建模-第七章背包问题.

ps 1 . 重量超出 ws C , 而此时价值密度值最小的是 w s 1
U 1 是此情形的上界 .
0 1 U max U , U 从而 是 z ( KP) 的上界 . 2
§2
ps Up jU 要证 ,只需 U C 1 0 1 ws 2、 U U1 是显然的; j 1 and 证 U0 U U U1 s 1 1 ps s 1 zopt (C ( KP)) 0 p j C ps 1 C(KP) 的最优解值 U p j w j 1 sC s p j 1 ws 1 p (w C ) s (*)
缺点:需要更多的分支运算 .
第七章 背包问题
考虑 KP 的松弛问题 :?
x j 0,1 x j 0,1
max
z pj xj
j 1
n
C((KP KP)) s.t.
w x
j 1 j
n
C(KP)如何求解?
j
C
第一个放不下的
0 x j 0,1 1 x j N 1,2,, n j
算法吗?
若
w x
j
j
,
则
xk 1 ,
否则 xk 0 ; step 3 若 k n , 则结束;
s 1
表示不超过 的最大整数.
Go on
第七章 背包问题
Theorem 2.1 的证明 Proof :
*
Go back
( p j 0)
要证 x* x
显然 C(KP) 的最优解必满足
w x
j 1 j
n
j
C
* x 设 是其最优解, 若存在 k s 使 xk 1
实验二,背包问题课件

在背包容量为J时
Y
第i个物品能否放入
N
根据放入后是否有 利决定是否放入
不放入,背包 价值不变
J++ N
J= =C
Y I--
2019/10/9
I= =1
N
4
Y
第一个物
品
Y
能否放入
N
根据放入后是否有 利决定是否放入
不放入,背包 价值不变
输出(j,m(I,j))矩阵
Y X[I]=0,不装入
for(int d=0;d<c;d++)
m[0][d]=0;
cout<<"输出(j,m(i,j))的矩阵:"<<endl;
for(int a=0;a<=n;a++)
{ for(int b=0;b<=c;b++)
cout<<m[a][b]<<" ";
cout<<endl; }
cout<<endl;
}2019/10/9
实验二
0/1背包问题
2019/10/9
1
程序流程图:
J--背包的现有容量 C--背包的最大容量 V(i)—物品的价值(I=1,2,3,4,5) M—背包的价值
2019/10/9
2
在背包容量为J时
Y
第n个物品能否放入
N
背包价值为V(n)
背包价值为0
J++ N
J= =C
Y
2019/10/9
9
void traceback()
{
cout<<“输出表示装入情况的数组(1表示装入,0表示不
动态规划-0-1背包ppt课件

22
矩阵连乘 ➢ 问题:设有给定n个矩阵{A1,A2,...,An},其中Ai与Ai+1是可乘的,i=1,2,...,n-1。考察这n个矩
阵的连乘积A1A2...An。 ➢ 假设给定两个矩阵A1,A2, 它们的维数分别是m*n,n*p,则计算A1A2的标准算法怎样设计?
63
01 5
00006666611
54
01 4
4 500006666611 6
0 0 14
00006666666
构造最优解
➢ 结果示例:
w
2
2
6
5 4
m( i , j) 1, 10,15 m(i+1, j)
m( i , j) x1=1
2, 8, 9
m(i+1 , j)
0 1 2 3 4 5 6 7 8 9 10 j
0 1 2 3 4 5 6 7 8 9 10 j
v
价值是6=m(4+1,5),
21
6
22
3
63
5
5 4000066
4
4 500006666666 6
当w4放入时,则要配合其前边的最优值,即w4的放入,使剩余物品(4+1..n)的最大容量变为jw4,此时背包中的最大容量为m(4+1,j-w4)的值0加上v4的值4,然后比较w4放入与否的总价 值,因此m(4,5)选择w4不放入背包,最优值是依然是6。
5
最优值过程分析
➢ 然后,我们在对物品5处理后的基础上,对物品4进行分析。此时我们的任务是要确定 m(4,0..10)11个元素的值。用同样的方法,对物品4的处理有两种情况:w4大于j和w4小 于j。
第六讲 动态规划背包问题

1<=i<=N, 0<=j<=M 时间复杂度O(NM) 时间复杂度
9
多层背包问题
件物品; 有N件物品 件物品 件物品Wi公斤 第i件物品 公斤 件物品 公斤; 件物品价值Ci元 第i件物品价值 元; 件物品价值 现有一辆载重M公斤的卡车 公斤的卡车; 现有一辆载重 公斤的卡车 件物品限制最多只能取Xi个 第i件物品限制最多只能取 个; 件物品限制最多只能取 问选取装载哪些物品, 问选取装载哪些物品,使得卡车运送的总价值最 大?
背包类动态规划问题
1
经典的背包问题( 背包 背包) 经典的背包问题(01背包)
件物品; 有N件物品 件物品 件物品Wi公斤 第i件物品 公斤 件物品 公斤; 件物品价值Ci元 第i件物品价值 元; 件物品价值 现有一辆载重M公斤的卡车 公斤的卡车; 现有一辆载重 公斤的卡车 问选取装载哪些物品,使得卡车运送的总价值 问选取装载哪些物品, 最大? 最大?
8
动态规划
表示前i件物品背包为 的最优解, 设F(i,j)表示前 件物品背包为 的最优解,则有, 表示前 件物品背包为j的最优解 则有,
F ( i − 1, j ), 不选第 i 件物品 F ( i − 1, j − w [ i ]) + c [ i ],只选主件 F ( i − 1, j − w [ i ] - w [ i1]) + c [ i ] + c [ i1], // 选主件和第 1件附件 F ( i , j ) = Max F ( i − 1, j − w [ i ] - w [ i 2 ]) + c [ i ] + c [ i 2 ], // 选主件和第 2 件附件 F ( i − 1, j − w [ i ] - w [ i1] - w [ i 2 ]) + c [ i ] + c [ i1] + c [ i 2 ], // 选主件和 2 件附件
(完整版)01背包问题

01背包问题,是用来介绍动态规划算法最经典的例子,网上关于01背包问题的讲解也很多,我写这篇文章力争做到用最简单的方式,最少的公式把01背包问题讲解透彻。
01背包的状态转换方程f[i,j] = Max{ f[i-1,j-Wi]+Pi( j >= Wi ), f[i-1,j] }只要你能通过找规律手工填写出上面这张表就算理解了01背包的动态规划算法。
首先要明确这张表是至底向上,从左到右生成的。
为了叙述方便,用e2单元格表示e行2列的单元格,这个单元格的意义是用来表示只有物品e时,有个承重为2的背包,那么这个背包的最大价值是0,因为e物品的重量是4,背包装不了。
对于d2单元格,表示只有物品e,d时,承重为2的背包,所能装入的最大价值,仍然是0,因为物品e,d都不是这个背包能装的。
同理,c2=0,b2=3,a2=6。
对于承重为8的背包,a8=15,是怎么得出的呢?根据01背包的状态转换方程,需要考察两个值,一个是f[i-1,j],对于这个例子来说就是b8的值9,另一个是f[i-1,j-Wi]+Pi;在这里,f[i-1,j]表示我有一个承重为8的背包,当只有物品b,c,d,e四件可选时,这个背包能装入的最大价值f[i-1,j-Wi]表示我有一个承重为6的背包(等于当前背包承重减去物品a的重量),当只有物品b,c,d,e四件可选时,这个背包能装入的最大价值f[i-1,j-Wi]就是指单元格b6,值为9,Pi指的是a物品的价值,即6由于f[i-1,j-Wi]+Pi = 9 + 6 = 15 大于f[i-1,j] = 9,所以物品a应该放入承重为8的背包以下是actionscript3 的代码public function get01PackageAnswer(bagItems:Array,bagSize:int):Array{var bagMatrix:Array=[];var i:int;var item:PackageItem;for(i=0;i<bagItems.length;i++){bagMatrix[i] = [0];}for(i=1;i<=bagSize;i++){for(varj:int=0;j<bagItems.length;j++){item = bagItems[j] as PackageItem;if(item.weight > i){//i背包转不下itemif(j==0){bagMatrix[j][i] = 0;}else{bagMatrix[j][i]=bagMatrix[j-1][i];}}else{//将item装入背包后的价值总和var itemInBag:int;if(j==0){bagMatrix[j][i] = item.value;continue;}else{itemInBag = bagMatrix[j-1][i-item.weight]+item.value;}bagMatrix[j][i] = (bagMatrix[j-1][i] > itemInBag ? bagMatrix[j-1][i] : itemInBag)}}}//find answervar answers:Array=[];var curSize:int = bagSize;for(i=bagItems.length-1;i>=0;i--){item = bagItems[i] as PackageItem;if(curSize==0){break;}if(i==0 && curSize > 0){answers.push();break;}if(bagMatrix[i][curSize]-bagMatrix[i-1][curSize-item.weight ]==item.value){answers.push();curSize -= item.weight;}}return answers;}PackageItem类public class PackageItem{public var name:String;public var weight:int;public var value:int;public function PackageItem(name:String,weight:int,value:int){ = name;this.weight = weight;this.value = value;}}测试代码varnameArr:Array=['a','b','c','d','e'];var weightArr:Array=[2,2,6,5,4];var valueArr:Array=[6,3,5,4,6];var bagItems:Array=[];for(vari:int=0;i<nameArr.length;i++){var bagItem:PackageItem = new PackageItem(nameArr[i],weightArr[i],valueArr[i]);bagItems[i]=bagItem;}var arr:Array = ac.get01PackageAnswer(bagItems,10);。
背包问题的贪心算法20页PPT文档

则用j比i好,∵装入A, V i 2 ;而装入B,Vi=3
对例。4.3的数据使用按效益值的非增次序的选择策略.
V 125,X 11 ,W 118 背包剩:C-18=2;物品2有次大效益值
(V2=24 )但w2=15,背包装不下物品2。使用 x2=2/15,刚好装满背
包
6
,且物品2的24/15 = v2/w2 较物品3的15/10= v3/w3效益值高。按 此选择策略,得②即(1, 2/15, 0),∑vixi=28.2 .此解是一个次优解。 显然,按物品效益值的非增次序装包不能得最优解。
背包问题:
与0-1背包问题类似,所不同的是在选择物品i装入背包时 ,可以选择物品i的一部分,而不一定要全部装入背包, 1≤i≤n。
这2类问题都具有最优子结构性质,极为相似,但背 包问题可以用贪心算法求解,而0-1背包问题却不能用 贪心算法求解。
2
例4.3 贪心算法不能求得0-1背包问题得最优解。
考虑背包问题: n=3,c=50kg,(v1,v2,v3)=(60,100,120), (w1,w2,w3)=(10,20,30). vi/wi=(6,5,4).贪心算法解是(1,1,0), ∑vixi=60+100 , ∑wixi=30;最优解是(0,1,1), ∑vixi=100+120, ∑wixi=50,
实际上,动态规划算法的确可以有效地解0-1背包问题。
3
4.2 背包问题
已知有n种物品和一个可容纳c重量的背包,每种物品i的
重量为wi。假定物品i的一部分放入背包会得到vixi的效益。其
中0≤xi≤1,vi>0 . 采用怎样的装包方法才会使装入背包物品的总
效益最大呢?即求解 n
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
刷表法——手推
【样例输入】package.in
10 4
21
for(int i=1;i<=n;++i)
Hale Waihona Puke 33for(int v=m;v>=w[i];--v)
45
f[v]=max(f[v],f[v-w[i]]+c[i])
79
【样例输出】package.out
12
i
W[i]
C[i]
i=0
0
0
i=1
2
1
i=2
理一件物品,作为一个阶段,共有n个 阶段 2、定义状态:
定义f[i][v]是前i件物品恰好放 入一个容量为v的背包,所得到的最大 价值 3、状态转移方程: 若第i件物品没有放入背包,则f[i][v]=f[i-
1][v] 若第i件物品放入背包,则f[i][v]=f[i-1][v-
w[i]]+c[i] 根据状态定义,f[i][v]=max(f[i-1][v],f[i-
【输出格式】 仅一行,一个数,表示最大总价值。
【样例输入】package.in 10 4 21 33 45 79
【样例输出】package.out 12
01背包
【问题描述】 一个旅行者有一个最多能用m公斤的
背包,现在有n件物品,它们的重量分别是 W1,W2,...,Wn,它们的价值分别为 C1,C2,...,Cn.若每种物品只有一件求旅行者 能获得最大总价值。 【输入格式】
1][v-w[i]]+c[i]) 4、临界值: 当i==0时,表示一件物品也没有, f[0][v]=0,数组f在main函数前定义即可
刷表法——手推
【样例输入】package.in 10 4
i
21
i=0
33
i=1
45 79
i=2
【样例输出】package.out
i=3
12
i=4
W[i]
C[i]
0
0
将01背包问题的基本思路加以改进,得到了这样一个清晰的方法。这说明01背包问 题的方程的确是很重要,可以推及其它类型的背包问题。
在f[i][v]=max{f[i-1][v-k*w[i]]+k*c[i]|0<=k*w[i]<= v}中,k的个数不确定,我们可以将其改 进:。
2
1
3
3
4
5
7
9
V=0 V=1 V=2 V=3 V=4 V=5 V=6 V=7 V=8 V=9 V=10
i=0 0 0 0 0 0 0 0 0 0 0 0
i=1 0 i=2 i=3 i=4
0
11
0 13
0 13
01 3
1 1 1 1 11 1 4 4 4 4 44 4 5 5688 9 9 5 5 6 9 9 10 12
这个方程非常重要,基本上所有跟背包相关的问题的方程都是由它衍生出来 的。所以有必要将它详细解释一下:“将前i件物品放入容量为v的背包中”这个 子问题,若只考虑第i件物品的策略(放或不放),那么就可以转化为一个只牵扯 前i-1件物品的问题。如果不放第i件物品,那么问题就转化为“前i-1件物品放入容 量为v的背包中”;如果放第i件物品,那么问题就转化为“前i-1件物品放入剩下 的容量为v-w[i]的背包中”,此时能获得的最大价值就是f [i-1][v-w[i]]再加上通过 放入第i件物品获得的价值c[i]。
算法优化:
for(int i=1;i<=n;++i) for(int v=m;v>=0;--v) if(v>=w[i]) f[i][v]=max(f[i-1][v],f[i-1][v-w[i]]+c[i]); else f[i][v]=f[i-1][v];
for(int i=1;i<=n;++i) for(int v=n;v>=w[i];--v) f[v]=max(f[v],f[v-w[i]]+c[i])
动态规划
第二节 背包问题
第二节 背包问题
一、01背包问题 问题:
有N件物品和一个容量为V的背包。第i件物品的费用(即体积,下同)是w[i] ,价值是c[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量 ,且价值总和最大。 基本思路:
这是最基础的背包问题,特点是:每种物品仅有一件,可以选择放或不放。 用子问题定义状态:即f[i][v]表示前i件物品(部分或全部)恰放入一个容量为v 的背包可以获得的最大价值。则其状态转移方程便是:f[i][v]=max{f[i-1][v],f[i1][v-w[i]]+c[i]}。
i=4
0 1 3 5 5 6 9 9 10 12
二、完全背包
问题: 有N种物品和一个容量为V的背包,每种物品都有无限件可用。第i种物品的费用
是w[i],价值是c[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量 ,且价值总和最大。
基本思路: 这个问题非常类似于01背包问题,所不同的是每种物品有无限件。也就是从每种
例题 9.11
【问题描述】 一个旅行者有一个最多能用m公斤的背包,现在有n件物品,它们的重量
分别是W1,W2,...,Wn,它们的价值分别为C1,C2,...,Cn.若每种物品只有一件求 旅行者能获得最大总价值。
【输入格式】 第一行:两个整数,M(背包容量,M<=200)和N(物品数量,N<=30); 第2..N+1行:每行二个整数Wi,Ci,表示每个物品的重量和价值。
3
3
i=3
4
5
i=4
7
9
V=0 V=1 V=2 V=3 V=4 V=5 V=6 V=7 V=8 V=9 V=10
i=0 0 0 0 0 0 0 0 0 0 0 0
F[v]
i=1 0
0
11
1 1 1 1 11 1
F[v]
i=2
0 13
4 4 4 4 44 4
F[v]
i=3
0 13
5 5688 9 9
F[v]
第一行:两个整数,M(背包容量, M<=200)和N(物品数量,N<=30);
第2..N+1行:每行二个整数Wi,Ci,表示每 个物品的重量和价值。 【输出格式】
仅一行,一个数,表示最大总价值。 【样例输入】package.in
10 4
21
33
45
79 【样例输出】package.out
12
1、确定阶段: 按照序号依次处理物品,每处
物品的角度考虑,与它相关的策略已并非取或不取两种,而是有取0件、取1件、取2件 ……等很多种。如果仍然按照解01背包时的思路,令f[i][v]表示前i种物品恰放入一个容量 为v的背包的最大权值。仍然可以按照每种物品不同的策略写出状态转移方程,像这样: f[i][v]=max{f[i-1][v-k*w[i]]+k*c[i]|0<=k*w[i]<= v}。
