ch.1-15 理想气体的熵
合集下载
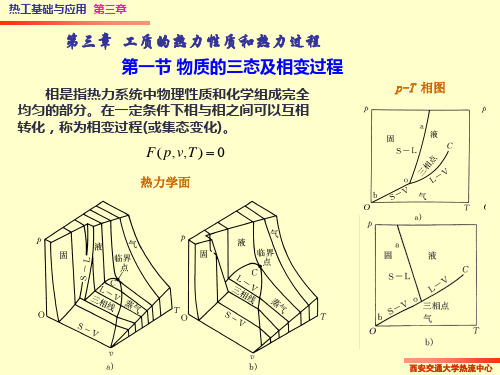
热工基础 第三章.理想气体的性质与热力过程

CV ,m McV xi M i cV ,i xi CV ,m,i
i 1 i 1
29
k
i 1 k
i 1 k
3-4 理想气体的热力过程
1.热力过程的研究目的与方法
(1)目的: 了解外部条件对热能与机械 能之间相互转换的影响,以便合理地安排 热力过程,提高热能和机械能转换效率。
V V1 V2 Vk Vi
i 1
k
25
3. 理想混合气体的成分 成分:各组元在混合气体中所占的数量份额。 (1) 成分的分类 1)质量分数 :某组元的质量与混合气体总质量
的比值称为该组元的质量分数。
k k mi wi , m mi wi 1 m i 1 i 1 2)摩尔分数 : 某组元物质的量与混合气体总物
22
3-3
理想混合气体
1. 理想混合气体的定义 由相互不发生化学反应的理想气体组成混合 气体,其中每一组元的性质如同它们单独存在一 样,因此整个混合气体也具有理想气体的性质。 混合气体的性质取决于各组元的性质与份额。 2. 理想混合气体的基本定律 (1)分压力与道尔顿定律 分压力: 某组元i单独占有混合气体体积V并处于 混合气体温度T 时的压力称为该组元的 分压力。用 pi 表示。
10
由比定容热容定义式可得
qV u cV dT T V
(4)比定压热容
cp
q p dT
据热力学第一定律,对微元可逆过程,
q dh vdp
11
焓也是状态参数, h h(T ,
p)
h h dh dT dp T p p T 对定压过程,dp 0 ,由上两式可得 h q p dT T p
i 1 i 1
29
k
i 1 k
i 1 k
3-4 理想气体的热力过程
1.热力过程的研究目的与方法
(1)目的: 了解外部条件对热能与机械 能之间相互转换的影响,以便合理地安排 热力过程,提高热能和机械能转换效率。
V V1 V2 Vk Vi
i 1
k
25
3. 理想混合气体的成分 成分:各组元在混合气体中所占的数量份额。 (1) 成分的分类 1)质量分数 :某组元的质量与混合气体总质量
的比值称为该组元的质量分数。
k k mi wi , m mi wi 1 m i 1 i 1 2)摩尔分数 : 某组元物质的量与混合气体总物
22
3-3
理想混合气体
1. 理想混合气体的定义 由相互不发生化学反应的理想气体组成混合 气体,其中每一组元的性质如同它们单独存在一 样,因此整个混合气体也具有理想气体的性质。 混合气体的性质取决于各组元的性质与份额。 2. 理想混合气体的基本定律 (1)分压力与道尔顿定律 分压力: 某组元i单独占有混合气体体积V并处于 混合气体温度T 时的压力称为该组元的 分压力。用 pi 表示。
10
由比定容热容定义式可得
qV u cV dT T V
(4)比定压热容
cp
q p dT
据热力学第一定律,对微元可逆过程,
q dh vdp
11
焓也是状态参数, h h(T ,
p)
h h dh dT dp T p p T 对定压过程,dp 0 ,由上两式可得 h q p dT T p
理想气体的内能、焓、比热容、熵介绍

一般用组成气体的含量与混合物总量的比值
来表示混合物的组成。
w 质量分数(mass fraction): i
mi m
y nn pp 摩尔分数(mole fraction): i
i
i
piV ni RT pV nRT
VV 容积分数(volume fraction): i
i
显然
w1 w2 wn 1
得
wi
yi
Mi M
由
wi
mi m
Vi i V
得
wi
i
i
3.4.3 混合物的密度、摩尔质量及折合气体常数
由密度的定义,混合物的密度为:
m m1 m2 mi 1V1 2V2 iVi
V
V
V
n
即得: 11 22 ii ii
单位摩尔数的物质温度升高1K所需要的热
量,称为摩尔比热容Cm (kJ/kmol.K)
C Mc c dqT 定容比热(specific
m
heat
at
constant
volume)
:
v
v
c 定压比热(specific heat at constant pressure) : p
qp dT
pV nRT pV mRgT
混合物的质量等于各组成气体质量之和:
n
m mi i 1
m m1 m2 mi mn
混合物物质的量等于各组成气体物质的量之和:
n
n ni n n1 n2 ni nn
i 1
工程热力学 第三章 理想气体的性质

11
比热容的概念
比热容是单位物量的物质升高1K或1℃所需 的热量。 根据物质的数量和经历的过程不同,可分为:
(1)比热容(质量热容) : 1kg物质的热容,c ,J/(kg·K)。 c q q dT dt
12
比热容的概念
(2)摩尔热容
1 mol物质的热容,Cm,J/(kmol· K)。 Cm Mc
s isi
❖1kg混合气体的比熵变为
d s
c i p,i
dT T
R i g,i
dip pi
❖1mol混合气体的熵变为
dmpp
49
课后思考题
❖理想气体的热力学能和焓是温度的单值函 数,理想气体的熵也是温度的单值函数吗?
❖气体的比热容cp、cv究竟是过程量还是状态 量
pp1p2 pK pi i1
41
道尔顿分压力定律
pi p
ni n
xi
pi xi p
即分压力与总压力之比等于摩尔分数(即气 体组分的摩尔数与总摩尔数之比)
42
亚美格分体积定律
❖混合气体中第 i 种组元处于与混合气体压力 和温度时所单独占据的体积称为该组元的 分体积,用 Vi 表示。
❖亚美格分体积定律:理想混合气体的总体 积等于各组元的分体积之和(仅适用于理 想气体)
的关系式
17
cv和cp的关系式
比热容比: c p cV
得 cp 1 Rg
联立式 cp cV Rg
cV
1
1
Rg
18
比热容和温度的关系
❖理想气体的 u 和 h 是温度的单值函数,所 以理想气体的 cV 和 cp 也是温度的单值函 数。
c ft a b t d t2 e t3
比热容的概念
比热容是单位物量的物质升高1K或1℃所需 的热量。 根据物质的数量和经历的过程不同,可分为:
(1)比热容(质量热容) : 1kg物质的热容,c ,J/(kg·K)。 c q q dT dt
12
比热容的概念
(2)摩尔热容
1 mol物质的热容,Cm,J/(kmol· K)。 Cm Mc
s isi
❖1kg混合气体的比熵变为
d s
c i p,i
dT T
R i g,i
dip pi
❖1mol混合气体的熵变为
dmpp
49
课后思考题
❖理想气体的热力学能和焓是温度的单值函 数,理想气体的熵也是温度的单值函数吗?
❖气体的比热容cp、cv究竟是过程量还是状态 量
pp1p2 pK pi i1
41
道尔顿分压力定律
pi p
ni n
xi
pi xi p
即分压力与总压力之比等于摩尔分数(即气 体组分的摩尔数与总摩尔数之比)
42
亚美格分体积定律
❖混合气体中第 i 种组元处于与混合气体压力 和温度时所单独占据的体积称为该组元的 分体积,用 Vi 表示。
❖亚美格分体积定律:理想混合气体的总体 积等于各组元的分体积之和(仅适用于理 想气体)
的关系式
17
cv和cp的关系式
比热容比: c p cV
得 cp 1 Rg
联立式 cp cV Rg
cV
1
1
Rg
18
比热容和温度的关系
❖理想气体的 u 和 h 是温度的单值函数,所 以理想气体的 cV 和 cp 也是温度的单值函 数。
c ft a b t d t2 e t3
工程热力学-03 理想气体u、h、s的计算

11
5、理想气体比定容热容cV0和比定压热容cp0的关系
(1) c=p0
d=h dT
d (u += pv) dT
d dT
(u
+
RgT=)
du dT
+
d dT
(RgT )
c p0 = cV 0 + Rg
(2)比热容比:比定压热容和比定容热容之比,符号 γ
γ = cp0
cV 0
cV 0
=
γ
1 −
1
Rg
(3-13a)
p
s= 2 − s1
cV 0 ln
p2 p1
+ cp0
ln
v2 v1
(3-14b)
19
若把理想气体的比热容看作定值:
= ds
cV 0
dT T
+
Rg
dv v
= ds
cp0
dT T
−
Rg
dp p
= ds
cV
0
dp p
+
cp0
dv v
s2= − s1
cV 0
ln T2 T1
+
Rg
ldu dT
(3-5)
任何过程中,单位质量的理想气体的温度升高1K时,比 热力学能增加的数值即等于其比定容热容cV0的值。
9
3、任意气体的比定压热容cp
按照比定压热容的定义式:cp
=
( δq dT
)p
设h=f (T , p)
δ=q
dh − vdp
=
(
∂h ∂T
1、分压力:混合物中的某种组成气体单独占有混合物的容积, 并具有与混合物相同温度时的压力。
理想气体
∆h = ∫ c p dT
T1
T2
平均比热容 平均比热容( 平均比热容(表) 定值比热容 热力性质表
∆u = cV ∆u = cV
t2
t1
⋅ (t 2 − t 1 ) ⋅ t 2 − cV
t1
∆h = c p
∆h = c p
t2 t1
⋅ (t 2 − t1 )
⋅ t2 − c p
t1 0° C
t2
0° C
热力学能 焓和熵
T p ∆s = c p ln 2 − Rg ln 2 T1 p1
∆h = c p ∆T = c p ∆t
ct =
t2
1
c 02°C ⋅t2 −c 01°C ⋅t1
t t
t2 −t1
定值比热容表
单原子气体
cV (C ,m) V
c p (Cp,m)
3 3 Rg ( R ) 2 2
双原子气体
0° C
⋅ t1
t2 0° C
⋅ t1
∆u = cV ∆T = cV ∆t
∆u = u 2 (T2 ) − u1 (T1 )
∆h = c p ∆T = c p ∆t
∆h = h2 (T2 ) − h1 (T1 )
西安交通大学热流中心
热工基础与应用 第三章
2、 理想气体的熵
ds =
δqre
T
=
du + pdv cV dT + pdv dT dv p / T = Rg / v = ds = cV + Rg → T T T v
混合气体 组成气体
1、分压力定律 : 分压力 :各组元在混合物温度
下单独占据混合物所占体积时 所产生的压力。
物理化学 03-03相变过程熵变

2
将环境看作一个巨大的热源: 将环境看作一个巨大的热源: T(环)=常数;Qr(环)=∆H(环) ; Q(环)=- 系) 常数; 环 = =-Q(系 环 常数 环 环 =-
P121 例3.5.1
Q(系) ∆S (环境 )=- T (环)
∆H ( 263 K ) = ∆H ( 273 K ) + m ∆ C p ∆T=-311.46kJ = Q( 系 )
-
§3.5 相变过程
1. 可逆相变
可逆相变—恒温恒压且无限接近平衡条件下进行的相变过程 恒温恒压且无限接近平衡条件下进行的相变过程
∆H 相变 Qr ∆ S= = T相变 T相变
2. 不可逆相变
在始末态之间设计可逆途径
P121 例3.5.1
1
H2O(l) 263K 100kPa ∆1S
不可逆相变 ∆S(263K) ∆2S 可逆相变 ∆S(273K)
B
T δQ T δQ δQ r r = [S AB (0 K ) − S A (0 K ) − S B (0 K )] + ∫ −∫ −∫ r 0K T AB 0 K T A 0 K T B T
7
2.热力学第三定律
=
∫
Tf
C o--,m (s ) p T T
0K Tb
o ∆ fus H mdT + Tf
+∫ +∫
C o-,m ( l ) p
Tf T
dT +
o ∆ vap H m-
Tb
C o-,m ( g ) p
Tb
T
dT + ∆ pg S o- (T ) g m
4.标准摩尔反应熵的计算 4.标准摩尔反应熵的计算
将环境看作一个巨大的热源: 将环境看作一个巨大的热源: T(环)=常数;Qr(环)=∆H(环) ; Q(环)=- 系) 常数; 环 = =-Q(系 环 常数 环 环 =-
P121 例3.5.1
Q(系) ∆S (环境 )=- T (环)
∆H ( 263 K ) = ∆H ( 273 K ) + m ∆ C p ∆T=-311.46kJ = Q( 系 )
-
§3.5 相变过程
1. 可逆相变
可逆相变—恒温恒压且无限接近平衡条件下进行的相变过程 恒温恒压且无限接近平衡条件下进行的相变过程
∆H 相变 Qr ∆ S= = T相变 T相变
2. 不可逆相变
在始末态之间设计可逆途径
P121 例3.5.1
1
H2O(l) 263K 100kPa ∆1S
不可逆相变 ∆S(263K) ∆2S 可逆相变 ∆S(273K)
B
T δQ T δQ δQ r r = [S AB (0 K ) − S A (0 K ) − S B (0 K )] + ∫ −∫ −∫ r 0K T AB 0 K T A 0 K T B T
7
2.热力学第三定律
=
∫
Tf
C o--,m (s ) p T T
0K Tb
o ∆ fus H mdT + Tf
+∫ +∫
C o-,m ( l ) p
Tf T
dT +
o ∆ vap H m-
Tb
C o-,m ( g ) p
Tb
T
dT + ∆ pg S o- (T ) g m
4.标准摩尔反应熵的计算 4.标准摩尔反应熵的计算
第三章(3) 理想气体热力学能、焓和熵变化量的计算

称为比热比或等熵指数。
五、理想气体熵变化量的计算
根据熵的定义式ds=δq/T及热力学第一定律的解析式:
δq=cvdT+ pdv δq=cpdT-vdp
两边同除以T,可得
ds=cvdT/T+ p/Tdv ds=cpdT/T-v/Tdp (1) (2)
由理想气体状态方程:pv=RT可知 p/T=R/v v/T=R/p
三、理想气体焓变化量的计算
根据焓的定义式 h=u+pv (流动功),对于理想气体,因 pv=RT,所以 H=u+RT=f(T) 因为焓是状态量,我们就可以选择压力不变的可逆过程来计
算理想气体焓的变化量。根据开口系统可逆稳定流动过程可知,
能量方程式可表示为: δq=dh –vdp(技术功)
对于定压过程,因dp=0、δq=cpdT,代入上式可得
例3-5:一绝热刚性容器被隔板分为容积相等的 A、B两个空间,
A侧装有1kg空气,压力pA=0.2MPa,温度TA=300K。B侧为真空, 如图所示。抽去隔板后,空气充满整个空间,达到新的平衡。 试求(1)气体的温度; (2)气体熵的变化量(视比热容为定值)。
dh=cpdT
当采用定值比热容时,则有:△h=cp △ T
结论:1)理想气体无论经历什么过程,其焓的变化量都等
于定压过程的加热量。
2) 热力学第一定律应用于理想气体的任意过程中
δq=cpdT+ δw
3)对于理想气体的可逆过程,可表示为
δq=cpdT-vdp(技术功)
四、理想气体比定压热容与比定容热容的关系
第三节 理想气体热力学能、焓和熵变化量的计算
1.上节回顾 2. 理想气体热力学能变化量的计算
3. 理想气体焓变化量的计算
热力学公式总结

热力学公式总结热力学公式,作为热力学研究的基础,是描述能量转化和热力学过程的数学表达式。
它们通过简洁的符号和方程式,揭示了物质和能量之间的相互关系。
以下是几个常见的热力学公式及其含义,让我们一起来了解一下吧。
1. 热力学第一定律:ΔU = Q - W热力学第一定律是能量守恒定律在热力学中的表达,它说明了一个封闭系统内部能量的变化等于系统所吸收的热量减去对外界做功的大小。
这个公式告诉我们,能量既不能被创造也不能被消灭,只能从一种形式转化为另一种形式。
2. 熵的定义:ΔS = Q/T熵是描述系统无序程度的物理量,它是热力学中的一个重要概念。
熵的增加代表了系统的无序性增加,而熵的减少则代表了系统的有序性增加。
这个公式告诉我们,熵的变化与系统所吸收的热量和温度有关,系统吸收的热量越多,熵的增加越大。
3. 理想气体状态方程:PV = nRT理想气体状态方程是描述理想气体性质的基本公式,它将气体的压力、体积、摩尔数和温度联系在一起。
这个公式告诉我们,当气体的压力、体积和摩尔数一定时,温度越高,气体的体积越大。
4. 热力学第二定律:ΔS ≥ 0热力学第二定律是热力学中的一个基本原理,它表明在一个孤立系统中,系统的熵不会减小,或者说系统总是趋向于更高的熵。
这个公式告诉我们,自然界中熵的增加是不可逆的,系统的有序性总是会不可避免地变差。
以上是几个常见的热力学公式,它们揭示了能量转化和热力学过程的规律。
通过理解和运用这些公式,我们可以更好地理解和分析能量转化和热力学过程,为实际问题的解决提供依据。
热力学公式的应用广泛,涵盖了能源、化学、物理等多个领域,对于推动科学技术的发展和改善人类生活质量起到了重要的作用。
希望今天的介绍能让大家对热力学公式有更深入的了解,并在实际应用中发挥出更大的作用。
