浙江省金丽衢十二校2020届高三下学期第二次联考技术试题 扫描版含答案
浙江省金丽衢十二校2024届高三下学期第二次联考数学试题(含答案与解析)_2761

金丽衢十二校2024学年高三第二次联考数学试题(考试时间为120分钟,试卷总分为150分)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.2.回答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上,写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回选择题部分一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合{}0,1,2A =,{|31,}B x x k k ==-∈N ,则A B = ( ) A. {}0,1,2B. {}1,2C. {}1D. {}22. 若复数z 满足:232i z z +=-,则z ( ) A. 2B.C.D. 53. 若函数()()ln e 1xf x ax =++为偶函数,则实数a 的值为( )A. 12-B. 0C.12D. 14. 双曲线2211x y a a -=-的离心率e 的可能取值为( )A.B.C.D. 25. 在ABC 中,“A ,B ,C 成等差数列且sin ,sin ,sin A B C 成等比数列”是“ABC 是正三角形”的( ) A. 充分不必要条件 B. 必要不充分条件 C. 充要条件D. 既不充分也不必要条件6. 已知抛物线21:2C x y =的焦点为F ,以F 为圆心的圆2C 交1C 于A ,B 两点,交1C 的准线于C ,D 两点,若四边形ABCD 是矩形,则圆2C 的方程为( )为A. 22(1)12x y +-=B. 22(1)16x y +-=C. 22132x y ⎛⎫+-= ⎪⎝⎭ D. 22142x y ⎛⎫+-= ⎪⎝⎭7. 已知函数()11,02ln ,0x x f x x x ⎧+≤⎪=⎨⎪>⎩若1212()()()f x f x x x =<,则21x x -的取值范围为( )A [e,)+∞B. 42ln )[2,-+∞C. []42ln 2,e -D. [e 1,)-+∞8. 在三棱锥D ABC -中,底面是边长为2的正三角形,若AD 为三棱锥D ABC -的外接球直径,且AC 与BD,则该外接球的表面积为( ) A.19π3B.28π3C. 7πD. 16π二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.9. 关于函数()22sin cos f x x x x =⋅+,下列说法正确的是( ) A. 最小正周期为2πB.关于点π6⎛-⎝中心对称 C.最大值2+D. 在区间5ππ,1212⎡⎤-⎢⎥⎣⎦上单调递减 10. 设定义在R 上的函数()f x 的导函数为()f x ',若R x ∀∈,均有()()()1xf x x f x '=+,则( ) A. ()00f = B. ()20f ''-=(()f x ''为()f x 的二阶导数) C. ()()221f f <D. 1x =-是函数()f x 的极大值点11. 已知正方体1111ABCD A B C D -,的棱长为1,点P 是正方形1111D C B A 上的一个动点,初始位置位于点1A 处,每次移动都会到达另外三个顶点.向相邻两顶点移动的概率均为14,向对角顶点移动的概率为12,如当点P 在点1A 处时,向点1B ,1D 移动的概率均为14,向点1C 移动的概率为12,则( ) A. 移动两次后,“PC =”的概率为38B. 对任意*n ∈N ,移动n 次后,“//PA 平面1BDC ”的概率都小于13.为C. 对任意*n ∈N ,移动n 次后,“PC ⊥平面1BDC ”的概率都小于12D. 对任意*n ∈N ,移动n 次后,四面体1P BDC -体积V 的数学期望()15E V <(注:当点P 在平面1BDC 上时,四面体1P BDC -体积为0)非选择题部分三、填空题:本题共3小题,每小题5分,共15分.12. 已知圆柱的轴截面面积为4,则该圆柱侧面展开图的周长最小值为__________.13. 某中学A 、B 两个班级有相同的语文、数学、英语教师,现对此2个班级某天上午的5节课进行排课,2节语文课,2节数学课,1节英语课,要求每个班级的2节语文课连在一起,2节数学课连在一起,则共有__________种不同的排课方式.(用数字作答)14. 设正n 边形的边长为1,顶点依次为12,,,n A A A ,若存在点P 满足120PA PA ⋅=u u u r u u u r,且11n k k PA ==∑u u u r ,则n 的最大值为__________.(参考数据:tan 360.73︒≈)四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15. 已知等差数列{}n a 的前n 项和为n S ,且2221n n S a n =+-. (1)求n a ;(2)求数列11n n a a +⎧⎫⎨⎬⎩⎭的前n 项和n T .16. 如图,在四棱锥P ABCD -中,四边形ABCD 是边长为2的正方形,平面PAD ⊥平面ABCD,PA PD ==,点E 是线段AD 的中点,2CM MP =.(1)证明:PE //平面BDM ; (2)求平面AMB 与平面BDM 的夹角.17. 某工厂生产某种元件,其质量按测试指标划分为:指标大于或等于82为合格品,小于82为次品,现抽取这种元件100件进行检测,检测结果统计如下表:的测试指标 [)20,76[)76,82[)82,88[)88,94[]94,100元件数(件) 121836304(1)现从这100件样品中随机抽取2件,若其中一件为合格品,求另一件也为合格品的概率; (2)关于随机变量,俄国数学家切比雪夫提出切比雪夫不等式:若随机变量X 具有数学期望()E X μ=,方差()2D X σ=,则对任意正数ε,均有()22P x σμεε-≥≤成立.(i )若1~100,2X B ⎛⎫ ⎪⎝⎭,证明:1(025)50P X ≤≤≤; (ii )利用该结论表示即使分布未知,随机变量的取值范围落在期望左右的一定范围内的概率是有界的.若该工厂声称本厂元件合格率为90%,那么根据所给样本数据,请结合“切比雪夫不等式”说明该工厂所提供的合格率是否可信?(注:当随机事件A 发生的概率小于0.05时,可称事件A 为小概率事件)18. 已知椭圆2222:1(0)x y L a b a b+=>>的左顶点()30A -,和下顶点B ,焦距为,直线l 交椭圆L 于C ,D (不同于椭圆的顶点)两点,直线AD 交y 轴于M ,直线BC 交x 轴于N ,且直线MN 交l 于P . (1)求椭圆L 标准方程;(2)若直线AD ,BC 的斜率相等,证明:点P 在一条定直线上运动.19. ①在微积分中,求极限有一种重要的数学工具——洛必达法则,法则中有结论:若函数()f x ,()g x 的导函数分别为()f x ',()g x ',且lim ()lim ()0x a x af xg x →→==,则 ()()lim lim ()()x a x a f x f x g x g x ''→→=. ②设0a >,k 是大于1的正整数,若函数()f x 满足:对任意[]0,x a ∈,均有()x f x f k ⎛⎫≥ ⎪⎝⎭成立,且()0lim 0x f x →=,则称函数()f x 为区间[]0,a 上的k 阶无穷递降函数. 结合以上两个信息,回答下列问题:(1)试判断()33f x x x =-是否为区间[]0,3上的2阶无穷递降函数;(2)计算:10lim(1)xx x →+;的(3)证明:3sin cos πx x x ⎛⎫< ⎪-⎝⎭,3π,π2x ⎛⎫∈ ⎪⎝⎭. 参考答案一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合{}0,1,2A =,{|31,}B x x k k ==-∈N ,则A B = ( ) A. {}0,1,2 B. {}1,2C. {}1D. {}2【答案】D 【解析】【分析】根据交集定义求解即可.【详解】因为{}0,1,2A =,{|31,}B x x k k ==-∈N , 所以{2}A B = . 故选:D.2. 若复数z 满足:232i z z +=-,则z 为( )A. 2B.C.D. 5【答案】C 【解析】【分析】利用共轭复数的概念及复数相等的充要条件求出z ,进而求出z . 【详解】设()i,,R z a b a b =+∈,则i,z a b =- 所以23i=32i z z a b +=--,即1,2a b ==,所以z ==.故选:C.3. 若函数()()ln e 1xf x ax =++为偶函数,则实数a 的值为( )A. 12-B. 0C.12D. 1【答案】A【解析】【分析】根据偶函数满足的关系即可化简求解. 【详解】()()ln e 1xf x ax =++的定义域为R ,()()()e 1ln e 1ln ln e 1e x xx x f x ax ax x ax -⎛⎫+-=+-=-=+-- ⎪⎝⎭,由于()()ln e 1xf x ax =++为偶函数,故()()f x f x -=,即()()()()ln e 11ln e 1120x x a x ax a x +-+=++⇒+=,故120a +=,解得12a =- 故选:A4. 双曲线2211x y a a -=-的离心率e 的可能取值为( )A.B.C.D. 2【答案】A 【解析】【分析】由题得到1a >或a<0,再利用离心率c e a ==.【详解】由(1)0a a ->,得到1a >或a<0,当1a >时,c e a ====<,当a<0,双曲线2211y x a a -=--,c e a ====<,所以1e <<故选:A.5. 在ABC 中,“A ,B ,C 成等差数列且sin ,sin ,sin A B C 成等比数列”是“ABC 是正三角形”的( ) A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件【答案】C 【解析】【分析】根据给定条件,利用等差、等比数列的定义,结合正余弦定理及充分条件、必要条件的定义判断即得.【详解】在ABC 中,由A ,B ,C 成等差数列,得2B A C =+,而πA B C ++=,则π3B =, 由sin ,sin ,sin A BC 成等比数列,得2sin sin sin B A C =,由正弦定理得2b ac =,由余弦定理得2222cos b a c ac B =+-,即22ac a c ac =+-,解得a c =,因此ABC 是正三角形;若ABC 是正三角形,则π3A B C ===,sin sin sin A B C ===, 因此A ,B ,C 成等差数列且sin ,sin ,sin A B C 成等比数列,所以“A ,B ,C 成等差数列且sin ,sin ,sin A B C 成等比数列”是“ABC 是正三角形”的充要条件. 故选:C6. 已知抛物线21:2C x y =的焦点为F ,以F 为圆心的圆2C 交1C 于A ,B 两点,交1C 的准线于C ,D 两点,若四边形ABCD 是矩形,则圆2C 的方程为( ) A. 22(1)12x y +-=B. 22(1)16x y +-=C. 22132x y ⎛⎫+-= ⎪⎝⎭D. 22142x y ⎛⎫+-= ⎪⎝⎭【答案】D 【解析】【分析】依题意知,圆2C 的圆心坐标为10,2F ⎛⎫⎪⎝⎭,且点F 为该矩形对角线的交点,利用点F 到直线CD 的距离与点F 到AB 的距离相等,可求得直线AB 的方程为:32y =,从而可求得A 点坐标,从而可求得圆2C 的半径,于是可得答案.【详解】解:由题可得:抛物线21:2C x y =的焦点为10,2F ⎛⎫ ⎪⎝⎭, 所以圆2C 的圆心坐标为10,2F ⎛⎫ ⎪⎝⎭,因为四边形ABCD 是矩形,且为BD 直径,AC 为直径,10,2F ⎛⎫ ⎪⎝⎭为圆2C 圆心, 所以点F 为该矩形对角线的交点,所以点F 到直线CD 的距离与点F 到AB 的距离相等, 故点F 到直线CD 的距离1d = , 所以直线AB 的方程为:32y = ,所以32A ⎫⎪⎭, 故圆2C 的半径2r AF === ,所以圆2C 的方程为22142x y ⎛⎫+-= ⎪⎝⎭. 故选:D【点睛】本题考查抛物线的简单性质,考查圆的标准方程的确定,分析得到点F 为该矩形ABCD 的两条对角线的交点是关键,考查作图、分析与运算能力,属于中档题.7. 已知函数()11,02ln ,0x x f x x x ⎧+≤⎪=⎨⎪>⎩若1212()()()f x f x x x =<,则21x x -的取值范围为( )A. [e,)+∞B. 42ln )[2,-+∞C. []42ln 2,e -D. [e 1,)-+∞【答案】B的【解析】【分析】由题意可知1211ln 2x x +=,转化为21222ln 2x x x x -=-+.结合图像构造函数()2ln 2h x x x =-+,(]0,e x ∈,求出函数值域即为本题答案.【详解】由题意可知1211ln 2x x +=,即122ln 2x x =-,所以21222ln 2x x x x -=-+. 由图像可得(]20,e x ∈,设()2ln 2h x x x =-+,(]0,e x ∈. 则22()1x h x x x-'=-=,(]0,e x ∈.令2()0x h x x -'==,则2x = 当()0h x '>时(]2,e x ∈,当()0h x '<时()0,2x ∈所以()2ln 2h x x x =-+在()0,2单调递减,在(]2,e 单调递增. 所以()h x 在2x =时取得最小值()242ln 2h =-, 可得2142ln [2,)x x -∈-+∞. 故选:B8. 在三棱锥D ABC -中,底面是边长为2的正三角形,若AD 为三棱锥D ABC -的外接球直径,且AC 与BD,则该外接球的表面积为( ) A.19π3B.28π3C. 7πD. 16π【答案】A 【解析】【分析】记球心为O ,取AB 中点为E 、BC 中点为F ,连接OE OF EF 、、,易得OE OF ==,1EF =,由cos OEF ∠=,即可求出21912r =,由此即可求出答案.【详解】如图所示:记球心为O ,取AB 中点为E 、BC 中点为F ,连接OE OF EF 、、, 记外接球半径为r ,的在Rt ABD中,BD =∥OE BD,OE =,在ABC 中,//EF AC ,112EF AC ==, 在Rt OBF中,OF =所以AC 与BD 所成角为OEF ∠,即cos OEF ∠=, 在OEF 中,OE OF ==,1EF =,所以12cos EFOEF OE ∠===解得:21912r =, 所以该外接球的表面积为:219194π4ππ123r =⨯= 故选:A.二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.9. 关于函数()22sin cos f x x x x =⋅+,下列说法正确的是( ) A. 最小正周期为2πB.关于点π6⎛-⎝中心对称 C.2+ D. 在区间5ππ,1212⎡⎤-⎢⎥⎣⎦上单调递减 【答案】BC 【解析】【分析】首先化简函数的解析式,再根据三角函数的性质,判断选项.【详解】())22sin cos sin 2cos 21f x x x x x x =⋅+=+,π2sin 23x ⎛⎫=++ ⎪⎝⎭,函数的最小正周期2ππ2T ==,故A 错误;πππ2sin 0633f ⎛⎫⎛⎫-=-++=+= ⎪ ⎪⎝⎭⎝⎭,所以函数()f x图象关于点π6⎛- ⎝中心对称,故B 正确;()π2sin 23f x x ⎛⎫=++ ⎪⎝⎭,所以函数的最大值为2,故C 正确;由5ππ,1212x ⎡⎤∈-⎢⎥⎣⎦,πππ2,322x ⎡⎤+∈-⎢⎥⎣⎦,函数sin y x =在区间ππ,22⎡⎤-⎢⎥⎣⎦单调递增, 所以函数()f x 在区间5ππ,1212⎡⎤-⎢⎥⎣⎦上单调递增,故D 错误. 故选:BC10. 设定义在R 上的函数()f x 的导函数为()f x ',若R x ∀∈,均有()()()1xf x x f x '=+,则( ) A. ()00f = B. ()20f ''-=(()f x ''为()f x 的二阶导数) C. ()()221f f < D. 1x =-是函数()f x 的极大值点【答案】AB 【解析】【分析】由()()()1xf x x f x '=+,令0x =,即可判断A ;由已知得()()f x f x x x'⎡⎤=⎢⎥⎣⎦,即得函数()e x f x c x=+,确定0c =,从而可得()()e xf x x c =+,求导数,即可判断B ;令()(),(0)f x g x x x=>,判断其单调性,即可判断C ;根据极值点与导数的关系可判断D.【详解】由R x ∀∈,()()()1xf x x f x '=+,令0x =,则()()()00100,0f f ∴==+,A 正确; 当0x ≠时,由()()()1xf x x f x '=+得()()()xf x f x xf x -'=,故()()()2f x x f x f x xx'⋅-=,即()()f x f x x x '⎡⎤=⎢⎥⎣⎦,则()e xf x c x =+(c 为常数),则()()e x f x x c =+, ()00f =满足该式,故()()e x f x x c =+,则()e e x x f x c x '=++,将()()e xf x x c =+代入()()()1xf x x f x '=+中,得()()()e e 1e x x xx c x x x c ++=++,即222e e e e x x x x x xc x x x c cx x ++=+++,而x ∈R ,故0c =,则()e x f x x =,()e e x xf x x ='+,()e e e e (2)x x x xf x x x ''=++=+,故()2e (22)0xf =''--=,B 正确;令()(),(0)f x g x x x=>,()e 0xg x '=>,故()g x 在(0),+∞上单调递增,故()()2121f f >,即()()221f f >,C 错误; 由于()e e x xf x x ='+,令()()0,e 10x f x x '>∴+>,即得1x >-,令()()0,e 10xf x x '<∴+<,即得1x <-,故()f x 在(1),-∞-上单调递减,在(1),-+∞上单调递增, 故1x =-是函数()f x 的极小值点,D 错误, 故选:AB11. 已知正方体1111ABCD A B C D -,的棱长为1,点P 是正方形1111D C B A 上的一个动点,初始位置位于点1A 处,每次移动都会到达另外三个顶点.向相邻两顶点移动的概率均为14,向对角顶点移动的概率为12,如当点P 在点1A 处时,向点1B ,1D 移动的概率均为14,向点1C 移动的概率为12,则( ) A. 移动两次后,“PC =”的概率为38B. 对任意*n ∈N ,移动n 次后,“//PA 平面1BDC ”的概率都小于13C. 对任意*n ∈N ,移动n 次后,“PC ⊥平面1BDC ”的概率都小于12D. 对任意*n ∈N ,移动n 次后,四面体1P BDC -体积V 的数学期望()15E V <(注:当点P 在平面1BDC 上时,四面体1P BDC -体积为0)【答案】ACD 【解析】【分析】先求出点P 在移动n 次后,点1111,,,A B C D 的概率,再结合由向量法求出线面垂直、线面平行和三棱锥的体积,对选项一一判断即可得出答案.【详解】设移动n 次后,点P 在点1111,,,A B C D 的概率分别为,,,n n n n a b c d , 其中11111110,,,,1424n n n n a b c d a b c d ====+++=, 111111111111111442111442111442111442n n n n n n n n n n n n n n n n a b d c b a c d c b d ad a c b ------------⎧=++⎪⎪⎪=++⎪⎨⎪=++⎪⎪⎪=++⎩,解得:111+42211142214nn n n n na cb d ⎧⎛⎫=-⎪ ⎪⎝⎭⎪⎪⎪⎛⎫=--⎨ ⎪⎝⎭⎪⎪==⎪⎪⎩, 对于A ,移动两次后,“PC =表示点P 移动两次后到达点1A ,所以概率为2211134228a ⎛⎫=+⨯-= ⎪⎝⎭,故A 正确;对于B ,以D 为坐标原点,建立如图所示的空间直角坐标系,所以()()()()1,0,0,0,0,0,1,1,0,0,1,0A D B C ,()()()()11111,0,1,0,0,1,1,1,1,0,1,1A D B C ,因为()()11,1,0,0,1,1DB DC == ,()()()1110,1,1,1,0,1,1,1,1B A D A A C =--=-=--,设平面1BDC 的法向量为(),,n x y z = ,则100n DB x y n DC y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩ , 取1y =,可得1,1x z =-=-,所以()1,1,1n =--,而110,0B A n D A n ⋅=⋅= ,11,B A D A ⊄平面1BDC ,所以当点P 位于1B 或1D 时,//PA 平面1BDC , 当P 移动一次后到达点1B 或1D 时,所以概率为1112423⨯=>,故B 错误; 对于C ,()11,1,1,A C n =--=所以当点P 位于1A 时,PC ⊥平面1BDC ,所以移动n 次后点P 位于1A ,则1111+4222nn a ⎛⎫=-< ⎪⎝⎭,故C 正确;对于D ,四面体1P BDC -体积V 的数学期望()11111111=n A BDC n B BDC n C BDC n D BDC E V a V b V c V d V ----⋅+⋅+⋅+⋅12BDC S == ()11,0,1DA = , 所以点1A 到平面1BDC的距离为11DA n d n ⋅===同理点111,,B C D 到平面1BDC所以111111111111,,03336A BDCB BDCD BDC C BDC V V V V ----======, 所以()11111111111=+0+42234646662n n E V ⎡⎤⎛⎫⎛⎫-⋅+⨯++⨯=-⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦,当n 为偶数,所以()11151=+662245nE V ⎛⎫≤< ⎪⎝⎭,当n 为奇数,所以()11111=66265nE V ⎛⎫-<< ⎪⎝⎭,故D 正确.故选:ACD.【点睛】关键点睛:本题的关键点是先求出点P 在移动n 次后,点1111,,,A B C D 的概率,再结合由向量法求出线面垂直、线面平行和三棱锥的体积,对选项一一判断即可得出答案.非选择题部分三、填空题:本题共3小题,每小题5分,共15分.12. 已知圆柱的轴截面面积为4,则该圆柱侧面展开图的周长最小值为__________.【答案】 【解析】【分析】将圆柱的母线长和底面圆半径分别设为,l r ,根据已知和基本不等式求出侧面展开图面积的最小值. 【详解】设圆柱的母线长和底面圆半径分别设为,l r ,根据已知得24lr =,由题意可得圆柱侧面展开图的周长可以表示为4π2L r l =+≥=侧,当且仅当4π2r l =时,即r =,l =.故答案为:13. 某中学的A 、B 两个班级有相同的语文、数学、英语教师,现对此2个班级某天上午的5节课进行排课,2节语文课,2节数学课,1节英语课,要求每个班级的2节语文课连在一起,2节数学课连在一起,则共有__________种不同的排课方式.(用数字作答) 【答案】8 【解析】【分析】由a 表示数学课,b 表示语文课,c 表示英语课,按上午的第1、2、3、4、5节课顺序,列出所有可能情况可得答案.【详解】由a 表示数学课,b 表示语文课,c 表示英语课, 按上午的第1、2、3、4、5节课排列,可得 若A 班排课为aabbc ,则B 班排课为bbcaa , 若A 班排课为bbaac ,则B 班排课为aacbb ,若A 班排课为aacbb ,则B 班排课为bbaac ,或B 班排课为cbbaa , 若A 班排课为bbcaa ,则B 班排课为aabbc ,或B 班排课为caabb , 若A 班排课为cbbaa ,则B 班排课为aacbb , 若A 班排课为caabb ,则B 班排课为bbcaa , 则共有8种不同的排课方式. 故答案为:8.14. 设正n 边形的边长为1,顶点依次为12,,,n A A A ,若存在点P 满足120PA PA ⋅=u u u r u u u r,且11n k k PA ==∑u u u r,则n 的最大值为__________.(参考数据:tan 360.73︒≈)【答案】5 【解析】【分析】由题意确定P 点的轨迹,分类讨论,结合向量的运算说明正六边形中以及7n ≥时不符合题意,说明5n =时满足题意,即可得答案.【详解】由题意知点P 满足120PA PA ⋅=u u u r u u u r,则P 点在以12A A 为直径的圆上, 当6n =时,设,,,B C D M 为123456,,,A A A A A A CD 的中点,如图,61||2||2|2|k k PA PB PC PD PB PM ==++=+∑ ,当,PB PM共线且方向时,即,,B P M 三点共线时,1||n k k PA =∑ 取最小值,此时1||2PB BM ==,||,则1||2PM = ,则min 2|2|31PB PM +=->,故6n =时,不满足题意;当5n =时,设,C N 为1235,A A A A 的中点,如图,541|||22|k K PA PC PN PA ==++∑ ,当4,PC PA共线且反向时,51||k K PA =∑ 取最小值,此时4,,,C P N A 共线,144442tan 3672,tan 72 3.13,|tan 72 1.56,||| 1.061tan 36211||22A A C CA PA CA ︒︒︒︒∠===⨯--≈≈=≈,453436||1sin 3610.59,|| 1.060.590.47,A A A A N PN ∠==⨯≈≈≈-=∴ ,则4min |22||120.47 1.06|1PC PN PA ++≈-⨯-=,则当4,PC PA 共线且同向时,必有4max |22|1PC PN PA ++>,故5n =时,存在点P 满足120PA PA ⋅=u u u r u u u r,且11n k k PA ==∑;当7n ≥时,如图,正七边形的顶点到对边的高h 必大于正六边形对边之间的高,依此类推,故此时不存在点P 满足120PA PA ⋅=u u u r u u u r,且11n k k PA ==∑;故n 的最小值为5, 故答案为:5【点睛】难点点睛:本题考查了平面向量的运算以及向量的模的最值问题,综合性较强,难度加大,难点在于要分类讨论正n 边形的情况,结合向量的加减运算,确定模的最值情况.四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15. 已知等差数列{}n a 的前n 项和为n S ,且2221n n S a n =+-. (1)求n a ;(2)求数列11n n a a +⎧⎫⎨⎬⎩⎭的前n 项和n T .【答案】(1)*1,2n a n n =+∈N(2)22323n T n =-+ 【解析】【分析】(1)根据,n n a S 关系求通项公式即可; (2)裂项相消法求和即可得解. 【小问1详解】 由2221n n S a n =+-①所以当2n ≥时,21122(1)1n n S a n --=+--②②-①得:122221n n n a a a n -=-+-,整理得:11,22n a n n -=-≥, 所以*1,2n a n n =+∈N . 【小问2详解】 由(1)知12n a n =+, 所以1111122131321232222n n a a n n n n n n +==-=-++⎛⎫⎛⎫++++ ⎪⎪⎝⎭⎝⎭, 所以122311112222222235572123323n n n T a a a a a a n n n +=+++=-+-++-=-+++ . .16. 如图,在四棱锥P ABCD -中,四边形ABCD 是边长为2的正方形,平面PAD ⊥平面ABCD,PA PD ==,点E 是线段AD 的中点,2CM MP =.的(1)证明:PE //平面BDM ; (2)求平面AMB 与平面BDM 的夹角. 【答案】(1)证明见解析(2)π3. 【解析】【分析】(1)连接EC 交BD 于N ,连接MN ,根据条件证明MN //PE 即得;(2)先证明PE ⊥平面ABCD ,依题建系,求出相关点和向量的坐标,分别求得平面AMB 与平面BDM 的法向量,最后由空间向量的夹角公式求解即得. 【小问1详解】如图,连接EC 交BD 于N ,连接MN ,由E 是AD 的中点可得11122DE AD BC ===, 易得DEN 与BCN △相似,所以12EN NC =, 又12PM MC =,所以MN //PE , 又MN ⊂平面,BDM PE ⊄平面BDM ,所以PE //平面BDM ; 【小问2详解】因平面PAD ⊥平面ABCD ,且平面PAD ⋂平面ABCD AD =,由PA PD ==,点E 是线段AD 的中点可得,PE AD ⊥又PE ⊂平面PAD ,故得PE ⊥平面ABCD .如图,取BC 的中点为F ,分别以,,EA EF EP为,,x y z 轴的正方向,建立空间直角坐标系.则()()0,0,0,1,0,0E A ,()()()()1,0,0,1,2,0,1,2,0,0,0,2D B C P --,()11221,2,2,,,3333PC PM PC ⎛⎫=--==-- ⎪⎝⎭ ,则124,,333M ⎛⎫- ⎪⎝⎭,.设平面AMB 的法向量为()1111,,n x y z =,由()4240,2,0,,,333AB AM ⎛⎫==- ⎪⎝⎭,则11111120424333n AB y n AM x y z ⎧⋅==⎪⎨⋅=-++=⎪⎩,故可取()11,0,1n = ; 设平面BDM 的法向量为()2222,,n x y z =,由()4442,2,0,,,333BD BM ⎛⎫=--=-- ⎪⎝⎭,则2222222220444333n BD x y n BM x y z ⎧⋅=--=⎪⎨⋅=--+=⎪⎩,故可取()21,1,0n =- . 故平面AMB 与平面BDM的夹角余弦值为1212121cos ,2n n n n n n ⋅〈〉===, 所以平面AMB 与平面BDM 的夹角为π3. 17. 某工厂生产某种元件,其质量按测试指标划分为:指标大于或等于82为合格品,小于82为次品,现抽取这种元件100件进行检测,检测结果统计如下表: 测试指标 [)20,76[)76,82[)82,88[)88,94[]94,100元件数(件) 121836304(1)现从这100件样品中随机抽取2件,若其中一件为合格品,求另一件也为合格品的概率; (2)关于随机变量,俄国数学家切比雪夫提出切比雪夫不等式:若随机变量X 具有数学期望()E X μ=,方差()2D X σ=,则对任意正数ε,均有()22P x σμεε-≥≤成立.(i )若1~100,2X B ⎛⎫ ⎪⎝⎭,证明:1(025)50P X ≤≤≤; (ii )利用该结论表示即使分布未知,随机变量的取值范围落在期望左右的一定范围内的概率是有界的.若该工厂声称本厂元件合格率为90%,那么根据所给样本数据,请结合“切比雪夫不等式”说明该工厂所提供的合格率是否可信?(注:当随机事件A 发生的概率小于0.05时,可称事件A 为小概率事件) 【答案】(1)2343(2)(i )证明见解析;(ii )不可信. 【解析】【分析】(1)由条件概率的公式进行求解即可; (2)(i )由1~100,2X B ⎛⎫⎪⎝⎭求出()()50,25E X D X ==,再结合切比雪夫不等式即可证明;(ii )设随机抽取100件产品中合格品的件数为X ,()100,0.9X B :,由切比雪夫不等式判断出()()97090200.0225400P X P X =≤-≥≤=,进而可得出结论. 【小问1详解】记事件A 为抽到一件合格品,事件B 为抽到两个合格品,()()222701003022100100C C C 161301,C 330C 330P AB P A -==== ()()()16123.30143P AB P B A P A ===∣ 【小问2详解】(i )由题:若1~100,2X B ⎛⎫⎪⎝⎭,则()()50,25E X D X == 又()()1001001C100,2k P X k P X k ⎛⎫====- ⎪⎝⎭所以()1025(0252P X P X ≤≤=≤≤或()175100)50252X P X ≤≤=-≥ 由切比雪夫不等式可知,()225150252525P X -≥≤= 所以()102550P X ≤≤≤;(ii )设随机抽取100件产品中合格品的件数为X ,假设厂家关于产品合格率为90%的说法成立,则()100,0.9X B :, 所以()()90,9E X D X ==,由切比雪夫不等式知,()()97090200.0225400P X P X =≤-≥≤=, 即在假设下100个元件中合格品为70个的概率不超过0.0225,此概率极小,由小概率原理可知,一般来说在一次试验中是不会发生的,据此我们有理由推断工厂的合格率不可信.18. 已知椭圆2222:1(0)x y L a b a b+=>>的左顶点()30A -,和下顶点B ,焦距为,直线l 交椭圆L 于C ,D (不同于椭圆的顶点)两点,直线AD 交y 轴于M ,直线BC 交x 轴于N ,且直线MN 交l 于P . (1)求椭圆L 的标准方程;(2)若直线AD ,BC 的斜率相等,证明:点P 在一条定直线上运动.【答案】(1)22:19x L y +=(2)证明见解析 【解析】【分析】(1)由顶点坐标和焦距可求出椭圆标准方程;(2)设直线AD ,BC 的斜率为k ,联立直线():3AD y k x =+和椭圆方程,得到()22,,D x y 联立直线:1BC y kx =-和椭圆方程()11,,C x y 由于AD //BC ,所以MP DP PNPC=,可得点()00,P x y ,利用消元法可得点P 的轨迹方程,即可得证. 【小问1详解】由已知得:3,a c ==1b =,所以椭圆22:19x L y +=【小问2详解】设直线,AD BC 的斜率为()()()112200,,,,,,k C x y D x y P x y .则直线():3AD y k x =+,直线:1BC y kx =-,得()10,3,,0M k N k ⎛⎫⎪⎝⎭联立()223,99y k x x y ⎧=+⎨+=⎩得()222219548190kxk x k +++-=,易知Δ0>.由222819319k x k --⨯=+,得22232719k x k -=+,于是()2226319k y k x k =+=+.同理:211221891,1919k k x y k k -==++ 由于AD //BC ,所以MP DP PN PC =,即20200023271911819k x x k k x x k k--+=--+,得0331x k =+①,同理0331ky k =+②,由①②得00330x y +-=, 故点P 在直线330x y +-=上运动.【点睛】关键点点睛:本题的关键是设出直线,AD BC 的方程,联立直线方程和椭圆方程,得到点,C D 的坐标,从而得解.19. ①在微积分中,求极限有一种重要的数学工具——洛必达法则,法则中有结论:若函数()f x ,()g x 的导函数分别为()f x ',()g x ',且lim ()lim ()0x a x af xg x →→==,则 ()()lim lim ()()x a x a f x f x g x g x ''→→=. ②设0a >,k 是大于1的正整数,若函数()f x 满足:对任意[]0,x a ∈,均有()x f x f k ⎛⎫≥ ⎪⎝⎭成立,且()0lim 0x f x →=,则称函数()f x 为区间[]0,a 上的k 阶无穷递降函数. 结合以上两个信息,回答下列问题:(1)试判断()33f x x x =-是否为区间[]0,3上的2阶无穷递降函数;(2)计算:10lim(1)xx x →+;(3)证明:3sin cos πx x x ⎛⎫< ⎪-⎝⎭,3π,π2x ⎛⎫∈ ⎪⎝⎭. 【答案】(1)()33f x x x =-不是区间[]0,3上的2阶无穷递降函数;(2)10lim(1)e xx x →+=(3)证明见解析 【解析】【分析】(1)根据函数()f x 为区间[]0,a 上k 阶无穷递降函数的定义即可判断;(2)通过构造()()=ln h x g x ,再结合()()lim lim ()()x a x a f x f x g x g x ''→→=即可得到结果;(3)通过换元令令πx t -=,则原不等式等价于23πtan sin ,0,2t t t t ⎛⎫⋅≥∈ ⎪⎝⎭,再通过构造函数()23tan sin π,0,2t t f t t t ⋅⎛⎫=∈ ⎪⎝⎭,根据题干中函数()f x 为区间π0,2⎡⎤⎢⎥⎣⎦上的k 阶无穷递降函数的定义证出()π1,0,2f t t ⎛⎫>∈ ⎪⎝⎭,即可证明结论.【小问1详解】 设()()373282x F x f x f x x ⎛⎫=-=- ⎪⎝⎭,由于()731082F =-<, 所以()2x f x f ⎛⎫≥⎪⎝⎭不成立, 故()33f x x x =-不是区间[]0,3上的2阶无穷递降函数.【小问2详解】设()1(1)xg x x =+,则()()()ln 11ln ln 1x g x x x x+=+=, 设()()ln 1x h x x+=,则0001ln(1)1lim ()lim lim 11x x x x x h x x →→→++===,所以0lim ln ()1x g x →=,得1lim(1)e xx x →+= 【小问3详解】的.令πx t -=,则原不等式等价于23πtan sin ,0,2t t t t ⎛⎫⋅≥∈ ⎪⎝⎭, 即证23tan sin π1,0,2t t t t ⋅⎛⎫≥∈ ⎪⎝⎭, 记()23tan sin π,0,2t t f t t t ⋅⎛⎫=∈ ⎪⎝⎭,则238tan sin 222t tt f t ⋅⎛⎫= ⎪⎝⎭, 所以()2233224cos tan sin 1218tan sin 1tan 1tan 22222tf t t t t t t t t t t f ⋅=⋅==>⎛⎫⋅-- ⎪⎝⎭, 即有对任意π0,2t ⎛⎫∈ ⎪⎝⎭,均有()2t f t f ⎛⎫> ⎪⎝⎭,所以()22n t t f t f f ⎛⎫⎛⎫>>> ⎪ ⎪⎝⎭⎝⎭, 因为00sin limlim cos 1x x xx x→→==,所以33233sin sin tan sin 12222lim lim lim lim lim 12cos cos 22222n n n n n n n n n n n n n n n t t t t t f t t t t t →+∞→+∞→+∞→+∞→+∞⎡⎤⎛⎫⎛⎫⋅ ⎪ ⎪⎢⎥⎛⎫⎝⎭⎝⎭⎢⎥===⋅= ⎪⎛⎫⎝⎭⎢⎥⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎣⎦⎝⎭⎝⎭⎝⎭, 所以()π1,0,2f t t ⎛⎫>∈ ⎪⎝⎭,证毕!【点睛】方法点睛:利用函数方法证明不等式成立问题时,应准确构造相应的函数,注意题干条件中相关限制条件的转化.。
2020届浙江省金丽衢十二校高三下学期第二次联考技术试卷及答案

2020届浙江省金丽衢十二校高三下学期第二次联考技术试卷
2020届浙江省金丽衢十二校高三下学期第ቤተ መጻሕፍቲ ባይዱ次联考技术试卷
2020届浙江省金丽衢十二校高三下学期第二次联考技术试卷
2020届浙江省金丽衢十二校高三下学期第二次联考技术试卷
2020届浙江省金丽衢十二校高三下学期第二次联考技术试卷
2020届浙江省金丽衢十二校高三下学期第二次联考技术试卷
2020届浙江省金丽衢十二校高三下学期第二次联考技术试卷
金丽衢十二校2020届高三生物下学期第二次联考试题含解析

B。 “选择放松”对人群中的致病基因频率影响很小
C。 多基因遗传病的发病风险随年龄的增加而升高
D. 对胎儿细胞的染色】D
【解析】
【分析】
1、一般认为,引起疾病的基因是有害的,称为“致病基因”。但随着基因技术研究的深入,我们又认识到基因也具有二重性。
【详解】A、一个神经元轴突末梢可分支形成多个突触小体,进而与骨骼肌形成多个突触,A正确;
B、A和a是等位基因,是控制相对性状的基因,他们控制的是同一性状,B错误;
C、细胞分化的实质是基因的选择性表达,所以核酸种类(mRNA)可发生变化,C正确;
D、非同源染色体上的非等位基因遗传遵循自由组合定律,如果非等位基因在同一条染色体上则并不遵循该定律,D错误;
故选C.
10.神经元是神经系统结构和功能的基本单位,下列有关叙述正确的是( )
【详解】A、氢键使水分蒸发时需要消耗大量的热,因为水分蒸发时要破坏氢键,因此出汗能有效地降低体温,水温的升高也需要较多的热,因为先要破坏氢键才能促进分子的运动。反之,水温的降低会形成较多的氢键,而氢键的形成又会释放热量,这就使得细胞内的温度变化比较缓和,A正确;
B、血浆中含有多种无机盐,包括Na+、K+、Ca2+、Mg2+等正离子,以及Cl-、HCO3—、H2PO4-等负离子,这些离子对于维持血浆的正常浓度、酸碱平衡和神经肌肉的兴奋性等都是非常重要的,但并不是在维持神经肌肉兴奋性中各种离子都能发挥作用,B错误;
B、肺炎双球菌属于原核生物,遗传物质为核酸中的DNA,新型冠状病毒为RNA病毒,遗传物质为核酸中的RNA,B正确;
C、肺炎双球菌为原核生物,无成形的细胞核,无各种复杂的细胞器,只含一种细胞器核糖体,新型冠状病毒无细胞结构,因此肺炎双球菌与新型冠状病毒都没有细胞核和线粒体,C正确;
2020年浙江省金丽衢十二校高考物理二模试卷含答案

高考物理二模试卷题号一二三四五六七总分得分一、单选题(本大题共13小题,共39.0分)1.下列物理量属于矢量的是()A. 速率B. 电势C. 磁感应强度D. 重力势能2.发现行星运动三大定律的科学家是()A. 牛顿B. 伽利略C. 卡文迪许D. 开普勒3.下列物理量及对应的单位不正确的是()A. 加速度m/s2B. 磁感应强度BC. 磁通量WbD. 电场强度V/m4.一物体沿直线运动,在t=0到t=6s的时间内的v-t图象如图所示,则这段时间内的路程为()A. 8mB. 4mC. 6mD. 0m5.把质量是0.2kg的小球放在竖立的弹簧上,并把球往下按至A的位置,如图甲所示。
迅速松手后,弹簧把球弹起,球升到最高位置C(图丙),途中经过位置B时弹簧正好处于自由状态(图乙)。
已知B、A的高度差为0.1m,C、B的高度差为0.2m,弹簧的质量和空气的阻力均可忽略。
则()A. 小球从状态乙到状态丙的过程中,动能先增大,后减小B. 小球从状态甲到状态丙的过程中,机械能一直不断增大C. 状态甲中,弹簧的弹性势能为0.6JD. 状态乙中,小球的动能为0.6J6.一真空中孤立的带电体,其周围的电场线及等势面如图所示,则下列说法正确的是()A. A点的电势比B点的电势高B. A点的场强比B点的场强大C. 一微小的带电体从A点移动到B点电场力做负功D. 一微小的带电体从A点移动到B点电场力做正功7.“辽宁舰质量为m=6×106kg,如图是“辽宁舰”在海上转弯时的照片,假设整个过程中辽宁舰做匀速圆周运动速度大小为20m/s,圆周运动的半径为1000m,下列说法中正确的是()A. 在A点时水对舰的合力指向圆心B. 在A点时水对舰的合力大小约为F=6.0×107NC. 在A点时水对舰的合力大小约为F=2.4×106ND. 在A点时水对舰的合力大小为08.如图所示,三块一样的蹄形磁铁并排放置在粗糙水平桌面上,S极在上,N极在下,导体棒AB单位长度的电阻为R,导体棒所在位置的磁感应强度相同。
2020年浙江省金丽衢十二校高考化学第二次联考试卷(附答案详解)
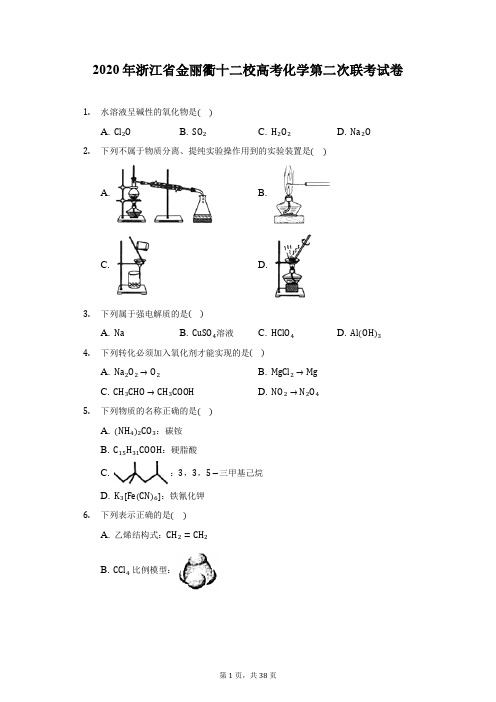
2020年浙江省金丽衢十二校高考化学第二次联考试卷1.水溶液呈碱性的氧化物是()A. Cl2OB. SO2C. H2O2D. Na2O2.下列不属于物质分离、提纯实验操作用到的实验装置是()A. B.C. D.3.下列属于强电解质的是()A. NaB. CuSO4溶液C. HClO4D. Al(OH)34.下列转化必须加入氧化剂才能实现的是()A. Na2O2→O2B. MgCl2→MgC. CH3CHO→CH3COOHD. NO2→N2O45.下列物质的名称正确的是()A. (NH4)2CO3:碳铵B. C15H31COOH:硬脂酸C. :3,3,5−三甲基己烷D. K3[Fe(CN)6]:铁氰化钾6.下列表示正确的是()A. 乙烯结构式:CH2=CH2B. CCl4比例模型:C. 氟离子的结构示意图:D. 氨基的电子式:7.下列说法不正确的是()A. 乙醇和乙醚互为同分异构体B. 红磷和白磷互为同素异形体C. 612C和 614C互为同位素D. 甲烷和异丁烷互为同系物8.下列说法正确的是()A. 石灰石是生产玻璃、水泥、炼铁的工业原料B. 石英砂高温下经焦炭氧化可制得粗硅C. 工业铝的冶炼,加入冰晶石是为了降低Al2O3的熔点,从而节约能耗D. 以硫黄原料,在沸腾炉中硫磺可直接氧化为SO39.下列说法正确的是()A. 检验醛基时,新制Cu(OH)2悬浊液可由NaOH溶液和过量CuSO4溶液混合制得B. 可通过铝热反应制备金属镁C. 可通过油脂的皂化反应制备甘油和肥皂D. 泡沫灭火器内简盛硫酸铝溶液,外简和内筒之间装有碳酸钠溶液10.下列说法不正确的是()A. 石油裂解的主要目的是获得乙烯、丙烯、丁二烯等短链不饱和烃B. 煤的干馏、气化、液化均涉及化学变化C. 绿色植物光合作用属于生物化学转换D. 汽油、柴油属于烃类物质,植物油、动物油属于酯类物质11.下列说法不正确的是()A. 挤少量牙膏溶于水,加入新制Cu(OH)2,振荡,若溶液呈绛蓝色,说明牙膏中可能含有甘油B. 受溴腐蚀致伤,先用苯或甘油洗涤伤口,再用水冲洗C. 可用碱式滴定管或移液管量取22.10mL KMnO4溶液D. 分离硝酸钾与氯化钠,先将混合物溶于水,再经蒸发浓缩、趁热过滤、冷却结晶、过滤、洗涤、干燥等系列操作完成12.下列说法不正确的是()A. 医用外科口罩用完后应投入中标志的垃圾箱中回收B. 口罩的过滤层材料为熔喷聚丙烯,聚两烯的链节与单体组成相同、结构不同C. 75%酒精可用于皮肤消毒,其原理是酒精能使构成细菌的蛋白质变性D. 84消毒液(NaClO)与洁厕灵(盐酸)不能混合使用,以防氯气中毒13.下列说法正确的是()A. 利用浓溴水可鉴别己烯、己烷、四氯化碳、苯酚、乙醇B. 乙酸乙酯中混有乙酸,可加入氢氧化钠固体,再通过加热蒸馏除去C. 为检验淀粉在敢性环境下是否完全水解,应在水解液中加入过量的氢氧化钠,然后加入少量碘水进行检验D. 蛋白质、纤维素、油脂、核酸的水解都属于由高分子转变成小分子的取代反应14.下列离子方程式不正确的是()A. CaCO3溶于醋酸:CaCO3+2CH3COOH=Ca2++2CH3COO−+CO2↑+H2OB. NH4HCO3中加入足量NaOH溶液:NH4++HCO3−+2OH−=CO32−+H2O+NH3⋅H2OC. 含1molFeBr2溶液中通入lmolCl2:2Fe2++4Br−+3Cl2=2Fe3++Br2+6Cl−D. NaHSO3溶液中加入少量H2O2:HSO3−+H2O2=SO42−+H2O+H+15.对于有机物,下列说法不正确的是()A. 能使酸性KMnO4溶液褪色B. 一定条件下能发生缩聚反应C. 1mol该有机物最多能与3mol氢气加成D. 所有原子可能共面16.下列说法正确的是()A. 同主族元素之间核电荷数可能相差8、16、26、32B. 第2周期元素(除氖外),随着核电荷数递增,最高正化合价从+1→+7C. 同主族元素的单质,随着核电荷数递增,熔沸点逐渐升高D. 稀有气体元素原子中,核外各电子层均已排满,形成稳定的电子层结构17.下列说法正确的是()A. 升高温度,0.1mol⋅L−1的氢氧化钠溶液pH值减小,碱性减弱B. 相同温度下浓度相等的苯酚钠溶液与醋酸钠溶液的pH:前者大于后者C. 室温下0.005mol⋅L−1的硫酸溶液中,由水电离出的氢离子浓度等于2×10−12mol⋅L−1D. 室温下pH相等的盐酸与醋酸溶液分别与同浓度的NaOH溶液中和,前者消耗的NaOH多18.如图装置是探究电解工作原理及氢氧燃料电池工作原理示意图,实验时,先闭合S1,断开S2,电解水一段时间后,再断开S1,闭合S2,二极管能持续发光,下列有关说法正确的是()A. 电解质溶液可以为NaOH、H2SO4或Na2SO4溶液B. 在闭合S1断开S2时,右侧多孔碳棒电极上失去电子,发生氧化反应,吸附氢气C. 若电解质溶液为NaOH,在断开S1闭合S2时,左侧多孔碳棒电极作正极,电极反应式为:H2−2e−+2OH−=2H2OD. 在断开S1闭合S2时,Na+向左侧多孔碳棒迁移,电子由负极经外电路流向正极,再由正极经电解液流向负极,构成回路19.下列说法正确的是()A. NH2COONH4(s)⇌2NH3(g)+CO2(g),增加NH2COONH4的量能加快正反应速率B. FeCl3⋅6H2O(s)⇌FeCl3(s)+6H2O(g),HCl气流能抑制反应进行C. NaCl(s)⇌Na+(aq)+Cl−(aq),加入KCl固体,能减少NaCl的溶解D. N2(g)+3H2(g)⇌2NH3(g),加压,有利于增加活化分子百分数,平衡向右移动20.关于阿伏加德罗常数N A,下列说法正确的是()A. KClO3+6HCl=3Cl2↑+KCl+3H2O,反应生成标准状况下6.72L氯气时转移电子数为0.6N AB. 将lmolCl2溶于水,溶液中2N(Cl2)+N(Cl−)+N(HClO)+N(ClO−)=2N A(N代表微粒数)C. H+(aq)+OH−(aq)=H2O(l),ΔH=−57.3kJ⋅mol−1,当2N A个醋酸分子与NaOH恰好中和时放热114.6kJD. 已知小分子的直径一般约为10−10m,1molFeCl3完全水解可生成N A个Fe(OH)3胶粒21.甲烷可消除NO2污染:CH4+2NO2⇌N2+CO2+2H2O,在2L密闭容器中控制不同温度,分别加入0.50molCH4和1.2molNO2,测得n(CH4)随时间变化的有关实验数据见如表:下列说法正确的是()A. 组别②中,0~20min内,NO2的降解速率为0.016mol⋅L−1⋅min−1B. 由实验数据可知实验控制的温度T1<T2C. 40min时,表格中省略的数据可能为0.18D. 组别①中,NO2的平衡转化率为80%22.可逆反应NO2(g)+CO(g)⇌CO2(g)+NO(g)反应过程中的能量变化如图所示,下列说法正确的是()A. 1molNO2与1molCO在处于过渡态时的能量是134kJB. 若反应开始时加入催化剂,能使E1变小、E2变大,所以正反应速率加快C. 1molNO2和1molCO断键所需的能量小于1molCO2和1molNO断键所衢的能量D. 该反应的反应热ΔH=+234kJ⋅mol−123.室温下,用0.100mol⋅L−1NaOH溶液分别滴定20.00mLamol⋅L−1的盐酸和醋酸溶液,滴定曲线如图所示,下列说法不正确的是()A. 窒温下,K a(CH3COOH)的数量级为10−5B. pH=7时,c(Cl−)=c(CH3COO−)C. V(NaOH)=10.00mL时,c(CH3COO−)>c(CH3COOH)D. V(NaOH)=20.00mL时,醋酸对应的溶液中存在c(H+)+c(CH3COOH)=c(OH−)24.将过氧化氢水溶液与饱和碳酸钠溶液置于反应釜中,控制温度在5℃以下进行反应,然后加入异丙醇使过碳酸钠(2Na2CO3⋅3H2O2)结晶、分离。
2020届金丽衢十二校第二次联考生物答案

2020届金丽衢十二校第二次联考生物参考答案与评分标准1-5:BDBDD 6-10:DDDCA 11-15:DCCCD 16-20:DCCBB 21-25:BAABD 26.(每空1分,共7分)(1)食物链与食物网(写全给分)腐食食物链(2)季相自然选择(3)均匀分布(4)害虫抗药性增强(或生物放大)利用害虫的天敌进行生物防治(或培育抗虫果树,写出生物防治也给分)27.(每空1分,共8分)(1)RuBP(或五碳糖或核酮糖二磷酸)三碳酸/3-磷酸甘油酸(2)基粒(3)RuBP和PEP(答全给分)为维管束鞘细胞的卡尔文循环提供CO2(4)碳反应脱落酸高温和高光强(答全给分)28.(每空1分,遗传图解3分,共9分)(1)染色体组染色体组型(或染色体核型)(2) AAX B X B、AAX B X b (答全给分)0或1或2(答全给分)(3)AX B:AX b:aX B:aX b-=6:2:3:1 1/2429.(每空1分,最后一空2分,共16分)(一)(1)排走冷空气(2)发酵过程中葡萄皮的色素进入到发酵液中两层纱布(写出纱布即给分)增加酒精含量与糖含量(答全给分);(3)等体积不需要有氧温度、食盐用量和腌制时间等;(二)(1)花药(或花粉)有丝分裂中期的染色体数目(写出染色体数目即给分)(2)细胞系(或细胞株)培养时间、人参细胞产量(或细胞数量、密度)(答全给分)(3)限制性核酸内切酶和DNA连接酶(答全给分)基因探针(或核酸探针、单抗特异探针)释放信号分子、吸引农杆菌;促进脱分化有利于形成愈伤组织(每写对一点给1分)30.(每空1分,曲线图3分,共10分)(一)①适量生理盐水②每隔一段时间测定癌细胞数量/癌细胞细胞周期时间(“每隔一段时间”必须写出,否则不给分)③对所得实验数据进行统计和分析(二)①(共3分,标题1分,横纵轴标示1分,曲线正确1分)②细胞周期的总长及各时期所占的比例/细胞周期的总长及各时期细胞所占的比例③RNA聚合酶影响cyclin B基因的表达、影响cyclin B蛋白与P蛋白的结合、影响CDK1的活性等④癌细胞表面特有的膜蛋白。
2020金丽衢十二校第二次联考数学试卷及答案

数学试题卷 第 4 页 (共 4 页)
2020 学年金丽衢十二校高三第二次联考
数学评分标准与参考答案
一、选择题(4×10=40 分)
题号 1
2
3
4
5
6
7
8
9
10
答案 B
D
A
B
C
A
D
D
A
C
二、填空题(多空题每题 6 分,单空题每题 4 分,共 36 分)
11.5; 12.-16, 20 ; 13.[2, 3) , 3 ; 14. 2 , 9 ;
交于 A, B 两点(AF<BF),点 C(不同于原点)在抛物线上,PC 不平行于 x 轴,且 PC 与抛
物线有且只有一个公共点.
当t 2
2
时,
AF
1 2
FB
.
(Ⅰ)求 p 的值;
(Ⅱ)若 CA,CB 分别与 x 轴交于 D, E ,设 ADF , BEF 和 ABC的面积分别为 S1, S2, S ,
A.74
B.73
C.70
D.0
5.过原点 O 作曲线 16a2 6x 8y a x2 y2 0a 0 的切线 OA, OB ,则 cos AOB
(▲)
A. 3 5
B. 4 5
C. 7 25
D. 24 25
6.已知 a 0, b 0 , 则“ ab ≥100 ”的一个充分不必要条件是( ▲ )
第Ⅱ卷(共 110 分)
二、填空题(本大题共 7 小题,多空题每题 6 分,单空题每题 4 分,共 36 分。) 11.设复数 z 满足: | z | z 1 3i ( i 是虚数单位),则 | z | ▲ . 12.已知 (x 1)4(1 2x)3 a0 a1x a2x2 a7x7 ,则 a0 a1 a7 = ▲ , a6 = ▲ . 13.函数 f (x) 3 cos x sin x , x (0, π) 的值域为 ▲ ,若 f (x) 2 , x (0, π)
浙江省金丽衢十二校2020届高三下学期第二次联考数学试题(解析版)

金丽衢十二校2019学年高三第二次联考数学试题第Ⅰ卷(共40分)一、选择题(本大题共10小题,每小题4分,共40分.在每个小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合{0,1,2,3,}I =集合{0,1},{0,3},M N ==则()I N M =I ð( )A. {0}B. {3}C. {0,2,3}D. ∅ 【答案】B【解析】【分析】根据交集、补集的定义计算可得;【详解】解:因为集合}{0,1,2,3I =,集合{0,1},{0,3}M N ==,所以{}2,3I M =ð,{}()3I N M =I ð故选:B【点睛】本题考查集合的运算,属于基础题.2.双曲线2231x y -=的渐进线方程为( )A. y =B. 2y x =±C. y =D. 3y x =±【答案】C【解析】【分析】先将双曲线的方程化为标准方程,求得,a b ,写出其渐进线方程. 【详解】因为双曲线的标准方程为:22113x y -=,所以1a b ==,所以双曲线的渐进线方程为b y x a=±=. 故选:C 【点睛】本题主要考查双曲线的几何性质,还考查了运算求解的能力,属于基础题.3.若实数x ,y 满足约束条件236021x y y x -+⎧⎨-⎩……,则z =3x +y 的最小值为( ) A. 13 B. 3 C. 2D. 1 【答案】C【解析】【分析】画出不等式表示的平面区域,根据z 的几何意义求解即可.【详解】22,12|1|22,1x x y x x x -≥⎧=-=⎨-<⎩Q∴该不等式组对应的平面区域,如下图所示3z x y =+可化为3y x z =-+平移直线3y x =-,当直线过点(0,2)A 时,z 取最小值即min 3022z =⨯+=故选:C【点睛】本题主要考查了线性规划求最值的应用,属于中档题.4.已知某几何体的三视图如图所示,则这个几何体的体积为( )A. 2B. 23C. 1D. 4 【答案】A【解析】【分析】将三视图还原可得一个以俯视图为底面直三棱柱,代入棱柱体积公式,可得答案.【详解】解:将三视图还原可得一个以俯视图为底面的直三棱柱, 所以112222V Sh ==⨯⨯⨯=. 故选:A.【点睛】本题考查由三视图求体积,根据已知分析出几何体形状,是解答的关键.5.设m ∈R ,已知圆1:C 221x y +=和圆2C :2268300x y x y m +--+-=,则“21m >”是“圆C 1和圆C 2相交”的( ) A. 充分而不必要条件 B. 必要而不充分条件C. 充要条件D. 既不充分也不必要条件 【答案】B 的【解析】【分析】根据题意先求出两圆心的距离12C C ,再利用圆C 1和圆C 2相交列不等式121212||r r C C r r -<<+求出m 的范围,即可得答案.【详解】解:由已知圆2C :()()22345x y m -+-=-,若圆C 1和圆C 2相交,则121||5C C <==<,解得2141m <<,“21m >”是“2141m <<”的必要而不充分条件.故选:B.【点睛】本题考查圆和圆的位置关系,考查充分性和必要性的判断,关键是熟练判断圆与圆的位置关系,是基础题.6.已知函数f (x )的定义域为D ,其导函数为()f x ',函数'sin ()()y x f x x D =⋅∈的图象如图所示,则f (x )( )A. 有极小值f (2),极大值f (π)B. 有极大值f (2),极小值f (0)C. 有极大值f (2),无极小值D. 有极小值f (2),无极大值【答案】D【解析】【分析】 通过sin x 的正负取值以及'sin ()x f x ⋅的正负取值,可判断函数()f x 在定义域D 上的单调性,进而可判断极值的取值情况.【详解】解:当()0,x π∈,sin 0x >,当()(),0,2x πππ∈-U ,sin 0x <则由图像可得当(),2x π∈-时,()0f x '≤,当()2,2x π∈时,()0f x '≥,故函数()f x 在(),2π-上单调递减,在()2,2π上单调递增,则由图像可得函数f (x )在定义域D 上,先减后增,有极小值f (2),无极大值.故选:D.【点睛】本题考查导函数的图像和原函数单调性之间的关系,考查函数在某点取得极值的条件,考查学生识图用图能力,是基础题.7.设01,a n R <<∈,随机变量X 的分布列是则随机变量X 的方差D (X )( )A. 既与n 有关,也与a 有关B. 与n 有关,但与a 无关C. 既与a 无关,也与n 无关D. 与a 有关,但与n 无关【答案】D【解析】【分析】根据分布列计算()E X n a =+,再计算()2D X a a =-,得到答案. 【详解】根据分布列得到()()()11E X n a n a n a =-++=+,故()()()()()()2223232112D X a n E X a n E X a a a a a a a =--++-=-+-+=-. 故选:D.【点睛】本题考查了根据分布列求方差,意在考查学生的计算能力和应用能力.8.设正数数列{}n a 满足12n n a a a S +++=L ,21n n S S S T =L ,1n n S T +=,则数列1n a ⎧⎫⎨⎬⎩⎭的前10项和属于( )A. (0,500)B. (500,1000)C. (1000,2000)D. (2000,3000) 【答案】A【解析】【分析】由已知可得211n n S S S S =-L ,对n 赋值分别求出123,,S S S ,猜想n S ,然后验证,进而可求出n a ,从而可求得数列1n a ⎧⎫⎨⎬⎩⎭的前10项和.【详解】因为21n n S S S T =L ,1n n S T +=,所以211n n S S S S =-L ,当1n =时,111S S =-,所以112S =, 当2n =时,1221S S S =-,即22112S S =-,所以223S =, 当3n =时,12331S S S S =-,即33113S S =-,所以334S =, 猜想:1n n S n =+,则11n T n =+,代入已知检验等式21n n S S S T =L ,1n n S T +=成立, 所以当2n ≥时,2211111(1)(1)n n n n n n n a S S n n n n n n ---+=-=-==+++,又1112a S ==, 所以1(1)n a n n =+,所以1(1)n n n a =+, 所以12101111223910330(0,500)a a a +++=⨯+⨯++⨯=∈L L . 故选:A.【点睛】本题主要考查数列和的概念及知n S 求n a ,属于中档题.9.在三棱锥P ABC -中,平面PBC ⊥平面ABC ,PCB ∠为钝角,D ,E 分别在线段AB ,AC 上,使得,AE PE AD PD ==,记直线PD ,PE ,PA 与平面ABC 所成角的大小分别为α,β,γ则( )A. 2αβγ<<B. 2βαγ<<C. 2αγβ<<D. 2βγα<<【答案】A【解析】【分析】根据题意,画出三棱锥P ABC -,作PH ⊥平面ABC ,即可得直线PD ,PE ,PA 与平面ABC 所成角,由三角形边角关系即可判断大小.【详解】三棱锥P ABC -中,平面PBC ⊥平面ABC ,PCB ∠为钝角,D ,E 分别在线段AB ,AC 上,使得,AE PE AD PD ==,作出几何关系如下图所示:作PH ⊥平面ABC ,连接,,DH EH AH ,则PDH ∠即为直线PD 与平面ABC 所成角α,即sin sin PH DPDH P α∠==, 则PEH ∠即为直线PE 与平面ABC 所成角β,即sin sin PH EPEH P β∠==, 则PAH ∠即为直线PA 与平面ABC 所成角γ,即sin sin PH A PAH P γ∠==, 且α,β,γ0,2π⎛⎤∈ ⎥⎝⎦.因为PCB ∠为钝角,,AD PD =所以PE PD <,则PH PH PD PE<,所以sin sin αβ<,即αβ<, 由E 在线段AC 上,平面PBC ⊥平面ABC ,所以EAP V 为钝角三角形,AEP ∠为钝角;AEH △为钝角三角形,AEH ∠为钝角; 由余弦定理可知222cos 02EA EP PA AEP EA EP+-∠=<⋅,因为AE PE =, 所以222EP PA <. 而22sin 22sin cos 2PH AH PH AH PA PA PAγγγ⨯==⨯⨯= 22sin sin 2PH AHPH AH AH AH PE PE PE AEPE ββ⨯<=⨯=⋅=⋅, 即sin 2sin AH AEγβ<⋅,因AEH ∠为钝角,所以1AH AE >,所以sin 2sin γβ>,即2γβ>, 综上可知2αβγ<<,故选:A【点睛】本题考查了直线与平面夹角的作法与大小比较,关键是找到直线与平面夹角,再由边角关系比较即可,属于难题.10.设t ∈R ,已知平面向量,a b r r 满足:||2||2a b ==r r ,且1a b ⋅=r r ,向量()c xa t x b =+-r r r ,若存在两个不同的实数[0,]x t ∈,使得2230c a c -⋅+=r r r ,则实数t ( )A. 有最大值为2,最小值为32 B. 无最大值,最小值为32 C. 有最大值为2,无最小值D. 无最大值,最小值为0 【答案】B【解析】【分析】利用向量的数量积公式得出2223,3a c x t c x t ⋅=+=+r r r ,从而将方程2230c a c -⋅+=r r r 化为2236230x x t t -+-+=,利用二次函数零点的分布求出t 的范围,即可得出答案. 【详解】设向量,a b r r 的夹角为θ ||||cos 2cos 1a b a b θθ⋅===r r r r Q ,1cos 2θ∴= [0,]θπ∈Q ,3πθ∴= ()2()()43a c xa t x b a xa t x b a x t x x t ⋅=+-⋅=+-⋅=+-=+r r r r r r r r 222222[()]2()()c xa t x b x a x t x a b t x b =+-=+-⋅+-⋅r r r r r r r 22222242223x xt x t xt x x t =+-+-+=+ 存在两个不同的实数[0,]x t ∈,使得2230c a c -⋅+=r r r即存在两个不同的实数[0,]x t ∈,使得2236230x x t t -+-+= 即22()3623f x x x t t =-+-+在[0,]t 内有两个不同的零点 .22(0)0230()048300026016f t t f t t t t t t ⎧⎧-+≥⎪⎪⎪-+≥⎪⎪⇒∆>⎨⎨<<⎪⎪-⎪⎪<-<>⎩⎪⎩……,解得3,22t ⎡⎫∈⎪⎢⎣⎭ 则实数t 的最小值为32,无最大值 故选:B【点睛】本题主要考查了数量积公式的应用,利用二次函数零点分布求参数范围,属于中档题. 第Ⅱ卷(共110分)二、填空题(本大题7小题,多空题每题6分,单空题每题4分,共36分.)11.复数z满足:1,z i ⋅=+其中i 为虚数单位,则z 对应的点位于复平面的第______象限;|z |=______.【答案】 (1). 四 (2). 2【解析】【分析】根据条件得到z =,根据复数的除法运算整理为z a bi =+的形式,即可求解.【详解】因为1,z i ⋅=所以z i === 所以z对应的点的坐标为)1-, 故z 对应的点位于复平面的第四象限,因为z i =,所以2z =.故答案为:四;2.【点睛】本题考查复数的运算及几何意义,复数模长的计算,考查运算能力,属于基础题.12.若二项式23()nx x -展开式中各项系数之和为64,则n =______;其展开式的所有二项式系数中最大的是______(用数字作答)【答案】 (1). 6 (2). 20【解析】【分析】取1x =得到264n =,解得6n =,再计算二项式系数最大值得到答案.【详解】取1x =得到(13)64-=n ,解得6n =;故二项式系数为6r C ,当3r =时,二项式系数最大为3665420321C ⨯⨯==⨯⨯. 故答案为:6;20.【点睛】本题考查了二项式定理,意在看考查学生的计算能力和应用能力. 13.设R,0,a b ∈>已知函数()21,12,1x a x f x b x x x π+-≤=⎨⎪+>⎪⎩是奇函数,则a =______;若函数()f x 是R 上的增函数,则b 的取值范围是______.【答案】 (1).12(2). 1,1⎤⎦ 【解析】【分析】由()00f =可算出12a =,由函数()f x 是R 上的增函数可得b y x x =+在()1,+∞上单调递增且2x y π=在1x =处的函数值要小于或者等于b y x x =+在1x =处的函数值,然后即可求出b 的取值范围.【详解】因为()f x 是奇函数,定义域为R所以()0210f a =-=,解得12a =因为函数()f x 是R 上的增函数 所以b y x x=+在()1,+∞上单调递增,所以1b ≤且2x y π=在1x =处的函数值要小于或者等于b y x x =+在1x =处的函数值12b π≤+,解得1b ≥-综上:b的取值范围是1,1⎤⎦ 故答案为:12;1,1⎤⎦ 【点睛】本题考查的是分段函数的奇偶性和单调性,考查了学生的转化能力和计算能力,属于中档题. 14.在ABC ∆中,内角A ,B ,C 的对边分别为a ,b ,c ,且b =4,C =2A ,3a =2c ,则cosA =______;a =______.【答案】 (1).34(2). 165 【解析】【分析】 由正弦定理可知3sin 2sin 2A A =,结合二倍角的正弦公式可求出3cos 4A =;由余弦定理结合32a c =可得22316323482a a a ⎛⎫+- ⎪⎝⎭=⋅,从而可求出165a =或4,由22C A π=<可排除4a =这一情况,进而可得正确答案. 【详解】解:由正弦定理知,sin sin a c A C=,因为32a c =,2C A =, 所以3sin 2sin24sin cos A A A A ==,即3cos 4A =; 由余弦定理知,2222216cos 28b c a c a A bc c+-+-==,因为32a c =, 所以22316323482a a a ⎛⎫+- ⎪⎝⎭=⋅,整理得,2536640a a -+=,解得165a =或4.因为3cos 42A =>,所以4A π<,则22C A π=<.当4a =时,6c =, 则2222224461cos 22448a b c C ab +-+-===-⨯⨯,此时2C π>不符合题意,因此165a =. 故答案为: 34;165【点睛】本题考查了正弦定理,考查了余弦定理,考查了二倍角公式.本题的关键是由正弦定理边角互化求出cos A .本题的易错点是未对a 的结果进行取舍.15.设F 是椭圆22143x y +=上右焦点,P 是椭圆上的动点,A 是直线34120x y --=的动点,则PA PF -的最小值为______.【答案】1-【解析】【分析】根据椭圆方程可知()1,0F ,设F '是椭圆22143x y +=上的左焦点,则()1,0F '-.根据椭圆的定义可知24PF PF a '+==,则()44PA PF PA PF PA PF ''-=--=+-, 即PA PF -的最小值即求PA PF '+的最小值即可,利用图象可知,PA PF '+的最小值,即当AF '垂直于直线34120x y --=时AF '的值,利用点到直线的距离公式求出AF '的值,进而可得出结论.【详解】解:Q F 是椭圆22143x y +=上的右焦点, 24a =,23b =, ∴2221c a b =-=,即()1,0F ,设F '是椭圆22143x y +=上的左焦点,则()1,0F '-. 根据椭圆的定义可知24PF PF a '+==. ∴4PF PF '=-,()44PA PF PA PF PA PF ''-=--=+-. 则PA PF -的最小值即求PA PF '+的最小值,根据图象可知,PA PF '+的最小值,即当AF '垂直于直线34120x y --=时AF '的值,则3AF '==. 则此时44341PA PF AF ''+-=-=-=-.所以PA PF -的最小值为1-.故答案为:1-.【点睛】本题考查椭圆的定义与性质,考查点到直线的距离公式,考查数形结合能力,属于中档题. 16.两个同样的红球、两个同样的黑球和两个同样的白球放入下列6个格中,要求同种颜色的球不相邻,则可能的放球方法共有______种.(用数字作答)【答案】30【解析】【分析】对于不相邻的问题,运用插空的方法,先排出红球,再将黑球插空在红球的空隙之中,再将白球插在红球和黑球的空隙中可得答案.【详解】第一步:先将两个相同红球,排成一排,只有一种排法,第二步:情况1:再在两个红球的空隙中插入一个黑球,剩下的一个黑球有122C =种排法, 再将两个相同的白球插在红球和黑球的空隙中有2510C =种排法,所以由分步乘法原理得共有21020⨯=种排法,所以情况1共有20种排法;情况2:两个黑球分别放在红球的两侧,有1种方法,再将1个白球放于两个红球之间,剩下的1个白球再在红球和黑球之间插空,有14C 4=种方法,因此对于情况2共有4种排列方法;情况3:两个黑球一起放在红球的一侧,有2种方法,再分别在相邻的红球和相邻的黑球之间各放一个白球,只有一种放法,因此情况3共有2种放法;情况4:两个黑球一起放在红球之间,有1种放法,再在两个黑球之间放一白球,红球和黑球的空隙中再插入1个白球,共有4种放法,因此情况4共有4种放法;根据分类计数原理可得:所有的放球方法共有20+4+2+430=种方法;故答案为:30.【点睛】本题考查排列、组合的运用,注意本题中同色的球是相同的,对于较难问题,我们可以采取分步来做,不相邻的问题运用插空法,属于中档题.17.已知函数()()()()ln ,3f x x x a g x ff x =-+=+有4个零点,则实数a 的取值范围为______. 【答案】()21,2e -【解析】【分析】利用导数求得函数()f x 的单调性与最值,得到10a ->,设函数()f x 的两个零点分别为12,x x ,则1201x x <<<,得出()13f x x +=有两个零点,再结合()23f x x +=,得出22x a <+,代入即可求解. 【详解】由题意,函数()ln f x x x a =-+,可得()111x f x x x-'=-=, 当01x <<时,()0f x '>,函数()f x 单调递增;当1x >时,()0f x '<,函数()f x 单调递递减, 所以当1x =时,函数()f x 取得最大值,最大值为()11f a =-,要使函数()f x 有零点,则10a ->,可得1a >,设函数()f x 的两个零点分别为12,x x ,则1201x x <<<,令()0g x =,即()()30f f x +=,则()13f x x +=,即()13f x x =-,则()13(3,1)f x x =-∈--有两个零点,又由()23f x x +=,即()23f x x =-,只需231x a -<-,即22x a <+,即(2)ln(2)20f a a +=+-<,解得22a e <-,综上可得:实数a 的取值范围是()21,2e -.【点睛】本题主要考查了利用导数研究函数的零点问题,以及函数与方程的综合应用,其中解答中利用导数求得函数的单调性,以及合理应用函数性质是解答的关键,着重考查转化思想,以及推理与运算能力. 三、解答题(本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤. 18.已知函数()()()4sin 0,02x x f ϕωϕπω=+><<的部分图象如图所示(),f x 经过()1,0,当2x =-时(),f x 取到最小值.(Ⅰ)求ω和φ的值;(Ⅱ)求函数()()()2g x f x f x =++的单调递增区间.【答案】(Ⅰ)6π=ω,116πϕ=. (Ⅱ)[]123,123k k -+,k Z ∈.【解析】【分析】(Ⅰ)根据图像中特殊点的位置,先求周期,进而求出ω的值,再代入特殊点,根据特殊点的对应关系可求出ϕ的值. (Ⅱ)根据题意求出()g x 的解析式,然后利用整体思想的应用求出函数的单调区间.【详解】解:(Ⅰ)由图像可知,34T =,∴ 12T =,则2=126ωππ=; 又()4s =16in 0f πϕ⎛⎫=+ ⎪⎝⎭,∴5+k 6πϕπ=.因为在1x =处为上升零点,且02ϕπ<<,所以116πϕ=. (Ⅱ)由(Ⅰ)可知,()6114sin 6x x f ππ⎛⎫=+⎪⎝⎭,11()4sin 4sin 6666x x g x ππππ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭8sin cos 666x x πππ==, 解22262x k k πππππ-≤≤+得:123123k x k -≤≤+, 所以()g x 的单调递增区间是[]123,123k k -+,k Z ∈.【点睛】本题考查根据三角函数的图像求解析式,考查三角函数式的恒等变换以及正弦函数性质的应用,考查学生的运算能力和转化能力,属于基础题.19.如图,三棱锥P ABC -的底面是边长为3的等边三角形,侧棱3,4,5,PA PB PC ===设点M ,N 分别为PC ,BC 的中点.(Ⅰ)求证:BC ⊥面AMN ;(Ⅱ)求直线AP 与平面AMN 所成角.【答案】(Ⅰ)见解析(Ⅱ)30°【解析】【分析】(Ⅰ)根据边长关系可以计算PB BC ⊥,由传递性可得MN BC ⊥,再根据等边三角形的性质可知AN BC ⊥,由此可证明. (Ⅱ)利用BC ⊥面AMN 的关系,过P 做面AMN 的垂线PQ ,则PAQ ∠为所求角,根据长度关系可求出角的正弦值,进而求出角的大小.【详解】(Ⅰ)因为3BC =,4,5,PB PC ==所以PBC ∆为直角三角形,由勾股定理逆定理可知PB BC ⊥,所以MN BC ⊥,在等边三角形ABC 中,N 为BC 中点,所以AN BC ⊥,又PB BC B ⋂=,所以BC ⊥面AMN .(Ⅱ)延长NM 到Q ,使NM MQ =,连接PQ ,AQ ,于是四边形PQNB 为平行四边形.所以PQ BN P , 根据前一问的结论可知PQ ⊥面AMN ,所以PAQ ∠直线直线AP 与平面AMN 所成角.在直角三角形PAQ 中,312sin 32PQ PAQ AP ∠===,所以30PAQ ∠=︒.【点睛】本题考查线面垂直的判定定理和线面角的求法,考查线面角的定义,熟练掌握线面角的定义是解题的关键,本题属于中档题.20.设数列{a n }的前n 项和为S n ,满足:()*21N n n n a S n n n -+∈+=.(Ⅰ)求证:数列1(1)n a n n ⎧⎫+⎨⎬+⎩⎭为等比数列; (Ⅱ)求S n ,并求S n 的最大值. 【答案】(Ⅰ)见解析(Ⅱ)1112n n S n =-+,1180. 【解析】【分析】(Ⅰ)由题得21n n n a S n n -+=+,①,1122n n n a S n n---+=-,(2)n ≥ ②,两式相减得1112(1)(1)n n a a n n n n -⎛⎫+=+ ⎪+-⎝⎭,即得数列1(1)n a n n ⎧⎫+⎨⎬+⎩⎭为等比数列; (Ⅱ)求出11121n n a n n ⎛⎫=-- ⎪+⎝⎭,再利用分组求和裂项相消法求出n S ;分析得到当5n ≥时,1n n S S ->,当4n ≤时,1n n S S -≤,即得n S 的最大值为4S 得解.【详解】解:(Ⅰ)因为21n n n a S n n-+=+,① 1122n n n a S n n---+=-,(2)n ≥, ② 由①-②可得, 当2n ≥时,122122n n n n a a n n n n ----=-+-, 所以122122(1)n n n n a a n n n n --++--=-+-, 所以1222122(1)n n n n a a +n n n n n n --+--=-++-, 所以1222212(11)(1)(1)n n n a a +=+n n n n n n n n n -----=-+-+- 整理得,1112(1)(1)n n a a n n n n-⎛⎫+=+ ⎪+-⎝⎭, 所以11(1)112(1)n n a n n a n n-⎛⎫+ ⎪+⎝⎭=+-, 又11122a +=,所以1(1)n a n n ⎧⎫+⎨⎬+⎩⎭为首项公比均为12的等比数列; (Ⅱ)由(Ⅰ)得11(1)2n n a n n +=+, 所以111112(1)21n n n a n n n n ⎛⎫=-=-- ⎪++⎝⎭, 所以1111111122231n n S n n ⎛⎫=---+-++- ⎪+⎝⎭L , 故有1112n n S n =-+, 因为111(1)12(1)(1)2n n n n n a n n n n +⎛⎫=-=- ⎪++⎝⎭, 令(1)()12n n n f n +=-,则1(1)(2)(1)()2n n n f n f n ++-+-=, 所以(1)(2)(3)(4)(5)f f f f f <=>>L ,又()10f =,()40f >,()50f <,所以当5n ≥时,0n a <即1n n S S ->,当4n ≤时,0n a ≥即1n n S S -≤,因此n S 的最大值为4111151680S =-=. 【点睛】本题主要考查数列性质的证明,考查分组求和裂项相消法求和,考查公式法求和,考查数列n S 的最值的求法,意在考查学生对这些知识的理解掌握水平和分析推理能力.21.已知抛物线2y ax =上一点()0,5M x 到焦点的距离为214,过()1,0P -作两条互相垂直的直线1l 和2l ,其中斜率为()0,k k >1l 与抛物线交于A ,B ,2l 与y 轴交于C ,点Q 满足:,.AP PB QA QB λλ==u u u r u u u r u u u r u u u r(1)求抛物线的方程;(2)求三角形PQC 面积的最小值.【答案】(1)2y x =; (2)12【解析】【分析】 (1)根据抛物线定义,()0,5M x 到焦点的距离等于到其准线的距离,求得抛物线方程;(2)应用设而不解,联立方程组,根与系数的关系,以及向量式,将点,Q C 的纵坐标均用k 表示出来,再表示出,PQ PC ,从而表示出三角形的面积,再求最值.【详解】解:(1)抛物线2y ax =化为标准方程为:21x y a=,其准线为14y a =-, 则1215()44a --=,得1a =,故抛物线的方程为2y x =. (2)由题1:(1)l y k x =+,21:(1)l y x k =-+,则1(0,)C k -, 设112200(,),(,),(,)A x y B x y Q x y ,则2(1)y k x y x =+⎧⎨=⎩,得20x kx k --=, 则12x x k +=,12x x k =-.由AP PB λ=u u u r u u u r ,则1122(1,)(1,)x y x y λ---=+,得12y y λ=-, QA QB λ=u u u r u u u r ,则10102020(,)(,)x x y y x x y y λ--=--,得1020y y y y λ-=-, 故101220y y y y y y --=-,得120122y y y y y =+ 又221212()y y x x k ==,21212(2)2y y k x x k k +=++=+,则20222k y k k=+,0||PQ ==2222k k k =+,||PC = 又PQC S ∆12PQ PC =⋅⋅2212k k k +=+, 令()g k =2212k k k++,0k > 则2222(1)()(2)k k g k k k --+'=+=22112(22(2)k k k k +---+则()g k在递减,在1()2++∞递增,故当12k +=时,()g k的最小值为12g ⎛+= ⎝⎭12, 故三角形PQC【点睛】本题考查了抛物线定义,直线与抛物线的位置关系,考查了设而不解,联立方程组,根与系数的关系,以及向量式化简等常用技巧,表示出三角形的面积公式后,表达式较复杂,可利用导数工具求最值. 22.已知函数())0f x a =>有两个不同的极值点. (Ⅰ)求实数a 的取值范围;(Ⅱ)若对任意R,m ∈存在[),,x e ∈+∞使得()f x m k -≥成立,证明:k < 【答案】(Ⅰ)1,2e ⎛⎫ ⎪⎝⎭;(Ⅱ)证明见解析.【解析】【分析】(Ⅰ)求得'()f x ,令()'0f x =,得到2ln 20a x x --+=,设2()ln 2a g x x x=--+, 利用导数求得函数()g x 的单调性与最值,列出不等式组,即可求解;(Ⅱ)由(Ⅰ)知1,2e a ⎛⎫∈ ⎪⎝⎭,得到()210a g e e=->,把对任意m R ∈,存在[)3,x ∈+∞,使得()f x m k -≥成立,转化为()()0022f x b f x k -≤≤,化简()0f x == 令()2ln ()x h x e x e x=<<,利用导数求得函数()h x 的单调性与极值,即可求解. 【详解】(Ⅰ)由函数())0f x a =>,则'2ln 2())a x f x x a --+=>, 令()'0f x =,可得2ln 20a x x--+=, 设2()ln 2a g x x x =--+,则'22()a x g x x -=,令()'0g x =,解得2x a =, 列表如下:所以()g x 的极大值为()()21ln 2g a a =-,又因为()2220a g e e =-<, 所以函数()f x 有两个不同的极值点等价于()0(2)0g a g a <⎧⎨>⎩,解得12e a <<, 因此实数a 的取值范围为1,2e ⎛⎫⎪⎝⎭; (Ⅱ)由(Ⅰ)知1,2e a ⎛⎫∈ ⎪⎝⎭,故()210a g e e =->, 设()g x 的较大零点为0x ,则()20,x e e∈, 且()0,x e x ∈,()'0f x >;()0,x x ∈+∞,()'0f x <,所以()f x 在()0,e x 上单调递增,在()0,x +∞上单调递减,从而()f x 有最大值为()0f x ,又当x e ≥时,()0f x >,故可设函数()f x 的值域为()(0,b f x ⎤⎦,其中0b ≥,由题意:对任意m R ∈,存在[)3,x ∈+∞,使得()f x m k -≥成立, 等价于()()0022f x b f x k -≤≤, 而()0f x =,且()000022ln 2x a a x x x -=-=,所以()0f x ==20e x e <<, 令()2ln ()x h x e x e x=<<,则'21ln ()0x h x x -=<, 所以()h x 在()2,e e 上单调递减, 所以1()()h x h e e <=,故()0f x < 因此()02f x k ≤<. 【点睛】本题主要考查导数在函数中的综合应用,以及不等式的证明,着重考查了转化与化归思想、分类讨论、及逻辑推理能力与计算能力,对于此类问题,通常要构造新函数,利用导数研究函数的单调性,求出最值,进而得出相应的含参不等式,从而求出参数的取值范围;也可分离变量,构造新函数,直接把问题转化为函数的最值问题.。
