解直角三角形的应用(方位角)
【教案】解直角三角形及方位角的应用

解直角三角形及方向角的应用教课目的【知识与技术】在理解解直角三角形的含义、直角三角形五个元素之间关系的基础上, 会运用勾股定理、直角三角形的两锐角互余及锐角三角函数解直角三角形.【过程与方法】经过综合运用勾股定理、直角三角形的两锐角互余及锐角三角函数解直角三角形 , 逐渐培育学生剖析问题、解决问题的能力 .【感情、态度与价值观】在研究学习的过程中 , 培育学生合作沟通的意识, 使学生认识到数与形相结合的意义与作用 , 领会到学好数学知识的作用, 并提升学生将数学知识应用于实际的意识 , 进而体验“从实践中来 , 到实践中去”的辩证唯心主义思想, 激发学生学习数学的兴趣 . 让学生在学习过程中感觉到成功的愉悦, 产生后继学习激情 , 增强学好数学的信心 .要点难点【要点】直角三角形的解法 .【难点】灵巧运用勾股定理、直角三角形的两锐角互余及锐角三角函数解直角三角形 .、教课过程一、复习回首师: 你还记得勾股定理的内容吗?生: 记得.学生表达勾股定理的内容.师: 直角三角形的两个锐角之间有什么关系呢?生: 两锐角互余 .师: 直角三角形中 ,30 °的角所对的直角边与斜边有什么关系?生:30 °的角所对的直角边等于斜边的一半.师: 很好!二、共同研究 , 获得新知1.观点 .师: 由 sinA=, 你能获得哪些公式 ?生甲 :a=c · sinA.生乙 :c=.师: 我们还学习了余弦函数和正切函数 , 也能获得这些式子的变形 . 这些公式有一个共同的特色 , 就是式子的右端起码有一条边 , 为何会是这样的呢 ?学生思虑 .生: 由于左侧的也是边 , 依据右侧边与角的关系计算出来的应是长度.师: 对! 解三角形就是由已知的一些边或角求另一些边和角 , 我们此刻看看解直角三角形的观点 .教师板书 :在直角三角形中 , 由已知的边角关系 , 求出未知的边与角 , 叫做解直角三角形 .2.练习教师多媒体课件出示 :(1) 如图 (1) 和(2), 依据图中的数据解直角三角形 ;师: 图(1) 中是已知一角和一条直角边解直角三角形的种类 , 你如何解决这个问题呢 ?生 1: 依据 cos60°=, 获得 AB=,而后把 AC边的长和 60°角的余弦值代入 , 求出 AB边的长 , 再用勾股定理求出 BC边的长 , ∠B 的度数依据直角三角形两锐角互余即可获得 .生2: 先用直角三角形两锐角互余获得∠B为30°, 而后依据30°的角所对的直角边等于斜边的一半 , 求出 AB的值 , 再由 sin60 °=获得 BC=AB· sin60 °, 进而获得 BC边的长 .师: 你们回答得都对 ! 还有没有其余的方法了 ?生 3: 能够求出 AB后用 AB的值和∠ B 的余弦求 BC的长 .生 4: 能够在求出 AB后不用三角函数 , 用勾股定理求出 BC.师: 同学们说出这几种做法都是对的. 下边请同学们看图 (2), 并解这个直角三角形 .学生思虑 , 计算 .师: 这两个题目中已经给出了图形, 此刻我们再看几道题 .教师多媒体课件出示 :【例 1】在 Rt △ABC中, ∠ C=90°, ∠B=42°6',c=287.4,解这个直角三角形.师: 你如何解答这道题呢 ?先做什么 ?生: 先画出图形 .师: 很好 ! 此刻请同学们画出大概图形.学生绘图 .教师找一世谈谈解这个直角三角形的思路 , 而后让同学们自己做 , 最后集体订下 .解: ∠A=90°-42 °6'=47 ° 54'.由 cosB=,得a=ccosB=287.4× 0.7420 ≈213.3.由 sinB= 得b=csinB=287.4 × 0.6704 ≈192.7.教师多媒体课件出示 :【例 2】在△ ABC中 , ∠ A=55° ,b=20 cm,c=30 cm. 求△ ABC的面积 S△ABC.( 精准到 0.1 cm 2 )师: 这道题是已知了三角形的两条边和一个角, 求三角形的面积 . 要先如何 ?学生思虑 .生: 先画出图形 .师: 对, 题中没有已知图形时 , 一般都要自己画出图形 . 而后呢 ?你能给出解这道题的思路吗 ?生 1: 先计算 AB边上的高 , 以 AB为底 ,AB 边上的高为三角形的高 , 依据三角形的面积公式 , 就能计算出这个三角形的面积了 .生 2: 还能够先计算 AC边上的高 , 而后用三角形的面积公式计算这个三角形的面积 .师: 很好 ! 我们此刻议论以 AB为底时求三角形面积的方法 , 如何求 AB边上的高呢 ?教师找一世回答 , 而后集体校正 .解: 如图 , 作 AB上的高 CD.在 Rt△ACD中,CD=AC·sinA=bsinA,∴S△ABC=AB· CD=bcsinA.当∠ A=55° ,b=20 cm,c=30 cm 时 , 有S△ABC=bcsinA= × 20×30sin55 °=×20×30× 0.8192≈245.8(cm 2).教师多媒体课件出示 :【例 3】如图 , 东西两炮台 A、 B 相距 2 000 米, 同时发现入侵敌舰 C,炮台 A测得敌舰 C 在它的南偏东 40°的方向 , 炮台 B 测得敌舰 C在它的正南方 , 试求敌舰与两炮台的距离 .( 精准到 1 米 )师: 这是一个与解直角三角形相关的实质问题, 你能将它转变为数学模型吗?学生思虑后回答 : 会.师: 这相当于已知了哪些条件, 让你求什么量 ?生: 已知直角三角形的一个锐角和一条直角边, 求它的斜边和另向来角边.师: 你回答得很好 ! 此刻请同学们计算一下.学生计算 , 教师巡视指导 , 最后集体校正 .解: 在 Rt△ABC中 ,∵∠ CAB=90°- ∠ DAC=50°,=tan ∠ CAB,∴BC=AB·tan ∠CAB=2 000×tan50 °≈ 2 384( 米)又∵ =cos50°,∴AC==≈3 111( 米).答: 敌舰与 A、B 两炮台的距离分别约为 3 111 米和 2 384 米.三、练习新知师: 此刻请同学们看课本第125 页练习 1 的第 (1) 、 (2) 题.教师找两生各板演 1 题, 其余同学在下边做 , 而后集体校正 .解:(1)∠A=90°-80 °=10° ,AB=≈≈ 172.81,AC=≈≈ 170.16,(2)BC===≈ 7.42.cosA===0.375,∠A≈67.976 °≈ 67°58'32 ″,∠B=90°- ∠A=22°1'28 ″.教师找一世板演课本第125 页练习的第 3 题, 其余同学在下边做 , 而后集体订正 .解:过点 A 向 DC作垂线 , 与 DC交于一点 E.AE=ADsin43°=6×sin43 °≈6× 0.682=4.092.S=(AB+DC)×AE=(4+8) × 4.092≈24.55.答: 梯形的面积为 24.55.四、稳固提升师: 同学们 , 经过方才的学习 , 相信大家都掌握了必定的解直角三角形及其应用题的方法 , 此刻我出几道习题来检测下大家学得怎么样 !教师多媒体课件出示习题:1.在△ ABC中, ∠C=90°, 以下各式中不正确的选项是 ( ) A.b=a· tanB B.a=b ·cosAC.c=D.c=【答案】 B2. 在 Rt△ABC中, ∠C=90°,a=35,b=28, 则 tanA= ,tanB=.【答案】3. 在 Rt△ABC中, ∠C=90°,c=10,b=5, 则∠ A= ,S △ABC=.【答案】 30°4.已知在 Rt △ABC中 , ∠ C=90° ,a=104,b=20.49, 求∠ A 和∠ B.( 可利用计算器进行运算 , 精准到 1° )【答案】∠ A=79°, ∠B=11°5.如图 , 在 Rt△ ABC中,BC=7.85,AB=11.40, 解这个直角三角形 .( 边长保存三个有效数字 , 角度精准到 1°)【答案】 AC=8.27,∠ A=44° , ∠ B=46°五、讲堂小结师: 本节课 , 我们学习了什么内容 ?学生回答 .师: 你还有什么不懂的地方吗?学生发问 , 教师解答 .教课反省本节课在教课过程中 , 能灵巧办理教材 , 敢于松手让学生经过自主学习、合作研究 , 达到理解并掌握知识的目的 , 并能运用知识解决问题 . 在本章开头 , 我率领学生复习了与解直角三角形相关的知识点 , 使学生在解决问题时能想到并能娴熟运用 . 在解有特别角的三角形时有不只一种解法 , 我鼓舞学生勇于讲话 , 给了他们展现自我的时机 , 锻炼他们表达自己想法的能力 , 而且加强了他们的自信心 .。
26.4 解直角三角形的应用 - 第1课时仰角、俯角、方位角问题课件(共23张PPT)

例1 如图,小明在距旗杆4.5 m的点D处,仰视旗杆顶端A,仰角(∠AOC)为50°;俯视旗杆底部B,俯角(∠BOC)为18°.求旗杆的高.(结果精确到0.1 m)
例题示范
知识点2 方向角方位角:由正南或正北方向线与目标方向线构成的锐角叫做方位角.如下图中的目标方向OA,OB,OC,OD的方向角分别表示________60°,________45°(或__________),_________80°及_________30°.
拓展提升
1.热气球的探测器显示,从热气球看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球与楼的水平距离为120 m,这栋楼有多高(结果取整数)?
分析:如图,α=30°,β=60°.在Rt△ABD中,α =30°,AD=120,所以利用解直角三角形的知识求出BD;类似地可以求出CD,进而求出BC.
第二十六章 解直角三角形
26.4 解直角三角形的应用
第1课时 仰角、俯角、方位角问题
学习目标
学习重难点
重点
难点
1.巩固解直角三角形有关知识,了解仰角、俯角、方向角的概念.2.运用解直角三角形知识解决与仰角、俯角和方位角有关的实际问题.
运用解直角三角形知识解决与仰角、俯角和方位角有关的实际问题.
将某些实际问题中的数量关系,归结为直角三角形中元素之间的关系,从而解决问题.
回顾复习
解直角三角形的应用典型习题(方位角)

1.如下图,某船以每小时36海里的速度向正东方向航行,在点A 测得某岛C 在北偏东60°方向上,航行半小时后到达点B 测得该岛在北偏东30°方向上,已知该岛周围16海里内有暗礁。
(1)说明点B 是否在暗礁区域内;(2)若继续向东航行有无触礁的危险?请说明理由。
2.如图,海岛A 四周20海里周围内为暗礁区,一艘货轮由东向西航行,在B 处见岛A 在北偏西60˚,航行24海里到C ,见岛A 在北偏西15˚,货轮继续向西航行,有无触礁的危险3.如图所示,A 、B 两城市相距100km .现计划在这两座城市间修筑一条高速公路(即线段AB ),经测量,森林保护中心P 在A 城市的北偏东30°和B 城市的北偏西45°的方向上.已知森林保护区的范围在以P 点为圆心,50km 为半径的圆形区域内.请问计划修筑的这条高速公路会不会穿越保护区.为什么?(参考数据:3 1.7322 1.414≈,≈)4.为打击索马里海盗,保护各国商船的顺利通行,我海军某部奉命前往该海域执行护航任务.某天我护航舰正在某小岛A 北偏西45°并距该岛20海里的B 处待命.位于该岛正西方向C 处的某外国商船遭到海盗袭击,船长发现在其北偏东60°的方向有我军护航舰(如图所示),便发出紧急求救信号.我护航舰接警后,立即沿BC 航线以每小时60海里的速度前去救援.问我护航舰需多少分钟可以到达该商船所在的位置C 处?(结果精确到个位)5.如图,某天然气公司的主输气管道从A 市的东偏北30°方向直线延伸,测绘员在A 处测得要安装天然气的M 小区在A 市东偏北60°方向,测绘员沿主输气管道步行2000米到达C 处,测得小区M 位于C 的北偏西60°方向,请你在主输气管道上寻找支管道连接点N ,使到该小区铺设的管道最短,并求AN 的长.6.如图,A 城气象台测得台风中心在A 城的正西方300千米处,以每小时10千米的速度向北偏东60º的BF 方向移动,距台风中心200千米的范围内是受这次台风影响的区域。
第一章直角三角形的边角关系-解直角三角形的应用复习-方位角(教案)

本节课将重点围绕方位角的求解与应用进行复习巩固,提高学生解决实际问题的能力。
二、核心素养目标
本节课的核心素养目标致力于培养学生的以下能力:
1.理解并运用数学知识:通过复习直角三角形的性质和解直角三角形的方法,加深对几何知识的理解和应用,提高解决实际问题的能力;
难点解释:学生在理解三角函数的概念时,容易混淆正弦、余弦、正切函数的定义及其应用场景。
(2)空间想象能力的培养:在求解方位角时,需要学生在脑海中构建直角三角形的空间模型。
难点解释:学生在解决方位角问题时,往往难以在脑海中形成清晰的空间图像,导致解题困难。
(3)实际问题的解决:将数学知识应用于实际情境,解决现实问题。
3.重点难点解析:在讲授过程中,我会特别强调解直角三角形的方法和方位角的计算这两个重点。对于难点部分,我会通过具体例题和图示来帮助大家理解。
(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与方位角相关的实际问题。
2.实验操作:为了加深理解,我们将进行一个简单的实验操作。通过测量和计算,演示方位角的基本原理。
第一章直角三角形的边角关系-解直角三角形的应用复习-方位角(教案)
一、教学内容
本节课为九年级数学课程,选取教材中“第一章直角三角形的边角关系-解直角三角形的应用复习”部分进行深入讲解。内容包括:
1.复习直角三角形的定义及性质;
2.掌握解直角三角形的方法;
3.介绍方位角的概念及应用;
4.通过实际例题,让学生掌握利用解直角三角形的方法求解方位角;
2.数学思维能力:在方位角的求解过程中,锻炼学生的逻辑推理和空间想象能力,提升数学思维水平;
用解直角三角形解方位角的应用教案(完美版)

在线分享文档用解直角三角形解方位角的应用一、教学目标(一)知识与技能巩固直角三角形中锐角的三角函数,学会解关于方位角的问题.(二)过程与方法逐步培养学生分析问题解决问题的能力,进一步渗透数形结合的数学思想和方法.(三)情感态度与价值观培养学生用数学的意识;渗透数学来源于实践又反过来作用于实践的辩证唯物主义观点.二、重、难点重点:能熟练运用有关三角函数知识.难点:解决实际问题.三、教学过程(一)明确目标讲评上课节课后作业(二)重点、难点的学习与目标完成过程教师出示例题.例1 如图,在山坡上种树,要求株距(相邻两树间的水平距离)是5.5m,测得斜坡的倾斜角是24°,求斜坡上相邻两树的坡面距离是多少(精确到0.1m).分析:1.例题中出现许多术语——株距,倾斜角,这些概念学生未接触过,比较生疏,而株距概念又是学生易记错之处,因此教师最好准备教具:用木板钉成一斜坡,再在斜坡上钉几个铁钉,利用这种直观教具更容易说明术语,符合学生的思维特点.2.引导学生将实际问题转化为数学问题画出图形(上图(2)).已知:Rt△ABC中,∠C=90°,AC=5.5,∠A=24°,求AB.3.学生运用解直角三角形知识完全可以独立解决例1.教师可请一名同学上黑在线分享文档板做,其余同学在练习本上做,教师巡视.答:斜坡上相邻两树间的坡面距离约是6.0米.教师引导学生评价黑板上的解题过程,做到全体学生都掌握.例2 如图6-30,沿AC方向开山修渠,为了加快施工速度,要从小山的另一边同时施工,从AC上的一点B取∠ABD=140°,BD=52cm,∠D=50°,那么开挖点E离D多远(精确到0.1m),正好能使A、C、E成一条直线?这是实际施工中经常遇到的问题.应首先引导学生将实际问题转化为数学问题.由题目的已知条件,∠D=50°,∠ABD=140°,BD=520米,求DE为多少时,A、C、E在一条直线上。
解直角三角形的应用-方向角问题-初中数学习题集含答案

一.填空题(共 5 小题) 1.(2018 秋•顺义区期末)轮船从 B 处以每小时 50 海里的速度沿南偏东 30 方向匀速航行,在 B 处观测灯塔 A 位于
南偏东 75 方向上,轮船航行半小时到达 C 处,在观测灯塔 A 北偏东 60 方向上,则 C 处与灯塔 A 的距离是 海里.
2.(2019 秋•东城区校级期中)如图,某货船以 24 海里 / 时的速度从 A 处向正东方向的 D 处航行,在点 A 处测得某 岛 C 在北偏东 60 的方向.该货船航行 30 分钟后到达 B 处,此时测得该岛在北偏东 30 的方向上.则货船在航行中 离小岛 C 的最短距离是 .
3.(2017 春•西城区校级期中)如图,在点 A 测得某岛 C 在北偏东 60 方向上,且距 A 点18 3 海里,某船以每小时 36 海里的速度从点 A 向正东方向航行,航行半小时后到达 B 点,此时测得岛 C 在北偏东 30 方向上,已知该岛周围 16 海里内有暗礁. B 点与 C 岛的距离是 B 点暗礁区域 (填内或外)
7.(2016•延庆县一模)如图,甲船在港口 P 的南偏西 60 方向,距港口 86 海里的 A 处,沿 AP 方向以每小时 15 海 里的速度匀速驶向港口 P .乙船从港口 P 出发,沿南偏东 45 方向匀速驶离港口 PC 2x ,现两船同时出发,2 小 时后乙船在甲船的正东方向.求乙船的航行速度.(结果精确到个位,参考数据: 2 1.414 , 3 1.732 , 5 2.236)
【分析】根据题中所给信息,求出 BCA 90 ,再求出 CBA 45 ,从而得到 ABC 为等腰直角三角形,然后根据 解直角三角形的知识解答.
【解答】解:根据题意,得 1 2 30 , Q ACD 60 , ACB 30 60 90 , CBA 75 30 45 , ABC 为等腰直角三角形, Q BC 50 0.5 25 , AC BC 25 (海里). 故答案为:25.
解直角三角形的应用(仰角和俯角问题)

计算角度证结果:检 查计算结果是 否满足三角形 内角和为180
度的条件
添加标题
确定已知条件:已知三角形的边长和角度
添加标题
利用正弦定理:sin/ = sinB/b = sinC/c
添加标题
利用余弦定理:cos = (b^2 + c^2 - ^2) / (2bc)
正弦定理:在直角三角形中 任意一边的长度等于其对角 的正弦值乘以斜边的长度
余弦定理:在直角三角形中 任意两边长度的平方和等于 斜边的平方
正切定理:在直角三角形中 任意一边的长度等于其对角 的正切值乘以斜边的长度
余切定理:在直角三角形中 任意两边长度的平方差等于 斜边的平方
正割定理:在直角三角形中 任意一边的长度等于其对角 的正割值乘以斜边的长度
确保测量工具的 准确性和稳定性
避免在危险区域 进行测量如高空、
高压电等
遵守操作规程确 保人身安全
做好防护措施如 佩戴安全帽、手
套等
及时清理现场避 免杂物影响测量
结果
遇到突发情况及 时停止操作并寻
求帮助
仰角和俯角为0度:此时三角形退化为直线无法求解
仰角和俯角为90度:此时三角形退化为直角三角形可以直接求解
全站仪等
测量误差:注 意测量误差对 仰角和俯角测 量结果的影响
测量环境:注 意测量环境的 影响如温度、 湿度、风速等
测量方法:注 意测量方法的 选择如直接测 量、间接测量
等
测量误差:测量工具的精度、测量人员的操作水平等
计算误差:计算过程中的舍入误差、公式使用错误等
环境误差:温度、湿度、光照等环境因素对测量结果的影响
添加文档副标题
目录
01.
02.
25.4 解直角三角形的应用(2)
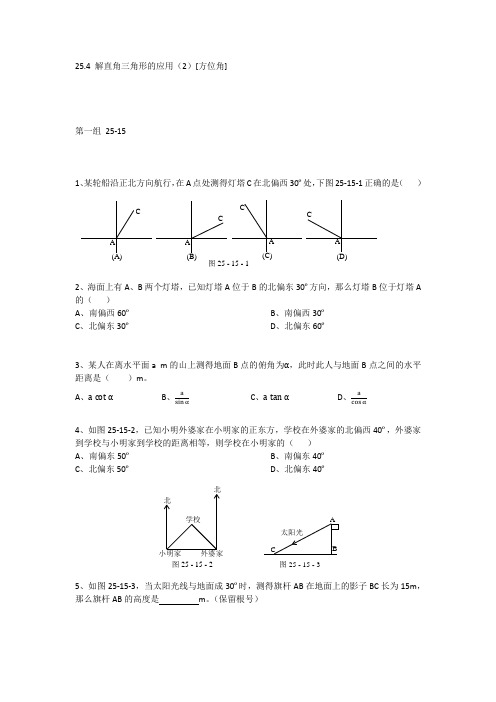
25.4 解直角三角形的应用(2)[方位角]第一组 25-151、某轮船沿正北方向航行,在A 点处测得灯塔C 在北偏西30º处,下图25-15-1正确的是( )2、海面上有A 、B 两个灯塔,已知灯塔A 位于B 的北偏东30º方向,那么灯塔B 位于灯塔A 的( )A 、南偏西60ºB 、南偏西30ºC 、北偏东30ºD 、北偏东60º3、某人在离水平面a m 的山上测得地面B 点的俯角为α,此时此人与地面B 点之间的水平距离是( )m 。
A 、a cot α B 、a sin αC 、a tan αD 、acos α4、如图25-15-2,已知小明外婆家在小明家的正东方,学校在外婆家的北偏西40º,外婆家到学校与小明家到学校的距离相等,则学校在小明家的( ) A 、南偏东50º B 、南偏东40º C 、北偏东50º D 、北偏东40º5、如图25-15-3,当太阳光线与地面成30º时,测得旗杆AB 在地面上的影子BC 长为15m ,那么旗杆AB 的高度是 m 。
(保留根号)图 25 - 15 - 1(D)A CA C CA CA 图 25 - 15 - 2小明家学校北北图 25 - 15 - 3BA太阳光C6、某人从A 点出发,向北偏东45º方向走到B 点,再从B 点出发,向南偏西15º方向走到C 点,那么∠ABC= 。
7、如图25-15-4,点B 在点A 北偏西30º方向,且AB=5km ,点C 在点B 北偏东60º方向,且BC=12km ,则A 到C 的距离是 。
8、如图25-15-5,一轮船以每小时20海里的速度沿正东方向航行,上午8时,该船在A 处测得某灯塔位于它的北偏东30º的B 处,上午9时行至C 处,测得灯塔恰好在它的正北方向,此时它与灯塔的距离是 海里。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B
CO 东
A
北
A
P
C
B
当堂练习
1、海中有一个小岛A,它的周围8海里内有暗礁,鱼 船跟踪鱼群由西向东航行。在B点测得小岛A在北偏 东60°方向上,航行12海里到达点D,这时测得小岛A 在北偏东30°方向上,如果鱼船不改变航线继续向东 航行,有没有触礁的危险?
A
B D
当堂练习
2、如图,某船以29.8海里/时的速度向正北方向航 行,在A处测得灯塔C在该船的北偏东32°方向上, 半小时后该船航行到点B处,发现此时灯塔C与船 的距离最短。 (1)在图上标出点B的位置; (2)求灯塔C到B处的距离(精确到0.1海里)。
北
D C
A
东
当堂练习
3、如图,小岛A在港口P的南偏西45°方向,距离港口 81海里处,甲船从小岛A出发,沿AP方向以9海里/时的 速度驶向港口;乙船从港口P出发,沿南偏东60°方向, 以18海里/时的速度驶离港口。已知两船同时出发。 (1)出发后几小时两船与港口P的距离相等? (2)出发后几小时乙船在甲船的正东方向?
A
N1
N
∴AD 在Rt△ADB中,
∵ tan30˚== t-a-ABn-DD-60=0x√-=-X--+--2x3-4-x
X=12
AD≈12×1.732 =20.784 > 20
答:货轮无触礁危险。
DC
X
24海 B 里
当堂练习
4、如图,海关缉私艇在A处接到情报,在A的北偏西 60°方向的B处发现一可疑船只正以24海里/时的速度向 正东方向航行,于是该艇立即沿北偏西45°方向前进, 经过1小时航行,恰好在C处截住可疑船只,求缉私艇 的速度。
复习
如图,在高为300m的山顶上,测得一 建筑物顶端与底端的俯角分别为30°和 60°,求该建筑物的高。
A C
300m
BD
探究
例题:如图,一艘海轮位于灯塔P的北偏东65°方向, 距离灯塔80海里的A处,它正沿着正南方向航行一段 时间后,到达位于灯塔P的南偏东34°方向上的B处, 这时,海轮所在的B处距离灯塔P有多远?
北 P东
AHale Waihona Puke 二、探究例、如图,海岛A四周20海里周围内为暗礁区,一艘货 轮由东向西航行,,航行24海里到C,在B处见岛A在北 偏西60˚.在c见岛A在北偏西30˚,货轮继续向西航行,有 无触礁的危险?
解:过点A作AD⊥BC于D,
设 则 在Rt△ACDDC=中x,, BD=X+24
AD
∵ tan∠DDCC3A=------
