第8章最优消费和投资离散时间
第8章 相关分析-2. 离散相关

第8章 相关分析2. 离散相关与离散序列的卷积运算一样,离散序列的相关运算也可以分为线性相关和循环相关两种类型。
2.1 基本定义线性相互关的计算对应公式(8-1)的离散化形式,计算离散序列][n x 和][n y 的线性互相关,可得:∑+∞-∞=+⋅=i xy n i y i x n r ][][][ (8-6)对有限长度的离散序列][n x ,1,1,0-=L n 、][n y ,1,1,0-=P n ,且二者的长度分别为L 和P 。
那么,有如下公式成立:∑--=+⋅=nP i xy n i y i x n r 10][][][ (8-7)当P n i ≥+时,0][=+n i y ,所以公式(8-7)中的求和上限为n P --1。
因为序列][n r xy 下标n 的取值范围为:11-≤≤-P n M ,所以与线性卷积的长度一样,序列][n x 和][n y 的线性互相关序列的最大长度也是1-+P L 。
与离散Fourier 变换的相关特性对应的是循环相关(或称圆周相关),循环互相关的定义已在第二章中出现过,笔者在下面重新书写一遍。
∑-=+⋅=10])[(][][N i N xy n i y i x n r (8-8)其中,N n i )(+表示)(n i +除以N 的余数,][n r xy 下标n 的取值范围为:2/2/N n N <≤-。
可以利用循环相关来计算两个序列的线性相关,只是要对原有序列进行补零处理。
把长度为L 的序列][n x 和长度为P 的序列][n y 补零后拓展序列长度为N 的新序列][n x 和][n y ,只要满足1-+≥P L N ,两个新序列的循环相关就等同于原有两个序列的线性相关。
与连续函数的互相关函数一样,互相关序列][n r xy 既不是偶序列,也不是奇序列,但满足等式:][][n N r n r yx xy -=。
2.2 快速算法计算两个长度相等的序列的循环相关时,如果直接采用公式(8-8)的定义,计算量是非常大的,尤其在N 较大的情况下。
第八章资产组合理论

如果我们的资产组合中的风险资产仍然 是债券基金与股票基金,但是,现在我 们也投资于年收益率为5%的无风险的国 库券,那会发生什么情况呢?我们从图 解开始,图8 - 6显示了根据表8 - 1计算出 的股票基金与债券基金的联合概率分布 的机会集合。
两条可能的资本配置线( C A L)从无风险 利率( rf=5%)连到两种可行的资产组合。
8.2 两种风险资产的资产组合
在上一节我们考虑了几种证券等权重的分散资 产组合。现在开始研究有效分散,这可以构建 任意给定期望收益条件下的最低风险的资产组 合。
两种资产的资产组合相对易于分析,它们体现 的原则与思考可以适用于多种资产的资产组合。 我们将考察一个包括两个共同基金的资产组合, 一个是专门投资于长期债券的债券资产组合D, 一个是专门投资于股权证券的股票基金E,表8 - 1列出了影响这些基金收益率的参数,这些参 数可以从真实的基金中估计得出。
在上一节,我们推导了资产组合中两种风险资产的比例, 在此基础上,我们引入第三种选择—无风险的资产组合。 这可以使我们处理好资金在三种关键资产:股票、债券与 无风险货币市场证券之间的配置,一旦投资者掌握了这个 原则,他将可以很容易地构造由多种风险资产组成的资产 组合。
最优风险资产组合:两种风险资产和一种 无风险资产
低于组合中各个资产的标准差。
信号与系统 第8章 离散时间系统的时域与变换域分析

4
8.1.1 线性时不变离散时间系统
例8.1-1 设某离散系统激励x[n]与响应y[n]之间的关系为
y[n] = nx[n],判断该系统是否为线性时不变系统。
1 M2
1
M2
k M1
(x1[n
k]
x1[n
k ])
1
M2
1
M2
M1 M 2 1 kM1 x1[n k] M1 M 2 1 kM1 x2[n k]
y1[n] y2[n]
该系统满足叠加性,所以该系统是线性系统。
(3)假设输入信号为x[n]= x1[n-m],则输出信号为
y[n]
y[n] = x[n] + ay[n-1] = a n
此范围仅限于n ≥ 0,
故
y[n] = anu[n] 12
8.2 常系数线性差分方程的求解
N
M
ak y[n k] br x[n r]
k 0
r0
(8.2-2)
8.2.1 线性常系数差分方程的时域经典法求解
一般地,常系数线性差分方程的解由齐次解和特解组成。
的完全解。
其中激励信号为x[n] n2,且边界条件为 y[1] 1
解:(1)齐次解为 yh[n] C(2)n
(2)将 x[n] n代2 入差分方程的右端,得自由项为
2n 1
从而特解为 yp[n] D1n D2
其中,D1和D2为待定系数,代入原方程得
3D1n 3D2 2D1 2n 1
第8章_离散模型(投影版)
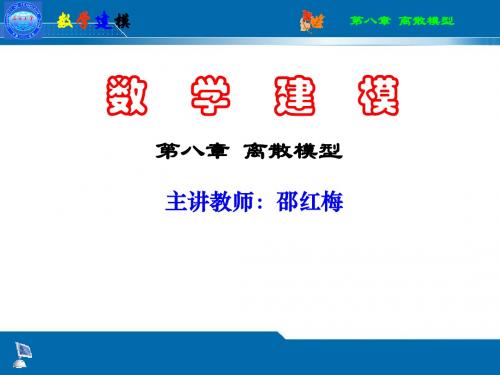
A的秩为1,A的惟一非零特征根为n
由成对比较阵求 A的任一列向量都是对应于特征根n的特征向量
A的归一化特征向量可作为权向量
权向量的特征根 法
对于不一致(但在允许范围内)的成对比较阵A,建议用对应于最大特征 根λ的特征向量作为权向量w ,即A w = A λ 层次分析模型
数学建模
一致性检验 对A确定不一致的允许范围 n阶一致阵A的惟一非零特征根为n
aij · ajk=(wi / wj) · (wj / wk)= wi / wk= aik
所以当aij离一致性的要求不远时, 表示诸因素 n阶一致阵A有下列性质 C1 ,…,Cn对上 A的特征根和特征向量也与一致阵的相差不大。
如果一个正互反阵A满足aij · ajk = aik , i,j,k = 1,2,…,n 因为矩阵A的特征根和特征向量连续地依赖于矩阵的元素aij, 则A称为一致性矩阵,简称一致阵。
随机一致性指标RI的数值 4 0.90 5 6 7 n RI 1 0 2 0 3 0.58 8 9 10 11
计算A'的一致性指标 CI 1,2阶的正互反 是因为
表中n = 1,2时RI = 0,
随机一致性指标RI之比称为一致性比率CR。 CI A的不一致程度在容许范围之内,可用其 CR 0.1 RI 特征向量作为权向量:通过一致性检验 层次分析模型
1.12 1.24 1.32 1.41 1.45 1.49 1.51 0.1的选取是带有 一定主观信度的 对于n≥3的成对比较阵A,将它的一致性指标 CI与同阶(指n相同)的
数学建模
第八章 离散模型
―选择旅游地”中准则层对目标的权向量及一致性检验
3 1 1/ 2 4 3 2 1 7 5 5 A 1 / 4 1 / 7 1 1 / 2 1 / 3 1 / 3 1 / 5 2 1 1 当检验不通过时, 1 1 / 3 1 / 5 3 1 要重新进行成对比较, 或对已有的A进行修正。
信号与系统_第八章 z变换、离散时间系统的z域分析

Re(z)
C是包围X(z)zn-1所有极点之逆时针闭合积分路线,通常选 择z平面收敛域内以原点为中心的圆。
➢ 求X(z)的反z变换的三种方法 ✓留数法 ✓幂级数展开和长除法 ✓部分分式展开法
中国民航大学 CAUC
8.3 逆z变换
二、部分分式展开法求逆z变换(1)
✓ 步骤 (1)将X(z)除以z,得到X(z)/z=X1(z); (2)将X1(z)按其极点展成部分分式(其方法与拉氏变换 的部分分式展开完全一致);
3.x(n)为左边序列
x(n)是无始有终的序列,即当n n2 时, x(n)=0 。
X (z)
n2
x(n)
z
n
x(n)z n
jIm(z)
n
n n2
✓若n20,0z RX2
0
RX2 Re(z)
✓若n20,0z RX2
中国民航大学 CAUC
8.2 z变换的收敛域
4.x(n)为双边序列
x(n)是从n =延伸到n = 的序列 。
(3)X(z)=zX1(z),得到X(z)的部分分式展开式;
(4)对X(z)的每一个部分分式进行反z变换,就得到X(z) 对应的序列x(n)。
[例]求 X (z)
z2
( z 1) 的逆z变换。
(z 1)( z 0.5)
中国民航大学 CAUC
8.3 逆z变换
二、部分分式展开法求逆z变换(2)
[例]求收敛域分别为z1和 z1 两种情况下, X (z) 1 2z 1
➢X(z)收敛域的确定必须同时依赖于 ✓ 序列的性质(有限长,右边,左边,双边) ✓ 是对x(n)进行单边还是双边z变换 ✓ X(z)的极点
中国民航大学 CAUC
信号与系统第8章 离散时间系统的z域分析

零状态响应为
Yf
(z)
(1 z 1 z 2 ) 2 3z 1 z 2
1 1 z 1
1/ 6 0.5 5 / 6 1 z1 1 z1 1 0.5z1
yf [k] Z 1{Yf (z)}{1/ 6 0.5(1)k (5/ 6)(0.5)k}u[k]
y[k] yx[k] yf [k] {1/ 6 3.5(1)k (4 / 3)(0.5)k}u[k]
离散时间信号与系统的Z域分析
• 离散时间信号的Z域分析 • 离散时间系统的Z域分析 • 离散时间系统函数与系统特
性
离散时间信号的Z域分析
• 理想取样信号的拉普拉斯变换 • 单边Z变换定义 • 单边Z变换的收敛域 • 常用序列的Z变换 • 单边Z变换的性质 • Z反变换
理想取样信号的拉普拉斯变换
fs (t) f (t) (t kT) f (kT) (t kT)
Re(z)
三、常用序列的Z变换
1) Z{ (k)} 1, z 0
2) 3)
Z{u(k)} 1 1 z
Z{aku(k)}
1 , 1
1 a
z
z
1
1 z
a
4)
Z{e
j0k
u(k
)}
1
e
1
j0
z
1
z z e j0
5)
Z{e-
j0k u (k
)}
1
1 e- j0
z
1
z z e- j0
z e j0 z e j0
解代数方程
二阶系统响应的z域求解
y[k] a1 y[k 1] a2 y[k 2] b0 f [k] b1 f [k 1] k 0
初始状态为y[1], y[2] 对差分方程两边做Z变换,利用
离散数学第8章图论
第8章 图论
两图同构的必要条件:
(1) 结点数相等; (2) 边数相等; (3) 度数相同的结点数相等。 但这不是充分条件。例如下图中(a)、(b)两图虽然满足以上 3条件,但不同构。(a)中的x应与(b)中的y对应,因为次数都是3。 但(a)中的x与两个次数为1的点u,v邻接,而(b)中的y仅与一个次数 为1的点w邻接。
A
C
B
第8章 图论
8.1 图的基本概念
8.1.1 图 定义8.1―1 一个图G是一个三重组〈V(G),E(G),ΦG〉,其中
V(G)是一个非空的结点(或叫顶点)集合,E(G)是边的集合,ΦG是从
边集E到结点偶对集合上的函数。一个图可以用一个图形表示。 例1设G=〈V(G),E(G),ΦG〉,其中V(G)={a,b,c,d},E(G)={e1,e2,e3,e4, e5,e6,e7},ΦG(e1)=(a,b),ΦG(e2)=(a,c),ΦG(e3)=(b,d), ΦG(e4)=(b,c),ΦG(e5)=(d,c),ΦG(e6)=(a,d),ΦG(e7)=(b,b)
第8章 图论
定理8.2―2在一个具有n个结点的简单图G=〈V,E〉
中,如果经v1有一条简单回路,则经v1有一条长度不超过n 的基本回路。
定义 8.2―3 在图 G=〈V,E〉中 , 从结点 vi 到 vj 最短路径
的长度叫从 vi 到 vj 的距离 , 记为 d(vi,vj) 。若从 vi 到 vj 不存在 路径,则d(vi,vj)=∞。 注意,在有向图中,d(vi,vj)不一定等于d(vj,vi),但一般地 满足以下性质:
其中V3=V1∩V2,E3=E1∩E2,记为G3=G1∩G2。 (3)G1与G2的差,定义为图G3=〈V3,E3〉,记为G3=G1-G2。 其中E3=E1-E2,V3=(V1-V2)∪{E3中边所关联的顶点}。 (4)G1与G2的环和,定义为图G3=〈V3,E3〉, G3=(G1∪G2)-(G1∩G2),记为G3=G1G2。
陈后金《信号与系统》(第2版)课后习题(离散时间信号与系统的z域分析)

第8章离散时间信号与系统的z域分析8-1 根据定义求以下序列的单边z变换及其收敛域。
解:根据序列单边z变换的定义即可求出上述信号的z变换及收敛域。
8-2 根据单边z变换的位移性质,求以下序列的z变换及其收敛域。
解:单边z变换的位移特性有以下3种形式(8-1)(8-2)(8-3)对于因果序列的位移,利用式(8-1);非因果序列的位移,利用式(8-2)和(8-3)。
(1)利用因果序列的位移特性,有(2)利用因果序列的位移特性,有(3)利用因果序列的位移特性,有(4)利用因果序列的位移特性,有(5)由于,直接应用指数信号的z变换,可得(6)将改写成,利用因果序列的位移特性,可得8-3 根据z变换的性质,求以下序列的单边z变换及其收敛域。
解:利用z变换的性质求信号z变换的关键是根据待分析信号的构成,确定合适的信号作为基本信号,采用相应的z变换性质。
(1)由,以及z域微分特性,有(2)将改写为利用(1)题结果及因果序列的位移特性,可得(3)将改写为利用的z变换及z域微分特性,有故(4)将改写为利用(3)题结论及因果序列的位移特性,可得(5)将改写为利用卷积特性(6)利用(5)题结果及指数加权特性,有8-4 求以下周期序列的单边z变换。
解:周期为N的单边周期序列可以表示为第一个周期序列及其位移的线性组合,即这样,若计算出的z变换,利用因果序列的位移特性和线性特性,则可求得其单边周期序列的变换为(1)可表示为利用的变换及因果序列的位移特性,可得(2)将改写为利用(1)题的结果及卷积特性,可得8-5 已知,利用z变换的性质,求下列各式的单边z变换及其收敛域。
解:本题的关键是判断各信号是经过什么运算得到的,然后根据其运算,利用相应的z变换性质即可求出它们的z变换。
(1)利用因果序列的位移特性,可得(2)利用指数加权特性,可得(3)利用(1)题结果及指数加权特性,可得(4)利用z域微分特性,可得(5)利用(4)题结果及线性加权特性,可得(6)可以表示为,利用卷积特性可得(7)可以表示为,利用卷积特性可得(8)可以表示为,利用因果序列的位移特性及卷积特性,可得8-6 已知因果序列的z变换式,试求的初值和终值解:利用初值定理和终值定理即可求出的初值和终值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
为了找到最优投资比例w(1) ,只要对f [w(1)]求导,并令一阶导数等于0 就可以了, 容易得到:
再考察当股票价格p = 50 时的情形, 我们发现仍 旧可以使用上式。因为
依然表示股票价格上涨一倍的情况下,投资在两种 资产上,给投资者带来的期末财富的期望效用; 而
则是投资机会相对较差时,期末财富的效用水平。 所以最优解还是w(1) =13 /19 ,因此这个最优投 资比例决策独立于1 时刻股票价格和财富的绝对 水平。
逆向归纳法:从倒数第一期,即T -1期开始。 这就是说,我们必须获得t = 1时期,股票 价格在p = 200或者p = 50 两种情况下的最
优投资比例,这是一个单期静态优化问题。 一旦获得了t =1时的相应结果w(1) 和W(1) , 就可以按照同样的结构,进一步推测t = 0
时刻的最优投资比例,从而一层层地逐步 解决了问题。
第8章 最优消费和投资:离散时间
基本分析框架
典型消费者个人将生存一段时期[0,T],他会有一 个大于0 的初始财富或者说资源禀赋W(0) ;在生 存过程中,他会获得一些非资本(non-capital) 收入(t) (例如工资);在生存的每一天中,他 必须决定把可供支配的财富(资源),用于当前 消费C 和投资积累I 上(投资将提供下一时刻的资 本收入);在最后时刻留下一部分遗产W(T ) 给 后人。这时,两个基本选择问题,即消费多少 (也就是投资多少)和如何投资(资产组合), 必须同时被决定。消费者这种不断的选择行为的 目的就是使得他们终身效用最大化。
Байду номын сангаас
目前的任务就是找到 最优的投资决策变量 (最优控制) w(0) 和 w(1) ,使以上最优化 问题得以解决。
模型求解
“向前”推导的方法:即从t = 0 时刻开始,事先 决定一个策略w(0) ,但它是不是最优还不清楚。 根据w(0) ,我们仅仅能够知道t =1时刻的期望财 富水平的函数表达式,但是最大化这个函数得到 的“最优的”w(0) ,并不一定是最优决策过程 [w(0), w(1)]的必然组成部分,除非可以明确地知 道在所有不同情况状态下的w(1) ,并且它是惟一 的。因此向前推导的方法是行不通的。
w(0) =13 /19, w(1) = 13/19
尽管实际的问题要比这个简单的例子复杂得多, 但从上述求解过程中,仍然可以归纳出最优个人 消费/投资决策的动态规划解法的最显著特征—— 即它是向后追溯的。而这正是贝尔曼最优化原理 的体现。
一般情形
现在考察多期离散时间情况下,个人最优 消费/投资决策问题的标准建模方法和它的 一般解法。
目标函数
其中T 是投资者的寿命;C(t) 是 投资者年龄为t 时选择的消费数 量;W (t) 是t 时刻的财富(或 者遗产);Et (.) t是基于t 时刻 所有已经揭示出的信息的条件 期望算子。Ut[C (t), t] 是效用函 数,在整个定义域内,它被假 定是单调递增和凹的;U2[W (T),T] 是基于期末财富或者 说遗产的效用函数(bequest valuation function),它也是单 调递增和凹的。
简单地说,它表示在每 一时点上,股票价格要 么以4/9 的概率上涨一倍, 要么以(1-4/9)的概率 下跌一半。用w(0) 和w(1) 表示该投资者在0、1 时 刻上,投资于风险资产 (股票)上的财富分额。
(3)投资者的非资本收入为0,效用函数 具有以下特定形式:
U (x) =
(4)为了简化分析,假定投资者也不进行 任何消费,这样最优决策的惟一目标就是 最大化他来自最终财富的期望效用。
“一个最优策略有这样的特征:无论初始状态和初始决策 是什么,余下的决策在考虑到第一个决策导致的状态的影 响下,都必须是最优的策略。”
简单地说,这就意味着任何最优过程的最后一段过程必定 是最优的。这一原则将在后面的分析中一再的出现。
简化的例子
假定: (1)典型个人生存两个时期,他可以在两个时点
第一步: t = 1时刻
假定此时的财富W(1) 为任意一正数(它是 由上一期t = 0 时的最优决策所产生的)。 投资到股票上的财富比例为w(1) ,则投向 无风险资产上的就是1- w(1) 。我们来计算 最后的t = 2 时刻,积累的财富的期望效用 是多少。先考虑当股票价格p = 200时的情 形,根据二项树模型:
第二步: t = 0 时刻
根据上面的推理,我们只要知道1 时刻的财 富水平W(1) ,就可以知道最终财富的期望 效用水平是多少,而1 时期的财富水平 W(1) ,也是由同第一步类似的决策过程所 决定的,即:
同样对f [w(0)]求导数,并令一阶导数等于0,得到 最优化条件还是:w(0) = 13 /19 。因此最优投资 决策方案就是:
约束条件
其中 就是非资本收入,广 义上I 泛指各种投资,但这 里实际上仅仅包括对市场上 可交易的有价证券的投资。 经济体系中的风险, 就源自
于非资本收入和投资机会集 合(investment opportunity set)(也即资本收入)的不 确定性。
最优消费/投资决策:离散时间
所谓随机最优控制,就是试图在一个由随机因素驱动的成 长路径上,通过采用适当的策略来最优化目标函数。这里 的消费多少和如何投资,就是由投资者决定的控制变量 (controlled variable )或者说决策(decision),通过一 系列遵循某种原则的最优的决策,即最优策略(policy), 个人可以得到最大的效用满足。这里的原则,指的就是贝 尔曼(Bellman R.)最优化原则(principle of optimality):
上,即t = 0 、1上做决策( t = 3时,他就死亡 了);他被赋予一定量的初始资源W(0) > 0 。 (2)理想化的资本市场上存在两种资产。一种是 无风险的现金或者债券,它的价格在任何时刻都 没有变化,始终为1;另一种是有风险的股票,它 的价格过程假定由以下二项树描绘
股票价格运动的二项树模型
