高一数学集合与简易逻辑
高一数学集合与简单逻辑公式

高一数学集合与简单逻辑公式集合是高一数学必修1第1章的内容,高中数学的基本概念之一,下面是店铺给大家带来的高一数学集合与简单逻辑公式,希望对你有帮助。
高一数学集合与简单逻辑公式任一xaxb,记作ab高中数学ab,baa=bab={x|xa,且xb}ab={x|xa,或xb}card(ab)=card(a)+card(b)-card(ab)(1)命题原命题若p则q逆命题若q则p否命题若p则q逆否命题若q,则p(2)四种命题的关系(3)ab,a是b成立的充分条件ba,a是b成立的必要条件ab,a是b成立的充要条件1.集合元素具有①确定性②互异性③无序性2.集合表示方法①列举法②描述法③韦恩图④数轴法3.集合的运算⑴a(bc)=(ab)(ac)⑵cu(ab)=cuacubcu(ab)=cuacub4.集合的性质⑴n元集合的子集数:2n真子集数:2n-1;非空真子集数:2n-2高一数学集合常考知识点1.集合的有关概念1)集合(集):某些指定的对象集在一起就成为一个集合(集).其中每一个对象叫元素注意:①集合与集合的元素是两个不同的概念,教科书中是通过描述给出的,这与平面几何中的点与直线的概念类似。
②集合中的元素具有确定性(a?A和a?A,二者必居其一)、互异性(若a?A,b?A,则a≠b)和无序性({a,b}与{b,a}表示同一个集合)。
③集合具有两方面的意义,即:凡是符合条件的对象都是它的元素;只要是它的元素就必须符号条件2)集合的表示方法:常用的有列举法、描述法和图文法3)集合的分类:有限集,无限集,空集。
4)常用数集:N,Z,Q,R,N*2.子集、交集、并集、补集、空集、全集等概念1)子集:若对x∈A都有x∈B,则A B(或A B);2)真子集:A B且存在x0∈B但x0 A;记为A B(或,且 )3)交集:A∩B={x| x∈A且x∈B}4)并集:A∪B={x| x∈A或x∈B}5)补集:CUA={x| x A但x∈U}高一数学集合练习1.(20 13年高考四川卷)设集合A={1,2,3},集合B={ -2,2},则A∩B 等于( B )(A) (B){2}(C){-2,2} (D){-2,1,2,3}解析:A∩B={2},故选B.2.若全集U={-1,0,1,2},P={x∈Z|x2<2},则∁UP等于( A )(A){2} (B){0,2}(C){-1,2} (D){-1,0,2}解析:依题意得集合P={-1,0,1},故∁UP={2}.故选A.3.已知集合A={x|x>1},则(∁RA)∩N的子集有( C )(A)1个 (B)2个 (C)4个 (D)8个解析:由题意可得∁RA={x|x≤1},所以(∁RA)∩N={0,1},其子集有4个,故选C.4.(2013年高考全国新课标卷Ⅰ)已知集合A={x|x2-2x>0},B={x|-(A)A∩B= (B)A∪B=R(C)B⊆A (D)A⊆B解析:A={x|x>2或x<0},∴A∪B=R,故选B.5.已知集合M={x ≥0,x∈R},N={y|y=3x2+1,x∈R},则M∩N等于( C )(A) (B){x|x≥1}(C){x|x>1} (D){x|x≥1或x<0}解析:M={x|x≤0或x>1},N={y|y≥1}={x|x≥1}.∴M∩N={x|x>1},故选C.。
集合与简易逻辑

如:应把集合{1,2,2}改写成 {1,2}
(3) 无序性: 集合中的元素是平等的,没有先后顺序, 因此判定两个集合是否一样,仅需比较它们的元素是否 一样,不需考查排列顺序是否一样.
如:集合{1,2,3}和{1,3,2}表示同一集合。
二、元素与集合之间的关系: 若a是集合A的元素, 就说 a 属于集合 A , 记作 a∈A ; 若a不是集合A的元素, 则 a 不属于集合 A , 记作 aA。 例如:A={1,2,3,4,5}
Q 有理数集记作______;
R 实数集记作_______;
四、集合的常用表示方法:
“地球上的四大洋”组成的集合可以表示 为: {太平洋,大西洋,印度洋,北冰洋}.
方法一:列举法——把集合中的元素一一 列举出来写在大(花)括号{ }内表示集合的 方法。
例1:用列举法表示下列集合:
{ 2, 3, 5, 7 } (1)小于10的所有质数组成的集合__________; (2)由大于3小于10的整数组成的集合 { 4, 5, 6, 7 ,8 ,9 } ___________________; { -4, 4} (3)方程x2-16=0的实数解组成的集合_________;
3 则3∈A , A 2
集合常用大写字母A,B,C,D,……标记, 元素常用小写字母a,b,c,d,……标记。
三、常用数集及其记法:
数的集合简称数集。 一些常用数集及其记法:
N 非负整数集(即自然数集) 记作_______;
N*或 N+ 正整数集记作_____________;
Z 整数集记作_______;
例2:用描述法表示下列集合:
集合与简易逻辑知识点总结- 高三数学一轮复习

知识点总结1 集合与简易逻辑一、集合(一)元素与集合1.集合的含义某些指定对象的部分或全体构成一个集合.构成集合的元素除了常见的数、点等数学对象外,还可以是其他对象.2.集合元素的特征(1)确定性:集合中的元素必须是确定的,任何一个对象都能明确判断出它是否为该集合中的元素.(2)互异性:集合中任何两个元素都是互不相同的,即相同元素在同一个集合中不能重复出现.(3)无序性:集合与其组成元素的顺序无关.3.元素与集合的关系元素与集合之间的关系包括属于(记作a A ∈)和不属于(记作a A ∉)两种.4.集合的常用表示法集合的常用表示法有列举法、描述法、图示法(韦恩图).5.常用数集的表示 数集 自然数集 正整数集 整数集 有理数集 实数集符号 NN ∗或N + Z Q R (二)集合间的基本关系1.集合A 为集合B 的子集 ,记作A B ⊆(或B A ⊇),读作“A 包含于B ”(或“B 包含A ”).(2)真子集:若A B ⊆,且存在b B ∈,但b A ∉,则集合A 是集合B 的真子集,记作AB (或B A ⊃≠). 读作“A 真包含于B ”或“B 真包含A ”.(3)相等:对于两个集合A 与B ,如果A B ⊆,同时B A ⊆,那么集合A 与B 相等,记作A =B .(4)空集:把不含任何元素的集合叫做空集,记作∅;(三)集合的基本运算(1)交集:由所有属于集合A 且属于集合B 的元素组成的集合,叫做A 与B 的交集,记作A B ⋂, 即{}|A B x x A x B ⋂=∈∈且.(2) 并集:由所有属于集合A 或属于集合B 的元素组成的集合,叫做A 与B 的并集,记作A B ⋃,(3) 即{}|A B x x A x B ⋃=∈∈或.(3)补集:对于一个集合A ,由全集U 中不属于集合A 的所有元素组成的集合称为集合A 相对于全集U 的补集,简称为集合A 的补集,记作U C A ,即{|,}U C A x x U x A =∈∉且.(四)集合的运算性质(1)集合的运算性质:①交换律:A ∪B =B ∪A ;A ∩B =B ∩A ;②结合律:(A ∪B )∪C =A ∪(B ∪C );(A ∩B )∩C =A ∩(B ∩C );③分配律:(A ∩B )∪C =(A ∪C )∩(B ∪C );(A ∪B )∩C =(A ∩C )∪(B ∩C );【集合常用结论】1.子集个数:含有n个元素的有限集合M,其子集个数为2n;其真子集个数为2n-1;其非空子集个数为2n-1;其非空真子集个数为2n-2.2. 是任何集合的子集,是任何非空集合的真子集.3.∁U(A∪B)=(∁U A)∩(∁U B);∁U(A∩B)=(∁U A)∪(∁U B);4.A∪B=A⇔B⊆A;A∩B=B⇔B⊆A.5.集合运算中的常用方法若已知的集合是不等式的解集,用数轴求解;若已知的集合是点集,用数形结合法求解;若已知的集合是抽象集合,用Venn图求解.二、简易逻辑(一).全称命题、特称(存在性)命题及其否定(1)全称命题p:∀x∈M,p(x),其否定为特称(存在性)命题:¬p:∃x0∈M,¬p(x0).(2)特称(存在性)命题p:∃x0∈M,p(x0),其否定为全称命题:¬p:∀x∈M,¬p(x).(二).充分条件与必要条件的判定方法(1)定义法:若p⇒q,则p是q的充分条件(或q是p的必要条件);若p⇒q,且q⇏p,则p是q的充分不必要条件(或q是p的必要不充分条件).(2)集合法:利用集合间的包含关系。
高中数学——11、集合、简易逻辑

集合、简易逻辑常用数集符号自然数集N (包括0),正整数集N *或N +,整数集Z ,实数集R 集合1、互异性例:集合{a 2,0,1}与集合{b 2,0,-1}相等,根据互异性,a 2=-1、b 2=12、元素、集合间的关系(韦恩图):元素与集合∈∉,集合与集合⊆ ⊊⊄ (注:集合A ⊆集合B ,集合A 可以是Ø,集合A 、B 可以相等)3、空集:Ø,无任何元素,是任何集合的子集(注:{Ø}与Ø不同,{Ø}包含1个元素Ø,Ø无元素)(注:空集必须分类讨论)4、交集∩,并集∪,补集(全集U 中不属于集合A 的元素集合,C U A ) 例:A={x |1≤x ≤3},B={x |mx+1=0},A ∩B ≠Ø,求m 的范围 补集思想,令A ∩B =Ø,则B =Ø(m=0)或-m1<1或>3,求出m 的集合M ,C R M 即所求范围5、常见元素类型(1)数集例:{x|x 2+3x-4=0},表示方程x 2+3x-4=0的解(2)点集例:{(x ,y )|y=x 2+3x-4},表示函数y=x 2+3x-4图像上点的坐标6、集合子集的个数含有n 个元素的集合,子集个数为2n ,非空集合个数为2n -1简易逻辑1、复合命题:或∨、且∧、非﹁p∨q:一真即真(特称命题∃:“存在……”)p∧q:一假即假(全称命题∀:“对于所有……”)2、原命题(若p,则q)与逆否命题(若﹁q,则﹁p)同真同假3、对于命题“若p,则q”,否命题与命题的否定(否定命题)(1)否命题:若﹁p,则﹁q(2)命题的否定(否定命题):若p,则﹁q(注:命题的否定考的多,否命题考的少)(3)全称命题、特称命题的否定例1:否定全称命题“∀实数x,x2>0”先改为“若p,则q”,“若x为实数,则x2>0”→否定即﹁q,“若x为实数,∃实数x,x2≤0”,即“∃实数x,x2≤0”例2:否定特称命题“∃平行四边形,不是矩形”先改为“若p,则q”,“若一个平面图形是平行四边形,∃一个平行四边形,不是矩形”→否定即﹁q,“若一个平面图形是平行四边形,则它是矩形”,即“∀平行四边形,是矩形”4、充分必要条件p是q的充分必要条件,p⇔q(1)充分条件:p⇒q(2)必要条件:p⇐q(注:利用集合理解充分必要条件p⇒q,即集合P⊆Q,p⇐q,即集合P⊇Q)。
必修1、选修1-1 集合与简易逻辑

作“������或������” ;对于“������ ∨ ������”形式的命题判断真假的方法是:一真则真; (2)且:一般地,用联结词“且”把命题������和命题������联结起来,就得到一个新的命题,记作������ ∧ ������,读 作“������且������” ;对于“������ ∧ ������”形式的命题判断真假的方法是:一假则假; (3)非:一般地,对于一个命题全盘否定,就得到一个新的命题,记作“¬ ������” ,读作“非������”或读作 “������的否定” ;对于“¬ ������”形式的命题判断真假的方法是:真假相对; 4、全称量词与存在量词: (1)全称量词和全称命题: 全称量词:短语“所有的” “任意一个” “任意的”等在逻辑中通常称为全称量词,用符号“∀”表示; 全称命题:含有全称量词的命题称为全称命题; 全称命题的表达形式:������: ∀������ ∈ ������, ������ ������ ; 全称命题的否定形式:¬ ������: ∂������������ ∈ ������, ¬ ������ ������������ ; (全称命题的否定是特称命题) (2)存在量词和特称命题: 存在量词:短语“至少有一个” “存在一个”等在逻辑中通常称为存在量词,用符号“∂”表示; 特称命题:含有存在量词的命题称为特称命题; 特称命题的表达形式:������: ∂������������ ∈ ������, ������ ������������ ; 特称命题的否定形式:¬ ������: ∀������ ∈ ������, ¬ ������ ������ ; (特称命题的否定是全称命题)
(二)集合的运算——交集、并集、补集
1、交集: 一般地, 由所有属于集合������并且属于������的所有元素组成的集合, 称为集合������与集合������的交集, 记作������ ∩ ������, 读作������交������,即������ ∩ ������ = ������ ������ ∈ ������且������ ∈ ������ ;
高中数学 知识点归纳 1集合与简易逻辑
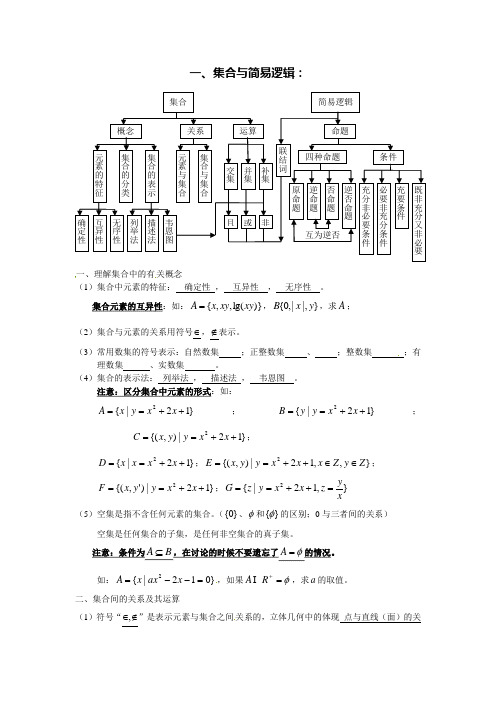
一、集合与简易逻辑:一、理解集合中的有关概念(1)集合中元素的特征: 确定性 , 互异性 , 无序性 。
集合元素的互异性:如:)}lg(,,{xy xy x A =,}|,|,0{y x B ,求A ; (2)集合与元素的关系用符号∈,∉表示。
(3)常用数集的符号表示:自然数集 ;正整数集 、 ;整数集 ;有理数集 、实数集 。
(4)集合的表示法: 列举法 , 描述法 , 韦恩图 。
注意:区分集合中元素的形式:如:}12|{2++==x x y x A ;}12|{2++==x x y y B ;}12|),{(2++==x x y y x C ;}12|{2++==x x x x D ;},,12|),{(2Z y Z x x x y y x E ∈∈++==;}12|)',{(2++==x x y y x F ;},12|{2xyz x x y z G =++==(5)空集是指不含任何元素的集合。
(}0{、φ和}{φ的区别;0与三者间的关系) 空集是任何集合的子集,是任何非空集合的真子集。
注意:条件为B A ⊆,在讨论的时候不要遗忘了φ=A 的情况。
如:}012|{2=--=x ax x A ,如果φ=+R A ,求a 的取值。
二、集合间的关系及其运算(1)符号“∉∈,”是表示元素与集合之间关系的,立体几何中的体现 点与直线(面)的关系 ;符号“⊄⊂,”是表示集合与集合之间关系的,立体几何中的体现 面与直线(面)的关系 。
(2)_}__________{_________=B A ;____}__________{_________=B A ; _}__________{_________=A C U (3)对于任意集合B A ,,则:①A B B A ___;A B B A ___;B A B A ___; ②⇔=A B A ;⇔=A B A ;⇔=U B A C U ;⇔=φB A C U ;③=B C A C U U ; )(B A C U =;(4)①若n 为偶数,则=n ;若n 为奇数,则=n ;②若n 被3除余0,则=n ;若n 被3除余1,则=n ;若n 被3除余2,则=n ;三、集合中元素的个数的计算:(1)若集合A 中有n 个元素,则集合A 的所有不同的子集个数为_________,所有真子集的个数是__________,所有非空真子集的个数是 。
高一数学集合与简易逻辑综合知识精讲

高一数学集合与简易逻辑综合【本讲主要内容】集合与简易逻辑综合集合、子集、交集、并集、补集等概念,绝对值不等式、一元二次不等式的解法,简易逻辑。
【知识掌握】 【知识点精析】1. 集合:一般地,某些指定的对象集在一起就成为一个集合;2. 子集:一般地,对于两个集合A 与B ,如果集合A 的任何..一个元素都是集合B 的元素,我们就说集合A 包含于集合B ,或集合B 包含集合;3. 交集:一般地,由所有属于A 且属于B 的元素所组成的集合,叫做A ,B 的交集;4. 并集:一般地,由所有属于集合A 或属于集合B 的元素所组成的集合,叫做A ,B 的并集;5. 补集:一般地,设S 是一个集合,A 是S 的一个子集(即S A ⊆),由S 中所有不属于A 的元素组成的集合,叫做S 中子集A 的补集(或余集);6. )0a (a x ><的解集是。
{}a x x |x <<-;)0a (a |x |>>的解集是{}a x a x |x -<>或;7. 一元二次不等式的解法;8. 简易逻辑:命题:可以判断真假的语句叫做命题。
逻辑联结词:“或”、“且”、“非”这些词叫做逻辑联结词。
简单命题和复合命题不含逻辑联结词的命题叫做简单命题。
简单命题是不含其他命题作为其组成部分(在结构上不能再分解成其他命题)的命题。
由简单命题和逻辑联结词构成的命题叫做复合命题。
四种命题及它们的关系【解题方法指导】例1. 已知全集{}的质数不大于20U ,A ,B 是U 的两个子集,且满足{}5,3B C A U = ,{}19,7A C B U = ,(U C A ) (U C B)= {}17,2。
求集合A 和B 。
解法一:(直接解法)依题意,{}5,3B C A U = ,则{}A 5,3⊆,且{}B C 5,3U ⊆。
从而知3,5A ∈,且∉B 。
同理,由B A C U {}19,7,知7,19,且7,19∉A由(A C U ) (U C B ){}17,2,知2,17∉A ,且2,17 ∉B因为{}19,17,13,11,7,5,3,2U ,观察11和13这两个元素,不外乎下面几种情况:①若11 ,11 ,则A C U ,且 U CB ,这与(AC U ) (U C B )={}17,2矛盾;②若11∈A ,11B ∉,则 U C B ,这与A U C B ={}5,3矛盾;③若11 ∉A ,11∈B ,则A C U ,这与B AC U = {}19,7矛盾;④若11 ∈A ,11 ∈B ,则11∈(A B )。
高一数学 集合与简易逻辑

芯衣州星海市涌泉学校高一数学集合与简易逻辑 第一题集合、子集、交集、并集1由小于10的所有质数组成的集合是。
2由不大于50的所有质数组成的集合是。
3设全集U=Z ,M={10}x N x ∈≤,P={23}x Z x ∈-≤≤。
那么M P =,M P =,U M C P =。
4由1,2,3这三个数字抽出一部分或者者全部数字〔没有重复〕所组成的自然数有。
5由1,2,3这三个数字抽出一部分或者者全部数字所组成的自然数中,不超过321的有个,其中3的倍数有个。
6集合{a,b}的子集有,其中真子集有个。
7假设{a}⊆A ⊆{a,b,c},那么集合A 的个数有个。
8设U=Z ,M={2,}x x k k z =∈,N={21,}x x k k z =+∈,P={21,}x x k k z =±∈,Q={41,}x x k k z =±∈,那么以下结论不正确的选项是〔〕A ,U C MN =B ,U C P M =C ,P Q =∅D ,U C M N P Q === 9设A={2}x x >-,B={3}x x <,那么A B =。
10设A={12}x x -<<,B={13}x x <<,那么A B =。
11设A={(,)46}x y y x =-+,B={(,)53}x y y x =-,那么A B =。
12设A=2{46}yy x =--,B=2{530}y x y --=,那么A B =,A B = 13设A=2{46}y y x =--,B=2{50}y x y m --=,假设A B ≠∅,那么实数m 的取值范围是,假设A B R ≠,那么实数m 的取值范围是。
第二题一元二次不等式与含绝对值不等式的根本解法1〔1〕不等式5005x -≤的解集是;〔2〕不等式257x +>的解集是 2不等式5527x <-≤的解集是。
3不等式11x x-≤的解集是。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
升庵中学高一数学组1
第一章
集合与简易逻辑测试
班级
姓名
一选择题:只有唯一正确结论(每小题5分,共60分)
(1)下面有四个命题:①集合N 中最小的数是
1;②0是自然数;③
1,2,3是不大于3的
自然数组成的集合;④,a N b N ,则2a b 。
其中正确的命题的个数是(
)
A 0
B 1
C 2
D 3
(2)下面6种表示法:①
1,2x y ;②
1
,/
2
x x y y
;③
1,2;④1,2;
⑤
1,2;⑥,/12x y x y 或。
能正确表示方程组
20
30
x y
x
y 的解集的是
A ①②③④⑤⑥
B ②③④⑤
C ②⑤ D
②⑤⑥
(3)已知集合/12,/35A x a x
a B x x 。
则能使A B 成立的实数a 的
取值范围是()
A
/34
a x B
/34
a x C
/34
a x D
(4)设全集2,3,5,2,5,5U U A
a C A
则a 的值是(
)
A 2
B 8
C 2或8
D
2或8
(5)全集,,,,,,,,U U
a b c d e A
a b B
C A 则集合B 的个数是(
)
A 5
B 6
C 7
D 8
(6)已知集合1,1,2M ,集合2
/,N
y y
x x
M ,则M
N
()
A
1,2,4
B
1,4 C
1
D
(7)设集合1,2,,2,3M
N
则满足P
M
N 的集合P 的个数是
()
A 6个
B 7个
C 8个
D 9个
(8)已知全集2
/12200,U x N x
x P 集合3,4,6,8
,集合
3589Q ,,,,。
