2014年石家庄一模数学(理科)试卷与答案
河北省正定中学2014届高三数学上学期质检一模拟试题

高三年级质检一模拟考试 数 学一、选择题. (每小题5分,共60分)1. 已知i 是虚数单位,若复数(1i)(2i)a ++是纯虚数,则实数a 等于 ( )A .2B .12 C .12- D .2- 2. 已知集合}|{},023|{2a x x N x x x M >=>-+=,若N M ⊆,则实数a 的取值范围是( )A .),3[+∞B .),3(+∞C .]1,(--∞D .)1,(--∞3. 若n S 为等差数列{a n }的前n 项和,369-=S ,10413-=S ,则5a 与7a 的等比中项为( ) A.24 B.24- C.32 D.24± 4.设n m ,是两条不同直线,βα,是两个不同的平面,下列命题正确的是( ) A .βα//,//n m 且,//βα则n m // B . βα⊥⊥n m ,且 βα⊥,则 n m ⊥ C .,,,n m n m ⊥⊂⊥βα 则βα⊥ D .,//,//,,ββααn m n m ⊂⊂则βα//5.阅读程序框图,若输出的S 的值等于16,那么在程序框图中的 判断框内应填写的条件是 ( )A .i >5B .i >6C .i >7D .i >86. 若 函 数 R x x x x f ∈+=,cos 3sin )(ωω,又0)(,2)(=-=βαf f , 且|α-β|的最小值为3,4πω则正数的值为( )A .13B .23C .43D .327. 已知n xx )32(+展开式中各项系数和为625,则展开式中含x 项的系数为( )A .216B. 224 C .240 D .2508. 如图是函数b ax x x f ++=2)(的部分图象,则函数)('ln )(x f x x g += 的零点 所在的区间是( ) A.)2141(, B.)121(, C.)21(, D.)32(,ABC ∆c b a ,,C B A ,,0sin cos 2sin cos =+-+BB A A cb a +9.已知双曲线22221(0,0)x y a b a b-=>>的左,右焦点是F 1,F 2,设P 是双曲线右支上一点,121F F F P 在上的投影的大小恰好为1||F P ,且它们的夹角为6π,则双曲线的离心率e为( )A .212+ B .312+ C .31+ D .21+10.已知平面向量0,(,)a b a a b ≠≠满足2a =,且b 与b a -的夹角为30,则b 的最大值为( )A .2B .3C .4D .511. 在中,分别是角所对边的边长,若,则的值是( )A .1B .2C .3D .212. 已知定义在R 上的函数()f x 满足:222,[0,1)()2,[1,0)x x f x x x ⎧+∈=⎨-∈-⎩,且(2)()f x f x +=,25()2x g x x +=+,则方程()()f x g x =在区间[5,1]-上的所有实根之和为( )A .-5B .-6C .-7D .-8二、填空题(每小题5分,共20分). 13.设变量x ,y 满足约束条件⎩⎪⎨⎪⎧2x +y -2≥0,x -2y +4≥0,x -1≤0,则目标函数z =2y -3x 的最大值为14.在航天员进行的一项太空实验中,要先后实施6个程序,其中程序A 只能出现在第一或最后一步,程序B 和C 在实施时必须相邻,则实验顺序的编排方法共有 种.(用数字作答)15. 如图,某几何体的正视图和俯视图都是矩形,侧视图是等腰直角三角形,则该几何体的外接球的体积为 . 16. 设抛物线x y C 16:2=的焦点为F ,过点)0,4(-Q 的 直线l 与抛物线C 相交于,A B 两点,若||2||QB QA =,则 直线l 的斜率=k . 三 解答题17.(本小题满分10分)在△ABC 中,,,a b c 分别为内角A, B, C 的对边,2sin (2)sin (2)sin a A b c B c b C =+++. (1)求A 的大小;(2)求sin sin B C +的最大值.18.(本小题满分12分)已知数列{}n a 的首项123a =,121nn n a a a +=+,1,2,3,n =…. (Ⅰ)证明:数列1{1}na -是等比数列;(Ⅱ)求数列{}nna 的前n 项和n S .19.(本小题满分12分)现有4个人去参加春节联欢活动,该活动有甲、乙两个项目可供参加者选择. 为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个项目联欢,掷出点数为1或2的人去参加甲项目联欢,掷出点数大于2的人去参加乙项目联欢.(Ⅰ)求这4人中恰好有2人去参加甲项目联欢的概率;(Ⅱ)求这4个人中去参加甲项目联欢的人数大于去参加乙项目联欢的人数的概率; (Ⅲ)用X ,Y 分别表示这4个人中去参加甲、乙项目联欢的人数,记||X Y ξ=-,求随 机变量ξ的分布列与数学期望E ξ.20.(本小题满分12分)如图:四棱锥P-ABCD 中,底面ABCD 是平行四边形,∠ACB =90°,平面PAD ⊥平面ABCD ,PA =BC =1,PD =,E 、F 分别为线段PD 和BC 的中点.(I) 求证:CE ∥平面PAF ;(II) 在线段BC 上是否存在一点G ,使得平面PAG 和平面PGC 所成二面角的大小为60°?若存在,试确定G 的位置;若不存在,请说明理由.21.(本小题满分12分)已知椭圆2222:1(0)x y C a b a b +=>>与双曲线1322=-y x 的离心率互为倒数,且直线02=--y x 经过椭圆的右顶点.(Ⅰ)求椭圆C 的标准方程;(Ⅱ)设不过原点O 的直线l 与椭圆C 交于、N M 两点 ,且直线OM 、MN 、ON的斜率依次成等比数列,求△OMN 面积的取值范围.22.(本小题满分l2分)已知函数)1(ln )(--=x a x x f ,a ∈R .(I)讨论函数)(x f 的单调性; (Ⅱ)当1≥x 时,)(x f ≤1ln +x x恒成立,求a 的取值范围.答案一 选择题1-5 ACDBA 6-10 BABCC 11-12 BC 二 填空题13. 4 14. 96 15.86π 16. 223±17.解:(1)由正弦定理得,22(2)(2)a b c b c b c =+++,即222a b c bc =++,由余弦定理得,2222cos a b c bc A =+-⋅.∴2221cos 222b c a bc A bc bc +--===-, ∵(0,)A ∈π,∴3A 2π=. (2)由(1)得3C B π=-,这时 sin sin sin sin()3B C B B π+=+-=31cos sin 22B B +sin()3B π=+,∵(0,)B π∈3,∴当32B ππ+=,即6B π=时,sin sin B C +的最大值为1.18 解:(Ⅰ)121n n n a a a +=+,∴ 111111222n n n n a a a a ++==+⋅, ∴ 11111(1)2n na a +-=-,又123a =,∴11112a -=,∴数列1{1}n a -是以为12首项,12为公比的等比数列. …………4分(Ⅱ)由(Ⅰ)知1111111222n n n a -+-=⋅=,即1112n n a =+, ……………6分∴2n n n nn a =+. 设23123222n T =+++…2n n +, ① ……8分则23112222n T =++ (1122)n n n n +-++,② ……………………9分 由①-②得2111222n T =++ (111)11(1)1122112222212n n n n n n n n n +++-+-=-=---,............10分 ∴11222n n n n T -=--.又123+++ (1)2n n n ++=. …………11分19解:依题意,这4个人中,每个人去参加甲项目联欢的概率为13,去参加乙项目联欢的概率为23.设“这4个人中恰有i 人去参加甲项目联欢”为事件i A ,(0,1,2,3,4)i =,则4412()()()33i i ii P A C -=.(Ⅰ)这4个人中恰好有2人去参加甲项目联欢的概率22224128()()()3327P A C ==--------4分(Ⅱ)设“这4人中去参加甲项目联欢的人数大于去参加乙项目联欢的人数”为事件B ,34B A A =⋃, 故334434441211()()()()()()3339P B P A P A C C =+=+=. ∴这4人中去参加甲项目联欢的人数大于去参加乙项目联欢的人数的概率为19.-------8分(III)ξ的所有可能取值为0,2,4. 28(0)()27P P A ξ===,1340(2)()(),81P P A P A ξ==+=0417(4)()(),81P P A P A ξ==+= 所以ξ的分布列是14881E ξ=.-----------------------------------------------------12 20.(1)取PA 中点为H ,连结CE 、HE 、FH ,因为H 、E 分别为PA 、PD 的中点,所以HE ∥AD,AD HE 21=, 因为ABCD 是平行四边形,且F 为线段BC 的中点 所以FC ∥AD,AD FC 21= 所以HE ∥FC,FC HE = 四边形FCEH 是平行四边形 所以EC ∥HF 又因为PAF HF PAF CE 平面平面⊂⊄, 所以CE ∥平面PAF ……………4分(2)因为四边形ABCD 为平行四边形且∠ACB =90°, 所以CA ⊥AD 又由平面PAD ⊥平面ABCD 可得 CA ⊥平面PAD 所以CA ⊥PA由PA =AD =1,PD PA ⊥AD …………5分 所以可建立如图所示的平面直角坐标系A-xyz因为PA=BC=1,AB=2所以AC=1所以(1,1,0),(1,0,0),(0,0,1)B C P -假设BC 上存在一点G ,使得平面PAG 和平面PGC 所成二面角的大小为60°, 设点G 的坐标为(1,a ,0),01≤≤-a 所以)1,0,0(),0,,1(==AP a AG 设平面PAG 的法向量为),,(z y x m = 则⎩⎨⎧==+00z ay x 令0,1,=-==z y a x所以)0,1,(-=a m又(0,,0),(1,0,1)CG a CP ==- 设平面PCG 的法向量为),,(z y x n = 则0ay x z =⎧⎨-+=⎩令1,0,1===z y x 所以)1,0,1(=n ……………9分因为平面PAG 和平面PGC 所成二面角的大小为60°,所以2121,cos 2=•+=〉〈a a n m 所以1±=a 又01≤≤-a 所以1-=a ……………11分 所以线段BC 上存在一点G ,使得平面PAG 和平面PGC 所成二面角的大小为60°点G即为B 点……12分21、(Ⅰ)∵双曲线的离心率为332,所以椭圆的离心率23==a c e , 又∵直线02=--y x 经过椭圆的右顶点,∴右顶点为()0,2,即 2=a ……2分∴1,3==b c ∴椭圆方程为1422=+y x……4分 . E. H22.(Ⅰ))(x f 的定义域为),,0(+∞xaxx f -=1)(', 若,0≤a 则'()0,f x >)(x f ∴在),0(+∞上单调递增,……………2分若0,a >则由0)('=x f 得ax 1=,当)1,0(a x ∈时,,0)('>x f 当),1(+∞∈a x 时,0)('<x f ,)(x f ∴在)1,0(a上单调递增,在),1(+∞a 单调递减.所以当0a ≤时,()f x 在),0(+∞上单调递增,当0a >时, ()f x 在)1,0(a上单调递增,在),1(+∞a单调递减.……………4分(Ⅱ)1)1(ln 1ln )(2+--=+-x x a x x x x x f , 令)1)(1(ln )(2≥--=x x a x x x g ,ax x x g 21ln )(-+=',令()()ln 12F x g x x ax '==+-,12()axF x x-'=,………………6分 (1)a 0,≤若()0F x '>,[)g (x)1,g (x)g (1)1-2a 0'''+∞≥=>在递增,[)0)1()(,,1)(=≥+∞∴g x g x g 递增在,不符合题意从而,01x lnx-f (x)≥+.……………8分 (2)1110a ,),()0,(()(1,,)2122x F x g x a a ''<<>∴∈若当在递增, g (x)g (1)1-2a,''>=从而以下论证(1)同一样,所以不符合题意.……………10分[)1(3),()01,2a F x '≥≤+∞若在恒成立, [)02a -1(1)g (x)g 1,(x)g ≤='≤'+∞'∴递减,在,[)01ln )(,0)1()(,,1g(x)≤+-=≤∴+∞x xx f g x g 递减在从而, 综上所述,a 的取值范围是⎪⎭⎫⎢⎣⎡+∞,21………………12分。
河北省石家庄2014届高三上学期期末质检数学理试卷扫描版含答案

2014年石家庄市高中毕业班教学质量检测(一)高三数学(理科答案)一、选择题:本大题共12小题,每小题5分.1-5 DDCBB 6-10 DCAAD 11-12 CC 二、填空题:本大题共4小题,每小题5分,共20分..13 200 143315 1+ 16 223n n -+三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.所以()f x 的最大值是2……………5分(Ⅱ)令442x k πππ+=+∈k (Z ),……………7分则416k x ππ=+()k z ∈,……………9分 而直线x m =是函()y f x =的对称轴,所以416k m ππ=+∈k (Z )………………10分 18. 解:(Ⅰ)设等差数列{}n a 的公差为0≠d . 因为346S a =+,所以63223311++=⨯+d a da . ① 因为1413,,a a a 成等比数列,所以2111(12)(3)a a d a d +=+. ② ……2分 由①,②可得:13,2a d ==. ……………………………………4分 所以21n a n =+. ……………………………………6分 (Ⅱ)由题意1212+=+n nb ,设数列}{n b 的前n 项和为n T ,122+=n nc ,)(422*121)1(21N n c c n n n n ∈==++++,所以数列}{n c 为以8为首项,以4为公比的等比数列 (9)分所以238(14)28.143n n n T n n +--=+=+- ……………………………………12分19. 解:(Ⅰ)各组的频率分别是0.1,0.2,0.3,0.2,0.1,0.1……………2分 所以图中各组的纵坐标分别是0.01,0.02,0.03,0.02,0.01,0.01……………4分……………5分(Ⅱ)ξ的所有可能取值为:0,1,2,3 ……………6分()22642251061545150=,104522575C C p C C ξ==⋅=⋅=()21112646442222510510415624102341=,1045104522575C C C C C p C C C C ξ⋅==⋅+⋅=⋅+⋅= ()111224644422225105104246666222=,1045104522575C C C C C p C C C C ξ⋅==⋅+⋅=⋅+⋅= ()124422510461243=,104522575C C p C C ξ==⋅=⋅=……………10分所以ξ的分布列是:ξ1 2 3p15753475 2275475……………11分 所以ξ的数学期望65E ξ=…………………12分 20.解法一:(Ⅰ)设BD OC F ⋂=,连接EF ,E F 、分别是PC 、OC 的中点,则//EFPO ,……………1分已知CD ⊥平面PAD ,CD ⊂平面ABCD ,所以平面ABCD ⊥平面PAD ,PABOEDCFH 又PA PD =,O 为AD 的中点,则PO AD ⊥,而平面ABCD PAFD AD ⋂=平面,所以PO ⊥平面ABCD , 所以EF⊥平面ABCD ,又AB ⊂平面ABCD ,所以AB EF ⊥; ……………3分在ABD ∆中,222ABBD AD +=,AB BD ⊥;又EF BD F ⋂=,所以AB ⊥平面BED ,又DE ⊂平面BED ,所以⊥AB DE . ……………6分 (Ⅱ)在平面ABCD 内过点A 作AHCO ⊥交CO 的延长线于H ,连接HE ,AE ,因为PO ⊥平面ABCD ,所以POC ⊥平面ABCD , 平面POC ⋂平面ABCD AH =,所以AH ⊥平面POC ,PC ⊂平面POC ,所以AH ⊥PC ;在APC ∆中,AP AC =,E 是PC 中点,故AE PC ⊥;所以PC⊥平面AHE ,则PC ⊥HE .所以AEH ∠是二面角O PC A --的平面角……………10分 设222PO AD BC CD ====,而222AE AC EC =-,AE =所以二面角O PC A --.……………12分 解法二:因为CD ⊥平面PAD ,CD ⊂平面ABCD ,所以平面ABCD ⊥平面PAD ,又PA PD =,O 是AD 的中点,则PO AD ⊥,且平面ABCD PAFD AD ⋂=平面, 所以PO ⊥平面ABCD ……………2分如图,以O 为原点,以,,OB OD OP 分别为x 轴、y 轴、z 轴的正方向建立空间直角坐标系.(0,1,0)A -(1,0,0)B (1,1,0)C (0,1,0)D 11(,,1)22E (0,0,2)P ……………4分(1,1,0)AB =11(,,1)22DE =-,0AB DE ⋅=,所以AC DE ⊥……………6分A(Ⅱ)(1,2,0)AC =,(1,1,2)PC =-, 设平面PAC 的法向量为(,,)x y z =m ,00AC PC ⋅=⇒⋅=令2x =,得又0BD PO ⋅=,0BD OC ⋅=,所以平面POC 的法向量(1,1,0)BD =-,……………10分,|||BDBD BD ⋅==m -, 所以二面角O PC A --.……………12分 21.解:(Ⅰ)由已知,可设椭圆C 的方程为)0(12222>>=+b a by a x ,因为a PF PF 232)332()11()332()11(||||222221==+-+++=+,所以23a =,22b =,所以,椭圆C 的方程为22132x y +=…………………4分(也可用待定系数法1)1(912122=-+a a ,或用332122=-=a a a b ) (2)当直线l 斜率存在时,设直线l :(1)y k x =+,由22132(1)x y y k x ⎧+=⎪⎨⎪=+⎩得2222(23)6360k x k x k +++-=,设1122(,),(,)A xy B x y ,21223623k x x k -=+,2122623k x x k -+=+……………6分 所以12||x x -==,设内切圆半径为r ,因为2ABF ∆的周长为4a =,2142ABF S a r =⨯⨯=,所以当2ABF ∆的面积最大时,内切圆面积最大,又21212121||||||2ABF S F F y y y y =-=-#12||||k x x =-=……………8分 令2232t k =+≥,则223t k -=,所以2ABF S===<……………10分 又当k 不存在时,12||y y -=23r ==,4=9S π圆故当k 不存在时圆面积最大, 4=9S π圆,此时直线方程为1x =-. …………………12分 (也可以设直线1-=my x l :,避免对k 的讨论,参照以上解法,按相应步骤给分) 22.解:(I )()f x 的定义域为(0,)+∞.其导数1'()f x a x=-.………1分 ①当0a ≤时,'()0f x >,函数在(0,)+∞上是增函数;…………2分②当0a >时,在区间1(0,)a 上,'()0f x >;在区间1(,)a+∞上,'()0f x <. 所以()f x 在1(0,)a 是增函数,在1(,)a+∞是减函数.……………4分(II )①由(I )知,当0a ≤时,函数()f x 在(0,)+∞上是增函数,不可能有两个零点 当0a >时,()f x 在1(0,)a 是增函数,在1(,)a +∞是减函数,此时1()f a为函数()f x 的最大值,当0)1(≤a f 时,)(x f 最多有一个零点,所以11()ln 0f a a=>,解得01a <<,…6分此时,2211a e a e <<,且011)1(<-=+--=e ae a ef ,)10(ln 231ln 22)(2222<<--=+--=a a e a a e a ae f令a e a a F 2ln 23)(--=,则022)(2222>-=+-='a ae a e a x F ,所以)(a F 在0(,)1上单调递增,所以03)1()(2<-=<e F a F ,即0)(22<ae f所以a 的取值范围是0(,)1…………………8分 ②证法一:12121ln 1ln x x a x x ++==.设1ln ()(0)x g x x x +=> . 2ln '()xg x x =-. 当01x << 时,'()0g x > ;当1x > 时,'()0g x < ;所以()g x 在(0,1) 上是增函数,在(1,)+∞ 上是减函数.()g x 最大值为(1)1g = .由于12()()g x g x = ,且01a << ,所以12121ln 1ln 01x x x x ++<=< ,所以111x e<<. 下面证明:当01x <<时,221ln 1x x x -<+ .设221(x)ln (0)1x h x x x -=->+ ,则2222(1)'()0(1)x h x x x -=>+ .()h x 在(0,1] 上是增函数,所以当01x <<时, ()(1)0h x h <= .即当01x <<时,221ln 1x x x -<+.. 由101x <<得1()0h x < .所以211211ln 1x x x -<+.所以112111ln 21x x x x +<+ ,即12121x a x <+,112()1x x a ->,112ln ln()0x x a+->. 又111ln ax x =+ ,所以1121ln()0ax x a-+->,112ln()1ax x a+->. 所以111112222()ln()()1ln()10f x x a x x ax a a a a-=---+=-+-> . 即122()()f x f x a->. 由1210x x a <<<,得121x a a ->.所以122x x a -<,1222x x a+>> . …………………12分 ②证法二:由(II )①可知函数()f x 在1(0,)a 是增函数,在1(,)a+∞是减函数..1ln )(+-=ax x x f 所以01)1(,011)1(>-=<-=+--=a f e a e a ef .故111x e<< 第二部分:分析:因为a x 101<<,所以a x a 121>-.只要证明:0)2(1>-x a f 就可以得出结论 下面给出证明:构造函数:)10).((ln )2()2ln()()2()(ax ax x x a a x a x f x a f x g ≤<-----=--= 则:0)2()1(22121)(2<--=+--='ax x a x a a x a x x g 所以函数)(x g 在区间]1,0(a 上为减函数.a x 101<<,则0)1()(1=>ag x g ,又0)(1=x f 于是0)()(1)2()2ln()2(11111>=-+---=-x g x f x aa x a x a f . 又0)(2=x f 由(1)可知 122x a x ->.即2221>>+ax x …………………12分。
河北省石家庄市2014届高三数学第一次模拟考试A卷 文(石家庄一模)新人教A版

河北省石家庄市2014届高三数学第一次模拟考试A 卷 文(石家庄一模)新人教A 版一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知i 为虚数单位,a R ∈ ,若(1)(1)a a i -++ 是纯虚数,则a 的值为 A. -1或1 B. 1 C. -1 D. 32. 设不等式20x x -≤的解集为M, 函数()lg(1)f x x =-的定义域为N ,则M ∩N=A. (-1, 0]B. [0, 1)C.(0,1)D. [0.1]3.函数()tan(2)3f x x π=-的单调递增区间是 A. 5[,]()212212k k k Z ππππ-+∈ B.5(,)()212212k k k Z ππππ-+∈C.2(,)()63k k k Z ππππ++∈ D.5[,]()1212k k k Z ππππ-+∈4. 已知12123113,log ,log 23a b c === ,则A. a b c >>B. b c a >>C. c b a >>D. b a c >>5. 登山族为了了解某山高y (km)与气温x (°C )之间的关系,随机统计了4次山高与相应的气温,并制作了对照表:A. -10B. -8C. -6D. -4 6.已知等差数列{}n a ,且35710133()2()48a a a a a ++++= ,则数列{}n a 的前13项之和为A. 24B. 39C. 52D.1047. 执行右面的程序框图,若输出的结果为3,则可输入的实数x 值的个数为A. 1B. 2C. 3D. 4 8.三棱锥S-ABC 及其三视图中的正视图和侧视图如图所示,则棱SB 的长为气温(0C ) 18 13 10 -1山高 (km) 24 34 38 64SACB正视图A. 211B. 4 2C. 38D. 16 39. 在∆ABC 中,角A 、B 、C 所为,,a b c 且满足对的边长分别sin cos c A C =,则sinA+sinB 的最大值是A. 1B. 2C. 3D. 310. 双曲线22221(0,0)x y a b a b -=>>的左、右焦点分别为F1,F2,渐近线分别为12,l l ,点P 在第一象限内且在1l 上,若2l ⊥PF1,2l∥PF2,则该双曲线的离心率为 A. 5 B. 2 C. 3 D. 2 11. 已知()f x 是定义在R 上的以3为周期的偶函数,若(1)1,f < 23(5)1a f a -=+ ,则实数a 的取值范围为A. 14a -<<B. 21a -<<C. 10a -<<D.12a -<<12.设直线l 与曲线3()21f x x x =++有三个不同的交点A 、B 、C, 且|AB|=|BC|=10 ,则直线l 的方程为A. 51y x =+B. 41y x =+C 1y =+ D.31y x =+二、填空题:本大题共4小题,每小题5分,共20分.13. 抛物线24y x =-的焦点坐标为14. 若,x y 满足约束条件⎩⎪⎨⎪⎧x ≥0x +2y ≥32x +y ≤3, 则z x y =-的最大值是15. 在三棱锥P-ABC 中,侧棱PA,PB,PC 两两垂直,PA=1,PB=2,PC=3,则三棱锥的外接球的表面积为______16. 已知O 为锐角∆ABC 的外心,AB=6,AC=10,AO x AB y AC =+,且2105x y +=,则边BC 的长为 _______三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17. (本小题满分12分) 已知{}n a 是各项均为正数的等比数列,且12342,32.a a a a ⋅=⋅=(I)求数列{}n a 的通项公式; (II)设数列{}n b 的前n 项为2nS n ()nN ,求数列{}n n a b 的前n 项和.18. (本小题满分12分)如图,在三棱柱ABC-A1B1C1中,AB ⊥AC ,顶点1A 在底面ABC 上的射影恰为点B ,且AB=AC=A1B=2. (Ⅰ)证明:平面1A AC ⊥平面1AB B;(Ⅱ)若点P 为11B C 的中点,求三棱锥P ABC -与四棱锥111P AA B A -的体积之比.19.(本小题满分12分)某城市要建成宜商、宜居的国际化新城,该城市的东城区、西城区分别引进8个厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.(Ⅰ)根据茎叶图判断哪个区域厂家的平均分较高;(Ⅱ)规定85分以上(含85分)为优秀厂家,若从该两个区域各选一个优秀厂家,求得分差距不超过5的概率.图①CEO 1O 2A O 2图②20. (本小题满分12分)椭圆C:22221(0)x y a b a b +=>> 的离心率为32,过其右焦点F 与长轴垂直的弦长为1.(I)求椭圆C 的方程;(II)设椭圆C 的左,右顶点分别为A ,B ,点P 是直线1x =上的动点,直线PA 与椭圆的另一交点为M ,直线PB 与椭圆的另一交点为N,求证:直线MN 经过一定点.21. (本小题满分12分)已知函数()ln (1)(1)()f x x x x ax a a R =---+∈ . (I)若a =0,判断函数()f x 的单调性;(II)若1x >时,()f x <0恒成立,求a 的取值范围.请考生在第22〜24三题中任选一题做答,如果多做,则按所做的第一题记分. 22. (本小题满分10分)选修4-1:几何证明选讲已知⊙O1和⊙O2相交于A ,B 两点,过A 点作⊙O1的切线交⊙O2于点E ,连接EB 并延长交⊙O1于点C ,直线CA 交⊙O2于点D.(Ⅰ) 当点D 与点A 不重合时(如图①),证明ED2=EB ·EC ;(II) 当点D 与点A 重合时(如图②),若BC=2,BE=6,求⊙O2的直径长.23. (本小题_分10分)选修4-4:坐标系与参数方程在直角坐标系中,曲线C1的参数方程为:2cos ,,x y αα=⎧⎪⎨=⎪⎩(α为参数),以原点为极点,x轴的正半轴为极轴,并取与直角坐标系相同的长度单位,建立极坐标系,曲线C2的极坐标方程为:cos ρθ=.(I)求曲线C2的直角坐标方程;(II)若P ,Q 分别是曲线C1和C2上的任意一点,求|PQ|的最小值.24. (本小题满分10分)选修4-5:不等式选讲 已知函数()2(0)f x ax ax a a =-+-> .(I)当a =1时,求()f x x ≥的解集;(II )若不存在实数x ,使()f x <3成立,求a 的取值范围.2014年石家庄市高中毕业班第一次模拟考试 数学(文科)答案 一、选择题:A 卷答案:1-5 CBBAC 6-10 CCBDB 11-12AD B 卷答案:1-5 DBBAD 6-10 DDBCB 11-12AC 二、填空题:13.1(0,)16-14. 015.14π16.三、解答题:(解答题按步骤给分,本答案只给出一或两种答案,学生除标准答案的其他解法,参照标准酌情设定,且只给整数分)17解:(Ⅰ)设等比数列na 的公比为q ,由已知得21251232a qa q ,,……………2分又∵10a ,0q,解得112a q,,………………3分∴12nna ;…………………5分(Ⅱ)由2nS n 得,211nS n ,∴当2n时,121nn nb S S n ,………………7分当1n 时,11b 符合上式,∴21nb n ,(n*N )……………8分,∴1212nn na b n ,12113252212nn T n ,2312123252232212n n nT n n ,………………10分两式相减得 21122222122323nnnnT n n ,∴2323nnT n .……………………12分18.证明:(Ⅰ)由题意得:1A B ⊥面ABC ,∴1A B AC⊥, ------2分又AB AC ⊥,1ABA B B=∴AC ⊥面1AB B, ------3分 ∵AC ⊂面1A AC , ∴平面1A AC ⊥平面1AB B; ------5分(Ⅱ)在三棱锥ABC P -中,因为AB AC ⊥, 所以底面ABC 是等腰直角三角形,又因为点P 到底面的距离B A h 1==2,所以34213131=⋅⋅⋅=⋅=∆-h AB AC h S V ABC ABC P . ------6分由(Ⅰ)可知AC ⊥面1AB B,因为点P 在11B C 的中点,所以点P 到平面B B AA 11距离2h 等于点1C 到平面B B AA 11的距离的一半,即12=h .------8分341223131312121111=⋅⋅⋅=⋅⋅=⋅=-h B A AB h S V B B AA B B AA P 四边形, ------10分所以三棱锥ABC P - 与四棱锥111A B AA P -的体积之比为1:1. ------12分19. 解:(Ⅰ)东城区的平均分较高.(结论正确即给分)……………………5分 (Ⅱ)从两个区域各选一个优秀厂家,则所有的基本事件共15种,………………7分 满足得分差距不超过5的事件(88,85)(88,85)(89,85)(89,94)(89,94)(93,94)(93,94)(94,,94)(94,,94)共9种.……………10分所以满足条件的概率为35.………………12分20.解:(Ⅰ)依题意23==a c e ,过焦点F与长轴垂直的直线x=c与椭圆12222=+b y a x联立解答弦长为a b 22=1,……………2分 所以椭圆的方程1422=+y x .………………4分(Ⅱ)设P(1,t)3210t t k PA =+-=,直线)2(3:+=x ty l PA ,联立得:22(2),3 1.4t y x x y ⎧=+⎪⎪⎨⎪+=⎪⎩即()0361616942222=-+++t x t x t ,可知2216362,49M t x t --=+所以2218849M t x t -=+, 则222188,4912.49M M t x t t y t ⎧-=⎪⎪+⎨⎪=⎪+⎩……………………6分同理得到22282,414.41N N t x t t y t ⎧-=⎪⎪+⎨⎪=⎪+⎩………………8分 由椭圆的对称性可知这样的定点在x 轴, 不妨设这个定点为Q()0,m ,………………10-分又m t t t t k MQ-+-+=948189412222 , m t t t t k NQ -+-+=1428144222 ,NQMQ k k =,()28326240m t m --+=,4m =.……………12分21.解:(Ⅰ)若0a =,()ln 1f x x x x =-+,'()ln f x x ='(0,1),()0,()x f x f x ∈<为减函数,'(1,),()0,()x f x f x ∈+∞>为增函数 (4)分(Ⅱ)ln (1)(1)0,x x x ax a ---+<在()1,+∞恒成立.01若0a =, ()ln 1f x x x x =-+,'()ln f x x =,'(1,),()0,()x f x f x ∈+∞>∴为增函数.()(1)0f x f ∴>=,即()0f x <不成立;0a ∴=不成立.……………………6分021x >,(1)(1)ln 0,x ax a x x --+-<在()1,+∞恒成立, 不妨设(1)(1)()ln ,x ax a h x x x --+=-,()1,x ∈+∞ ()2'221(1)1()x ax a ax x a h x x x -+---+=-=-,()1,x ∈+∞………………8分'121()0,1,a h x x x a -===,若0a <,则211ax a -=<,1x >,'()0h x >,()h x 为增函数,()h x >(1)0h =(不合题意);若102a <<,1(1,)ax a -∈,'()0h x >,()h x 为增函数,()h x >(1)0h =(不合题意);若12a ≥,(1,)x ∈+∞,'()0h x <,()h x 为减函数,()h x <(1)0h =(符合题意).……………11分综上所述若1x >时,()0f x <恒成立,则12a ≥.………………12分22.解:(Ⅰ)连接AB ,在EA 的延长线上取点F ,如图①所示. ∵AE 是⊙O1的切线,切点为A , ∴∠FAC =∠ABC,.……………1分 ∵∠FAC =∠DAE ,∴∠ABC =∠DAE,∵∠ABC 是⊙O2内接四边形ABED 的外角, ∴∠ABC =∠ADE,……………2分 ∴∠DAE =∠ADE.………………3分∴EA =ED,∵EC EB EA •=2, ∴EC EB ED •=2.………………5分 (Ⅱ)当点D 与点A 重合时,直线CA 与⊙O2只有一个公共点, 所以直线CA 与⊙O2相切.……………6分 如图②所示,由弦切角定理知:︒⨯=∠=∠∠=∠∠=∠∠=∠18021ABE ABC MAEPAC ABE MAE ABC PAC 因又∴AC 与AE 分别为⊙O1和⊙O2的直径.…………8分∴由切割线定理知:EA2=BE·CE,而CB =2,BE =6,CE=8∴EA2=6×8=48,AE =34.故⊙O2的直径为34.………………10分图(2)O 2O 1ABMP CE23.解: (Ⅰ)θρcos = ,…………………2分.…………………4分(ααsin 2,cos 2),)0,21(2C (Ⅱ)设P2PC ===…………………6分1cos ,2α∴=,2min PC =,…………………8分min 12PQ =.……………………10分24.解:(Ⅰ)当a=1时,()21f x x x x=-+-≥2x ≥当时,解得3x ≥;当21<<x 时,解得1≤x ,∴无解1x ≤当时,解得1x ≤;……………………………3分综上可得到解集}31{≥≤x x x 或.……………………5分(Ⅱ)依题意, ,()3x f x ∀∈≥R 对都有,则()()3222)(≥-=---≥-+-=a a ax ax a ax ax x f ,……………8分232351(a a a a -≥-≤-∴≥≤-或或舍)5a ∴≥…………………10分ϑρρcos 2=41212222=+⎪⎭⎫ ⎝⎛-=+y x x y x。
2014石家庄一模数学试卷(理)
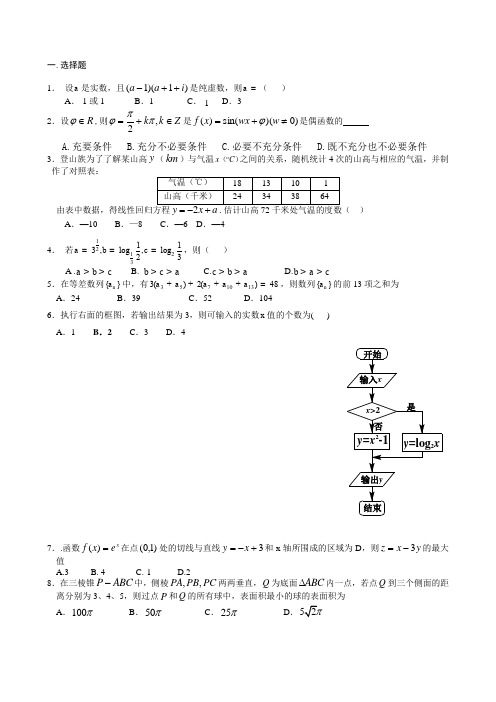
一.选择题1. 设a 是实数,且)1)(1(i a a ++-是纯虚数,则a =( )A .-1或1B .1C .-1D .3 2.设R ∈ϕ,则Z k k ∈+=,2ππϕ是)0)(sin()(≠+=w wx x f ϕ是偶函数的A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件 3.登山族为了了解某山高y (km )与气温)(C x 之间的关系,随机统计4次的山高与相应的气温,并制作了对照表:由表中数据,得线性回归方程.估计山高72千米处气温的度数( )A .—10B .—8C .—6D .—4 4. 若12123113,log ,log 23a bc ===,则( ) A .a b c >> B. b c a >> C.c b a >> D.b a c >>5.在等差数列{}n a 中,有35710133()2()48a a a a a ++++=,则数列{}n a 的前13项之和为 A .24B .39C .52D .1046.执行右面的框图,若输出结果为3,则可输入的实数x 值的个数为( ) A .1 B .2 C .3D .47..函数xe xf =)(在点)1,0(处的切线与直线3+-=x y 和x 轴所围成的区域为D ,则y x z 3-=的最大值A.3B. 4C.-1D.28.在三棱锥P ABC -中,侧棱,,PA PB PC 两两垂直,Q 为底面ABC ∆内一点,若点Q 到三个侧面的距离分别为3、4、5,则过点P 和Q 的所有球中,表面积最小的球的表面积为 A .100π B .50π C .25π D .9.双曲线22221(0,0)x y a b a b -=>> 的左、右焦点分别为1F ,2F ,渐近线分别为12,l l ,点P 在第一象限内且在1l 上,若12PF l ⊥,22l PF ∥,则双曲线的离心率是( ) AB .2CD10.在ABC ∆中角A,B,C 所对的边分别为a,b,c 且满足C a A c cos sin =则C A sin 2sin +的最大值( )A .1B .22 C .2D11.设直线l 与曲线321y x x =++有三个不同的交点,,A B C ,且AB BC ==l 的方程为A 15+=x yB 14+=x yC 13+=x y D.31y x =+12. 设{}(),()()max (),()(),()()g x f x g x f x g x f x f x g x ≤⎧=⎨>⎩,若函数2()h x x px q =++的图像经过不同两点(,0),(,0)αβ,且存在整数n ,使得1n n αβ<<<+成立,则 ( B) {}.max (),(1)1A h n h n +> {}.m a x (),(1)1B h n h n +<{}1.max (),(1)8C h n h n +≥ .D {}1m a x (),(1)2h nh n +≤二.填空题 13.=+-⎰dx x x )211(12 14. 三棱锥S ABC -及其三视图中的主视图和左视图如图所示,则棱SB 的长为左视图主视图15.已知函数()x a x f 3cosπ=,a 等于抛掷一颗骰子得到的点数,则()x f y =在[]4,0上有5个以下或6个以上零点的概率是16.若实数,,,a b c d 满足()223ln 20b a a c d +-+-+=,则()()22a cb d -+-的最小值为______ . 三.解答题17.已知{}n a 是各项均为正数的等比数列,且122a a ?,3432a a ?.(1)求{}n a 的通项公式;(2)设数列{}n b 满足3121113521n n b b b b a n +++++=--L (n Î*N ),求数列{}n b 的前n 项和n T .18.(理)(本小题满分12分) 如图,在三棱柱111A B C A B C-中,A B A C ⊥,顶点1A 在底面ABC 上的射影恰为点B ,且12A B A C A B ===. (Ⅰ)证明:平面1A AC ⊥平面1AB B ;(Ⅱ)若点P 为11B C 的中点,并求出二面角1P AB A --的平面角的余弦值.CBA 1C 1B 1A19.(理)现有甲、乙、丙、丁四人独立参加天津卫视《非你莫属》应聘节目,根据各人综合表现,甲、乙成功应聘的概率均为12,丙、丁成功应聘的概率均为(01)t t <<,设ξ表示成功应聘的人数. (1)若甲、乙有且只有一个人成功应聘的概率与丙、丁都成功应聘的概率相等,求t 的值; (2)求ξ的分布列及数学期望(用t 表示);(3)若恰好有两个人成功应聘的概率最大,试求t 的取值范围.20.椭圆2222:1(0)x y C a b a b +=>>的离心率为3,过右焦点F 与长轴垂直的弦长为83.(I )求椭圆的方程;(II )设椭圆的左、右顶点分别为A 、B ,点P 是直线2x =上的动点,直线PA 与椭圆的另一交点为M ,直线PB 与椭圆的另一交点为N .求证:直线MN 经过一定点.21.(理)已知函数()2()2ln(1)f x x x ax x =++--,()ln(1)g x x =+ ()a R ∈, (1) 若0a =,()()()m x f x g x =-求()m x 的极值点;(2) 已知12x x <,对于任意20x >, 有()()12g x f x =成立,求a 的取值范围.选修系列4-1.已知⊙O 1和⊙O 2相交于A 、B 两点,过A 点作⊙O 1的切线交⊙O 2于点E ,连接EB 并延长交⊙O 1于点C ,直线CA 交⊙O 2于点D .(1)如图(1)所示,当点D 与点A 不重合时,证明EC EB ED ∙=2(2) 如图(2) 当点D 与点A 重合时,直线AC 与⊙O 2有怎样的位置关系?此时若BC =2,BE =6,求⊙O 2的直径.线1C 的参数方4-4.在直角坐标系中,曲程:)(s i2c o 2为参量ααα⎩⎨⎧==y x 以原点为极点,x 轴正半轴为极轴,并取与直角坐标系相同的单位长度,建立极坐标系 曲线2C :θρcos =(1)求曲线2C 的普通方程(2)若P,Q 分别是曲线1C 和2C 上的任意一点,求PQ 最小距离 4-5.已知)0(2)( a a ax ax x f -+-=, (1)当的解集时x x f a≥=)(1(2)若不存在实数3)( x f x 使,求a 的取值范围.图(2)图(1)。
数学_2014年河北省石家庄市某校高考数学三模试卷(二)(理科)(含答案)

2014年河北省石家庄市某校高考数学三模试卷(二)(理科)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的1. 设集合M ={−1, 0, 1},N ={a, a 2}则使M ∩N =N 成立的a 的值是( ) A 1 B 0 C −1 D 1或−12. 复数51+2i 的共轭复数为( )A −53−103i B −53+103i C 1−2i D 1+2i3. 直线m 、n 和平面a 、β.下列四个命题中, ①若m // a ,n // a ,则m // n ;②若m ⊂α,n ⊂α,m // β,n // β,则α // β; ③若α⊥β,m ⊂α,则m ⊥β;④若α⊥β,m ⊥β,m ⊄α,则m // α, 其中正确命题的个数是( ) A 0 B 1 C 2 D 34. 设ω>0,函数y =sin(ωx +π3)+2的图象向右平移4π3个单位后与原图象重合,则ω的最小值是( )A 23 B 43 C 32 D 35. 若实数x ,y 满足约束条件{y ≥0x −y ≥02x −y −2≤0,则z =x +2y 的取值范围是( )A [0, 1]B [1, 6]C [0, 6]D [2, 6]6. 设f(x)={2e x−1,x <2log 3(x 2−1),x ≥2则不等式f(x)<2的解集为( )A (√10, +∞)B (−∞, 1)∪[2, √10)C (1, 2]∪(√10, +∞)D (1, √10)7. 已知四棱锥P −ABCD ,现要在四棱锥的各个面上涂色,有4种不同的颜色可供选择,要求相邻的面不同色,则不同的涂色方法有( )种. A 60 B 120 C 48 D 728. 假设你家订了一份早报,送报人可能在早上6:30−7:30之间把报纸送到你家,你父亲离开家去上班的时间在早上7:00−8:00之间,则你父亲离开家前能得到报纸的概率为( )A 13 B 712 C 78 D 189. 已知点P 为△ABC 内一点,且PA →+2PB →+3PC →=0→,则△APB ,△APC ,△BPC 的面积之比等于( )A 9:4:1B 1:4:9C 3:2:1D 1:2:310. 函数f(x)=Asin(ωx +ϕ)+b 的图象如图所示,则S =f(0)+f(1)+...+f(2014)等于( )A 0B 40252 C 40292D 4031211. 在抛物线y=x2+ax−5(a≠0)上取横坐标为x1=−4,x2=2的两点,经过两点引一条割线,有平行于该割线的一条直线同时与抛物线和圆5x2+5y2=36相切,则抛物线顶点的坐标为()A (−2, −9)B (0, −5)C (2, −9)D (1, 6)12. 已知函数f(x)满足f(x)=2f(1x ),当x∈[1, 3]时,f(x)=lnx,若在区间[13,3]内,函数g(x)=f(x)−ax,有三个不同的零点,则实数a的取值范围是()A [ln33,1e) B [ln33,2e) C (0,12e) D (0,1e)二、填空题:本大题共4小题,每题5分.13. 若将函数f(x)=x5表示为f(x)=a0+a1(1+x)+a2(1+x)2+...a5(1+x)5,其中a0,a1,a2,…,a5为实数,则a0+a3=________.14. 已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的外接球的表面积等于14πcm3.15. 设F1,F2是焦距等于6的双曲线C:x2a2−y2b2=1(a>0, b>0)的两个焦点,P是C上一点,若|PF1|+|PF2|=6a,且△PF1F2的最小内角为30∘,则C的方程为________.16. △ABC中,∠C=90∘,M是BC的中点,若sin∠BAC=√33,则sin∠BAM=________.三、解答题:解答应写出文字说明,证明过程或演算步骤.17. 已知数列{a n}是等差数列,a2=6,a5=12;数列{b n}的前n项和是S n,且S n+12b n= 1.(1)求数列{a n}和{b n}通项公式;(2)记c n=−2a n⋅logb n2,数列{c n}的前n项和为T n,若T n<m−20122对一切n∈N∗都成立,求最小正整数m.18. 每年的三月十二日,是中国的植树节,林管部门在植树前,为保证树苗的质量,都会在植树前对树苗进行检测.现从甲、乙两批树苗中各抽测了10株树苗的高度,规定高于128厘米的为“良种树苗”,测得高度如下(单位:厘米) 甲:137,121,131,120,129,119,132,123,125,133 乙:110,130,147,127,146,114,126,110,144,146(1)根据抽测结果,完成答题卷中的茎叶图,并根据你填写的茎叶图,对甲、乙两批树苗的高度作比较,写出对两种树苗高度的统计结论;(2)设抽测的10株甲种树苗高度平均值为x ¯,将这10株树苗的高度依次输入按程序框图进行运算,(如图)问输出的S 大小为多少?并说明S 的统计学意义;(3)若小王在甲批树苗中随机领取了5株进行种植,用样本的频率分布估计总体分布,求小王领取到的“良种树苗”株数X 的分布列.19. 如图,ABCD 为边长2的菱形,∠BAD =60∘,对角线交于点O ,沿BD 将BCD 折起,使二面角C −BD −A 为120∘,P 为折起后AC 上一点,且AP =2PC ,Q 为△ABD 的中心.(1)求证:PQ // 平面BCD ; (2)求证:PO ⊥平面ABD ;(3)求BP 与平面BCD 所成角的正弦值.20. 已知点A(4, 0),B(1, 0),若动点T 满足AB →⋅AT →=6|BT →|.(1)求动点T 的轨迹Γ;(2)在x 轴正半轴上是否存在一点P ,过该点的直线l (不与x 轴重合)与曲线Γ交于两点M ,N ,使得1|PM|2+1|PN|2为定值,若有求出P 点坐标和定值,若不存在,说明理由.21. 已知函数f(x)=lnx +1−x ax,其中a 为大于零的常数.(1)若函数f(x)在区间[1, +∞)内调递增,求a 的取值范围; (2)求函数f(x)在区间[1, 2]上的最小值;(3)求证:对于任意的n ∈N ∗,且n >1时,都有lnn >12+13+⋯+1n 成立.请考生在第(22)、(23)、(24)三题中任选一题作答.注意:只能做选定的题目.如果多做,则按所做的第一题计分,作答时用2B铅笔在答题卡上把所选题目对应题号下方的方框涂黑.【选修4-1:几何证明选讲】22. 如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,F为BA延长线上一点,且满足BD⋅BE=BA⋅BF.求证:(1)EF⊥FB;(2)∠DFB+∠DBC=90∘.【选修4-4:坐标系与参数方程】23. 在平面直角坐标系中,以原点为极点,x轴为极轴建立极坐标系,曲线C1的方程为:ρcosθ+ρsinθ=1,若曲线C1与C2相{x=√2cosθy=sinθ(θ为参数),曲线C2的极坐标方程为C2交于A、B两点.(1)求|AB|的值;(2)求点M(−1, 2)到A、B两点的距离之积.【选修4-5:不等式选讲】24. 在平面直角坐标系中,定义点P(x1, y1)、Q(x2, y2)之间的直角距离为L(P, Q)=|x1−x2|+|y1−y2|,点A(x, 1),B(1, 2),C(5, 2)(1)若L(A, B)>L(A, C),求x的取值范围;(2)当x∈R时,不等式L(A, B)≤t+L(A, C)恒成立,求t的最小值.2014年河北省石家庄市某校高考数学三模试卷(二)(理科)答案1. C2. D3. B4. C5. C6. B7. D8. C9. C10. D11. A12. A 13. 9 14. 14π 15.x 23−y 26=116. √6917. 解:(1)设{a n }的公差为d , 则a 2=a 1+d ,a 5=a 1+4d , ∵ a 2=6,a 5=12,∴ {a 1+d =6a 1+4d =12,解得a 1=4,d =2,∴ a n =4+2(n −1)=2n +2.∵ 数列{b n }的前n 项和是S n ,且S n +12b n =1,∴ 当n =1时,b 1=S 1, 由S 1+12b 1=1,得b 1=23,当n ≥2时,∵ S n =1−12b n ,S n−1=1−12b n−1,∴ S n −S n−1=12(b n−1−b n ),即b n =12(b n−1−b n ), ∴ b n =13b n−1,∴ {b n }是以23为首项,13为公比的等比数列,∴ b n =23⋅(13)n−1=2⋅(13)n .(2)∵ b n =2•(13)n , ∴ c n =−2c n ⋅log 3bn2=−2(2n+2)log 3(13)n=1n(n+1)=1n −1n+1,∴ T n =(1−12)+(12−13)+(13−14)+...+(1n−1n+1)=1−1n+1<1,由已知得m−20122≥1,∴ m ≥2014,∴ 最小正整数m =2014.…. 18. 解:(1)茎叶图略.---统计结论:①甲种树苗的平均高度小于乙种树苗的平均高度; ②甲种树苗比乙种树苗长得更整齐;③甲种树苗的中位数为127,乙种树苗的中位数为128.5;④甲种树苗的高度基本上是对称的,而且大多数集中在均值附近, 乙种树苗的高度分布较为分散.---(每写出一个统计结论得1分)(2)x ¯=127,S =135.−−−−S 表示10株甲树苗高度的方差,是描述树苗高度离散程度的量.S 值越小,表示长得越整齐,S 值越大,表示长得越参差不齐.---- (3)由题意,领取一株甲种树苗得到“良种树苗”的概率为12,则X ∼B(5,12)−−−所以随机变量X 的分布列为19. (1)证明:如图由ABCD 为菱形,则AC ⊥BD ,∠AOC =120∘,由Q 为三角形ABD 的重心,可得AQ =2QO ,又AP =2PC ,所以PQ // CO , 又PQ ⊄平面BCD ,CO ⊂平面BCD ,所以PQ // 平面BCD ;(2)证明:由题意OC =OA =2cos30∘=√3,在△AOC 中,由余弦定理可得 AC 2=3+3−2×√3×√3×cos120∘=9,所以AC =3, 又∠AOC =120∘,AO =CO ,∴ ∠PAO =30∘,在△PAO 中,OA =√3,AP =2,∠PAO =30∘,所以PO =1, 所以PO 2+OA 2=AP 2,所以PO ⊥OA ,又BD ⊥平面AOC ,所以PO ⊥BD ,又AO ∩BD =0, 所以PO ⊥平面ABD ;(3)解:建立如图所示的坐标系,则B(1, 0, 0),D(−1, 0, 0),C(0, √32, 32),P(0, 0, 1), ∴ BP →=(−1, 0, 1),CB →=(0, −√32, −32),CD→=(−1, −√32, −32), 设平面BCD 的法向量为m →=(x, y, z),则{x −√32y −32z =0−x −√32y −32z =0,取m →=(0, −√3, 1),设BP 与平面BCD 所成角为α,则sinα=|1√2⋅2|=√24. 20. 解:(1)设动点T(x, y), ∵ A(4, 0),B(1, 0),∴ AT →=(x −4, y),AB →=(−3, 0),BT →=(x −1, y), 代入AB →⋅AT →=6|BT →|,整理得:x 24+y 23=1;(2)假设存在定点P(m, 0)(m >0),使得1|PM|2+1|PN|2为定值.设M(x 1, y 1),N(x 2, y 2),直线l:x =ty +m ,则|PM|2=(x 1−m)2+y 12=(t 2+1)y 12,|PN|2=(t 2+1)y 22. ∴ 1|PM|2+1|PN|2=1(t 2+1)(1y 12+1y 22)=1(t 2+1)y 12+y 22y 12y 22=1(t 2+1)(y 1+y 2)2−2y 1y 2y 12y 22 (1)联立x =ty +m 与x 24+y 23=1,整理得:(3t 2+4)y 2+6tmy +3m 2−12=0.∴ y 1+y 2=−6tm3t 2+4,y 1y 2=3m 2−123t 2+4,代入(1)式得:1|PM|2+1|PN|2=1(t 2+1)⋅(−6tm 3t 2+4)2−2⋅3m 2−123t 2+4(3m 2−123t 2+4)2=t 2(18m 2+72)+96−24m 2t 2(3m 2−12)2+(3m 2−12)2.要使得上式为定值,须18m 2+72=96−24m 2,解得m =2√77, 此时1|PM|2+1|PN|2取到定值79. ∴ 当P 为(2√77,0)时,1|PM|2+1|PN|2取到定值79.21. 解:(1)∵ 函数f(x)=lnx +1−x ax,其中a 为大于零的常数,∴ f ′(x)=1x −1ax 2=x−1a x 2.∵ 函数f(x)在区间[1, +∞)内单调递增,∴ 当x ≥1时,f ′(x)≥0恒成立,即1a ≤x(a >0),x ∈[1, +∞)恒成立⇔1a≤[x]min ,(a >0)x ∈[1, +∞)⇔1a ≤1(a >0).解得a ≥1.即为所求的取值范围.(2)(I)由(1)可知:当a ≥1时,f(x)在区间[1, 2]上单调递增, ∴ 当x =1时,函数f(x)取得最小值,且f(1)=0.(II)当0<a ≤12时,1a ≥2,∴ 当x ∈[1, 2]时,f ′(x)≤0,∴ 函数f(x)在区间[1, 2]上单调递减,∴ 当x =2时,函数f(x)取得最小值,且f(2)=ln2−12a.(III)当12<a <1时,1<1a<2.令f ′(x)=0,则x =1a .当1<x <1a 时,f ′(x)<0;当1a <x <2时,f ′(x)>0.∴ 当x =1a 时,函数f(x)取得极小值,因为在区间[1, 2]内只有一个极小值,所以也即最小值,∴ 最小值为f(1a)=1−1a−lna .(3)由(1)可知:令a =1,则函数f(x)=lnx +1−x x在区间[1, +∞)上单调递增.再令x =n+1n,f(1+1n )>f(1),而f(1+1n )=lnn+1n−1n+1,f(1)=0,∴ ln(n +1)−lnn >1n+1.∴ lnn =(ln2−ln1)+(ln3−ln2)+...+[lnn −ln(n −1)]>12+13+...+1n , 即lnn >12+13+ (1)n .22. (1)证明:连接AD ,则∵ AB 是⊙O 的直径,∴ ∠ADB =90∘在△ADB 和△EFB 中,∵ BD ⋅BE =BA ⋅BF ,∴ BDBA =BFBE ….. 又∠DBA =∠EBF ,∴ △ADB ∽△EFB….. 则∠EFB =∠ADB =90∘,∴ EF ⊥FB….. (2)在△ADB 中,∠ADB =∠ADE =90∘又∠EFB =90∘∴ E 、F 、A 、D 四点共圆; … ∴ ∠DFB =∠AEB…..又AB 是⊙O 的直径,则∠ACB =90∘,∴ ∠DFB +∠DBC =∠AEB +∠DBC =90∘…23. 解:(1)利用sin 2θ+cos 2θ=1可得:曲线C 1的普通方程为x 22+y 2=1, 由C 2:ρcosθ+ρsinθ=1,可得:C 2的普通方程为x +y −1=0, 则C 2的参数方程为{x =−1−√22t y =2+√22t.(t 为参数),代入C 1得3t 2+10√2t +14=0, ∴ |AB|=|t 1−t 2|=√(t 1+t 2)2−4t 1t 2=4√23. (2)|MA|⋅|MB|=|t 1t 2|=143.24. 由定义得|x −1|+1>|x −5|+1,即|x −1|>|x −5|,两边平方得8x >24, 解得x >3,当x ∈R 时,不等式|x −1|≤|x −5|+t 恒成立, 也就是t ≥|x −1|−|x −5|恒成立,法一:令函数f(x)=|x −1|−|x −5|={−4x ≤12x −61<x ≤54x >5,所以f(x)max=4,要使原不等式恒成立只要t≥4即可,故t min=4.法二:运用绝对值不等式性质.因为|x−1|−|x−5|≤|(x−1)−(x−5)|=4,所以t≥4,t min=4.故t的最小值为:4.。
河北省石家庄市2014届高三调研数学(理)试题Word版无答案

第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知i 是虚数单位,则复数3(1)z i i =+∙的共轭复数是( )A .1i --B .1i -C .1i -+D .1i +2.设α表示直线,,αβγ表示不同的平面,则下列命题中正确的是( )A .若a α⊥且a b ⊥,则//b αB .若γα⊥且γβ⊥,则//αβC .若//a α且//a β,则//αβD .若//γα且//γβ,则//αβ3.若抛物线22y px =上一点0(2,)P y 到其准线的距离为4,则抛物线的标准方程为( )A .24y x =B .26y x =C .28y x =D .210y x =5.ABCD 沿对角线BD 折起,连结AC ,得到三棱锥C ABD -,其正视图、俯视图均为全等的等腰直角三角形(如图所示),则其侧视图的面积为( )A .2B .12C .1D .26.设变量,x y 满足约束条件:+222y x x y x ≥⎧⎪≤⎨⎪≥-⎩,则3z x y =-的最小值( )A .2-B .4-C .6-D .8-7.袋中装有完全相同的5个小球,其中有红色小球3个,黄色小球2个,如果不放回地依次摸出2个小球,则在第一次摸出红球的条件下,第二次摸出红球的概率是( )A .310B .35C . 12D .1410.已知函数12()|log |f x x =,若m n <,有()()f m f n =,则3m n +的取值范围是( )A.)+∞ B.)+∞ C .[4,)+∞ D .(4,)+∞11.已知点G 是ABC ∆的重心,若0120A ∠=,2AB AC ∙=-,则||AG 的最小值是( )A.3 B.2 C .23 D .3412.已知函数11,1()10ln 1,1x x f x x x ⎧+≤⎪=⎨⎪->⎩,则方程()f x ax =恰有两个不同实数根时,实数a 的取值范围是( )(注:e 为自然对数的底数)A .(1,0]-B .1(1,)10-C .211(1,0][,)10e -D .21(1,)e- 第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.某学校共有师生3200人,现用分层抽样的方法,从所有师生中抽取一个容量为160的样本,已知从学生中抽取的人数为150,那么该学校的教师人数是 .14.在ABC ∆中,若1BC =,3A π=,sin 2sin B C =,则AB 的长度为 .三、解答题 (本大题共6小题,共70.解答应写出文字说明、证明过程或演算步骤.)17.(本小题满分10分) 已知函数()sin(4)cos(4)44f x x x ππ=++-. (1)求函数()f x 的最大值;(2)若直线x m =是函数()f x 的对称轴,求实数m 的值.18. (本小题满分12分)已知公差不为0的等差数列{}n a 的前n 项和为n S ,346S a =+,且1413,,a a a 成等比数列.(1)求数列{}n a 的通项公式;(2)设21n an b =+,求数列{}n b 的前n 项和.19. (本小题满分12分)20. (本小题满分12分)21. (本小题满分12分)已知1(1,0)F -、2(1,0)F 为椭圆C 的左、右焦点,且点P 在椭圆C 上. (1)求椭圆C 的方程;(2)过1F 的直线l 交椭圆C 于,A B 两点,则2F AB ∆的内切圆的面积是否存在最大值? 若存在其最大值及此时的直线方程;若不存在,请说明理由.。
2014届河北省石家庄高中毕业班第一次质量检测文科数学试题(含答案解析)WORD精校版

石家庄2014届高三第一次教学质量检测(期末)文科数学(时间120分钟 满分150分)注意事项:1.本试卷分第Ⅰ卷(选择题))和第Ⅱ卷(非选择题)两部分.答卷前考生务必将自己的姓名、准考证号填写在答题卡上.2.回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.写在本试卷上无效.3.回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效. 4.考试结束后,将本试卷和答题卡一并交回.第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分,每小题给出的四个选项中,只有一项是符合题目要求的.1.已知i 是虚数单位,则复数z =(1+i)·i 3的共轭复数是 A .-1-i B .1-i C .-1+i D .1+i 2、集合A ={-1,0,1},B ={y|y =x 2+1,x ∈A},则A B =A 、{0}B 、{1} C.{0,1} D.{-1,0,1} 3.设a ,b 表示直线,α,β,γ表示不同的平面,则下列命题中正确的是 A .若a ⊥α且a ⊥b ,则b ∥α B .若γ⊥α且γ⊥β,则α∥βC .若a ∥α且a ∥β,则α∥βD .若γ∥α且γ∥β,则α∥β4.若抛物线y 2=2px 上一点P (2,y 0)到其准线的距离为4,则抛物线的标准方程为 A .y 2=4x B .y 2=6x C .y 2=8x D .y 2=10x 5.某程序框图如图所示,该程序运行后输出的k 的值是 A .4 B .5 C .6 D .76.把边长为2的正方形ABCD 沿对角线BD 折起,连结AC ,得到三棱锥C -ABD ,其正视图、俯视图均为全等的等腰直角三角形(如图所示),则其俯视图的面积为 A .32B . 12C .1D .227.设变量x ,y 满足约束条件:⎩⎪⎨⎪⎧y ≥x ,x +2y ≤2,x ≥-2,则z =x -3y 的最小值为A .-2B .-4C .-6D .-88.若双曲线x 2a 2-y 2b2=1(a >0,b >0)的右顶点为A ,过其左焦点F 作x 轴的垂线交双曲线于M ,N 两点,且MA NA>0,则该双曲线离心率的取值范围为正视图俯视图9.函数f (x )=sin x ·ln |x |的部分图象为10.已知球O ,过其球面上A ,B ,C 三点作截面,若O 点到该截面的距离等于球半径的一半,且AB =BC =2,∠B =120︒,则球O 的表面积为 A .64π3B .8π3C .4πD .16π911.已知各项均为正数的等比数列{n a }中,4a 与14a 的等比中项为,则7112a a +的值为A .16B .8C .D .412.已知函数则方程f (x )=ax 恰有两个不同的实根时,实数a 的取值范围是(注:e 为自然对数的底数)第Ⅱ卷(非选择题共90分)二、填空题:本大题共4小题,每小题5分,共20分.13.某学校共有师生3200人,先用分层抽样的方法,从所有师生中抽取一个容量为160的样本.已知从学生中抽取的人数为150,那么该学校的教师人数是__________. 14.在△ABC 中,内角A ,B ,C 的对边长分别为a ,b ,c ,若(a +b +c )(a +b -c )=ab ,则角C 的大小为为__________. 15.边长为1的菱形ABCD 中,,则__________.16.如右图,一个类似杨辉三角的数阵,则第n (n ≥2)的第3个数为__________.1 3 356 57 11 11 7 9 18 22 18 9……三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(本小题满分10分)已知函数f(x)=sin(4x+π4)+cos(4x-π4).(Ⅰ)求函数f(x)的最大值;(Ⅱ)若直线x=m是曲线y=f(x)的对称轴,求实数m的值.18.(本小题满分12分)已知公差不为0的等差数列{a n}的前n项和为S n,S3=a4+6,且a1,a4,a13成等比数列.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)设b n=2a n+1,求数列{b n}的前n项和.19.(本小题满分12分)2013年12月21日上午10时,省会首次启动重污染天气Ⅱ级应急响应,正式实施机动车车尾号限行,当天某报社为了解公众对“车辆限行”的态度,随机抽查了50人,将调查(Ⅰ)完成被调查人员的频率分布直方图;(Ⅱ)若从年龄在[55,65),[65,75)的被调查者中各随机选取1人进行进行追踪调查,求两人中至少有一人赞成“车辆限行”的概率.20.(本小题满分12分)如图,四棱锥P-ABCD中,底面ABCD是边长为1的正方形,CD⊥平面P AD,PA⊥AD,P A=2,E分别PC的中点,点P在棱PA上.(Ⅰ)求证:AC⊥DE;(Ⅱ)求三棱锥E-BDF的体积.21.(本小题满分12分)已知函数.(Ⅰ)当a=2时,求函数y=f(x)的单调区间;(II)当a>0时,函数y=f(x)在闭区间上的最大值为,求a的取值范围。
2014石家庄质检二数学理WORD解析版

2014年石家庄市高中毕业班复习教学质量检测(二) 高三数学(理科)解析版1.已知全集{}{}{}|15,1,2,3,1,2,u U x Z x A C B =∈≤≤==则A B ⋂=( )A .{}1,2B .{}1,3C .{}3D .{}1,2,3 【答案】 C【解析】{}{}{}{}|1512345,1,2,345u U x Z x C B B =∈≤≤==∴=,,,,,,{}{}1,2,3,3.A A B =∴⋂=2.已知i 为虚数单位,右图中复平面内的点A 表示复数z ,,则表示复数1zi+的点是( )。
A . MB .NC .PD .Q【答案】 D【解析】因为点A 的坐标为3,1(),所以3z i =+,所以23(3)(1)3342211(1)(1)22z i i i i i i ii i i i i ++--+--=====-+++- 所以表示复数1zi+的点的坐标为21(,-),故为点Q.3.利用计算机产生01之间的均匀随机数a ,则使关于x 的一元二次方程20x x a -+=无实根的概率为 ( )A.12 B. 14 C. 34 D. 23【答案】 C【解析】由一元二次方程20x x a -+=无实根,1140,4a a ∴∆=-<∴>,所以由几何概型可知P=34. 4.等差数列1239,,,,x x x x 的公差为1,随机变量ξ等可能的取值1239,,,,x x x x ,则方差()D ξ为 ( )A .103 B.203 C.109 D.209【答案】 B【解析】由题意可得12389559()99x x x x x x E x ξ++++=== 2222152585952222222221()[()()()()]91=[(4)(3)(2)(1)01234]916020 =(16941014916)993D x x x x x x x x ξ=-+-++-+--+-+--+++++++++++++==5.阅读如图所示的程序框图,则该算法的功能是 ( )A .计算数列{}21n -的前5项和B .计算数列{}21n -的前6项和C .计算数列{}12n -的前5项和D .计算数列{}12n -的前6项和【答案】 D【解析】依据程序01252222s =++++,所以数列的通项公式为12n n a -=,而共6项,所以选D.6.已知实数x y 、满足121,y y x x y m ≥⎧⎪≤-⎨⎪+≤⎩如果目标函数z x y =-的最小值为-2,则实数m 的值为 ( )A. 8B. 4C. 2D. 0【答案】 A【解析】可采用特值验证方法.()11,121y y x =⎧⎨=-⎩得A ,()11,1y m x y m=⎧-⎨+=⎩得,21121,33y x m m x y m =-⎧+-⎛⎫⎨ ⎪+=⎝⎭⎩得,把三个顶点分别代入z x y =-,显然()1,1不是使目标函数z x y =-取最小值-2的点,把()1,1m -代入2x y -=-,解得0m =;把121,33m m +-⎛⎫⎪⎝⎭代入2x y -=-,解得8m =.当0m =时0x y m +==,即121,0y y x x y ≥⎧⎪≤-⎨⎪+≤⎩无公共区域,即不满足题意,所以8m =.7.已知函数()cos()sin 4f x x x π=+,则函数()f x 的图象 ( )A.关于直线8x π=对称 B.关于点2(,)84π-对称 C.最小正周期为2T π= D.在区间(0,)8π上为减函数【答案】 A【解析】2222()cos()sin (cos sin )sin (sin cos sin )4222211cos 2212=(sin 2)(sin 2cos 21)sin(2)2224244f x x x x x x x x x x x x x x ππ=+=-=---=+-=+-当8x π=时,函数()f x 取到最大值1224-,所以8x π=是函数()f x 的图象 的一条对称轴.8.点A,B,C,D 在同一个球的球面上,2,22AB BC AC ===,若四面体ABCD 体积的最大值为43,则该球的表面积为 ( ) A.163πB. 8πC. 9πD. 12π【答案】 C【解析】当四面体ABCD 体积的最大时,球心O 和顶点D 的连线OD 垂直于平面ABC ,而ABC∆为直角三角形,11142223323ABC V S h h h ∆==⋅⋅⋅⋅=∴=,即D 点到Rt ABC ∆距离为2,由球的性质可知,直线DO Rt ABC ABC ⊥∆∆于外心,即AC 的中点1O ,则1OO A ∆为直角三角形,(如图所示)设球半径为R ,()2212,2,22AO OO h R R AO r R R ∴==-=-=∴-+=解得R=32, 2234492S R πππ⎛⎫∴=== ⎪⎝⎭9.已知两定点()2,0A -和()2,0B ,动点(),P x y 在直线:3l y x =+上移动,椭圆C 以A 、B 为焦点且经过点P ,则椭圆C 的离心率的最大值为 ( )A.226 B. 426 C. 213 D. 413【答案】 B【解析】由A 、B 为焦点,可知2c =,点P 经过椭圆C 且点(),P x y 在直线:3l y x =+上移动,所以线:3l y x =+与椭圆22221x y a b +=有交点,联系方程有222213x y a b y x ⎧+=⎪⎨⎪=+⎩得()2222222690ab x a x a a b +++-=,0∆≥,即()()42222236490a a b a a b -+-≥化简得:()2222229090a b a b a b -+≥∴-+≥, 解得222222294249a b b a c a a +≥=-=-∴-≥,即21326242226262c a a e a≥∴≥∴≤==,即离心率的最大值为426. 10.定义在区间[]0,1上的函数()f x 的图像如图所示,以()()0,0A f 、()()1,1B f 、()(),C x f x 为顶点的ABC ∆的面积记为函数()S x ,则函数()S x 的导函数()S x '的大致图像为 ( )【选项】A B C D【答案】 DDOC1OA【解析】由定义在区间[]0,1上的函数()f x 的图像可知,ABC ∆的面积记为函数()S x 的单调性变化为:增、减、增、减.所以数()S x 的导函数()S x '取值为:正,负,正,负.当C 移动到线段AB 上时, ()S x '不存在,因此导数图像分成两部分. 又由导数的几何意义可知,切线斜率在每部分都是由大变小.综合上述,故选D.11.已知函数,0.()ln ,0.xa e x f x x x ⎧≤=⎨->⎩,其中e 为自然对数的底数,若关于x 的方程(())0f f x =有且只有一个实数解,则实数a 的取值范围为( ) A.(,0)-∞ B.(,0)(0,1)-∞ C.(0,1) D.(0,1)(1,)+∞【答案】 B【解析】当0a =时,已知(())0f f x =有无数解,不符合题意。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
K1+478~K1+5888段左侧片石混凝土挡土墙第1部分2014年石家庄市高中毕业班第一次模拟考试试卷数学(理科)A卷(时间120分钟,满分150分)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知为虚数单位,,若是纯虚数,则的值为A. -1或1B.1C.-1D.32.若p:=2+k,k∈Z, q:是偶函数,则p是q的A.充要条件B. 充分不必要条件C.必要不充分条件D.既不充分也不必要条件3. 已知,则A.B.C.D.4.登山族为了了解某山高(km)与气温(°C)之间的关系,随机统计了4次山高与相应的气温,并制作了对照表:由表中数据,得到线性回归方程A.-10B.-8C. -6D. -45.已知等差数列,且,则数列的前13项之和为A. 24B. 39C. 52D. 1046. 执行右面的程序框图,若输出的结果为3,则可输入的实数值的个数为A. 1B. 2C.3D. 47. 曲线(其中e为自然对数的底数)在点(0, 1)处的切线与直线和轴所围成的区域D(包含边界),点为区域D内的动点,则的最大值为A. 3B. 4C. -1D.28.三棱锥S-ABC及其三视图中的正视图和侧视图如图所示,则棱SB的长为A. 211B.42C.38D. 1639. 在ABC中,角A、B、C所对的边长分别为, 且满足,则sinA+sinB的最大值是A. 1B.2C. 3D.310. 双曲线的左、右焦点分别为F1,F2,渐近线分别为,点P在第一象限内且在上,若⊥P F1,∥P F2,则该双曲线的离心率为A. 5B. 2C. 3D. 211.设直线与曲线有三个不同的交点A、B、C, 且|AB|=|BC|=10 ,则直线的方程为A.B.C D.12.设max{}=若函数的图象经过不同的两点,且存在整数n,使得n<<<n+1成立,则A. max{h(n),h(n+1)}>1B.max{h(n),h(n+1)}<1C. max{h(n),h(n+1)}>12D.max{h(n),h(n+1)}<12第II卷(非选择题,共90分)二、填空题:本大题共4小题,每小题5分,共20分.13.=14. 在三棱锥P-ABC中,侧棱PA,PB,PC两两垂直,Q为底面ABC内一点,若点Q到三个侧面的距离分别为3、4、5,则过点P和Q的所有球中,表面积最小的球的表面积为______15.已知函数为抛掷一颗骰子得到的点数,则函数在[0, 4]上零点的个数小于5或大于6的概率为16.若实数,b, c, d满足,则的最小值为__三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.17. (本小题满分12分)已知是各项均为正数的等比数列,且(I)求数列的通项公式;(II)18. (本小题满分12分)如图,在三棱柱ABC-A1B1C1中,AB⊥AC,顶点在底面上的射影恰为点,且AB=AC=A1B=2.(Ⅰ)证明:平面平面;(Ⅱ)若点为的中点,求出二面角的余弦值.19.(本小题满分12分)气温(0C)181310-1山高(km)24343864K1+478~K1+5888段左侧片石混凝土挡土墙第1部分现有甲、乙、丙三人参加某电视台的应聘节目《非你莫属》,若甲应聘成功的概率为12,乙、丙应聘成功的概率均为t2(0<t<2),且三个人是否应聘成功是相互独立的.(Ⅰ)若乙、丙有且只有一个人应聘成功的概率等于甲应聘成功是相互独立的,求t的值;(Ⅱ)记应聘成功的人数为ξ,若当且仅当ξ为2时概率最大,求E(ξ)的取值范围.20. (本小题满分12分)椭圆C: 的离心率为32,过其右焦点F与长轴垂直的弦长为1.(I)求椭圆C的方程;(II)设椭圆C的左,右顶点分别为A,B ,点P是直线上的动点,直线PA与椭圆的另一交点为M,直线PB与椭圆的另一交点为N,求证:直线M N经过一定点.21. (本小题满分12分)已知函数.(I)若=0,,求函数的极值点及相应的极值;(II)若对于任意,存在满足且成立,求的取值范围.请考生在第22〜24三题中任选一题做答,如果多做,则按所做的第一题记分.22. (本小题满分10分)选修4-1:几何证明选讲已知⊙O1和⊙O2相交于A,B两点,过A点作⊙O1的切线交⊙O2于点E,连接E B并延长交⊙O1于点C,直线CA交⊙O2于点D.(Ⅰ)当点D与点A不重合时(如图①),证明E D2=E B·E C;(II)当点D与点A重合时(如图②),若BC=2,B E=6,求⊙O2的直径长.23. (本小题_分10分)选修4-4:坐标系与参数方程在直角坐标系中,曲线C1的参数方程为:(为参数),以原点为极点,x轴的正半轴为极轴,并取与直角坐标系相同的长度单位,建立极坐标系,曲线C2的极坐标方程为:.(I)求曲线C2的直角坐标方程;(II)若P,Q分别是曲线C1和C2上的任意一点,求|PQ|的最小值.24. (本小题满分10分)选修4-5:不等式选讲已知函数.(I)当=1时,求的解集;(II )若不存在实数,使<3成立,求的取值范围.2014年石家庄市高中毕业班第一次模拟考试(数学理科答案)一、选择题:A卷答案:1---5CAACC 6---10CABDB11-12DBB卷答案:1---5DAADD6---10DABCB11-12CB11.提示:曲线关于(0,1)中心对称.12.提示:函数图象不随的变化而变化.二、填空题:13.14. 15.16.16.提示:可转化为上的动点与直线上动点的问题.三、解答题:(解答题按步骤给分,本答案只给出一或两种答案,学生除标准答案的其他解法,参照标准酌情设定,且只给整数分)17.解:(Ⅰ)设等比数列的公比为,由已知得……………2分又∵,,解得………………3分∴;…………………5分(Ⅱ)由题意可得,,()两式相减得,∴,()……………………7分当时,,符合上式,∴,()…………………………8分设,,………………10分两式相减得,∴.…………………12分(整理结果正确即可,不拘泥于形式)18.(本小题满分12分)K1+478~K1+5888段左侧片石混凝土挡土墙第1部分如图,在三棱柱中,,顶点在底面上的射影恰为点,.(Ⅰ)证明:平面平面;(Ⅱ)若点为的中点,求出二面角的余弦值.证明:(Ⅰ)由题意得:面,∴, ------2分又,∴面,------3分∵面,∴平面平面;------5分(Ⅱ)解法1:以A为原点,建立如图所示的空间直角坐标系,则因为P为棱的中点,故易求得.------6分设平面的法向量为则得令,则------8分而平面的法向量------9分则------11分由图可知二面角为锐角,故二面角的平面角的余弦值是.------12分解法2:过P做PP1//A1B1交A1C1的中点于P1,由(Ⅰ)可知P1A1,连接P1B,则为二面角的平面角,------8分在中,,,故二面角的平面角的余弦值是------12分19.解:(Ⅰ)由题意得,解得.……………3分(Ⅱ)的所有可能取值为0,1,2,3;;;.故的分布列为:……………………7分.…………………8分由题意得:,,,又因为所以解得的取值范围是.…………………11分.…………………12分20.解:(Ⅰ)依题意,过焦点F与长轴垂直的直线x=c与椭圆联立解答弦长为=1,……………2分所以椭圆的方程.………………4分(Ⅱ)设P(1,t),直线,联立得:即,可知所以,则……………………6分同理得到………………8分由椭圆的对称性可知这样的定点在轴,不妨设这个定点为Q,………………10-分又,,,,.……………12分21.解:(Ⅰ),,为减函数;为增函数,所以只有一个极小值点,极小值为0.……………………4分(Ⅱ) 设依题意即求在上存在零点时的取值范围.又当时,,且在定义域内单调递增,所以只需要在上恒成立.即,在上恒成立.即,在上恒成立.…………7分K1+478~K1+5888段左侧片石混凝土挡土墙第1部分 若,显然不成立,因为由第一问知在为增函数,故,即在恒成立,不妨设,,,…………………9分若,则,若,,所以为增函数,(不合题意),若,若,,为增函数,(不合题意),若,若,,为减函数,(符合题意),综上所述,若时,恒成立,则.……………………………12分22.解:(Ⅰ)连接AB,在E A的延长线上取点F,如图①所示.∵A E是⊙O1的切线,切点为A,∴∠F AC=∠ABC,.……………1分∵∠F AC=∠DA E,∴∠ABC=∠DA E,∵∠ABC是⊙O2内接四边形AB E D的外角,∴∠ABC=∠AD E,……………2分∴∠DA E=∠AD E.………………3分∴E A=E D,∵,∴.………………5分(Ⅱ)当点D与点A重合时,直线CA与⊙O2只有一个公共点,所以直线CA与⊙O2相切.……………6分如图②所示,由弦切角定理知:∴AC与A E分别为⊙O1和⊙O2的直径.…………8分∴由切割线定理知:E A2=B E·C E,而CB=2,B E=6,C E=8∴E A2=6×8=48,A E=.故⊙O2的直径为.………………10分23.解:(Ⅰ),…………………2分.…………………4分(Ⅱ)设P(),…………………6分,,…………………8分.……………………10分24.解:(Ⅰ)当a=1时,,解得;当时,解得,无解,解得;……………………………3分综上可得到解集.……………………5分(Ⅱ)依题意,,则,……………8分(舍),所以…………………10分不开口,没有人知道你想要什么;不去做,任何想法都只在脑海里游泳;不迈出脚步,永远找不到你前进的方向。
其实你很强,只是懒惰帮了你倒忙。
