第12章--MATLAB-Simulink系统仿真-习题答案
MATlab 仿真部分习题答案
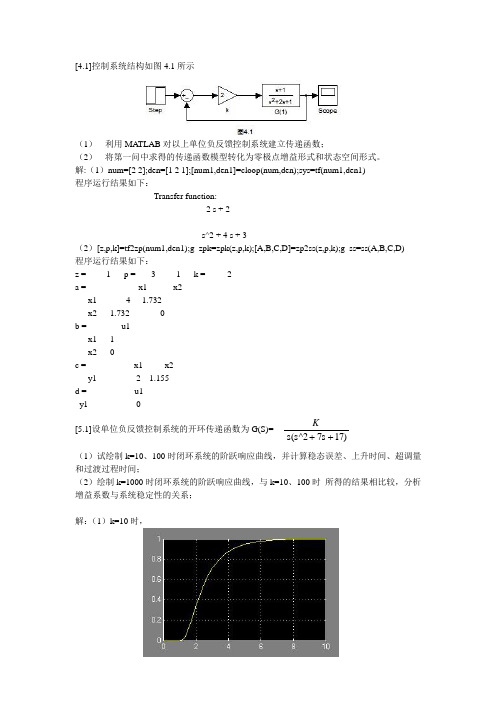
[4.1]控制系统结构如图4.1所示(1)利用MATLAB对以上单位负反馈控制系统建立传递函数;(2)将第一问中求得的传递函数模型转化为零极点增益形式和状态空间形式。
解:(1)num=[2 2];den=[1 2 1];[num1,den1]=cloop(num,den);sys=tf(num1,den1)程序运行结果如下:Transfer function:2 s + 2-------------s^2 + 4 s + 3(2)[z,p,k]=tf2zp(num1,den1);g_zpk=zpk(z,p,k);[A,B,C,D]=zp2ss(z,p,k);g_ss=ss(A,B,C,D)程序运行结果如下:z = -1 p = -3 -1 k = 2a = x1 x2x1 -4 -1.732x2 1.732 0b = u1x1 1x2 0c = x1 x2y1 2 1.155d = u1y1 0K[5.1]设单位负反馈控制系统的开环传递函数为G(S)=+s(s^2+7s17)(1)试绘制k=10、100时闭环系统的阶跃响应曲线,并计算稳态误差、上升时间、超调量和过渡过程时间;(2)绘制k=1000时闭环系统的阶跃响应曲线,与k=10、100时所得的结果相比较,分析增益系数与系统稳定性的关系;解:(1)k=10时,K=100时,K=10时,利用MA TLAB工作区输入程序:num=[10];den=[1,7,17,0];[z,p,k]=tf2zp( num,den);运行得z,p,k的值p= -3.5+2.1794*i -3.5-2.1794*i k=10G=zpk([ ],[-3.5+2.1794*i,-3.5-2.1794*i],10);c=dcgain(G);[y,t]=step(G);plot(t,y)[Y,K]=max(y);timetopeak=t(k);percentovershoot=100*(y-c)/cn=1;while y(n)<c n=n+1;end risetime=t(n) i=length(t);while(y(i)>0.98*c&y(i)<1.02*c) i=i-1;End setllingtime=t(i) 运行程序结果为:稳定值c=0.5882,响应时间setllingtime=1.0096s,上升时间risetime=1.1989s,最大峰值时间timetopeak=1.4356,超调量percentovershoot=0.555% 同理得k=100时,稳定值c=5.882,响应时间setllingtime=1.0096s, 上升时间risetime=1.1989s,最大峰值时间timetopeak=1.4356,超调量percentovershoot=0.555%(3)k=1000时,由其响应曲线可知,增益系数越大,其稳定性越差。
Matlab与控制系统仿真部分习题答案

【4.2】程序:num=[5,0];den=conv([1,1],conv([1,2],[1,3])); [numc,denc]=cloop(num,den);[z,p,k]=tf2zp(numc,denc);[A,B,C,D]=tf2ss(numc,denc);g_zp=zpk(z,p,k)g_tf=tf(numc,denc)g_ss=ss(A,B,C,D)运行结果:Zero/pole/gain:5 s----------------------------------(s+0.4432) (s^2 + 5.557s + 13.54)Transfer function:5 s----------------------s^3 + 6 s^2 + 16 s + 6a =x1 x2 x3x1 -6 -16 -6x2 1 0 0x3 0 1 0b =u1x1 1x2 0x3 0c =x1 x2 x3y1 0 5 0d =u1y1 0【4.3】程序:A=[0 0 0 -1;1 0 0 -2;0 1 0 -3;0 0 1 -4]; B=[0;0;0;1];C=[1 0 0 0];g_ss=ss(A,B,C,D)[num,den]=ss2tf(A,B,C,D);g_tf=tf(num,den)[z,p,k]=ss2zp(A,B,C,D);g_zpk=zpk(z,p,k)运行结果:a =x1 x2 x3 x4x1 0 0 0 -1x2 1 0 0 -2x3 0 1 0 -3x4 0 0 1 -4b =u1x1 0x2 0x3 0x4 1c =x1 x2 x3 x4y1 1 0 0 0d =u1y1 0Continuous-time model.Transfer function:-3.109e-015 s^3 - s^2 - 3.331e-015 s - 4.441e-016 -------------------------------------------------s^4 + 4 s^3 + 3 s^2 + 2 s + 1Zero/pole/gain:- s^2----------------------------------------------(s+0.6724) (s+3.234) (s^2 + 0.0936s + 0.4599)【5.1】(1)程序num=[0,10];den=conv([1,0],[1,7,17]); [numc,denc]=cloop(num,den,-1); G=tf(numc,denc)[y,t]=step(G);plot(t,y,'b-')C=dcgain(G);n=1;while y(n)<0.1*Cn=n+1;endm=1;while y(m)<0.9*Cm=m+1;endrisetime=t(m)-t(n)[Y,k]=max(y); percentovershoot=100*(Y-C)/Ci=length(t);while(y(i)>0.98*C)&(y(i)<1.02*C) i=i-1;endsettlingtime=t(i)运行结果:Transfer function:10-----------------------s^3 + 7 s^2 + 17 s + 10risetime =2.7312percentovershoot =-0.4399settlingtime =5.1372图:0123456700.10.20.30.40.50.60.70.80.91(2)程序k=[10,100,1000];t=linspace(1,20,200);num=1;den=conv([1,0],[1,7,17]);for j=1:3;s1=tf(num*k(j),den);sys=feedback(s1,1)y(:,j)=step(sys,t);endplot(t,y(:,1),'r',t,y(:,2),'b',t,y(:,3),'g')gtext('k=10');gtext('k=100');gtext('k=1000') 运行结果:Transfer function:10-----------------------s^3 + 7 s^2 + 17 s + 10Transfer function:100------------------------s^3 + 7 s^2 + 17 s + 100Transfer function:1000-------------------------s^3 + 7 s^2 + 17 s + 1000图:024681012141618200.20.40.60.811.21.41.61.8图:02468101214161820-3-2-1123422【6.1】程序:(1)num1=[1,1];den1=conv([1,0,0],conv([1,2],[1,4]));sys1=tf(num1,den1)rlocus(sys1)运行结果:-12-10-8-6-4-2024-8-6-4-202468Root LocusReal Axis I m a g i n a r y A x i s(2)num2=[1,1];den2=conv([1,0],conv([1,-1],[1,4,16]));sys2=tf(num2,den2)rlocus(sys2)运行结果:-10-8-6-4-2024-8-6-4-202468Root LocusReal Axis I m a g i n a r y A x i s(3)num3=[1,8];den3=conv([1,0,0],conv([1,3],conv([1,5],conv([1,7],[1,15])))); sys3=tf(num3,den3)rlocus(sys3)运行结果:-30-25-20-15-10-5051015-20-15-10-505101520Root LocusReal Axis I m a g i n a r y A x i s【6.3】程序:num=[1,2];den=conv([1,0],conv([1,4],conv([1,8],[1,2,5])));sys=tf(num,den)rlocus(sys)[k,poles]=rlocfind(sys)运行结果:Transfer function:s + 2---------------------------------------s^5 + 14 s^4 + 61 s^3 + 124 s^2 + 160 sSelect a point in the graphics windowselected_point =0.0296 + 2.2826i k =135.8815poles =-7.3248-5.41040.0145 + 2.3021i0.0145 - 2.3021i -1.2939图:-20-15-10-5051015-15-10-551015Root LocusReal Axis I m a g i n a r y A x i s【7.3】程序(1)画波特图num=[50];den=conv([1,0],conv([1,10],[3,1]));sys=tf(num,den)sys1=feedback(sys,1)bode(sys)grid图(1)-150-100-50050100M a g n i t u d e (d B)10-210-1100101102103-270-225-180-135-90P h a s e (d e g )Bode DiagramFrequency (rad/sec)程序(2)画奈奎斯特图num=[50];den=conv([1,0],conv([1,10],[3,1]));sys=tf(num,den)sys1=feedback(sys,1)nyquist(sys)grid图(2)-16-14-12-10-8-6-4-20-300-200-100100200300Nyquist DiagramReal Axis I m a g i n a r y A x i s程序(3)画零极点图num=[50];den=conv([1,0],conv([1,10],[3,1]));sys=tf(num,den)sys1=feedback(sys,1)pzmap(sys1)gird图(3)P ole-Zero MapReal Axis I m a g i n a r y A x i s -12-10-8-6-4-20-1.5-1-0.50.511.5程序(4)计算相角裕量和幅值裕量num=[50];den=conv([1,0],conv([1,10],[3,1]));sys=tf(num,den)sys1=feedback(sys,1)[gm,pm,wcg,wcp]=margin(sys)运行结果Transfer function:50---------------------3 s^3 + 31 s^2 + 10 sTransfer function:50--------------------------3 s^3 + 31 s^2 + 10 s + 50gm =2.0667pm =7.5615wcg =1.8257wcp =1.2645程序(5)绘制阶跃响应曲线num=[50];den=conv([1,0],conv([1,10],[3,1])); sys=tf(num,den)sys1=feedback(sys,1)step(sys1)图(5)00.20.40.60.811.21.41.61.82Step ResponseTime (sec)A m p l i t u d e【7.4】程序如下:num=[300];den=conv([1,0,0],conv([0.2,1],[0.02,1]));sys=tf(num,den)margin(sys)grid波特图如下:-150-100-50050100M a g n i t u d e (d B )10-1100101102103-360-315-270-225-180P h a s e (d e g )Bode DiagramGm = Inf , P m = -78 deg (at 11 rad/sec)Frequency (rad/sec)【9.3】程序:A=[-2 2 -1;0 -2 0;1 -4 0];B=[0;0;1];C=[1,0,0];D=0;M=ctrb(A,B)m=rank(M)if m==3;disp('系统可控')elsedisp('系统不可控')endN=obsv(A,C)n=rank(N)if n==3;disp('系统可观')elsedisp('系统不可观') endsys=ss(A,B,C,D) [num,den]=ss2tf(A,B,C,D) sys1=tf(num,den)[z,p,k]=ss2zp(A,B,C,D)运行结果:M =0 -1 20 0 01 0 -1m =2系统不可控N =1 0 0-2 2 -13 -4 2n =2系统不可观a =x1 x2 x3x1 -2 2 -1x2 0 -2 0x3 1 -4 0b =u1x1 0x2 0x3 1c =x1 x2 x3y1 1 0 0d =u1y1 0 Continuous-time model.0 0 -1 -2den =1 4 5 2Transfer function:-s - 2---------------------s^3 + 4 s^2 + 5 s + 2z =-2p =-1-1-2k = -1【10.1】(1)程序:A=[0,1,0,0;0,5,0,0;0,0,-7,0;0,0,0,-8]; B=[0;1;0;1];C=[1,2,3,4];D=zeros(1,1);G_ss=ss(A,B,C,D)运行结果:a =x1 x2 x3 x4x1 0 1 0 0x2 0 5 0 0x3 0 0 -7 0x4 0 0 0 -8u1x1 0x2 1x3 0x4 1c =x1 x2 x3 x4y1 1 2 3 4d =u1y1 0(2):程序:[num1,den1]=ss2tf(A,B,C,D); p=roots(den1)i=0;for k=1:1:length(p)if real(p(k))>0i=i+1;endendif i>0disp('系统不稳定');elsedisp('系统稳定');end运行结果:p =5.0000-8.0000-7.0000系统不稳定(3)(4)程序:AA=[0,1,0;0,5,0;0,0,-8];BB=[0;1;1];P=[-1,-2,-8];K=acker(AA,BB,P);i=4;K(4)=0;Kpp=eig(A-B*K)sys1=tf(num1,den1);[y1,t]=step(sys1);plot(t,y1)hold onA_feedback=A-B*K;[num2,den2]=ss2tf(A_feedback,B,C,D); sys2=tf(num2,den2);[y2,t]=step(sys2);plot(t,y2,'r')gridgtext('反馈前')gtext('反馈后')运行结果:K =2 8 0 0pp =-8-2-1-7图形:01234560123456【13.1】程序:A=[0,1;0,0];B=[0;1];C=[1,0];D=zeros(1,1);G_ss=ss(A,B,C,D)M=ctrb(A,B);if rank(M)==2disp('系统完全能控'); elsedisp('系统不完全能控'); endS=[1,0];N=obsv(A,S);if rank(N)==2disp('(A,S)可观测'); elsedisp('(A,S)不可观测'); endR=1;Q=[1,0;0,0];[K,P,E]=Lqr(A,B,Q,R)A_new=A-B*K;G_new=ss(A_new,B,C,D);t=linspace(0,5,100)';y1=step(G_ss,t);y2=step(G_new,t);plot(t,y1,'r:',t,y2,'b-')gridgtext('反馈前')gtext('反馈后')运行结果:a =x1 x2x1 0 1x2 0 0b =u1x1 0x2 1c =x1 x2y1 1 0d =u1y1 0Continuous-time model. 系统完全能控(A,S)可观测K =1.0000 1.4142P =1.4142 1.00001.0000 1.4142E =-0.7071 + 0.7071i-0.7071 - 0.7071i图形:00.51 1.52 2.53 3.54 4.5502468101214。
MATLAB-SIMULINK讲解完整版

点击图3-2中“树状结构目录窗口”中各模块库名前带 “+”的小方块可展开二级子模块库的目录。“模块窗口” 中显示的是用户在“树状结构目录窗口”中选中的模块库所 包含的模块图标。如果显示的模块图标前带“+”的小方块, 表明该图标下还有三级目录,直接点击该图标可在该窗口中 展现三级目录下的模块图标。
为了叙述方便,本书将模块库中以图标形式表示的典型 环节称为模块,将用典型环节模块组成的系统仿真模型简称 为模型。
在SIMULINK中创建子系统一般有两种方法。
1) 通过“子系统”模块的方法 该方法要求在用户的模型里添加一个称为Subsystem的 子系统模块,然后再往该模块里加入组成子系统的各种模块。 这种方法适合于采用自上而下设计方式的用户,具体实现步 骤如下: (1) 新建一个空白模型。 (2) 打开“端口和子系统”(Ports&Subsystems)模块库, 选取其中的“子系统”(Subsystem)模块并把它复制到新建的 仿真平台窗口中。
第3章 SIMULINK应用基础
3.1 SIMULINK仿真环境 3.2 SIMULINK的基本操作 3.3 SIMULINK系统建模 3.4 SIMULINK运行仿真 3.5 SIMULINK模块库 3.6 SIMULINK系统仿真应用 习题
3.1 SIMULINK仿真环境 SIMULINK是MATLAB的一个分支产品,主要用来实 现对工程问题的模型化及动态仿真。SIMULINK体现了模块 化设计和系统级仿真的思想,采用模块组合的方法使用户能 够快速、准确地创建动态系统的计算机模型,使得建模仿真 如同搭积木一样简单。SIMULINK现已成为仿真领域首选的 计算机环境。
单击模块,拖曳模块到合适的位置,松开鼠标按键
方法 1:选中模块,选择菜单命令[Format>Rotate Block], 模块顺时针旋转 90°;选择菜单命令[Format>Flip Block],
MATLAB语言:Simulink系统仿真习题与答案

一、单选题1、将模块连接好之后,如果要分出一根连线,操作方法是()。
A.把鼠标指针移到分支点的位置,按住鼠标左键拖曳到目标模块的输入端B.双击分支点的位置,按住鼠标左键拖曳到目标模块的输入端C.把鼠标指针移到分支点的位置,按下Ctrl键并按住鼠标拖曳到目标模块的输入端D.把鼠标指针移到分支点的位置,按下Shift键并按住鼠标拖曳到目标模块的输入端正确答案:C2、在一个模型窗口上按住一个模块并同时按Shift键移动到另一个模型窗口,则()。
A.在两个模型窗口都有这个模块B.在后一个窗口有这个模块C.在前一个窗口有这个模块D.在两个窗口都有模块并添加连线正确答案:A3、为子系统定制参数设置对话框和图标,使子系统本身有一个独立的操作界面,这种操作称为子系统的()。
A.包装B.封装C.集成D.组合正确答案:B4、使用S函数时,要在模型编辑窗口添加()。
A.Sine Wave模块B.S-Program模块C.Subsystem模块D.S-Function模块正确答案:D二、多选题1、启动Simulink的方法有()。
A.在命令行窗口中输入simulink命令B.在“主页”选项卡中单击SIMULINK命令组中的“Simulink”命令按钮C.在“主页”选项卡中单击“文件”命令组中的“新建”命令按钮D.在“主页”选项卡中单击“文件”命令组中的“新建脚本”命令按钮正确答案:A、B、C2、根据控制信号的控制方式不同,条件执行子系统分为()。
A.事件驱动子系统B.使能子系统C.触发子系统D.使能加触发子系统正确答案:B、C、D3、以下关于S函数的描述中,正确的有()。
A.利用S函数可以对Simulink模块库进行扩充B.S函数只能用MATLAB语言编写C.S函数有现成的模板程序D.S函数模块能够被封装正确答案:A、C、D三、判断题1、建立系统仿真模型是在Simulink模型编辑窗口中进行的。
正确答案:√2、利用触发子系统能够将锯齿波转换为方波。
MATLAB及Simulink应用实验指导书+答案

《MATLAB及应用》实验指导书班级:姓名:学号:总评成绩:汽车工程系电测与汽车数字应用中心目录实验04051001 MATLAB语言基础1实验04051002 MATLAB科学计算及绘图4实验04051003 MATLAB综合实例编程6实验04051001MATLAB 语言基础1实验目的1) 熟悉MATLAB 的运行环境 2) 掌握MATLAB 的矩阵和数组的运算 3) 掌握MATLAB 符号表达式的创建 4) 熟悉符号方程的求解2实验内容说明:从下面的题目、第1~4章课后习题中任选10题,学号为奇数的选择奇数号题,学号为偶数的选择偶数号题,并在答案之前标注题目来源,例如“课本第1章题2”、“指导书题3”等。
可以采用notebook 格式输出结果(关于notebook 请查阅其他参考资料,或上网搜索) 例如:课本第4章题1.一个半径为r 的求体积V 和表面积A 分别为:334r V π=、24r A π= a.给出以下程序的伪代码描述:计算当30≤≤r 米时的V 和A ,并同时绘制V 相对于A 的图形。
b.编写和运行部分a 中所描述的程序。
解:clc,clear; r=0:0.1:3; V=4/3*pi*r.^3; A=4*pi*r.^2; plot(A,V);grid on; xlabel('Surface Area'); ylabel('Volume');1.在一个已知的测量矩阵T(100×100)中,删除整行全为0的行,删除整列内容全为0的整列(判断某列元素是否为0方法:检查T(: ,i).*(T(: ,j))是否为0)。
2.假设汽车系在下列各年度的人口统计如表所示试用一个二维矩阵STU表示上述数据,并请计算出下列各数值:(1)汽车系在2002~2006年之间的每年平均新生、毕业生人数。
(2)5年来汽车系共有多少毕业生?(3)在哪几年,新生数目比毕业生多?(4)5年来每年的毕业生对新生的比例平均值为何?3.完成下列矩阵运算:(1) 使用randn 产生一个(10×10)的矩阵A(2) 计算B=(A+A ’)/2。
MATLAB控制系统各种仿真例题(包括simulink解法)

一、 控制系统的模型与转换1. 请将下面的传递函数模型输入到matlab 环境。
]52)1)[(2(24)(32233++++++=s s s s s s s G )99.02.0)(1(568.0)(22+--+=z z z z z H ,T=0.1s >> s=tf('s');G=(s^3+4*s+2)/(s^3*(s^2+2)*((s^2+1)^3+2*s+5));GTransfer function:s^3 + 4 s + 2------------------------------------------------------s^11 + 5 s^9 + 9 s^7 + 2 s^6 + 12 s^5 + 4 s^4 + 12 s^3>> num=[1 0 0.56];den=conv([1 -1],[1 -0.2 0.99]);H=tf(num,den,'Ts',0.1)Transfer function:z^2 + 0.56-----------------------------z^3 - 1.2 z^2 + 1.19 z - 0.992. 请将下面的零极点模型输入到matlab 环境。
请求出上述模型的零极点,并绘制其位置。
)1)(6)(5()1)(1(8)(22+++-+++=s s s s j s j s s G )2.8()6.2)(2.3()(1511-++=----z z z z z H ,T=0.05s>>z=[-1-j -1+j];p=[0 0 -5 -6 -j j];G=zpk(z,p,8)Zero/pole/gain:8 (s^2 + 2s + 2)--------------------------s^2 (s+5) (s+6) (s^2 + 1)>>pzmap(G)>> z=[0 0 0 0 0 -1/3.2 -1/2.6];p=[1/8.2];H=zpk(z,p,1,'Ts',0.05)Zero/pole/gain:z^5 (z+0.3125) (z+0.3846)-------------------------(z-0.122)Sampling time: 0.05>>pzmap (H )num=[0,7.1570,-6.4875 ];den=[1,-2.2326,1.7641,-0.4966];sysd=tf(num,den,0.05,'variable','z^-1')Transfer function:7.157 z^-1 - 6.487 z^-2-----------------------------------------1 - 2.233 z^-1 + 1.764 z^-2 - 0.4966 z^-3Sampling time: 0.05二、 线性系统分析1. 请分析下面传递函数模型的稳定性。
MATLAB与控制系统仿真练习题(含图)及答案
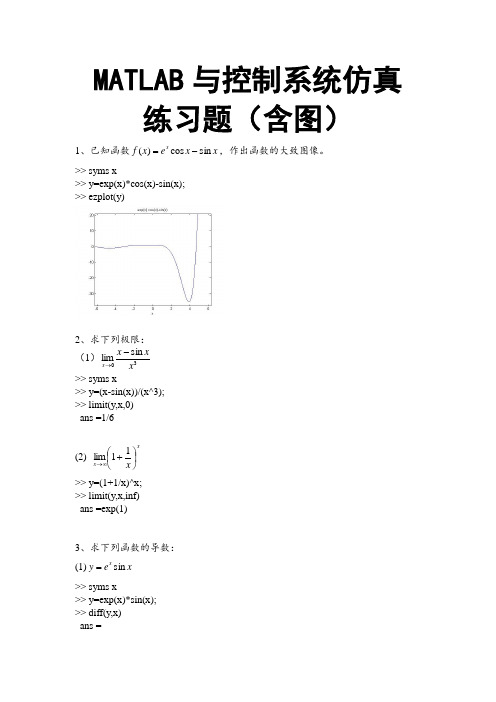
MATLAB 与控制系统仿真练习题(含图)1、已知函数x x e x f x sin cos )(-=,作出函数的大致图像。
>> syms x>> y=exp(x)*cos(x)-sin(x); >> ezplot(y)2、求下列极限:(1)30sin lim xx x x -→ >> syms x>> y=(x-sin(x))/(x^3);>> limit(y,x,0)ans =1/6(2) xx x ⎪⎭⎫ ⎝⎛+∞→11lim >> y=(1+1/x)^x;>> limit(y,x,inf)ans =exp(1)3、求下列函数的导数:(1)x e y x sin =>> syms x>> y=exp(x)*sin(x);>> diff(y,x)ans =exp(x)*sin(x)+exp(x)*cos(x)(2) x e x x y 22sin +=>> syms x>> y=sin(x)+x^2*exp(2*x);>> diff(y,x)ans =cos(x)+2*x*exp(2*x)+2*x^2*exp(2*x)4、求.)1(532⎰-dx x x 和.sin ⎰xdx e x(1).)1(532⎰-dx x xsyms x>> int(x^2*(1-x^3)^5)ans =-1/18*x^18+1/3*x^15-5/6*x^12+10/9*x^9-5/6*x^6+1/3*x^3(2).sin ⎰xdx e x>> int(exp(x)*sin(x))ans =-1/2*exp(x)*cos(x)+1/2*exp(x)*sin(x)5、求.)(102⎰-dx x x 和.1102⎰-dx x x (1) .)(102⎰-dx x x>> syms x>> int(x-x^2,0,1)ans =1/6(2) .1102⎰-dx x x>> syms x>> int(x*(1-x^2)^0.5,0,1)ans =1/36、已知二元函数),(cos )sin(2xy xy z +=试求y x z x z y z x z ∂∂∂∂∂∂∂∂∂222,,,。
第12章--MATLAB-Simulink系统仿真-习题答案

第12章--M A T L A B-S i m u l i n k系统仿真-习题答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第12章 MATLAB Simulink系统仿真习题12一、选择题1.启动Simulink后,屏幕上出现的窗口是()。
AA.Simulink起始页 B.Simulink Library Browser窗口C.Simulink Block Browser窗口 D.Simulink模型编辑窗口2.模块的操作是在()窗口中进行的。
DA.Library Browser B.Model BrowserC.Block Editer D.模型编辑3.Integrator模块包含在()模块库中。
BA.Sources B.Continuous C.Sinks D.Math Operations 4.要在模型编辑窗口中复制模块,不正确的方法是()。
B A.单击要复制的模块,按住鼠标左键并同时按下Ctrl键,移动鼠标到适当位置放开鼠标B.单击要复制的模块,按住鼠标左键并同时按下Shift键,移动鼠标到适当位置放开鼠标C.在模型编辑窗口选择Edit→Copy命令和Edit→Paste命令D.右键单击要复制的模块,从快捷菜单中选择Copy命令和Paste命令5.已知仿真模型如图12-41(a)所示,示波器的输出结果如图12-41(b)所示。
(a)仿真模型3(b )示波器输出结果图12-41 习题仿真模型及仿真结果则XY Graph 图形记录仪的输出结果是( )。
CA .正弦曲线B .余弦曲线C .单位圆D .椭圆二、填空题1.Simulink (能/不能)脱离MATLAB 环境运行。
2.建立Simulink 仿真模型是在 窗口进行的。
模型编辑窗口3.Simulink 仿真模型通常包括 、系统模块和 三种元素。
信号源(Source ),信宿(Sink )4.由控制信号控制执行的子系统称为 ,它分为 、 和 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
,
第12章 MATLAB Simulink系统仿真
习题12
一、选择题
1.启动Simulink后,屏幕上出现的窗口是()。
A
A.Simulink起始页 B.Simulink Library Browser窗口
C.Simulink Block Browser窗口 D.Simulink模型编辑窗口
2.模块的操作是在()窗口中进行的。
D
A.Library Browser B.Model Browser
(
C.Block Editer D.模型编辑
3.Integrator模块包含在()模块库中。
B
A.Sources B.Continuous C.Sinks D.Math Operations 4.要在模型编辑窗口中复制模块,不正确的方法是()。
B
A.单击要复制的模块,按住鼠标左键并同时按下Ctrl键,移动鼠标到适当位置放开鼠标
B.单击要复制的模块,按住鼠标左键并同时按下Shift键,移动鼠标到适当位置放开鼠标
C.在模型编辑窗口选择Edit→Copy命令和Edit→Paste命令
D.右键单击要复制的模块,从快捷菜单中选择Copy命令和Paste命令
|
5.已知仿真模型如图12-41(a)所示,示波器的输出结果如图12-41(b)所示。
(a)仿真模型
(b )示波器输出结果
图12-41 习题仿真模型及仿真结果
则XY Graph 图形记录仪的输出结果是( )。
C
A .正弦曲线
B .余弦曲线
C .单位圆
D .椭圆
】
二、填空题
1.Simulink (能/不能)脱离MATLAB 环境运行。
2.建立Simulink 仿真模型是在 窗口进行的。
模型编辑窗口
3.Simulink 仿真模型通常包括 、系统模块和 三种元素。
信号源(Source ),信宿(Sink )
4.由控制信号控制执行的子系统称为 ,它分为 、 和 。
条件执行子系统,使能子系统,触发子系统,使能加触发子系统。
5.为子系统定制参数设置对话框和图标,使子系统本身有一个独立的操作界面,这种操作称为子系统的 。
封装(Masking )
%
三、应用题
1.利用Simulink 仿真来实现摄氏温度到华氏温度的转换:9325f c T T =
+。
2.利用Simulink 仿真)5cos 2513cos 91(cos 8)(2t ωt ωt ωπ
A t x ++=
,取A=1,ω=2π。
3.设系统微分方程为 '(1)2y x y y =+⎧⎨=⎩
试建立系统模型并仿真。
4.设计一个实现下面函数模块的子系统并对子系统进行封装。
Output = (Input1+ I nput2)×Input3-Input4
5.已知y=kx+b,其中x为输入,k、b为待定参数,试采用S函数实现模块,并封装和测试该模块。
