届文科数学立体几何大题训练

合集下载

届高三数学立体几何专项训练(文科)

高三数学立体几何专题(文科)（一）吴丽康 2019-111.如图，四棱锥P-ABCD 中，底面ABCD 为矩形，PA ⊥平面ABCD ，E 为PD 的点. （Ⅰ）证明：PB //平面AEC ；（Ⅱ）设AP=1，AD=，三棱锥P-ABD 的体积V=，求A 点到平面PBD 的距离.2. 如图，四棱锥P -ABCD 中，AB ∥CD ，AB ＝2CD ，E 为PB 的中点．(1)求证：CE ∥平面PAD ；(2)在线段AB 上是否存在一点F ，使得平面PAD ∥平面CEF ？若存在，证明你的结论，若不存在，请说明理由．3如图，在四棱锥P －ABCD 中，平面PAC ⊥平面ABCD ，且PA ⊥AC ，PA ＝AD ＝2，四边形ABCD 满足BC ∥AD ，AB ⊥AD ，AB ＝BC ＝1.点E ，F 分别为侧棱PB ，PC 上的点，且PE PB ＝PF PC＝λ(λ≠0)． (1)求证：EF ∥平面PAD ；(2)当λ＝12时，求点D 到平面AFB 的距离． 4.如图，四棱柱ABCD －A1B1C1D1的底面ABCD 是正方形．(1)证明：平面A1BD ∥平面CD1B1；(2)若平面ABCD ∩平面B1D1C ＝直线l ，证明：B1D1∥l.5..如图，四边形ABCD 是平行四边形，点P 是平面ABCD 外一点， M 是PC 的中点，在DM 上取一点G ，过G 和AP 作平面交平面BDM 于GH.求证：AP∥GH.6.如图，在四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，PA＝AB＝BC，E是PC的中点．证明：(1)CD⊥AE；(2)PD⊥平面ABE.7.(2018北京通州三模,18)如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,四边形ABCD为正方形,△PAB为等边三角形,E是PB中点,平面AED与棱PC 交于点F.(1)求证:AD∥EF; (2)求证:PB⊥平面AEFD;(3)记四棱锥P-AEFD的体积为V1,四棱锥P-ABCD的体积为V2,直接写出的值.8...如图，在四棱锥P-ABCD中，底面ABCD是∠DAB＝60°且边长为a的菱形，侧面PAD为正三角形，其所在平面垂直于底面ABCD，若G为AD的中点．(1)求证：BG⊥平面PAD；(2)求证：AD⊥PB；(3)若E为BC边的中点，能否在棱PC上找到一点F，使平面DEF⊥平面ABCD？并证明你的结论．9.(2016·高考北京卷)如图，在四棱锥P-ABCD中，PC⊥平面ABCD，AB∥DC，DC⊥AC.(1)求证：DC⊥平面PAC；(2)求证：平面PAB⊥平面PAC；(3)设点E为AB的中点．在棱PB上是否存在点F，使得PA∥平面CEF？说明理由．10..如图，在四棱锥P－ABCD中，底面ABCD是矩形，点E在棱PC上(异于点P，C)，平面ABE与棱PD交于点F.(1)求证：AB∥EF；(2)若AF⊥EF，求证：平面PAD⊥平面ABCD.11..如图，在四棱锥P－ABCD中，PA⊥平面ABCD，PA＝AB＝BC＝3，AD＝CD＝1，∠ADC＝120°，点M是AC与BD的交点，点N在线段PB上，且PN＝1PB.4(1)证明：MN∥平面PDC；(2)求直线MN与平面PAC所成角的正弦值．12..(2016·高考四川卷)如图，在四棱锥P ABCD中，PA⊥CD，AD∥BC，∠ADC＝∠PAB＝90°，BC＝CD＝1AD．2(1)在平面PAD内找一点M，使得直线CM∥平面PAB，并说明理由；(2)证明：平面PAB⊥平面PBD．13．(2016·高考江苏卷)如图，在直三棱柱ABC A1B1C1中，D，E分别为AB，BC的中点，点F在侧棱B1B上，且B1D⊥A1F，A1C1⊥A1B1.求证：(1)直线DE∥平面A1C1F；(2)平面B1DE⊥平面A1C1F.14.【2014,19】如图，三棱柱中，侧面为菱形，的中点为，且平面.（1）证明：（2）若,求三棱柱的高.15.(2017天津,文17)如图,在四棱锥P-ABCD中,AD⊥平面PDC,AD∥ BC, PD⊥PB,AD=1,BC=3,CD=4,PD=2.(1)求异面直线AP 与BC 所成角的余弦值;(2)求证:PD ⊥平面PBC;(3)求直线AB 与平面PBC 所成角的正弦值.16.(2016·高考浙江卷)如图，在三棱台ABC DEF 中，平面BCFE ⊥平面ABC ，∠ACB ＝90°，BE ＝EF ＝FC ＝1，BC ＝2，AC ＝3.(1)求证：BF ⊥平面ACFD ；(2)求直线BD 与平面ACFD 所成角的余弦值．17..(2018·全国Ⅲ)如图，矩形ABCD 所在平面与半圆弧CD 所在平面垂直， M 是CD 上异于C ，D 的点．(1)证明：平面AMD ⊥平面BMC.(2)在线段AM 上是否存在点P ，使得MC ∥平面PBD ？说明理由．立体几何中的翻折问题18...如图(1)，在直角梯形ABCD 中，AD ∥BC ，∠BAD ＝π2，AB ＝BC ＝12AD ＝a ，E 是AD 的中点，O 是AC 与BE 的交点．将△ABE 沿BE 折起到图(2)中△A1BE 的位置，得到四棱锥A1-BCDE.(1)证明：CD ⊥平面A1OC ；(2)当平面A1BE ⊥平面BCDE 时，四棱锥A1-BCDE 的体积为362，求a 的值．19.．如图1，在直角梯形ABCD 中，∠ADC ＝90°，AB ∥CD ，AD ＝CD ＝12AB ＝2， E 为AC 的中点，将△ACD 沿AC 折起，使折起后的平面ACD 与平面ABC 垂直，如图2.在图2所示的几何体D －ABC 中：(1)求证：BC ⊥平面ACD ；(2)点F 在棱CD 上，且满足AD ∥平面BEF ，求几何体F －BCE 的体积．20．如图，长方体ABCD-A1B1C1D1中，AB ＝16，BC ＝10，AA1＝8.点E ，F 分别在A1B1，D1C1上，过点E 、F 的平面α与此长方体的面相交，交线围成一个正方形EFGH.(1)求证：A1E ＝D1F ；(2)判断A1D 与平面α的关系．高三数学立体几何专题(文科)1解析：（Ⅰ）设AC 的中点为O ，连接EO. 在三角形PBD 中，中位线EO//PB ，且EO 在平面AEC 上，所以PB//平面AEC.（Ⅱ）∵AP=1，，，，∴，作AH ⊥PB 角PB 于H ，由题意可知BC ⊥平面PAB ，∴BC ⊥AH ，故AH ⊥平面PBC ．又，故A 点到平面PBC 的距离.2.(1)证明：如图所示，取PA 的中点H ，连接EH ，DH ，因为E 为PB 的中点，所以EH ∥AB ，EH ＝12AB ，又AB ∥CD ，CD ＝12AB ．所以EH ∥CD ，EH ＝CD ，因此四边形DCEH 是平行四边形，所以CE ∥DH ，又DH ⊂平面PAD ，CE ⊄平面PAD ，所以CE ∥平面PAD ．(2)如图所示，取AB 的中点F ，连接CF ，EF ，所以AF ＝12AB ，又CD ＝12AB ，所以AF ＝CD ，又AF ∥CD ，所以四边形AFCD 为平行四边形，所以CF ∥AD ，又CF ⊄平面PAD ，所以CF ∥平面PAD ，由(1)可知CE ∥平面PAD ，又CE ∩CF ＝C ，故平面CEF ∥平面PAD ，故存在AB 的中点F 满足要求．3.(1)证明 ∵PE PB ＝PF PC ＝λ(λ≠0)，∴EF ∥BC.∵BC ∥AD ，∴EF ∥AD. 又EF ⊄平面PAD ，AD ⊂平面PAD ，∴EF ∥平面PAD.(2)解 ∵λ＝12，∴F 是PC 的中点，在Rt △PAC 中，PA ＝2，AC ＝2，∴PC ＝PA2＋AC2＝6，∴PF ＝12PC ＝62.∵平面PAC ⊥平面ABCD ，且平面PAC ∩平面ABCD ＝AC ， PA ⊥AC ，PA ⊂平面PAC ，∴PA ⊥平面ABCD ，∴PA ⊥BC.又AB ⊥AD ，BC ∥AD ，∴BC ⊥AB ，又PA ∩AB ＝A ，PA ，AB ⊂平面PAB ，∴BC ⊥平面PAB ，∴BC ⊥PB ，∴在Rt △PBC 中，BF ＝12PC ＝62. 连接BD ，DF ，设点D 到平面AFB 的距离为d ，在等腰三角形BAF 中，BF ＝AF ＝62，AB ＝1， ∴S △ABF ＝54，又S △ABD ＝1，点F 到平面ABD 的距离为1， ∴由VF －ABD ＝VD －AFB ，得13×1×1＝13×d ×54，解得d ＝455，即点D 到平面AFB 的距离为455. 4.证明 (1)由题设知BB1∥DD1且BB1＝DD1，所以四边形BB1D1D是平行四边形，所以BD∥B1D1.又BD⊄平面CD1B1，B1D1⊂平面CD1B1，所以BD∥平面CD1B1.因为A1D1∥B1C1∥BC且A1D1＝B1C1＝BC，所以四边形A1BCD1是平行四边形，所以A1B∥D1C.又A1B⊄平面CD1B1，D1C⊂平面CD1B1，所以A1B∥平面CD1B1.又因为BD∩A1B＝B，BD，A1B⊂平面A1BD，所以平面A1BD∥平面CD1B1.(2)由(1)知平面A1BD∥平面CD1B1，又平面ABCD∩平面B1D1C＝直线l，平面ABCD∩平面A1BD＝直线BD，所以直线l∥直线BD，在四棱柱ABCD－A1B1C1D1中，四边形BDD1B1为平行四边形，所以B1D1∥BD，所以B1D1∥l.5.连接AC交BD于点O，连接MO，因为PM＝MC，AO＝OC，所以PA∥MO，因为PA⊄平面MBD，MO⊂平面MBD，所以PA∥平面MBD．因为平面PAHG∩平面MBD＝GH，所以AP∥GH.6.[证明] (1)在四棱锥P-ABCD中，因为PA⊥底面ABCD， CD⊂平面ABCD，所以PA⊥CD，因为AC⊥CD，且PA∩AC＝A，所以CD⊥平面PAC，而AE⊂平面PAC，所以CD⊥AE.(2)由PA＝AB＝BC，∠ABC＝60°，可得AC＝PA.因为E是PC的中点，所以AE⊥PC.由(1)知AE⊥CD，且PC∩CD＝C，所以AE⊥平面PCD．而PD⊂平面PCD，所以AE⊥PD．因为PA⊥底面ABCD，所以PA⊥AB．又因为AB⊥AD且PA∩AD＝A，所以AB⊥平面PAD，而PD⊂平面PAD，所以AB⊥PD．又因为AB∩AE＝A，所以PD⊥平面ABE.7.(1)证明因为ABCD为正方形,所以AD∥BC.因为AD⊄平面PBC,BC⊂平面PBC,所以AD∥平面PBC.因为AD⊂平面AEFD,平面AEFD∩平面PBC=EF,所以AD∥EF.(2)证明因为四边形ABCD是正方形,所以AD⊥AB.因为平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,AD⊂平面ABCD,所以AD⊥平面PAB.因为PB⊂平面PAB,所以AD⊥PB.因为△PAB为等边三角形,E是PB中点,所以PB⊥AE.因为AE⊂平面AEFD,AD⊂平面AEFD,AE∩AD=A,所以PB⊥平面AEFD.(3)解由(1)知,V1=VC-AEFD,VE-ABC=VF-ADC=VC-AEFD=V1,∴VBC-AEFD=V1,则VP-ABCD=V1+V1=V1,∴.8.[解] (1)证明：在菱形ABCD中，∠DAB＝60°，G为AD的中点，所以BG⊥AD．又平面PAD⊥平面ABCD，平面PAD∩平面ABCD＝AD，所以BG⊥平面PAD．(2)证明：如图，连接PG.因为△PAD为正三角形，G为AD的中点，所以PG⊥AD．由(1)知，BG⊥AD，又PG∩BG＝G，所以AD⊥平面PGB．因为PB⊂平面PGB，所以AD⊥PB．(3)当F为PC的中点时，满足平面DEF⊥平面ABCD．证明如下：取PC的中点F，连接DE、EF、DF.在△PBC中，FE∥PB，在菱形ABCD中，GB∥DE.而FE⊂平面DEF，DE⊂平面DEF，EF∩DE＝E，PB⊂平面PGB，GB⊂平面PGB，PB∩GB＝B，所以平面DEF∥平面PGB．因为BG⊥平面PAD，PG⊂平面PAD，所以BG⊥PG.又因为PG⊥AD，AD∩BG＝G，所以PG⊥平面ABCD．又PG⊂平面PGB，所以平面PGB⊥平面ABCD，所以平面DEF⊥平面ABCD．9.【解】(1)证明：因为PC⊥平面ABCD，所以PC⊥DC.又因为DC⊥AC，且PC∩AC＝C，所以DC⊥平面PAC.(2)证明：因为AB∥DC，DC⊥AC，所以AB⊥AC.因为PC⊥平面ABCD，所以PC⊥AB．又因为PC∩AC＝C，所以AB⊥平面PAC.又AB⊂平面PAB，所以平面PAB⊥平面PAC.(3)棱PB上存在点F，使得PA∥平面CEF.理由如下：如图，取PB中点F，连接EF，CE，CF.又因为E为AB的中点，所以EF∥PA.又因为PA⊄平面CEF，且EF⊂平面CEF，所以PA∥平面CEF.10.证明(1)因为四边形ABCD是矩形，所以AB∥CD.又AB⊄平面PDC，CD⊂平面PDC，所以AB∥平面PDC，又因为AB⊂平面ABE，平面ABE∩平面PDC＝EF，所以AB∥EF.(2)因为四边形ABCD是矩形，所以AB⊥AD.因为AF⊥EF，(1)中已证AB∥EF，所以AB⊥AF.又AB ⊥AD ，由点E 在棱PC 上(异于点C)，所以点F 异于点D ，所以AF ∩AD ＝A ，AF ，AD ⊂平面PAD ，所以AB ⊥平面PAD ，又AB ⊂平面ABCD ，所以平面PAD ⊥平面ABCD.11.(1)证明因为AB ＝BC ，AD ＝CD ，所以BD 垂直平分线段AC.又∠ADC ＝120°，所以MD ＝12AD ＝12，AM ＝32.所以AC ＝ 3. 又AB ＝BC ＝3，所以△ABC 是等边三角形，所以BM ＝32，所以BM MD ＝3，又因为PN ＝14PB ，所以BM MD ＝BN NP＝3，所以MN ∥PD. 又MN ⊄平面PDC ，PD ⊂平面PDC ，所以MN ∥平面PDC.(2)解因为PA ⊥平面ABCD ，BD ⊂平面ABCD ，所以BD ⊥PA ，又BD ⊥AC ，PA ∩AC ＝A ，PA ，AC ⊂平面PAC ，所以BD ⊥平面PAC.由(1)知MN ∥PD ，所以直线MN 与平面PAC 所成的角即直线PD 与平面PAC 所成的角，故∠DPM 即为所求的角．在Rt △PAD 中，PD ＝2，所以sin ∠DPM ＝DM DP ＝122＝14，所以直线MN 与平面PAC 所成角的正弦值为14. 12.【解】 (1)取棱AD 的中点M(M ∈平面PAD)，点M 即为所求的一个点．理由如下：因为AD ∥BC ，BC ＝12AD ，所以BC ∥AM ，且BC ＝AM ，所以四边形AMCB 是平行四边形，从而CM ∥AB ．又AB ⊂平面PAB ，CM ⊄平面PAB ，所以CM ∥平面PAB ．(说明：取棱PD 的中点N ，则所找的点可以是直线MN 上任意一点)(2)证明：由已知，PA ⊥AB ，PA ⊥CD ，因为AD ∥BC ，BC ＝12AD ，所以直线AB 与CD 相交．所以PA ⊥平面ABCD ，从而PA ⊥BD ．连接BM ，因为AD ∥BC ，BC ＝12AD ，所以BC ∥MD ，且BC ＝MD ．所以四边形BCDM 是平行四边形．所以BM ＝CD ＝12AD ，所以BD ⊥AB ．又AB ∩AP ＝A ，所以BD ⊥平面PAB ．又BD ⊂平面PBD ，所以平面PAB ⊥平面PBD ．13.[证明] (1)在直三棱柱ABC A1B1C1中，A1C1∥AC.在△ABC 中，因为D ，E 分别为AB ，BC 的中点，所以DE ∥AC ，于是DE ∥A1C1.又DE ⊄平面A1C1F ，A1C1⊂平面A1C1F ，所以直线DE ∥平面A1C1F.(2)在直三棱柱ABC A1B1C1中，A1A ⊥平面A1B1C1.因为A1C1⊂平面A1B1C1，所以A1A ⊥A1C1.又A1C1⊥A1B1，A1A ⊂平面ABB1A1，A1B1⊂平面ABB1A1，A1A∩A1B1＝A1，所以A1C1⊥平面ABB1A1.因为B1D ⊂平面ABB1A1，所以A1C1⊥B1D ．又B1D ⊥A1F ，A1C1⊂平面A1C1F ，A1F ⊂平面A1C1F ，A1C1∩A1F ＝A1，所以B1D ⊥平面A1C1F.因为直线B1D ⊂平面B1DE ，所以平面B1DE ⊥平面A1C1F14.证明：(Ⅰ)连接 BC1，则O 为B1C 与BC1的交点，∵AO ⊥平面BB1C1C. ∴AO ⊥B1C ， …2分因为侧面BB1C1C为菱形，∴BC1⊥B1C，…4分∴BC1⊥平面ABC1，∵AB平面ABC1，故B1C⊥AB.…6分(Ⅱ)作OD⊥BC，垂足为D，连结AD，∵AO⊥BC，∴BC⊥平面AOD，又BC平面ABC，∴平面ABC⊥平面AOD，交线为AD，作OH⊥AD，垂足为H，∴OH⊥平面ABC. …9分∵∠CBB1=60°，所以ΔCBB1为等边三角形，又BC=1，可得OD=，由于AC⊥AB1，∴，∴，由OH·AD=OD·OA，可得OH=，又O为B1C的中点，所以点B1到平面ABC的距离为，所以三棱柱ABC-A1B1C1的高高为。

立体几何测试题(文科).docx

立体几何文科试题一、选择题：本大题共12 小题，在每小题给出的四个选项中，只有一项是符合题目要求的．1、设有直线m、n和平面、 . 下列四个命题中，正确的是( )A. 若m∥ , n∥ , 则m∥nB. 若m, n, m∥ , n∥ , 则∥C. 若， m, 则mD. 若， m， m, 则m∥2、已知直线 l , m与平面，，满足I l，l //， m和 m，则有A．且 l m B．且 m //C． m // 且 l m D． // 且r0,1,r r r r3.若a 1 ， b1,1,0 ，且a b a ，则实数的值是（）A .－ 1 B.0 C.1 D.－ 24、已知平面α⊥平面β，α∩β= l ，点 A∈α， A l，直线 AB∥ l ，直线 AC⊥l，直线 m∥α， m∥β，则下列四种位置关系中，不一定成立的是（）．．．A. AB∥ mB. AC⊥ mC. AB∥βD. AC⊥β5一个几何体的三视图及长度数据如图，则几何体的表面积与体积分别为8、某几何体的三视图如图所示，当 a b 取最大值时，这个几何体的体积为（A．1B．1C．2D．163329、已知A, B,C , D在同一个球面上 , AB平面 BCD, BC CD , 若 AB6, AC球面距离是（）A. B.4253C. D.33310、四面体ABCD的外接球球心在CD 上，且 CD 2，AB 3 ，在外接球面上AππC．2πD．5πA．B．633611、半径为 2cm的半圆纸片做成圆锥放在桌面上，一阵风吹倒它，它的最高处距桌面（A． 4cm B． 2cm C．23cm D．3cm12、有一正方体，六个面上分别写有数字1、 2、 3、 4、 5、 6，有三个人从不同的角3 的对面的数字为 m，4 的对面的数字为 n，那么 m+n 的值为（）A．3B． 7C． 8D． 11A 72,3B 82，3C 73D 832，2,22二．填空题：本大题共 4 个小题。

高中数学立体几何大题练习(文科)

立体几何大题练习（文科）：1．如图，在四棱锥S﹣ABCD中，底面ABCD是梯形，AB∥DC，∠ABC=90°，AD=SD，BC=CD=，侧面SAD⊥底面ABCD．（1）求证：平面SBD⊥平面SAD；（2）若∠SDA=120°，且三棱锥S﹣BCD的体积为，求侧面△SAB的面积．【分析】（1）由梯形ABCD，设BC=a，则CD=a，AB=2a，运用勾股定理和余弦定理，可得AD，由线面垂直的判定定理可得BD⊥平面SAD，运用面面垂直的判定定理即可得证；（2）运用面面垂直的性质定理，以及三棱锥的体积公式，求得BC=1，运用勾股定理和余弦定理，可得SA，SB，运用三角形的面积公式，即可得到所求值．【解答】（1）证明：在梯形ABCD中，AB∥DC，∠ABC=90°，BC=CD=，设BC=a，则CD=a，AB=2a，在直角三角形BCD中，∠BCD=90°，可得BD=a，∠CBD=45°，∠ABD=45°，由余弦定理可得AD==a，则BD⊥AD，由面SAD⊥底面ABCD．可得BD⊥平面SAD，又BD⊂平面SBD，可得平面SBD⊥平面SAD；（2）解：∠SDA=120°，且三棱锥S﹣BCD的体积为，由AD=SD=a，在△SAD中，可得SA=2SDsin60°=a，△SAD的边AD上的高SH=SDsin60°=a，由SH⊥平面BCD，可得×a××a2=，解得a=1，由BD⊥平面SAD，可得BD⊥SD，SB===2a，又AB=2a，在等腰三角形SBA中，边SA上的高为=a，则△SAB的面积为×SA×a=a=．【点评】本题考查面面垂直的判定定理的运用，注意运用转化思想，考查三棱锥的体积公式的运用，以及推理能力和空间想象能力，属于中档题．2．如图，在三棱锥A﹣BCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，点E、F（E与A、D不重合）分别在棱AD，BD上，且EF⊥AD．求证：（1）EF∥平面ABC；（2）AD⊥AC．【分析】（1）利用AB∥EF及线面平行判定定理可得结论；（2）通过取线段CD上点G，连结FG、EG使得FG∥BC，则EG∥AC，利用线面垂直的性质定理可知FG⊥AD，结合线面垂直的判定定理可知AD⊥平面EFG，从而可得结论．【解答】证明：（1）因为AB⊥AD，EF⊥AD，且A、B、E、F四点共面，所以AB∥EF，又因为EF⊂平面ABC，AB⊂平面ABC，所以由线面平行判定定理可知：EF∥平面ABC；（2）在线段CD上取点G，连结FG、EG使得FG∥BC，则EG∥AC，因为BC⊥BD，FG∥BC，所以FG⊥BD，又因为平面ABD⊥平面BCD，所以FG⊥平面ABD，所以FG⊥AD，又因为AD⊥EF，且EF∩FG=F，所以AD⊥平面EFG，所以AD⊥EG，故AD⊥AC．【点评】本题考查线面平行及线线垂直的判定，考查空间想象能力，考查转化思想，涉及线面平行判定定理，线面垂直的性质及判定定理，注意解题方法的积累，属于中档题．3．如图，在三棱柱ABC﹣A1B1C1中，CC1⊥底面ABC，AC⊥CB，点M和N分别是B1C1和BC的中点．（1）求证：MB∥平面AC1N；（2）求证：AC⊥MB．【分析】（1）证明MC1NB为平行四边形，所以C1N∥MB，即可证明MB∥平面AC1N；（2）证明AC⊥平面BCC1B1，即可证明AC⊥MB．【解答】证明：（1）证明：在三棱柱ABC﹣A1B1C1中，因为点M，N分别是B1C1，BC的中点，所以C1M∥BN，C1M=BN．所以MC1NB为平行四边形．所以C1N∥MB．因为C1N⊂平面AC1N，MB⊄平面AC1N，所以MB∥平面AC1N；（2）因为CC1⊥底面ABC，所以AC⊥CC1．因为AC⊥BC，BC∩CC1=C，所以AC⊥平面BCC1B1．因为MB⊂平面BCC1B1，所以AC⊥MB．【点评】本题考查线面平行的判定，考查线面垂直的判定与性质，考查学生分析解决问题的能力，属于中档题．4．如图，在四棱锥P﹣ABCD中，底面ABCD为直角梯形，AD||BC，PD⊥底面ABCD，∠ADC=90°，AD=2BC，Q为AD的中点，M为棱PC的中点．（Ⅰ）证明：PA∥平面BMQ；（Ⅰ）已知PD=DC=AD=2，求点P到平面BMQ的距离．【分析】（1）连结AC交BQ于N，连结MN，只要证明MN∥PA，利用线面平行的判定定理可证；（2）由（1）可知，PA∥平面BMQ，所以点P到平面BMQ的距离等于点A到平面BMQ的距离．【解答】解：（1）连结AC交BQ于N，连结MN，因为∠ADC=90°，Q为AD的中点，所以N为AC的中点．…（2分）当M为PC的中点，即PM=MC时，MN为△PAC的中位线，故MN∥PA，又MN⊂平面BMQ，所以PA∥平面BMQ．…（5分）（2）由（1）可知，PA∥平面BMQ，所以点P到平面BMQ的距离等于点A到平面BMQ的距离，所以V P=V A﹣BMQ=V M﹣ABQ，﹣BMQ取CD的中点K，连结MK，所以MK∥PD，，…（7分）又PD⊥底面ABCD，所以MK⊥底面ABCD．又，PD=CD=2，所以AQ=1，BQ=2，，…（10分）=V A﹣BMQ=V M﹣ABQ=.，…（11分）所以V P﹣BMQ则点P到平面BMQ的距离d=…（12分）【点评】本题考查了线面平行的判定定理的运用以及利用三棱锥的体积求点到直线的距离．5．如图，在直三棱柱ABC﹣A1B1C1中，BC⊥AC，D，E分别是AB，AC的中点．（1）求证：B1C1∥平面A1DE；（2）求证：平面A1DE⊥平面ACC1A1．【分析】（1）证明B1C1∥DE，即可证明B1C1∥平面A1DE；（2）证明DE⊥平面ACC1A1，即可证明平面A1DE⊥平面ACC1A1．【解答】证明：（1）因为D，E分别是AB，AC的中点，所以DE∥BC，…（2分）又因为在三棱柱ABC﹣A1B1C1中，B1C1∥BC，所以B1C1∥DE…（4分）又B1C1⊄平面A1DE，DE⊂平面A1DE，所以B1C1∥平面A1DE…（6分）（2）在直三棱柱ABC﹣A1B1C1中，CC1⊥底面ABC，又DE⊂底面ABC，所以CC1⊥DE…（8分）又BC⊥AC，DE∥BC，所以DE⊥AC，…（10分）又CC1，AC⊂平面ACC1A1，且CC1∩AC=C，所以DE⊥平面ACC1A1…（12分）又DE⊂平面A1DE，所以平面A1DE⊥平面ACC1A1…（14分）【点评】本题考查线面平行、线面垂直、面面垂直的判定，考查学生分析解决问题的能力，属于中档题．6．在四棱锥P﹣ABCD中，PC⊥底面ABCD，M，N分别是PD，PA的中点，AC⊥AD，∠ACD=∠ACB=60°，PC=AC．（1）求证：PA⊥平面CMN；（2）求证：AM∥平面PBC．【分析】（1）推导出MN∥AD，PC⊥AD，AD⊥AC，从而AD⊥平面PAC，进而AD ⊥PA，MN⊥PA，再由CN⊥PA，能证明PA⊥平面CMN．（2）取CD的中点为Q，连结MQ、AQ，推导出MQ∥PC，从而MQ∥平面PBC，再求出AQ∥平面，从而平面AMQ∥平面PCB，由此能证明AM∥平面PBC．【解答】证明：（1）∵M，N分别为PD、PA的中点，∴MN为△PAD的中位线，∴MN∥AD，∵PC⊥底面ABCD，AD⊂平面ABCD，∴PC⊥AD，又∵AD⊥AC，PC∩AC=C，∴AD⊥平面PAC，∴AD⊥PA，∴MN⊥PA，又∵PC=AC，N为PA的中点，∴CN⊥PA，∵MN∩CN=N，MN⊂平面CMN，CM⊂平面CMN，∴PA⊥平面CMN．解（2）取CD的中点为Q，连结MQ、AQ，∵MQ是△PCD的中位线，∴MQ∥PC，又∵PC⊂平面PBC，MQ⊄平面PBC，∴MQ∥平面PBC，∵AD⊥AC，∠ACD=60°，∴∠ADC=30°．∴∠DAQ=∠ADC=30°，∴∠QAC=∠ACQ=60°，∴∠ACB=60°，∴AQ∥BC，∵AQ⊄平面PBC，BC⊂平面PBC，∴AQ∥平面PBC，∵MQ∩AQ=Q，∴平面AMQ∥平面PCB，∵AM⊂平面AMQ，∴AM∥平面PBC．【点评】本题考查线面垂直、线面平行的证明，考查空间中线线、线面、面面间的位置关系，考查推理论证能力、运算求解能力、空间想象能力，考查化归与转化思想、数形结合思想、函数与方程思想，是中档题．7．如图，在四棱锥P﹣ABCD中，底面ABCD是边长为2的正方形，侧面PAD⊥底面ABCD，且PA=PD=AD，E、F分别为PC、BD的中点．（1）求证：EF∥平面PAD；（2）求证：面PAB⊥平面PDC．【分析】（1）连接AC，则F是AC的中点，E为PC 的中点，证明EF∥PA，利用直线与平面平行的判定定理证明EF∥平面PAD；（2）先证明CD⊥PA，然后证明PA⊥PD．利用直线与平面垂直的判定定理证明PA⊥平面PCD，最后根据面面垂直的判定定理即可得到面PAB⊥面PDC．【解答】证明：（1）连接AC，由正方形性质可知，AC与BD相交于BD的中点F，F也为AC中点，E为PC中点．所以在△CPA中，EF∥PA，又PA⊂平面PAD，EF⊄平面PAD，所以EF∥平面PAD；（2）平面PAD⊥平面ABCD平面PAD∩面ABCD=AD⇒CD⊥平面PAD⇒CD⊥PA正方形ABCD中CD⊥ADPA⊂平面PADCD⊂平面ABCD又，所以PA2+PD2=AD2所以△PAD是等腰直角三角形，且，即PA⊥PD．因为CD∩PD=D，且CD、PD⊂面PDC所以PA⊥面PDC又PA⊂面PAB，所以面PAB⊥面PDC．【点评】本题考查直线与平面垂直的判定，直线与平面平行的判定的应用，考查逻辑推理能力．8．如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD为菱形，且PA=AD=2，BD=2，E、F分别为AD、PC中点．（1）求点F到平面PAB的距离；（2）求证：平面PCE⊥平面PBC．【分析】（1）取PB的中点G，连接FG、AG，证得底面ABCD为正方形．再由中位线定理可得FG∥AE且FG=AE，四边形AEFG是平行四边形，则AG∥FE，运用线面平行的判定定理可得EF∥平面PAB，点F与点E到平面PAB的距离相等，运用线面垂直的判定和性质，证得AD⊥平面PAB，即可得到所求距离；（2）运用线面垂直的判定和性质，证得BC⊥平面PAB，EF⊥平面PBC，再由面面垂直的判定定理，即可得证．【解答】（1）解：如图，取PB的中点G，连接FG、AG，因为底面ABCD为菱形，且PA=AD=2，，所以底面ABCD为正方形．∵E、F分别为AD、PC中点，∴FG∥BC，AE∥BC，，，∴FG∥AE且FG=AE，∴四边形AEFG是平行四边形，∴AG∥FE，∵AG⊂平面PAB，EF⊄平面PAB，∴EF∥平面PAB，∴点F与点E到平面PAB的距离相等，由PA⊥平面ABCD，可得PA⊥AD，又AD⊥AB，PA∩AB=A，AD⊥平面PAB，则点F到平面PAB的距离为EA=1．（2）证明：由（1）知AG⊥PB，AG∥EF，∵PA⊥平面ABCD，∴BC⊥PA，∵BC⊥AB，AB∩BC=B，∴BC⊥平面PAB，由AG⊂平面PAB，∴BC⊥AG，又∵PB∩BC=B，∴AG⊥平面PBC，∴EF⊥平面PBC，∵EF⊂平面PCE，∴平面PCE⊥平面PBC．【点评】本题考查空间点到平面的距离，注意运用转化思想，考查线面平行和垂直的判定和性质，以及面面垂直的判定，熟练掌握定理的条件和结论是解题的关键，属于中档题．9．在四棱锥P﹣ABCD中，底面ABCD为直角梯形，∠BAD=∠ADC=90°，DC=2AB=2AD，BC⊥PD，E，F分别是PB，BC的中点．求证：（1）PC∥平面DEF；（2）平面PBC⊥平面PBD．【分析】（1）由中位线定理可得PC∥EF，故而PC∥平面DEF；（2）由直角梯形可得BC⊥BD，结合BC⊥PD得出BC⊥平面PBD，于是平面PBC ⊥平面PBD．【解答】证明：（1）∵E，F分别是PB，BC的中点，∴PC∥EF，又PC⊄平面DEF，EF⊂平面DEF，∴PC∥平面DEF．（2）取CD的中点M，连结BM，则AB DM，又AD⊥AB，AB=AD，∴四边形ABMD是正方形，∴BM⊥CD，BM=CM=DM=1，BD=，∴BC=，∴BD2+BC2=CD2，∴BC⊥BD，又BC⊥PD，BD∩PD=D，∴BC⊥平面PBD，又BC⊂平面PBC，∴平面PBC⊥平面PBD．【点评】本题考查了线面平行，面面垂直的判定，属于中档题．10．如图，在三棱锥A﹣BCD中，E，F分别为BC，CD上的点，且BD∥平面AEF．（1）求证：EF∥平ABD面；（2）若AE⊥平面BCD，BD⊥CD，求证：平面AEF⊥平面ACD．【分析】（1）利用线面平行的性质可得BD∥EF，从而得出EF∥平面ABD；（2）由AE⊥平面BCD可得AE⊥CD，由BD⊥CD，BD∥EF可得EF⊥CD，从而有CD⊥平面AEF，故而平面AEF⊥平面ACD．【解答】证明：（1）∵BD∥平面AEF，BD⊂平面BCD，平面BCD∩平面AEF=EF，∴BD∥EF，又BD⊂平面ABD，EF⊄平面ABD，∴EF∥平ABD面．（2）∵AE⊥平面BCD，CD⊂平面BCD，∴AE⊥CD，由（1）可知BD∥EF，又BD⊥CD，∴EF⊥CD，又AE∩EF=E，AE⊂平面AEF，EF⊂平面AEF，∴CD⊥平面AEF，又CD⊂平面ACD，∴平面AEF⊥平面ACD．【点评】本题考查了线面平行、线面垂直的性质，面面垂直的判定，属于中档题．。

立体几何常考题型练习(文科生用)

立体几何常考题型练习(毛艺瑾用)出题人：王春生概念选择题1、设,αβ是两个不同的平面，,l m 是两条不同的直线，以下命题正确的是 A ．若//,//l ααβ,则//l β B ．若,//l ααβ⊥，则l β⊥ C ．若,l ααβ⊥⊥,则//l β D ．若//,l ααβ⊥,则l β⊥2.已知直线m n ,与平面αβ，，下列命题中错误．．的是 A 。

若 m n αα,⊥⊥，则m n // B.若 m n ββ,//⊥，则m n ⊥ C.若 m n αβαβ,,⊥⊥⊥,则m n ⊥D 。

若 m n n α//,⊂，则m α//3。

已知n m ,是两条不重合的直线，α,β是两个不重合的平面，给出下列四个命题:其中正确命题的个数是（1)若βαα⊥,//m ，则β⊥m ； (2)βαβα⊥⊥⊥⊥则且若,,,m n m n ； (3）若αβ⊥,m α⊄，m β⊥,则//m α；（4)若n m ,是异面直线，,//,,//,m m n n αββα⊂⊂则//αβ．A.1B.2 C 。

3 D.4三视图：1．某几何体的三视图如图所示，且该几何体的体积是3，则正视图中的x 的值是A ．2B ．92C ．32D ．3第1题图正视图侧视图x2．某几何体的三视图如图所示，则该几何体的体积为 A ．83B ．103C ．4D ．33．已知某几何体的三视图如图所示，三视图是边长为1的等腰直角三角形和边长为1的正方形，则该几何体的体积为A ．16B ．13C ．12D ．23外接球问题1、某四棱锥的三视图如图所示，则该四棱锥外接球的表面积是A ．172π B ．34πC ．17342π D ．1734π2、一个几何体的三视图如右图所示，则该几何体外接球的表面积为A ．π3B ．π2C ．316πD ．以上都不对1FAEC OBDM3、三棱锥P ABC -中，15AB BC ==，6AC =，PC ⊥平面ABC ，2PC =，则该三棱锥的外接球表面积为 A ．253π B ．252π C ．833π D ．832π几何证明计算题1．如图，AB 为圆O 的直径,点E 、F 在圆O 上,EF AB //，矩形ABCD 的边BC 垂直于圆O 所在的平面，且2=AB ，1==EF AD 。

高三文科数学立体几何综合题训练

ACABCE FP1A 1C 1BBA高三文科数学立体几何综合题训练1.如图，四边形ABCD 与''ABB A 都是边长为a 的正方形，点E 是A A '的中点，'A A ⊥平面ABCD .（I ）求证：C A '//平面BDE ；（II ）求证：平面AC A '⊥平面BDE ．2.如图，在四棱锥ABCD -P 中，底面ABCD 是矩形，侧棱PD ⊥底面ABCD ， DC PD =，E 是PC 的中点，作EF ⊥PB 交PB 于点F . （1）证明：PA ∥平面EDB ；（2）证明：PB ⊥平面EFD .3.在棱长为2的正方体1111D C B A ABCD -中，E 、F 分别为1DD 、DB 的中点。

（1）求证：EF//平面11D ABC ；（2）求证：EF C B 1⊥；（3）求三棱锥EFC B -1的体积V 。

4.在直三棱柱111C B A ABC -中， AC=4,CB=2,AA 1=260=∠ACB ，E 、F 分别是BC C A ,11的中点。

（1）证明：平面⊥AEB 平面C C BB 11；（2）证明：//1F C 平面ABE ；(3)设P 是BE 的中点，求三棱锥F C B P 11-的体积。

5.如图，四边形A B C D 为矩形，AD ⊥平面ABE2,AE EB BC === F 为C E 上的点，且B F ⊥平面AC E ，.BD AC G =（1）求证：A E ⊥平面BC E ；（2）求证：//A E 平面BFD ；（3）求三棱锥E A D C -的体积.6.如图，在侧棱垂直于底面的三棱柱ABC —A 1B 1C 1中，AC=3，AB=5，AA 1=BC=4，点D 是AB 的中点。

（Ⅰ）求证：1AC BC ⊥；（Ⅱ）求证：1//AC 平面CDB 1；（Ⅲ）求三棱锥A 1—B 1CD 的体积。

A 1B 1C 1D 1ABC DE7.正方形AD EF 与梯形A B C D 所在的平面互相垂直, ,//,22AD CD AB CD CD AB AD ⊥==. (Ⅰ)求证：B C B E ⊥；(Ⅱ)在E C 上找一点M ,使得//B M 平面A D E F ,请确定M 点的位置,并给出证明．8.三棱柱111A B C A B C -中，侧棱与底面垂直，90ABC ∠=，12AB BC BB ===， ,M N分别是AB ，1A C 的中点．（Ⅰ）求证：M N ∥平面11BCC B ；（Ⅱ）求证：M N ⊥平面11A B C ；（Ⅲ）求三棱锥M -11A B C 的体积．9.如图,长方体1111D C B A ABCD -中，11==AA AB ,2=AD ,E 是BC 的中点. (Ⅰ)求证：直线//1BB 平面DE D 1； (Ⅱ)求证：平面AE A 1⊥平面DE D 1； (Ⅲ)求三棱锥DE A A 1-的体积.10.如图，P A 垂直于矩形A B C D 所在的平面，AD PA 2==，CD =，E 、F 分别是A B 、P D 的中点。

立体几何大题练习(文科)(含详解)

立体几何大题练习（文科）1．在正三棱柱111ABC A B C -中，点D 是BC 的中点.（1）求证： 1A C 面1AB D ；（2）设M 是棱1CC 上的点，且满足1BM B D ⊥.求证：面1AB D ⊥面ABM .2．直三棱柱111ABC A B C -中， 5AB =， 3AC =， 4BC =，点D 是线段AB 上的动点.（1）当点D 是AB 的中点时，求证： 1AC 平面1B CD ；（2）线段AB 上是否存在点D ，使得平面11ABB A ⊥平面1CDB ？若存在，试求出AD 的长度；若不存在，请说明理由.3．如图，在四棱锥P ABCD -中，底面ABCD 为直角梯形， //AB CD ， AB AD ⊥， 2CD AB ==， PAB ∆与PAD ∆均为等边三角形，点E 为CD 的中点.（1）证明：平面PAE ⊥平面ABCD ；（2）若点F 在线段PC 上且2CF PF =，求三棱锥F BEC -的体积.4．在如图所示的多面体A B C D E 中，已知//AB DE ， AB AD ⊥，ACD ∆是正三角形，22AD DE AB ===， BC = F 是CD 的中点.（1）求证： //AF 平面BCE ；（2）求证：平面BCE ⊥平面CDE ；（3）求D 到平面BCE 的距离.5．如图，在五面体ABCDEF 中，底面ABCD 为正方形， EF DC ，平面ABCD ⊥平面CDEF ， AE CF ⊥.(1)求证： CF DE ⊥；(2)若CF DE =， 24DC EF ==，求五面体ABCDEF 的体积.6．如图，在四棱椎E ABCD -中， AE DE ⊥， CD ⊥平面ADE ， AB ⊥平面ADE ， 6CD DA ==， 2AB =， 3DE =.(1)求证：平面ACE ⊥平面CDE ；(2)在线B 段DE 上是否存在一点F ，使AF 平面BCE ？若存在，求出EF ED的值；若不存在，说明理由.7．如图，在三棱锥P ABCD -中，底面ABCD 为梯形， //,24,3AB CD BD AD ADB π==∠=，点P 在底面ABCD 内的正投影为点M ，且M 为AD 的中点.（1）证明： AB ⊥平面PAD ；（2）若,BC DC PD PB =⊥，求四棱锥P ABCD -的体积.8．如图，四面体PABC 中， PA ⊥平面ABC ， 1PA =， 1AB =， 2AC =，BC =.（1）求四面体PABC 的四个面的面积中，最大的面积是多少？（2）证明：在线段PC 上存在点M ，使得AC BM ⊥，并求PMMC 的值.9．在如图所示的五面体ABCDEF 中，四边形ABCD 为菱形，且60DAB ∠=， //EF 平面ABCD ， 22EA ED AB EF ====， M 为BC 中点.（1）求证： //FM 平面BDE ；（2）若平面ADE ⊥平面ABCD ，求F 到平面BDE 的距离.10．如图，三棱柱111ABC A B C -中，侧面11BB C C 是菱形，其对角线的交点为O ，且1AB AC =， 1AB B C ⊥.⑴ 求证： AO ⊥平面11BB C C ；(2)设1160B BC B AC ∠=∠=︒，若三棱锥1A BCC -的体积为1，求点1C 到平面1ABB 的距离.立体几何大题练习（文科）1．在正三棱柱111ABC A B C -中，点D 是BC 的中点.（1）求证： 1A C 面1AB D ；（2）设M 是棱1CC 上的点，且满足1BM B D ⊥.求证：面1AB D ⊥面ABM .试题解析：（1）设11A B AB O ⋂=，连OD .因为四边形11AA B B 是矩形，∴O 是1A B 的中点.又D 是BC 的中点，∴1AC OD . 又1AC ⊄面1AB D ， OD ⊂面1AB D ， ∴1A C 面1AB D .（2）因为ABC ∆是正三角形， D 是BC 的中点，∴AD BC ⊥.∵平面ABC ⊥面11BB C C ，又平面ABC ⊥面11BB C C BC =， AD ⊂面ABC .∴AD ⊥面11BB C C ，∵BM ⊂面11BB C C ，∴AD BM ⊥.又∵1BM B D ⊥， 1AD B D D ⋂=， AD ， 1B D ⊂面1AB D ，∴BM ⊥面1AB D ，又BM ⊂面ABM ，∴面1AB D ⊥面ABM .2．直三棱柱111ABC A B C -中， 5AB =， 3AC =， 4BC =，点D 是线段AB 上的动点.（1）当点D 是AB 的中点时，求证： 1AC 平面1B CD ；（2）线段AB 上是否存在点D ，使得平面11ABB A ⊥平面1CDB ？若存在，试求出AD 的长度；若不存在，请说明理由.【试题解析】（1）如图，连接1BC ，交1B C 于点E ，连接DE ，则点E 是1BC 的中点，又点D 是AB 的中点，由中位线定理得1DE AC ，因为DE ⊂平面1B CD ， 1AC ⊄平面1B CD ，所以1AC 平面1B CD .（2）当CD AB ⊥时平面11ABB A ⊥平面1CDB .证明：因为1AA ⊥平面ABC ， CD ⊂平面ABC ，所以1AA CD ⊥．又CD AB ⊥， 1AA AB A ⋂=，所以CD ⊥平面11ABB A ，因为CD ⊂平面1CDB ，所以平面11ABB A ⊥平面1CDB ，故点D 满足CD AB ⊥.因为5AB =， 3AC =， 4BC =，所以222AC BC AB +=，故ABC ∆是以角C 为直角的三角形，又CD AB ⊥，所以95AD =.3．如图，在四棱锥P ABCD -中，底面ABCD 为直角梯形， //AB CD ， AB AD ⊥， 2CD AB ==， PAB ∆与PAD ∆均为等边三角形，点E 为CD 的中点.（1）证明：平面PAE ⊥平面ABCD ；（2）若点F 在线段PC 上且2CF PF =，求三棱锥F BEC -的体积.试题解析：（1）证明：连接BD ，由于//AB CD ，点E 为CD 的中点，DE AB =， AB AD ⊥，所以四边形ABED 为正方形，可得BD AE ⊥，设BD 与AE 相交于点O ，又△PAB 与△PAD 均为等边三角形，可得PB PD =，在等腰△PBD 中，点O 为BD 的中点，所以BD PO ⊥，且AE 与PO 相交于点O ，可得BD ⊥平面PAE ，又BD ⊂平面ABCD ，所以平面PAE ⊥平面ABCD ．（2）由2CD AB ==，△PAB 与△PAD 均为等边三角形，四边形ABED 为正方形， BD 与AE 相交于点O ，可知3OA OP ==， PA =PO AO ⊥，又平面PAE ⊥平面ABCD ，所以PO ⊥平面ABCD ，设点F 到平面BCE 的距离为h ，又2CF PF =，所以223h PO =⋅=，BEC S ∆= 12BE CE ⋅⋅= 192⨯=， F BEC V -= 13BCE S h ∆⋅⋅= 19263⨯⨯=，所以，三棱锥F BEC -的体积为6． 4．在如图所示的多面体A B C D E 中，已知//AB DE ， AB AD ⊥， ACD ∆是正三角形，22AD DE AB ===， BC = F 是CD 的中点.（1）求证： //AF 平面BCE ；（2）求证：平面BCE ⊥平面CDE ；（3）求D 到平面BCE 的距离.【试题解析】（Ⅰ）取CE 的中点M ，连接,BM MF ，因F 为CD 的中点，所以1//2MF ED ，又AB // 12ED , 所以//MF AB ，四边形ABMF 为平行四边形，所以MB//AF ,因为BM ⊂平面BCE ， AF ⊄平面BCE ，所以//AF 平面.BCE（Ⅱ）因为ACD ∆是正三角形，所以2AC AD CD ===,在ABC ∆中， 1,2,AB AC BC ===所以222AB AC BC +=，故AB AC ⊥，∴DE ⊥AC ，又DE ⊥AD ,AC∩AD=A∴DE ⊥平面ACD∴DE ⊥AF,又AF ⊥CD ，由（Ⅰ）得BM ∥AF∴DE ⊥BM, BM ⊥CD ，DE∩CD=D∴BM ⊥平面CDE ，BM ⊂平面BCE∴平面BCE ⊥平面CDE（Ⅲ）连接DM ，由于DE =DC∴DM ⊥CE由（Ⅱ）知，平面BCE ⊥平面CDE ，∴DM ⊥平面BCE所以DM 为D 到平面BCE 的距离，DM所以D 到平面BCE5．如图，在五面体ABCDEF 中，底面ABCD 为正方形， EF DC ，平面ABCD ⊥平面CDEF ， AE CF ⊥.(1)求证： CF DE ⊥；(2)若CF DE =， 24DC EF ==，求五面体ABCDEF 的体积.试题解析：（Ⅰ）因为平面ABCD ⊥平面CDEF ，平面ABCD ∩平面CDEF ＝CD ，AD ⊥CD ，所以AD ⊥平面CDEF ，又CF ⊂平面CDEF ，则AD ⊥CF ．又因为AE ⊥CF ，AD ∩AE ＝A ，所以CF ⊥平面AED ，DE ⊂平面AED ，从而有CF ⊥DE ．（Ⅱ）连接FA ，FD ，过F 作FM ⊥CD 于M ，因为平面ABCD ⊥平面CDEF 且交线为CD ，FM ⊥CD ，所以FM ⊥平面ABCD ．因为CF ＝DE ，DC ＝2EF ＝4，且CF ⊥DE ，所以FM ＝CM ＝1，所以五面体的体积V ＝V F －ABCD ＋V A －DEF ＝＋＝．6．如图，在四棱椎E ABCD -中， AE DE ⊥， CD ⊥平面ADE ， AB ⊥平面ADE ， 6CD DA ==， 2AB =， 3DE =.(1)求证：平面ACE ⊥平面CDE ；(2)在线段DE 上是否存在一点F ，使AF 平面BCE ？若存在，求出EF ED的值；若不存在，说明理由. 解析：(1)证明：因为CD ⊥平面ADE ， AE ⊂平面ADE ，所以CD AE ⊥，又因为AE DE ⊥， CD DE D ⋂=，所以AE ⊥平面CDE ，又因为AE ⊂平面ACE ，所以平面ACE ⊥平面CDE .(2)结论：在线段DE 上存在一点F ，且13EF ED =，使AF 平面BCE . 解：设F 为线段DE 上一点，且13EF ED =，过点F 作FM CD 交CE 于M ，则13FM CD =. 因为CD ⊥平面ADE ， AB ⊥平面ADE ，所以CD AB .又因为3CD AB =，所以MF AB =， FM AB ，所以四边形ABMF 为平行四边形，则AF BM . 又因为AF ⊄平面BCE ， BM ⊂平面BCE ，所以AF 平面BCE .7．如图，在三棱锥P ABCD -中，底面ABCD 为梯形， //,24,3AB CD BD AD ADB π==∠=，点P 在底面ABCD 内的正投影为点M ，且M 为AD 的中点.（1）证明： AB ⊥平面PAD ；（2）若,BC DC PD PB =⊥，求四棱锥P ABCD -的体积.试题解析：（1）2,4,3AD BD ADB π==∠=，由余弦定理得， 222AB BD AD AB =∴=+，故AB AD ⊥又点P 在底面ABCD 内的正投影为点M ， PM ∴⊥平面ABD ，又AB ⊂平面ABDPM AB ∴⊥，又,,PM AD M PM AD ⋂=⊂平面PAD ， AB PAD ∴⊥（2）连接PM ⊥平面,ABD AD ⊂平面,ABD PM AD ∴⊥又M 为AD 的中点， 1MD AM ∴==设PM h =，则PD BM PB =====222PD PB PD PB BD ⊥∴+=，即2211316,1h h h +++=∴=//,AB CD AB AD CD AD ⊥∴⊥，又3ADB π∠=∴在等腰BCD ∆中， 1,,cos 2662BC DC CDB CD BD ππ=∠=∴==,3CD ∴=∴梯形ABCD 的面积为122⨯⨯=⎝113P ABCD V -∴==8．如图，四面体PABC 中， PA ⊥平面ABC ， 1PA =， 1AB =， 2AC =， BC =.（1）求四面体PABC 的四个面的面积中，最大的面积是多少？（2）证明：在线段PC 上存在点M ，使得AC BM ⊥，并求PM MC 的值. 试题解析：（1）由题设AB ＝1，AC ＝2，BC可得222AB BC AC +=,所以AB BC ⊥,由PA ⊥平面ABC ，BC 、AB ⊂平面ABC ,所以PA BC ⊥， PA AB ⊥,所以PB =又由于PA∩AB ＝A ，故BC ⊥平面PAB,PB ⊂平面PAB,所以BC PB ⊥,所以ACB ∆， PAC ∆, PAB ∆, PCB ∆均为直角三角形，且PCB ∆的面积最大，12PCB S ∆==．（2）证明：在平面ABC 内，过点B 作BN ⊥AC ，垂足为N ．在平面PAC 内，过点N 作MN ∥PA 交PC 于点M ，连接BM ．由PA ⊥平面ABC 知PA ⊥AC ，所以MN ⊥AC ．由于BN ∩MN ＝N ，故AC ⊥平面MBN ．又BM ⊂平面MBN ，所以AC ⊥BM ．因为ABN ∆与ACB ∆相似， 12AB AB AN AC ⋅==，从而NC ＝AC －AN ＝．由MN ∥PA ，得＝＝．9．在如图所示的五面体ABCDEF 中，四边形ABCD 为菱形，且60DAB ∠=， //EF 平面ABCD ，22EA ED AB EF ====， M 为BC 中点.（1）求证： //FM 平面BDE ；（2）若平面ADE ⊥平面ABCD ，求F 到平面BDE 的距离.试题解析：（1）取CD 中点N ，连接,MN FN ，因为,N M 分别为,CD BC 中点，所以//MN BD ，又BD ⊂平面BDE ，且MN ⊄平面BDE ，所以//MN 平面BDE ，因为//EF 平面ABCD ， EF ⊂平面ABEF ，平面ABCD ⋂平面ABEF AB =，所以//EF AB ．又222AB CD DN EF ====， //AB CD ，所以//EF CD ， EF DN =.所以四边形EFND 为平行四边形.所以//FN ED .又ED ⊂平面BDE 且FN ⊄平面BDE ，所以//FN 平面BDE ，又FN MN N ⋂=，所以平面//MFN 平面BDE .又MF ⊂平面MFN ，所以//FM 平面BDE .（2）由（1）得//FM 平面BDE ，所以F 到平面BDE 的距离等于M 到平面BDE 的距离．取AD 的中点H ，连接,EH BH ，因为四边形ABCD 为菱形，且60DAB ∠=， 2EA ED AB EF ===，所以EH AD ⊥， BH AD ⊥，因为平面ADE ⊥平面ABCD ，平面ADE ⋂平面ABCD AD =，所以EH ⊥平面ABCD ， EH BH ⊥，因为EH BH ==BE =所以12BDE S ∆==，设F 到平面BDE 的距离为h ，又因为11422BDM BCD S S ∆∆===，所以由E BDM M BDE V V --=，得113232h =⨯⨯，解得5h =. 即F 到平面BDE 的距离为5． 10．如图，三棱柱111ABC A B C -中，侧面11BB C C 是菱形，其对角线的交点为O ，且1AB AC =， 1AB B C ⊥.⑴ 求证： AO ⊥平面11BB C C ；(2)设1160B BC B AC ∠=∠=︒，若三棱锥1A BCC -的体积为1，求点1C 到平面1ABB 的距离. 试题解析：（1)证明：∵四边形11BB C C 是菱形，∴11B C BC ⊥,∵11,AB B C AB BC B ⊥⋂=,∴1B C ⊥平面1ABC ，又AO ⊂平面1ABC ，∴1B C AO ⊥．∵1AB AC =, O 是1BC 的中点，∴1AO B C ⊥，∵11B C BC O ⋂=，∴AO ⊥平面11BB C C .(2)设菱形11BB C C 的边长为x ，又160B BC ∠=︒，∴1BB C ∆是等边三角形，则1B C x =．由（1)知1AO B C ⊥，又O 是1B C 的中点， ∴1AB AC =，又160B AC ∠=︒，∴1AB C ∆是等边三角形，则11AC AB B C x ===，在Rt ACO ∆中，AO x ==，∴1131111sin12013328A BCC BCC V S AO x x x x -∆=⋅=⨯⋅⋅⋅=⋅=，解得2x =. 在Rt ABO ∆中，BO x ===，在Rt BCO ∆中，AB x ===11122ABB S AB ∆=⨯==，设点1C 到平面1ABB 的距离为h ，由111111C ABB A BB C A BCC V V V ---===，得111133ABB S h h ∆⋅⋅==，解得h =，即点1C 到平面1ABB.。

高考立体几何文科大题及答案

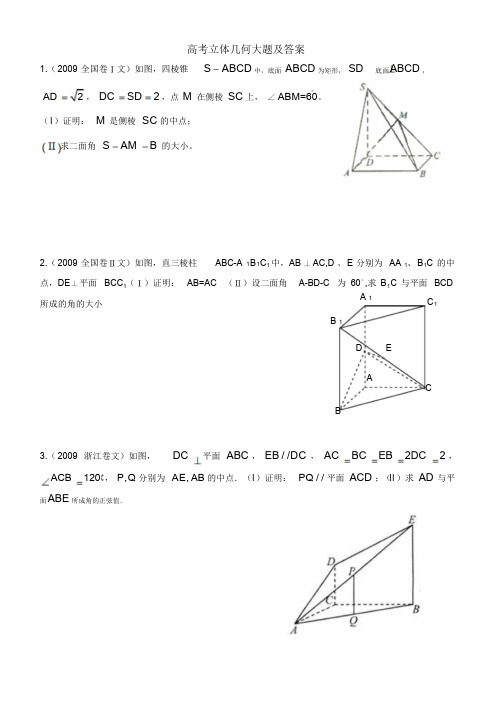
高考立体几何大题及答案1.（2009 全国卷Ⅰ文）如图，四棱锥S ABCD中，底面ABCD 为矩形，SD 底面ABCD ，AD 2 ，DC SD 2，点M 在侧棱SC上，∠ABM=60。

（I）证明：M 是侧棱SC的中点；求二面角S AM B的大小。

2.（2009 全国卷Ⅱ文）如图，直三棱柱ABC-A 1B1C1 中，AB ⊥AC,D 、E 分别为AA 1、B1C 的中点，DE⊥平面BCC1（Ⅰ）证明：AB=AC （Ⅱ）设二面角A-BD-C 为60°,求B1C 与平面BCD所成的角的大小A 1 C1 B 1D EAC B3.（2009 浙江卷文）如图，DC 平面ABC ，EB / /DC ，AC BC EB 2DC 2 ，ACB 120 ，P,Q 分别为AE, AB 的中点．（I）证明：PQ / / 平面ACD ；（II ）求AD 与平面ABE所成角的正弦值．4.（2009 北京卷文）如图，四棱锥P ABCD 的底面是正方形，PD 底面ABCD ，点E 在棱PB 上.（Ⅰ）求证：平面AEC 平面PDB ；（Ⅱ）当PD 2AB 且 E 为PB 的中点时，求AE 与平面PDB 所成的角的大小.5.（2009 江苏卷）如图，在直三棱柱ABC A1B1C1 中，E、F 分别是 A B 、A1C 的中点，点D1在B C 上，A1D B1C1 1 。

求证：（1）EF∥平面ABC ；（2）平面A FD 平面BB1C1C .16.（2009安徽卷文）如图，ABCD的边长为2的正方形，直线l与平面ABCD平行，g和F式l上的两个不同点，且EA=ED，FB=FC，和是平面ABCD内的两点，和都与平面ABCD垂直，（Ⅰ）证明：直线垂直且平分线段AD：（Ⅱ）若∠EAD=∠EAB=60°，EF=2，求多面体ABCDEF的体积。

7.（2009江西卷文）如图，在四棱锥P ABCD中，底面ABCD是矩形，PA平面ABCD，PA AD4，AB2．以BD的中点O为球心、BD为直径的球P面交PD于点M．（1）求证：平面ABM⊥平面PCD；（2）求直线PC与平面ABM所成的角；M（3）求点O到平面ABM的距离．DAOBC8.（2009四川卷文）如图，正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直，△ABE是等腰直角三角形，AB AE,FA FE,AEF45（I）求证：EF平面BCE；（II）设线段CD、AE的中点分别为P、M，求证：PM∥平面BCE（III）求二面角F BD A的大小。

立体几何文科练习题

立体几何文科练习题1. 塔的高度某座塔的阴影长度为30m，同时日照角度为60°。

求塔的高度。

解析：设塔的高度为h，则根据正切函数的定义，有tan 60° = h / 30即√3 = h / 30解得h = 30√3 m2. 球的体积和表面积已知一颗球的直径为12cm，求其体积和表面积。

解析：球的半径为直径的一半，即 r = 12 / 2 = 6 cm球的体积公式为V = (4/3)πr³，代入 r = 6 cm，π取近似值3.14，计算得V ≈ 904.32 cm³球的表面积公式为S = 4πr²，代入 r = 6 cm，π取近似值3.14，计算得S ≈ 452.16 cm²3. 圆台的体积一个圆台的上底半径为5 cm，下底半径为10 cm，高度为15 cm，求圆台的体积。

解析：圆台的体积公式为V = (1/3)πh(r₁² + r₂² + r₁r₂)，其中 h 为高度，r₁、r₂分别为上底半径和下底半径代入 h = 15 cm，r₁ = 5 cm，r₂ = 10 cm，π取近似值3.14，计算得V ≈ 1301.67 cm³4. 正方体的对角线长度一个正方体的边长为a，求其对角线长度。

解析：对角线的长度可以通过勾股定理求解。

正方体的对角线可以看作是一个空间对角线：l = √(a² + a² + a²) = √3a5. 圆锥的斜高一个圆锥的半径为4 cm，母线长度为10 cm，求圆锥的斜高。

解析：圆锥的斜高可以通过勾股定理求解。

将圆锥展开图看作一个直角三角形，斜高即为斜边，母线为直角边，半径为另一直角边。

斜高的长度l = √(10² + 4²) = √116 ≈ 10.77 cm6. 圆柱的体积和侧面积一个圆柱的底面半径为8 m，高度为20 m，求圆柱的体积和侧面积。

文科立体几何模拟试题答案

文科立体几何模拟试题答案一、选择题1. 若一个正方体的棱长为2cm，则其对角线的长度为？A. 2√2 cmB. 2√3 cmC. 4 cmD. √8 cm答案：B2. 一个圆锥的底面半径为3cm，高为4cm，其侧面展开图的扇形的中心角为？A. 90°B. 120°C. 150°D. 180°答案：D3. 一个球的表面积为4πR²，若该球的体积为16π，则其半径R为？A. 2B. 4C. 2√2D. √16答案：A4. 一个圆柱的底面直径为6cm，高为10cm，其侧面积为？A. 60π cm²B. 36π cm²C. 90π cm²D. 180π cm²答案：A5. 一个锥体的底面半径为r，高为h，侧面展开图是一个等腰三角形，其底边长为？A. πrB. 2πrC. √(2h² + r²)D. √(h² + 4r²)答案：D二、填空题1. 一个正方体的体积为64cm³，其棱长为______。

答案：4cm2. 一个球的体积为64π，其表面积为______。

答案：64π cm²3. 一个圆柱的底面半径为5cm，高为12cm，其体积为______。

答案：942π cm³4. 一个锥体的底面半径为3cm，高为6cm，其侧面展开图的扇形的中心角为______。

答案：120°5. 一个正四面体的边长为a，其表面积为______。

答案：√3a²三、解答题1. 一个正方体的棱长为3cm，求其内切球的体积。

解：正方体的内切球即为正方体的对角线所形成的球体，其半径r为正方体棱长的一半，即r = 3/2 cm。

根据球体体积公式V = 4/3πr³，代入r值得到V = 4/3π(3/2)³ = 9π cm³。

2. 一个圆锥的底面半径为2cm，高为5cm，求其侧面展开图的扇形的弧长。

文科立体几何大题训练

文科立体几何大题训练1．如图，四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=AD，∠BAD=∠ABC=90°．（1）证明：直线BC∥平面PAD；（2）若△PCD面积为2，求四棱锥P﹣ABCD的体积．2．如图，在三棱锥P﹣ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA=AB=BC=2，D为线段AC的中点，E为线段PC上一点．（1）求证：PA⊥BD；（2）求证：平面BDE⊥平面PAC；（3）当PA∥平面BDE时，求三棱锥E﹣BCD的体积．3．如图，四棱锥P﹣ABCD中，PA⊥底面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点．（Ⅰ）证明MN∥平面PAB；（Ⅱ）求四面体N﹣BCM的体积．4．如图，在三棱锥P﹣ABC中，PA=PB=AB=2，BC=3，∠ABC=90°，平面PAB⊥平面ABC，D，E分别为AB，AC中点．（1）求证：DE∥平面PBC；（2）求证：AB⊥PE；（3）求三棱锥P﹣BEC的体积．5．如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD是菱形，PA=AB=2，E为PA 的中点，∠BAD=60°．（Ⅰ）求证：PC∥平面EBD；（Ⅱ）求三棱锥P﹣EDC的体积．6．如图，在三棱锥D﹣ABC中，DA=DB=DC，E为AC上的一点，DE⊥平面ABC，F为AB的中点．（Ⅰ）求证：平面ABD⊥平面DEF；（Ⅱ）若AD⊥DC，AC=4，∠BAC=45°，求四面体F﹣DBC的体积．7．如图，四边形ABCD是正方形，平面ABCD⊥平面ABE，AF∥BE，AB⊥BE，AB=BE=2，AF=1．（Ⅰ）求证：AC⊥平面BDE；（Ⅱ）求证：AC∥平面DEF；（III）求三棱锥D﹣FEB的体积．8．如图，四棱锥S﹣ABCD中，底面ABCD是菱形，其对角线的交点为O，且SA=SC，SA⊥BD．（1）求证：SO⊥平面ABCD；（2）设∠BAD=60°，AB=SD=2，P是侧棱SD上的一点，且SB∥平面APC，求三棱锥A﹣PCD 的体积．文科立体几何大题训练参考答案与试题解析一．解答题（共8小题）1．如图，四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=AD，∠BAD=∠ABC=90°．（1）证明：直线BC∥平面PAD；（2）若△PCD面积为2，求四棱锥P﹣ABCD的体积．【解答】（1）证明：四棱锥P﹣ABCD中，∵∠BAD=∠ABC=90°．∴BC∥AD，∵AD⊂平面PAD，BC⊄平面PAD，∴直线BC∥平面PAD；（2）解：四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=AD，∠BAD=∠ABC=90°．设AD=2x，则AB=BC=x，CD=，O是AD的中点，连接PO，OC，CD的中点为：E，连接OE，则OE=，PO=，PE==，△PCD面积为2，可得：=2，即：，解得x=2，PO=2．则V P﹣ABCD=×（BC+AD）×AB×PO==4．2．如图，在三棱锥P﹣ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA=AB=BC=2，D为线段AC的中点，E为线段PC上一点．（1）求证：PA⊥BD；（2）求证：平面BDE⊥平面PAC；（3）当PA∥平面BDE时，求三棱锥E﹣BCD的体积．【解答】解：（1）证明：由PA⊥AB，PA⊥BC，AB⊂平面ABC，BC⊂平面ABC，且AB∩BC=B，可得PA⊥平面ABC，由BD⊂平面ABC，可得PA⊥BD；（2）证明：由AB=BC，D为线段AC的中点，可得BD⊥AC，由PA⊥平面ABC，PA⊂平面PAC，可得平面PAC⊥平面ABC，又平面PAC∩平面ABC=AC，BD⊂平面ABC，且BD⊥AC，即有BD⊥平面PAC，BD⊂平面BDE，可得平面BDE⊥平面PAC；（3）PA∥平面BDE，PA⊂平面PAC，且平面PAC∩平面BDE=DE，可得PA∥DE，又D为AC的中点，可得E为PC的中点，且DE=PA=1，由PA⊥平面ABC，可得DE⊥平面ABC，可得S△BDC=S△ABC=××2×2=1，则三棱锥E﹣BCD的体积为DE•S△BDC=×1×1=．3．如图，四棱锥P﹣ABCD中，PA⊥底面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点．（Ⅰ）证明MN∥平面PAB；（Ⅱ）求四面体N﹣BCM的体积．【解答】证明：（Ⅰ）取BC中点E，连结EN，EM，∵N为PC的中点，∴NE是△PBC的中位线∴NE∥PB，又∵AD∥BC，∴BE∥AD，∵AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，∴BE=BC=AM=2，∴四边形ABEM是平行四边形，∴EM∥AB，∴平面NEM∥平面PAB，∵MN⊂平面NEM，∴MN∥平面PAB．解：（Ⅱ）取AC中点F，连结NF，∵NF是△PAC的中位线，∴NF∥PA，NF==2，又∵PA⊥面ABCD，∴NF⊥面ABCD，如图，延长BC至G，使得CG=AM，连结GM，∵AM CG，∴四边形AGCM是平行四边形，∴AC=MG=3，又∵ME=3，EC=CG=2，∴△MEG的高h=，∴S△BCM===2，∴四面体N﹣BCM的体积V N﹣BCM===．4．如图，在三棱锥P﹣ABC中，PA=PB=AB=2，BC=3，∠ABC=90°，平面PAB⊥平面ABC，D，E分别为AB，AC中点．（1）求证：DE∥平面PBC；（2）求证：AB⊥PE；（3）求三棱锥P﹣BEC的体积．【解答】证明：（1）∵D，E分别为AB，AC的中点，∴DE∥BC，又DE⊄平面PBC，BC⊂平面PBC，∴DE∥平面PBC．（2）连接PD，∵DE∥BC，又∠ABC=90°，∴DE⊥AB，又PA=PB，D为AB中点，∴PD⊥AB，又PD∩DE=D，PD⊂平面PDE，DE⊂平面PDE，∴AB⊥平面PDE，又PE⊂平面PDE，∴AB⊥PE．（3）∵平面PAB⊥平面ABC，平面PAB∩平面ABC=AB，PD⊥AB，PD⊂平面PAB，∴PD⊥平面ABC，∵△PAB是边长为2的等边三角形，∴PD=，∵E是AC的中点，∴．5．如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD是菱形，PA=AB=2，E为PA 的中点，∠BAD=60°．（Ⅰ）求证：PC∥平面EBD；（Ⅱ）求三棱锥P﹣EDC的体积．【解答】（Ⅰ）证明：连接AC，BD，设AC与BD相交于点O，连接OE．由题意知，底面ABCD是菱形，则O为AC的中点，又E为AP的中点，∴OE∥CP，∵OE⊂平面BDE，PC⊄平面BDE，∴PC∥平面BDE；（Ⅱ）解：∵E为PA的中点，∴，∵四边形ABCD是菱形，∴AC⊥BD，又∵PA⊥平面ABCD，∴PA⊥BD，又PA∩AC=A，∴DO⊥平面PAC，即DO是三棱锥D﹣PCE的高，DO=1，则．6．如图，在三棱锥D﹣ABC中，DA=DB=DC，E为AC上的一点，DE⊥平面ABC，F为AB的中点．（Ⅰ）求证：平面ABD⊥平面DEF；（Ⅱ）若AD⊥DC，AC=4，∠BAC=45°，求四面体F﹣DBC的体积．【解答】证明：（Ⅰ）∵DE⊥平面ABC，AB⊂平面ABC，∴AB⊥DE，又F为AB的中点，DA=DB，∴AB⊥DF，DE，DF⊂平面DEF，DE∩DF=D，∴AB⊥平面DEF，又∵AB⊂平面ABD，∴平面ABD⊥平面DEF．（Ⅱ）∵DA=DB=DC，E为AC上的一点，DE⊥平面ABC，∴线段DA、DB、DC在平面ABC的投影EA，EB，EC满足EA=EB=EC∴△ABC为直角三角形，即AB⊥BC由AD⊥DC，AC=4，∠BAC=45°，∴AB=BC=2，DE=2，∴S△FBC==2，∴四面体F﹣DBC的体积V F﹣DBC=V D﹣FBC==．7．如图，四边形ABCD是正方形，平面ABCD⊥平面ABE，AF∥BE，AB⊥BE，AB=BE=2，AF=1．（Ⅰ）求证：AC⊥平面BDE；（Ⅱ）求证：AC∥平面DEF；（III）求三棱锥D﹣FEB的体积．【解答】（Ⅰ）证明：∵四边形ABCD是正方形，∴AC⊥BD．又∵平面ABEF⊥平面ABCD，平面ABEF∩平面ABCD=AB，AB⊥BE，BE⊂平面ABEF，∴BE⊥平面ABCD．又∵AC⊂平面ABCD．∴BE⊥AC，又BE∩BD=B，∴AC⊥平面BDE；（Ⅱ）证明：取DE的中点G，连结OG，FG，∵四边形ABCD为正方形，∴O为BD的中点．则OG∥BE，且．由已知AF∥BE，且，则AF∥OG且AF=OG，∴四边形AOGF为平行四边形，则AO∥FG，即AC∥FG．∵AC⊄平面DEF，FG⊂平面DEF，∴AC∥平面DEF；（Ⅲ）解：∵平面ABCD⊥平面ABEF，四边形ABCD是正方形，平面ABEF∩平面ABCD=AB，∴AD∥BC，AD⊥AB．由（Ⅰ）知，BE⊥平面ABCD，AD⊂平面ABCD，∴BE⊥AD∴AD⊥平面BEF．∴．8．如图，四棱锥S﹣ABCD中，底面ABCD是菱形，其对角线的交点为O，且SA=SC，SA⊥BD．（1）求证：SO⊥平面ABCD；（2）设∠BAD=60°，AB=SD=2，P是侧棱SD上的一点，且SB∥平面APC，求三棱锥A﹣PCD 的体积．【解答】解：（1）证明：∵底面ABCD是菱形；∴对角线BD⊥AC；又BD⊥SA，SA∩AC=A；∴BD⊥平面SAC，SO⊂平面SAC；∴BD⊥SO，即SO⊥BD；又SA=SC，O为AC中点；∴SO⊥AC，AC∩BD=O；∴SO⊥平面ABCD；（2）如图，连接PO；∵SB∥平面APC，SB⊂平面SBD，平面SBD∩平面APC=PO；∴SB∥PO；在△SBD中，O是BD的中点，PO∥SB，∴P是SD的中点；取DO中点，并连接PE，则PE∥SO，SO⊥底面ACD；∴PE⊥底面ACD，且PE=；根据已知条件，Rt△ADO中AD=2，∠DAO=30°，∴DO=1；∴在Rt△SDO中，SD=2，SO=；∴；又；∴V三棱锥A﹣PCD=V三棱锥P﹣ACD=．。

立体几何大题练习(文科)

1．如图，在三棱锥A﹣BCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，点E、F（E与A、D不重合）分别在棱AD，BD上，且EF⊥AD．求证：（1）EF∥平面ABC；（2）AD⊥AC．2．如图，在直三棱柱ABC﹣A1B1C1中，BC⊥AC，D，E是AB，AC的中点．（1）求证：B1C1∥平面A1DE；（2）求证：平面A1DE⊥平面ACC1A1．3．如图，在四棱锥P﹣ABCD中，底面ABCD是边长为2的正方形，侧面PAD⊥底面ABCD，且PA=PD=AD，E、F分别为PC、BD的中点．（1）求证：EF∥平面PAD；（2）求证：面PAB⊥平面PDC．4．如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD为菱形，且PA=AD=2，BD=2，E、F分别为AD、PC中点．（1）求点F到平面PAB的距离；（2）求证：平面PCE⊥平面PBC．5．在四棱锥P﹣ABCD中，底面ABCD为直角梯形，∠BAD=∠ADC=90°，DC=2AB=2AD，BC ⊥PD，E，F分别是PB，BC的中点．求证：（1）PC∥平面DEF；（2）平面PBC⊥平面PBD．6．如图，在三棱锥A ﹣BCD 中，E ，F 分别为BC ，CD 上的点，且BD ∥平面AEF ．（1）求证：EF ∥平ABD 面；（2）若AE ⊥平面BCD ，BD ⊥CD ，求证：平面AEF ⊥平面ACD ．7．已知四棱锥中，⊥平面，是直角梯形，，90º，．（1）求证：⊥；（2）在线段上是否存在一点，使//平面，若存在，指出点的位置并加以证明；若不存在，请说明理由ABCD P -PA ABCD ABCD BC AD //BAD ∠AD BC 2=AB PD PB E AE PCD E。

高三立体几何习题(文科含答案)

23正视图图1侧视图图22 俯视图 2图3立几习题21假设直线l 不平行于平面a ，且l a ∉，则 A ．a 内的所有直线与异面 B ．a 内不存在与l 平行的直线 C ．a 内存在唯一的直线与l 平行 D ．a 内的直线与l 都相交 2.1l ，2l ，3l 是空间三条不同的直线，则以下命题正确的选项是〔A 〕12l l ⊥，23l l ⊥13//l l ⇒〔B 〕12l l ⊥，23//l l ⇒13l l ⊥〔C 〕233////l l l ⇒1l ，2l ，3l 共面〔D 〕1l ，2l ，3l 共点⇒1l ，2l ，3l 共面3．如图1 ~ 3，某几何体的正视图〔主视图〕，侧视图〔左视图〕和俯视图分别是等边三角形，等腰三角形和菱形，则该几何体的体积为 A ．3 B ．4 C ．3 D ．24.某几何体的三视图如下图，则它的体积是〔〕 A.283π- B.83π-D.23π5、如图，在四棱锥ABCD P -中，平面PAD ⊥平面ABCD ，AB=AD ，∠BAD=60°，E 、F 分别是AP 、AD的中点求证：〔1〕直线E F ‖平面PCD ；（2）平面BEF ⊥平面PAD5〔本小题总分值13分〕如图，ABEDFC为多面体，平面ABED与平面ACFD垂直，点O在线段AD上，OD=，△OAB，△OAC，△ODE，△ODF都是正三角形。

OA=，21∥；〔Ⅰ〕证明直线BC EF-的体积.〔Ⅱ〕求棱锥F OBED6.〔本小题共14分〕如图，在四面体PABC中，PC⊥AB，PA⊥BC,点D,E,F,G分别是棱AP,AC,BC,PB的中点.〔Ⅰ〕求证：DE∥平面BCP；〔Ⅱ〕求证：四边形DEFG为矩形；〔Ⅲ〕是否存在点Q，到四面体PABC六条棱的中点的距离相等？说明理由.7．〔本小题总分值12分〕如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，点E在线段AD上，且CE∥AB。

高中文科数学：立体几何专题1

高三文科数学: 立体几何专题一. 选择题:1.圆柱被一个平面截去一部分后与半球（半径为r）组成一个几何体, 该几何体三视图中的正视图和俯视图如图所示, 若该几何体的表面积为16+20π, 则r=（A）1 (B) 2 (C) 4 (D) 82.如图, 网格纸上小正方形的边长为1, 粗线画出的是某几何体的三视图, 则此几何体的体积为（A）6（B）9（C）12（D）183. 在一个几何体的三视图中, 正视图与俯视图如右图所示, 则相应的侧视图可以为4.平面α截球O的球面所得圆的半径为1, 球心O到平面α的距离为, 则此球的体积为（A）6π（B）43π（C）46π（D）63π5. 若m, n是两条不同的直线, α, β是两个不同的平面, 则下列命题不正确的是()A. 若α∥β, m⊥α, 则m⊥βB. 若m∥n, m⊥α, 则n⊥αC．若m∥α, m⊥β, 则α⊥βD．若α∩β＝m, 且n与α, β所成的角相等, 则m⊥n二. 填空题:6.已知正四棱锥的体积为, 底面边长为, 则以为球心, 为半径的球的表面积为________。

7. 已知两个圆锥有公共底面, 且两圆锥的顶点和底面的圆周都在同一个球面上. 若圆锥底面面积是这个球面面积的, 则这两个圆锥中, 体积较小者的高与体积较大者的高的比值为______________.8．已知平面α, β和直线m, 给出条件：①m∥α；②m⊥α；③m⊂α；④α∥β.当满足条件________时, 有m⊥β.(填所选条件的序号)三、解答题:9．如图, 四边形ABCD为菱形, G为AC与BD的交点, BE⊥平面ABCD.（Ⅰ）证明: 平面AEC⊥平面BED；（Ⅱ）若∠ABC=120°, AE⊥EC, 三棱锥E—ACD的体积为, 求该三棱锥的侧面积10. 如图,在四棱锥中,,,,⊥,E和F分别是CD和PC的中点,平面PAD⊥底面ABCD,PA ADBE平面PAD;(3)平面BEF⊥平面PCD 求证:(1)PA⊥底面ABCD;(2)//11. 如图在直棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=3,D是BC的中点,点E在菱BB1上运动.(I) 证明:AD⊥C1E;(II)当异面直线AC,C1E 所成的角为60°时,求三棱锥C1-A2B1E的体积.。

立体几何文科练习题(精品).docx

立体几何1.用斜二测画法画出长为6,宽为4的矩形水平放置的直观图，则该直观图面积为（）A.12B. 24C. 6>/2D. 12^22.设是不同的直线，6Z,”是不同的平面，下列命题中正确的是（）A.若mlla.n ± f3.m Ln ,则a L/3B.若mlla.n±/?,m,则a//”C.若mlla.n ±[3.mlIn ,则a ±D.若ml ta.n ± /3.ml In ,则a 11 /33.如图，棱长为1的正方体ABCD-A^C.D.中，P为线段A.B ±的动点，则下列结论错谖的是A. DC X 1B.平面D.A.P±平面A.APc. ZAPD]的最大值为90° D. AP + PD l的最小值为』2 +1 1 4.一个几何体的三视图如图所示（单位：m）,则该几何体的体积为 m3. : 口2 1正视图侧视图I，1』5.若某几何体的三视图如图所示，则此几何体的体积等于. r* * it,2俯视图6.如图是一个几何体的三视图，则该几何体的体积是7 .如图，一个盛满水的三棱锥容器，不久发现三条侧棱上各有一个小洞D,E,F ,且知SD : DA = SE : EB = CF : FS = 2 :1,若仍用这个容器盛水，则最多可盛水的体积是原来的.8.如图，四边形ABCD为正方形，QA_L平面ABCD, PD〃QA, QA=AB=- PD.⑴证明：PCU平面DCQ；⑵求棱锥Q-ABCD的体积与棱锥P- DCQ的体积的比值.［来7T 9.如图所示的多面体中，ABCD是菱形，3DE尸是矩形，面ABCD, ZBAD = ~.3(1)求证：平面BCF H平面AEQ.(2)若BF = BD = a,求四棱锥A-BQEF的体积。

10.在四棱锥 P —A3CQ 中，底面ABCD为矩形，PD 1 ^ABCD , AB = 1, BC = 2, PD =的,G、F分别为AP、CQ的中点.(1)求证：AD 1 PC；(2)求证：FG〃平面BCP；11.如图，多面体AEDBFC的直观图及三视图如图所示，M,N分别为AF,BC的中点.(1)求证：MN 〃平面CDEF ；(2)求多面体A - CDEF的体积.12.如图，在三棱锥P-ABC中，ZABC = 90°,(1)求证：EFtmABC；(2)求证：平面AEF L平面PAB.P平面ABC , E, F分别为PB, PC的中点.B13.如图,在二棱锥 P—ABC 中，D, E, F 分别为棱 PC, AC, AB 的中点.已知 PAXAC, PA=6, BC=8, DF=5.求证:(1)直线PA〃平面DFE；(2)平面BDE±平面ABC.14.如图.直二棱柱ABC —AiBiCi中，AB= AC,点D、E分别是棱BC, CG上的点(点D不同于点C),且ADXDE, F为BC的中点.求证：(1)平面ADE_L平面BCCB(2)直线AF〃平面ADE.参考答案1. C【解析】试题分析：斜二测法：要求长边，宽减半，直角变为45°角，则面积为：6x2xsin45° = 6& 考点：直观图与立体图的大小关系.2. C【解析】试题分析：此题只要举出反例即可，A,B中由可得nil (3,则可以为任意角度的两平面,A, B均错误.C, D中由n V (3,mll n可得m L (3 ,则有all /3 ,故C正确，D错误.考点：线，面位置关系.3. C【解析】试题分析:g项侦回，「.A正确；"5恤M，.IB正确;当0<A/<g 时，ZAPD］为钝角，3错；将面AA X B与面ABB^沿人3展成平面图形，线段人。

立体几何文科练习题

立体几何文科练习题立体几何文科练习题立体几何是数学中的一个重要分支，它研究的是空间中的图形和体积。

虽然在理科中占据重要地位，但是立体几何也可以在文科中发挥重要作用。

本文将介绍一些立体几何的文科练习题，帮助读者加深对立体几何的理解。

1. 三维建模与艺术立体几何在艺术领域中有着广泛的应用。

请你思考一下，如果你是一位雕塑家，你将如何运用立体几何的知识来设计和制作一件雕塑作品？你可以考虑使用什么样的形状、线条和结构，以及如何使用不同的材料来表达你的创意。

通过这个练习，你可以发现立体几何与艺术之间的联系，以及如何将理论应用于实践。

2. 城市规划与空间布局城市规划是一个复杂而综合的领域，其中立体几何的概念经常被应用。

请你思考一下，如果你是一位城市规划师，你将如何使用立体几何的知识来设计一个城市的空间布局？你可以考虑如何合理利用有限的土地资源，如何设计道路和建筑物的位置，以及如何创造一个舒适和谐的城市环境。

通过这个练习，你可以体会到立体几何在实际问题中的应用，以及如何将理论转化为实践。

3. 数字游戏与谜题立体几何可以被应用于数字游戏和谜题中，这是一个有趣而具有挑战性的练习。

请你设计一个立体几何的数字游戏或谜题，让玩家通过解题来加深对立体几何的理解。

你可以考虑使用不同的图形和体积计算，以及设计不同的难度级别。

通过这个练习，你可以锻炼自己的创造力和逻辑思维能力，同时加深对立体几何的理解。

4. 空间感知与导航立体几何在空间感知和导航中起着重要作用。

请你思考一下，为什么我们能够准确地判断物体的位置和方向？立体几何的概念如何帮助我们在空间中导航？你可以考虑使用平面图、立体图和坐标系来解释这个问题。

通过这个练习，你可以深入理解立体几何在我们日常生活中的应用，以及它对我们空间感知的影响。

通过以上的练习题，我们可以看到立体几何在文科领域中的重要性和应用价值。

无论是艺术、城市规划、数字游戏还是空间感知，立体几何都能为我们提供新的视角和解决问题的方法。

高三数学立体几何专项训练(文科)(教育课资)

2020届高三数学立体几何专题(文科)吴丽康 2019-111.如图，四棱锥P -ABCD 中，底面ABCD 为矩形，P A ⊥平面ABCD ，E 为PD 的点. （Ⅰ）证明：PB // 平面AEC ；（Ⅱ）设AP=1，AD =，三棱锥P -ABD 的体积V =，求A 点到平面PBD 的距离.2. 如图，四棱锥P ABCD 中，AB ∥CD ，AB ＝2CD ，E 为PB 的中点． (1)求证：CE ∥平面P AD ；(2)在线段AB 上是否存在一点F ，使得平面P AD ∥平面CEF ？若存在，证明你的结论，若不存在，请说明理由．3如图，在四棱锥P －ABCD 中，平面P AC ⊥平面ABCD ，且P A ⊥AC ，P A ＝AD ＝2，四边形ABCD 满足BC ∥AD ，AB ⊥AD ，AB ＝BC ＝1.点E ，F 分别为侧棱PB ，PC 上的点，且PE PB ＝PFPC＝λ(λ≠0)． (1)求证：EF ∥平面P AD ；(2)当λ＝12时，求点D 到平面AFB 的距离．3434.如图，四棱柱ABCD－A1B1C1D1的底面ABCD是正方形．(1)证明：平面A1BD∥平面CD1B1；(2)若平面ABCD∩平面B1D1C＝直线l，证明：B1D1∥l.5..如图，四边形ABCD是平行四边形，点P是平面ABCD外一点，M是PC的中点，在DM上取一点G，过G和AP作平面交平面BDM于GH.求证：AP∥GH.6.如图，在四棱锥PABCD中，P A⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，P A＝AB＝BC，E是PC的中点．证明：(1)CD⊥AE；(2)PD⊥平面ABE.7.(2018北京通州三模,18)如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,四边形ABCD为正方形,△PAB为等边三角形,E是PB中点,平面AED与棱PC交于点F.(1)求证:AD∥EF; (2)求证:PB⊥平面AEFD;(3)记四棱锥P-AEFD的体积为V1,四棱锥P-ABCD的体积为V2,直接写出V1的值.V28...如图，在四棱锥PABCD中，底面ABCD是∠DAB＝60°且边长为a的菱形，侧面P AD为正三角形，其所在平面垂直于底面ABCD，若G为AD的中点．(1)求证：BG⊥平面P AD；(2)求证：AD⊥PB；(3)若E为BC边的中点，能否在棱PC上找到一点F，使平面DEF⊥平面ABCD？并证明你的结论．9.(2016·高考北京卷)如图，在四棱锥PABCD中，PC⊥平面ABCD，AB∥DC，DC⊥AC.(1)求证：DC⊥平面P AC；(2)求证：平面P AB⊥平面P AC；(3)设点E为AB的中点．在棱PB上是否存在点F，使得P A∥平面CEF？说明理由．10..如图，在四棱锥P－ABCD中，底面ABCD是矩形，点E在棱PC上(异于点P，C)，平面ABE与棱PD交于点F.(1)求证：AB∥EF；(2)若AF⊥EF，求证：平面P AD⊥平面ABCD.11..如图，在四棱锥P －ABCD 中，P A ⊥平面ABCD ，P A ＝AB ＝BC ＝3，AD ＝CD ＝1，∠ADC ＝120°，点M 是AC 与BD 的交点，点N 在线段PB 上，且PN ＝14PB .(1)证明：MN ∥平面PDC ；(2)求直线MN 与平面P AC 所成角的正弦值．12..(2016·高考四川卷)如图，在四棱锥P ABCD 中，P A ⊥CD ，AD ∥BC ，∠ADC ＝∠P AB ＝90°，BC ＝CD ＝12AD ．(1)在平面P AD 内找一点M ，使得直线CM ∥平面P AB ，并说明理由； (2)证明：平面P AB ⊥平面PBD ．13．(2016·高考江苏卷)如图，在直三棱柱ABC A 1B 1C 1中，D ，E 分别为AB ，BC 的中点，点F 在侧棱B 1B 上，且B 1D ⊥A 1F ，A 1C 1⊥A 1B 1. 求证：(1)直线DE ∥平面A 1C 1F ；(2)平面B 1DE ⊥平面A 1C 1F .14.【2014,19】如图，三棱柱111C B A ABC -中，侧面C C BB 11为菱形，C B 1的中点为O ，且⊥AO 平面C C BB 11. （1）证明：;1AB C B ⊥（2）若1AB AC ⊥,,1,601==∠BC CBB 求三棱柱111C B A ABC -的高.15.(2017天津,文17)如图,在四棱锥P-ABCD 中,AD ⊥平面PDC,AD ∥ BC, PD ⊥PB, AD=1,BC=3,CD=4,PD=2.(1)求异面直线AP 与BC 所成角的余弦值;(2)求证:PD ⊥平面PBC;(3)求直线AB 与平面PBC 所成角的正弦值.16.(2016·高考浙江卷)如图，在三棱台ABC DEF 中，平面BCFE ⊥平面ABC ， ∠ACB ＝90°，BE ＝EF ＝FC ＝1，BC ＝2，AC ＝3. (1)求证：BF ⊥平面ACFD ；(2)求直线BD 与平面ACFD 所成角的余弦值．17..(2018·全国Ⅲ)如图，矩形ABCD 所在平面与半圆弧CD 所在平面垂直， M 是CD 上异于C ，D 的点．(1)证明：平面AMD ⊥平面BMC .(2)在线段AM 上是否存在点P ，使得MC ∥平面PBD ？说明理由．立体几何中的翻折问题18...如图(1)，在直角梯形ABCD 中，AD ∥BC ，∠BAD ＝π2，AB ＝BC ＝12AD ＝a ，E 是AD 的中点，O 是AC 与BE 的交点．将△ABE 沿BE 折起到图(2)中△A 1BE 的位置，得到四棱锥A 1BCDE .(1)证明：CD ⊥平面A 1OC ；(2)当平面A 1BE ⊥平面BCDE 时，四棱锥A 1BCDE 的体积为362，求a 的值．19.．如图1，在直角梯形ABCD 中，∠ADC ＝90°，AB ∥CD ，AD ＝CD ＝12AB ＝2，E 为AC 的中点，将△ACD 沿AC 折起，使折起后的平面ACD 与平面ABC 垂直，如图2.在图2所示的几何体D －ABC 中： (1)求证：BC ⊥平面ACD ；(2)点F 在棱CD 上，且满足AD ∥平面BEF ，求几何体F －BCE 的体积．20．如图，长方体ABCD A 1B 1C 1D 1中，AB ＝16，BC ＝10，AA 1＝8.点E ，F 分别在A 1B 1，D 1C 1上，过点E 、F 的平面α与此长方体的面相交，交线围成一个正方形EFGH .(1)求证：A 1E ＝D 1F ；(2)判断A 1D 与平面α的关系．2020届高三数学立体几何专题(文科)1解析：（Ⅰ）设AC 的中点为O ，连接EO . 在三角形PBD 中，中位线EO //PB ，且EO 在平面AEC 上，所以PB //平面AEC . （Ⅱ）∵AP =1，3AD =，-3P ABD V =， -11=32P ABD V PA AB AD ∴⋅⋅⋅33==AB ，∴32AB =，作AH ⊥PB 角PB 于H ，由题意可知BC ⊥平面P AB ，∴BC ⊥AH ，故AH ⊥平面PBC ．又313PA AB AH PB ⋅==，故A 点到平面PBC 的距离313. 2.(1)证明：如图所示，取P A 的中点H ，连接EH ，DH ，因为E 为PB 的中点，所以EH ∥AB ，EH ＝12AB ，又AB ∥CD ，CD ＝12AB ．所以EH ∥CD ，EH ＝CD ，因此四边形DCEH 是平行四边形，所以CE ∥DH ，又DH ⊂平面P AD ，CE ⊄平面P AD ，所以CE ∥平面P AD ． (2)如图所示，取AB 的中点F ，连接CF ，EF ，所以AF ＝12AB ，又CD ＝12AB ，所以AF ＝CD ，又AF ∥CD ，所以四边形AFCD 为平行四边形，所以CF ∥AD ，又CF ⊄平面P AD ，所以CF ∥平面P AD ，由(1)可知CE ∥平面P AD ，又CE ∩CF ＝C ，故平面CEF ∥平面P AD ，故存在AB 的中点F 满足要求．3.(1)证明 ∵PE PB ＝PFPC ＝λ(λ≠0)，∴EF ∥BC .∵BC ∥AD ，∴EF ∥AD .又EF ⊄平面P AD ，AD ⊂平面P AD ，∴EF ∥平面P AD . (2)解 ∵λ＝12，∴F 是PC 的中点，在Rt △P AC 中，P A ＝2，AC ＝2，∴PC ＝P A 2＋AC 2＝6，∴PF ＝12PC ＝62.∵平面P AC ⊥平面ABCD ，且平面P AC ∩平面ABCD ＝AC ，P A ⊥AC ，P A ⊂平面P AC ，∴P A ⊥平面ABCD ，∴P A ⊥BC .又AB ⊥AD ，BC ∥AD ，∴BC ⊥AB ，又P A ∩AB ＝A ，P A ，AB ⊂平面P AB ， ∴BC ⊥平面P AB ， ∴BC ⊥PB ，∴在Rt △PBC 中，BF ＝12PC ＝62.连接BD ，DF ，设点D 到平面AFB 的距离为d ，在等腰三角形BAF 中，BF ＝AF ＝62，AB ＝1， ∴S △ABF ＝54，又S △ABD ＝1，点F 到平面ABD 的距离为1， ∴由V F －ABD ＝V D －AFB ，得13×1×1＝13×d ×54，解得d ＝455，即点D 到平面AFB 的距离为455.4.证明 (1)由题设知BB 1∥DD 1且BB 1＝DD 1，所以四边形BB 1D 1D 是平行四边形，所以BD ∥B 1D 1.又BD ⊄平面CD 1B 1，B 1D 1⊂平面CD 1B 1，所以BD ∥平面CD 1B 1.因为A 1D 1∥B 1C 1∥BC 且A 1D 1＝B 1C 1＝BC ，所以四边形A 1BCD 1是平行四边形，所以A 1B ∥D 1C .又A 1B ⊄平面CD 1B 1，D 1C ⊂平面CD 1B 1，所以A 1B ∥平面CD 1B 1.又因为BD ∩A 1B ＝B ，BD ，A 1B ⊂平面A 1BD ，所以平面A 1BD ∥平面CD 1B 1. (2)由(1)知平面A 1BD ∥平面CD 1B 1，又平面ABCD ∩平面B 1D 1C ＝直线l ，平面ABCD ∩平面A 1BD ＝直线BD ，所以直线l ∥直线BD ，在四棱柱ABCD －A 1B 1C 1D 1中，四边形BDD 1B 1为平行四边形，所以B 1D 1∥BD ，所以B 1D 1∥l .5.连接AC 交BD 于点O ，连接MO ，因为PM ＝MC ，AO ＝OC ，所以P A ∥MO ，因为P A ⊄平面MBD ，MO ⊂平面MBD ，所以P A ∥平面MBD ．因为平面P AHG ∩平面MBD ＝GH ，所以AP ∥GH .6.[证明] (1)在四棱锥P ABCD 中，因为P A ⊥底面ABCD ， CD ⊂平面ABCD ，所以P A ⊥CD ，因为AC ⊥CD ，且P A ∩AC ＝A ，所以CD ⊥平面P AC ，而AE ⊂平面P AC ，所以CD ⊥AE . (2)由P A ＝AB ＝BC ，∠ABC ＝60°，可得AC ＝P A . 因为E 是PC 的中点，所以AE ⊥PC .由(1)知AE ⊥CD ，且PC ∩CD ＝C ，所以AE ⊥平面PCD ．而PD ⊂平面PCD ，所以AE ⊥PD ．因为P A ⊥底面ABCD ，所以P A ⊥AB ．又因为AB ⊥AD 且P A ∩AD ＝A ，所以AB ⊥平面P AD ，而PD ⊂平面P AD ，所以AB ⊥PD ．又因为AB ∩AE ＝A ，所以PD ⊥平面ABE .7.(1)证明因为ABCD 为正方形,所以AD ∥BC.因为AD ⊄平面PBC,BC ⊂平面PBC,所以AD ∥平面PBC. 因为AD ⊂平面AEFD,平面AEFD ∩平面PBC=EF, 所以AD ∥EF. (2)证明因为四边形ABCD 是正方形,所以AD ⊥AB.因为平面PAB ⊥平面ABCD,平面PAB ∩平面ABCD=AB,AD ⊂平面ABCD, 所以AD ⊥平面PAB.因为PB ⊂平面PAB,所以AD ⊥PB. 因为△PAB 为等边三角形,E 是PB 中点,所以PB ⊥AE.因为AE ⊂平面AEFD,AD ⊂平面AEFD,AE ∩AD=A,所以PB ⊥平面AEFD. (3)解由(1)知,V 1=V C-AEFD ,V E-ABC =V F-ADC =23V C-AEFD =23V 1,∴V BC-AEFD =53V 1,则V P-ABCD =V 1+53V 1=83V 1, ∴V 1V 2=38.8.[解] (1)证明：在菱形ABCD 中，∠DAB ＝60°，G 为AD 的中点，所以BG ⊥AD ．又平面P AD ⊥平面ABCD ，平面P AD ∩平面ABCD ＝AD ，所以BG ⊥平面P AD ．(2)证明：如图，连接PG.因为△P AD为正三角形，G为AD的中点，所以PG⊥AD．由(1)知，BG⊥AD，又PG∩BG＝G，所以AD⊥平面PGB．因为PB⊂平面PGB，所以AD⊥PB．(3)当F为PC的中点时，满足平面DEF⊥平面ABCD．证明如下：取PC的中点F，连接DE、EF、DF.在△PBC中，FE∥PB，在菱形ABCD中，GB∥DE.而FE⊂平面DEF，DE⊂平面DEF，EF∩DE＝E，PB⊂平面PGB，GB⊂平面PGB，PB∩GB＝B，所以平面DEF∥平面PGB．因为BG⊥平面P AD，PG⊂平面P AD，所以BG⊥PG.又因为PG⊥AD，AD∩BG＝G，所以PG⊥平面ABCD．又PG⊂平面PGB，所以平面PGB⊥平面ABCD，所以平面DEF⊥平面ABCD．9.【解】(1)证明：因为PC⊥平面ABCD，所以PC⊥DC.又因为DC⊥AC，且PC∩AC＝C，所以DC⊥平面P AC.(2)证明：因为AB∥DC，DC⊥AC，所以AB⊥AC.因为PC⊥平面ABCD，所以PC⊥AB．又因为PC∩AC＝C，所以AB⊥平面P AC.又AB⊂平面P AB，所以平面P AB⊥平面P AC.(3)棱PB上存在点F，使得P A∥平面CEF.理由如下：如图，取PB中点F，连接EF，CE，CF.又因为E为AB的中点，所以EF∥P A.又因为P A⊄平面CEF，且EF⊂平面CEF，所以P A∥平面CEF.10.证明(1)因为四边形ABCD是矩形，所以AB∥CD.又AB⊄平面PDC，CD⊂平面PDC，所以AB∥平面PDC，又因为AB⊂平面ABE，平面ABE∩平面PDC＝EF，所以AB∥EF.(2)因为四边形ABCD是矩形，所以AB⊥AD.因为AF⊥EF，(1)中已证AB∥EF，所以AB⊥AF.又AB⊥AD，由点E在棱PC上(异于点C)，所以点F异于点D，所以AF∩AD＝A，AF，AD⊂平面P AD，所以AB⊥平面P AD，又AB⊂平面ABCD，所以平面P AD⊥平面ABCD.11.(1)证明因为AB ＝BC ，AD ＝CD ，所以BD 垂直平分线段AC .又∠ADC ＝120°，所以MD ＝12AD ＝12，AM ＝32. 所以AC ＝ 3. 又AB ＝BC ＝3，所以△ABC 是等边三角形，所以BM ＝32，所以BM MD ＝3，又因为PN ＝14PB ，所以BM MD ＝BN NP＝3，所以MN ∥PD . 又MN ⊄平面PDC ，PD ⊂平面PDC ，所以MN ∥平面PDC .(2)解因为P A ⊥平面ABCD ，BD ⊂平面ABCD ，所以BD ⊥P A ，又BD ⊥AC ，P A ∩AC ＝A ，P A ，AC ⊂平面P AC ，所以BD ⊥平面P AC .由(1)知MN ∥PD ，所以直线MN 与平面P AC 所成的角即直线PD 与平面P AC 所成的角，故∠DPM 即为所求的角．在Rt △P AD 中，PD ＝2，所以sin ∠DPM ＝DM DP ＝122＝14，所以直线MN 与平面P AC 所成角的正弦值为14. 12.【解】 (1)取棱AD 的中点M (M ∈平面P AD )，点M 即为所求的一个点．理由如下：因为AD ∥BC ，BC ＝12AD ，所以BC ∥AM ，且BC ＝AM ，所以四边形AMCB 是平行四边形，从而CM ∥AB ．又AB ⊂平面P AB ，CM ⊄平面P AB ，所以CM ∥平面P AB ．(说明：取棱PD 的中点N ，则所找的点可以是直线MN 上任意一点)(2)证明：由已知，P A ⊥AB ，P A ⊥CD ，因为AD ∥BC ，BC ＝12AD ，所以直线AB 与CD 相交．所以P A ⊥平面ABCD ，从而P A ⊥BD ．连接BM ，因为AD ∥BC ，BC ＝12AD ，所以BC ∥MD ，且BC ＝MD ．所以四边形BCDM 是平行四边形．所以BM ＝CD ＝12AD ，所以BD ⊥AB ．又AB ∩AP ＝A ，所以BD ⊥平面P AB ．又BD ⊂平面PBD ，所以平面P AB ⊥平面PBD ．13.[证明] (1)在直三棱柱ABC A 1B 1C 1中，A 1C 1∥AC .在△ABC 中，因为D ，E 分别为AB ，BC 的中点，所以DE ∥AC ，于是DE ∥A 1C 1.又DE ⊄平面A 1C 1F ，A 1C 1⊂平面A 1C 1F ，所以直线DE ∥平面A 1C 1F .(2)在直三棱柱ABC A 1B 1C 1中，A 1A ⊥平面A 1B 1C 1.因为A 1C 1⊂平面A 1B 1C 1，所以A 1A ⊥A 1C 1.又A 1C 1⊥A 1B 1，A 1A ⊂平面ABB 1A 1，A 1B 1⊂平面ABB 1A 1，A 1A ∩A 1B 1＝A 1，所以A 1C 1⊥平面ABB 1A 1.因为B 1D ⊂平面ABB 1A 1，所以A 1C 1⊥B 1D ．又B 1D ⊥A 1F ，A 1C 1⊂平面A 1C 1F ，A 1F ⊂平面A 1C 1F ，A 1C 1∩A 1F ＝A 1，所以B 1D ⊥平面A 1C 1F .因为直线B 1D ⊂平面B 1DE ，所以平面B 1DE ⊥平面A 1C 1F14.证明：(Ⅰ)连接 BC 1，则O 为B 1C 与BC 1的交点，∵AO ⊥平面BB 1C 1C . ∴AO ⊥B 1C ， …2分因为侧面BB 1C 1C 为菱形，∴BC 1⊥B 1C ，…4分∴BC 1⊥平面ABC 1，∵AB ⊂平面ABC 1，故B 1C ⊥AB . …6分(Ⅱ)作OD ⊥BC ，垂足为D ，连结AD ，∵AO ⊥BC ，∴BC ⊥平面AOD ，又BC ⊂平面ABC ，∴平面ABC ⊥平面AOD ，交线为AD ，作OH ⊥AD ，垂足为H ，∴OH ⊥平面ABC . …9分∵∠CBB 1=60°，所以ΔCBB 1为等边三角形，又BC =1，可得OD =3，由于AC ⊥AB 1，∴11122OA B C ==，∴2274AD OD OA =+=，由 OH·AD=OD·OA ，可得OH=21，又O 为B 1C 的中点，所以点B 1到平面ABC 的距离为217，所以三棱柱ABC -A 1B 1C 1的高高为21。

立体几何测精彩试题(卷)(文科)

立体几何文科试题一、选择题：本大题共12小题，在每小题给出的四个选项中，只有一项是符合题目要求的． 1、设有直线m 、n 和平面α、β.下列四个命题中，正确的是( )A.若m ∥α,n ∥α,则m ∥nB.若m ⊂α,n ⊂α,m ∥β,n ∥β,则α∥βC.若α⊥β，m ⊂α,则m ⊥βD.若α⊥β，m ⊥β，m ⊄α,则m ∥α 2、已知直线,l m 与平面αβγ，，满足//l l m βγαα=⊂，，和m γ⊥，则有A ．αγ⊥且l m ⊥B ．αγ⊥且//m βC ．//m β且l m ⊥D ．//αβ且αγ⊥ 3.若()0,1,1a =-，()1,1,0b =，且()a b a λ+⊥，则实数λ的值是（） A .－1 B.0 C.1 D.－24、已知平面α⊥平面β，α∩β= l ，点A ∈α，A ∉l ，直线AB ∥l ，直线AC ⊥l ，直线m ∥α，m ∥β，则下列四种位置关系中，不一定．．．成立的是（） A. AB ∥mB. AC ⊥mC. AB ∥βD. AC ⊥β5一个几何体的三视图及长度数据如图，则几何体的表面积与体积分别为()3,27+A ()328，+B()2327，+C ()23,28+D6、已知长方体的表面积是224cm ，过同一顶点的三条棱长之和是6cm ，则它的对角线长是（） A.14cm B. 4cm C. 32cm D. 23cm7、已知圆锥的母线长5l cm =，高4h cm =，则该圆锥的体积是____________3cmA. 12π B 8π C. 13π D. 16π8、某几何体的三视图如图所示，当b a +取最大值时，这个几何体的体积为（）A ．61B ．31C ．32D ．21 9、已知,,,A B C D 在同一个球面上,,AB BCD ⊥平面,BC CD ⊥若6,AB =213,AC =8AD =,则,B C 两点间的球面距离是（） A.3πB. 43πC. 23πD. 53π10、四面体ABCD 的外接球球心在CD 上，且2CD =，3=AB ，在外接球面上A B ，两点间的球面距离是（）A ．π6B ．π3C ．2π3 D ．5π611、半径为2cm 的半圆纸片做成圆锥放在桌面上，一阵风吹倒它，它的最高处距桌面（）A ．4cmB ．2cmC ．cm 32D ．cm 312、有一正方体，六个面上分别写有数字1、2、3、4、5、6，有三个人从不同的角度观察的结果如图所示.如果记3的对面的数字为m ，4的对面的数字为n ，那么m+n 的值为（）A ．3B ．7C ．8D ．11二．填空题：本大题共4个小题。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2０17届文科数学立体几何大题训练
1. 如图,三棱锥A —BPC 中，AP ⊥ＰC ，AC ⊥BC ，M 为AB 中点,D 为ＰB 中点，且△ＰＭB 为正三角形．
（Ⅰ）求证：DM //平面ＡP Ｃ；
（Ⅱ）求证:平面ＡBC ⊥平面APC ;
(Ⅲ）若ＢＣ=4,ＡＢ=20,求三棱锥D —BCM 的体积．
2. 如图1,在四棱锥ABCD P -中,⊥PA 底面ABCD ，面ABCD 为正方形,E 为侧棱PD 上一点，F 为AB 上一点.该四棱锥的正(主）视图和侧（左)视图如图2所示. （Ⅰ）求四面体PBFC 的体积; （Ⅱ)证明:AE ∥平面PFC ;
（Ⅲ)证明：平面PFC ⊥平面PCD .
3. 如图,四棱柱P ABCD -中， .//,,AB PAD AB CD PD AD F ⊥=平面是DC 上的点且1
,2
DF AB PH =为PAD ∆中AD 边上的高．
（Ⅰ）求证：//AB 平面PDC ; (Ⅱ）求证：PH BC ⊥;
（Ⅲ）线段PB 上是否存在点E ,使EF ⊥平面PAB ？说明理由.
4. 如图,在四棱锥中,底面
为菱形，,为的中点。

（1）若
，求证：平面
;
（2）点在线段
上，
，试确定
的值,使；
F A
B
D P
C
H
5. ．如图，
是矩形中边上的点，为边的中点,,现将沿边折至位置，且平面平面. ⑴ 求证：平面平面;
⑵ 求四棱锥的体积.
6．如图,在四棱锥P ABCD -中，平面PAD ⊥平面ABCD ,90ABC BCD ∠=∠=,
PA PD DC CB a ====,2AB a =,E 是PB 中点,H 是AD 中点.
(Ⅰ）求证：//EC 平面APD ；（Ⅱ）求三棱锥E BCD -的体积. E ABCD AD F CD 2
43
AB AE AD ===ABE ∆BE PBE ∆PBE ⊥BCDE PBE ⊥PEF P BEFC -P
B
C
D F
E
B
C D A
F
E
(1)
(2)
7. 如图,在三棱锥S ABC -中,侧面SAB 与侧面SAC 均为等边三角形, 90BAC ∠=°,O 为BC 中点.
（Ⅰ)证明:SO ⊥平面ABC ；
（Ⅱ）求异面直线B Ｓ与AC 所成角的大小．
８. 如图，已知A Ｂ平面A ＣD ,DE ∥A Ｂ,△ＡC Ｄ是正三角形,,且F 是CD 的中点．
(Ⅰ）求证AF ∥平面BCE ；
(Ⅱ）设AB =1,求多面体ABCDE 的体积． ⊥2AD DE AB ==O
S
B
A
C
９.如图,是矩形中边上的点,为边的中点，，现将沿边折至位置,且平面平面． ⑴ 求证:平面平面; ⑵ 求四棱锥的体积.
10. 右图为一组合体，其底面
为正方形,平面，，且
(Ⅰ）求证：平面； (Ⅱ）求四棱锥
的体积；
（Ⅲ)求该组合体的表面积. E ABCD AD F CD 2
43
AB AE AD ===ABE ∆BE PBE ∆PBE ⊥BCDE PBE ⊥PEF P BEFC -ABCD PD ⊥ABCD //EC PD 22PD AD EC ===//BE PDA B CEPD -
P
B
C
E
D F
E
(1)
(2)
11. 四棱锥中,底面为平行四边形,侧面底面,为
的中点，已知，
(Ⅰ)求证：；
(Ⅱ)在上求一点,使平面;
（Ⅲ)求三棱锥的体积.
12. 在三棱柱111ABC A B C -中,底面是边长为的正三角形，点1A 在底面ABC 上的射影O 恰是BC 中点. （Ⅰ)求证:1AA BC ⊥；
(Ⅱ）当侧棱1AA 和底面成45角时，求11A BB C C V - （Ⅲ)若D 为侧棱1AA 上一点,当
为何值时,11BD A C ⊥.
S ABCD -ABCD SBC ⊥ABCD E SD 45222ABC AB BC ∠===，， 3.SB SC ==SA BC ⊥BC F //EC SAF D EAC -32DA
D
A 1
13．如图，已知三棱锥,
，为中
点，为中点,且是正三角形,.
(1)求证:平面平面； (2）求三棱锥的体积．
14．在四棱锥P-AB ＣD 中,底面ABCD 是矩形，ＰＡ＝AD=4,AB=2，P Ｂ＝２5，PD=42，E 是PD 的中点 (1)求证：AE ⊥平面PCD;
(2)若F 是线段B Ｃ的中点，求三棱锥F-ACE 的体积。

ABC P - 90=∠ACB D AB CB ,20,4==AB M PB PDB ∆PC PA ⊥PAC ⊥ABC BCD M -D
P
M
C
B
A
1５．如图，在正四棱锥ABCD P -中，底面是边长为2的正方形，侧棱6=
PA ，E 为
BC 的中点,F 是侧棱PD 上的一动点。

(1)证明:BF AC ⊥；
(2)当直线ACF PE 平面//时，求三棱锥
ACD F -的体积.
16. 如图,在直三棱柱(即侧棱与底面垂直的三棱柱）111ABC A B C -中，90,
ACB ∠=122AC AA BC ===，D 为1AA 的中点.
（I ）求证:平面1B CD ⊥平面11B C D ； (ＩＩ）求1C 到平面1B CD 的距离．
17．如图，斜三棱柱中,侧面底面ＡBC ，底面A ＢC 是边长为2的等边三角形，侧面是菱形，，E 、Ｆ分别是、AB 的中点. 求证:(1）；
（2)求三棱锥的体积.
1８. 如图所示，四棱锥P-AB ＣＤ的底面A ＢCD 是边长为1的菱形，∠BCD ＝6０︒
,Ｅ是CD 的中点,ＰＡ⊥底面ABCD,ＰA=2.
(1）证明：平面P ＢＥ⊥平面PA Ｂ； (2)求P Ｃ与平面P ＡB 所成角的余弦值。

111A B C ABC -11AA C C ⊥11AA C C 160A AC ∠=11A C EC ABC ⊥平面1A EFC - A
B
F
C
C 1
E A 1
B 1
第18题图
１9．如图，斜三棱柱111A B C ABC -中，侧面11AA C C ⊥底面A ＢＣ，侧面11AA C C 是菱形，
160A AC ∠=，E 、F 分别是11A C 、AB 的中点．
求证：（1)ＥＦ∥平面11BB C C ; （2）平面CEF ⊥平面A ＢC
２0．已知△ＢCD 中，∠ＢCD =90°,BC =CD =１,ＡＢ⊥平面BCD ，∠ＡD Ｂ=６０°,E 、F 分
别是ＡC 、AD 上的动点，且
)10(,<<==λλAD
AF
AC AE ﻩ（Ⅰ）求证：不论λ为何值,总有平面ＢＥF ⊥平面AB Ｃ；（Ⅱ）当λ为何值时，平面BE Ｆ⊥平面ＡＣD ？
A
1
E F
E
D
B
A
C。