材力期末练习10答案
材力期末练习10答案
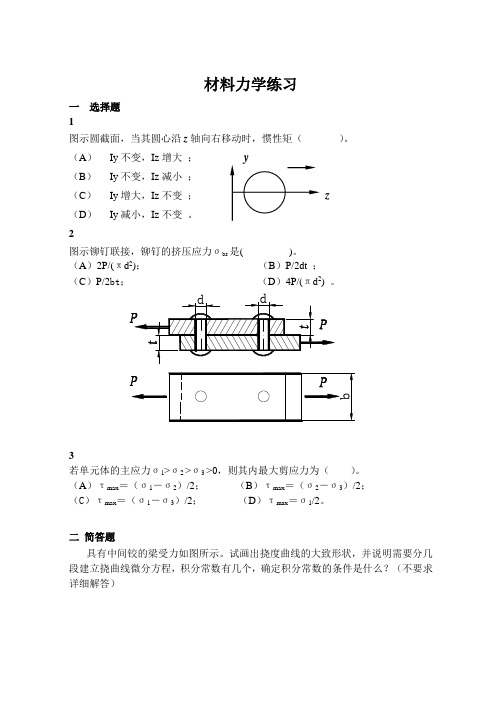
材料力学练习一选择题1图示圆截面,当其圆心沿z轴向右移动时,惯性矩()。
(A)Iy不变,Iz增大;(B)Iy不变,Iz减小;(C)Iy增大,Iz不变;z(D)Iy减小,Iz不变。
2图示铆钉联接,铆钉的挤压应力σbs是( )。
(A)2P/(πd2);(B)P/2dt ;(C)P/2bt;(D)4P/(πd2) 。
Array 3若单元体的主应力σ1>σ2 >σ3 >0,则其内最大剪应力为()。
(A)τmax=(σ1-σ2)/2;(B)τmax=(σ2-σ3)/2;(C)τmax=(σ1-σ3)/2;(D)τmax=σ1/2。
二简答题具有中间铰的梁受力如图所示。
试画出挠度曲线的大致形状,并说明需要分几段建立挠曲线微分方程,积分常数有几个,确定积分常数的条件是什么?(不要求详细解答)45°30°三 计算题 第1题图示结构AC 、BC 杆均为直径d =20 mm 的圆截面直杆,材料许用应力[б]=160 MPa ,求此结构的允许载荷[ F ]。
第2题已知变截面钢杆,I 段为d 1=20mm 的圆形截面,II 段为a 2=25mm 的正方形截面, III 段为d 3=12mm 的圆形截面,各段长度如图所示。
若此杆在轴向压力P 作用下在第II 段上产生σ2=-30Mpa 的应力,E =210GPa ,求此杆的总缩短量。
第3题钢制空心圆轴的外径D =100 mm ,内径d =50mm 。
若要求轴在2m 内的最大扭转角不超过1.5o ,材料剪切弹性模量G =82 GPa 。
求:1.该轴所能承受的最大扭矩; 2.此时轴内的最大剪应力。
0.2m 0.2m 0.4m P I IIIII P第4题作梁的剪力、弯矩图。
第5题图示为一铸铁梁,许用拉应力 [σt ] =30MPa ,许用压应力 [σc ] =60MPa , I z = 7.63×10-6m 4,试校核此梁的强度。
材料力学B精选题10

能 量 法1. 试就图示杆件的受载情况,证明构件内弹性应变能的数值与加载次序无关。
证:先加F 1后加F 2,则221212()/(2)/(2)/(2)V F a b EA F a EA F F a EA ε 1=+++ 先加F 2后加F 1,则222112/(2)()/(2)/(2)V F a EA F a b EA F F a EA ε 2=+++ 所以 V ε 1 = V ε 22. 直杆的支承及受载如图,试证明当F 1=2F /3时, 杆中应变能最小,并求出此时的应变能值。
解:1AC F F F =- ;1BC F F =-22221111()2/(2)/(2)(23/2)/()V F F l EA F l EA F FF F l EA ε=-+=-+1/0V F ε∂∂=: 1230F F -+= , 12/3F F =2min /(3)V F l EA ε =3. 图示杆系的各杆EA 皆相同,杆长均为a 。
求杆系内的总应变能,并用功能原理求A 、B 两点的相对线位移∆AB 。
解: 25/(6)V F a EA ε=视CD 相对固定2⨯F ∆AB /4 = 5F 2a /(6EA )∆AB = 5Fa /(3EA ) ( 拉开 )4. 杆AB 的拉压刚度为EA ,求(a) 在F 1及F 2二力作用下,杆的弹性应变能; (b) 令F 2为变量,F 2为何值时,杆中的应变能最小?此时杆的应变能是多少? 答: N 12AC F F F =-, N 2BC F F =-(a) 22122()2/(2)/(2)V F F l EA F l EA ε=-+221122(23/2)/()l F F F F EA =-+(b) 2/0V F ε∂∂=,12230F F -+=,212/3F F = 此时 21min /(3)V F l EA ε=5. 力F 可以在梁上自由移动。
为了测定F 力作用在C 点时梁的弯曲轴线,可以利用千分表测各截面的铅垂位移。
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第10章 组合受力与变形杆件的强度计算

解:危险截面在 A 处,其上之内力分量为: 弯矩: M y = FP1 a , M z = FP2 H 扭矩: M x = FP2 a 轴力: FNx = FP1 在截面上垂直与 M 方向的垂直线 ab 与圆环截 求得 M y 与 M z 的矢量和 M 过截面中心, 面边界交于 a、b 两点,这两点分别受最大拉应力和最大压应力。但由于轴向压力的作用,最 大压应力值大于最大拉应力值,故 b 点为危险点,其应力状态如图所示。 10-7 试求图 a 和 b 中所示之二杆横截面上最大正应力及其比值。 解: (a)为拉弯组合
7
y
y
A
O
0.795
B
14.526
+13.73MPa
z
(a)
O O
+14.43MPa
(b)
C
y
A
C
B B
y
A
O O
B
z
12.6mm
14.1mm
zC
−15.32MPa
16.55MPa
zC
z
(c)
(d)
习题 10-9 解图
∴
+ σ max
= 14.526 − 0.795 = 13.73 MPa
− σ max = −14.526 − 0.795 = −15.32 MPa
Ebh
由此得
2 FP 6e
e=
10-9
ε1 − ε 2 h × ε1 + ε 2 6
图中所示为承受纵向荷载的人骨受力简图。试:
1.假定骨骼为实心圆截面,确定横截面 B-B 上的应力分布; 2.假定骨骼中心部分(其直径为骨骼外直径的一半)由海绵状骨质所组成,忽略海绵状承受 应力的能力,确定横截面 B-B 上的应力分布;
《工程力学(工程静力学与材料力学)(第3版)》考试试卷(附答案)(10)

工程力学考试答卷(10)1.(5分)结构对称的梁在反对称载荷作用下:弯矩图对称,剪力图反对称;弯矩图反对称,剪力图对称;弯矩图和剪力图都对称;弯矩图和剪力图都反对称。
正确答案是B。
2.(5分)关于材料的力学一般性能,有如下结论,请判断哪一个是正确的:脆性材料的抗拉能力低于其抗压能力;(B)脆性材料的抗拉能力高于其抗压能力;(C)韧性材料的抗拉能力高于其抗压能力;正确答案是A。
(D)脆性材料的抗拉能力等于其抗压能力。
3.(5分)关于斜弯曲的主要特征有以下四种答案,请判断哪一种是正确的。
(A) My≠0,Mz≠0,FNx≠0;,中性轴与截面形心主轴不一致,且不通过截面形心;(B) My≠0,Mz≠0,FNx=0,中性轴与截面形心主轴不一致,但通过截面形心;(C) My≠0,Mz≠0,FNx=0,中性轴与截面形心主轴平行,但不通过截面形心;(D) My≠0,Mz≠0,FNx≠0,中性轴与截面形心主轴平行,但不通过截面形心。
正确答案是B。
4.(5分)两根长度相等、直径不等的圆轴受扭后,轴表面上母线转过相同的角度。
设直径大的轴和直径小的轴的横截面上的最大剪应力分别为τ1max和τ2max,材料的切变模量分别为G1和G2。
关于τ1max和τ2max的大小,有下列四种结论,请判断哪一种是正确的。
(A)τ1max>τ2max;(B)τ1max<τ2max;(C)若G1>G2,则有τ1max>τ2max;正确答案是C。
(D)若G1>G2,则有τ1max<τ2max。
5.(10分)截面为工字形的立柱受力如图所示。
试求此力向截面形心C平移的结果。
解:r =(-50, 125, 0)mm F =(0, 0, -100)kN F 向C 平移,得 FR =(0, 0, -100)kN1000000.1250.05-)(-=⨯==kj i F r F M M C C=(-12.5, -5, 0)kN ·m6.(10分)图示芯轴AB 与轴套CD 的轴线重合,二者在B 、C 处连成一体;在D 处无接触。
材料力学性能习题及解答库

第一章习题答案一、解释下列名词1、弹性比功:又称为弹性比能、应变比能,表示金属材料吸收弹性变形功的能力。
2、滞弹性:在弹性范围内快速加载或卸载后,随时间延长产生附加弹性应变的现象。
3、循环韧性:金属材料在交变载荷下吸收不可逆变形功的能力,称为金属的循环韧性。
4、包申格效应:先加载致少量塑变,卸载,然后在再次加载时,出现σe升高或降低的现象。
5、解理刻面:大致以晶粒大小为单位的解理面称为解理刻面。
6、塑性、脆性和韧性:塑性是指材料在断裂前发生不可逆永久(塑性)变形的能力。
韧性:指材料断裂前吸收塑性变形功和断裂功的能力,或指材料抵抗裂纹扩展的能力7、解理台阶:高度不同的相互平行的解理平面之间出现的台阶叫解理台阶;8、河流花样:当一些小的台阶汇聚为在的台阶时,其表现为河流状花样。
9、解理面:晶体在外力作用下严格沿着一定晶体学平面破裂,这些平面称为解理面。
10、穿晶断裂和沿晶断裂:沿晶断裂:裂纹沿晶界扩展,一定是脆断,且较为严重,为最低级。
穿晶断裂裂纹穿过晶内,可以是韧性断裂,也可能是脆性断裂。
11、韧脆转变:指金属材料的脆性和韧性是金属材料在不同条件下表现的力学行为或力学状态,在一定条件下,它们是可以互相转化的,这样的转化称为韧脆转变。
二、说明下列力学指标的意义1、E(G):E(G)分别为拉伸杨氏模量和切变模量,统称为弹性模量,表示产生100%弹性变形所需的应力。
2、σr、σ0.2、σs: σr :表示规定残余伸长应力,试样卸除拉伸力后,其标距部分的残余伸长达到规定的原始标距百分比时的应力。
σ0.2:表示规定残余伸长率为0.2%时的应力。
σs:表征材料的屈服点。
3、σb:韧性金属试样在拉断过程中最大试验力所对应的应力称为抗拉强度。
4、n:应变硬化指数,它反映了金属材料抵抗继续塑性变形的能力,是表征金属材料应变硬化行为的性能指标。
5、δ、δgt、ψ:δ是断后伸长率,它表征试样拉断后标距的伸长与原始标距的百分比。
(仅供参考)《材料力学》第五版-刘鸿文第9-10章习题答案

湖北汽车工业学院 材料力学 主讲教师:马迅
9.16 10号工字梁的C端固定,A端铰支于空心钢管AB上。 钢管的内径和外径分别为30mm和40mm,B端亦为铰支。 当300N的重物落于梁的A端时,校核AB杆的稳定性。规 定稳定安全系数nst=2.5。
解: 包含一次静不定、冲击载荷 和屈曲三类问题。
解题思路: 利用变形协调条件求解静不定问
=
64 1× 2/cos30o 2
= 44.6N
2杆的许可载荷
[N2 ] =
Pcr n
=
44.6 N = 24.8N 1.8
P=12.4N
HAII MAXUN
1
2012-6-1
1/8
Printed with FinePrint - purchase at PDF created with pdfFactory trial version
Kd =1+
1+ 2×50=4 ∆ st
σ st max
=
M max W
= 37.5MPa
( yc )d = Kd ∆st = 0.05m (σ max )d = Kdσ max = 150MPa
HAII MAXUN
4
2012-6-1
4/8
Printed with FinePrint - purchase at PDF created with pdfFactory trial version
湖北汽车工业学院 材料力学 主讲教师:马迅
附加习题9-4:立柱CD为圆截面,材料的E=200Gpa, σp=200MPa。稳定安全系数nst=2,校核立柱的稳定性。
解:
λP =
π 2E = σPFra bibliotekπ 2 200 ×109 200 × 106
《材料力学》第五版_刘鸿文第9_10章习题答案

−P
0
P
− 2P P
0
0
2P
0
−P
P
− 2P 0
0
解: a、c 桁架 b 桁架
Pcr =
Pb ≥ Pc = Pa
π 2 EI ( 2l ) 2 π 2 EI Pcr = (l ) 2
HAII MAXUN
N ≤ Pcr = 2 P N ≤ Pcr = P
π 2 EI 2 2l 2 π 2 EI P= (l ) 2 P=
8.5 ×1.43 (14 − 8.5) × 9.63 4 4 Iy = + cm = 407cm 12 12
9.6 × 143 (9.6 − 1.4) × 8.53 4 4 Iz = + cm = 1780cm 12 12
iy =
λP =
Iy A
=
407 cm = 2.51cm iz = 64.7
湖北汽车工业学院
材料力学
主讲教师:马迅
10.14 材料相同、长度相等的变截面杆和等截面杆,若两 杆的最大横截面面积相同,问哪一根杆件承受冲击的能 力强?设变截面杆直径为d的部分长为2/5l。假设H较 大,近似把动载系数取为 2H 2H 解:
Kd = 1+ 1+ ∆ st ≈ ∆ st
3 2 lW lW Nl 4Wl ∆st = ∑ = 5 + 5 = π π EA 5Eπ E D2 E d 2 4 4
湖北汽车工业学院
材料力学
主讲教师:马迅
第9+10章习题
教材:9.13、9.16、10.14 附加习题: 9-1、9-2、9-3、9-4、10-2、10-4
附加习题9-2: 1、2杆均为圆截面,直径相同,d=8mm, 材料的E=120GPa,适用欧拉公式的临界柔度为90,规定 稳定性安全系数nst=1.8,求结构的许可载荷P。 解: 应用平衡条件有
材力第十章

向力 Fz = 10 kN;在齿轮 2 上,作用有切向力 F'y = 5 kN、径向力 F'z = 1.82 kN。若许用应力 [ ]=100 MPa,试根据第四强度理论确定轴径。
题 10-13 图 解:将各力向该轴轴线简化,得其受力图如图 10-13a 所示。内力图( M z , M y 和 T )分 别示如图 b,c 和 d。
其相当应力为 (b)
比较式(a)和(b)可知,该轴真正的危险点是截面 A-A 上水平直径的左端点,其相当应力如 式(b)所示。 顺便指出,本题计算相当应力的另一种方法是先求 ( ) 与 τ ( ) ,再求 σ r3 ( ) 。这里的
5
从截面 A-A 上左边水平半径量起,以顺钟向为正。将 σ r3 ( ) 对 求导,寻找其极值位置,找 到的极值位置是 0 ,由此确定的危险点同上述真正的危险点,相当应力当然也同式(b)。
5.19 102 m 51.9 mm
10-16
图示钢质拐轴,承受铅垂载荷 F1 与水平载荷 F2 作用。已知轴 AB 的直径为
d,轴与拐臂的长度分别为 l 与 a,许用应力为[],试按第四强度理论建立轴 AB 的强度条件。
题 10-16 图 解:将载荷 F1 与 F2 平移到截面 B 的形心,得轴 AB 的受力如图 b 所示。 显然,固定端处的横截面 A 为危险截面,该截面的轴力、扭矩与弯矩分别为
试求偏心距 a 的许用值。
题 10-8 图 解:1.确定内力
FN 250kN,M y Fa 2.50 105 a (N m) M z 0.050F 0.050 250103 N m 1.25104 N m
2.计算 Iz,Iy 及 A
0.100 0.1203 0.080 0.0803 4 )m 1.099105 m 4 12 12 3 0.020 0.100 0.080 0.0203 4 Iy ( 2 )m 3.39 106 m 4 12 12 A (0.100 0.020 2 0.080 0.020)m2 5.60 103 m 2 Iz (
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
材料力学练习
一选择题
1
图示圆截面,当其圆心沿z轴向右移动时,惯性矩()。
(A)Iy不变,Iz增大;
(B)Iy不变,Iz减小;
(C)Iy增大,Iz不变;z
(D)Iy减小,Iz不变。
2
图示铆钉联接,铆钉的挤压应力σbs是( )。
(A)2P/(πd2);(B)P/2dt ;
(C)P/2bt;(D)4P/(πd2) 。
Array 3
若单元体的主应力σ1>σ 2 >σ 3 >0,则其内最大剪应力为()。
(A)τmax=(σ1-σ2)/2;(B)τmax=(σ2-σ3)/2;
(C)τmax=(σ1-σ3)/2;(D)τmax=σ1/2。
二简答题
具有中间铰的梁受力如图所示。
试画出挠度曲线的大致形状,并说明需要分几段建立挠曲线微分方程,积分常数有几个,确定积分常数的条件是什么?(不要求
详细解答)
三 计算题 第1题
图示结构AC 、BC 杆均为直径d =20 mm 的圆截面直杆,材料许用应力[б]=160 MPa ,求此结构的允许载荷[ F ]。
第2题
已知变截面钢杆,I 段为d 1=20mm 的圆形截面,II 段为a 2=25mm 的正方形截面, III 段为d 3=12mm 的圆形截面,各段长度如图所示。
若此杆在轴向压力P 作用下在第II 段上产生σ2=-30Mpa 的应力,E =210GPa ,求此杆的总缩短量。
第3题
钢制空心圆轴的外径D =100 mm ,内径d =50mm 。
若要求轴在2m 内的最大扭转角不超过1.5o ,材料剪切弹性模量G =82 GPa 。
求:1.该轴所能承受的最大扭矩; 2.此时轴内的最大剪应力。
0.2m
0.2m
0.4m
P
II
P
第4题
作梁的剪力、弯矩图。
第5题
图示为一铸铁梁,许用拉应力 [σt ] =30MPa ,许用压应力 [σc ] =60MPa , I z = 7.63×10-6m 4,试校核此梁的强度。
第6题
叠加法求D 点的挠度。
EI 已知。
第7题
边长a=20mm 的正方形截面杆受力与支承如图所示。
已知材料的[σ]=50MPa ,试求许用载荷[P]。
第8题
水平放置的直径为20mm 的圆截面直角折杆受力如图所示,已知P=200N ,材料的许用应力为[σ]=170MPa 。
试用第三强度理论确定折杆的长度a 的许用值。
第9题
圆轴AD ,在C 、B 处分别装有直径2m 和1m 的大、小两个轮子。
沿大轮切向作用铅直力kN P 3=,提起小轮切向重物
Q 。
轴的[]M P a 60=σ。
m CD AB BC 122===。
按第三强度理论设计轴径。
第10题
图示结构,①、②杆材料、长度相同,已知:Q =90kN, E=200Gpa, l =0.8m, λP =99.3, λs =57, 经验公式σcr =304-1.12λ(MPa), n st =3。
校核结构的稳定性。
答案
一 选择题 1
C 2 B 3 C 二 简答题
1。
分3段积分,共有6个积分常数 2。
确定积分常数的条件是: x =0,w 1=0; θ1=0 x =l ,w 1= w 2;
x =2l , w 2=0;w 2= w 3; θ2=θ3;
三 计算题 第1题
以C 节点为研究对象,根据平衡方程解出
F F N 2
131-=
F F N 132-=
由BC 杆的拉伸强度条件得KN F 7.68][=
第2题
解:σII =–P/A II , P=30×252×10–3=18.75kN,
mm 272.01242002540020
4
20010
2101075.182
223
3
3
1
i
i 3
1
i
-=⎪⎭⎫ ⎝⎛⨯⨯++⨯⨯⨯⨯⨯-
=-
=∆=
∆∑
∑==ππi i A l E
P l
l
第3题
1.确定轴所能承受的最大扭矩
根据
[]p
x
M
G I θθ=
≤
由已知条件知,允许的θ值为
1.51.5/2m /m
1802
πθ⨯==
⨯
弧度
于是
p
1.5π1802
x
M
G I ≤
⨯
由于
4
4
(1)
1.532
1802
x G D M παπ-=
⨯
⨯
4
2410
3
501.50.118.210
100321802
9.8710N m
π⎡⎤⎛⎫⨯⨯-⨯⨯⎢⎥ ⎪⎝⎭⎢⎥⎣⎦=
⨯⨯=⨯⋅ 2.最大剪应力
3
6
max 3
4
p
9.87101653.610Pa=53.6M Pa π0.1(10.5)
x
M
W τ⨯⨯==
=⨯⨯-
第4题 第5题
KN R A 5.2= KN R B 5.10=
由弯矩图可知危险截面为B 截面,m KN M
B
⋅-=4
B 截面上,[]t
z
B
t MPa I y M
σ
σ<=⨯⨯⨯⨯=
=
--26.2710
63.710
521046
3
3
1
[]c
z
B
t M P a I y M
σ
σ<=⨯⨯⨯⨯=
=
--1.4610
63.710
881046
3
3
2
较大弯矩为m KN M
C
⋅=5.2 []t
z
C
t M P a I y M
σ
σ<=⨯⨯⨯⨯=
=
--83.2810
63.710
88105.26
3
3
2
+
-
M
4KN.m
2.5KN.m
Q
M
故结构安全
第6题
(a )=(b )+(b )+(c )+(d )
()↑=
)EI
39
m w D (
第7题
∑=0x
F
︒=30cos P F Ax
∑=0A
M
By F P 120602
1=⨯⨯
P F By 25.0=
P M
M
F N c
Ax 015.0 0.866P max
====
[]σσ≤+
=
W
M A
F C Ax max
kN P 73.3≤
第8题
B
解:(1)求Q
15.0⨯=⨯P Q
kN P Q 6322=⨯==∴
(2)作内力图
m kN M
n
⋅=3
m kN M
B
⋅=⨯=625.25.025.5
m kN M
C
⋅=⨯=875.15.075.3
(3)设计轴径d m kN M
M
n
B
⋅=+=+986.33
625
.22
2
22
[]σπσ
≤+=
3
22
323
d
M
M n
xd
[]
(
)mm m M
M
d n
B
87810
878.010
6010
3
625
.232
321
3
6
3
2
2
3
22=⨯=⨯⨯⨯+=
+≥
∴-πσπ
第9题
危险截面为固定端,弯矩Pa M 2= 扭矩Pa T =
[]σπσ≤=
+=3
2
2
3532d
Pa
W T
M
z
r mm a 299
≤
第10题。
