电子测量部分习题答案
电子测量技术课后题答案

④判断: 测量次数为 9 次,置信概率 99%,查表可得 G=2.32
GS (V ) = 2.32 × 0.13 = 0.30
比较可得无残差大于 0.30 的数据 1.4 解: ①平均值
∴测得数据无异常
1 n 1 X i = (52.953 + 52.959 + 52.961 + 52.950 + 52.955 + 52.950 + 52.949 + 52.954 + 52.955) ∑ n i =1 9 = 52.954 X =
计算扩展不确定度. 参考答案: A 类评定: u1=0.084KΩ B 类评定: u2=0.019KΩ 合成标准不确定度为: uc = u12 + u2 2 = 0.086 K Ω
v=u4/( u14/v1+ u24/v2) ≈ 9 扩展不确定度评定,按 t 分布处理, 概率可取 95%, 查 t 分布表得到包含因子 扩展不确定度评定 U95=K95 uc =2.26x0.086=0.19 KΩ 完整的测量结果为:R=(13.40±0.19) KΩ (K95=2.26,P=95%) Veff=9 1.11 解:y= x1 x2 ⋅ x 3 3 =x 1 ⋅ x 2
20ns / div ~ 0.5s / div 10 20ns / div 显示一个周期波形时,被测信号的周期范围为 × 10div ~ 0.5s / div × 10div 10 即20ns ~ 5s 1 1 ~ ,即50 MHz ~ 0.2 Hz 则被测信号的频率范围为 20ns 5s 带有扫描扩展“×10”功能的示波器,其Dt的总范围为 2.17 解:
电子测量技术课后习题答案

2.4 有一个100V 的被测电压,若用0.5 级、量程为0-300V 和1.0 级、量程为0-100V 的两只电压表测量,问哪只电压表测得更准些?为什么?答:要判断哪块电压表测得更准确,即判断哪块表的测量准确度更高。
(1)对量程为0-300V、±0.5 级电压表,根据公式有% 100 % % 100 1x s x x x m x % 5 . 1 % 100 100 % 5 . 0 300 (2)对量程为0-100V、±1.0 级电压表,同样根据公式有% 100 % % 100 2 x s x x x m x % 0 . 1 % 100 100 % 0 . 1 100 从计算结果可以看出,用量程为0-100V、±1.0 级电压表测量所产生的示值相对误差小,所以选用量程为0-100V、±1.0 级电压表测量更准确。
2.9 测量上限为500V 的电压表,在示值450V 处的实际值为445V,求该示值的:(1)绝对误差(2)相对误差(3)引用误差(4)修正值答:(1)绝对误差V V V A x x 5 450 445 (2)相对误差% 12 . 1 % 100 445 5 % 100x x x (3)引用误差% 0 . 1 % 100 500 5 % 100m m x x (4)修正值V x c 5 2.10 对某电阻进行等精度测量10 次,数据如下(单位kΩ):0.992、0.993、0.992、0.991、0.993、0.994、0.997、0.994、0.991 、0.998。
试给出包含误差值的测量结果表达式。
答:1).将测量数据按先后次序列表。
n )(V V i )(V i )( 2 2 V i n )(V V i )(Vi )(2 2 V i 1 0.992 -0.0015 0.00000225 6 0.9940.0005 0.00000025 2 0.993 -0.0005 0.00000025 7 0.997 0.0035 0.00001225 3 0.992 -0.0015 0.00000225 8 0.994 0.0005 0.00000025 4 0.991 -0.0025 0.00000625 9 0.991 -0.0025 0.00000625 5 0.993 -0.0005 0.00000025 10 0.998 0.0045 0.00002025 2).用公式 n i i x n x 1 求算术平均值。
电子测量技术与仪器(第3版)课后习题答案

课后习题
目前本课程教材选用北京理工大学出版社出版的《电子测量技术与仪器》主编王川2010年7月第一版,教学过程中在教材里选择合适的习题作为课后习题,参考答案如下:
第一章
1-1见教材P4
1-2见教材P5
1-3 Δx1=1v,Δx2 =1v ,γA1=10% , γA2=1%
1-4 (1)Δx=0.03v ,c=-0.03v
(2) γA=0.86%
(3)1.0级
第二章
2-1见教材P13-14
2-3见教材P23
2-4见教材P26
第三章
3-2
正弦波三角波方波
有效值表 1.77V 1.44V 2.5V
均值表 1.77V 1.39V 2.76V
峰值表 1.77V 1.77V 1.77V
3-3选均值表较为合适,均值表的波形误差相对较小
3-6见教材P57-59
3-10(1)甲为4位乙为4位半
(2)当乙的基本量程为2V时,乙具有超量程能力,甲没有超量程能力
(3)0.01mV
第四章
4-1见教材P98-99
4-4(1)先让所用通道的垂直耦合接地,确定电压为零的位置,然后换到直流耦合,测量高低电平的电压大小。
(2)分别读取方波波形上升沿10%—90%的时间长度与下降沿90%—10%的时间长度,即为前沿时间和后沿时间。
4-11见教材P117
第五章
5-2见教材P134
5-9见教材P146
第六章
6-2见教材P168-169
6-3见教材P165-166
6-5测频量化误差分别为±0.00001%,±0.0001%,±0.001%。
电子测量习题答案2
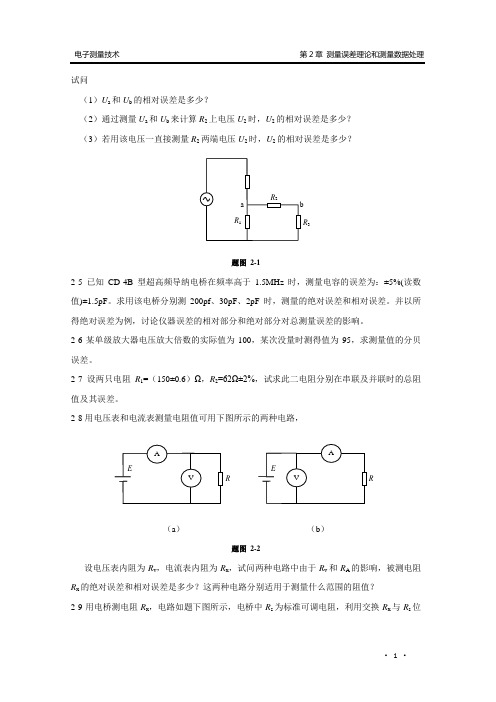
试问(1)U a 和U b 的相对误差是多少?(2)通过测量U a 和U b 来计算R 2上电压U 2时,U 2的相对误差是多少?(3)若用该电压一直接测量R 2两端电压U 2时,U 2的相对误差是多少?题图 2-12-5已知CD-4B 型超高频导纳电桥在频率高于1.5MHz 时,测量电容的误差为:±5%(读数值)±1.5pF 。
求用该电桥分别测200pf 、30pF 、2pF 时,测量的绝对误差和相对误差。
并以所得绝对误差为例,讨论仪器误差的相对部分和绝对部分对总测量误差的影响。
2-6某单级放大器电压放大倍数的实际值为100,某次没量时测得值为95,求测量值的分贝误差。
2-7设两只电阻R 1=(150±0.6)Ω,R 2=62Ω±2%,试求此二电阻分别在串联及并联时的总阻值及其误差。
2-8用电压表和电流表测量电阻值可用下图所示的两种电路,(a ) (b )题图 2-2设电压表内阻为R v ,电流表内阻为R x ,试问两种电路中由于R v 和R A 的影响,被测电阻R x 的绝对误差和相对误差是多少?这两种电路分别适用于测量什么范围的阻值?2-9用电桥测电阻R x ,电路如题下图所示,电桥中R s 为标准可调电阻,利用交换R x 与R s 位RE A V R EV A R 1 R 2 R 3ab置的方法对R x 进行两次测量,试证明R x 的测量值R 1及R 2的误差△R 1及△R 2无关。
题图 2-32-10用某电桥测电阻,当电阻的实际值为102Ω时测得值为100Ω,同时读数还有一定的分散性,在读数为100Ω附近标准偏差为0.5Ω,若用该电桥测出6个测得值为100Ω的电阻串联起来,问总电阻的确定性系统误差和标准偏差各是多少?系统误差和标准偏差的合成方法有何区别?2-11具有均匀分布的测量数据,(1)当置倍概率为100%时若它的置信区间为[M (x )-Cδ(x )],M (x)+Cδ(x )],问这里C 应取多大?(2)若取置信区间为[M (x )-2δ(x )], M (x )+2δ(x )],问置信概率为多大?2-12对某信号源的输出电压频率进行8次测量,数据如下(单位Hz ):1000.82,1000.79,1000.85,1000.84,1000.78,1000.91,1000.76,1000.82(1)试求其有限次测量的数学期望与标准差的估计值。
电子测量技术基础章节练习题及答案

第1章习题答案1、选择题(单项选择题)(1) 在测量中,绝对误差与其真值之比称为 C 。
A. 示值误差B. 随机误差C. 相对误差D. 引用误差(2) 仪表指示值与实际值之间的差值称为 A 。
A. 绝对误差B. 相对误差C. 示值相对误差D. 引用误差(3) 仪器仪表的准确度等级通常是用 D 来表示。
A. 绝对误差B. 相对误差C. 示值相对误差D. 引用相对误差(4) 测得信号的频率为0.0760MHz,这个数字的有效数字有 B 位。
A. 三B. 四C. 五D. 六(5) 测得信号的周期为2.4751μs,经整理保留三位有效数字,即为 C 。
A. 2.47μsB. 2.475μsC. 2.48μsD. 2.4751μs(6) 一定条件下,测量结果的大小及符号保持恒定或按照一定规律变化的误差称为 A 。
A. 系统误差B. 随机误差C. 粗大误差D. 绝对误差(7) 测量为8mA的电流时,若希望误差不超过0.2mA,则最好选用下列哪项方案? AA. 在1.5级电流表的10mA量程上测量B. 在5.0级电流表的10mA量程上测量C. 在2.5级电流表的10mA量程上测量D. 在2.5级电流表的100mA量程上测量2、判断题(正确的在后面括号内打对号、错误的打叉号)(1) 测量结果就是指被测量的数值量。
(×)(2) 测量结果的绝对误差越小,测量结果就越准确。
(√)(3) 测量结果的绝对误差与修正值等值同号。
(×)(4) 测量结果的绝对误差就是误差的绝对值。
(×)(5) 在测量过程中,粗大误差又称偶然误差,是由仪器精度不够产生的。
(×)3、简答题(1) 什么是测量?答:测量是人类对客观事物取得数量概念的认识过程,测量结果是由数值(大小及符号) 和单位构成,没有单位的测量结果是没有物理意义。
(2) 什么是电子测量?答:应用各类现代电子测量仪器所进行的测量活动称之为电子测量。
电子测量课后习题答案

电子测量课后习题答案电子测量是电子工程领域中的一个重要分支,它涉及到对电子信号的各种参数进行准确测量。
以下是一些电子测量课后习题的答案示例,供同学们参考:习题一:解释什么是数字多用表,并说明其主要功能。
数字多用表是一种多功能的电子测量仪器,它能够测量电压、电流、电阻等多种电子参数。
其主要功能包括:1. 直流电压测量:测量电路中的直流电压。
2. 交流电压测量:测量电路中的交流电压。
3. 电阻测量:测量电路元件的电阻值。
4. 电流测量:测量电路中的电流。
5. 电容测量:测量电路中的电容值。
6. 二极管测试:检测二极管的正向压降。
7. 温度测量:测量温度传感器输出的电压值。
习题二:简述示波器的基本工作原理。
示波器是一种用于观察和测量电信号波形的仪器。
其基本工作原理如下:1. 信号输入:将待测信号通过探头输入到示波器。
2. 垂直放大:信号通过垂直放大器放大,以适应屏幕显示。
3. 水平扫描:水平扫描产生周期性的扫描线,与输入信号同步。
4. 显示:经过放大和扫描的信号在屏幕上形成波形,供观察和分析。
习题三:解释什么是频率计,并说明其应用。
频率计是一种测量周期性信号频率的仪器。
其应用包括:1. 测试电子设备的时钟频率。
2. 测量无线电信号的频率。
3. 校准其他测量仪器的频率响应。
4. 在实验室中测量实验信号的频率特性。
习题四:如何使用万用表测量电路中的电流?使用万用表测量电路中的电流步骤如下:1. 选择适当的电流测量范围。
2. 断开待测电路。
3. 将万用表设置为电流测量模式。
4. 将万用表串联到电路中。
5. 闭合电路,观察万用表读数。
习题五:什么是信号发生器,它有哪些类型?信号发生器是一种产生特定频率和波形的电子信号的设备。
其类型包括:1. 正弦波信号发生器:产生正弦波形的信号。
2. 方波信号发生器:产生方波形的信号。
3. 脉冲信号发生器:产生脉冲波形的信号。
4. 函数信号发生器:可以产生多种波形的信号。
请注意,以上内容仅为示例,具体的习题答案应根据实际的课程内容和习题要求进行编写。
《电子测量技术》CH1-CH4习题参考答案

f 0 min
=
f i1 N1 10
+
fi2 N 2
= 1K ´1000 + 100K ´ 720 = 72100KHz = 72.1MHz 10
当 N1 , N 2 分别取最大值时 f0 最大,
f 0 max
=
f i1N1 10
+
fi2 N 2
= 1K ´1100 + 100K ´1000 = 10110KHz = 100.11MHz 10
即 y ' = y = 5 = 0.5 cm。 k 10
7
5、被测脉冲信号峰峰值为 8V,经衰减量为 10 倍的探头引入示波器,“倍率”置“×5”位,“偏 转灵敏度微调”置“校正”位,要想在荧光屏上获得峰峰高度为 8cm 的波形,“Y 轴偏转灵敏 度”开关“V/cm”应置哪一挡?
解:设 Y 轴偏转灵敏度开关置为 x V/cm,则有峰峰值为 8cm ´ x ´ 10 ¸ 5 = 8 V,所以
答:不考虑倍率开关时,
y1
=
VP-P h
= 5 =1 5
cm,由于倍率开关为“×5”,屏幕上波形偏转
增大 5 倍,所以屏幕上峰与峰之间的距离为 y = k1 ´ y1 = 5 ´1 = 5 cm。如果采用探头,对
输入有 10 倍衰减,输入示波器的电压减小 10 倍,相应屏幕上峰与峰之间的距离减小 10 倍,
解: f » 350 = 350 = 8.75MHz tr 40
f B ³ 3 f = 3 ´ 8.75MHz = 26.25MHz
2、用双踪示波器测量信号相位差,显示波形如图所示,已知 AB = 3cm,AC = 24cm,试求
这两个信号的相位差 Δψ。
电子测量课后习题答案

Rx
R2
Rx
R2 R3
R4
100 4781 1000
输入量x1、x2、x3之间互不相关,试计算y的扩展不 确定度。
解:
测量的数学模型为:
y f (x1, x2, x3) x1 x2x33
幂指数分别为:
p1 1,
p2
1 2
,
p3
3 2
由于各输入量的估计值互不相关,则:
3
ucrel y
[ piurel (xi )]2
i1
(2%)2
(
1 2
f 1 正弦波的频率范围:
t
2 Hz~50MHz
上限频率为: 50MHz
2.17 某示波器荧光屏的水平长度为10 cm,要 求显示频率为10 MHz的正弦信号的两个完整 周期的波形。求示波器应具有的时基因数。
Uy
t
Dt x
t 10cm
2• 1 10106
10
2 108 s/cm
2.18 有一正弦信号,使用偏转因数为10 mV/div 的示波器进行测量,测量时信号经过 10∶1 的 衰减探极加到示波器,测得荧光屏上波形的高 度为6.5 div,问该信号的峰值是多少?
)
1.5%
2
(
3 2
)
1.0%
2
2.61%
各输入量的自由度为:
1 8, 2 6,
3 10
有效自由度为:
eff
ucrel4 ( y) 3 [ piurel (xi )]4
i 1
i
(2.61%)4
(1 2%)4 0.51.5%4 (1.51%)4 18.134
8
6
10
取
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.3 已知可变频率振荡器频率f 1=2.4996~4.5000MHz ,固定频率振荡器频率f 2=2.5MHz ,若以f 1和f 2构成一差频式信号发生器,试求其频率覆盖系数,若直接以f 1构成一信号发生器,其频率覆盖系数又为多少? 解:因为差频式信号发生器f 0= f 1-f 2所以输出频率范围为:400Hz ~2.0000MHz频率覆盖系数301055000Hz400MHz0000.2⨯===k如果直接以f 1构成一信号发生器,则其频率覆盖系数8.1.4996MHz2MHz5000.40≈='k3.4 简述高频信号发生器主要组成结构,并说明各组成部分的作用? 答:高频信号发生器主要组成结构图如下图所示:(1)主振级产生具有一定工作频率范围的正弦信号,是信号发生器的核心。
(2)缓冲级主要起阻抗变换作用,用来隔离调制级对主振级可能产生的不良影响,以保证主振级工作的稳定。
(3)调制级主要进行幅度调制和放大后输出,并保证一定的输出电平调节和输出阻抗。
(4)输出级进一步控制输出电压的幅度,使最小输出电压达到μV 数量级。
3.5 要求某高频信号发生器的输出频率f =8~60MHz ,已知其可变电容器的电容C 的变化范围为50pF~200pF ,请问该如何进行波段划分,且每个波段对应的电感应为多大?解:2502002121minmax maxmin min max ===C CLC LC f f k ==ππ 而5.7Hz80MHz6==∑k ,n k k =∑ 高频信号发生器原理框图输出443.3255.0875.08.1lg 5.7lg 9.0lg lg ≈====∑k k n由MHz 8pF2002121maxmin ==L LC f ππ=,所以H 979.10μ=L相邻波段的电感值满足:21k L L nn =-,所以可以计算得出 H 495.01μ=LH 124.02μ=LH 031.01μ=L3.8 简述各种类型的信号发生器的主振器的组成,并比较各自特点。
答:(1)低频信号发生器的主振器组成为:RC 文氏桥式振荡器,其特点是频率稳定,易于调节,并且波形失真小和易于稳幅。
(2)高频信号发生器的主振器组成为:LC 三点式振荡电路,主振级的电路结构简单,输出功率不大,一般在几到几十毫瓦的范围内。
(3)脉冲信号发生器的主振器组成为:可采用自激多谐振荡器、晶体振荡器或锁相振荡器产生矩形波,也可将正弦振荡信号放大、限幅后输出,作为下级的触发信号。
对主振级输出波形的前、后沿等参数要求不很高,但要求波形的一致性要好,并具有足够的幅度。
3.9 XFG-7高频信号发生器的频率范围为f=100kHz~30MHz ,试问应划分几个波段?(为答案一致,设k=2.4) 解:而30000KHz10MHz3==∑k ,n k k =∑84.7334.0477.24.29.0lg 300lg 9.0lg lg ≈==⨯==∑k k n3.10 简述合成信号源的的各种频率合成方法及其优缺点。
答:合成信号源的的各种频率合成方法主要有模拟直接合成法,数字直接合成法和锁相环频率合成法。
模拟直接合成法特点:虽然转换速度快(μs 量级),但是由于电路复杂,难以集成化,因此其发展受到一定限制。
数字直接合成法:基于大规模集成电路和计算机技术,尤其适用于函数波形和任意波形的信号源,将进一步得到发展。
但目前有关芯片的速度还跟不上高频信号的需要,利用DDS 专用芯片仅能产生100MHz 量级正弦波,其相位累加器可达32位,在基准时钟为100MHz 时输出频率分辨力可达0.023Hz ,可贵的是这一优良性能在其它合成方法中是难以达到的。
锁相环频率合成法:虽然转换速度慢(ms 量级),但其输出信号频率可达超高频频段甚至微波、输出信号频谱纯度高、输出信号的频率分辨力取决于分频系数N ,尤其在采用小数分频技术以后,频率分辨力大力提高。
3.11 简述直接数字频率合成原理,试设计一个利用微处理器产生任意波形发生器的方案,并讨论如何提高任意波形的频率?答:在存储器里存储任意波形的数字量,通过微处理器以一定的时间间隔读取数据,并送D/A 转换器进行转换,并将电压信号送滤波器进行滤波,一直以相同的转换时间间隔取下一个数进行转换,这样就可得到任意波形发生器。
提高任意波形频率的方法有:(1)减小读取时间间隔,并采用转换速度较快的D/A 转换器; (2)采用读取时间短的存储器; (3)一个周期转换的点数减小。
3.12有一频率合成器如图3.37所示,求: (1)f 0的表达式; (2)f 0的范围;(3)最小步进频率。
解:由图可知:(1)3011f f f N -=232100N f f = 所以10022110f N f N f += (2)1000~5601=N6000~50002=N图3.37 题3.12图MHz KHz KHzKHz f f f 650.556501001500010560100500056021min 0==⨯+⨯=+= MHz KHz KHzKHz f f f 060.1010060100160001010001006000100021max 0==⨯+⨯=+= (3)因为N1和N2均可改变,但f0表达式中,N2的系数小,所以N2变化1得到的f0的变化最小,即f0的最小步进频率为Hz KHzf f 10100110020===∆ 3.13 计算下图所示锁相环的输出频率范围及步进频率。
解:(a )m f n f r 0=,所以n m f f r =0,步进maxn fr (b )10N f f P f rH r -=,所以rH r f P N f f +=1,步进maxP fr (c )设VCO1输出频率为f 1,则111N f f r =,111N f f r =, 2022110N f f N f r =+,2211222112221010)10()10(N f Nf N f N N f N f N f f r r r r r +=+=+= )1000~720(10010)1100~1000(10kHz kHz f +=(b) 图3.38 题3.13图(c )MHzkHz kHz f L 1.7272010010100010=⨯+⨯=MHz kHz kHz f H 11.100100010010110010=⨯+⨯=步进Hz kHz 1001011=⨯ 3.15 AD9850 DDS 中如果时钟频率f c =125MHz ,相位累加器宽度N =32位,频率控制字k=0100000H ,这时输出频率为多少?解:k=0100000H ,所以A 20=1,因为DDS :Hz MHz A f A f A f A f A f f c c c c c out 578125.30517212522222122012032131302311===++⋅⋅⋅++=30.518KHz =4.3 分析通用计数器测量频率和周期的误差,以及减小误差的方法。
答:通用计数器测量频率的误差:即±1误差和标准频率误差。
一般总误差可采用分项误差绝对值合成,即)1(cc x x x f f T f f f ∆+±=∆ 通用计数器测量周期的误差:主要有三项,即量化误差、转换误差以及标准频率误差。
其合成误差可按下式计算 ⎪⎪⎭⎫⎝⎛∆+⨯+±=∆c c m n c x n x x f f U U f T T T π21101 减少测频误差的方法:在x f 一定时,闸门时间T 选得越长,测量准确度越高 减少测周误差的方法:1)采用多周期测量可提高测量准确度; 2)提高标准频率,可以提高测周分辨力; 3)测量过程中尽可能提高信噪比V m /V n 。
4.8 用计数式频率计测量频率,闸门时间(门控时间)为l s 时,计数器读数为5400,这时的量化误差为多大?如将被测信号倍频4倍,又把闸门时间扩大到5倍,此时的量化误差为多大?解:(1)量化误差%019.0154001±=±=±=∆Tf N N x (2)量化误差%00095.020%019.02015411±=±=±=⨯±=''±='∆Tf T f T f N N x x x4.9用一个7位电子计数器测量一个f x =5MHz 的信号频率,试分别计算当“闸门时间”置于1s 、0.1s 和10ms 时,由±1误差产生的测频误差。
解:闸门时间为1s 时,±1误差71021511-⨯±=⨯±=±=∆MHz T f N N x 闸门时间为0.1s 时,±1误差61021.0511-⨯±=⨯±=±=∆MHz T f N N x 闸门时间为10ms 时,±1误差510201.0511-⨯±=⨯±=±=∆MHz T f N N x 4.10 用某计数式频率计测频率,已知晶振频率f c 的相对误差为Δf c /f c =±5×10-8,门控时间T =1s ,求:(1)测量f x =10MHz 时的相对误差;(2)测量f x =10KHz 时的相对误差,并找出减小测量误差的方法。
解:测频±1误差)1(cc x s x x f f f T f f ∆+±=∆ (1)786105.1)105101011(--⨯±=⨯+⨯⨯±=∆x x f f (2)483100005.1)105101011(--⨯±=⨯+⨯⨯±=∆x x f f 对相同闸门时间下,当被测频率越高时,测频相对误差越小,同时晶振频率误差影响也越大。
4.11 用某计数式频率计测周期,已知晶振频率f c 的相对误差为Δf c /f c =±5×10-8,时基频率为10MHz ,周期倍乘100。
求测量10μs 周期时的测量误差。
解:计数器测周期误差4866100005.1)105101010101001()101(---⨯=⨯+⨯⨯⨯⨯±=∆+±=∆c c C x n x x f f f T T T 4.12 用某电子计数器测一个f x =10Hz 的信号频率,当信号的信噪比S/N =20dB 时,分别计算当“周期倍乘”置于×1和×100时,由于转换误差所产生的测周误差,并讨论计算结果。
解:由转换误差产生的测周误差为:mnn xxU U T T ⨯⨯=∆π1021 因为:20lg20=n m U U ,所以10=nm U U所以“周期倍乘”置于×1时:0282.010121=⨯⨯=∆πx x T T 所以“周期倍乘”置于×100时:000282.010110021=⨯⨯⨯=∆πxxT T 由测周误差可知,增大“周期倍乘”可以减少由转换误差产生的测周误差。
