圆锥曲线的切点弦方程培训资料

合集下载

圆锥曲线切点弦的性质及其应用

圆锥曲线切点弦的性质及其应用
圆锥曲线切点弦：融会贯通几何与动力学，开启创新之路。

圆锥曲线切点弦是椭圆曲线的重要特性，它联系着椭圆的焦点和它的椭圆杆（即椭圆的直径）。

它的形状随着半焦距的变化而变化，特
别是在不同的椭圆形状和焦距之间形成的拐角处。

它的性质主要有以
下几点：
1. 确定椭圆曲线的所有焦点，涉及到椭圆曲线圆锥曲线切点弦的计算。

2. 定义和计算椭圆曲线的一系列弦上的垂直线段，两条垂直线段之间
形成拐角处。

3. 弦上的点分为两种，一种是椭圆曲线切点弦上的点，另一种是椭圆
曲线周边环上的点。

应用：
1. 通过圆锥曲线切点弦，可以计算激光切割机机头运动轨迹。

2. 也可以用圆锥曲线切点弦来计算图形的面积。

3. 圆锥曲线切点弦特性也可以用来解决物体移动时其运动轨迹在椭圆曲线上的性质与特性。

圆锥曲线的切线与切点弦方程

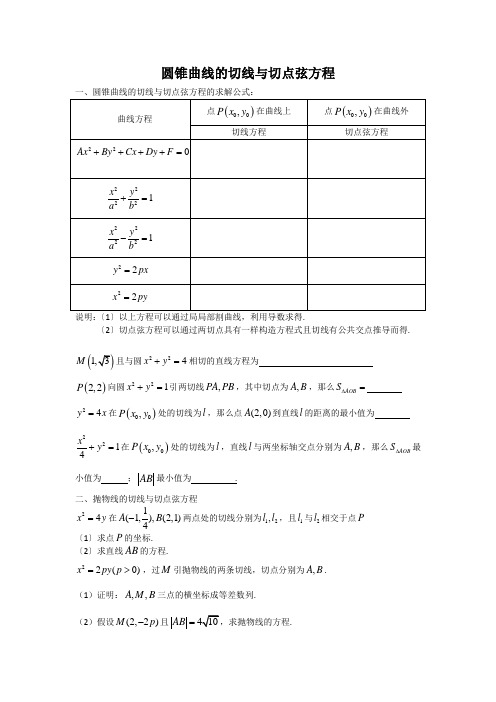
圆锥曲线的切线与切点弦方程说明：〔1〕以上方程可以通过局局部割曲线，利用导数求得.〔2〕切点弦方程可以通过两切点具有一样构造方程式且切线有公共交点推导而得.(M 且与圆224x y +=相切的直线方程为 ()2,2P 向圆221x y +=引两切线,PA PB ，其中切点为,A B ，那么AOB S ∆=24y x =在()00,P x y 处的切线为l ，那么点(2,0)A 到直线l 的距离的最小值为 2214x y +=在()00,P x y 处的切线为l ，直线l 与两坐标轴交点分别为,A B ，那么AOB S ∆最小值为；AB 最小值为 .二、抛物线的切线与切点弦方程24x y =在1(1,),(2,1)4A B -两点处的切线分别为12,l l ，且1l 与2l 相交于点P 〔1〕求点P 的坐标.〔2〕求直线AB 的方程.22(0)x py p =>，过M 引抛物线的两条切线，切点分别为,A B .（1）证明：,,A M B 三点的横坐标成等差数列.（2）假设(2,2)M p -且AB =.24x y =，过点P 的直线l 交抛物线于,A B 两点，分别以,A B 为切点的两切线12,l l . 〔1〕假设(2,2)P ，求1l 与2l 交点M 的轨迹方程.〔2〕假设点P 为抛物线的焦点F ，证明：〔i 〕MF AB ⊥；〔ii 〕MA MB ⊥.C ：22x py =的焦点(0,)F c (0)c >到直线l ：20x y --=的距离为322，设P 为直线l 上点，过点P 作抛物线的两条切线12,l l ，求切点分别为,A B .〔1〕求抛物线C 的方程；〔2〕当00(,)P x y 为定点时，求直线AB 的方程；〔3〕当P 在直线上运动时，求FA FB ⋅的最小值. 1C ：22221x y a b+=的两个焦点1(2,0)F -，2(2,0)F ，点(2,3)A 在椭圆上，过点A 的直线l 与抛物线2C ：24x y =交于,B C 两点，抛物线2C 在,B C 两点处的切线分别为12,l l 且1l 与2l 相交于点P .〔1〕求椭圆1C 的方程；〔2〕是否存在满足1212PF PF AF AF +=+的点P ，假设存在，请指出个数？假设不存在说明理由.。

专题14 圆锥曲线切线方程微点1 圆锥曲线切线方程的求法

专题14 圆锥曲线切线方程微点1 圆锥曲线切线方程的求法专题14 圆锥曲线切线方程微点1 圆锥曲线切线方程的求法【微点综述】圆锥曲线的切线方程问题侧重于考查圆锥曲线的性质、标准方程以及直线方程的几种形式．此类问题的难度一般不大，对同学们的抽象思维和分析能力的要求较高．下面主要探讨一下求圆锥曲线的切线方程的方法及常用结论．一、圆锥曲线切线方程方法 1．向量法在求圆的切线方程时，可巧妙利用圆心和切点的连线垂直于切线的性质来建立关系式．在运用向量法解题时，可先给各条线段赋予方向，求得各条直线的方向向量，然后根据“互相垂直的两个向量的数量积为0”的性质建立圆心、切点、切线之间的关系式，从而求得切线的方向向量以及直线的方程．例11．已知圆O 的方程是()()222x a y b r -+-=，求经过圆上一点()00,M x y 的圆的切线l 的方程． 2．变换法设椭圆方程为22221x y a b +=，我们作变换：,,x au y bv =⎧⎨=⎩则可把椭圆化为单位圆：221u v +=，从而可将求椭圆的切线方程问题转化为求圆的切线问题．例22．求过椭圆221169x y +=上一点M ⎛ ⎝⎭的切线l 方程． 3．判别式法可以利用一元二次方程根的判别式来求圆锥曲线的切线方程，这种方法也是中学阶段的常用方法之一．思维导图：设切线方程⇒联立切线与椭圆的方程⇒消去y （或x ）得到关于x （或y ）的一元二次方程⇒Δ0=求切线斜率⇒写出切线方程．注意：过双曲线的对称中心不可能作出直线与双曲线相切．例33．求经过点()2,1M 的双曲线：2222x y -=的切线l 的方程． 4．导数法我们知道，导数的几何意义是：该函数曲线在某一点上的切线的斜率，那么在求圆锥曲线的切线方程时，可对曲线的方程进行求导，便可得到曲线在切点处切线的斜率或切点的坐标，根据直线的点斜式方程即可求得切线的方程．例44．设为,A B 曲线2:4x C y =上两点，,A B 的横坐标之和为4．设M 为曲线C 上一点，C在M 处的切线与直线AB 平行，且AM BM ⊥，求直线AB 的方程．例55．证明：过椭圆C ：22221x y m n+=(m >n >0)上一点Q (x 0，y 0)的切线方程为00221x x y y m n +=．5．几何性质法通过对椭圆、双曲线以及抛物线的几何性质的研究，我们知道：（1）若焦点为12,F F 的椭圆或双曲线上有一点M ，则12F MF ∠的平分线一定与圆锥曲线相切；（2）若焦点为F 的抛物线上有一点M ，过M 作准线的垂线，垂足为N ，则FN 的中点P 与M 的连线PM 必与抛物线相切．据此，我们也可以利用圆锥曲线的几何性质作出其切线，然后再求出切线的方程．例66．求抛物线2:8C y x =上经过点()8,8M 的切线l 的方程．例77．过抛物线准线上任一点作抛物线的切线，则过两切点的弦必过焦点．例8（2022乙卷理科）8．已知抛物线C ：()220x py p =>的焦点为F ，且F 与圆M ：()2241y x ++=上点的距离的最小值为4． (1)求p ；(2)若点P 在M 上，P A ，PB 为C 的两条切线，A ，B 是切点，求△P AB 面积的最大值．【强化训练】（2022桃城区校级模拟）9．已知圆22:1C x y +=，直线:2l x =，P 为直线l 上的动点，过点P 作圆C 的切线，切点分别为A ，B ，则直线AB 过定点（）A ．1,02⎛⎫ ⎪⎝⎭B ．(0,2)C ．(2,1)D ．1,12⎛⎫ ⎪⎝⎭（2022聊城一模）10．已知圆22:1C x y +=，直线:20l x y ++=，P 为直线l 上的动点，过点P 作圆C 的两条切线，切点分别为A ，B ．则直线AB 过定点（） A ．11,22⎛⎫-- ⎪⎝⎭B ．()1,1--C ．11,22⎛⎫- ⎪⎝⎭D ．11,22⎛⎫- ⎪⎝⎭（2022迎泽区校级月考）11．已知圆()22:14C x y -+=.动点P 在直线280x y +-=上，过点P 引圆的切线，切点分别为,A B ，则直线AB 过定点______.12．过圆2216x y +=外一点P （4，2）向圆引切线． (1)求过点P 的圆的切线方程；(2)若过点P 的直线截圆所得的弦长为(3)若过P 点引圆的两条切线，切点分别为1P 、2P ，求过切点1P 、2P 的直线方程．（2021春·黑龙江期中）13．已知点(10,3)P 在椭圆222:199x y C a +=上.若点()00,N x y 在圆222:M x y r +=上，则圆M 过点N 的切线方程为200x x y y r +=.由此类比得椭圆C 在点P 处的切线方程为（）A ．13311x y+= B ．111099x y += C ．11133x y += D ．199110x y += （2020．新课标△）14．已知△M ：222220x y x y +---=，直线l ：220x y ++=，P 为l 上的动点，过点P 作△M 的切线,PA PB ，切点为,A B ，当||||PM AB ⋅最小时，直线AB 的方程为（） A ．210x y --= B ．210x y +-= C ．210x y -+= D ．210x y ++=（2022宿州期末）15．定义：若点()00,P x y 在椭圆()222210x y a b a b+=>>上，则以 P 为切点的切线方程为：00221x x y y a b +=.已知椭圆 22:132x y C +=，点M 为直线260x y --=上一个动点，过点M 作椭圆C 的两条切线 MA ，MB ，切点分别为A ，B ，则直线AB 恒过定点（） A ．11,23⎛⎫- ⎪⎝⎭B ．11,23⎛⎫- ⎪⎝⎭C ．12,23⎛⎫- ⎪⎝⎭D ．12,23⎛⎫- ⎪⎝⎭（2022金安区校级期末）16．已知椭圆具有如下性质：若椭圆的方程为()222210x y a b a b+=>>，则椭圆在其上一点()00,A x y 处的切线方程为00221x x y ya b+=，试运用该性质解决以下问题；椭圆221:12x C y +=，点B 为1C 在第一象限中的任意一点，过B 作1C 的切线l ，l 分别与x 轴和y 轴的正半轴交于,C D 两点，则OCD 面积的最小值为（） A ．1BCD ．2（2022吉安期末理）17．过圆222x y r +=上一定点(),o o P x y 的圆的切线方程为20o x x y y r +=.此结论可推广到圆锥曲线上.过椭圆221124x y +=上的点()3,1A -作椭圆的切线l .则过A 点且与直线l 垂直的直线方程为（） A ．20?x y +-= B ．30x y --= C ．2330x y +-= D ．3100x y --=（2022大连期末）18．已知()11,M x y 为圆22:1C x y +=上一点，则过C 上点M 的切线方程为________，若()22,N x y 为椭圆2222:1(0)x y E a b a b+=>>上一点，则过E 上点N 的切线方程为_____________. （2022泸县校级一模）19．椭圆223144x y +=上点P (1,1)处的切线方程是______．（2022金安区校级模拟）20．一般情况下，过二次曲线Ax2+By2=C （ABC ≠0）上一点M （x0，y0）的切线方程为Ax0x+By0y=C ，．若过双曲线22221(0,0)x y a b a b -=>>上一点M （x0，y0）（x0＜0）作双曲线的切线l ，已知直线l 过点N 0,2b ⎛⎫⎪⎝⎭，且斜率的取值范围是⎣，则该双曲线离心率的取值范围是______．（2022兴庆区校级一模）21．已知()00,P x y 是抛物线()220y px p =>上的一点，过P 点的切线方程的斜率可通过如下方式求得在22y px =两边同时求导，得：2'2yy p =，则'py y=，所以过P 的切线的斜率0p k y =.试用上述方法求出双曲线22y x 12－＝在P 处的切线方程为_________.（2022亳州期末）22．已知椭圆C 的方程为()222210x y a b a b+=>>，离心率12e =，点P (2，3)在椭圆上．(1)求椭圆C 的方程(2)求过点P 的椭圆C 的切线方程(3)若从椭圆一个焦点发出的光线照到点P 被椭圆反射，证明：反射光线经过另一个焦点．（2022福州二模）23．已知椭圆C ：()222210x y a b a b+=>>的离心率为12，点31,2⎛⎫ ⎪⎝⎭在椭圆C 上．(1)求椭圆C 的方程；(2)若椭圆C 的两条切线交于点M （4，t ），其中t R ∈，切点分别是A 、B ，试利用结论：在椭圆22221x y a b+=上的点()00,x y 处的椭圆切线方程是00221x x y y a b +=，证明直线AB 恒过椭圆的右焦点2F ；(3)试探究2211AF BF +的值是否恒为常数，若是，求出此常数；若不是，请说明理由．（2022香坊区校级三模）24．已知点1(,2)2D -，过点D 作抛物线21:C x y =的两切线，切点为,A B .（1）求两切点,A B 所在的直线方程；（2）椭圆22221(0)x y a b a b +=>>（1）中直线AB 与椭圆交于点P ，Q ，直线,,PQ OP OQ 的斜率分别为k ，1k ，2k ，若123k k k +=，求椭圆的方程. （2022渝中区校级月考）25．已知椭圆22122:1x y C a b+=()0a b >>的离心率为12，过点)E的椭圆1C 的两条切线相互垂直.（△）求椭圆1C 的方程；（△）在椭圆1C 上是否存在这样的点P ，过点P 引抛物线22:4C x y =的两条切线12,l l ，切点分别为,B C ，且直线BC 过点()1,1A ？若存在，指出这样的点P 有几个（不必求出点的坐标）；若不存在，请说明理由. （2022杭州模拟）26．已知曲线1C 上任意一点到()0,1F 的距离比到x 轴的距离大1，椭圆2C 的中心在原点，一个焦点与1C 的焦点重合，长轴长为4．(1)求曲线1C 和椭圆2C 的方程；(2)椭圆2C 上是否存在一点M ，经过点M 作曲线1C 的两条切线,MA MB （,A B 为切点）使得直线AB 过椭圆的上顶点，若存在，求出切线,MA MB 的方程，不存在，说明理由．参考答案：1．()()()()200x a x a y b y b r --+--=【分析】设切线l 上任意一点N 的坐标是(),x y ，利用0OM ON ⋅=化简整理可得. 【详解】设切线l 上任意一点N 的坐标是(),x y ，由已知得圆心(),O a b ，()()0000,,,OM x a y b MN x x y y ∴=--=--，又0OM ON ⋅=，即()0000()()()0x x x a y y y b --+--= 所以()()()()()()00000x a x a x a y b y b y b ----+----=⎡⎤⎡⎤⎣⎦⎣⎦， △过圆上的点()00,M x y 的圆的切线l 的方程是：()()()()()()220000x a x a y b y b x a y b --+--=-+-，又()()22200x a y b r -+-=，△所求圆的切线l 的方程为()()()()200x a x a y b y b r --+--=．2．340x y +-=【分析】令,43yx u v ==，利用伸缩变换求得椭圆和点M 在新坐标系下的方程和坐标，然后由圆的切线方程和伸缩变换公式可得.【详解】令,43y x u v ==，则椭圆在新坐标系uOv 下的方程是：221u v +=，点M ⎛ ⎝⎭在新坐标系uOv 下的坐标是：⎝⎭，设过圆221u v +=上的点⎝⎭的切线方程为(22v k u -=-（易得斜率必存在），即(v k u =221u v +=整理得2221(1)(1)(21)02k u k u k k +-+--=由题意可知，22222(1)2(1)(21)0k k k k k =--+--=Δ，整理得2(1)0k +=即1k =-，所以切线方程为(v u =-，即：u v +=∴过椭圆上一点M 的切线l的方程是：43x y+340x y +-=． 3．10x y --=【分析】设直线，与双曲线联立，结合判别式分析，即得解【详解】若直线斜率不存在，过点()2,1M 的直线方程为：2x =，代入2222x y -=可得21y =，与双曲线有两个交点，不是切线；若直线斜率存在，设l 的方程是：()12y k x -=-，即：21y kx k =-+，将它代入方程2222x y -=整理得：()()()222214218840k x k k x k k ---+-+=，由已知20210,k -∆=≠，即()()()2224214218840k k k k k -----+=⎡⎤⎣⎦，解得：1k =，故所求切线l 的方程为：21y x =-+，即：10x y --=． 4．7y x =+【分析】在求得直线AB 的斜率后，便可运用导数法对抛物线的方程求导，得出点M 的坐标，再根据韦达定理和弦长公式求得切线的方程．【详解】设()()1122,,,A x y B x y ，则2212121212,,,444x x x x y y x x ≠==+=，于是直线AB 的斜率为121212121212()()14()4y y x x x x x x k x x x x -+-+====--，由24x y =，得2x y '=．设()33,M x y ，由题意可知：312x =，解得32x =，()2,1M ∴．设直线AB 的方程为y x m =+，故线段的中点为()2,2N m +，1MN m =+将y x m =+代入24x y =得2440x x m --=，当()1610m ∆=+>，即当1m >-时，12x =+22x =-从而可得12AB x =-= 因为AM BM ⊥，且BN AN =，因为直角三角形斜边上的中线等于斜边的一半，所以BN AN MN ==，所以2AB MN =，即()21m =+，解得7m =，直线AB 的方程为7y x =+． 5．证明见解析【分析】方法一：分0y >，0y <和0y =，当0y >，0y <时，利用导数求切线方程可得；方法二：设直线方程联立椭圆方程，利用判别式等于0求切点横坐标，然后可得切线方程. 【详解】法一：由椭圆C ：22221x y m n+=，则有22221y x n m =-当0y >时，y =2nx y m '=-，△当00y >时，2000222001x n n n k x x y mm m y n =-=-=-⋅． △切线方程为()200020x n y y x x m y -=-⋅-，整理为：222222220000n x x m y y m y n x m n +=+=，两边同时除以22m n 得：00221x x y ym n+=．同理可证：00y <时，切线方程也为00221x x y ym n+=．当0=0y 时，切线方程为x m =±满足00221x x y ym n+=．综上，过椭圆上一点00(,)Q x y 的切线方程为00221x x y ym n+=．法二：当斜率存在时，设切线方程为y kx t =+，联立方程：22221x y m ny kx t ⎧+=⎪⎨⎪=+⎩可得222222()n x m kx t m n ++=，化简可得： 22222222()2()0n m k x m ktx m t n +++-=，△由题可得：42222222244()()0m k t m n m k t n ∆=-+-=，化简可得：2222t m k n =+，△式只有一个根，记作0x ，220222m kt m kx n m k t =-=-+，0x 为切点的横坐标，切点的纵坐标200n y kx t t =+=，所以2020x m k y n =-，所以2020n x k m y =-，所以切线方程为：2000020()()n x y y k x x x x m y -=-=--，化简得：00221x x y ym n+=．当切线斜率不存在时，切线为x m =±，也符合方程00221x x y ym n+=，综上：22221x y m n+=在点00(,)x y 处的切线方程为00221x x y y m n +=．6．280x y -+=【分析】根据线段NF 的垂直平分线经过点M 即可求得切线方程.【详解】由抛物线2:8C y x =可得其焦点()2,0F ，准线方程为：2x =-，过点()8,8M 作准线的垂线，设垂足为N ，则N 的坐标为()2,8-，又设FN 的中点为P ，则P 的坐标为()0,4，如图所示：故直线PM 的方程为：84480y x --=-，即280x y -+=，△切线l 的方程为280x y -+=． 7．答案见解析.【分析】根据两切线方程分别为：()11y y p x x =+，()22y y p x x =+，且均过均过点P ，可知弦AB 方程为：02p y y p x ⎛⎫=- ⎪⎝⎭.【详解】以22y px =（p ＞0）为例说明．设点00(,)Q x y 是抛物线22y px =上的任意一点，则过点00(,)Q x y 且与抛物线相切的直线方程为00()y y k x x -=-，联立2002()y pxy y k x x ⎧=⎨-=-⎩得：222222000000(222)20k x k x p ky x k x y kx y -+-++-=，因为二者相切，所以Δ0=，即222222000000(222)4(2)0k x p ky k k x y kx y +--+-=，化简得：0p k y =，又2002y px =，代入00()y y k x x -=-得：()00y y p x x =+，即抛物线22y px =在00(,)Q x y 处的切线方程为()00yy p x x =+. 设准线上任一点0,2p P y ⎛⎫- ⎪⎝⎭，切点分别为()11,A x y 、()22,B x y ，则切线方程分别为：()11y y p x x =+，()22y y p x x =+两切线均过点P ，则满足1012p y y p x ⎛⎫=-+ ⎪⎝⎭，2022p y y p x ⎛⎫=-+ ⎪⎝⎭．故过两切点的弦AB 方程为：02p y y p x ⎛⎫=- ⎪⎝⎭，则弦AB 过焦点．【点睛】（1）点()00,P x y 是抛物线()220y mx m =≠上一点，则抛物线过点P 的切线方程是：()00y y m x x =+；（2）点()00,P x y 是抛物线()220x my m =≠上一点，则抛物线过点P 的切线方程是：()00x x m y y =+．8．(1)p ＝2(2)【分析】（1）先求42pFM =+，点F 到圆M 上的点的距离的最小值即为FM r -. （2）求出AB =和点P 到直线AB的距离d =322(6)2144PABb S ⎛⎫--+= ⎪⎝⎭△，根据b 的范围即可求最大值.（1）0,2p F ⎛⎫⎪⎝⎭到圆心4(0,)M -的距离42p FM +，所以点F 到圆M 上的点的距离的最小值为4142pFM r -=+-=，解得p ＝2；（2）由（1）知，抛物线的方程为24x y =，即214y x =，则12y x '=，设切点()11,A x y ，()22,B x y ，则易得PA l ：21124x x y x =-，△PB l ：22224x x y x =-，△联立△△可得1212,24x x x x P +⎛⎫⎪⎝⎭，设AB l ：y kx b =+，联立抛物线方程，消去y 并整理可得2440x kx b --=， △216160k b ∆=+>，即20k b +>，且124x x k +=，124x x b =-， △(2,)P k b -△AB ==点P 到直线AB 的距离d =△()322142PABS AB d k b ==+△△，又点(2,)P k b -在圆M ：()2241y x ++=上，故()22144b k --=，代入△得，332222(6)2112154444PAB b b b S ⎛⎫--+⎛⎫-+-== ⎪ ⎪⎝⎭⎝⎭△，而[]5,3p y b =-∈--，△当b ＝5时，()max=PAB S【点睛】(1)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似，一般要用到根与系数的关系；(2)有关直线与抛物线的弦长问题，要注意直线是否过抛物线的焦点，若过抛物线的焦点，可直接使用公式|AB |＝x 1＋x 2＋p ，若不过焦点，则必须用一般弦长公式． 9．A【分析】设(2,)P t ，圆心C 的坐标为(0,0)，可得以线段PC 为直径的圆N 的方程，两圆方程作差，得两圆公共弦AB 的方程可得答案．【详解】因为P 为直线l 上的动点，所以可设(2,)P t ，由题意可得圆心C 的坐标为(0,0)，以线段PC 为直径的圆N 的圆心为1,2⎛⎫⎪⎝⎭t P所以方程为2220x y x ty +--=，两圆方程作差，即得两圆公共弦AB 的方程为210x ty +-=，()210-+=x ty ，所以直线AB 过定点1,02⎛⎫⎪⎝⎭．故选：A. 10．A【分析】由P A △AC ，PB △BC 可知点A 、B 在以PC 为直径的圆上，设点P 坐标，写出以PC 为直径的圆的方程，然后可得直线AB 方程，再由直线方程可确定所过定点. 【详解】根据题意，P 为直线l ：20x y ++=上的动点，设P 的坐标为(),2t t --，过点P 作圆C 的两条切线，切点分别为A ，B ，则P A △AC ，PB △BC ，则点A 、B 在以PC 为直径的圆上，又由C （0，0），(),2P t t --，则以PC 为直径的圆的方程为：()()20x x t y y t -+++=，变形可得：()2220x y tx t y +-++=，则有22221(2)0x y x y tx t y ⎧+=⎨+-++=⎩，联立可得：()120tx t y -++=，变形可得：()120y t x y +--=，即直线AB 的方程为()120y t x y +--=，变形可得：()120y t x y +--=，则有1200y x y +=⎧⎨-=⎩，解可得1212x y ⎧=-⎪⎪⎨⎪=-⎪⎩，故直线AB 过定点11,22⎛⎫-- ⎪⎝⎭. 故选：A ． 11．118,77⎛⎫ ⎪⎝⎭【分析】根据题意，设P 的坐标为(82,)t t -，由圆的切线的性质分析可得则A 、B 在以CP 为直径的圆上，进而可得该圆的方程，进而分析可得直线AB 为两圆的公共弦所在直线的方程，由圆与圆的位置关系分析可得直线AB 的方程，据此分析可得答案．【详解】根据题意，动点P 在直线280x y +-=上，设P 的坐标为(82,)t t -，圆22:(1)4C x y -+=，圆心为(1,0)，过点P 引圆的切线，切点分别为A ，B ，则PA CA ⊥，PB CB ⊥，则A 、B 在以CP 为直径的圆上，该圆的方程为(1)[(82)](0)()0x x t y y t ---+--=，变形可得：22(92)(82)0x y t x ty t +---+-=，又由A 、B 在圆C 上，即直线AB 为两圆的公共弦所在直线的方程，则有2222230(92)(82)0x y x x y t x ty t ⎧+--=⎨+---+-=⎩，则直线AB 的方程为(711)(22)x t x y -=--，则有7110220x x y -=⎧⎨--=⎩，解可得：11787x y ⎧=⎪⎪⎨⎪=⎪⎩；故直线AB 恒过定点11(7，8)7；故答案为：11(7，8)7．【点睛】本题考查直线与圆的位置关系、公共弦方程求法、直线过定点问题，考查函数与方程思想、转化与化归思想，考查逻辑推理能力和运算求解能力，求解时注意两圆相减可得公共弦直线方程的应用. 12．(1)x ＝4或34200x y +-= (2)y ＝2或43100x y --= (3)280x y +-=【分析】（1）分k 不存在和k 存在两种情况讨论，利用圆心到直线距离等于半径，求解即可；（22，结合圆心到直线距离公式，可得解；（3）由题意12,,,P O P P 四点共圆，且PO 为直径，写出圆的方程，过切点1P 、2P 的直线即为圆22420x y x y +--=与圆2216x y +=的交线，求解即可. （1）当切线斜率不存在时，过点P （4，2）的直线为x ＝4，圆心到直线距离等于半径，故x ＝4为切线；当切线的斜率存在时，设切线方程为()24y k x -=-，即420kx y k --+=．4=，即430k +=解得：34k =-，此时切线方程为34200x y +-=．△过点P 的圆的切线方程为x ＝4或34200x y +-=；（2）由（1）知，所求切线斜率存在，设直线方程为420kx y k --+=．△r ＝4，且弦长为△圆心到直线420kx y k --+=的距离2d ==，即2340k k -= 解得k ＝0或43k =．△所求直线方程为y ＝2或43100x y --=；（3）由题意，1122,OP PP OP PP ⊥⊥ 故12,,,P O P P 四点共圆，且PO 为直径 △P （4，2），△以PO 为直径的圆圆心为(2,1)，半径||2PO r == 故圆的方程为()()22215x y -+-=，由于12,P P 也在圆2216x y +=上，故过切点1P 、2P 的直线为圆22420x y x y +--=与圆2216x y +=的公共弦两圆方程作差可得过1P 、2P 的直线方程为280x y +-=． 13．C【分析】先根据点在椭圆上，求得2a ，再类比可得切线方程. 【详解】因为点(10,3)P 在椭圆222:199x y C a +=上，故可得21009199a +=，解得2110a =；由类比可得椭圆C 在点P 处的切线方程为： 103111099x y +=，整理可得11133x y+=. 故选：C.【点睛】本题考查由椭圆上一点的坐标求椭圆方程，以及类比法的应用，属综合基础题. 14．D【分析】由题意可判断直线与圆相离，根据圆的知识可知，四点,,,A P B M 共圆，且AB MP ⊥，根据 44PAMPM AB SPA ⋅==可知，当直线MP l ⊥时，PM AB ⋅最小，求出以 MP 为直径的圆的方程，根据圆系的知识即可求出直线AB 的方程．【详解】圆的方程可化为()()22114x y -+-=，点 M 到直线l 的距离为2d =>，所以直线 l 与圆相离．依圆的知识可知，四点,,,A P B M 四点共圆，且AB MP ⊥，所以14442PAMPM AB SPA AM PA ⋅==⨯⨯⨯=，而PA =，当直线MP l ⊥时，min MP ， min 1PA =，此时PM AB ⋅最小． △()1:112MP y x -=-即 1122y x =+，由1122220y x x y ⎧=+⎪⎨⎪++=⎩解得，10x y =-⎧⎨=⎩．所以以MP 为直径的圆的方程为()()()1110x x y y -++-=，即 2210x y y +--=，两圆的方程相减可得：210x y ++=，即为直线AB 的方程．故选：D.【点睛】本题主要考查直线与圆，圆与圆的位置关系的应用，以及圆的几何性质的应用，意在考查学生的转化能力和数学运算能力，属于中档题． 15．C【解析】设()26,M t t +，()11,A x y ，()22,B x y ，即可表示出MA 的方程，又M 在MA 上，即可得到()1126132x t y t++=，即可得到直线AB 的方程，从而求出直线AB 过的定点；【详解】解：因为点M 在直线260x y --=上，设()26,M t t +，()11,A x y ，()22,B x y ，所以MA 的方程为11132x x y y+=，又M 在MA 上，所以()1126132x t y t ++=△，同理可得()2226132x t y t ++=△；由△△可得AB 的方程为()26132x t yt++=，即()22636x t yt ++=，即()()431260x y t x ++-=，所以4301260x y x +=⎧⎨-=⎩，解得1223x y ⎧=⎪⎪⎨⎪=-⎪⎩，故直线恒过定点12,23⎛⎫- ⎪⎝⎭故选：C 16．C【解析】设1111(,),(0,0)B x y x y >>，根据题意，求得过点B 的切线l 的方程，即可求得C 、D 坐标，代入面积公式，即可求得OCD 面积S 的表达式，利用基本不等式，即可求得答案. 【详解】设1111(,),(0,0)B x y x y >>，由题意得，过点B 的切线l 的方程为：1112x xy y +=，令0y =，可得12(,0)C x ，令0x =，可得11(0,)D y ，所以OCD 面积111112112S x y x y =⨯⨯=，又点B 在椭圆上，所以221112x y +=，所以121111121111122x y S x y x y x x y y +===+≥=当且仅当11112x y y x =，即111,x y ==时等号成立，所以OCD. 故选：C【点睛】解题的关键是根据题意，直接写出过点B 的切线方程，进而求得面积S 的表达式，再利用基本不等式求解，考查分析理解，计算化简的能力，属基础题. 17．A【解析】根据类比推理，可得直线l 的方程，然后根据垂直关系，可得所求直线方程.【详解】过椭圆221124x y +=上的点()3,1A -的切线l 的方程为31124x y-+=，即40x y --=，切线l 的斜率为1，与直线l 垂直的直线的斜率为-1，过A 点且与直线l 垂直的直线方程为(13)y x +=-一，即20x y +-=. 故选：A【点睛】本题考查类比推理以及直线的垂直关系，属中档题. 18． 111x x y y +=22221x x y ya b+= 【分析】由OM 垂直切线可求出切的斜率，再利用点斜式可求出过C 上点M 的切线方程；利用导数的几何意义在点()22,N x y 处切线的斜率，再利用点斜式求出直线方程【详解】解：因为11OM y k x =，切线与直线OM ，所以所求切线的斜率为11x y -，所以所求的切线方程为1111()x y y x x y -=--，即221111y y y x x x -=-+，得221111x x y y x y +=+，因为点()11,M x y 为圆22:1C x y +=上一点，所以22111x y +=，所以过C 上点M 的切线方程为111x x y y +=；当20y >时，设0y >，由22221x y a b +=得22221y x b a=- 22222y a x b a -= △22222()b y a x a =-△y = △1'222()(2)2b y a x x a-=-⋅-1222()bx a x a -=--=△过点()22,N x y的切线的斜率为△过点()22,N x y的切线的方程为22)y y x x -=-△点()22,N x y 在椭圆上，△2222221x y a b+=，222222222,a y a y b x a b b=+=， △2222()bx b y y x x a ay -=-⋅-，即222222()b xy y x x a y -=-- 2222222222a y y a y b x x b x -=-+，2222222222a y y b x x a y b x +=+，△222222a y y b x x a b +=，△所求的切线方程为22221x x y ya b+=，当20y <时，同理可得其切线方程为22221x x y ya b+=所以过E 上点()22,N x y 的切线方程为22221x x y ya b+=，故答案为：111x x y y +=；22221x x y ya b+= 【点睛】此题考查圆锥曲线的切线方程的求法，属于中档题 19．340x y +-=【分析】由导数的几何意义即可求得切线方程.【详解】△椭圆223144x y +=，△y >0时，y △23xy -'=， △x ＝1时，13y '=-，即切线斜率13k =-，△椭圆223144x y +=上点P (1,1)处的切线方程是()1113y x -=--，即340x y +-=．故答案为：340x y +-=． 20．【分析】求得切线方程，将N 代入切线方程，即可求得M 点坐标，求得切线方程，根据斜率公式及离心率公式即可求得答案．【详解】双曲线在M （x 0，y 0）的切线方程为00221x x y ya b-=，将N 代入切线方程，解得y 0＝﹣2b ，代入双曲线方程解得：x 0，21y b =，即y2bx +，由斜率的取值范围是⎣1≤b a ≤2，由双曲线的离心率e ＝c a1≤22b a ≤4，∴双曲线离心率的取值范围，故答案为:．【点睛】本题考查双曲线的切线方程的应用及离心率公式，考查转化思想，属于中档题．21．20-=x y【详解】分析：结合题中的方法类比求解切线方程即可.详解：用类比的方法对2212y x ＝－两边同时求导得，22x yy x y y '∴'=＝，，0002|2x x x k y y =∴='＝， △切线方程为2(y x ，整理为一般式即：20x y －.点睛：“新定义”主要是指即时定义新概念、新公式、新定理、新法则、新运算五种，然后根据此新定义去解决问题，有时还需要用类比的方法去理解新的定义，这样有助于对新定义的透彻理解.对于此题中的新概念，对阅读理解能力有一定的要求.但是，透过现象看本质，它们考查的还是基础数学知识，所以说“新题”不一定是“难题”，掌握好三基，以不变应万变才是制胜法宝. 22．(1)2211612x y +=；(2)280x y +-=； (3)证明见解析.【分析】（1）根据已知条件列方程组即可求出,,a b c .（2）由直线与椭圆相切，根据判别式Δ0=即可求出直线斜率k . （3）利用向量数量积证明直线1PF 与2F P 关于直线m 对称即可；【详解】（1）由题意可得：2222212491c a a b c a b ⎧=⎪⎪=+⎨⎪⎪+=⎩，解得216a =，212b =，△椭圆C 的方程为：2211612x y +=；（2）显然，过点P (2，3)的切线存在斜率，设切线l 的斜率为k ，则l ：3(2)y k x -=-，由22116123(2)x y y k x ⎧+=⎪⎨⎪-=-⎩得()()222348231648120k x k kx k k +--+--=，因为直线l 与椭圆C 相切，∴()()()2222Δ64234341648120k k k k k =--+--=，化为：24410k k ++=，解得12k =-．△求过点P 的椭圆切线方程为280x y +-=．（3）证明：△椭圆C 的方程为：2211612x y +=，则椭圆左右焦点分别为()12,0F -，()22,0F ， △过点P 的椭圆切线方程为280x y +-=， △过点P 的椭圆法线方程为m ：210x y --=，法线的方向向量()1,2m =--， △()14,3PF =--，()20,3PF =-， △1112cos ,PF mPF m PF m⋅==-，2222cos ,PF mPF m PF m⋅==- △直线1PF ，2F P 关于直线m 对称；△从椭圆一个焦点发出的光线照到点P ，被椭圆反射后，反射光线一定经过另一个焦点．【点睛】求椭圆的标准方程有两种方法：△定义法：根据椭圆的定义，确定a 2，b 2的值，结合焦点位置可写出椭圆方程．△待定系数法：若焦点位置明确，则可设出椭圆的标准方程，结合已知条件求出a ，b ；若焦点位置不明确，则需要分焦点在x 轴上和y 轴上两种情况讨论，也可设椭圆的方程为Ax 2＋By 2＝1(A >0，B >0，A ≠B )． 23．(1)22143x y +=(2)证明见解析(3)是，常数为43【分析】（1）代入点坐标，结合2221b e a=-求解即可；（2）根据结论设出切线方程，两条切线交于点M （4，t ），可得点A 、B 的坐标都适合方程13tx y +=，求出定点坐标即可；（3）联立直线AB 与椭圆，点点距公式表示22,AF BF ，结合韦达定理化简即得解【详解】（1）△椭圆C ：()222210x y a b a b+=>>的离心率为12，点31,2⎛⎫ ⎪⎝⎭在椭圆C 上．△222314b e a =-=，△221914a b +=，△，由△△得：24a =，23b =，△椭圆C 的方程为22143x y +=．（2）证明：设切点坐标()11,A x y ，()22,B x y ，则切线方程分别为11143x x y y+=，22143x x y y +=．又两条切线交于点M （4，t ），即1113t x y +=，2213tx y +=，即点A 、B 的坐标都适合方程13tx y +=，令0y =，可得1x = 故对任意实数t ，点（1，0）都适合这个方程，故直线AB 恒过椭圆的右焦点()21,0F ．（3）将直线AB 的方程13tx y =-+，代入椭圆方程，得223141203t y y ⎛⎫-++-= ⎪⎝⎭，即2242903t y ty ⎛⎫+--= ⎪⎝⎭， △122612t y y t +=+，1222712y y t =-+，不妨设10y >，20y <，21AF y =，同理22BF y =，△211212221111y y y y y y AF BF -⎫+=-=⎪⎭1243==，△2211AF BF +的值恒为常数43． 24．（1）2y x =+；（2）2214812x y +=. 【分析】（1）设出切点，利用切点处的导数是斜率，表示出切线方程，1(,2)2D -在切线上，求出两解，分别对应切点,A B 坐标，则方程可求. （2a b 、的一个关系；联立直线和椭圆方程，用上韦达定理，结合123k k k +=，再建立a b 、的一个关系，则椭圆方程可求. 【详解】解：（1）设切点11(,)A x y 22(,)B x y ，则221122,x y x y ==切线的斜率为2y x '=，所以抛物线上过11(,)A x y 点的切线的斜率为12x ，切线方程为()2111112,2y y x x x y x x x -=-=-，1(,2)2D -在切线上，所以21120x x --=，12x =或11x =-，当12x =时，2114y x ==；当11x =-，2111y x ==，不妨设()(2,4),1,1A B -，1AB k =，所以两切点,A B 所在的直线方程2y x =+.（2）由e =2234c a =，又222c a b =-，所以224a b =.222244y x x y b=+⎧⎨+=⎩，得225161640x x b ++-=， 21651645P Q P Q x x b x x ⎧+=-⎪⎪⎨-⎪=⎪⎩， 21,Q PP Qk k y y x x ==， 1k =，又因为123k k k +=，()()3,3,223P Q P Q Q P Q Q P P P Q P Q P Qx x x x y y x y x y x x x x x x ++++===+，()2P Q P Q x x x x +=，22161642,1255b b --⨯==，248a =，所以椭圆的方程2214812x y +=.【点睛】以直线和抛物线、椭圆的位置关系为载体，考查求直线方程、椭圆方程的方法；中档题.25．(△)22143x y +=；(△)满足条件的点P 有两个.【详解】试题分析：(1) 结合椭圆的离心率可求得1c =，则椭圆方程为22143x y +=.(2)由题意首先求得切线方程的参数形式，据此可得直线BC 的方程为002x y x y =-，则点P 的轨迹方程为112y x =-，原问题转化为直线112y x =-与椭圆1C 的交点个数，即满足条件的点P 有两个. 试题解析：（△）由椭圆的对称性，不妨设在x 轴上方的切点为M ，x 轴下方的切点为N ，则1NE k =，NE的直线方程为y x =因为椭圆22122:1x y C a b+= ()0a b >>的离心率为12，所以椭圆22122:143x y C c c+=，所以22221,43y x x y c c ⎧=⎪⎨+=⎪⎩ 0∆=，则1c =，所以椭圆方程为22143x y +=.（△）设点()11,B x y ，()22,C x y ，()00,P x y ，由24x y =，即214y x =，得12y x '=，△抛物线2C 在点B 处的切线1l 的方程为()1112x y y x x -=-，即2111122x y x y x =+-， △21114y x =，△112x y x y =-.△点()00,P x y 在切线1l 上，△10012x y x y =-.△ 同理，20022x y x y =-.△ 综合△、△得，点()11,B x y ，()22,C x y 的坐标都满足方程002xy x y =-. △经过()11,B x y ，()22,C x y 两点的直线是唯一的， △直线BC 的方程为002x y x y =-， △点()1,1A 在直线BC 上，△00112y x =-， △点P 的轨迹方程为112y x =-.又△点P 在椭圆1C 上，又在直线112y x =-上， △直线112y x =-经过椭圆1C 内一点()0,1-， △直线112y x =-与椭圆1C 交于两点. △满足条件的点P 有两个.26．(1)21:4C x y =，222:134x y C +=(2)2y =-【分析】(1)依据曲线1C 和椭圆的定义求方程.(2) 假设点M 存在，设切线方程，M 即在抛物线又在椭圆上找到等量关系.【详解】（1）由曲线1C 上任意一点到F （0，1）的距离比到x 轴的距离大1，根据抛物线的定义，曲线1C 为以F （0，1）为焦点的抛物线，则曲线1C ：24x y =；设椭圆2C 的方程()222210y x a b a b+=>>，由24a =，a ＝2，c ＝1，2223b a c =-=，△椭圆2C ：22143y x +=；（2）若存在，由题意设AB 方程：y ＝kx +2代入24x y =，化简得2480x kx --=，设()11,A x y ，()22,B x y ，则124x x k +=，128x x =-，△ 由于12y x '=，△切线MA 方程为：()11112y y x x x -=-，即2111124y x x x =-，△同理切线MB 方程为：2221124y x x x =-，△ 由△△得1212,24x x x x M +⎛⎫⎪⎝⎭，△M （2k ，-2），又M （2k ，-2）在椭圆上，24113k +=可得：k ＝0，△M （0，-2）k ＝0代入△有：1x =2x =-△椭圆2C 上存在一点M （0，-2）符合题意，此时两条切线的方程为2y =-．【点睛】本题要证明切点弦过定点，设切点弦的直线方程，得到韦达定理，然后通过切点写出两条切线方程，可以得到交点M 的坐标，由点M 的特性可以求出M 坐标，进而求出切点，写出切线方程．。

高考高频考点(圆锥曲线)3、圆的切线、切点弦结论

第3讲圆的切线、切点弦结论知识与方法1求过圆()()222:C x a y b r −+−=上一点()00,P x y 的圆C 的切线的步骤如下：（1）先验证经过点P 且垂直于x 轴的直线是否和圆C 相切，若是，如图1所示，所求切线为0x x =，问题求解完毕；若否，则进行下一步；（2）设切线斜率为k ，如图2所示，由PC ⊥切线，求出k ，用点斜式写出切线的方程，问题求解完毕.上述问题的结论：圆C 上点P 处的切线的方程为()()()()200x a x a y b y b r −−+−−=. 2求过圆()()222:C x a y b r −+−=外一点()00,P x y 的圆C 的切线的步骤如下：（1）先验证过点P 且垂直于x 轴的直线是否和圆相切，若是，如图3所示，其中一条切线为0x x =（2）设切线的斜率为k ，用点斜式写出切线的方程，由圆心到切线的距离d r =，解出k ，求得切线方程.3.过圆()()222:C x a y b r −+−=外一点()00,P x y 作圆C 的两条切线，切点分别为A 和B ，如图4所示，则切点弦AB 所在直线的方程为()()()()200x a x a y b y b r −−+−−=典型例题【例l 】圆()22:14C x y −+=在点(P 处的切线方程为______.【解析】显然点P 在圆C 上，故所求切线的方程为()()0114x −−=，化简得：30x +=.【答案】30x +=变式1 圆22:230C x y x +−−=在点(2,P 处的切线方程为______.【解析】易验证点P 在圆C 上，故所求切线的方程为222302xx +−−⋅−=，化简得：50x −=【反思】过圆C 上的点()00,P x y 作圆C 的切线，则切线的方程可以在圆C 的一般式方程中将2x 换成0x x ，将2y 换成0y y ，将x 换成02x x +，将y 换成02y y+得到.【答案】50x −=变式2 已知圆()22:14C x y −+=，则：（1）圆C 的过点()2,0P −的切线方程为_______；（2）圆C 的过点()3,1Q 的切线方程为_______ 【解析】（1）显然过点P 且斜率不存在的直线2x =−与圆C 不相切，故可设切线的方程为()2y k x =+，即20kx y k −+=2=，解得：k =，故圆C 的过点P 的切线方程为)25y x =±+；（2）易得过点Q 且斜率不存在的直线3x =与圆C 相切，设另一条切线的方程为()13y m x −=−，即130mx y m −+−=2=，解得：34m =−，所以该切线的方程为()3134y x −=−−，化简得：34130x y +−=，综上所述，圆C 的过点Q 的切线方程为3x =或34130x y +−=.【答案】（1）)2y x =+；（2）3x =或34130x y +−= 【例2】已知圆22:4O x y +=外一点()2,3P ，过点P 作圆C 的两条切线，切点分别为A 和B ，则直线AB 的方程为_______【解析】由题意，切点弦AB 所在直线的方程为234x y +=，即2340x y +−= 【答案】2340x y +−=变式1 已知圆22:2410C x y x y +−−+=外一点()2,1P −，过点P 作圆C 的两条切线，切点分别为A 和B ，则直线AB 的方程为______.【解析】由题意，切点弦AB 所在直线的方程为212241022x yx y −++−+−⋅−⋅+= 化简得：310x y +−=【反思】过圆C 外的点()00,P x y 作圆C 的两条切线，则切点弦所在直线的方程，可在圆C 的一般式方程中将2x 换成0x x ，将2y 换成0y y ，将x 换成02x x +，将y 换成02y y+得到. 【答案】310x y +−=变式2 已知圆22:4Q x y +=，P 为直线:4l y x =+上一点，过点P 作圆O 的两条切线，切点分别为A 和B ，若四边形PAOB 的面积为12，则直线AB 的方程为______.【解析】如图，AP =，所以四边形PAOB 的面积122S AP AO =⨯⋅=由题意，12=，解得:PO =由题意，点P 在直线:4l y x =+上，故可设(),4P m m +，则PO == 解得：6m =−或2，当6m =−时，()6,2P −−，此时直线AB 的方程为624x y −−=，化简得：320x y ++= 当2m =时，()2,6P ，此时直线AB 的方程为264x y +=，化简得：320x y +−=，所以直线AB 的方程为320x y ++=或320x y +−=【答案】320x y ++=或320x y +−=变式3 已知圆22:4O x y +=，P 为直线:260l x y ++=上一点，过点P 作圆C 的两条切线，切点分别为A 和B ，当四边形PACB 的面积最小时，则直线AB 的方程为______.【解析】如图，AP =，所以四边形PACB 的面积122S AP AO =⨯⋅=PO 最小时，S 也最小，此时PO l ⊥，易求得PO 的方程为20x y −=，联立20260x y x y −=⎧⎨++=⎩解得：65x =−，125y =−，所以612,55P ⎛⎫−− ⎪⎝⎭，故直线AB 的方程为612455x y −−=，化简得：36100x y ++=.【答案】36100x y ++=变式4 已知直线:4l y x =+与x 轴交于点T ，过直线l 上的动点P 作圆22:4O x y +=的两条切线，切点分别为A 、B ，设AB 中点为M ，则TM 的最小值为（）A. B. D.3【解析】如图，因为点P 在直线:4l y x =+上，所以可设(),4P m m +，则切点弦AB 所在直线的方程为()44mx m y ++=即()440m x y y ++−=，所以直线AB 过定点()1,1Q −，又M 为AB 中点，所以OM AB ⊥，故点M 在以OQ 为直径的圆上，从而点M 的轨迹是以11,22G ⎛⎫− ⎪⎝⎭为半径的圆，显然点()4,0T −在该圆外，所以minTMTG ==.【反思】当动点P 在与圆C 相离的某一定直线上运动时，过点P 作圆C 的两条切线，则切点弦所在的直线是过定点的直线，熟悉这一模型，本题的求解就不困难了. 【答案】A强化训练1.（★★）圆22:40C x y x +−=在点(P 处的切线方程为（）A.20x +−=B.40x +−=C.40x +=D.20x +=【解析】显然点P 在圆C 上，故所求切线的方程为11402xx y +⋅+−⋅=，化简得：20x +=.【答案】D2.（★★）已知圆()22:11C x y +−=，则：（1）圆C 的过点()0,2P −的切线方程为______；（2）圆C 的过点()1,1Q −的切线方程为______.【解析】（1）显然过点P 且斜率不存在的直线0x =与圆C 不相切，故可设切线的方程为()()20y k x −−=−，即20kx y −−=1=，解得：k =±C 的过点P的切线方程为2y =±−；（2）易得过点Q 且斜率不存在的直线1x =与圆C 相切，设另一条切线的方程为()()11y m x −−=−，即10mx y m −−−=1=，解得：34m =−，所以该切线的方程为()()3114y x −−=−−，化简得：3410x y ++=，综上所述，圆C 的过点Q 的切线方程为1x =或3410x y ++=【答案】（1）2y =±−；（2）1x =或3410x y ++=3.（★★）已知圆()22:12C x y −+=外一点()2,2P ，过点P 作圆C 的两条切线，切点分别为A 和B ，则直线AB 的方程为______.【解析】由题意，切点弦AB 所在直线的方程为()()21122x y −−+=，化简得：230x y +−=. 【答案】230x y +−=4.（★★）已知圆()()22:129C x y −+−=外一点()4,2P −，过点P 作圆C 的两条切线，切点分别为A 和B ，则直线AB 的方程为______.【解析】由题意，切点弦AB 所在直线的方程为()()()()4112229x y −−−+−−=，化简得：45x =−.【答案】45x =−5.（★★）已知圆22:2440C x y x y +−−−=外一点()4,1P −−，过点P 作圆C 的两条切线，切点分别为A 和B ，则直线AB 的方程为______.【解析】由题意，切点弦AB 所在直线的方程为414244022x y x y −−−−−⋅−⋅−=，化简得：5320x y +−=.【答案】5320x y +−=6.（★★★）已知圆22:2440C x y x y +−−−=，P 为直线:20l x y ++=上一点，过点P 作圆C 的两条切线，切点分别为A 和B ，若四边形PACB 的面积为12，则直线AB 的方程为______.【解析】如图，AP ==所以四边形PACB 的面积122S AP AC =⨯⋅=由题意，12=，解得：5PC =，由题意，点P 在直线20x y ++=上，故可设(),2P m m −−，则PC =5=，解得：4m =−或1，当4m =−时()4,2P −，此时直线AB 的方程为4242244022x yx y −++−+−⋅−⋅−=，化简得：45x =−，当1m =时，()1,3P −，此时直线AB 的方程为133244022x yx y +−+−−⋅−⋅−=，化简得：15y =，所以直线AB 的方程为45x =−或15y =.【答案】45x =−或15y =7.（★★★）已知圆22:2440C x y x y +−−−=，P 为直线:20l x y ++=上一点，过点P 作圆C 的两条切线，切点分别为A 和B ，当四边形PACB 的面积最小时，则直线AB 的方程为______.【解析】()()22222440129x y x y x y +−−−=⇒−+−=⇒圆心()1,2C ，半径3r =.如图，AP ==所以四边形PACB 的面积122S AP AC =⨯⋅= 所以当PC 最小时，S 也最小，此时，PC l ⊥，故PC 的方程为21y x −=−，即10x y −+=，联立1020x y x y −+=⎧⎨++=⎩解得：32x =−，12y =−，即31,22P ⎛⎫−− ⎪⎝⎭，所以直线AB 的方程为()()311122922x y ⎛⎫⎛⎫−−−+−−−= ⎪ ⎪⎝⎭⎝⎭，化简得：5530x y ++=.【答案】5530x y ++=8.（★★★★）已知P 为抛物线2:4C y x =上的动点，过P 作圆()22:44M x y −+=的两条切线，切点分别为A 和B ，则当四边形PAMB 的面积最小时，直线AB 的方程为______.【解析】如图，AP ==，所以四边形PAMB 的面积122S AP AM =⨯⋅=，所以当PM 最小时，S 也最小，由题意，()4,0M ，可设()2,2P t t ，则()()2222242244416212PM t t t t t =−+=−+=−+，故当t =PM 取得最小值，此时(2,P ±，所以直线AB 的方程为()()2444x −−±=，化简得：20x ±−=.【答案】20x +−=或20x =−=9.（★★★★）已知圆22:2440C x y x y +−−−=，P 为直线:20l x y ++=上的动点，过点P 作圆C 的两条切线，切点分别为A 和B ，AB 的中点为Q ，若点T 的坐标为111,1010⎛⎫⎪⎝⎭，则TQ 的最小值为______.【解析】()()22222440129x y x y x y +−−−=⇒−+−=⇒圆心()1,2C ，半径3r =，设(),2P m m −−，则切点弦AB 所在直线的方程为()()()()112229m x m y −−+−−−−=，化简得：()140m x y x y −+−−=，所以直线AB 过定点41,55K ⎛⎫− ⎪⎝⎭，如图，显然CQ KQ ⊥，所以点Q 的轨迹是以CK 为直径的圆，其圆心为111,1010G ⎛⎫ ⎪⎝⎭，CK ==，因为GT =min 12TQ GT GK =−=.【答案】10。

圆锥曲线的切点弦方程及其应用

圆锥曲线的切点弦方程及其应用摘要：切点弦的问题是圆锥曲线中的重要内容之一，是近几年高考的热点考题，切点弦涉及到的问题，难度较大，技巧性强，计算繁琐，学生遇到此类问题较为棘手，束手无策，这里通过类比推理，探究其规律，掌握其性质，触类旁通，化繁就简，降低难度，进一步提高学习效率。

关键词：圆锥曲线；弦方程；应用1.内容解析1.切点弦的概念：过曲线C（圆，椭圆，双曲线，抛物线）外一点（对非封闭曲线是开口外一点）引两条切线，可以得到两个切点，连接切点即为切点弦。

2.微专题概述：圆锥曲线的切点弦方程是平面解析几何中的一类难点问题，围绕切点弦命制的解析几何试题具有内涵深刻、灵活多变的特点。

本专题在讲解一道课本习题即“过圆上一点圆的切线问题”的求解方法的基础上，立足学生思维的“最近发展区”，通过设置环环紧扣的问题串，最后得出椭圆、双曲线、抛物线的切点弦的一般性结论。

本微专题坚持“以小见大、微中知著”，最终达到启迪学生思维、开阔数学视野、培养类比归纳能力的目的；另一方面，客观题中熟练掌握切点弦方程结论，可以帮助学生有效简化解题过程、提高解题速度。

1.本专题所蕴含的数学思想方法及教学策略分析思想方法：数形结合思想、化归与转化思想、特殊与一般的思想教学策略：讲授法、分组讨论法、引导启示法立足高三年级学生实际、对基本概念和知识点采取讲授的方法；通过设置环环相扣的问题串，让学生分组讨论，教师引导实现同类知识的的迁移和整合归纳；注重问题串的整体性，在问题串的引领下，引导启示学生进行系列、连续的思维活动，使学生思维达到新高度。

1.教学目标1.知识与技能（1）掌握圆锥曲线在某点处的切点弦方程；（2）会用切点弦方程解决一些实际问题；（3）通过复习渗透数形结合、类比的思想，逐步培养学生分析问题和解决问题的能力。

2.过程与方法首先，通过对过圆上一点的圆的切线的求法的研究，进而设置一些列有较强逻辑关系的问题串，采取学生小组讨论法、教师启发引导法从而完成教学目标。

课题∶圆锥曲线的切线方程和切点弦方程

课题：圆锥曲线的切线方程和切点弦方程主讲人：安庆一中李治国教学目标：（1）.掌握圆锥曲线在某点处的切线方程及切点弦方程。

（2）.会用切线方程及切点弦方程解决一些问题。

（3）通过复习渗透数形结合、类比的思想，逐步培养学生分析问题和解决问题的能力。

(4) 掌握曲线与方程的关系。

教学重点：切线方程及切点弦方程的应用教学难点：如何恰当使用切线方程及切点弦方程教学过程：1. 引入：通过09年安徽省高考题及近几年各省考察圆锥曲线的实例引出本节课。

2. 知识点回顾：1.2. 3.4. 圆锥曲线切线的几个性质：性质1 过椭圆的准线与其长轴所在直线的交点作椭圆的两条切线，则切点弦长等于该椭圆的通径．同理:双曲线,抛物线也有类似的性质性质2 过椭圆的焦点F 1的直线交椭圆于A ，B 两点，过A ，B 两点作椭圆的切线交于点P ，则P 点的轨迹是焦点的对应的准线，并且同理:双曲线,抛物线也有类似的性质3. 例题精讲：练习1：抛物线与直线围成的封闭的图形的面积为，若直线l 与抛物线相切，且平行于直线，则直线l 的方程为例1：设抛物线的焦点为F ，动点P 在直线22200(,)x y r M x y +=过圆上一点的切线方程:200xx yy r +=00221xx yy a b +=220022(,)1x y P x y a b +=设为椭圆上的点，则过该点的切线方程为：220022(,)1x y P x y a b -=设为双曲线上的点，则过该点的切线方程为：00221xx yy a b -=00(,)2P x y px =2设为抛物线y 上的点，则过该点的切线方程为：00()yy p x x =+1PF AB ⊥1F :20l x y --=2:C y x =2(0)y ax a =>1x =43260x y -+=上运动，过P 作抛物线C 的两条切线PA 、PB ，且与抛物线C 分别相切于A 、B 两点.求△APB 的重心G 的轨迹方程.4. 圆锥曲线的切点弦方程:1.2.3.4. 练习2：例题3：5.小结: 1．判断直线与圆锥曲线的位置关系时，注意数形结合；2. 掌握求曲线方程的方法：3. 两种方程两种思想作业： 6. 反思220022(,)1x y P x y a b +=设为椭圆外一点，过该点作椭圆的两条切线，切点为A ，B 则弦AB 的方程为：22200(,)P x y x y r +=设为圆外一点，则切点弦的方程为：200xx yy r +=220022(,)1x y P x y a b -=过为双曲线的两支作两条切线，则切点弦方程为：00221xx yy a b -=00(,)2P x y px =2设为抛物线y 开口外一点，则切点弦的方程为：00()yy p x x =+22221(,0). x y P m a bA B AB ±=≠对于圆锥曲线，过点，（m 0）作两条切线，切点为，则直线恒过定点22x 21,4312A,B AB OMN y P x y +=+=已知椭圆是在直线位于第一象限上一点，由P 向已知椭圆作两切线，切点分别为，问当直线与两坐标轴围成的三角形面积最小，最小值为多少？2l y x+3P y 2A,B.PAB P x ==∆已知是直线：上一点，过点作抛物线的两条切线，切点分别为求面积的最小值。

圆锥曲线的切线切点弦总结归纳(转换坐标系法)

圆锥曲线的切线、切点弦推论总结归纳1、椭圆切线推论：已知椭圆C 方程22221x y a b+=（a>b>0），C 上一点P （00,y x ），过点P 且与C 相切的切线L 方程为：12020=+byy a x x 。

12222=+by a x'2'2()()1x y +=推导：如图所示，当切线'L 斜率存在且不为0时（即切线L 斜率存在且不为0），设'OP 、'L 的斜率分别为1k ，2k ，0010000y ay b k x bx a-==-，由圆的切线性质易知'OP ⊥'L ，即121k k ⋅=-，∴02101bx k k ay -==-，∴由点斜式易得'L 方程为：''0000()y bx xy x b ay a -=--，又'',x yx y a b ==，∴ 0000()y bx x y x b b ay a a-=--，即为椭圆切线L 方程，化简如下：0000y y bx x x b ay a --=-⋅，000022()()y y y x x x b a --=-，2200002222x x y y x y a b a b +=+，又点P(00,y x )是椭圆上一点，∴2200221x y a b +=，即切线L 方程化简后为：0022x x y ya b+=1；易知当切线L 斜率为0时，P （0,b ±），切线L 方程为：y b =±，满足上式；当切线L 斜率不存在时，P （,0a ±）切线L 方程为：x a =±，也满足上式。

综上，推导完毕。

2、直线与椭圆位置关系判定推论：已知椭圆C 方程12222=+by a x （a>b>0），一直线L 方程为：0Ax By C ++=,则L 与C 相交⇔2222A a B b +>2C ；L 与C 相切⇔2222A a B b +=2C ；L 与C 相离⇔2222A a B b +<2C 。

圆锥曲线的切点弦、中点弦、切线

圆锥曲线的切点弦、中点弦、切线
圆锥曲线中点弦公式：py-αx=pβ-α^2。

立体几何定义：以直角三角形的直角边所在直线为旋转轴，其余两边旋转360度而成的曲面所围成的几何体叫做圆锥。

旋转轴叫做圆锥的轴。

垂直于轴的边旋转而成的曲面叫做圆锥的底面。

不垂直于轴的边旋转而成的曲面叫做圆锥的侧面。

曲线，是微分几何学研究的主要对象之一。

直观上，曲线可看成空间质点运动的轨迹。

微分几何就是利用微积分来研究几何的学科。

为了能够应用微积分的知识，我们不能考虑一切曲线，甚至不能考虑连续曲线，因为连续不一定可微。

这就要我们考虑可微曲线。

第1页共1页。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2011年江西高考一道试题解法的推广一圆锥曲线的切点弦方程
圆锥曲线问题是高考的重点，曲线的切线又是近几年的热点，这类题对学生的要求比较高，充分考查学生的逻辑思维能力，本文在对江西高考试题分析的基础上归纳总结出圆、椭圆、抛物线、双曲线的切点弦方程的求法。

背景知识
I I 2 2 2
已知圆C:x y r r 0 ,点A x o,y o是圆C上一点，求以点A为切点的切线方程.
分析：易知以A x o, y o为切点的直线方程为：xx o yy o r2r 0
（2oii年江西高考理科第14题）
2 2 i
问题1：若椭圆笃爲1的焦点在x轴上，过点1,丄作圆x2 y21的切线，切
a b 2
点分别为A B，直线AB恰好经过椭圆的右焦点和上顶点，则椭圆方程是___________ .
解：设A x1,y1 ,B x2, y2
•••点A B在圆x2 y21上,则
过点A为，屮的切线方程为L「X1X y1y 1.
过点B x2,y2的切线方程为L2: x2x y2y 1.
1 1 1
由于L1, L2经过点1, 则捲y1 1x y 1.
2 2 2
1
故刘，如,x2,y2均为方程x y 1的解。

1
经过A、B两点的直线方程AB : x — y 1 .
2
2 2
设椭圆务与1的右焦点为c,o，上顶点为o,b .
a b
由于直线AB经过椭圆右焦点和上顶点。

K
c 1,- 1 即b 2
2
2,22
a b c 5
2 2
故椭圆方程为—1.
5 4
由此题的解题方法，可得到如下推广: 结论一：（圆的切点弦方程）
线MN 的方程为：ax by r 2.
x 2
问题2 :过椭圆一
4
2
y
1外一点P 1,2作椭圆的两切线，切点为M 、N 求直线MN
3
的方程.
1 a b 0外一点P X o ,y 0作椭圆的两切线，切点为
M 、N 则直线MN 的方程为：X
o 2X
耳 1
a b
2
问题3：过抛物线y 4x 外一点P 1, 2作抛物线两切线，切点分别为 M 、N , 求直线MN 的方程。

解：设 M 为，％ , N x 2, y 2
贝U 过
M 、N 的
切线方程为
%y 2 x X 1 ,y 2y 2 x x ?
由于过M 、N 的切线都经过P 1, 2则 2y 1 2 X 1 1 ,2y 2
2 X 2 1
•••直线MN 的方程为 2y 2
X 1即X y 1
结论三：（抛物线的切点弦方程）
过抛物线y 2px p 0外一点P x 0, y 0作两切线，切点为 M 、N ，则直线MN 的方程为yy 0 p x x 0
x_j
X %y 1,X 2X
1
4
3
4
3
由于两切线都过P 1,2，则小
%y 1 ① X 2X y 2y
1 ②
2y . 4
3 4 3
x
N ，
所以直线MN 的方程为:
这两式表示直线 —
1经过M 、
4 3
N 的切线方程分别为;
结论二：（椭圆的切点弦方
程）
过圆x
y 2 r 2 r 0，外一点P a,b 作圆的两切线，切点为
M 、N ，则直
解：设 M ^,y 1 ,N x 2,y 2 则过 M 、
2 2
过椭圆冷厶
a 2
b 2
2 2
问题4 :过双曲线—
y
5 4
1外一点P 3,3作双曲线两切线，切点分别为求直线MN的方程。

解：设两切点的坐标为M x-\,y-\ , N x2, y2则两切线方程为
y i y1榔河
1，
54，54
由于两切线均过P3,3则
3X j3y i3x2
1, 2
3y2
5454
故X i, y i,X2,y2均为方
程
呈弐3y1的解，
54
则过M、N的直
线方程
为：
3x3y1
54
结论四：（双曲线的切点弦方程）
2 2
过双曲线务每1外一点P X o,y o作双曲线两切线，切点分别为
a b
N则直线MN的方程为：等罟「。