试题精选_山东省德州市平原县第一中学2015届高三上学期第一次月考数学(理)调研试卷(扫描版)_精校完美版
山东省德州市高三数学上学期第一次模拟试卷 理(含解析)
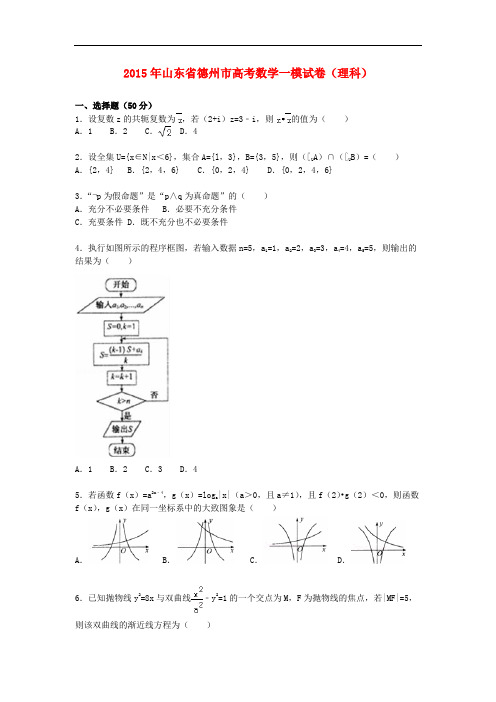
2015年山东省德州市高考数学一模试卷(理科)一、选择题(50分)1.设复数z的共轭复数为,若(2+i)z=3﹣i,则的值为()A.1 B.2 C.D.42.设全集U={x∈N|x<6},集合A={l,3},B={3,5},则(∁U A)∩(∁U B)=()A.{2,4} B.{2,4,6} C.{0,2,4} D.{0,2,4,6}3.“¬p为假命题”是“p∧q为真命题”的()A.充分不必要条件B.必要不充分条件C.充要条件 D.既不充分也不必要条件4.执行如图所示的程序框图,若输入数据n=5,a1=1,a2=2,a3=3,a4=4,a5=5,则输出的结果为()A.1 B.2 C.3 D.45.若函数f(x)=a2x﹣4,g(x)=log a|x|(a>0,且a≠1),且f(2)•g(2)<0,则函数f(x),g(x)在同一坐标系中的大致图象是()A.B.C.D.6.已知抛物线y2=8x与双曲线﹣y2=1的一个交点为M,F为抛物线的焦点,若|MF|=5,则该双曲线的渐近线方程为()A.5x±3y=0 B.3x±5y=0 C.4x±5y=0 D.5x±4y=07.棱长为2的正方体被一平面截得的几何体的三视图如图所示,那么被截去的几何体的体积是()A.B.C.4 D.38.已知D是不等式组所确定的平面区域,则圆x2+y2=4与D围成的区域面积为()A.B.C.πD.9.设m,n是正整数,多项式(1﹣2x)m+(1﹣5x)n中含x一次项的系数为﹣16,则含x2项的系数是()A.﹣13 B.6 C.79 D.3710.已知函数f(x)是定义在R上的奇函数,其导函数为f′(x),当x<0时,2f(x)+xf′(x)<0恒成立,则f(1),2014,2015在大小关系为()A.2015<2014<f(1)B.2015<f(1)<2014C.f(1)<2015<2014D.f(1)<2014<2015二、填空题(25分)11.某校对全校1600名男女学生的视力状况进行调查,现用分层抽样的方法抽取一个容量是200的样本,已知女生比男生少抽10人,则该校的女生人数是人.12.= .13.若不等式|x+1|+|2x﹣1|>a恒成立,则a的取值范围是.14.将函数f(x)=2sin(ωx﹣)(ω>0)的图象向左平移个单位,得到函数y=g (x)的图象,若y=g(x)在[0,]上为增函数,则ω的最大值为.15.设函数f(x)、g(x)的定义域分别为D J,D E,且D J⊆D E.若对于任意x⊆D J,都有g(x)=f(x),则称函数g(x)为f(x)在D E上的一个延拓函数.设f(x)=e x(x+1)(x<0),g(x)为f(x)在R上的一个延拓函数,且g(x)是奇函数,给出以下命题:①当x>0时,g(x)=e﹣x(x﹣1);②函数g(x)有5个零点;③g(x)>0的解集为(﹣1,0)∪(1,+∞);④函数g(x)的极大值为1,极小值为﹣1;⑤∀x1,x2∈R,都有|g(x1)﹣g(x2)|<2其中正确的命题是(填上所有正确的命题序号)三、解答题(75分)16.在△ABC中,角A,B,C对边分别是a,b,c,满足.(1)求角A的大小;(2)求sinA•sinB•sinC的最大值,并求取得最大值时角B,C的大小.17.正三棱柱ABC﹣A1B1C1的所有棱长都为4,D为的CC1中点.(1)求证:AB1⊥平面A1BD;(2)求二面角A﹣A1D﹣B的余弦值.18.某科技公司组织技术人员进行新项目研发,技术人员将独立地进行项目中不同类型的实验A,B,C,若A,B,C实验成功的概率分别为.(1)对A,B,C实验各进行一次,求至少有一次实验成功的概率;(2)该项目要求实验A,B各做两次,实验C做3次,如果A实验两次都成功则进行实验B 并获奖励10000元,两次B实验都成功则进行实验C并获奖励30000元,3次C实验只要有两次成功,则项目研发成功并获奖励60000元(不重复得奖).且每次实验相互独立,用X 表示技术人员所获奖励的数值,写出X的分布列及数学期望.19.单调递增数列{a n}的前n项和为S n,且满足4S n=a n2+4n.(1)求数列{a n}的通项公式;(2)数列{b n}满足,求数列{b n}的前n项和T n.20.已知函数f(x)=x﹣alnx+(a∈R)(1)求f(x)的单调区间;(2)若在[1,e](e=2.71828…)上任取一点x0,使得f(x0)≤0成立,求a的取值范围.21.已知椭圆C的中心在原点,焦点在x轴上,离心率等于,它的一个顶点恰好在抛物线x2=8y的准线上.(1)求椭圆C的标准方程;(2)点P(2,),Q(2,﹣)在椭圆上,A,B是椭圆上位于直线PQ两侧的动点.(i)若直线AB的斜率为,求四边形APBQ面积的最大值;(ii)当A,B运动时,满足∠APQ=∠BPQ,试问直线AB的斜率是否为定值,请说明理由.2015年山东省德州市高考数学一模试卷(理科)参考答案与试题解析一、选择题(50分)1.设复数z的共轭复数为,若(2+i)z=3﹣i,则的值为()A.1 B.2 C.D.4考点:复数代数形式的乘除运算.专题:数系的扩充和复数.分析:把已知的等式变形,然后利用复数代数形式的乘除运算化简求得z,再由得答案.解答:解:由(2+i)z=3﹣i,得,∴=.故选:B.点评:本题考查了复数代数形式的乘除运算,考查了复数的基本概念,是基础题.2.设全集U={x∈N|x<6},集合A={l,3},B={3,5},则(∁U A)∩(∁U B)=()A.{2,4} B.{2,4,6} C.{0,2,4} D.{0,2,4,6}考点:交、并、补集的混合运算.专题:计算题.分析:列举出全集U中的元素,求出A与B的补集,找出两补集的交集即可.解答:解:∵全集U={x∈N|x<6}={0,1,2,3,4,5},集合A={l,3},B={3,5},∴∁U A={0,2,4,5},∁U B={0,1,2,4},则(∁U A)∩(∁U B)={0,2,4}.故选C点评:此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.3.“¬p为假命题”是“p∧q为真命题”的()A.充分不必要条件B.必要不充分条件C.充要条件 D.既不充分也不必要条件考点:必要条件、充分条件与充要条件的判断.专题:简易逻辑.分析:根据复合命题之间的关系进行判断.解答:解:若¬p为假命题,则p为真命题.若p∧q为真命题,则p,q都为真命题,故“¬p为假命题”是“p∧q为真命题”的必要不充分条件,故选:B.点评:本题主要考查充分条件和必要条件的判断,根据复合命题之间的关系是解决本题的关键.4.执行如图所示的程序框图,若输入数据n=5,a1=1,a2=2,a3=3,a4=4,a5=5,则输出的结果为()A.1 B.2 C.3 D.4考点:程序框图.专题:图表型;算法和程序框图.分析:模拟执行程序,依次写出每次循环得到的S,k的值,当k=6时,满足条件k>5,退出循环,输出S的值为3,从而得解.解答:解:模拟执行程序,可得输入数据n=5,a1=1,a2=2,a3=3,a4=4,a5=5,S=0,k=1S=1,k=2不满足条件k>5,S=,k=3不满足条件k>5,S=2,k=4不满足条件k>5,S=,k=5不满足条件k>5,S=3,k=6满足条件k>5,退出循环,输出S的值为3.故选:C.点评:本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结果,属于基础题.5.若函数f(x)=a2x﹣4,g(x)=log a|x|(a>0,且a≠1),且f(2)•g(2)<0,则函数f(x),g(x)在同一坐标系中的大致图象是()A.B.C.D.考点:函数的图象.专题:函数的性质及应用.分析:先由条件f(2)•g(2)<0确定a的取值范围,然后利用指数函数和对数函数的性质去判断f(x),g(x)的图象.解答:解:由题意f(x)=a2x﹣4是指数型的,g(x)=log a|x|是对数型的且是一个偶函数,由f(2)•g(2)<0,可得出g(2)<0,故log a2<0,故0<a<1,由此特征可以确定C、D两选项不正确,且f(x)=a2x﹣4是一个减函数,由此知A不对,B选项是正确答案故选:B.点评:本题主要考查了函数图象的识别和应用.判断函数图象要充分利用函数本身的性质,由f(2)•g(2)<0确定a的取值范围,是解决本题的关键.6.已知抛物线y2=8x与双曲线﹣y2=1的一个交点为M,F为抛物线的焦点,若|MF|=5,则该双曲线的渐近线方程为()A.5x±3y=0 B.3x±5y=0 C.4x±5y=0 D.5x±4y=0考点:双曲线的简单性质.专题:圆锥曲线的定义、性质与方程.分析:求得抛物线的焦点和准线方程,设M(m,n),则由抛物线的定义可得m=3,进而得到M的坐标,代入双曲线的方程,可得a,再由渐近线方程即可得到所求.解答:解:抛物线y2=8x的焦点F(2,0),准线方程为x=﹣2,设M(m,n),则由抛物线的定义可得|MF|=m+2=5,解得m=3,由n2=24,可得n=±2.将M(3,)代入双曲线﹣y2=1,可得﹣24=1,解得a=,即有双曲线的渐近线方程为y=±x.即为5x±3y=0.故选A.点评:本题考查抛物线和双曲线的定义、方程和性质,主要考查抛物线的定义和双曲线的渐近线方程,考查运算能力,属于基础题.7.棱长为2的正方体被一平面截得的几何体的三视图如图所示,那么被截去的几何体的体积是()A.B.C.4 D.3考点:由三视图求面积、体积.专题:计算题;空间位置关系与距离.分析:三视图中长对正,高对齐,宽相等;由三视图想象出直观图,一般需从俯视图构建直观图,该几何体为正方体沿体对角线截成.解答:解:该几何体为正方体沿体对角线截成,其分成两部分的几何体的体积相等,而正方体的体积V=23=8,故被截去的几何体的体积是=4,故选C.点评:三视图中长对正,高对齐,宽相等;由三视图想象出直观图,一般需从俯视图构建直观图,本题考查了学生的空间想象力,识图能力及计算能力.8.已知D是不等式组所确定的平面区域,则圆x2+y2=4与D围成的区域面积为()A.B.C.πD.考点:两直线的夹角与到角问题;二元一次不等式(组)与平面区域.专题:直线与圆.分析:作出不等式组对应的平面区域,根据区域的图形进行求面积即可.解答:解:作出不等式组对应的平面区域,则公共区域如图:则直线x﹣2y=0的斜率k=,直线x+3y=0的斜率k=,则两直线的夹角θ满足tanθ=||=1,则θ=,则阴影部分对应的面积之和S==,故选:A.点评:本题主要考查二元一次不等式组的应用以及圆的扇形面积的求解,根据直线所成的角求出两条直线的夹角是解决本题的关键.9.设m,n是正整数,多项式(1﹣2x)m+(1﹣5x)n中含x一次项的系数为﹣16,则含x2项的系数是()A.﹣13 B.6 C.79 D.37考点:二项式系数的性质.专题:二项式定理.分析:由含x一次项的系数为﹣16利用二项展开式的通项公式求得2m+5n=16 ①.,再根据m、n为正整数,可得m=3、n=2,从而求得含x2项的系数.解答:解:由于多项式(1﹣2x)m+(1﹣5x)n中含x一次项的系数为•(﹣2)+•(﹣5)=﹣16,可得2m+5n=16 ①.再根据m、n为正整数,可得m=3、n=2,故含x2项的系数是•(﹣2)2+•(﹣5)2=37,故选:D.点评:本题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于基础题.10.已知函数f(x)是定义在R上的奇函数,其导函数为f′(x),当x<0时,2f(x)+xf′(x)<0恒成立,则f(1),2014,2015在大小关系为()A.2015<2014<f(1)B.2015<f(1)<2014C.f(1)<2015<2014D.f(1)<2014<2015考点:利用导数研究函数的单调性;函数奇偶性的性质;导数的运算.专题:函数的性质及应用;导数的概念及应用.分析:首先利用换元法设g(x)=x2f(x),进一步利用函数的导数求出函数g(x)的单调性,再利用函数的奇偶性求出函数在对称区间里的单调性,最后求出函数大小关系.解答:解:已知函数f(x)是定义在R上的奇函数,其导函数为f′(x),则:设函数g(x)=x2f(x)则:g′(x)=2xf(x)+x2f′(x)=g′(x)=x(2f(x)+xf′(x))当x<0时,2f(x)+xf′(x)<0恒成立,则:函数g′(x)>0所以函数在x<0时,函数g(x)为单调递增函数.由于函数f(x)是定义在R上的奇函数,则:函数g(x)=x2f(x)为奇函数.所以:在x>0时,函数g(x)为单调递增函数.所以:g()即:故选:D点评:本题考查的知识要点:利用函数的导数求函数的单调性,函数的奇偶性和函数单调性的关系.二、填空题(25分)11.某校对全校1600名男女学生的视力状况进行调查,现用分层抽样的方法抽取一个容量是200的样本,已知女生比男生少抽10人,则该校的女生人数是760 人.考点:分层抽样方法;频率分布直方图.专题:概率与统计.分析:先计算出样本中女学生人数,再根据分层抽样的性质计算出该校女生的人数.解答:解:根据题意,设样本中女生人数为x,则(x+10)+x=200,解得x=95,所以该校的女生人数是人,故答案为:760.点评:本题考查分层抽样,先计算中样本中男女学生的人数是解决本题的关键,属基础题.12.= e2.考点:定积分.专题:计算题.分析:欲求定积分,先求原函数,由于(lnx)′=,( x2)′=2x,故2x+的原函数是x2+lnx,从而问题解决.解答:解:∵(lnx)′=,( x2)′=2x,∴=x2|1e+lnx|1e=e2﹣1+lne﹣ln1=e2故答案为:e2点评:本小题主要考查定积分、定积分的应用、原函数的概念解法等基础知识,考查运算求解能力.属于基础题.13.若不等式|x+1|+|2x﹣1|>a恒成立,则a的取值范围是(﹣∞,).考点:绝对值不等式的解法.专题:不等式的解法及应用.分析:化简f(x)=|x+1|+|2x﹣1|的解析式,利用f(x)的单调性可得函数f(x)的最小值为f()=,由此求得a的范围.解答:解:设f(x)=|x+1|+|2x﹣1|=,由于函数f(x)在(﹣∞,﹣1]、(﹣1,)上都是减函数,在[,+∞)上是增函数,故当x=时,函数f(x)取得最小值为f()=.再根据题意可得>a,故答案为:(﹣∞,).点评:本题主要考查绝对值的意义,绝对值不等式的解法,函数的恒成立问题,函数的单调性的应用,体现了转化的数学思想,属于基础题.14.将函数f(x)=2sin(ωx﹣)(ω>0)的图象向左平移个单位,得到函数y=g (x)的图象,若y=g(x)在[0,]上为增函数,则ω的最大值为 2 .考点:由y=Asin(ωx+φ)的部分图象确定其解析式.专题:计算题.分析:函数的图象向左平移个单位,得到函数y=g(x)的表达式,然后利用在上为增函数,说明,利用周期公式,求出ω的不等式,得到ω的最大值.解答:解:函数的图象向左平移个单位,得到函数y=g(x)=2sinωx,y=g(x)在上为增函数,所以,即:ω≤2,所以ω的最大值为:2.故答案为:2.点评:本题是基础题,考查由y=Asin(ωx+φ)的部分图象确定其解析式,注意函数的周期与单调增区间的关系,考查计算能力,常考题型,题目新颖.15.设函数f(x)、g(x)的定义域分别为D J,D E,且D J⊆D E.若对于任意x⊆D J,都有g(x)=f(x),则称函数g(x)为f(x)在D E上的一个延拓函数.设f(x)=e x(x+1)(x<0),g(x)为f(x)在R上的一个延拓函数,且g(x)是奇函数,给出以下命题:①当x>0时,g(x)=e﹣x(x﹣1);②函数g(x)有5个零点;③g(x)>0的解集为(﹣1,0)∪(1,+∞);④函数g(x)的极大值为1,极小值为﹣1;⑤∀x1,x2∈R,都有|g(x1)﹣g(x2)|<2其中正确的命题是①③⑤(填上所有正确的命题序号)考点:抽象函数及其应用.专题:函数的性质及应用.分析:利用题目提供的信息,可得g(x)在D J上的解析式,然后通过函数的奇偶性可求得其在对称区间上解析式,综合结论即可得答案.解答:解:①由题意得,若x>0时,则﹣x<0,g(x)为f(x)在R上的一个延拓函数,且g(x)是奇函数,则g(x)=f(x)=e x(x+1)(x<0),∴g(﹣x)=e﹣x(﹣x+1)=﹣g(x),∴g(x)=e﹣x(x﹣1),(x>0),故①正确;②∵g(x)=e x(x+1)(x<0),此时g′(x)=e x(x+2),令其等于0,解得x=﹣2,且当x∈(﹣∞,﹣2)上导数小于0,函数单调递减;当x∈(﹣2,0)上导数大于0,函数单调递增,x=﹣2处为极小值点,且g(﹣2)>﹣1,且在x=﹣1处函数值为0,且当x<﹣1是函数值为负.又∵奇函数的图象关于原点中心对称,故函数f(x)的图象应如图所示:由图象可知:函数g(x)有3个零点,故②错误;③由②知函数g(x)>0的解集为(﹣1,0)∪(1,+∞),故③正确,;④由②知函数在x=﹣2处取得极小值,极小值为g(﹣2)=e﹣2(﹣2+1)=﹣e﹣2,根据奇函数的对称性可知在x=2处取得极大值,极大值为g(2)=e﹣2,故④错误;⑤当x<0时,g(x)=e x(x+1),则当x→0时,g(x)→1,当x>0时,g(x)=e﹣x(x﹣1),则当x→0时,g(x)→﹣1,即当x<0时,﹣1<﹣e﹣2<g(x)<1,即当x>0时,﹣1<g(x)<e﹣2<1,故有对∀x1,x2∈R,|g(x2)﹣g(x1)|<2恒成立,即⑤正确.故正确的命题是①③⑤,故答案为:①③⑤点评:本题主要考查新定义的应用,主要考查利用函数奇偶性求函数解析式的方法,在解题时注意对于新定义的理解,有一定的难度.三、解答题(75分)16.在△ABC中,角A,B,C对边分别是a,b,c,满足.(1)求角A的大小;(2)求sinA•sinB•sinC的最大值,并求取得最大值时角B,C的大小.考点:余弦定理;平面向量数量积的运算.专题:解三角形.分析:(1)由.利用数量积运算可得:2bccosA=a2﹣(b+c)2,展开再利用余弦定理可得2bccosA=﹣2bccosA﹣2bc,化为cosA=﹣.(2)由,可得,.利用两角和差的正弦公式、倍角公式可得sinA•sinB•sinC==﹣,由.可得,当=时,sinA•sinB•sinC取得最大值,即可得出.解答:解:(1)∵=cbcosA,.∴2bccosA=a2﹣(b+c)2,展开为:2bccosA=a2﹣b2﹣c2﹣2bc,∴2bccosA=﹣2bccosA﹣2bc,化为cosA=﹣,∵A∈(0,π).∴.(2)∵,∴,.∴sinA•sinB•sinC===﹣==﹣=﹣,∵.∴,当=时,即时,sinA•sinB•sinC取得最大值,此时B=C=.点评:本题考查了数量积运算、余弦定理、两角和差的正弦公式、倍角公式、三角函数的单调性,考查了推理能力与计算能力,属于难题.17.正三棱柱ABC﹣A1B1C1的所有棱长都为4,D为的CC1中点.(1)求证:AB1⊥平面A1BD;(2)求二面角A﹣A1D﹣B的余弦值.考点:用空间向量求平面间的夹角;直线与平面垂直的判定;二面角的平面角及求法.专题:空间位置关系与距离;空间角.分析:(1)通过建立如图所示的空间直角坐标系,利用数量积⇔,即可证明AB1⊥平面A1BD;(2)利用两个平面的法向量的夹角即可得到二面角.解答:(1)证明:取BC中点O,连接AO,∵△ABC为正三角形,∴AO⊥BC,∵在正三棱柱ABC﹣A1B1C1中,平面ABC⊥平面BCC1B1,∴AO⊥平面BCC1B1,取B1C1中点为O1,以O为原点,,,的方向为x,y,z轴的正方向,建立空间直角坐标系,则.∴,,.∵,.∴,,∴AB1⊥面A1BD.(2)设平面A1AD的法向量为,.,∴,∴,⇒,令z=1,得为平面A1AD的一个法向量,由(1)知AB1⊥面A1BD,∴为平面A1AD的法向量,,由图可以看出:二面角A﹣A1D﹣B是锐角.∴二面角A﹣A1D﹣B的余弦值为.点评:熟练掌握:通过建立如图所示的空间直角坐标系的方法,利用数量积与垂直的关系证明线面垂直;利用两个平面的法向量的夹角得到二面角.18.某科技公司组织技术人员进行新项目研发,技术人员将独立地进行项目中不同类型的实验A,B,C,若A,B,C实验成功的概率分别为.(1)对A,B,C实验各进行一次,求至少有一次实验成功的概率;(2)该项目要求实验A,B各做两次,实验C做3次,如果A实验两次都成功则进行实验B 并获奖励10000元,两次B实验都成功则进行实验C并获奖励30000元,3次C实验只要有两次成功,则项目研发成功并获奖励60000元(不重复得奖).且每次实验相互独立,用X 表示技术人员所获奖励的数值,写出X的分布列及数学期望.考点:离散型随机变量的期望与方差;离散型随机变量及其分布列.专题:概率与统计.分析:(1)设A,B,C实验成功分别记为事件A,B,C,且相互独立.记事件至少有一次实验成功为D,则P(D)=1﹣=1﹣,即可得出.(II)X的取值分别为,0,10000,30000,60000.则P(X=0)包括实验A第一次不成功或第一次成功而第二次不成功,P(X=10000)包括实验A两次成功,而B第一次不成功或第一次成功而第二次不成功,(X=30000)包括实验A,B的各两次实验都成功,而实验C的三次都不成功或三次实验中只有一次成功,P(X=60000)包括实验A,B的各两次实验都成功,而实验C的三次中都成功或三次中有两次成功,进而得出X分布列与数学期望.解答:解:(1)设A,B,C实验成功分别记为事件A,B,C,且相互独立.记事件至少有一次实验成功为D,则P(D)=1﹣=1﹣=1﹣=.(II)X的取值分别为,0,10000,30000,60000.则P(X=0)=+=,P(X=10000)=×=,P(X=30000)==,P(X=60000)=×=,X分布列为:X 0 10000 30000 60000P(X)X的数学期望E(X)=+++=21600元.点评:本题考查了随机变量的分布列及其数学期望、相互独立事件的概率、相互对立事件的概率计算公式,考查了推理能力与计算能力,属于中档题.19.单调递增数列{a n}的前n项和为S n,且满足4S n=a n2+4n.(1)求数列{a n}的通项公式;(2)数列{b n}满足,求数列{b n}的前n项和T n.考点:数列的求和;数列递推式.专题:等差数列与等比数列.分析:(1)由4S n=a n2+4n,利用递推关系可得:,变为(a n﹣2+a n﹣1)(a n﹣2﹣a n﹣1)=0,利用数列{a n}是单调递增数列,可得a n﹣a n﹣1=2.利用等差数列的通项公式即可得出;(2)由数列{b n}满足,可得=.再利用“错位相减法”、等比数列的前n项和公式即可得出.解答:解:(1)∵4S n=a n2+4n.∴当n=1时,4a1=+4,解得a1=2;当n≥2时,+4(n﹣1),∴4a n=4S n﹣4S n﹣1=a n2+4n﹣,化为,变为(a n﹣2+a n﹣1)(a n﹣2﹣a n﹣1)=0,∴a n+a n﹣1=2或a n﹣a n﹣1=2.∵数列{a n}是单调递增数列,a n+a n﹣1=2应该舍去,∴a n﹣a n﹣1=2.∴数列{a n}是等差数列,首项为2,公差为2,∴a n=2+2(n﹣1)=2n.(2)∵数列{b n}满足,∴=,∴=.∴数列{b n}的前n项和T n=+…+,=+…+,∴=++…+=﹣=,∴.点评:本题考查了递推式的应用、“错位相减法”、等差数列与等比数列的通项公式与前n 项和公式、对数的运算性质、数列的单调性,考查了推理能力与计算能力,属于难题.20.(13分)(2015•德州一模)已知函数f(x)=x﹣alnx+(a∈R)(1)求f(x)的单调区间;(2)若在[1,e](e=2.71828…)上任取一点x0,使得f(x0)≤0成立,求a的取值范围.考点:利用导数研究函数的单调性;利用导数求闭区间上函数的最值.专题:导数的综合应用.分析:(1)先求导,再分类讨论,得到函数的单调区间;(2)由题意,只要求出函数f(x)min≤0即可,利用导数和函数的最值的关系,进行分类讨论,即可得到a的范围.解答:解:(1)∵f(x)=x﹣alnx+(a∈R),∴f′(x)=1﹣﹣==,①当1+a≤0时,即a≤﹣1时,在x∈(0,+∞)上,f′(x)>0,∴函数f(x)在(0,+∞)上单调递增,②当a+1>0时,即a>﹣1时,在(0,1+a)上f′(x)<0,在(1+a,+∞)上,f′(x)>0,∴函数f(x)在(0,1+a)上单调递减,在(1+a,+∞)上单调递增,(2)在[1,e](e=2.71828…)上任取一点x0,使得f(x0)≤0成立,∴函数f(x)=x﹣alnx+在[1,e]的最小值小于或等于0,由(1)知,当a≤﹣1时,在[1,e]上为增函数,f(x)min=f(1)=1+1+a≤0,解得a≤﹣2,当a>﹣1时①当1+a≥e时,即a≥e﹣1时,f(x)在[1,e]上单调递减,∴f(x)min=f(e)=e+﹣a≤0,解得a≥,∵>e﹣1,∴a≥;②当1+a≤1,即a≤0,f(x)在[1,e]上单调递增,∴f(x)min=f(1)=1+1+a≤0,解得a≤﹣2,与a>﹣1矛盾;③当1<1+a<e,即0<a<e﹣1时,f(x)min=f(1+a),∵0<ln(1+a)<1,∴0<aln(1+a)<a,∴f(1+a)=a+2﹣aln(1+a)>2,此时f(1+a)≤0不成立,综上所述若在[1,e](e=2.71828…)上任取一点x0,使得f(x0)≤0成立a的范围为a≥,或a≤﹣2点评:本题主要考查函数的单调性及最值,以及分类讨论的思想,转化思想,属于中档题.21.已知椭圆C的中心在原点,焦点在x轴上,离心率等于,它的一个顶点恰好在抛物线x2=8y的准线上.(1)求椭圆C的标准方程;(2)点P(2,),Q(2,﹣)在椭圆上,A,B是椭圆上位于直线PQ两侧的动点.(i)若直线AB的斜率为,求四边形APBQ面积的最大值;(ii)当A,B运动时,满足∠APQ=∠BPQ,试问直线AB的斜率是否为定值,请说明理由.考点:椭圆的简单性质.专题:圆锥曲线中的最值与范围问题.分析:(1)设椭圆C的标准方程为(a>b>0),由椭圆的一个顶点恰好在抛物线x2=8y的准线y=﹣2上,可得﹣b=﹣2,解得b.又,a2=b2+c2,联立解得即可.(2)(i)设A(x1,y1),B(x2,y2),直线AB的方程为y=,与椭圆方程联立化为﹣12=0,由△>0,解得,利用根与系数的关系可得:x1﹣x2|=.四边形APBQ面积S=,利用二次函数的单调性即可得出.(ii)由∠APQ=∠BPQ,则PA,PB的斜率互为相互数,可设直线PA的斜率为k,则PB的斜率为﹣k,直线PA的方程为:=k(x﹣2),与椭圆的方程联立化为+4﹣16=0,利用根与系数的关系、斜率计算公式即可得出.解答:解:(1)设椭圆C的标准方程为(a>b>0),∵椭圆的一个顶点恰好在抛物线x2=8y的准线y=﹣2上,∴﹣b=﹣2,解得b=2.又,a2=b2+c2,∴a=4,,可得椭圆C的标准方程为.(2))(i)设A(x1,y1),B(x2,y2),直线AB的方程为y=,联立,化为﹣12=0,由△>0,解得,∴,x1x2=3t2﹣12,∴|x1﹣x2|==.四边形APBQ面积S==,当t=0时,S max=12.(ii)∵∠APQ=∠BPQ,则PA,PB的斜率互为相反数,可设直线PA的斜率为k,则PB的斜率为﹣k,直线PA的方程为:=k(x﹣2),联立,化为+4﹣16=0,∴x1+2=,同理可得:x2+2==,∴x1+x2=,x1﹣x2=,k AB===.∴直线AB的斜率为定值.点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得△>0及其根与系数的关系、弦长公式、斜率计算公式、四边形面积最大值,考查了推理能力与计算能力,属于难题.。
山东省德州市第一中学2015届高三数学10月月考试卷 理(含解析)

山东省德州市第一中学2015届高三数学10月月考试卷 理(含解析)注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明一、选择题(题型注释)1.已知集合A {}3,2,1,0=,集合 {|||2}B x N x =∈≤ ,则AB =( )A .{}3B .{}2,1,0C .{}2,1 D .{}3,2,1,0 【答案】B【解析】试题分析:因为{|||2}B x N x =∈≤{}2,1,0,1,2--= ,A {}3,2,1,0=, 所以AB {}2,1,0=.考点:集合的交集.2.若0()3f x '=-,则000()()lim h f x h f x h h→+--=( )A .3-B .6-C .9-D .12-【答案】B 【解析】 试题分析:由题意可得:000()()limh f x h f x h h→+--=()()()()()622lim 2lim 0'000000-==+-+=+-+→→x f h h x f h x f h h x f h x f h h . 考点:导数的定义及应用.3.函数)ln()(2x x x f -=的定义域为( )A.)1,0(B.]1,0[C.),1()0,(+∞-∞D.),1[]0,(+∞-∞ 【答案】C 【解析】试题分析:因为)ln()(2x x x f -=,所以0102<>⇒>-x x x x 或,所以函数)ln()(2x x x f -=的定义域为),1()0,(+∞-∞ .考点:函数的定义域.4.已知函数||5)(x x f =,)()(2R a x ax x g ∈-=,若1)]1([=g f ,则=a ( ) A.1 B.2 C.3 D.-1 【答案】A 【解析】试题分析:由题意可得:()[]()10115111=⇒=-⇒==-=-a a a f g f a .考点:幂函数方程求解.5.已知)(),(x g x f 分别是定义在R 上的偶函数和奇函数,且1)()(23++=-x x x g x f ,则=+)1()1(g f ( )A.3-B.1-C.1D.3 【答案】C 【解析】试题分析:因为1)()(23++=-x x x g x f ,所以()()111=---g f ,又因为)(),(x g x f 分别是定义在R 上的偶函数和奇函数, 所以()()111=+g f . 考点:函数奇偶性的应用.6.已知集合A {}4,1,0,2=,B ={k |k R ∈,22k A -∈,2k A -∉},则集合B 中所有元素之和为( )A .2B .-2C .0D 【答案】B 【解析】试题分析:当2222-=⇒=-k k 或2=k ,又因为A k ∉-2,所以2-=k 符合题意;当2,2022-==⇒=-k k k ,A k ∉-2,所以2,2-==k k 符合题意;当3,3122-==⇒=-k k k ,A k ∉-2,所以3,3-==k k 符合题意;当6,6422-==⇒=-k k k ,A k ∉-2,所以6,6-==k k 符合题意;所以{}6,6,3,3,2,2,2----=B ,所以集合B 中所有元素之和为-2. 考点:元素与集合的关系. 7.曲线1x y xe-=在点(1,1)处切线的斜率等于( )A .2eB .eC .2D .1【答案】C 【解析】试题分析:由1x y xe-=可得:11'--+=x x xe ey ,所以2|001'=+==e e y x ,所以曲线1x y xe-=在点()1,1处切线的斜率2=k . 考点:导数的几何意义. 8..若12()2(),f x x f x dx =+⎰则1()f x dx =⎰( )A.1-B.13-C.13D.1 【答案】B【解析】 试题分析:令()dx x f m ⎰=1,则()()m x dx x f xx f 22212+=+=⎰,所以()()()()m m dx x dx m x dx dx x f x dx x f m 2312221021021010210+=+=+=⎪⎭⎫ ⎝⎛+==⎰⎰⎰⎰⎰, 所以()313110-=⇒-=⎰dx x f m考点:定积分的应用. 9.下列四个图中,函数=y 10111n x x ++的图象可能是( )A B C D【答案】C 【解析】试题分析:因为xx y ln 10=是奇函数,所以向左平移一个单位可得:11ln 10++=x x y ,所以11ln 10++=x x y 的图像关于()0,1-中心对称,故排除A,D当2-<x 时,0<y 恒成立,所以应选C 考点:函数的图像.10.如图所示的是函数d cx bx x x f +++=23)(的大致图象,则2221x x +等于( )A .32 B .34 C .38D .916【答案】D【解析】试题分析:由图像可得:⎪⎩⎪⎨⎧=-=-=⇒⎪⎩⎪⎨⎧=+++==+-+-0210248001d c b d c b d d c b , 所以()2232'--=x x x f ,由题意可得:21,x x 是函数d cx bx x x f +++=23)(的两个极值点,故21,x x 是方程()0'=x f 的根,所以32,322121-==+x x x x ,则()9162212212221=-+=+x x x x x x . 考点:利用导数研究函数极值.第II 卷(非选择题)请点击修改第II 卷的文字说明 评卷人 得分二、填空题(题型注释)11.物体运动方程为23t S =-,则2t =时瞬时速度为 【答案】4ln 2 【解析】试题分析:由题意可得:2ln 2't s =,所以当2t =时瞬时速度为2ln 42ln 2|22'===t s考点:导数的几何意义. 12.已知()f x =2lg()1a x+-是奇函数,则实数a 的值是 【答案】1- 【解析】试题分析:因为()⎪⎭⎫⎝⎛+-=a x x f 12lg ,所以对于定义域内的所有x 的有()()x f x f -=-,即:⇒-+-=+++⇒⎪⎭⎫⎝⎛-+-=⎪⎭⎫ ⎝⎛+++⇒⎪⎭⎫ ⎝⎛+--=⎪⎭⎫ ⎝⎛++ax a x x ax a ax a x x ax a a x a x 211221lg 12lg 12lg 12lg()()111221222222-=⇒⎪⎩⎪⎨⎧==+⇒-+=-a a a x a a x考点:奇函数性质的应用.13.如图所示,已知抛物线拱形的底边弦长为a ,拱高为b ,其面积为____________.【答案】23ab 【解析】试题分析:建立如图所示的坐标系:所以设抛物线的方程为224x a b y -=所以函数与x 轴围成的部分的面积为3|34)4(22322222ab x a b dx x a b s aa a a =⎪⎭⎫ ⎝⎛-=-=--⎰,所以阴影部分的面积为323abab ab =-.考点:定积分的应用.14.不等式632(2)(2)x x x x -+>+-的解集为____________. 【答案】{}|12x x x <->或 【解析】试题分析:原不等式等价于623(2)(2).x x x x +>+++设3()f x x x =+,则()f x 在R 上单调增.所以,原不等式等价于22()(2)212f x f x x x x x >+⇔>+⇔<->或 所以原不等式的解集为:{}|12x x x <->或. 考点:解不等式.15.已知()f x 为R 上增函数,且对任意x R ∈,都有()34xf f x ⎡⎤-=⎣⎦,则(2)f =____________.【答案】10【解析】试题分析:令()3xt f x =-,则()4f t =且()3xf x t =+,所以()341tf t t t =+=⇒=,所以()13xf x =+,所以()221310f =+=.考点:函数单调性的应用. 评卷人 得分三、解答题(题型注释)16.已知函数()f x 的定义域为(2,2)-,函数()(1)(32)g x f x f x =-+-(1)求函数()g x 的定义域;(2)若()f x 是奇函数,且在定义域上单调递减,求不等式()0g x ≤的解集.【答案】(1)15(,)22;(2)1,22⎛⎤ ⎥⎝⎦.【解析】试题分析:(1)由题意可得:1321215232222x x x x -⎧--⎧⎪⇒⎨⎨--⎩⎪⎩<<<<<<<<,解此不等式组即可得出函数()g x 的定义域15(,)22;(2)由不等式()0g x ≤可得(1)(32)f x f x -+-根据单调性得2121223222123x x x x x --⎧⎪--⇒⎨⎪--⎩<<<<<≤≥进而可得不等式()0g x ≤的解集. 试题解析:(1)由题意可知:1321215232222x x x x -⎧--⎧⎪⇒⎨⎨--⎩⎪⎩<<<<<<<<,解得1522x << 3分∴函数()g x 的定义域为15(,)224分(2)由()0g x ≤得(1)(32)f x f x -+-≤0, ∴(1)(32)f x f x -≤-- 又∵()f x 是奇函数, ∴(1)(23)f x f x -≤- 8分又∵()f x 在(2,2)-上单调递减,∴2121223222123x x x x x --⎧⎪--⇒⎨⎪--⎩<<<<<≤≥ 11分∴()0g x ≤的解集为1,22⎛⎤ ⎥⎝⎦考点:函数的定义域、奇偶性、单调性的应用.17.已知曲线 32y x x =+- 在点 0P 处的切线 1l 平行直线410x y --=,且点 0P 在第三象限.(1)求0P 的坐标;(2)若直线 1l l ⊥ , 且 l 也过切点0P ,求直线 l的方程.【答案】(1)(1,4)--;(2)4170x y ++=. 【解析】试题分析:(1)根据曲线方程求出导数,因为已知直线410x y --=的斜率为4,根据切线与已知直线平行得到斜率都为4,所以令导数等于4得到关于x 的方程,求出方程的解,即为0p 的横坐标,又因为切点在第三象限,所以即可写出满足条件的切点坐标;(2)直线1l 的斜率为4,根据垂直两直线的斜率之积等于1-,可得直线l 的斜率为14-,又由(1)可知切点的坐标,即可写出直线l 的方程.试题解析:由32y x x =+-,得231y x '=+, 2分 由1l 平行直线410x y --=得2314x +=,解之得1x =±.当1x =时,0y =; 当1x =-时,4y =-. 4分 又∵点0P 在第三象限,∴切点0P 的坐标为(1,4)-- 6分 (2)∵直线1l l ⊥, 1l 的斜率为4, ∴直线l 的斜率为14-, 8分 ∵l 过切点0P ,点0P 的坐标为 (-1,-4) ∴直线l 的方程为14(1)4y x +=-+11分 即4170x y ++= 12分 考点:利用导数研究曲线方程.18.若实数0x 满足00()f x x =,则称0x x =为()f x 的不动点.已知函数3()3f x x bx =++, 其中b 为常数.(1)求函数()f x 的单调递增区间;(2)若存在一个实数0x ,使得0x x =既是()f x 的不动点,又是()f x 的极值点.求实数b 的值;【答案】(1)当0b ≥时,()f x 的单调递增区间为(,)-∞+∞,当0b <时,()f x 的单调递增区间为(,-∞,)+∞;(2)3b =-. 【解析】试题分析:(1)首先求出函数的导函数2()3f x x b '=+,然后根据b 的取值范围讨论导数的正负进而得出函数的单调区间;(2)由题意可得:203000303x b x bx x ⎧+=⎨++=⎩,解方程组可得3b =-.试题解析:(1)因3()3f x x bx =++,故2()3f x x b '=+. 1分 当0b ≥时,显然()f x 在R 上单增; 3分当0b <时,由知x >x <分 所以,当0b ≥时,()f x 的单调递增区间为(,)-∞+∞;当0b <时,()f x的单调递增区间为(,-∞,)+∞ 6分(2)由条件知203000303x b x bx x ⎧+=⎨++=⎩,于是300230x x +-=, 8分即2000(1)(223)0x x x -++=,解得01x = 11分从而3b =-. 12分 考点:函数性质的综合应用.19.统计表明,某种型号的汽车在匀速行驶中每小时的耗油量y (升)关于行驶速度x (千米/小时)的函数解析式可以表示为:3138(0120)12800080y x x x =-+<≤,已知甲、乙两地相距100千米(1)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升? (2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升? 【答案】(1)17.5;(2)以80千米/小时的速度匀速行驶时耗油最少,最少为11.25升. 【解析】试题分析:利用基本不等式解决实际问题时,应先仔细阅读题目信息,理解题意,明确其中的数量关系,并引入变量,依题意列出相应的函数关系式,然后利用基本不等式求解;(2)在求所列函数的最值时,若用基本不等式时,等号取不到时,可利用函数的单调性求解;(3)基本不等式具有将“和式”转化为“积式”和将“积式”转化为“和式”的放缩功能,常常用于比较数的大小或证明不等式,解决问题的关键是分析不等式两边的结构特点,选择好利用基本不等式的切入点.试题解析:(1)当40x =时,汽车从甲地到乙地行驶了1002.540=小时, 2分 要耗油313(40408) 2.517.512800080⨯-⨯+⨯= 4分答当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油17.5升 5分(2)当速度为x 千米/小时时,汽车从甲地到乙地行驶了100x小时,设油耗为()h x 升, 依题意得313100()(8)12800080h x x x x =-+⋅218001512804x x =+- (0120x <≤) 7分方法一则332280080()640640x x h x x x-'=-= (0120x <≤) 8分 令()0h x '=,解得80x =,列表得所以当80x =时,()h x 有最小值(80)11.25h =. 11分 方法二 2180015()12804h x x x =+-214004001512804x x x =++- 8分154≥-=11.25 10分 当且仅当214004001280x x x==时成立,此时可解得80x = 11分 答:当汽车以80千米/小时的速度匀速行驶时,从甲地到乙地耗油最少,最少为11.25升. 12分考点:基本不等式及函数模型的应用. 20.已知函数()ln f x x =(0)x ≠,函数1()()(0)()g x af x x f x '=+≠' (1)当0x ≠时,求函数()y g x =的表达式;(2)若0a >,函数()y g x =在(0,)+∞上的最小值是2 ,求a 的值;(3)在(2)的条件下,求直线2736y x =+与函数()y g x =的图象所围成图形的面积. 【答案】(1)()a y g x x x ==+;(2)1a =;(3)2ln 23ln 247-+.【解析】试题分析:(1)对x 的取值分类讨论,化简绝对值求出()'fx 得到0x >和0x <导函数相等,代入到()g x 即可;(2)根据基本不等式得到()g x 的最小值即可求出a ;(3)根据(2)知()1g x x x=+,首先联立直线与函数解析式求出交点,利用定积分求出直线与函数图像围成的区域的面积即可.试题解析:(1)∵()ln f x x =,∴当0x >时,()ln f x x =,1()f x x'=当0x <时,()ln()f x x =-,11()(1)f x x x'=⋅-=-. ∴当0x ≠时,函数()a y g x x x==+. 4分 (2)∵由(1)知当0x >时,()a g x x x =+, ∴当0,0a x >>时, ()≥g xx =时取等号.∴函数()y g x =在(0,)+∞上的最小值是∴依题意得2=∴1a =. 8分 (3)由27361y x y x x ⎧=+⎪⎪⎨⎪=+⎪⎩解得2121322,51326x x y y ⎧==⎧⎪⎪⎪⎨⎨=⎪⎪=⎩⎪⎩ ∴直线2736y x =+与函数()y g x =的图象所围成图形的面积 232271()()36S x x dx x ⎡⎤=+-+⎢⎥⎣⎦⎰=2ln 23ln 247-+ 13分 考点:导数及函数单调性、定积分的应用.21.设关于x 的方程210x mx --=有两个实根,,αβαβ<,函数()221x m f x x -=+. (1)求()()f f ααββ+的值;(2)判断()f x 在区间(),αβ的单调性,并加以证明;(3)若,λμ均为正实数,证明:f f λαμβμαλβαβλμλμ⎛⎫⎛⎫++-<- ⎪ ⎪++⎝⎭⎝⎭【答案】(1)()f αα+()2f ββ=;(2)单调递增;(3)见解析.【解析】试题分析:(1)因为,αβ是方程的210x mx --=的两个实根,利用韦达定理即可得到()f x的解析式,求出()(),f f αβ进而即可求出()()f f ααββ+的值;(2)利用导数及二次函数的图像来讨论导数的正负,即可判断函数的单调性;(3)首先求出,λαμβμαλβλμλμ++++的取值范围,然后根据函数的单调性判断出函数值的取值范围,把两个函数值相减即可得到要证的结论.试题解析:(1)∵,αβ是方程210x mx --=的两个根, ∴m αβ+=,1αβ=-, 1分∴()221mf ααα-=+,又m αβ=+,∴()222()1f ααβαβααααβ-+-==+-1α=,3分 即()1f αα=,同理可得()1f ββ=∴()f αα+()2f ββ= 4分(2)∵()2222(1)(1)x mx f x x --'=-+, 6分将m αβ=+代入整理的()222()()(1)x x f x x αβ--'=-+ 7分又()(),,0x f x αβ'∈>,∴()f x 在区间(),αβ的单调递增; 8分(3)∵λαμβαλμ+-+()0μβαλμ-=>+,λαμββλμ+-+()0μαβλμ-=<+ ∴λαμβαβλμ+<<+ 10分由(2)可知()()()f f f λαμβαβλμ+<<+,同理()()()f f f μαλβαβλμ+<<+()()f f f f λαμβμαλβαβλμλμ⎛⎫⎛⎫++-<- ⎪ ⎪++⎝⎭⎝⎭ 12分由(1)可知1()f αα=,1()f ββ=,1αβ=-, ∴11()()||||||f f αβαβαβαβαβ--=-==-∴f f λαμβμαλβαβλμλμ⎛⎫⎛⎫++-<- ⎪ ⎪++⎝⎭⎝⎭14分考点:函数与方程、函数的单调性、不等式的证明.。
山东省德州一中2015届高三上学期10月月考数学(理)试题

山东省德州一中2015届高三上学期10月月考数学(理)试题(解析版)【试卷综析】试卷贴近中学教学实际,在坚持对五个能力、两个意识考查的同时,注重对数学思想与方法的考查,体现了数学的基础性、应用性和工具性的学科特色.以支撑学科知识体系的重点内容为考点挑选合理背景,考查更加科学.试卷从多视角、多维度、多层次地考查数学思维品质,考查考生对数学本质的理解,考查考生的数学素养和学习潜能.第Ⅰ卷(选择题 共50分)一、选择题:每小题5分,共10题,50分.【题文】1.已知集合A ={0,1, 2,3},集合 {|||2}B x N x =∈≤ ,则A B =( )A .{ 3 }B .{0,1,2}C .{ 1,2}D .{0,1,2,3}【知识点】交集的运算.A1【答案解析】B 解析:因为{|||2}B x N x =∈≤{}|22x x =-≤≤,所以A B ={0,1,2},故选B.【思路点拨】先解出集合B ,再求A B 即可.【题文】2.若0()3f x '=-,则 )A .3-B .6-C .9-D .12- 【知识点】导数的概念.B11【答案解析】B B.【思路点拨】利用导数的概念解之即可.【题文】3.函数)ln()(2x x x f -=的定义域为( )A.)1,0(B. ]1,0[C. ),1()0,(+∞-∞D. ),1[]0,(+∞-∞ 【知识点】函数的定义域.B1【答案解析】C 解析:若使原函数有意义,则20x x ->,解得1x >或0x <,即函数的定义域为),1()0,(+∞-∞ ,故选C.【思路点拨】若使原函数有意义,解一元二次不等式即可.【题文】4.已知函数||5)(x x f =,)()(2R a x ax x g ∈-=,若1)]1([=g f ,则=a ( ) A.1 B. 2 C. 3 D. -1【知识点】函数的值.B1【答案解析】A 解析:由题意得:()11g a =-,所以()|1|151a f a --==,解得1a =,故选A.【思路点拨】先由题意得()1g ,然后解方程|1|51a -=即可.【题文】5.已知)(),(x g x f 分别是定义在R 上的偶函数和奇函数,且1)()(23++=-x x x g x f ,则=+)1()1(g f ( )A. 3-B. 1-C. 1D. 3 【知识点】奇函数、偶函数的性质.B4【答案解析】C 解析:因为)(),(x g x f 分别是定义在R 上的偶函数和奇函数,所以()()f x f x -=,g()()x g x -=-,又因为1)()(23++=-x x x g x f ,故32()g()1f x x x x ---=-++,即32()()1f x g x x x +=-++,则=+)1()1(g f 1,故选C.【思路点拨】先由题意的()()f x f x -=,g()()x g x -=-,再结合1)()(23++=-x x x g x f 可求出32()()1f x g x x x +=-++,进而得到结果.【题文】6.已知集合A ={2,0,1,4},B ={k |k R ∈,22k A -∈,2k A -∉},则集合B 中所有元素之和为( )A .2B .-2C .0D 【知识点】集合中元素的特性.A1【答案解析】B 解析:因为22k A -∈,所以有下列情况成立:(1)22k -=2,解得2k =±,当2k =时,20k A -=∈不满足题意,舍去,故2k =-;(2)22k -=0(3)22k -=1(4)22k -=4 所以集合B 中所有元素之和为2-,故选B.【思路点拨】由22k A -∈分情况讨论即可得到结果. 【题文】7.曲线1x y xe-=在点(1,1)处切线的斜率等于( )A .2eB .eC .2D .1 【知识点】导数的几何意义.B11【答案解析】C 解析:因为1()x f x xe-=,所以()1()1x f x x e-'=+,则()11(1)112k f e -'==+=,故选C.【思路点拨】先对原函数求导,再利用导数的几何意义求出斜率即可. 【题文】8则1()f x dx =⎰( )A.1-B.【答案解析】B 解析:设()1m f x dx =⎰,则2()2f x x m =+,故选B.【思路点拨】本题考查了定积分以及微积分基本定理的应用. 【题文】9.下列四个图中,函数 )ABCD【知识点】函数的图像;函数的性质.B8【答案解析】C 解析:令1t x =+,则原函数转化为于坐标原点对称,可排除A,D;又因为当0x >时,函数值为正值,故排除B,则答案为C. 【思路点拨】借助于函数的性质结合排除法即可.【题文】10.如图所示的是函数d cx bx x x f +++=23)(的大致图象,则2221x x +等于( )A B C D【答案解析】C 解析:由图象知()0f x =的根为0,1,2,\d=0,\()322()0f x x bx cx x x bx c =++=++=,\20x bx c ++=的两根为1和2,\3,2b c =-=,\32()32f x x x x =-+,\2()362f x x x ¢=-+,Q 12,x x 为23620x x -+=的两根,\122x x +=,选C.【思路点拨】由图象知()0f x =的根为0,1,2,求出函数解析式,12,x x 为23620x x -+=的两根,结合根与系数的关系求解.第Ⅱ卷(非选择题 共100分)二、填空题:每小题5分,共5题,25分.11.物体运动方程为23t S =-,则2t =时瞬时速度为 【知识点】导数的几何意义.B11【答案解析】4ln 2 解析:由题意得:2ln 2t S '=,当2t =时瞬时速度为22|2ln 24ln 2t S ='==,故答案为:4ln 2。
山东省德州市高三数学上学期1月月考试题 理1

高三数学(理)月考试题(2016/1/11)(时间120分钟,满分150分)一、选择题(每小题5分,共计50分) 1.设i 是虚数单位,复数7412ii+=+( ) A . 32i -B .32i +C . 23i +D . 23i -2.集合{}{}20,2A x x a B x x =-≥=<,若R C A B ⊆,则实数a 的取值范围是( ) A . []0,4B .(],4-∞C . (),4-∞D . ()0,43.设0.50322,log 2,log 0.1a b c ===,则 A.a b c <<B. c a b <<C. c b a <<D. b c a <<4.下列四个结论:①若0x >,则sin x x >恒成立;②命题“若sin 0,0x x x -==则”的逆命题为“若0sin 0x x x ≠-≠,则”; ③“命题p q ∨为真”是“命题p q ∧为真”的充分不必要条件; ④命题“,ln 0x R x x ∀∈->”的否定是“000,ln 0x R x x ∃∈-≤”. 其中正确结论的个数是( ) A .1个B .2个C .4个D .3个5.直线10x my ++=与不等式组30,20,20x y x y x +-≥⎧⎪-≥⎨⎪-≤⎩表示的平面区域有公共点,则实数m 的取值范围是( )A . 14,33⎡⎤⎢⎥⎣⎦B . 41,33⎡⎤--⎢⎥⎣⎦C . 3,34⎡⎤⎢⎥⎣⎦D . 33,4⎡⎤--⎢⎥⎣⎦6.已知某几何体的三视图,则该几何体的体积是( )A .12B .24C .36D .487.设01a <<,则函数11x y a =-的图象大致为( )8.已知向量()()0,sin ,1,2cos a x b x ==,函数()()2237,22f x a bg x a b =⋅=+-,则()f x 的图象可由()g x 的图象经过怎样的变换得到( )A .向左平移4π个单位长度 B . 向左平移2π个单位长度 C .向右平移4π个单位长度D . 向右平移2π个单位长度9. 已知函数()()()sin 0f x A x ωϕϕπ=+<<的图象如图所示,若()00053,,sin 36f x x x ππ⎛⎫=∈ ⎪⎝⎭,则的值为10.设()ln f x x =,若函数()()g x f x ax =-在区间(]0,3上有三个零点,则实数a 的取值范围是 A.10,e ⎛⎫ ⎪⎝⎭B. ln 31,3e ⎡⎫⎪⎢⎣⎭C.ln 30,3⎛⎤⎥⎝⎦D.ln 3,3e ⎛⎫⎪⎝⎭二、解答题(每小题5分共计25分)11.已知()sin cos 0,,tan αααπα-=∈=则 .12.已知平面向量()()1,22,.23a b m a b a b ==-⊥+=,,且则 . 13.函数1lg 1y x ⎛⎫=-⎪⎝⎭的定义域是 . 14. 设甲、乙两个圆柱的底面积分别为12S S 、,体积分别为12υυ,,若它们的侧面积相等,且1122169S S υυ=,则的值为.15.给出下列四个命题:①命题“,cos 0x R x ∀∈>”的否定是“,cos 0x R x ∃∈≤”; ②a 、b 、c 是空间中的三条直线,a//b 的充要条件是a c b c ⊥⊥且; ③命题“在△ABC 中,若,sin sin A B A B >>则”的逆命题为假命题;④对任意实数()()()(),000x f x f x x x x ''-=>><<有,且当时,f ,则当x 0时,f . 其中的真命题是 .(写出所有真命题的编号) 三、解答题:16.已知函数()()21cos cos 0,2f x x x x x R ωωωω=-->∈的图像上相邻两个最高点的距离为π.(I )求函数()f x 的单调递增区间;(II )若ABC ∆三个内角A 、B 、C的对边分别为()0,sin a b c c f C B ===、、,且3sin A ,求a ,b 的值.17. 已知数列{}n a 前n 项和n S 满足:21n n S a += (I )求数列{}n a 的通项公式; (II )设()()11211n n n n a b a a ++=++,数列{}n b 的前n 项和为n T ,求证:14n T <.18. 在如图所示的空间几何体中,平面ACD ⊥平面ABC ,ACD ACB ∆∆与是边长为2的等边三角形,BE=2,BE 和平面ABC 所成的角为60°,且点E 在平面ABC 上的射影落在ABC ∠的平分线上. (I )求证:DE//平面ABC ;(II )求二面角E BC A --的余弦值. 19. (本小题满分12分)如图正方形ABCD 的边长为ABCD的边长为BDEF 是平行四边形,BD 与AC 交于点G ,O 为GC的中点,FO FO =⊥平面ABCD.(I )求证:AE//平面BCF ;(II)若FO =,求证CF ⊥平面AEF..20. (本小题满分13分)已知函数()ln ,f x x mx m R =-∈.(I )求()f x 的单调区间; (II )若()[)1211m f x m x-≤-++∞在,上恒成立,求实数m 的取值范围. 21(本小题满分14分).如图,在△ABC 中,已知∠ABC=45°,O 在AB 上,且OB=OC=AB ,又PO ⊥平面ABC ,DA ∥PO ,DA=AO=PO . (Ⅰ)求证:PD ⊥平面COD ;(Ⅱ)求二面角B ﹣DC ﹣O 的余弦值.高三数学(理)月考试题答案一、 选择题1.A2.B3.C 4、D 5、D 6、A 7、B 8、C 9、D 10、D 二.填空题11. -1 12.(-4,7) 13.32[log ,)+∞ 14. 4315.①④ 三、解答题18.解析:(Ⅰ)证明:由题意知,ABC ∆,ACD ∆都是边长为2的等边三角形,取AC 中点O ,连接,BO DO ,则BO AC ⊥,DO AC ⊥,又∵平面ACD ⊥平面ABC ,∴DO ⊥平面ABC ,作EF ⊥平面ABC , 那么//EF DO ,根据题意,点F 落在BO 上, ∴60EBF ∠=︒,易求得∴四边形DEFO 是平行四边形,∴//DE OF ,∴//DE 平面 ABC …………6分(Ⅱ)建立如图所示的空间直角坐标系O xyz -,可知平面ABC 的一 个法向量为1(0,0,1)n =,,(1,0,0)C -,设平面BCE 的一个法向量为2(,,)n x y z =, 则,2200n BC n BE ⎧⋅=⎪⎨⋅=⎪⎩可求得(3,n =-分1213,13||||n n n n n n ⋅>==⋅又由图知,所求二面角的平面角是锐角, 所以二面角E BC A --的余弦值为分21.【解析】:(Ⅰ)证明:设OA=1,则PO=OB=2,DA=1,由DA∥PO,PO⊥平面ABC,知DA⊥平面ABC,∴DA⊥AO.从而,在△PDO中,∵PO=2,∴△PDO为直角三角形,故PD⊥DO.又∵OC=OB=2,∠ABC=45°,∴CO⊥AB,又PO⊥平面ABC,∴PO⊥OC,又PO,AB⊂平面PAB,PO∩AB=O,∴CO⊥平面PAB.故CO⊥PD.∵CO∩DO=O,∴PD⊥平面COD.-------------7分(Ⅱ)解:以OC,OB,OP所在射线分别为x,y,z轴,建立直角坐标系如图.则由(Ⅰ)知,C(2,0,0),B(0,2,0),P(0,0,2),D(0,﹣1,1),∴,由(Ⅰ)知PD⊥平面COD,∴是平面DCO的一个法向量,设平面BDC的法向量为,∴,∴,令y=1,则x=1,z=3,∴,∴,由图可知:二面角B﹣DC﹣O为锐角,二面角B﹣DC﹣O的余弦值为.--14分。
2015年山东省德州市高考一模数学试卷(理科)【解析版】

2015年山东省德州市高考数学一模试卷(理科)一、选择题(50分)1.(5分)设复数z的共轭复数为,若(2+i)z=3﹣i,则的值为()A.1B.2C.D.42.(5分)设全集U={x∈N|x<6},集合A={l,3},B={3,5},则(∁U A)∩(∁U B)=()A.{2,4}B.{2,4,6}C.{0,2,4}D.{0,2,4,6} 3.(5分)“¬p为假命题”是“p∧q为真命题”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.(5分)执行如图所示的程序框图,若输入数据n=5,a1=1,a2=2,a3=3,a4=4,a5=5,则输出的结果为()A.1B.2C.3D.45.(5分)若函数f(x)=a2x﹣4,g(x)=log a|x|(a>0,且a≠1),且f(2)•g (2)<0,则函数f(x),g(x)在同一坐标系中的大致图象是()A.B.C.D.6.(5分)已知抛物线y2=8x与双曲线﹣y2=1的一个交点为M,F为抛物线的焦点,若|MF|=5,则该双曲线的渐近线方程为()A.5x±3y=0B.3x±5y=0C.4x±5y=0D.5x±4y=0 7.(5分)棱长为2的正方体被一平面截得的几何体的三视图如图所示,那么被截去的几何体的体积是()A.B.C.4D.38.(5分)已知D是不等式组所确定的平面区域,则圆x2+y2=4与D 围成的区域面积为()A.B.C.πD.9.(5分)设m,n是正整数,多项式(1﹣2x)m+(1﹣5x)n中含x一次项的系数为﹣16,则含x2项的系数是()A.﹣13B.6C.79D.3710.(5分)已知函数f(x)是定义在R上的奇函数,其导函数为f′(x),当x <0时,2f(x)+xf′(x)<0恒成立,则f(1),2014,2015在大小关系为()A.2015<2014<f(1)B.2015<f(1)<2014C.f(1)<2015<2014D.f(1)<2014<2015二、填空题(25分)11.(5分)某校对全校1600名男女学生的视力状况进行调查,现用分层抽样的方法抽取一个容量是200的样本,已知女生比男生少抽10人,则该校的女生人数是人.12.(5分)(2x+)dx=.13.(5分)若不等式|x+1|+|2x﹣1|>a恒成立,则a的取值范围是.14.(5分)将函数f(x)=2sin(ωx﹣)(ω>0)的图象向左平移个单位,得到函数y=g(x)的图象,若y=g(x)在[0,]上为增函数,则ω的最大值为.15.(5分)设函数f(x)、g(x)的定义域分别为D J,D E,且D J⊆D E.若对于任意x⊆D J,都有g(x)=f(x),则称函数g(x)为f(x)在D E上的一个延拓函数.设f(x)=e x(x+1)(x<0),g(x)为f(x)在R上的一个延拓函数,且g(x)是奇函数,给出以下命题:①当x>0时,g(x)=e﹣x(x﹣1);②函数g(x)有5个零点;③g(x)>0的解集为(﹣1,0)∪(1,+∞);④函数g(x)的极大值为1,极小值为﹣1;⑤∀x1,x2∈R,都有|g(x1)﹣g(x2)|<2其中正确的命题是(填上所有正确的命题序号)三、解答题(75分)16.(12分)在△ABC中,角A,B,C对边分别是a,b,c,满足.(1)求角A的大小;(2)求sin A•sin B•sin C的最大值,并求取得最大值时角B,C的大小.17.(12分)正三棱柱ABC﹣A1B1C1的所有棱长都为4,D为的CC1中点.(1)求证:AB1⊥平面A1BD;(2)求二面角A﹣A1D﹣B的余弦值.18.(12分)某科技公司组织技术人员进行新项目研发,技术人员将独立地进行项目中不同类型的实验A,B,C,若A,B,C实验成功的概率分别为.(1)对A,B,C实验各进行一次,求至少有一次实验成功的概率;(2)该项目要求实验A,B各做两次,实验C做3次,如果A实验两次都成功则进行实验B并获奖励10000元,两次B实验都成功则进行实验C并获奖励30000元,3次C实验只要有两次成功,则项目研发成功并获奖励60000元(不重复得奖).且每次实验相互独立,用X表示技术人员所获奖励的数值,写出X的分布列及数学期望.19.(12分)单调递增数列{a n}的前n项和为S n,且满足4S n=a n2+4n.(1)求数列{a n}的通项公式;(2)数列{b n}满足a n+1+log2b n=log2a n,求数列{b n}的前n项和T n.20.(13分)已知函数f(x)=x﹣alnx+(a∈R)(1)求f(x)的单调区间;(2)若在[1,e](e=2.71828…)上任取一点x0,使得f(x0)≤0成立,求a的取值范围.21.(14分)已知椭圆C的中心在原点,焦点在x轴上,离心率等于,它的一个顶点恰好在抛物线x2=8y的准线上.(1)求椭圆C的标准方程;(2)点P(2,),Q(2,﹣)在椭圆上,A,B是椭圆上位于直线PQ两侧的动点.(i)若直线AB的斜率为,求四边形APBQ面积的最大值;(ii)当A,B运动时,满足∠APQ=∠BPQ,试问直线AB的斜率是否为定值,请说明理由.2015年山东省德州市高考数学一模试卷(理科)参考答案与试题解析一、选择题(50分)1.(5分)设复数z的共轭复数为,若(2+i)z=3﹣i,则的值为()A.1B.2C.D.4【解答】解:由(2+i)z=3﹣i,得,∴=.故选:B.2.(5分)设全集U={x∈N|x<6},集合A={l,3},B={3,5},则(∁U A)∩(∁U B)=()A.{2,4}B.{2,4,6}C.{0,2,4}D.{0,2,4,6}【解答】解:∵全集U={x∈N|x<6}={0,1,2,3,4,5},集合A={l,3},B ={3,5},∴∁U A={0,2,4,5},∁U B={0,1,2,4},则(∁U A)∩(∁U B)={0,2,4}.故选:C.3.(5分)“¬p为假命题”是“p∧q为真命题”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【解答】解:若¬p为假命题,则p为真命题.若p∧q为真命题,则p,q都为真命题,故“¬p为假命题”是“p∧q为真命题”的必要不充分条件,故选:B.4.(5分)执行如图所示的程序框图,若输入数据n=5,a1=1,a2=2,a3=3,a4=4,a5=5,则输出的结果为()A.1B.2C.3D.4【解答】解:模拟执行程序,可得输入数据n=5,a1=1,a2=2,a3=3,a4=4,a5=5,S=0,k=1S=1,k=2不满足条件k>5,S=,k=3不满足条件k>5,S=2,k=4不满足条件k>5,S=,k=5不满足条件k>5,S=3,k=6满足条件k>5,退出循环,输出S的值为3.故选:C.5.(5分)若函数f(x)=a2x﹣4,g(x)=log a|x|(a>0,且a≠1),且f(2)•g (2)<0,则函数f(x),g(x)在同一坐标系中的大致图象是()A.B.C.D.【解答】解:由题意f(x)=a2x﹣4是指数型的,g(x)=log a|x|是对数型的且是一个偶函数,由f(2)•g(2)<0,可得出g(2)<0,故log a2<0,故0<a<1,由此特征可以确定C、D两选项不正确,且f(x)=a2x﹣4是一个减函数,由此知A不对,B选项是正确答案故选:B.6.(5分)已知抛物线y2=8x与双曲线﹣y2=1的一个交点为M,F为抛物线的焦点,若|MF|=5,则该双曲线的渐近线方程为()A.5x±3y=0B.3x±5y=0C.4x±5y=0D.5x±4y=0【解答】解:抛物线y2=8x的焦点F(2,0),准线方程为x=﹣2,设M(m,n),则由抛物线的定义可得|MF|=m+2=5,解得m=3,由n2=24,可得n=±2.将M(3,)代入双曲线﹣y2=1,可得﹣24=1,解得a=,即有双曲线的渐近线方程为y=±x.即为5x±3y=0.故选:A.7.(5分)棱长为2的正方体被一平面截得的几何体的三视图如图所示,那么被截去的几何体的体积是()A.B.C.4D.3【解答】解:该几何体为正方体沿体对角线截成,其分成两部分的几何体的体积相等,而正方体的体积V=23=8,故被截去的几何体的体积是=4,故选:C.8.(5分)已知D是不等式组所确定的平面区域,则圆x2+y2=4与D 围成的区域面积为()A.B.C.πD.【解答】解:作出不等式组对应的平面区域,则公共区域如图:则直线x﹣2y=0的斜率k=,直线x+3y=0的斜率k=,则两直线的夹角θ满足tanθ=||=1,则θ=,则阴影部分对应的面积之和S==,故选:A.9.(5分)设m,n是正整数,多项式(1﹣2x)m+(1﹣5x)n中含x一次项的系数为﹣16,则含x2项的系数是()A.﹣13B.6C.79D.37【解答】解:由于多项式(1﹣2x)m+(1﹣5x)n中含x一次项的系数为•(﹣2)+•(﹣5)=﹣16,可得2m+5n=16 ①.再根据m、n为正整数,可得m=3、n=2,故含x2项的系数是•(﹣2)2+•(﹣5)2=37,故选:D.10.(5分)已知函数f(x)是定义在R上的奇函数,其导函数为f′(x),当x <0时,2f(x)+xf′(x)<0恒成立,则f(1),2014,2015在大小关系为()A.2015<2014<f(1)B.2015<f(1)<2014C.f(1)<2015<2014D.f(1)<2014<2015【解答】解:已知函数f(x)是定义在R上的奇函数,其导函数为f′(x),则:设函数g(x)=x2f(x)则:g′(x)=2xf(x)+x2f′(x)=g′(x)=x(2f(x)+xf′(x))当x<0时,2f(x)+xf′(x)<0恒成立,则:函数g′(x)>0所以函数在x<0时,函数g(x)为单调递增函数.由于函数f(x)是定义在R上的奇函数,则:函数g(x)=x2f(x)为奇函数.所以:在x>0时,函数g(x)为单调递增函数.所以:g()即:故选:D.二、填空题(25分)11.(5分)某校对全校1600名男女学生的视力状况进行调查,现用分层抽样的方法抽取一个容量是200的样本,已知女生比男生少抽10人,则该校的女生人数是760人.【解答】解:根据题意,设样本中女生人数为x,则(x+10)+x=200,解得x=95,所以该校的女生人数是人,故答案为:760.12.(5分)(2x+)dx=e2.【解答】解:∵(lnx)′=,(x2)′=2x,∴=x2|1e+lnx|1e=e2﹣1+lne﹣ln1=e2故答案为:e213.(5分)若不等式|x+1|+|2x﹣1|>a恒成立,则a的取值范围是(﹣∞,).【解答】解:设f(x)=|x+1|+|2x﹣1|=,由于函数f(x)在(﹣∞,﹣1]、(﹣1,)上都是减函数,在[,+∞)上是增函数,故当x=时,函数f(x)取得最小值为f()=.再根据题意可得>a,故答案为:(﹣∞,).14.(5分)将函数f(x)=2sin(ωx﹣)(ω>0)的图象向左平移个单位,得到函数y=g(x)的图象,若y=g(x)在[0,]上为增函数,则ω的最大值为2.【解答】解:函数的图象向左平移个单位,得到函数y=g(x)=2sinωx,y=g(x)在上为增函数,所以,即:ω≤2,所以ω的最大值为:2.故答案为:2.15.(5分)设函数f(x)、g(x)的定义域分别为D J,D E,且D J⊆D E.若对于任意x⊆D J,都有g(x)=f(x),则称函数g(x)为f(x)在D E上的一个延拓函数.设f(x)=e x(x+1)(x<0),g(x)为f(x)在R上的一个延拓函数,且g(x)是奇函数,给出以下命题:①当x>0时,g(x)=e﹣x(x﹣1);②函数g(x)有5个零点;③g(x)>0的解集为(﹣1,0)∪(1,+∞);④函数g(x)的极大值为1,极小值为﹣1;⑤∀x1,x2∈R,都有|g(x1)﹣g(x2)|<2其中正确的命题是①③⑤(填上所有正确的命题序号)【解答】解:①由题意得,若x>0时,则﹣x<0,g(x)为f(x)在R上的一个延拓函数,且g(x)是奇函数,则g(x)=f(x)=e x(x+1)(x<0),∴g(﹣x)=e﹣x(﹣x+1)=﹣g(x),∴g(x)=e﹣x(x﹣1),(x>0),故①正确;②∵g(x)=e x(x+1)(x<0),此时g′(x)=e x(x+2),令其等于0,解得x=﹣2,且当x∈(﹣∞,﹣2)上导数小于0,函数单调递减;当x∈(﹣2,0)上导数大于0,函数单调递增,x=﹣2处为极小值点,且g(﹣2)>﹣1,且在x=﹣1处函数值为0,且当x<﹣1是函数值为负.又∵奇函数的图象关于原点中心对称,故函数f(x)的图象应如图所示:由图象可知:函数g(x)有3个零点,故②错误;③由②知函数g(x)>0的解集为(﹣1,0)∪(1,+∞),故③正确,;④由②知函数在x=﹣2处取得极小值,极小值为g(﹣2)=e﹣2(﹣2+1)=﹣e﹣2,根据奇函数的对称性可知在x=2处取得极大值,极大值为g(2)=e﹣2,故④错误;⑤当x<0时,g(x)=e x(x+1),则当x→0时,g(x)→1,当x>0时,g(x)=e﹣x(x﹣1),则当x→0时,g(x)→﹣1,即当x<0时,﹣1<﹣e﹣2<g(x)<1,即当x>0时,﹣1<g(x)<e﹣2<1,故有对∀x1,x2∈R,|g(x2)﹣g(x1)|<2恒成立,即⑤正确.故正确的命题是①③⑤,故答案为:①③⑤三、解答题(75分)16.(12分)在△ABC中,角A,B,C对边分别是a,b,c,满足.(1)求角A的大小;(2)求sin A•sin B•sin C的最大值,并求取得最大值时角B,C的大小.【解答】解:(1)∵=cb cos A,.∴2bc cos A=a2﹣(b+c)2,展开为:2bc cos A=a2﹣b2﹣c2﹣2bc,∴2bc cos A=﹣2bc cos A﹣2bc,化为cos A=﹣,∵A∈(0,π).∴.(2)∵,∴,.∴sin A•sin B•sin C===﹣==﹣=﹣,∵.∴,当=时,即时,sin A•sin B•sin C取得最大值,此时B=C=.17.(12分)正三棱柱ABC﹣A1B1C1的所有棱长都为4,D为的CC1中点.(1)求证:AB1⊥平面A1BD;(2)求二面角A﹣A1D﹣B的余弦值.【解答】(1)证明:取BC中点O,连接AO,∵△ABC为正三角形,∴AO⊥BC,∵在正三棱柱ABC﹣A1B1C1中,平面ABC⊥平面BCC1B1,∴AO⊥平面BCC1B1,取B1C1中点为O1,以O为原点,,,的方向为x,y,z轴的正方向,建立空间直角坐标系,则.∴,,.∵,.∴,,∴AB1⊥面A1BD.AD的法向量为,(2)设平面A.,∴,∴,⇒,令z=1,得为平面A 1AD的一个法向量,由(1)知AB1⊥面A1BD,∴为平面A1AD的法向量,,由图可以看出:二面角A﹣A1D﹣B是锐角.∴二面角A﹣A1D﹣B的余弦值为.18.(12分)某科技公司组织技术人员进行新项目研发,技术人员将独立地进行项目中不同类型的实验A,B,C,若A,B,C实验成功的概率分别为.(1)对A,B,C实验各进行一次,求至少有一次实验成功的概率;(2)该项目要求实验A,B各做两次,实验C做3次,如果A实验两次都成功则进行实验B并获奖励10000元,两次B实验都成功则进行实验C并获奖励30000元,3次C实验只要有两次成功,则项目研发成功并获奖励60000元(不重复得奖).且每次实验相互独立,用X表示技术人员所获奖励的数值,写出X的分布列及数学期望.【解答】解:(1)设A,B,C实验成功分别记为事件A,B,C,且相互独立.记事件至少有一次实验成功为D,则P(D)=1﹣=1﹣=1﹣=.(II)X的取值分别为,0,10000,30000,60000.则P(X=0)=+=,P(X=10000)=×=,P(X=30000)==,P(X=60000)=×=,X分布列为:X的数学期望E(X)=+++=21600元.19.(12分)单调递增数列{a n}的前n项和为S n,且满足4S n=a n2+4n.(1)求数列{a n}的通项公式;(2)数列{b n}满足a n+1+log2b n=log2a n,求数列{b n}的前n项和T n.【解答】解:(1)∵4S n=a n2+4n.∴当n=1时,4a1=+4,解得a1=2;当n≥2时,+4(n﹣1),∴4a n=4S n﹣4S n﹣1=a n2+4n﹣,化为,变为(a n﹣2+a n﹣1)(a n﹣2﹣a n﹣1)=0,∴a n+a n﹣1=2或a n﹣a n﹣1=2.∵数列{a n}是单调递增数列,a n+a n﹣1=2应该舍去,∴a n﹣a n﹣1=2.∴数列{a n}是等差数列,首项为2,公差为2,∴a n=2+2(n﹣1)=2n.(2)∵数列{b n}满足,∴=,∴=.∴数列{b n}的前n项和T n=+…+,=+…+,∴=++…+=﹣=,∴.20.(13分)已知函数f(x)=x﹣alnx+(a∈R)(1)求f(x)的单调区间;(2)若在[1,e](e=2.71828…)上任取一点x0,使得f(x0)≤0成立,求a的取值范围.【解答】解:(1)∵f(x)=x﹣alnx+(a∈R),∴f′(x)=1﹣﹣==,①当1+a≤0时,即a≤﹣1时,在x∈(0,+∞)上,f′(x)>0,∴函数f(x)在(0,+∞)上单调递增,②当a+1>0时,即a>﹣1时,在(0,1+a)上f′(x)<0,在(1+a,+∞)上,f′(x)>0,∴函数f(x)在(0,1+a)上单调递减,在(1+a,+∞)上单调递增,(2)在[1,e](e=2.71828…)上任取一点x0,使得f(x0)≤0成立,∴函数f(x)=x﹣alnx+在[1,e]的最小值小于或等于0,由(1)知,当a≤﹣1时,在[1,e]上为增函数,f(x)min=f(1)=1+1+a≤0,解得a≤﹣2,当a>﹣1时①当1+a≥e时,即a≥e﹣1时,f(x)在[1,e]上单调递减,∴f(x)min=f(e)=e+﹣a≤0,解得a≥,∵>e﹣1,∴a≥;②当1+a≤1,即a≤0,f(x)在[1,e]上单调递增,∴f(x)min=f(1)=1+1+a≤0,解得a≤﹣2,与a>﹣1矛盾;③当1<1+a<e,即0<a<e﹣1时,f(x)min=f(1+a),∵0<ln(1+a)<1,∴0<aln(1+a)<a,∴f(1+a)=a+2﹣aln(1+a)>2,此时f(1+a)≤0不成立,综上所述若在[1,e](e=2.71828…)上任取一点x0,使得f(x0)≤0成立a的范围为a≥,或a≤﹣221.(14分)已知椭圆C的中心在原点,焦点在x轴上,离心率等于,它的一个顶点恰好在抛物线x2=8y的准线上.(1)求椭圆C的标准方程;(2)点P(2,),Q(2,﹣)在椭圆上,A,B是椭圆上位于直线PQ两侧的动点.(i)若直线AB的斜率为,求四边形APBQ面积的最大值;(ii)当A,B运动时,满足∠APQ=∠BPQ,试问直线AB的斜率是否为定值,请说明理由.【解答】解:(1)设椭圆C的标准方程为(a>b>0),∵椭圆的一个顶点恰好在抛物线x2=8y的准线y=﹣2上,∴﹣b=﹣2,解得b=2.又,a2=b2+c2,∴a=4,,可得椭圆C的标准方程为.(2))(i)设A(x1,y1),B(x2,y2),直线AB的方程为y=,联立,化为﹣12=0,由△>0,解得,∴,x 1x2=3t2﹣12,∴|x1﹣x2|==.四边形APBQ面积S==,当t=0时,S max=12.(ii)∵∠APQ=∠BPQ,则P A,PB的斜率互为相反数,可设直线P A的斜率为k,则PB的斜率为﹣k,直线P A的方程为:=k(x﹣2),联立,化为+4﹣16=0,∴x1+2=,同理可得:x2+2==,∴x1+x2=,x1﹣x2=,k AB===.∴直线AB的斜率为定值.。
山东省德州市某中学2015届高三数学上学期10月月考试题 理 新人教A版

高三月考数学试题〔理〕须知事项:1.本试题分为第1卷和第2卷两局部,总分为150分,考试时间为120分钟.2.禁止使用计算器. 3.答卷之前将姓名、班级等信息填写在答题卡与答题纸的相应位置.4.答卷必须使用黑色0.5毫米中性笔,使用其它类笔不给分.画图题可先用铅笔轻轻画出,确定答案后,用中性笔重描. 禁止使用透明胶带,涂改液,修正带.5.选择题填涂在答题卡上,填空题的答案抄写在答题纸纸上.解答题必须写出详细的解题步骤,必须写在答题纸相应位置,否如此不予计分.第1卷〔选择题 共50分〕一、选择题:每一小题5分,共10题,50分.1.集合A ={0,1, 2,3} ,集合{|||2}B x N x =∈≤,如此A B =〔 〕A .{ 3 }B .{0,1,2}C .{1,2}D .{0,1,2,3}2.假设0()3f x '=-,如此000()()limh f x h f x h h →+--=〔 〕A .3-B .6-C .9-D .12-3.函数)ln()(2x x x f -=的定义域为〔 〕 A.)1,0( B. ]1,0[ C. ),1()0,(+∞-∞ D. ),1[]0,(+∞-∞4.函数||5)(x x f =,)()(2R a x ax x g ∈-=,假设1)]1([=g f ,如此=a 〔 〕 A.1 B. 2 C. 3 D. -15.)(),(x g x f 分别是定义在R 上的偶函数和奇函数,且1)()(23++=-x x x g x f ,如此=+)1()1(g f 〔 〕A. 3-B. 1-C. 1D. 36.集合A ={2,0,1,4},B ={k |k R ∈,22k A -∈,2k A -∉},如此集合B 中所有元素之和为〔 〕A .2B .-2C .0D .27.曲线1x y xe -=在点〔1,1〕处切线的斜率等于 〔 〕A .2eB .eC .2D .18.假设120()2(),f x x f x dx =+⎰如此1()f x dx =⎰〔 〕A.1-B.13-C.13 D.19.如下四个图中,函数y=10111n x x ++的图象可能是〔 〕ABCD10.如下列图的是函数d cx bx x x f +++=23)(的大致图象,如此2221x x +等于〔 〕A .32B .34C .38D .316第2卷〔非选择题 共100分〕二、填空题:每一小题5分,共5题,25分.11.物体运动方程为23tS =-,如此2t =时瞬时速度为12.()f x =是奇函数,如此实数a 的值是13.如下列图,抛物线拱形的底边弦长为a ,拱高为b ,其面积为____________.14.不等式632(2)(2)x x x x -+>+-的解集为____________.15.()f x 为R 上增函数,且对任意x R ∈,都有()34xf f x ⎡⎤-=⎣⎦,如此(2)f =____________.三、解答题:共6小题,75分.写出必要文字说明、证明过程与演算步骤.16.(本小题总分为12分)函数()f x 的定义域为(2,2)-,函数()(1)(32)g x f x f x =-+- 〔Ⅰ〕求函数()g x 的定义域;〔Ⅱ〕假设()f x 是奇函数,且在定义域上单调递减,求不等式()0g x ≤的解集.17.(本小题总分为12分)曲线32y x x =+- 在点 0P 处的切线 1l 平行直线410x y --=,且点 0P 在第三象限. 〔Ⅰ〕求P 的坐标;〔Ⅱ〕假设直线 1l l ⊥ , 且 l 也过切点P ,求直线 l 的方程.18.〔本小题总分为12分〕 假设实数x 满足00()f x x =,如此称x x =为()f x 的不动点.函数3()3f x x bx =++, 其中b 为常数.〔Ⅰ〕求函数()f x 的单调递增区间; 〔Ⅱ〕假设存在一个实数0x ,使得x x =既是()f x 的不动点,又是()f x 的极值点.求实数b 的值;19.〔本小题总分为12分〕统计明确,某种型号的汽车在匀速行驶中每小时的耗油量y 〔升〕关于行驶速度x 〔千米/小时〕的函数解析式可以表示为:3138(0120)12800080y x x x =-+<≤甲、乙两地相距100千米〔Ⅰ〕当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升? 〔Ⅱ〕当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升? 20.(本小题总分为13分)函数()ln f x x =(0)x ≠,函数1()()(0)()g x af x x f x '=+≠'〔Ⅰ〕当0x ≠时,求函数()y g x =的表达式;〔Ⅱ〕假设0a >,函数()y g x =在(0,)+∞上的最小值是2 ,求a 的值;〔Ⅲ〕在〔Ⅱ〕的条件下,求直线2736y x =+与函数()y g x =的图象所围成图形的面积.21.〔本小题总分为14分〕设关于x 的方程012=--mx x 有两个实根βαβα<,,,函数()122+-=x m x x f 。
【山东版】2015届高三上学期月考(1)数学(理)含答案

2015 届上学期高三一轮复习第一次月考数学(理)试题【山东版】注意事项:1. 本试题共分 22 大题,全卷共 150 分。
考试时间为 120 分钟。
2.第 I 卷一定使用 2B 铅笔填涂答题纸相应题目的答案标号,改正时,要用橡皮擦洁净。
3. 第 II 卷一定使用 0.5 毫米的黑色墨水署名笔书写在答题纸的指定地点,在底稿纸和本卷上答题无效。
作图时,可用 2B 铅笔,要求字体工整、字迹清楚。
第 I 卷(共 60分) 一、选择题 (本大题共 12 个小题;每题5 分,共 60 分.在每题给出的4 个选项中,只有一项切合题目要求 .) 1.已知会合 A1,1 , Bx 1 2x4 ,则 AB 等于()A . 1,0,1B . 1C .1,1D . 0,12+ x ,则 fx + f 2的定义域为 ()2.设 f(x)= lg 2- x2 xA . (- 4,0)∪ (0,4)B . (-4,- 1)∪ (1,4)C . (- 2,- 1)∪ (1,2)D . (- 4,- 2)∪(2,4)3.命题 “全部能被 2 整除的整数都是偶数”的否认是 ()A .全部不可以被 2 整除的整数都是偶数B .全部能被 2 整除的整数都不是偶数C .存在一个不可以被 2 整除的整数是偶数D .存在一个能被 2 整除的整数不是偶数21 x , x 1的取值范围是 ()4.设函数 f ( x)log 2 ,则知足 f ( x) 2 的 x1 x, x 1A . [ 1,2]B .[0, 2]C . [1,+ )D .[0,+ )5.若函数 f ( x) x 2a(a R ) ,则以下结论正确的选项是()xA . a R , f ( x) 在 (0, ) 上是增函数B .C . aR , f ( x) 是偶函数D .a R , f ( x) 在 (0, ) 上是减函数a R , f ( x) 是奇函数6.一个篮球运动员投篮一次得3 分的概率为 a ,得 2 分的概率为 b ,不得分的概率为c ,[a, b, c(0,1)] ,已知他投篮一次得分的希望是2 1)2,则的最小值为(a3b32 28 C .14 16A .B .3D .3337.已知函数 f ( x) 的定义域为 (3 2a, a 1),且 f (x 1) 为偶函数 ,则实数 a 的值能够是()2B .2C.4D.6A .38 .已知函数 f ( x)x 49( x1) ,当x=a时 , f (x)获得最小值,则在直角坐标系中,函数x11 x 1g( x) ( )的大概图象为9.对于会合 M 、N,定义 M- N= { x|x∈ M 且 x? N} ,M⊕ N= (M- N)∪ (N- M),设 A= { y|y= 3x, x∈ R} ,B={ y|y=- (x- 1)2+ 2, x∈ R} ,则 A⊕ B 等于 ()A . [0,2)B. (0,2]C.(-∞,0]∪(2,+∞ )D. (-∞, 0)∪ [2,+∞)10.已知函数f ( x) x22x 3在区间 [0, t] 上有最大值32t的取值范围是(),最小值,则A.[1,)B.[0, 2]C.( ,2]D.[1,2]11.对于随意两个正整数m,n,定义某种运算“※”以下 :当m, n都为正偶数或正奇数时 , m※n = m n ;当m, n中一个为正偶数 ,另一个为正奇数时,m※n=mn.则在此定义下 ,会合M {( a, b) a ※ b12,a N , b N}中的元素个数是 ()A.10 个B.15 个C.16 个D.18 个12.已知函数 y= f( x)的周期为 2,当 x∈ [ - 1,1]时 f(x)= x2,那么函数 y= f(x)的图象与函数y=|lgx|的图象的交点共有 ()A.10个 B.9 个C.8 个D.1 个第 II 卷(非选择题,共90分)二、填空题 (本大题共 4 小题,每题 4 分,共 16 分 ,请将答案填在答题纸上)x≥1,13.已知会合 A= {( x, y)| x≤y,} ,会合 B= {( x, y)|3x+ 2y- m= 0} ,若 A∩B≠? ,则实数 m 的2x- y≤1最小值等于 __________ .1114.若 (a+ 1)2< (3- 2a) 2,则 a 的取值范围是 __________ .15.用二分法求方程2的正实根的近似解(精准度 0.001)时,假如我们选用初始区间是[1.4,1.5] ,x = 2则要达到精准度要求起码需要计算的次数是__________ 次.16.以下结论中是真命题的是__________( 填序号 ).2b① f(x)= ax + bx +c 在 [0,+ ∞)上是增函数的一个充足条件是- 2a <0; ②已知甲: x + y ≠3,乙: x ≠1或 y ≠2,则甲是乙的充足不用要条件; ③数列 { a n }( n ∈ N *)是等差数列的充要条件是P n n ,S n是共线的.n三、解答题 :本大题共 6 小题,共 74 分,解答应写出文字说明,证明过程或演算步骤. 17. (本小题满分 12 分)已知会合 A = { x ∈ R| 3≥ 1},会合 B = { x ∈R|y =- x 2+ x - m + m 2} ,若 A ∪ B = A ,务实数 m 的取x + 1值范围.18.(本小题满分 12 分)已知函数 f( x)= x 2+ 4ax + 2a + 6.(1) 若函数 f(x)的值域为 [0,+ ∞),求 a 的值;(2) 若函数f(x)的函数值均为非负数,求f(a)= 2- a|a + 3|的值域.19.(本小题满分12 分)已知函数f (x)log 4(4x1) kx(kR) 为偶函数.(Ⅰ )求 k 的值 ;(Ⅱ )若方程f ( x)log 4 (a 2xa)有且只有一个根, 务实数a 的取值范围 .20.(本小题满分 12 分)提升过江大桥的车辆通行能力可改良整个城市的交通状况.在一般状况下,大桥上的车流速度 v(单位:千米 /小时 )是车流密度 x(单位:辆 /千米 )的函数,当桥上的车流密度达到200 辆 / 千米时,造成堵塞,此时车流速度为0;当车流密度不超出 20 辆 /千米时,车流速度为 60 千米 /小时.研究表示:当20≤x ≤ 200时,车流速度 v 是车流密度 x 的一次函数.(1) 当 0≤x ≤ 200时,求函数 v(x)的表达式; (2) 当车流密度x 为多大时,车流量(单位时间内经过桥上某观察点的车辆数,单位:辆/小时 )f(x)= x ·v(x)能够达到最大,并求出最大值.(精准到 1 辆/小时 )21.(本小题满分 12 分)22已知 p : ? x ∈R,2x >m(x + 1), q : ? x 0∈ R ,x 0+ 2x 0- m -1= 0,且p ∧ q为真,务实数m 的取值范围.22.(本小题满分 14 分)设函数 f ( θ)= 3sin θ+ cos θ,此中, 角 θ的极点与坐标原点重合, 始边与 x 轴非负半轴重合,终边经过点 P(x , y),且 0≤θ≤π.1 , 3(1) 若点 P 的坐标为 (2),求 f( θ)的值;2x +y ≥1(2) 若点 P(x , y)为平面地区 Ω: x ≤1,上的一个动点,试确立角θ的取值范围,并求函数 f( θ)y ≤1的最小值和最大值.参照答案一、选择题1. B Bx 1 2x 4 { x 0 x 2} ,所以 A B {1} ,选 B .2. B由2 x0 ,得 f(x) 的定义域为 {x| - 2<x < 2}.2 xx22< < 2,-< 2.解得 x ∈ (- 4,- 1)∪ (1, 4) .故- 2 2< x3 .D 否认原题结论的同时要把量词做相应改变,应选D.4.Dx 2 是一个偶函数 .5.C 对于 a 0 时有 fx6.D1) ,即函数 f ( x) 对于 x 1对称 ,7.B 因为函数 f (x1) 为偶函数 ,所以 f ( x 1) f ( x所以区间 (3 2a, a 1) 对于 x1 对称 ,所以32a a 11,即 a 2 ,所以选 B .28 By x4 9x 1+9 5 ,因为 x 1 ,所以 x 1 0, 90 ,所以由均值不等式x 1x 1x 1 得 yx 1+ x 9 5 2 ( x 1) 9 5 1,当且仅当 x19,1 x 1x 1即2时取等号 ,所以 a2 ,所以1 x 11 x1(x 1) 9 , x 1 3, x 2 g (x) ( )( ),又所以a21g( x)( 1) x1( ) x 1 , x 12 ,所以选 B.22x 1 , x19. C由题可知,会合 A = {y|y > 0} , B = {y|y ≤ 2},所以 A - B = {y|y > 2} , B - A = {y|y ≤ 0},所以 A ⊕ B = (- ∞, 0]∪ (2,+ ∞),应选 C.12 .A画出两个函数图象可看出交点有10 个.二、填空题13. 5A ∩B ≠? 说明直线与平面地区有公共点, 所以问题转变成: 求当 x ,y 知足拘束条件 x ≥1,x ≤y,2x - y ≤1时,目标函数 m = 3x + 2y 的最小值. 在平面直角坐标系中画出不等式组表示的可行域.能够求得在点 (1,1) 处,目标函数 m = 3x + 2y 获得最小值 5.231∵函数 yx 2 在定义域 (0,+ ∞)上递减,∴ a + 1> 0, 3- 2a > 0, a + 1>3- 2a ,14. (, )3 2即 2< a <3.320.115. 7设起码需要计算n 次,则 n 知足 0.001 ,即 2n 100 ,因为 27128 ,故要达到精准7 次.2n度要求起码需要计算16. ②③① f(x) = ax 2+ bx + c 在 [0,+ ∞)上是增函数,则必有 a > 0,b 0 ,故①不正确.② x2a= 1 且 y = 2,则 x + y = 3. 进而逆否命题是充足不用要条件,故②正确.③若 {a n } 是等差数列,则 S n = An2+ Bn ,即 S n n= An + B ,故③正确.三、解答题x-20} = (- 1,2],17 解:由题意得: A = {x ∈ R| x+1 B = {x ∈ R|x 2-x + m - m 2≤ 0}= {x ∈ R|(x - m)(x -1+ m)≤ 0}由 A ∪B =A 知 B? A ,得- 1< m ≤2,- 1< 1- m ≤2,解得:- 1< m < 2.18 解: (1) ∵函数的值域为 [0,+ ∞),∴ = 16a 2- 4(2a +6) =0, ∴ 2a 2- a - 3= 0, ∴ a =- 1 或 a =3 .2(2) ∵对全部 x ∈ R 函数值均为非负,∴= 8 (2a 23- a- 3) ≤0,∴- 1≤a ≤ ,∴ a + 3> 0,2∴ f(a)= 2- a|a +3|=- a 2- 3a + 2=- (a+ 3)217 (a [-1, 3]) .24 2∵二次函数 f(a)在 [-1,3] 上单一递减,2∴ f ( 3) ≤ f(a) -≤ 1)f(,即-19≤ f(a) ,≤4∴ f(a)的值域为 [ -19, 4].24419 解:( 1)因为 f (x) 为偶函数,所以f ( x)f ( x)即 log 4 ( 4 x1) kxlog 4 (4x 1) kx ,∴ log 4 4 x 1log 4 (4 x1) 2kx14x∴(2k1) x0 , ∴k21 xlog 4 ( 4x1log 4 (4x1)1) log 4 2x(2)依题意知:f (x)1)x log 4 42log 4 (4x2∴由 f ( x) log 4 (a 2x a) 得 log 4 (4x 1) log 4 (a2 x a) log 4 2x∴4x 1 (a2x a) 2 x ﹡(a 2xa) 0令 t 2 x ,则 *变成 (1 a)t 2at1 0只要其有一正根 .(1) a1,t1 不合题意a 2 4(1 a) 0经考证知足 a 2xa 0a1(2) * 式有一正一负根,t 1t 2 1 0 1 a(3)两相等正根,0 a 2 2 2 经考证 a 2x a 0 a 2 2 2 20 解: (1) 由题意:当 0≤ x ≤ 20时, v(x) =60;当 20≤ x ≤ 200时,设 v(x) =ax + b ,再由已知得200a + b = 0, 20a +b = 60,解得 a =- 1 , b =200.3360, 0 x<20故函数 v(x) 的表达式为 v(x)=1 x),20x 200(2003(2) 依题意并由 (1) 可得60x,0 x<20f(x)= 1x), 20.x(200x 2003当 0≤x ≤20时, f(x) 为增函数,故当 x = 20 时,其最大值为 60×20= 1200;当 20≤x ≤200时, f(x)= 1x(200x) ≤f(x)= 1 (x+200x )210000 ,3323当且仅当 x = 200- x ,即 x =100 时,等号建立.所以,当 x = 100 时, f(x) 在区间 [20,200] 上获得最大值10000.3综上,当 x = 100 时, f(x) 在区间 [0,200] 上获得最大值 10000 ≈ 3333,3即当车流密度为 100 辆 / 千米时 ,车流量能够达到最大,最大值约为 3333 辆 /小时.21 解: 2x > m(x 2+ 1) 可化为 mx 2 -2x + m < 0.若 p : ? x ∈ R, 2x > m(x 2+ 1)为真,则 mx 2- 2x + m < 0 对随意的 x ∈R 恒建立.当 m = 0 时,不等式可化为- 2x <0,明显不恒建立;当 m ≠0时,有 m < 0, = 4-4m 2<0,∴ m <- 1.若 q : ? x 0∈ R , x 20 + 2x 0- m - 1=0 为真,则方程 x 2+ 2x - m - 1= 0 有实根, ∴ =4+ 4(m + 1) ≥0,∴ m ≥- 2.又 p ∧ q 为真,故 p 、 q 均为真命题. ∴ m <- 1 且 m ≥- 2,∴- 2≤m<- 1.22 解: (1) 由点 P 的坐标和三角函数的定义可得sin θ=3, cos θ=1.22于是 f(θ)= 3 3 1 = 2.sin θ+ cos θ= 322(2)作出平面地区 Ω(即三角地区 ABC) 以下图,此中 A(1,0) , B(1,1) , C(0,1) .于是 0≤θ≤.2又 f( θ)= 3 sin θ+ cos θ= 2sin( θ+ ) ,且≤θ+ ≤ ,6663故当 θ+= 2,即 θ= 时, f( θ)获得最大值,且最大值等于 2 ;6 3当 θ+= ,即 θ= 0 时, f( θ)获得最小值,且最小值等于 1.6 6。
2015年山东省高考数学一模试卷(理科)含解析答案

2015年山东省高考数学一模试卷(理科)一、选择题(共10小题,每小题5分,满分50分)1.(5分)(2015•山东一模)复数z=|(﹣i)i|+i5(i为虚数单位),则复数z的共轭复数为()A.2﹣i B.2+i C.4﹣i D.4+i【考点】:复数代数形式的乘除运算.【专题】:数系的扩充和复数.【分析】:直接利用复数模的公式求复数的模,再利用虚数单位i的运算性质化简后得z,则复数z的共轭复数可求.【解析】:解:由z=|(﹣i)i|+i5=,得:.故选:A.【点评】:本题考查复数模的求法,考查了虚数单位i的运算性质,是基础题.2.(5分)(2015•山东一模)若[﹣1,1]⊆{x||x2﹣tx+t|≤1},则实数t的取值范围是()A.[﹣1,0] B.[2﹣2,0] C.(﹣∞,﹣2] D.[2﹣2,2+2]【考点】:集合的包含关系判断及应用.【专题】:计算题;函数的性质及应用;集合.【分析】:令y=x2﹣tx+t,由题意,将集合的包含关系可化为求函数的最值的范围.【解析】:解:令y=x2﹣tx+t,①若t=0,则{x||x2≤1}=[﹣1,1],成立,②若t>0,则y max=(﹣1)2﹣t(﹣1)+t=2t+1≤1,即t≤0,不成立;③若t<0,则y max=(1)2﹣t+t=1≤1,成立,y min=()2﹣t•+t≥﹣1,即t2﹣4t﹣4≤0,解得,2﹣2≤t≤2+2,则2﹣2≤t<0,综上所述,2﹣2≤t≤0.故选B.【点评】:本题考查了集合的包含关系的应用,属于基础题.3.(5分)(2015•山东一模)已知M(2,m)是抛物线y2=2px(p>0)上一点,则“p≥1”是“点M到抛物线焦点的距离不少于3”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条【考点】:必要条件、充分条件与充要条件的判断.【专题】:简易逻辑.【分析】:根据抛物线的定义和性质,利用充分条件和必要条件的定义即可得到结论.【解析】:解:抛物线的交点坐标为F(,0),准线方程为x=﹣,则点M到抛物线焦点的距离PF=2﹣(﹣)=2+,若p≥1,则PF=2+≥,此时点M到抛物线焦点的距离不少于3不成立,即充分性不成立,若点M到抛物线焦点的距离不少于3,即PF=2+≥3,即p≥2,则p≥1,成立,即必要性成立,故“p≥1”是“点M到抛物线焦点的距离不少于3”的必要不充分条件,故选:B【点评】:本题主要考查充分条件和必要条件的判断,利用抛物线的定义和性质是解决本题的关键.4.(5分)(2015•山东一模)若m是2和8的等比中项,则圆锥曲线x2+的离心率为()A.B.C.或D.或【考点】:圆锥曲线的共同特征;等比数列的性质.【专题】:计算题.【分析】:先根据等比中项的性质求得m的值,分别看当m大于0时,曲线为椭圆,进而根据标准方程求得a和b,则c可求得,继而求得离心率.当m<0,曲线为双曲线,求得a,b和c,则离心率可得.最后综合答案即可.【解析】:解:依题意可知m=±=±4当m=4时,曲线为椭圆,a=2,b=1,则c=,e==当m=﹣4时,曲线为双曲线,a=1,b=2,c=则,e=故选D【点评】:本题主要考查了圆锥曲线的问题,考查了学生对圆锥曲线基础知识的综合运用,对基础的把握程度.5.(5分)(2015•山东一模)在△ABC中,若b=2,A=120°,三角形的面积S=,则三角形外接圆的半径为()A.B. 2 C.2D. 4【考点】:正弦定理.【专题】:解三角形.【分析】:由条件求得c=2=b,可得B的值,再由正弦定理求得三角形外接圆的半径R的值.【解析】:解:△ABC中,∵b=2,A=120°,三角形的面积S==bc•sinA=c•,∴c=2=b,故B=(180°﹣A)=30°.再由正弦定理可得=2R==4,∴三角形外接圆的半径R=2,故选:B.【点评】:本题主要考查正弦定理的应用,属于基础题.6.(5分)(2015•山东一模)某几何体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此几何体的外接球的表面积为()A.3π B.4π C.2π D.【考点】:由三视图求面积、体积.【专题】:空间位置关系与距离.【分析】:如图所示,该几何体是正方体的内接正四棱锥.因此此几何体的外接球的直径2R=正方体的对角线,利用球的表面积计算公式即可得出.【解析】:解:如图所示,该几何体是正方体的内接正四棱锥.因此此几何体的外接球的直径2R=正方体的对角线,其表面积S=4πR2=3π.故选:A.【点评】:本题考查了正方体的内接正四棱锥、球的表面积计算公式,考查了推理能力与计算能力,属于基础题.7.(5分)(2015•山东一模)定义max{a,b}=,设实数x,y满足约束条件,则z=max{4x+y,3x﹣y}的取值范围是()A.[﹣8,10] B.[﹣7,10] C.[﹣6,8] D.[﹣7,8]【考点】:简单线性规划.【专题】:分类讨论;转化思想;不等式的解法及应用.【分析】:由约束条件作出可行域,结合新定义得到目标函数的分段函数,然后化目标函数为直线方程的斜截式,数形结合得到最优解,求出最优解的坐标,代入目标函数得答案.【解析】:解:由约束条件作出可行域如图,由定义max{a,b}=,得z=max{4x+y,3x﹣y}=,当x+2y≥0时,化z=4x+y为y=﹣4x+z,当直线y=﹣4x+z过B(﹣2,1)时z有最小值为4×(﹣2)+1=﹣7;当直线y=﹣4x+z过A(2,2)时z有最大值为4×2+1×2=10;当x+2y<0时,化z=3x﹣y为y=3x﹣z,当直线y=3x﹣z过B(﹣2,1)时z有最小值为3×(﹣2)﹣1=﹣7;当直线y=﹣4x+z过A(2,﹣2)时z有最大值为4×2﹣1×(﹣2)=10.综上,z=max{4x+y,3x﹣y}的取值范围是[﹣7,10].故选:B.【点评】:本题是新定义题,考查了简单的线性规划,考查了数形结合及数学转化思想方法,是中档题.8.(5分)(2015•山东一模)函数y=log3(x+3)﹣1(a>0,且a≠1)的图象恒过定点A,若点A在直线mx+ny+1=0上,其中m,n均大于0,则的最小值为()A.2 B. 4 C.8 D.16【考点】:基本不等式;对数函数的图像与性质.【专题】:函数的性质及应用;不等式的解法及应用.【分析】:现根据对数函数图象和性质求出点A的坐标,再根据点在直线上,代入化简得到2m+n=1,再根据基本不等式,即可求出结果【解析】:解:∵y=log3(x+3)﹣1(a>0,且a≠1)的图象恒过定点A,当x+3=1时,即x=﹣2时,y=﹣1,∴A点的坐标为(﹣2,﹣1),∵点A在直线mx+ny+1=0上,∴﹣2m﹣n+1=0,即2m+n=1,∵m,n均大于0,∴=+=2+++2≥4+2=8,当且仅当m=,n=时取等号,故的最小值为8,故选:C【点评】:本题考查了对数函数图象和性质以及基本不等式,属于中档题9.(5分)(2015•山东一模)已知△ABC中,内角A、B、C所对的边分别为a,b,且acosC+c=b,若a=1,c﹣2b=1,则角B为()A.B.C.D.【考点】:余弦定理;正弦定理.【专题】:解三角形.【分析】:已知等式利用正弦定理化简,整理求出cosA的值,求出A的度数,利用余弦定理列出关系式,把a与sinA的值代入得到关于b与c的方程,与已知等式联立求出b与c 的值,再利用正弦定理求出sinB的值,即可确定出B的度数.【解析】:解:已知等式利用正弦定理化简得:sinAcosC+sinC=sinB=sin(A+C)=sinAcosC+cosAsinC,由sinC≠0,整理得:cosA=,即A=,由余弦定理得:a2=b2+c2﹣2bccosA,即1=b2+c2﹣bc①,与c﹣2b=1联立,解得:c=,b=1,由正弦定理=,得:sinB===,∵b<c,∴B<C,则B=.故选:B.【点评】:此题考查了正弦、余弦定理,以及特殊角的三角函数值,熟练掌握定理是解本题的关键.10.(5分)(2015•山东一模)设定义在D上的函数y=h(x)在点P(x0,h(x0))处的切线方程为l:y=g(x),当x≠x0时,若>0在D内恒成立,则称P为函数y=h(x)的“类对称点”,则f(x)=x2﹣6x+4lnx的“类对称点”的横坐标是()A.1 B.C.e D.【考点】:利用导数研究曲线上某点切线方程.【专题】:计算题;新定义;导数的概念及应用;导数的综合应用.【分析】:当a=4时,函数y=H(x)在其图象上一点P(x0,f(x0))处的切线方程为y=g (x)=(2x0+﹣6)(x﹣x0)++x02﹣6x0+4lnx0.由此能推导出y=h(x)存在“类对称点”,是一个“类对称点”的横坐标.【解析】:解:当a=4时,函数y=h(x)在其图象上一点P(x0,h(x0))处的切线方程为:y=g(x)=(2x0+﹣6)(x﹣x0)+x02﹣6x0+4lnx0,设m(x)=h(x)﹣g(x)=x2﹣6x+4lnx﹣(2x0+﹣6)(x﹣x0)﹣x02+6x0﹣4lnx0,则m(x0)=0.m′(x)=2x+﹣6﹣(2x0+﹣6)=2(x﹣x0)(1﹣)=(x﹣x0)(x﹣)若x0<,φ(x)在(x0,)上单调递减,∴当x∈(x0,)时,m(x)<m(x0)=0,此时<0;若x0,φ(x)在(,x0)上单调递减,∴当x∈(,x0)时,m(x)>m(x0)=0,此时<0;∴y=h(x)在(0,)∪(,+∞)上不存在“类对称点”.若x0=,(x﹣)2>0,∴m(x)在(0,+∞)上是增函数,当x>x0时,m(x)>m(x0)=0,当x<x0时,m(x)<m(x0)=0,故>0.即此时点P是y=f(x)的“类对称点”综上,y=h(x)存在“类对称点”,是一个“类对称点”的横坐标.故选B.【点评】:本题考查函数的单调增区间的求法,探索满足函数在一定零点下的参数的求法,探索函数是否存在“类对称点”.解题时要认真审题,注意分类讨论思想和等价转化思想的合理运用,此题是难题.二、填空题:本大题共5小题,每小题5分,共25分.11.(5分)(2015•山东一模)已知函数f(x)=|2x﹣a|+a,若不等式f(x)≤6的解集为{x|﹣2≤x≤3},则实数a的值为a=1.【考点】:其他不等式的解法.【专题】:不等式的解法及应用.【分析】:不等式即|2x﹣a|≤6﹣a,解得a﹣3≤x≤3.再由已知不等式的解集为{x|﹣2≤x≤3},可得a﹣3=﹣2,由此求得实数a的值.【解析】:解:由题意可得,不等式即|2x﹣a|≤6﹣a,∴a﹣6≤2x﹣a≤6﹣a,解得a﹣3≤x≤3.再由不等式的解集为{x|﹣2≤x≤3},可得a﹣3=﹣2,故a=1,故答案为a=1.【点评】:本题主要考查绝对值不等式的解法,体现了等价转化的数学思想,属于基础题.12.(5分)(2015•山东一模)已知点A(2,0)抛物线C:x2=4y的焦点为F,射线FA与抛物线C相交于点M,与其准线相交于点N,则|FM|:|MN|=1:.【考点】:抛物线的简单性质.【专题】:圆锥曲线的定义、性质与方程.【分析】:求出抛物线C的焦点F的坐标,从而得到AF的斜率k=﹣.过M作MP⊥l于P,根据抛物线物定义得|FM|=|PM|.Rt△MPN中,根据tan∠MNP=,从而得到|PN|=2|PM|,进而算出|MN|=|PM|,由此即可得到|FM|:|MN|的值.【解析】:解:∵抛物线C:x2=4y的焦点为F(0,1),点A坐标为(2,0),∴抛物线的准线方程为l:y=﹣1,直线AF的斜率为k==﹣,过M作MP⊥l于P,根据抛物线物定义得|FM|=|PM|,∵Rt△MPN中,tan∠MNP=﹣k=,∴=,可得|PN|=2|PM|,得|MN|==|PM|因此可得|FM|:|MN|=|PM|:|MN|=1:.故答案为:1:.【点评】:本题给出抛物线方程和射线FA,求线段的比值.着重考查了直线的斜率、抛物线的定义、标准方程和简单几何性质等知识,属于中档题.13.(5分)(2015•山东一模)已知函数则=.【考点】:定积分.【专题】:导数的综合应用.【分析】:=,由定积分的几何意义可知:表示上半圆x2+y2=1(y≥0)的面积,即可得出.利用微积分基本定理即可得出dx=.【解析】:解:=,由定积分的几何意义可知:表示上半圆x2+y2=1(y≥0)的面积,∴=.又dx==e2﹣e.∴==好.故答案为:.【点评】:本题考查了定积分的几何意义、微积分基本定理,属于中档题.14.(5分)(2015•山东一模)把座位编号为1、2、3、4、5的五张电影票全部分给甲、乙、丙、丁四个人,每人至少一张,至多两张,且分得的两张票必须是连号,那么不同的分法种数为96.(用数字作答)【考点】:排列、组合及简单计数问题.【专题】:概率与统计.【分析】:根据题意,先将票分为符合题意要求的4份,可以转化为将1、2、3、4、5这五个数用3个板子隔开,分为四部分且不存在三连号的问题,用插空法易得其情况数目,再将分好的4份对应到4个人,由排列知识可得其情况数目,由分步计数原理,计算可得答案.【解析】:解:先将票分为符合条件的4份,由题意,4人分5张票,且每人至少一张,至多两张,则三人一张,1人2张,且分得的票必须是连号,相当于将1、2、3、4、5这五个数用3个板子隔开,分为四部分且不存在三连号.在4个空位插3个板子,共有C43=4种情况,再对应到4个人,有A44=24种情况,则共有4×24=96种情况.故答案为96.【点评】:本题考查排列、组合的应用,注意将分票的问题转化为将1、2、3、4、5这五个数用3个板子隔开,分为四部分的问题,用插空法进行解决.15.(5分)(2015•山东一模)已知函数f(x)=xe x,记f0(x)=f′(x),f1(x)=f′(x0),…,f n(x)=f′n﹣1(x)且x2>x1,对于下列命题:①函数f(x)存在平行于x轴的切线;②>0;③f′2012(x)=xe x+2014e x;④f(x1)+x2<f(x2)+x1.其中正确的命题序号是①③(写出所有满足题目条件的序号).【考点】:导数的运算.【专题】:导数的概念及应用.【分析】:根据导数的几何意义判断①正确,根据导数和函数的单调性判断②错;根据导数的运算,得到③正确,根据导数与函数的单调性的关系判断④错【解析】:解:对于①,因为f′(x)=(x+1)e x,易知f′(﹣1)=0,函数f(x)存在平行于x轴的切线,故①正确;对于②,因为f′(x)=(x+1)e x,所以x∈(﹣∞,﹣1)时,函数f(x)单调递减,x∈(﹣1,+∞)时,函数f(x)单调递增,故>0的正负不能定,故②错;对于③,因为f1(x)=f′(x0)=xe x+2e x,f2(x)=f′(x1)=xe x+3e x,…,f n(x)=f′n﹣1(x)=xe x+(n+1)e x,所以f′2012(x)=f2013(x)=xe x+2014e x;故③正确;对于④,f(x1)+x2<f(x2)+x1等价于f(x1)﹣x1<f(x2)﹣x2,构建函数h(x)=f(x)﹣x,则h′(x)=f′(x)﹣1=(x+1)e x﹣1,易知函数h(x)在R上不单调,故④错;故答案为:①③【点评】:本题考查了导数的几何意义以及导数和函数的单调性的关系,以及导数的运算法则,属于中档题三、解答题:本大题共6小题,共75分,解答时应写出必要的文字说明、证明过程或演算步骤.16.(12分)(2015•山东一模)已知函数f(x)=2sinx+2sin(x﹣).(1)求f(x)的单调递增区间;(2)在△ABC中,角A,B,C的对边分别为a,b,c.已知f(A)=,a=b,证明:C=3B.【考点】:两角和与差的正弦函数;正弦定理.【专题】:计算题;三角函数的图像与性质;解三角形.【分析】:(1)运用两角差的正弦公式,即可化简,再由正弦函数的单调增区间,即可得到;(2)由f(A)=,及0<A<π,即可得到A=,再由正弦定理,及边角关系,即可得证.【解析】:(1)解:函数f(x)=2sinx+2sin(x﹣)=2(sinx+sinx﹣cosx)=2(sinx﹣cosx)=2sin(x﹣),令2kπ﹣≤x﹣≤2k,k∈Z,则2kπ﹣≤x≤2kπ,则f(x)的单调递增区间是[2kπ﹣,2kπ],k∈Z.(2)证明:由f(A)=,则sin(A﹣)=,由0<A<π,则﹣<A﹣<,则A=,由=,a=b,则sinB=,由a>b,A=,B=,C=,故C=3B.【点评】:本题考查三角函数的化简,正弦函数的单调区间,考查正弦定理及边角关系,注意角的范围,属于中档题.17.(12分)(2015•山东一模)2008年中国北京奥运会吉祥物由5个“中国福娃”组成,分别叫贝贝、晶晶、欢欢、迎迎、妮妮.现有8个相同的盒子,每个盒子中放一只福娃,每种福娃的数量如下表:福娃名称贝贝晶晶欢欢迎迎妮妮数量1 1 1 2 3从中随机地选取5只.(Ⅰ)求选取的5只恰好组成完整“奥运吉祥物”的概率;(Ⅱ)若完整地选取奥运会吉祥物记10分;若选出的5只中仅差一种记8分;差两种记6分;以此类推.设ξ表示所得的分数,求ξ的分布列及数学期望.【考点】:离散型随机变量及其分布列;离散型随机变量的期望与方差.【专题】:概率与统计.【分析】:(Ⅰ)根据排列组合知识得出P=运算求解即可.(Ⅱ)确定ξ的取值为:10,8,6,4.分别求解P(ξ=10),P(ξ=8),P(ξ=6),P(ξ=4),列出分布列即可.【解析】:解:(Ⅰ)选取的5只恰好组成完整“奥运吉祥物”的概率P===,(Ⅱ)ξ的取值为:10,8,6,4.P(ξ=10)==,P(ξ=8)=,P(ξ=6)==,P(ξ=4)==ξ的分布列为:ξ 10 8 6 4P﹣Eξ==7.5.【点评】:本题综合考查了运用排列组合知识,解决古典概率分布的求解问题,关键是确定随机变量的数值,概率的求解,难度较大,仔细分类确定个数求解概率,属于难题.18.(12分)(2015•山东一模)在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1).将△AEF沿EF折起到△A1EF的位置,使二面角A1﹣EF﹣B成直二面角,连结A1B、A1P(如图2)(1)求证:A1E⊥平面BEP(2)求直线A1E与平面A1BP所成角的大小;(3)求二面角B﹣A1P﹣F的余弦值.【考点】:与二面角有关的立体几何综合题;直线与平面垂直的判定;直线与平面所成的角.【专题】:空间角.【分析】:(1)设正三角形ABC的边长为3.在图1中,取BE的中点D,连结DF.由已知条件推导出△ADF是正三角形,从而得到EF⊥AD.在图2中,推导出∠A1EB为二面角A1﹣EF﹣B的平面角,且A1E⊥BE.由此能证明A1E⊥平面BEP.(2)建立分别以EB、EF、EA为x轴、y轴、z轴的空间直角坐标系,利用向量法能求出直线A1E与平面A1BP所成的角的大小.(3)分别求出平面A1FP的法向量和平面BA1F的法向量,利用向量法能求出二面角B﹣A1P﹣F的余弦值.【解析】:(1)证明:不妨设正三角形ABC 的边长为3.在图1中,取BE的中点D,连结DF.∵AE:EB=CF:FA=1:2,∴AF=AD=2,而∠A=60度,∴△ADF是正三角形,又AE=DE=1,∴EF⊥AD.在图2中,A1E⊥EF,BE⊥EF,∴∠A1EB为二面角A1﹣EF﹣B的平面角.由题设条件知此二面角为直二面角,∴A1E⊥BE.又BE∩EF=E,∴A1E⊥平面BEF,即A1E⊥平面BEP.(2)建立分别以EB、EF、EA为x轴、y轴、z轴的空间直角坐标系,则E(0,0,0),A(0,0,1),B(2,0,0),F(0,,0),P (1,,0),则,.设平面ABP的法向量为,由平面ABP知,,即令,得,.,,∴直线A1E与平面A1BP所成的角为60度.(3),设平面A1FP的法向量为.由平面A1FP知,令y 2=1,得,.,所以二面角B﹣A1P﹣F的余弦值是.【点评】:本题考查直线与平面垂直的证明,考查直线与平面所成的角的求法,考查二面角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.19.(12分)(2015•山东一模)数列{a n}中,a1=1,当n≥2时,其前n项和为S n,满足S n2=a n (S n﹣).(1)求S n的表达式;(2)设b n=,数列{b n}的前n项和为T n,不等式T n≥(m2﹣5m)对所有的n∈N*恒成立,求正整数m的最大值.【考点】:数列的求和;数列递推式.【专题】:等差数列与等比数列.【分析】:(1)当n≥2时,a n=S n﹣S n﹣1,代入利用等差数列的通项公式即可得出;(2)利用“裂项求和”、一元二次不等式的解法即可得出.【解析】:解:(1)∵S n2=a n(S n﹣)=.化为,∴数列是首项为==1,公差为2的等差数列.故=1+2(n﹣1)=2n﹣1,∴S n=.(2)b n===,故T n=+…+=.又∵不等式T n≥(m2﹣5m)对所有的n∈N*恒成立,∴≥(m2﹣5m),化简得:m2﹣5m﹣6≤0,解得:﹣1≤m≤6.∴正整数m的最大值为6.【点评】:本题考查了递推式的应用、“裂项求和”、等差数列的通项公式、一元二次不等式的解法,考查了推理能力与计算能力,属于中档题.20.(13分)(2015•山东一模)在平面直角坐标系xOy中,椭圆G的中心为坐标原点,左焦点为F1(﹣1,0),P为椭圆G的上顶点,且∠PF1O=45°.(Ⅰ)求椭圆G的标准方程;(Ⅱ)已知直线l1:y=kx+m1与椭圆G交于A,B两点,直线l2:y=kx+m2(m1≠m2)与椭圆G交于C,D两点,且|AB|=|CD|,如图所示.(ⅰ)证明:m1+m2=0;(ⅱ)求四边形ABCD的面积S的最大值.【考点】:直线与圆锥曲线的综合问题;椭圆的标准方程.【专题】:综合题.【分析】:(Ⅰ)根据F1(﹣1,0),∠PF1O=45°,可得b=c=1,从而a2=b2+c2=2,故可得椭圆G的标准方程;(Ⅱ)设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4).(ⅰ)直线l1:y=kx+m1与椭圆G联立,利用韦达定理,可求AB,CD的长,利用|AB|=|CD|,可得结论;(ⅱ)求出两平行线AB,CD间的距离为d,则,表示出四边形ABCD的面积S,利用基本不等式,即可求得四边形ABCD的面积S取得最大值.【解析】:(Ⅰ)解:设椭圆G的标准方程为.因为F1(﹣1,0),∠PF1O=45°,所以b=c=1.所以,a2=b2+c2=2.…(2分)所以,椭圆G的标准方程为.…(3分)(Ⅱ)设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4).(ⅰ)证明:由消去y得:.则,…(5分)所以===.同理.…(7分)因为|AB|=|CD|,所以.因为m1≠m2,所以m1+m2=0.…(9分)(ⅱ)解:由题意得四边形ABCD是平行四边形,设两平行线AB,CD间的距离为d,则.因为m1+m2=0,所以.…(10分)所以=.(或)所以当时,四边形ABCD的面积S取得最大值为.…(12分)【点评】:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查弦长的计算,考查三角形的面积,同时考查利用基本不等式求最值,正确求弦长,表示出四边形的面积是解题的关键.21.(14分)(2015•山东一模)已知函数f(x)=aln(x+1)﹣ax﹣x2.(Ⅰ)若x=1为函数f(x)的极值点,求a的值;(Ⅱ)讨论f(x)在定义域上的单调性;(Ⅲ)证明:对任意正整数n,ln(n+1)<2+.【考点】:利用导数求闭区间上函数的最值;利用导数研究函数的单调性;利用导数研究函数的极值.【专题】:导数的综合应用.【分析】:(I)由,f′(1)=0,知,由此能求出a.(Ⅱ)由,令f′(x)=0,得x=0,或,又f(x)的定义域为(﹣1,+∞),讨论两个根及﹣1的大小关系,即可判定函数的单调性;(Ⅲ)当a=1时,f(x)在[0,+∞)上递减,∴f(x)≤f(0),即ln(x+1)≤x+x2,由此能够证明ln(n+1)<2+.【解析】:解:(1)因为,令f'(1)=0,即,解得a=﹣4,经检验:此时,x∈(0,1),f'(x)>0,f(x)递增;x∈(1,+∞),f'(x)<0,f(x)递减,∴f(x)在x=1处取极大值.满足题意.(2),令f'(x)=0,得x=0,或,又f(x)的定义域为(﹣1,+∞)①当,即a≥0时,若x∈(﹣1,0),则f'(x)>0,f(x)递增;若x∈(0,+∞),则f'(x)<0,f(x)递减;②当,即﹣2<a<0时,若x∈(﹣1,,则f'(x)<0,f(x)递减;若,0),则f'(x)>0,f(x)递增;若x∈(0,+∞),则f'(x)<0,f(x)递减;③当,即a=﹣2时,f'(x)≤0,f(x)在(﹣1,+∞)内递减,④当,即a<﹣2时,若x∈(﹣1,0),则f'(x)<0,f(x)递减;若x∈(0,,则f'(x)>0,f(x)递增;若,+∞),则f'(x)<0,f(x)递减;(3)由(2)知当a=1时,f(x)在[0,+∞)上递减,∴f(x)≤f(0),即ln(x+1)≤x+x2,∵,∴,i=1,2,3,…,n,∴,∴.【点评】:本题考查函数极值的意义及利用导数研究函数的单调性,证明:对任意的正整数n.解题时要认真审题,注意导数的合理运用,恰当地利用裂项求和法进行解题.。
