2020年高中物理竞赛辅导课件★★ 准静态过程 功 热量
合集下载
准静态过程 功 热量 内能 热力学第一定律 等体过程 等压过程 摩尔热容等温过程和绝热过程
V2 V
Qp
E2
E1
W
等压膨胀过程：气体吸收的热 量，一部分用于内能的增加， 一部分用于对外作功。
p
等 压
p
( p,V2 ,T2 )
2
( p,V1,T1)
1
压
W
缩
o V2
V1 V
Qp
E1
W
E2
等压压缩过程：外界对气体作 的功和内能的减少均转化为热 量放出。
等压过程中，W 与 △E始终同号
Q
m' M
解 1）等温过程
W12 '
RT ln V2 ' V1
2.80104 J
2）氢气为双原子气体
(i 2) i 1.40
T2
T1
(V1 V2
)
1
753K
p
p2
2 T2
p2' T2' T1
Q0
p1
2'
T1
T 常量 1
o V2 V2' V1 10 V1 V
怎么求？
由热力学第一定律
dQT dWT pdV
Q T
WT
p RT
V2 V1
pdV
V
p
p1
1 ( p1,V1,T )
p2
( p2 ,V2 ,T )
2
o V1 dV V2 V
恒
温
谁做功？
热
源
T
QT
WT
V2
V1
RT V
dV
RT
ln V2 V1
RT ln p1
2020高中物理竞赛辅导课件(基础热力学)6功 热量(共18张PPT)
（Ａ）
例4．要使一热力学系统的内能增加，可以通 过____________或___________两种方式，或 者两种方式兼用来完成． 热力学系统的状态发生变化时，其内能的改变 量只决定于______，而与_______无关．
外界对系统作功 向系统传递热量 始末两个状态 所经历的过程
谢谢观看！
热量
热是物体中大量微粒机械运动的宏观表现
热量从温度高的物体传递到温度低的物体 或者从物体的高温部分传到低温部分 一定热量的产生（或消失）总是伴随着等 量的其他某种形式能量（如机械能、电能） 的消失（或产生）
热力学第一定律
绝热功与系统的内能 热量定义 热力学第一定律
绝热功与系统的内能
如果一个系统经过一个过程，其状态的变化完全是由 于机械的或电磁的作用，则称此过程为绝热过程。在 绝热过程中外界对系统所作的功为绝热功。
2020高中物理竞赛
基础热力学篇
功 热量
热力学过程 功 热量
热力学过程
当系统的状态随时间变化时，
我们就说系统在经历一个热力
学过程，简称过程。
理想气体自由膨胀
驰豫时间：系统平衡态破坏后需要经过一段 时间才能达到新的平衡态
非静态过程：在热力学过程中系统经历 的是一系列非平衡态
准静态过程：在热力学过程进行中的 每一时刻，系统都处于平衡态
气体自由膨胀过程
初态
真空
末 态
功
力学中
dW
F
ds
dW Pe Sdl dV Sdl
dW PedV
功的图示
在无摩擦准静态过程中 dW PdV
系统体积由V1变为V2，外界对系统作总功为
W V2 PdV
V1
系统对外界所作的功 W
例4．要使一热力学系统的内能增加，可以通 过____________或___________两种方式，或 者两种方式兼用来完成． 热力学系统的状态发生变化时，其内能的改变 量只决定于______，而与_______无关．
外界对系统作功 向系统传递热量 始末两个状态 所经历的过程
谢谢观看！
热量
热是物体中大量微粒机械运动的宏观表现
热量从温度高的物体传递到温度低的物体 或者从物体的高温部分传到低温部分 一定热量的产生（或消失）总是伴随着等 量的其他某种形式能量（如机械能、电能） 的消失（或产生）
热力学第一定律
绝热功与系统的内能 热量定义 热力学第一定律
绝热功与系统的内能
如果一个系统经过一个过程，其状态的变化完全是由 于机械的或电磁的作用，则称此过程为绝热过程。在 绝热过程中外界对系统所作的功为绝热功。
2020高中物理竞赛
基础热力学篇
功 热量
热力学过程 功 热量
热力学过程
当系统的状态随时间变化时，
我们就说系统在经历一个热力
学过程，简称过程。
理想气体自由膨胀
驰豫时间：系统平衡态破坏后需要经过一段 时间才能达到新的平衡态
非静态过程：在热力学过程中系统经历 的是一系列非平衡态
准静态过程：在热力学过程进行中的 每一时刻，系统都处于平衡态
气体自由膨胀过程
初态
真空
末 态
功
力学中
dW
F
ds
dW Pe Sdl dV Sdl
dW PedV
功的图示
在无摩擦准静态过程中 dW PdV
系统体积由V1变为V2，外界对系统作总功为
W V2 PdV
V1
系统对外界所作的功 W
2020年高中物理竞赛(力学篇)01运动的描述：描述质点运动的四个物理量(共12张PPT)
2020全国高中奥林匹克竞赛 物理
力学篇 （基础版）
P
一. 描述质点运动的四个物理量
1.位置矢量（单位：米）
位置矢量（位矢）： r 运动方程： r r(t)
O
vΓ
r(t)
Δs
P 2
2.位移：
r r2 r1 r(t2) r(t1)
P 1
v
rv 1
Δrvr
Г
2
直角 坐标系中
r
r
xi
( x2
v1 Δv
v2
或位矢对时间的二阶导数
r、av
描述质点运动状态的物理量 描述质点运动状态变化的物理量
直角坐标系中
加速度
a
dv
dv x
i
dv y
j
dv z
k
dt dt dt
dt
axi ay j azk
加速度大小
a a
a
2 x
a
2 y
az
2
任意曲线运动都可以视为沿x,y,z轴的三个各自独 立的直线运动的叠加（矢量加法）。
速度大小
v v
vx2
v
2 y
vz2
平均速度
v
r
x
i
y
j
z
k
t t t t
vxi vy j vzk
v
v(t )
速率（单位：米/秒）
平均速率
v s t
瞬时速率 v lim s ds t0 t dt
P
r r Q
O r r
注意 速度是矢量，速率是标量。
一般情况 v v (s r)
单向直线运动情况
——运动的独立性原理或运动叠加原理
力学篇 （基础版）
P
一. 描述质点运动的四个物理量
1.位置矢量（单位：米）
位置矢量（位矢）： r 运动方程： r r(t)
O
vΓ
r(t)
Δs
P 2
2.位移：
r r2 r1 r(t2) r(t1)
P 1
v
rv 1
Δrvr
Г
2
直角 坐标系中
r
r
xi
( x2
v1 Δv
v2
或位矢对时间的二阶导数
r、av
描述质点运动状态的物理量 描述质点运动状态变化的物理量
直角坐标系中
加速度
a
dv
dv x
i
dv y
j
dv z
k
dt dt dt
dt
axi ay j azk
加速度大小
a a
a
2 x
a
2 y
az
2
任意曲线运动都可以视为沿x,y,z轴的三个各自独 立的直线运动的叠加（矢量加法）。
速度大小
v v
vx2
v
2 y
vz2
平均速度
v
r
x
i
y
j
z
k
t t t t
vxi vy j vzk
v
v(t )
速率（单位：米/秒）
平均速率
v s t
瞬时速率 v lim s ds t0 t dt
P
r r Q
O r r
注意 速度是矢量，速率是标量。
一般情况 v v (s r)
单向直线运动情况
——运动的独立性原理或运动叠加原理
9.4准静态过程中功和热量的计算 课件-2020-2021学年高中物理竞赛
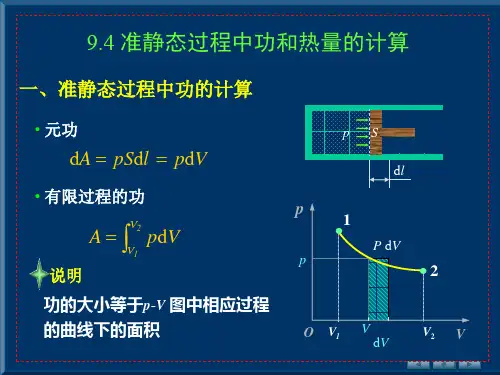
• 有限过程的功
A V2 pdV V1
说明 功的大小等于p-V 图中相应过程 的曲线下的面积
pS
dl
p
•1
P dV
p
•2
O V1
V dV
V2 V
二、 准静态过程中热量的计算
1. 热容 热容
物体温度升高1 K 所吸收的热量
比热容 单位质量的物体温度升高1 K 所吸收的热量
摩尔热容
1 mol 理想气体，经某一过程 x，吸热 Q，温度变化 T
违背第二定律开尔文表述
假设不成立
三、 热力学第二定律的实质，就是揭示了自然界的一 切自发过程都是单方向进行的不可逆过程。
9.11 卡诺定理
1. 在温度分别为T1 与T2 的两个给定热源之间工作的一切可 逆热机，其效率 相同，都等于可逆卡诺热机的效率，即
1 Q2 1 T2
Q1
T1
2. 在相同的高、低温热源之间工作的一切不可逆热机，其
Cx
lim
T 0
Q T
注意: 热容是过程量
2. 热量计算
mol 气体，经历某一个准静态过程 x，温度由 T1 变化 到 T2 ，吸热 Qx
Qx
T2 T1
CxdT
Cx —— 摩尔热容
若Cx与温度无关时（摩尔热容），则
Q Cx (T2 T2 )
9.3 功 热量 内能 热力学第一定律
热力学系统与外界传递能量的两种方式 做功 传热
94准静态过程中功和热量的计算一准静态过程中功的计算lpsaddvpddl?元功sp?21vvvpadovp1v2v??12dv?有限过程的功功的大小等于pv图中相应过程的曲线下的面积说明vppdv二准静态过程中热量的计算1
A V2 pdV V1
说明 功的大小等于p-V 图中相应过程 的曲线下的面积
pS
dl
p
•1
P dV
p
•2
O V1
V dV
V2 V
二、 准静态过程中热量的计算
1. 热容 热容
物体温度升高1 K 所吸收的热量
比热容 单位质量的物体温度升高1 K 所吸收的热量
摩尔热容
1 mol 理想气体，经某一过程 x，吸热 Q，温度变化 T
违背第二定律开尔文表述
假设不成立
三、 热力学第二定律的实质，就是揭示了自然界的一 切自发过程都是单方向进行的不可逆过程。
9.11 卡诺定理
1. 在温度分别为T1 与T2 的两个给定热源之间工作的一切可 逆热机，其效率 相同，都等于可逆卡诺热机的效率，即
1 Q2 1 T2
Q1
T1
2. 在相同的高、低温热源之间工作的一切不可逆热机，其
Cx
lim
T 0
Q T
注意: 热容是过程量
2. 热量计算
mol 气体，经历某一个准静态过程 x，温度由 T1 变化 到 T2 ，吸热 Qx
Qx
T2 T1
CxdT
Cx —— 摩尔热容
若Cx与温度无关时（摩尔热容），则
Q Cx (T2 T2 )
9.3 功 热量 内能 热力学第一定律
热力学系统与外界传递能量的两种方式 做功 传热
94准静态过程中功和热量的计算一准静态过程中功的计算lpsaddvpddl?元功sp?21vvvpadovp1v2v??12dv?有限过程的功功的大小等于pv图中相应过程的曲线下的面积说明vppdv二准静态过程中热量的计算1
高二物理竞赛功、热量 课件
无限小过程 系统无限小 做功值，它 不表示对 A 的全微分
功，热均为在过程中传递的能量，即过程量。 内能为状态函数。
5
对于理想气体，内能只与温度有关：
E i RT
2 对于准静态过程，。
注意：一个系统与外界的热传递不一定引起系统本身温 度的变化。 例1：等温过程（膨胀或压缩）
热库T
6
等温过程
1. 过程特征 系统温度保持不变，即 dT = 0，T = const.
(3) A —— 系统对外界做功，A 为正值，即A > 0； 外界对系统做功，A 为负值，即A < 0 （即系统对外做负功）。
4
对于任一无限小的过程（即初态与末态相距很近的过 程），热力学第一定律应写为：
dQ = dE + dA
无限小过程 的无限小热 量，它不表 示对Q 的全 微分
无限小过程 内能的增量
对于1mol物质，分别有摩尔定压热容Cp,m 和摩尔定体热容 CV,m 。 对于1kg物质，分别有定压比热 cp 和定体比热 cV 。
14
Cm
dQ m dT
1 dQ
dT
M
或：Cm = Mc
注意：由于dQ是一个过程量，故同一种理想气体在不同的
过程中，热容、比热容及摩尔热容是不同的。
13
定压热容：系统在压强保持不变的过程中的热容，记为
Cp。
Cp
dQ dT p
定体热容：系统在体积保持不变的过程中的热容，记为Cv。
CV
dQ dT V2来自系统经历一有限的准静态过程，体积由V1 变为 V2，则 系统对外界所做的总功为：
A dA V2 pdV V1
以气体膨胀做功为例，气体从初态( I )变化到末态(Ⅱ)用 上式求出的功的大小，根据定积分的意义可知，即为 p-V 状态图过程曲线下的面积。
2020年高中物理竞赛-热学A(联赛版)04热力学第一定律：应用(共12张PPT)
CV molT
RTVmol Vmol b
2a Vmol
H0
H p
T
H Vmol
T
Vmol p
T
2aVmol (Vmol b)2 RTbVm3ol 2a(Vmol b)2 RTVm3ol
从摩尔焓得：
H Vmol
T
2a(Vmol b)2 RTbVm2ol Vm2ol (Vmol b)2
3
RbT1 2a
1
与试验比较: 包科达书，p172
上转换温度：T1u 2a / Rb 下转换温度：T1d 2a / 9Rb
最大压强：p1 / T1 0 p10 a / 3b2 对应温度： T10 8a / 9Rb
Q
的热量称为该系统的热容 (C)。特殊标度下
C lim T 0 T
有：比热容 (c)、 摩尔热容 (Cmol)、等.
等体过程 V 0 Q (U pV )V (U )V
CV
lim (Q)V T 0 T
lim (U )V T 0 T
U T V
等压过程 Qp (U pV ) p [(U pV )] p 定义焓 (Enthalpy, 状态函数) H U pV (Q) p (H ) p
实验表明：常温常压下节流后，一般气体温度下降（T2 < T1）， 氢、氦等气体温度上升（T2 > T1）。这种气体节流膨胀后温度发生 变化的现象称为节流效应，也称焦耳—汤姆逊效应，且T2 < T1 的 称为正效应， T2 > T1 的称为负效应。
定义： T1 T2 , 0 正效应（电冰箱），反之，负效应
2020高中物理竞赛
热学A
第二节 热力学第一定律的应用 （一）准静态过程
05准静态过程内能热量和功
2
Байду номын сангаас
准静态过程只有在进行的 “ 无限缓慢 ” 的条件 下才可能实现。 下才可能实现。实际过程则要求系统状态发生变化的 特征时间远远大于弛豫时间τ才可近似看作准静态过 特征时间远远大于弛豫时间 才可近似看作准静态过 程。 对于一个平衡态，我们可以用状态参量来描述。 对于一个平衡态，我们可以用状态参量来描述。 作为准静态过程中间状 P A 态的平衡态， 态的平衡态 ， 具有确定的状 态参量值。 态参量值。 对 于 简 单 系 统 可 用 P—V 图 V 过程曲线 上的一点来表示这个平衡态。 上的一点来表示这个平衡态 。 B 系统的准静态变化过程可用P 系统的准静态变化过程可用 P— o 图上的一条曲线表示。 V图上的一条曲线表示。 V 非准静态过程不能用状态图上的一条曲线来表示。 非准静态过程不能用状态图上的一条曲线来表示。 准静态过程是一种理想的极限， 准静态过程是一种理想的极限，但作为热力学 的基础，我们要着重讨论它。 的基础，我们要着重讨论它。 3
5
2.气体作功的计算 . 只考虑无摩擦准静态过程的功。 只考虑无摩擦准静态过程的功。 b b 由功的定义： 由功的定义： = A dA = Fdr cosθ
P
dV S
∫
压力 F = PS 元功
a
∫
a
dx
dA = Fdx = PSdx= PdV dA = PdV 体积变化从 V1—V2，在整个 P 1
因热量与过程有关，故同一系统， 因热量与过程有关，故同一系统，在不同过程中 的热容量有不同的值。常用的定容热量与定压热容量。 的热容量有不同的值。常用的定容热量与定压热容量。 等容过程：引入等容摩尔热容 V，表示在等容过程中， 等容过程：引入等容摩尔热容C 表示在等容过程中 表示在等容过程中， 等容过程 容摩尔热容 1 mol 气体升高单位温度所吸收的热量。 气体升高单位温度所吸收的热量。
Байду номын сангаас
准静态过程只有在进行的 “ 无限缓慢 ” 的条件 下才可能实现。 下才可能实现。实际过程则要求系统状态发生变化的 特征时间远远大于弛豫时间τ才可近似看作准静态过 特征时间远远大于弛豫时间 才可近似看作准静态过 程。 对于一个平衡态，我们可以用状态参量来描述。 对于一个平衡态，我们可以用状态参量来描述。 作为准静态过程中间状 P A 态的平衡态， 态的平衡态 ， 具有确定的状 态参量值。 态参量值。 对 于 简 单 系 统 可 用 P—V 图 V 过程曲线 上的一点来表示这个平衡态。 上的一点来表示这个平衡态 。 B 系统的准静态变化过程可用P 系统的准静态变化过程可用 P— o 图上的一条曲线表示。 V图上的一条曲线表示。 V 非准静态过程不能用状态图上的一条曲线来表示。 非准静态过程不能用状态图上的一条曲线来表示。 准静态过程是一种理想的极限， 准静态过程是一种理想的极限，但作为热力学 的基础，我们要着重讨论它。 的基础，我们要着重讨论它。 3
5
2.气体作功的计算 . 只考虑无摩擦准静态过程的功。 只考虑无摩擦准静态过程的功。 b b 由功的定义： 由功的定义： = A dA = Fdr cosθ
P
dV S
∫
压力 F = PS 元功
a
∫
a
dx
dA = Fdx = PSdx= PdV dA = PdV 体积变化从 V1—V2，在整个 P 1
因热量与过程有关，故同一系统， 因热量与过程有关，故同一系统，在不同过程中 的热容量有不同的值。常用的定容热量与定压热容量。 的热容量有不同的值。常用的定容热量与定压热容量。 等容过程：引入等容摩尔热容 V，表示在等容过程中， 等容过程：引入等容摩尔热容C 表示在等容过程中 表示在等容过程中， 等容过程 容摩尔热容 1 mol 气体升高单位温度所吸收的热量。 气体升高单位温度所吸收的热量。
10-1 准静态过程 功 内能和热量
总热量：
Q Q
10-1 准静态过程 功 内能和热量
10.2
热力学第一定律
第10章 热力学定律
10.2.1 热力学第一定律 某一过程，系统从外界吸热 Q，对外 界做功 A，系统内能从初始态 E1变为 E2，则由能量守恒：
A ΔE Q
内能是状态量， A、 Q是过程量
对微元过程：
Q dE A
热一律的另一种表述： 第一类永动机制不成 对准静态过程： Q E2 E1
V2
V1
pdV
10.2.2 热容
C
Q
dT
单位：J/mol· K
• 摩尔热容量 C ，
• 比热容 c ， 单位：J/kg· K
Q 为过程量
C为过程量
经常用到1摩尔物质在等体过程以及在等压过程中的热 容量，称为摩尔定体热容和摩尔定压热容，分别定义 为：
CV ,m
i R 2
C P ,m
i2 R 2
2i i
i=3
单原子气体：
双原子气体： 多原子气体：
1.67
i=5
i=6
1.40
1.33
用 C
V ,m
CP,mγ值和实验比较，常温下符合很好
t 200 C
CV ,m R 2
P 1.01105 pa
CP ,m R 2
P
A
(PB,VB,TB)
V2
V1
pdV
O
VA
dV
VB
V
说明 δA>0：系统对外做功 系统所作的功在数值上 等于P-V 图上过程曲线 以下的面积。
作功与过程有关 。
p 下，气体准静态地由体积 V1 例 计算在等压 的过程系统对外界所做的功。
高中物理竞赛课件 第七章 热力学基础 (共67张PPT)
E i RT dE i RdT
2
2
CP
dQP dT
dQP
dE
PdV
i 2
RdT
RdT
PV RT d（PV） PdV VdP PdV RdT
14
单原子：i 3 双原子：i 5 多原子：i 6 二、三种等值过程
5
3
7
5
8
6
1.等容过程 特征：dV 0 dA 0
p
过程方程：
(1)状态d的体积Vd; (2)整个过程对外所做的功;
(3)整个过程吸收的热量.
p
2p1
c
解: (1)由绝热过程方程：
TcVc 1 TdVd 1
p1
ab
d
1
得：Vd
Tc Td
1
Vc
根据题意：
Td
Ta
p1V1 R
o v1 2v1
v
Vc 2V1
Tc
pcVc R
4 p1V1 R
4Ta
5
3
27
(2)整个过程对外所做的功;
真空
T
T0
2V0
∵绝热过程
(E E0） A 0
而 A=0
V0 1T0 （2V0） 1T T P0V0 P（2V0） P
E E0 （T T0）
始末两态满足 P0V0 P（2V0）
状态方程
T0
T
P
1 2
P0
26
例7-4 1mol单原子理想气体,由状态a(p1,V1)先等压加热至体积增大1倍,再等体加热至压 力增大1倍,最后再经绝热膨胀,使其温度降至初始温度,如图所示,试求:
i 2 1
1
i
物理课件4.14.2准静态过程功热量
当外界对系统所做的功为正时 ，系统能量增加；当外界对系 统所做的功为负时，系统能量 减少。
03 准静态过程热量的计算
CHAPTER
热量的定义
热量
在热传递过程中，系统之 间由于温差而发生的能量 转移的量度。
单位
在国际单位制中，热量的 单位是焦耳（J）。
热量与温度的关系
热量与温度变化量成正比 ，即 ΔQ = m × c × ΔT， 其中 m 是质量，c 是比热 容，ΔT 是温度变化量。
当 θ = 90° 时，cosθ = 0，表示力不 做功，即 W = 0。
当 θ > 90° 时，cosθ < 0，表示力做 负功，即 W < 0。
准静态过程功的物理意义
准静态过程功的物理意义是表 示系统能量的转化或转移。
在准静态过程中，系统能量的 变化量等于外界对系统所做的 功，是 描述力的空间效果的一个物理量 。
02
它等于力与物体在力的方向上通 过的位移的乘积。
准静态过程功的计算公式
准静态过程功的计算公式为：W = Fs cosθ，其中 F 是力，s 是位移，θ 是力与位移之间的夹角。
当 θ < 90° 时，cosθ > 0，表示力 做正功，即 W > 0。
准静态过程与动态过程的比较
动态过程能量耗散大，系统状态 随时间变化显著；准静态过程能 量耗散小，系统状态随时间变化
缓慢。
动态过程需要更多的外部能量输 入来维持系统状态的改变；准静
态过程则不需要。
在热力学计算中，准静态过程的 热力学性质更容易计算和处理。
02 准静态过程功的计算
CHAPTER
功的定义
准静态过程热量的计算公式
准静态过程
《准静态过程功热量》课件
• 案例一：汽车发动机冷却系统 * 描述：准静态过程功热量在汽车发动机冷却系统中的应用，如何通过计算准静态过程功热量来优化 冷却效果。 * 涉及知识点：准静态过程功热量的计算方法，汽车发动机冷却系统的原理。
• * 描述：准静态过程功热量在汽车发动机冷却系统中的应用，如何通过计算准静态过程功热量来优化冷却效果。 • * 涉及知识点：准静态过程功热量的计算方法，汽车发动机冷却系统的原理。
• 案例四：新能源领域的应用 * 描述：准静态过程功热量在新能源领域的应用，如何通过计算准静态过程功热量来优化新能源设备的 性能。 * 涉及知识点：准静态过程功热量的计算方法，新能源领域的原理和应用。
• * 描述：准静态过程功热量在新能源领域的应用，如何通过计算准静态过程功热量来优化新能源设备的性能。 • * 涉及知识点：准静态过程功热量的计算方法，新能源领域的原理和应用。
总结与展望
总结：准静态过程功热量的重要性及在各个领域的应用前 景
准静态过程功热量在热力学中 的地位和作用
准静态过程功热量在不同领域 的应用案例
准静态过程功热量在节能减排、 环境保护等领域的重要性
未来准静态过程功热量研究的 发展方向和挑战
研究方向：深入 研究准静态过程 功热量的基本原 理和应用领域， 探索新的理论和 方法，提高其准 确性和可靠性。
• 案例三：工业生产过程中的热量控制 * 描述：准静态过程功热量在工业生产过程中的热量控制中的应用，如何通过计算准静态过程 功热量来实现精确的温度控制。 * 涉及知识点：准静态过程功热量的计算方法，工业生产过程中的热量控制原理。
• * 描述：准静态过程功热量在工业生产过程中的热量控制中的应用，如何通过计算准静态过程功热量来实现精确的温度控制。 • * 涉及知识点：准静态过程功热量的计算方法，工业生产过程中的热量控制原理。
• * 描述：准静态过程功热量在汽车发动机冷却系统中的应用，如何通过计算准静态过程功热量来优化冷却效果。 • * 涉及知识点：准静态过程功热量的计算方法，汽车发动机冷却系统的原理。
• 案例四：新能源领域的应用 * 描述：准静态过程功热量在新能源领域的应用，如何通过计算准静态过程功热量来优化新能源设备的 性能。 * 涉及知识点：准静态过程功热量的计算方法，新能源领域的原理和应用。
• * 描述：准静态过程功热量在新能源领域的应用，如何通过计算准静态过程功热量来优化新能源设备的性能。 • * 涉及知识点：准静态过程功热量的计算方法，新能源领域的原理和应用。
总结与展望
总结：准静态过程功热量的重要性及在各个领域的应用前 景
准静态过程功热量在热力学中 的地位和作用
准静态过程功热量在不同领域 的应用案例
准静态过程功热量在节能减排、 环境保护等领域的重要性
未来准静态过程功热量研究的 发展方向和挑战
研究方向：深入 研究准静态过程 功热量的基本原 理和应用领域， 探索新的理论和 方法，提高其准 确性和可靠性。
• 案例三：工业生产过程中的热量控制 * 描述：准静态过程功热量在工业生产过程中的热量控制中的应用，如何通过计算准静态过程 功热量来实现精确的温度控制。 * 涉及知识点：准静态过程功热量的计算方法，工业生产过程中的热量控制原理。
• * 描述：准静态过程功热量在工业生产过程中的热量控制中的应用，如何通过计算准静态过程功热量来实现精确的温度控制。 • * 涉及知识点：准静态过程功热量的计算方法，工业生产过程中的热量控制原理。
2020年高中物理竞赛辅导课件：热学(气体动理论)01平衡态(共14张PPT)
⑶T (temperature) ①开氏温标(Kelvin scale) 单位：K ②摄氏温标(Celsius scale) 单位：℃
Tc=Tk-273.15 目前，Tmin=2.4 1011K (激光冷却法)
⒉ P-V图 P A
0
点——平衡态
线——准静态过程(过程
B
中的每一时刻，系统都
V 几乎处于平衡态)
PV M RT ——理想气体状态方程
M mol
(Clapeyrons equation)
M——气体质量(kg) Mmol——摩尔质量(kg/mol) R=8.31 J/molK
——普适气体常量or摩尔气体常量
状态方程的另一形式： P=nkT
n——分子数密度(m-3)
k=R/NA=1.3810-23J/K ——玻尔兹曼(Boltzmann)常量
2020
全国高中生物理学奥林匹克竞赛
普通物理学
（含竞赛真题练习）
热学（Thermology）
——研究与热现象有关的规律
热现象：大量分子无规则运动(热运动)的集 体表现
热力学系统：由大量分子组成的系统
研究方法：
⒈微观法：对大量分子的行为作统计分析， 建立宏观量与微观量的联系。
⒉宏观法：以实验为基础，研究系统与外界 的相互作用规律。
气体动理论 (Kinetic Theory of Gases)
主要内容： 压强公式 温度的微观解释 能量均分定理 理想气体的内能 麦克斯韦速率分布率 *玻尔兹曼分布率 *分子的平均碰撞频率与平均自由程
§1.1 平衡态 (Equilibrium State) ——在不受外界影响的条件下，系统的宏 观性质不随时间改变的状态。
[来历] P 1 M RT V M mol
2020年高中物理竞赛辅导课件★★功 功率
单位: 瓦特 符号W 1W＝1J·s－1
当额定功率一定时,负荷力越大,可达到的 速率就越小;负荷力越小,可达到的速率就越大。 这就是为什么汽车在上坡时走得慢,下坡时走得 快的道理。
3
例1.如图所示,一匹马以平行于圆弧形路面的拉力 拉着质量为m的车沿半径为R的圆弧形路面极
缓慢地匀速移动,车与路面的滑动摩擦系数为，
b
a
r 6ti
d(
r xi
)
x
0
6tdx
2 0
6t
3t2 m
dt
36
(J)
8
例. 速度大小为v0=20m/s的风作用于面积为S=25m2 的船帆上, 作用力 F aSρ(v0 v)2/ 2 , 其中a为无
量纲的常数, ρ为空气密度，v为船速。
(1)求风的功率最大时的条件；
(2) a=l, v=15m/s, =1.2kg/m,
第4章 功和能
Work & Energy
第1节 功 功率
Work & Power
1. 功 ——力的空间积累效应
力F 将质点由 ar移动到 b，
相应于元位r移 dA F
drr dr
, 力F对质点所做的功为: ——元功 r t+dt
b
所做的总功
Aab ab
r F
b
a
F
r dr
r
dr cos
t
dr
(1) 力对质点所做的功, 不仅与始、末位置有关， 而且往往与路径有关。
(2) 功是标量，但有正负, 且与参考系有关。
2
2. 功率 ——做功的快慢 功率：力在单位时间内所做的功
平均功率：
P
高中物理竞赛教程(超详细)第六讲热力学第一定律
高中物理竞赛热学教程第一讲温度和气体分子运动论第二讲热力学第一定律第二讲热力学第一定律§2.1 改变内能的两种方式热力学第一定律2．1． 1、作功和传热作功可以改变物体的内能。
如果外界对系统作功W。
作功前后系统的内能分别为E1、E2，则有E2E1W没有作功而使系统内能改变的过程称为热传递或称传热。
它是物体之间存在温度差而发生的转移内能的过程。
在热传递中被转移的内能数量称为热量，用 Q 表示。
传递的热量与内能变化的关系是E2E1Q做功和传热都能改变系统的内能，但两者存在实质的差别。
作功总是和一定宏观位移或定向运动相联系。
是分子有规则运动能量向分子无规则运动能量的转化和传递；传热则是基于温度差而引起的分子无规则运动能量从高温物体向低温物体的传递过程。
2．1． 2、气体体积功的计算1、准静态过程一个热力学系统的状态发生变化时，要经历一个过程，当系统由某一平衡态开始变化，状态的变化必然要破坏平衡，在过程进行中的任一间状态，系统一定不处于平衡态。
如当推动活塞压缩气缸中的气体时，气体的体积、温度、压强均要发生变化。
在压缩气体过程中的任一时刻，气缸中的气体各部分的压强和温度并不相同，在靠近活塞的气体压强要大一些，温度要高一些。
在热力学中，为了能利用系统处于平衡态的性质来研究过程的规律，我们引进准静态过程的概念。
如果在过程进行中的任一时刻系统的状态发生的实际过程非常缓慢图地进行时，各时刻的状态也就非常接近平衡态，过程就成了准静态过程。
因此，准静态过程就是实际过程非常缓慢进行时的极限情况A hB h 2-1-1对于一定质量的气体，其准静态过程可用p V图、p T图、v T图上的一条曲线来表示。
注意，只有准静态过程才能这样表示。
2、功在热力学中，一般不考虑整体的机械运动。
热力学系统状态的变化，总是通过做功或热传递或两者兼施并用而完成的。
在力学中，功定义为力与位移这两个矢量的标积。
在热力学中，功的概念要广泛得多，除机械功外，主要的有：流体体积变化所作的功；表面张力的功；电流的功。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
5
2020年高中物理竞赛辅导课件★★
一 准静态过程（理想化的过程）
从一个平衡态到另一平衡态所经过的每 一中间状态均可近似当作平衡态的过程 .
砂子 活塞 气体
p
p1 1 ( p1,V1,T1)
p2
2 ( p2 ,V2 ,T2 )
o V1 V2 V
1
二 功（过程量）
1 功是能量传递和转换的量度，它引 起系统热运动状态的变化.
T1 Q T2
4
物理学
第五版
13-1 准静态过程 功 热量
功与热量的异同
（1）都是过程量：与过程有关；
（2）等效性：改变系统热运动状态作用相同；
1 cal = 4.18 J ， 1 J = 0.24 cal
（3）功与热量的物理本质不同 .
宏观运动
功 分子热运动
热量
分子热运动
分子热运动
第十三章 热力学基础
宏观运动能量
热运动能量
2
物理学
第五版
13-1 准静态过程 功 量
2 准静态过程功的计算
dW Fdl pSdl
dW pdV
W V2 pdV V1
注意： 作功与过程有关 .
第十三章 热力学基础
3
三 热 量（过程量）
通过传热方式传递能量的量度，系统 和外界之间存在温差而发生的能量传递 .
T1 T2