数学建模-公交车调度问题
公交车调度数学建模
公交车调度数学建模公交车调度摘 要本文通过对给定数据进行统计分析，将数据按１８个时段、两个行驶方向进行处理，计算出各个时段各个站点以及两个方向的流通量，从而将远问题转化为对流通量的处理。
首先，利用各时段小时断面最高流通量计算出各时段各方向的最小发车次数，进行适当的调整，确定了各时段两个方向的发车次数。
假定采用均匀发车的方式。
继而求出各时段两个方向发车间隔，经部分调整后，列出0A 站和13A 站的发车时刻表，并给出了时刻表的合理性证明，从而制定调度方案。
根据调度方案采用逐步累加各时段新调用的车辆数算法，求出公交车的发配车辆数为５７辆。
其次，建立乘客平均待车时间和公交车辆实际利用率与期望利用率的差值这两个量化指标，并用这两个指标来评价调度方案以如何的程度照顾到乘客和公交公司双方利益。
前者为4.2分钟，后者为13.88%。
最后，我们以上述两个指标为优化目标，以乘客的等车时间数学期望值和公交车辆的满载率的数学期望为约束指标，建立了一个双目标的优化模型。
并且给出了具体的求解方法，特别指出的是，给出了计算机模拟的方法求解的进程控制图。
通过了对模型的分析，提出了采集数据的 采集数据方法的建议。
注释：第i 站乘客流通量：∑=ik 1（第k 站的上车的人数与第k 站的下车人数的差值）;总的乘客等车时间：∑=m i 1∑=nj 1(第i 时段第j 站等车乘客数)⨯(第I 时段第j 站等待时间)；乘客平均等车时间：总的乘客等车时间与总乘客数的比值；实际利用率：总实际乘客流通量与公司车辆总最大客运量的比值；期望利用率：总期望乘客流通量与公司车辆总最大客运量的比值一、问题的提出一条公交线路上行方向共１４站，下行方向功１３站，给定典型的一个工作日两个运行方向各站上下车的乘客数量统计。
该线路用同一型号的大客车，每辆标准载客１００人，据统计客车在该线路上运行的平均速度为２０公里／小时。
运营调度要求，乘客候车时间一般不要超过１０分钟，早高峰是一般不要超过５分钟，车辆满载率不应超过１２０％，一般也不要低与１００％，一般也不要地狱５０％。
公交线路的车辆调度问题_2001年全国大学生数学建模竞赛B题
发车间隔 / min
13 13 13 11 11 11 11 11
9
第1期
何永强, 黄 剑, 陆新根: 公交线路的车辆调度问题
17
为了顾及双方的利益, 取 为 0. 5, 所以可得 5 00- 6 00 的发车间隔为 11min 以后各个时间段都是用
这种方法进行求解见表 3, 并根据发车间隔可以制定出发车时间表, 见表 4.
表 3 各时间段的发车间隔
表 4 各时间段的调度方案
时间段
6 00 9 00 9 00 16 00 16 00 19 00 19 00 20 00 22 00 23 00
发车间隔 / min 2 11 4 11 15
时间段
5 00 6 00 6 00 9 00 9 00 16 00 16 00 19 00 19 00 22 00 22 00 23 00
( 5) 汽车的运行时间只包括乘客上下车时间和必要的运行时间, 不考虑其它时间.
( 6) 在同一时间段内按等间隔发车, 以方便工人操作.
( 7) 假设车上载客人数小于 50 为空车. 以( 50- 此刻车上人数) 为缺载人数
总空车时间= i 号车缺载人数 运行时间
( 8) 假设未搭上车的乘客为留乘乘客,
11
12
和车公里数减少了, 总留乘时间必然增加. 它们
13
分别代表了公交公司的利益和乘客的利益. 此
14
时间主要考虑两个方面, 总留乘时间和车公里
15
数, 为了计算方便, 现使它们的量纲一致. 即车
1 02 82 9277. 4 8642. 2 8140. 8 7166. 7 6651. 7 6327. 1 6067. 5
总留乘时间= ( 第 i 个车站留乘人数) ( 留乘时间)
数学建模-2001年地公交车调度问题
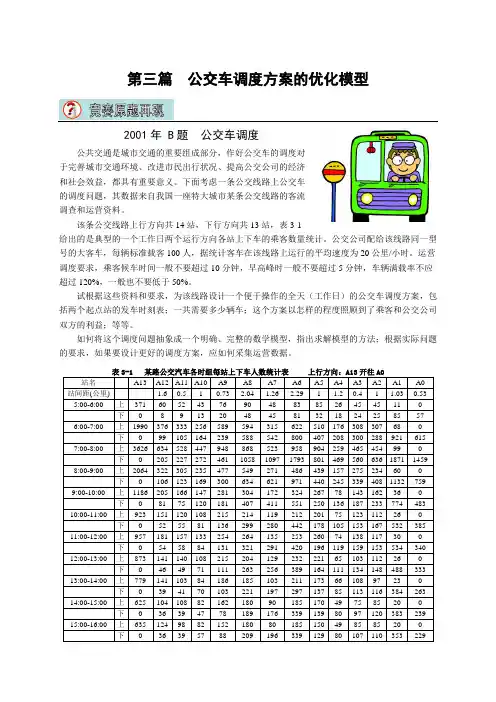
第三篇公交车调度方案的优化模型2001年 B题公交车调度Array公共交通是城市交通的重要组成部分，作好公交车的调度对于完善城市交通环境、改进市民出行状况、提高公交公司的经济和社会效益，都具有重要意义。
下面考虑一条公交线路上公交车的调度问题，其数据来自我国一座特大城市某条公交线路的客流调查和运营资料。
该条公交线路上行方向共14站，下行方向共13站，表3-1给出的是典型的一个工作日两个运行方向各站上下车的乘客数量统计。
公交公司配给该线路同一型号的大客车，每辆标准载客100人，据统计客车在该线路上运行的平均速度为20公里/小时。
运营调度要求，乘客候车时间一般不要超过10分钟，早高峰时一般不要超过5分钟，车辆满载率不应超过120%，一般也不要低于50%。
试根据这些资料和要求，为该线路设计一个便于操作的全天（工作日）的公交车调度方案，包括两个起点站的发车时刻表；一共需要多少辆车；这个方案以怎样的程度照顾到了乘客和公交公司双方的利益；等等。
如何将这个调度问题抽象成一个明确、完整的数学模型，指出求解模型的方法；根据实际问题的要求，如果要设计更好的调度方案，应如何采集运营数据。
公交车调度方案的优化模型*摘要：本文建立了公交车调度方案的优化模型，使公交公司在满足一定的社会效益和获得最大经济效益的前提下，给出了理想发车时刻表和最少车辆数。
并提供了关于采集运营数据的较好建议。
在模型Ⅰ中，对问题1建立了求最大客容量、车次数、发车时间间隔等模型，运用决策方法给出了各时段最大客容量数，再与车辆最大载客量比较，得出载完该时组乘客的最少车次数462次，从便于操作和发车密度考虑，给出了整分发车时刻表和需要的最少车辆数61辆。
模型Ⅱ建立模糊分析模型，结合层次分析求得模型Ⅰ带给公司和乘客双方日满意度为（0.941，0.811）根据双方满意度围和程度，找出同时达到双方最优日满意度(0.8807,0.8807)，且此时结果为474次50辆；从日共需车辆最少考虑，结果为484次45辆。
公共自行车调度问题-数学建模
公共自行车调度问题-数学建模1、-1-名目名目一、问题引入一、问题引入................................................................... ..................................................................... ...3二、问题分析二、问题分析................................................................... .............................................2、...........................32.1第一问分析................................................................... ......................................................42.2第二问分析................................................................... ..................................................3、....42.3第三问分析................................................................... ......................................................4三、模型假设和符号说明三、模型假设和符号说明................................................................... ....................................................53.1模型假4、设................................................................... ..........................................................53.2符号系统.............................................................................................................................6四、模型建立四、模型建立...........5、.................................................................. ..............................................................64.1模型分类................................................................... ..........................................................64.2租赁点安排方案建模.........6、.................................................................. .............................74.3调度车调度方案建模................................................................... .....................................84.3.1一辆调度车调度方案........................................................7、.....................................84.3.2多辆调度车调度方案................................................................... ..........................94.4租赁点数目和位置确实定................................................................... ............................114.5调度时间的模型................8、..............................................................................................12五、五、模型的求解模型的求解................................................................... ................................................................135.0经纬度转换为横纵坐标...........................9、.................................................................. ......135.1求解最短路径................................................................... ...............................................135.2模型一次运行后的单车重安排求解..................................................................10、............145.3求解安排方案的预估—校正算法................................................................... ...............165.4求解调度方案的启发式算法................................................................... .......................165.4.1算法简介....................................................11、...........................................................165.4.2算法内容................................................................... ............................................175.4.3约束条件................................................................... ........................12、....................185.4.4算法流程图................................................................... ........................................195.5租赁点位置................................................................... ....................................................205.6计算结果......13、................................................................. ....................................................205.6.1第一问结果................................................................... ........................................205.6.2第二问结果...................................14、................................................................. .......215.6.3第三问结果................................................................... ........................................23六、模型检验六、模型检验................................................................... ...........15、 (26)七、模型优缺点以及改良七、模型优缺点以及改良................................................................... ..................................................267.1安排方案的优点................................................................... ....16、........................................277.2调度方案的缺优点................................................................... ........................................277.3新增节点模型的优缺点................................................................... ................................277.4模型和算17、法的改良................................................................... ........................................28-2-7.4.1算法的改良................................................................... ........................................287.4.2模型的改良......................................18、................................................................. ....28八、。
数学建模-2001年的公交车调度问题
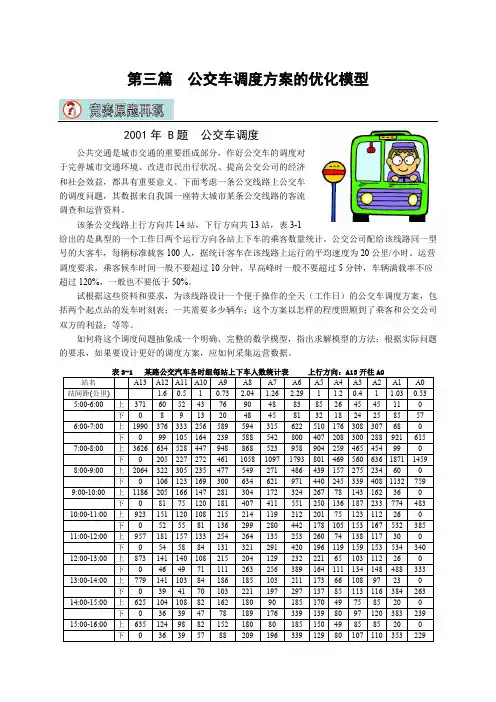
第三篇公交车调度方案的优化模型2001年 B题公交车调度Array公共交通是城市交通的重要组成部分，作好公交车的调度对于完善城市交通环境、改进市民出行状况、提高公交公司的经济和社会效益，都具有重要意义。
下面考虑一条公交线路上公交车的调度问题，其数据来自我国一座特大城市某条公交线路的客流调查和运营资料。
该条公交线路上行方向共14站，下行方向共13站，表3-1给出的是典型的一个工作日两个运行方向各站上下车的乘客数量统计。
公交公司配给该线路同一型号的大客车，每辆标准载客100人，据统计客车在该线路上运行的平均速度为20公里/小时。
运营调度要求，乘客候车时间一般不要超过10分钟，早高峰时一般不要超过5分钟，车辆满载率不应超过120%，一般也不要低于50%。
试根据这些资料和要求，为该线路设计一个便于操作的全天（工作日）的公交车调度方案，包括两个起点站的发车时刻表；一共需要多少辆车；这个方案以怎样的程度照顾到了乘客和公交公司双方的利益；等等。
如何将这个调度问题抽象成一个明确、完整的数学模型，指出求解模型的方法；根据实际问题的要求，如果要设计更好的调度方案，应如何采集运营数据。
公交车调度方案的优化模型*摘要：本文建立了公交车调度方案的优化模型，使公交公司在满足一定的社会效益和获得最大经济效益的前提下，给出了理想发车时刻表和最少车辆数。
并提供了关于采集运营数据的较好建议。
在模型Ⅰ中，对问题1建立了求最大客容量、车次数、发车时间间隔等模型，运用决策方法给出了各时段最大客容量数，再与车辆最大载客量比较，得出载完该时组乘客的最少车次数462次，从便于操作和发车密度考虑，给出了整分发车时刻表和需要的最少车辆数61辆。
模型Ⅱ建立模糊分析模型，结合层次分析求得模型Ⅰ带给公司和乘客双方日满意度为（0.941，0.811）根据双方满意度范围和程度，找出同时达到双方最优日满意度(0.8807,0.8807)，且此时结果为474次50辆；从日共需车辆最少考虑，结果为484次45辆。
数学建模论文校园公交车调度问题--大学毕业设计论文
西南交通大学2012年新秀杯数学建模竞赛题目：A题组别：大二组西南交通大学教务处西南交通大学实验室及设备管理处西南交通大学数学建模创新实践基地校园通行车路线的设计摘要本文主要研究的是校园交通车的站点设置、在固定停车和招手即停两种模式结合下的运载能力、运行路线和时间安排以及相应行驶方案的规划问题。
问题一中，我们对校园通行车现有行车路线网络和常停站点进行了调查和分析。
首先，在数据处理阶段，将站点实体间的线路选择抽象为图论最短路模型,用Matlab软件画出三条主要的行车线路，然后利用GIS空间分析方法解决单个交通线路上站点规划问题。
该方法依据乘客出行时间最短确定单个线路上的站点个数，结合GIS缓冲区分析和叠合分析，在路线上做站点设置的适宜性讨论，提出基于最优化理论和GIS空间分析技术的站点规划方法，确定站点的位置，从而提供一种可行的行驶方案。
问题二中，考虑固定停车和招手即停相结合的方案，我们首先将最佳行驶路线定义为车辆运行时间最短的路线，将图论中经典的Dijkstra算法（单源最短路径）进行改进，结合哈密尔顿图，以结点之间的时间作为权数，利用C++编程得到最佳推销员回路，也就是通行车行驶的最佳路径。
考虑到招手即停模式具有极大的随机性，为了便于调度，我们首先对乘车人次密度分布进行了调查和分析，并通过随机模拟出概率分布值较大的区域，将其抽象为一假想固定停车点，这样就将模型简化为固定停车点最佳行驶路径的问题。
根据已得到的乘车时段分布规律和学校实际的作息时间表，按照模糊聚类分析法将一工作日数单位时间段划分为更概括的高峰期、低潮期和一般期，并应用Matlab中的fgoalattain进行非线性规划求出实际发车数，以及应用时间步长法估计发车间隔，从而给出两种模式结合下通行车每周运行的车辆数、路线和时刻表。
问题三中，我们首先对校区师生乘车需求人数进行了描述性统计，从乘车人数的均值、方差、峰度以及正态性四个角度对样本进行检测，找到相关的分布规律与结论，即每日在各时段中的乘车人数分布相似。
最新公交车调度数学建模
公交车调度数学建模公交车调度摘 要本文通过对给定数据进行统计分析，将数据按１８个时段、两个行驶方向进行处理，计算出各个时段各个站点以及两个方向的流通量，从而将远问题转化为对流通量的处理。
首先，利用各时段小时断面最高流通量计算出各时段各方向的最小发车次数，进行适当的调整，确定了各时段两个方向的发车次数。
假定采用均匀发车的方式。
继而求出各时段两个方向发车间隔，经部分调整后，列出0A 站和13A 站的发车时刻表，并给出了时刻表的合理性证明，从而制定调度方案。
根据调度方案采用逐步累加各时段新调用的车辆数算法，求出公交车的发配车辆数为５７辆。
其次，建立乘客平均待车时间和公交车辆实际利用率与期望利用率的差值这两个量化指标，并用这两个指标来评价调度方案以如何的程度照顾到乘客和公交公司双方利益。
前者为4.2分钟，后者为13.88%。
最后，我们以上述两个指标为优化目标，以乘客的等车时间数学期望值和公交车辆的满载率的数学期望为约束指标，建立了一个双目标的优化模型。
并且给出了具体的求解方法，特别指出的是，给出了计算机模拟的方法求解的进程控制图。
通过了对模型的分析，提出了采集数据的 采集数据方法的建议。
注释：第i 站乘客流通量：∑=ik 1（第k 站的上车的人数与第k 站的下车人数的差值）;总的乘客等车时间：∑=mi 1∑=nj 1(第i 时段第j 站等车乘客数)⨯(第I 时段第j 站等待时间)；乘客平均等车时间：总的乘客等车时间与总乘客数的比值； 实际利用率：总实际乘客流通量与公司车辆总最大客运量的比值； 期望利用率：总期望乘客流通量与公司车辆总最大客运量的比值一、问题的提出一条公交线路上行方向共１４站，下行方向功１３站，给定典型的一个工作日两个运行方向各站上下车的乘客数量统计。
该线路用同一型号的大客车，每辆标准载客１００人，据统计客车在该线路上运行的平均速度为２０公里／小时。
运营调度要求，乘客候车时间一般不要超过１０分钟，早高峰是一般不要超过５分钟，车辆满载率不应超过１２０％，一般也不要低与１００％，一般也不要地狱５０％。
一类公交车调度问题的数学模型及其解法
一类公交车调度问题的数学模型及其解法1. 背景介绍公交车作为城市交通的重要组成部分，其运营效率和服务质量直接影响市民出行体验。
而公交车调度问题则是保障公交线路运营效率和准时性的重要环节之一。
在日常运营中，由于路况、乘客量、车辆故障等影响因素，公交车的调度往往面临诸多挑战。
如何利用数学模型解决公交车调度问题成为了一个备受关注的课题。
2. 公交车调度问题的数学建模公交车调度问题的数学建模主要涉及到车辆的合理分配以及路线的优化规划。
在数学建模时，需要考虑的主要因素包括但不限于乘客量、车辆容量、交通状况、站点分布等。
而个体车辆的运行轨迹则需要综合考虑上述因素以及最优化算法对其进行分析。
3. 数学模型的构建针对上述因素，可以将公交车调度问题构建成一个复杂的优化模型。
该模型主要包括以下几个方面的内容：（1）乘客需求预测：通过历史数据和大数据分析，预测不同时段和不同线路的乘客需求，为车辆调度提供依据。
（2）车辆分配优化：根据乘客需求预测和实际路况，采用最优化算法确定每辆车的运行路线和发车间隔。
（3）站点排队优化：结合乘客上下车规律和站点的停靠条件，优化车辆在不同站点的排队顺序，以减少候车时间和提升服务效率。
（4）交通状况仿真：通过交通仿真模型，考虑城市交通状况对公交车运行的影响，提前对可能出现的拥堵情况进行预判，以调整车辆的发车时间和路线。
4. 数学模型的求解在构建好数学模型后，需要采用合适的方法对其进行求解。
常见的求解方法主要包括但不限于线性规划、遗传算法、模拟退火算法等。
在实际求解过程中，需要充分考虑不同方法的适用场景和对模型的拟合程度，以选择最合适的求解方法。
5. 案例分析以某市的公交系统为例，采用上述数学模型对其进行调度优化。
通过收集该市的实际路况数据、站点分布情况以及历史乘客需求数据，建立完整的数学模型。
然后运用遗传算法对其进行求解，得到了最优的车辆运行路线和发车间隔。
在模型求解后，将其应用于实际公交车调度中，并进行了一段时间的实际运行试验。
数学建模-2001年的公交车调度问题
第三篇公交车调度方案的优化模型2001年 B题公交车调度公共交通是城市交通的重要组成部分，作好公交车的调度对于完善城市交通环境、改进市民出行状况、提高公交公司的经济和社会效益，都具有重要意义。
下面考虑一条公交线路上公交车的调度问题，其数据来自我国一座特大城市某条公交线路的客流调查和运营资料。
该条公交线路上行方向共14站，下行方向共13站，表3-1给出的是典型的一个工作日两个运行方向各站上下车的乘客数量统计。
公交公司配给该线路同一型号的大客车，每辆标准载客100人，据统计客车在该线路上运行的平均速度为20公里/小时。
运营调度要求，乘客候车时间一般不要超过10分钟，早高峰时一般不要超过5分钟，车辆满载率不应超过120%，一般也不要低于50%。
试根据这些资料和要求，为该线路设计一个便于操作的全天（工作日）的公交车调度方案，包括两个起点站的发车时刻表；一共需要多少辆车；这个方案以怎样的程度照顾到了乘客和公交公司双方的利益；等等。
如何将这个调度问题抽象成一个明确、完整的数学模型，指出求解模型的方法；根据实际问题的要求，如果要设计更好的调度方案，应如何采集运营数据。
站名A13 A12 A11 A10 A9 A8 A7 A6 A5 A4 A3 A2 A1 A0 站间距(公里) 1.6 0.5 1 0.73 2.04 1.26 2.29 1 1.2 0.4 1 1.03 0.53 5:00-6:00 上371 60 52 43 76 90 48 83 85 26 45 45 11 0 下0 8 9 13 20 48 45 81 32 18 24 25 85 57 6:00-7:00 上1990 376 333 256 589 594 315 622 510 176 308 307 68 0 下0 99 105 164 239 588 542 800 407 208 300 288 921 615 7:00-8:00 上3626 634 528 447 948 868 523 958 904 259 465 454 99 0 下0 205 227 272 461 1058 1097 1793 801 469 560 636 1871 1459 8:00-9:00 上2064 322 305 235 477 549 271 486 439 157 275 234 60 0 下0 106 123 169 300 634 621 971 440 245 339 408 1132 759 9:00-10:00 上1186 205 166 147 281 304 172 324 267 78 143 162 36 0 下0 81 75 120 181 407 411 551 250 136 187 233 774 483 10:00-11:00 上923 151 120 108 215 214 119 212 201 75 123 112 26 0 下0 52 55 81 136 299 280 442 178 105 153 167 532 385 11:00-12:00 上957 181 157 133 254 264 135 253 260 74 138 117 30 0 下0 54 58 84 131 321 291 420 196 119 159 153 534 340 12:00-13:00 上873 141 140 108 215 204 129 232 221 65 103 112 26 0 下0 46 49 71 111 263 256 389 164 111 134 148 488 333 13:00-14:00 上779 141 103 84 186 185 103 211 173 66 108 97 23 0 下0 39 41 70 103 221 197 297 137 85 113 116 384 263 14:00-15:00 上625 104 108 82 162 180 90 185 170 49 75 85 20 0 下0 36 39 47 78 189 176 339 139 80 97 120 383 239 15:00-16:00 上635 124 98 82 152 180 80 185 150 49 85 85 20 0 下0 36 39 57 88 209 196 339 129 80 107 110 353 22916:00-17:00 上1493 299 240 199 396 404 210 428 390 120 208 197 49 0 下0 80 85 135 194 450 441 731 335 157 255 251 800 557 17:00-18:00 上2011 379 311 230 497 479 296 586 508 140 250 259 61 0 下0 110 118 171 257 694 573 957 390 253 293 378 1228 793 18:00-19:00 上691 124 107 89 167 165 108 201 194 53 93 82 22 0 下0 45 48 80 108 237 231 390 150 89 131 125 428 336 19:00-20:00 上350 64 55 46 91 85 50 88 89 27 48 47 11 0 下0 22 23 34 63 116 108 196 83 48 64 66 204 139 20:00-21:00 上304 50 43 36 72 75 40 77 60 22 38 37 9 0 下0 16 17 24 38 80 84 143 59 34 46 47 160 117 21:00-22:00 上209 37 32 26 53 55 29 47 52 16 28 27 6 0 下0 14 14 21 33 78 63 125 62 30 40 41 128 92 22:00-23:00 上19 3 3 2 5 5 3 5 5 1 3 2 1 0 下0 3 3 5 8 18 17 27 12 7 9 9 32 21站名A0 A2 A3 A4 A5 A6 A7 A8 A9 A10 A11 A12 A13 站间距(公里) 1.56 1 0.44 1.2 0.97 2.29 1.3 2 0.73 1 0.5 1.62 5:00-6:00 上22 3 4 2 4 4 3 3 3 1 1 0 0 下0 2 1 1 6 7 7 5 3 4 2 3 9 6:00-7:00 上795 143 167 84 151 188 109 137 130 45 53 16 0 下0 70 40 40 184 205 195 147 93 109 75 108 271 7:00-8:00 上2328 380 427 224 420 455 272 343 331 126 138 45 0 下0 294 156 157 710 780 849 545 374 444 265 373 958 8:00-9:00 上2706 374 492 224 404 532 333 345 354 120 153 46 0 下0 266 158 149 756 827 856 529 367 428 237 376 1167 9:00-10:00 上1556 204 274 125 235 308 162 203 198 76 99 27 0 下0 157 100 80 410 511 498 336 199 276 136 219 556 10:00-11:00 上902 147 183 82 155 206 120 150 143 50 59 18 0 下0 103 59 59 246 346 320 191 147 185 96 154 438 11:00-12:00 上847 130 132 67 127 150 108 104 107 41 48 15 0 下0 94 48 48 199 238 256 175 122 143 68 128 346 12:00-13:00 上706 90 118 66 105 144 92 95 88 34 40 12 0 下0 70 40 40 174 215 205 127 103 119 65 98 261 13:00-14:00 上770 97 126 59 102 133 97 102 104 36 43 13 0 下0 75 43 43 166 210 209 136 90 127 60 115 309 14:00-15:00 上839 133 156 69 130 165 101 118 120 42 49 15 0 下0 84 48 48 219 238 246 155 112 153 78 118 346 15:00-16:00 上1110 170 189 79 169 194 141 152 166 54 64 19 0 下0 110 73 63 253 307 341 215 136 167 102 144 425 16:00-17:00 上1837 260 330 146 305 404 229 277 253 95 122 34 0 下0 175 96 106 459 617 549 401 266 304 162 269 784 17:00-18:00 上3020 474 587 248 468 649 388 432 452 157 205 56 0 下0 330 193 194 737 934 1016 606 416 494 278 448 1249 18:00-19:00 上1966 350 399 204 328 471 289 335 342 122 132 40 0 下0 223 129 150 635 787 690 505 304 423 246 320 1010 19:00-20:00 上939 130 165 88 138 187 124 143 147 48 56 17 0 下0 113 59 59 266 306 290 201 147 155 86 154 398 20:00-21:00 上640 107 126 69 112 153 87 102 94 36 43 13 0 下0 75 43 43 186 230 219 146 90 127 70 95 319 21:00-22:00 上636 110 128 56 105 144 82 95 98 34 40 12 0 下0 73 41 42 190 243 192 132 107 123 67 101 290 22:00-23:00 上294 43 51 24 46 58 35 41 42 15 17 5 0 下0 35 20 20 87 108 92 69 47 60 33 49 136公交车调度方案的优化模型*摘要：本文建立了公交车调度方案的优化模型，使公交公司在满足一定的社会效益和获得最大经济效益的前提下，给出了理想发车时刻表和最少车辆数。
数学建模-公交车调度问题
第三篇公交车调度方案得优化模型2001年 B题公交车调度Array公共交通就是城市交通得重要组成部分,作好公交车得调度对于完善城市交通环境、改进市民出行状况、提高公交公司得经济与社会效益,都具有重要意义。
下面考虑一条公交线路上公交车得调度问题，其数据来自我国一座特大城市某条公交线路得客流调查与运营资料。
该条公交线路上行方向共１4站，下行方向共13站，表3—1给出得就是典型得一个工作日两个运行方向各站上下车得乘客数量统计。
公交公司配给该线路同一型号得大客车,每辆标准载客１00人,据统计客车在该线路上运行得平均速度为20公里／小时.运营调度要求，乘客候车时间一般不要超过10分钟,早高峰时一般不要超过5分钟，车辆满载率不应超过12０%,一般也不要低于5０％。
试根据这些资料与要求，为该线路设计一个便于操作得全天（工作日)得公交车调度方案,包括两个起点站得发车时刻表；一共需要多少辆车；这个方案以怎样得程度照顾到了乘客与公交公司双方得利益；等等。
如何将这个调度问题抽象成一个明确、完整得数学模型，指出求解模型得方法；根据实际问题得要求，如果要设计更好得调度方案,应如何采集运营数据.公交车调度方案得优化模型*摘要：本文建立了公交车调度方案得优化模型，使公交公司在满足一定得社会效益与获得最大经济效益得前提下，给出了理想发车时刻表与最少车辆数。
并提供了关于采集运营数据得较好建议。
在模型Ⅰ中，对问题１建立了求最大客容量、车次数、发车时间间隔等模型，运用决策方法给出了各时段最大客容量数，再与车辆最大载客量比较，得出载完该时组乘客得最少车次数４62次,从便于操作与发车密度考虑，给出了整分发车时刻表与需要得最少车辆数61辆。
模型Ⅱ建立模糊分析模型，结合层次分析求得模型Ⅰ带给公司与乘客双方日满意度为（0、941,０、811)根据双方满意度范围与程度，找出同时达到双方最优日满意度（0、88０7,0、８807），且此时结果为474次5０辆;从日共需车辆最少考虑,结果为48４次４５辆。
数学建模-2001年的公交车调度问题教学内容
数学建模-2001年的公交车调度问题第三篇公交车调度方案的优化模型2001年 B题公交车调度Array公共交通是城市交通的重要组成部分，作好公交车的调度对于完善城市交通环境、改进市民出行状况、提高公交公司的经济和社会效益，都具有重要意义。
下面考虑一条公交线路上公交车的调度问题，其数据来自我国一座特大城市某条公交线路的客流调查和运营资料。
该条公交线路上行方向共14站，下行方向共13站，表3-1给出的是典型的一个工作日两个运行方向各站上下车的乘客数量统计。
公交公司配给该线路同一型号的大客车，每辆标准载客100人，据统计客车在该线路上运行的平均速度为20公里/小时。
运营调度要求，乘客候车时间一般不要超过10分钟，早高峰时一般不要超过5分钟，车辆满载率不应超过120%，一般也不要低于50%。
试根据这些资料和要求，为该线路设计一个便于操作的全天（工作日）的公交车调度方案，包括两个起点站的发车时刻表；一共需要多少辆车；这个方案以怎样的程度照顾到了乘客和公交公司双方的利益；等等。
如何将这个调度问题抽象成一个明确、完整的数学模型，指出求解模型的方法；根据实际问题的要求，如果要设计更好的调度方案，应如何采集运营数据。
公交车调度方案的优化模型*摘要：本文建立了公交车调度方案的优化模型，使公交公司在满足一定的社会效益和获得最大经济效益的前提下，给出了理想发车时刻表和最少车辆数。
并提供了关于采集运营数据的较好建议。
在模型Ⅰ中，对问题1建立了求最大客容量、车次数、发车时间间隔等模型，运用决策方法给出了各时段最大客容量数，再与车辆最大载客量比较，得出载完该时组乘客的最少车次数462次，从便于操作和发车密度考虑，给出了整分发车时刻表和需要的最少车辆数61辆。
模型Ⅱ建立模糊分析模型，结合层次分析求得模型Ⅰ带给公司和乘客双方日满意度为（0.941，0.811）根据双方满意度范围和程度，找出同时达到双方最优日满意度(0.8807,0.8807)，且此时结果为474次50辆；从日共需车辆最少考虑，结果为484次45辆。
数学建模论文-公交车调度问题
对公交车调度问题的研究作者：摘要：本文根据所给的客流量及运营情况排出公交车调度时刻表，以及反映客运公司和乘客的利益有多个指标，建立了乘客的利益及公司利益两个目标函数的多目标规划数学模型。
基于多目标规划分析法，进行数值计算，从而得到原问题的一个明确、完整的数学模型，并在模型扩展中运用已建的计算机模拟系统对所得的结果和我们对于调度方案的想法进行分析和评价。
首先通过数据的分析，并考虑到方案的可操作性，将一天划为；引入乘客的利益、公司利益作为两个目标函数，建立了两目标优化模型。
通过运客能力与运输需求(实际客运量) 达到最优匹配、满载率高低体现乘客利益；通过总车辆数较少、发车次数最少表示公司利益建立两个目标函数。
应用matlab中的fgoalattain进行多目标规划求出发车数，以及时间步长法估计发车间隔和车辆数。
关键字：公交车调度；多目标规划；数据分析；数学模型；时间步长法，matlab一问题的重述：1、路公交线路上下行方向各24站，总共有L 辆汽车在运行，开始时段线路两端的停车场中各停放汽车m辆，每两车可乘坐S人。
这些汽车将按照发车时刻表及到达次序次发车，循环往返地运行来完成运送乘客的任务。
建立数学模型，根据乘客人数大小，配多少辆车、多长时间发一班车使得公交公司的盈利最高，乘客的抱怨程度最小。
假设公交车在运行过程中是匀速的速度为v。
1路公交车站点客流量见下表1 已知数据及问题的提出我们要考虑的是莆田市的一路公交线路上的车辆调度问题。
现已知该线路上行的车站总数N1 ( = 24 )，下行的车站总数N2 ( = 24 )，并且给出每一个站点上下车的人数。
公交线路总路程L（=L）；公交行驶的速度V=20km/ h；运营调度要求,车辆满载率不应超过r= 120 % ,一般也不要底于r= 50 %。
现要我们根据以上资料和要求,为该线路设计一个公交公司发车时间的调度方案、一共需要多少辆车、公交车道路行驶过程中的速度以及公交车车型的选择的方案。
数学建模的公交车调度问题
第三篇公交车调度方案的优化模型2001年 B题公交车调度公共交通是城市交通的重要组成部分，作好公交车的调度对于完善城市交通环境、改进市民出行状况、提高公交公司的经济和社会效益，都具有重要意义。
下面考虑一条公交线路上公交车的调度问题，其数据来自我国一座特大城市某条公交线路的客流调查和运营资料。
该条公交线路上行方向共14站，下行方向共13站，表3-1给出的是典型的一个工作日两个运行方向各站上下车的乘客数量统计。
公交公司配给该线路同一型号的大客车，每辆标准载客100人，据统计客车在该线路上运行的平均速度为20公里/小时。
运营调度要求，乘客候车时间一般不要超过10分钟，早高峰时一般不要超过5分钟，车辆满载率不应超过120%，一般也不要低于50%。
试根据这些资料和要求，为该线路设计一个便于操作的全天（工作日）的公交车调度方案，包括两个起点站的发车时刻表；一共需要多少辆车；这个方案以怎样的程度照顾到了乘客和公交公司双方的利益；等等。
如何将这个调度问题抽象成一个明确、完整的数学模型，指出求解模型的方法；根据实际问题的要求，如果要设计更好的调度方案，应如何采集运营数据。
公交车调度方案的优化模型*摘要：本文建立了公交车调度方案的优化模型，使公交公司在满足一定的社会效益和获得最大经济效益的前提下，给出了理想发车时刻表和最少车辆数。
并提供了关于采集运营数据的较好建议。
在模型Ⅰ中，对问题1建立了求最大客容量、车次数、发车时间间隔等模型，运用决策方法给出了各时段最大客容量数，再与车辆最大载客量比较，得出载完该时组乘客的最少车次数462次，从便于操作和发车密度考虑，给出了整分发车时刻表和需要的最少车辆数61辆。
模型Ⅱ建立模糊分析模型，结合层次分析求得模型Ⅰ带给公司和乘客双方日满意度为（0.941，0.811）根据双方满意度范围和程度，找出同时达到双方最优日满意度(0.8807,0.8807)，且此时结果为474次50辆；从日共需车辆最少考虑，结果为484次45辆。
数学建模论文校园公交车调度问题大学论文
西南交通大学2012年新秀杯数学建模竞赛题目：A题组别：大二组西南交通大学教务处西南交通大学实验室及设备管理处西南交通大学数学建模创新实践基地校园通行车路线的设计摘要本文主要研究的是校园交通车的站点设置、在固定停车和招手即停两种模式结合下的运载能力、运行路线和时间安排以及相应行驶方案的规划问题。
问题一中，我们对校园通行车现有行车路线网络和常停站点进行了调查和分析。
首先，在数据处理阶段，将站点实体间的线路选择抽象为图论最短路模型,用Matlab软件画出三条主要的行车线路，然后利用GIS空间分析方法解决单个交通线路上站点规划问题。
该方法依据乘客出行时间最短确定单个线路上的站点个数，结合GIS缓冲区分析和叠合分析，在路线上做站点设置的适宜性讨论，提出基于最优化理论和GIS空间分析技术的站点规划方法，确定站点的位置，从而提供一种可行的行驶方案。
问题二中，考虑固定停车和招手即停相结合的方案，我们首先将最佳行驶路线定义为车辆运行时间最短的路线，将图论中经典的Dijkstra算法（单源最短路径）进行改进，结合哈密尔顿图，以结点之间的时间作为权数，利用C++编程得到最佳推销员回路，也就是通行车行驶的最佳路径。
考虑到招手即停模式具有极大的随机性，为了便于调度，我们首先对乘车人次密度分布进行了调查和分析，并通过随机模拟出概率分布值较大的区域，将其抽象为一假想固定停车点，这样就将模型简化为固定停车点最佳行驶路径的问题。
根据已得到的乘车时段分布规律和学校实际的作息时间表，按照模糊聚类分析法将一工作日数单位时间段划分为更概括的高峰期、低潮期和一般期，并应用Matlab中的fgoalattain进行非线性规划求出实际发车数，以及应用时间步长法估计发车间隔，从而给出两种模式结合下通行车每周运行的车辆数、路线和时刻表。
问题三中，我们首先对校区师生乘车需求人数进行了描述性统计，从乘车人数的均值、方差、峰度以及正态性四个角度对样本进行检测，找到相关的分布规律与结论，即每日在各时段中的乘车人数分布相似。
公共自行车调度问题-数学建模论文
目录一、问题引入..................................................................................................................................... - 3 -二、问题分析..................................................................................................................................... - 3 -2.1第一问分析................................................................................................................... - 4 -2.2第二问分析................................................................................................................... - 4 -2.3第三问分析................................................................................................................... - 4 -三、模型假设和符号说明................................................................................................................. - 5 -3.1模型假设....................................................................................................................... - 5 -3.2符号系统....................................................................................................................... - 6 -四、模型建立..................................................................................................................................... - 6 -4.1模型分类....................................................................................................................... - 6 -4.2 租赁点分配方案建模.................................................................................................. - 7 -4.3 调度车调度方案建模.................................................................................................. - 8 -4.3.1一辆调度车调度方案....................................................................................... - 8 -4.3.2多辆调度车调度方案....................................................................................... - 9 -4.4租赁点数目和位置的确定......................................................................................... - 11 -4.5 调度时间的模型........................................................................................................ - 12 -五、模型的求解............................................................................................................................. - 13 -5.0经纬度转换为横纵坐标............................................................................................. - 13 -5.1 求解最短路径............................................................................................................ - 13 -5.2 模型一次运行后的单车重分配求解........................................................................ - 14 -5.3 求解分配方案的预估—校正算法............................................................................ - 16 -5.4 求解调度方案的启发式算法.................................................................................... - 16 -5.4.1算法简介......................................................................................................... - 16 -5.4.2算法内容......................................................................................................... - 17 -5.4.3约束条件......................................................................................................... - 18 -5.4.4算法流程图..................................................................................................... - 19 -5.5租赁点位置................................................................................................................. - 20 -5.6计算结果..................................................................................................................... - 20 -5.6.1第一问结果..................................................................................................... - 20 -5.6.2第二问结果..................................................................................................... - 21 -5.6.3第三问结果..................................................................................................... - 23 -六、模型检验................................................................................................................................... - 26 -七、模型优缺点以及改进............................................................................................................... - 26 -7.1分配方案的优点......................................................................................................... - 27 -7.2调度方案的缺优点..................................................................................................... - 27 -7.3新增节点模型的优缺点............................................................................................. - 27 -7.4模型和算法的改进..................................................................................................... - 28 -7.4.1算法的改进..................................................................................................... - 28 -7.4.2模型的改进..................................................................................................... - 28 -八、参考文献................................................................................................................................... - 30 -附录................................................................................................................................................... - 30 -一、问题引入近年来，随着经济的发展，我国各级城市的机动车保有量都进入了持续高速增长时期，但由此所引发的道路拥堵、空气污染也引起了政府以及百姓的极大关注。
《独创》数学建模-公交车调度模型建立
图 1 g13 t 函数图像（图的大小我注意）
5
对公交线路全天的上车乘客数的函数 g j t 求一阶导， g j ' t 则表示第 j 个公交车站
1.2
问题提出
本问题考虑一条公交线路上公交车的调度问题，其数据来自我国一座特大城市某条 公交线路的客流调查和运营资料。 该条公交线路上行方向共 14 站，下行方向共 13 站，第 3-4 页给出的是典型的一个 工作日两个运行方向各站上下车的乘客数量统计。 公交公司配给该线路同一型号的大客 车，每辆标准载客 100 人，据统计客车在该线路上运行的平均速度为 20 公里/小时。运 营调度要求，乘客候车时间一般不要超过 10 分钟，早高峰时一般不要超过 5 分钟，车 辆满载率不应超过 120%，一般也不要低于 50%。 试根据这些资料和要求，为该线路设计一个便于操作的全天（工作日）的公交车调 度方案，包括两个起点站的发车时刻表；一共需要多少辆车；这个方案以怎样的程度照 顾到了乘客和公交公司双方的利益；等等。 如何将这个调度问题抽象成一个明确、完整的数学模型，指出求解模型的方法；根据实 际问题的要求，如果要设计更好的调度方案，应如何采集运营数据。
2
一、 问题重述
1.1 问题背景
公共交通是城市交通的重要组成部分。城市的现代化，尤其是城市功能的完善，离 不开城市交通的优化和提高。近些年来，随着我国社会的发展和城市居民收入水平的提 高，家庭私人轿车在城市交通中逐渐占据了一定地位，但这并不会削弱和取代公共交通 的功能和作用。根据世界各国的经验，优良的公交服务对于减少城市的交通拥挤、环境 污染，提高交通资源的配置效益等方面都具有积极的作用。目前，我国仍有不少城市公 交服务还没有充分发挥作用，常常出现车辆拥挤与闲置等问题，其重要原因之一就是车 辆调度依赖主观经验， 缺少严密科学的设计。 作好公交车的调度对于完善城市交通环境、 改进市民出行状况、提高公交公司的经济和社会效益，都具有重要意义。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第三篇公交车调度方案得优化模型2001年 B题公交车调度Array公共交通就是城市交通得重要组成部分,作好公交车得调度对于完善城市交通环境、改进市民出行状况、提高公交公司得经济与社会效益,都具有重要意义。
下面考虑一条公交线路上公交车得调度问题，其数据来自我国一座特大城市某条公交线路得客流调查与运营资料。
该条公交线路上行方向共１4站，下行方向共13站，表3—1给出得就是典型得一个工作日两个运行方向各站上下车得乘客数量统计。
公交公司配给该线路同一型号得大客车,每辆标准载客１00人,据统计客车在该线路上运行得平均速度为20公里／小时.运营调度要求，乘客候车时间一般不要超过10分钟,早高峰时一般不要超过5分钟，车辆满载率不应超过12０%,一般也不要低于5０％。
试根据这些资料与要求，为该线路设计一个便于操作得全天（工作日)得公交车调度方案,包括两个起点站得发车时刻表；一共需要多少辆车；这个方案以怎样得程度照顾到了乘客与公交公司双方得利益；等等。
如何将这个调度问题抽象成一个明确、完整得数学模型，指出求解模型得方法；根据实际问题得要求，如果要设计更好得调度方案,应如何采集运营数据.公交车调度方案得优化模型*摘要：本文建立了公交车调度方案得优化模型，使公交公司在满足一定得社会效益与获得最大经济效益得前提下，给出了理想发车时刻表与最少车辆数。
并提供了关于采集运营数据得较好建议。
在模型Ⅰ中，对问题１建立了求最大客容量、车次数、发车时间间隔等模型，运用决策方法给出了各时段最大客容量数，再与车辆最大载客量比较，得出载完该时组乘客得最少车次数４62次,从便于操作与发车密度考虑，给出了整分发车时刻表与需要得最少车辆数61辆。
模型Ⅱ建立模糊分析模型，结合层次分析求得模型Ⅰ带给公司与乘客双方日满意度为（0、941,０、811)根据双方满意度范围与程度，找出同时达到双方最优日满意度（0、88０7,0、８807），且此时结果为474次5０辆;从日共需车辆最少考虑,结果为48４次４５辆。
对问题２,建立了综合效益目标模型及线性规划法求解.对问题３，数据采集方法就是遵照前门进中门出得规律,运用两个自动记录机对上下车乘客数记录与自动报站机(加报时间信息)作录音结合，给出准确得各项数据，返站后结合日期储存到公司总调度室。
关键词:公交调度；模糊优化法;层次分析;满意度§1 问题得重述一、问题得基本背景公交公司制定公交车调度方案,要考虑公交车、车站与乘客三方面因素。
我国某特大城市某条公交线路情况,一个工作日两个运营方向各个站上下车得乘客数量统计见表３－1.二、运营及调度要求1．公交线路上行方向共1４站,下行方向共13站;２.公交公司配给该线路同一型号得大客车，每辆标准载客１０0人,据统计客车在该线路上运营得平均速度为20公里/小时.车辆满载率不应超过1２0％，一般也不低于50％;3.乘客候车时间一般不要超过10分钟,早高峰时一般不要超过5分钟。
三、要求得具体问题1.试根据这些资料与要求,为该线路设计一个便于操作得全天(工作日)得公交车调度方案,包括两个起点站得发车时刻表;一共需要多少辆车;这个方案以怎样得程度照顾到了乘客与公交公司双方得利益,等等；2.如何将这个调度问题抽象成一个明确完整得数学模型，并指出求解方法;3．据实际问题得要求,如果要设计好更好得调度方案,应如何采集运营数据。
3、2问题得分析本问题得难点就是同时考虑到完善城市交通环境、改进市民出行状况、提高公交公司得经济与*本文获2001年全国一等奖。
队员：叶云，周迎春，齐欢，指导教师：朱家明等。
社会效益等诸多因素。
如果仅考虑提高公交公司得经济效益,则只要提高公交车得满载率,运用数据分析法可方便地给出它得最佳调度方案;如果仅考虑方便乘客出行，只要增加车辆数得次数，运用统计方法同样可以方便地给出它得最佳调度方案,显然这两种方案就是对立得。
于就是我们将此题分成两个方面，分别考虑到：⑴公交公司得经济效益，记为公司得满意度；⑵乘客得等待时间与乘车得舒适度，记为乘客得满意度.显然公交公司得满意度取决于每一趟车得满载率，且满载率越高，公交公司得满意度越高；乘客得满意度取决于乘客等待得时间与乘车得舒适度，而乘客等待时间取决于车辆得班次,班次越多等待时间越少,满意度越高；乘客得舒适度取决于就是否超载,超载人数越少,乘客越满意。
很明显可以知道公交公司得满意度与乘客得满意度相互矛盾，所以我们需要在这两个因素中找出一个合理得匹配关系,使得双方得满意度达到最好。
3、3 模型得假设1．道路:交通情况、路面状况良好，无交通堵塞与车辆损坏等意外情况；2.公交车：发车间隔取整分钟,行进中彼此赶不上且不超车,到达终点站后调头变为始发车;3。
乘客：在每时段内到达车站得人数可瞧作就是负指数分布，乘客乘车就是按照排队得先后有序原则乘车,且不用在两辆车得间隔内等待太久；4.数据：“人数统计表”中得数据来源准确、可信、稳定、科学;5．票价：乘车票价为定值，不因乘车远近而改变.3、4 定义与符号说明3、5 模型得建立与求解3．5．1 模型Ⅰ：相关量及车辆数得确定模型对问题1为设计便于操作得公交车调度方案,根据表3-1给出得一个工作日两个运营方向各个站上下车得乘客数量统计，假设各时段车辆平均足够载完在相等时间内到达得乘客，乘客也只能乘坐该路车而没有太大得不满，我们要设计两个起点站得发车时刻表,计算需要得车辆数,首先可建立以下各模型来求相关量。
1。
相关量⑴上下行各时间段内最大客容量:建立模型如下运用模型与表3-1中得上下车乘客数,算出上下行各时间段内最大客容量如下:上行：7１６，2943，5０18，2７05，１５28，1193，13５5，1２０0，1０40，881，8７1，213３，2722，8９7,464,410,275,19;下行：７,1０39,275２，３22３，1８22，1093,９86，８30，891,10１7，1302，219６，36１，2４１７,１091，781,774，33７、其直观得双峰直方图如图３-１。
图3—1 (1)上行各时间段内最大客容量图3—１（2）下行各时间段内最大客容量⑵车次数:因为座位数为100得客车满载率在5０％与１２0％之间，即，在满足客车满载率与载完各时段所有乘客前提下,由模型：,(其中Z+就是正整数）可计算每个时段得详细车次数如下:上行:６,２５，42，２3,13,10，12，10，9，８，8,18,24,8,4，４,3，4；下行：3，9，23，27,1６，10，9，7，8，9，1１,1９，3１,21,10,7,7,4.求与可得出全工作日可行得最少车次总数：.⑶安排发车时间间隔:用每个时段60分钟除以车次数，即：,经计算可得出该时段平均发车时间间隔依次如下：上行:10,2、4,１、4，2、６，4、6,６,5，6，6、7,7、5，7、5，3、３，2、5,7、5,15，15,20,20；下行：２０，6、7,2、6，2、２，3、８，６，6、7,8、6，７、5,６、7，5、5，3、１,1、9,2、８,6，8、６，2０。
由得值有分数出现,而现实中列车、客车等时刻表得最小单位为分钟，故间隔应取整数。
当取整数时，可直接安排等时间发车次。
当某个取小数时,不妨设与就是与相邻得两个连续整数且,由模型:可求出以为间隔得班次与以为间隔得班次，再分别以发车间隔；为与，兼顾发车密度，将此时间段进行适当划分。
将上述各与值代入方程组,可相应地求出具体得发车间隔得次数,考虑到公交车调度方案得可操作性与公交公司得利益所在,在同时段线路上得车辆不宜过多，我们对结果进行了分析比较,将相邻时间段内发车间隔相等得班次尽量安排在一起，并且对高峰时期发车得先后顺序作了调整，得出了全天（一个工作日）内得公交车调度方案,见表３－5。
2。
日所需车辆数由汽车平均速度20千米/小时与A0-A13得距离千米、A1３—Ａ0得距离千米,可求得车辆从起点站到终点站得时间约为４4分钟;又由假设可知车辆到达终点站后立即调头往回开且不跑空车，由于早高峰乘客数最多,故此时车辆实际占用数也应就是当日得上限,考虑到8：00之前从A13发出得车次每个时段都多于Ａ0发出得车次，且最大逆差数为即从A13多发出38辆车；8：00到９：00虽然从A0发来得车辆多于从A13发出得车辆，但从8：0０到8：４4仍要从A1３发出得1５辆车，由假设恰在8:44时对方开来得车辆到站并调头再结合动态车辆有8辆赶不上时差。
故早高峰车辆实际占用为61辆,也即当天共需开动得车辆最少为61辆。
3。
5．２ 模型Ⅱ 最小车次数线性规划模型问题明显可瞧作就是一个排队随机服务系统，我们把汽车瞧作就是“顾客”,将各个车站瞧作就是“服务台"，则此公交系统可瞧作就是一个顾客不消失得、单通道多级服务台串联得排队系统。
因此，这里所遇到得，主要就是排队问题。
归纳起来,需要考虑三种活动：①首站发车活动：根据发车时刻表确定；②到达中途站活动：在中途站主要考虑与计算上下车人数、车上得总人数与上下车时间；③到达终点站调头活动:在终点站根据发车时刻表确定。
我们先考上行时乘客在站得逗留时间，即乘客在站得等待时间，它包括相邻两趟车到达站得时间间隔即发车间隔与乘客上下车得服务时间.因为假设每个乘客上车时间与下车时间不计，即＝0.可以得出：,故此问题可以转化为满足下列条件下得公交公司全天得总利益取最大得规划问题：①乘客等待时间在一般时间段不超过10分钟；②早高峰时间段不超过５分钟;③各个时间段内得最大满载率不超过12０%;④各个时间段内得最小满载率不超过５0%。
公交公司全天得总利益为全天所有车辆运行公里数最小,因为线路长度一定，只要考虑站车次即可得出目标函数：利用模I 中得数据，我们可以求出各个时间段内得发车次数与间隔,因为此解法就是在满足乘客得情况下求得最小解，所以乘客等待时间得满意度为1０0％,但就是从舒适度考虑,上下行分别有11与9人不满意,所以乘客总满意度为８６、１％，公交公司满意度为(10９+1１1)/２40×100％＝９1、7％,按模型Ⅰ方法考虑，此时结果为最少车辆数50辆,最少运行474车次. 3。
５.3 模型Ⅲ 满意度分析模型1.前期工作准备工作 ⑴满意度得层次分析据问题分析，我们在设计两个起点站得发车时刻表时，应着重考虑到此时刻表带给公交公司与乘客两者得利益,即公交公司与乘客对应得日平均满意度与，各时段得满意度与。
为此,我们采用层次分析法来讨论影响总体性能得两个相关因素。
在乘客源一定得情况下,影响得最主要因素就是车上得载客量,一般情况.在多个站点位置固定得条件下,影响得最主要因素就是乘客得等车时间与车上得平均载客量。
设,分别就是各时段乘客因等车时间与得影响而产生得满意度，则即可表示为:=Ａ，其中A 就是关于因素,得权重集.考虑到，对于乘客，,对得影响就是不相等得.上下车得乘客都在动态得变化着，但对车辆而言,车辆得满载率达120％时,最大超载得20%由于缺少座位,而注重舒适度得影响，而无暇过分顾及等待时间得影响；而１00％得乘客因为有座,而无需过分考虑舒适，更多得就是考虑等车时间得影响.又设，其中，、分别就是因素、得重要程度，用层次分析中成对比较法,可知：,同时，Ａ应满足归一性与非负性条件,即：。