华东师大版数学八年级上册2.定理与证明PPT
华师大版八年级数学上册《定理与证明》优质课课件

• 15、一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。2021年7月2021/7/292021/7/292021/7/297/29/2021
• 16、提出一个问题往往比解决一个更重要。因为解决问题也许仅是一个数学上或实验上的技能而已,而提出新的问题,却需要有创造性的想像力,而且标志着科学的真正进步。2021/7/292021/7/29July 29, 2021
(两直线平行,同位角相等)
∵ ∠3=∠1 ( 对顶角相等 )
∴∠1=∠2 ( 等量代换 )
命题证明的步骤: 1.根据题意,画出图形; 2.根据题设、结论,结合图形,写出
已知、求证; 3.经过分析,找出由已知推出求证的
途径,写出证明过程.
根据下列命题,画出图形,并结合 图形写出已知、求证(不写证明过程): 1)垂直于同一直线的两直线平行; 2)内错角相等,两直线平行; 3)一个角的平分线上的点到这个角的两边
OE平分∠AOB, OF平分∠BOC
求证:OE⊥OF
E
B
证明:∵OE平分∠AOB,
12 F
∴∠1=
OF平分∠BOC
1
2∠AOB,
∠2= 1
2
A ∠BOC
O
C
又∠AOB、∠BOC互为邻补角
∵ ∠AOB+∠BOC=180° ∴∠1+∠2= 1 (∠AOB+∠BOC)=90° ∴ OE⊥OF 2
如何判断一个命题是假命题?
• 17、儿童是中心,教育的措施便围绕他们而组织起来。2021/7/292021/7/292021/7/292021/7/29
• 2、Our destiny offers not only the cup of despair, but the chalice of opportunity. (Richard Nixon, American President )命运给予我们的不是失望之酒,而是机会之杯。二〇二一年六月十七日2021年6月17日星期四 • 3、Patience is bitter, but its fruit is sweet. (Jean Jacques Rousseau , French thinker)忍耐是痛苦的,但它的果实是甜蜜的。10:516.17.202110:516.17.202110:5110:51:196.17.202110:516.17.2021 • 4、All that you do, do with your might; things done by halves are never done right. ----R.H. Stoddard, American poet做一切事都应尽力而为,半途而废永远不行6.17.20216.17.202110:5110:5110:51:1910:51:19 • 5、You have to believe in yourself. That's the secret of success. ----Charles Chaplin人必须相信自己,这是成功的秘诀。-Thursday, June 17, 2021June 21Thursday, June 17, 20216/17/2021
华东师大版八年级上册数学知识点集及思维导图
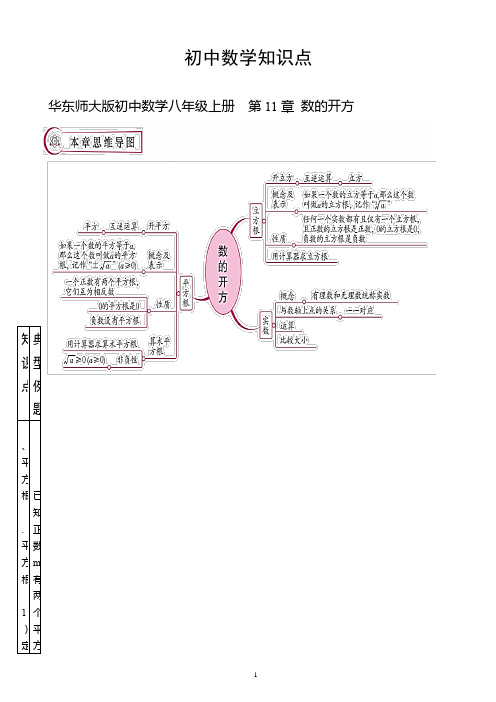
初中数学知识点华东师大版初中数学八年级上册 第11章 数的开方 知识点 典型例题、平方根 .平方根 1)定 已知正数m 有两个平方义:如果一个数的平方等于a ,那么这个数叫做a 的平方根.(2)表示方法:)0(,≥±a a . (3)性质:正数有两个互为相反数的平方根;零的平方根是零;负数没有平方根.2.算术平方根 (1)定义:正数a 的正的平方根,叫做a 的算术平方根.0的算术平方根是0.(2)表示方法:)0(,≥a a .(3)重要性质:双重非负性:)0(,0≥≥a a其他具有非负性的式子:a n a n ,(2为正整数).运算性质:如果几个非负数的和为0,那么每一个非负数都为0. (4)运算性质:一个非负数的算术平方根的平方等于它本身,)0(,)(2≥=a a a . 一个实数的平方的算术平方根等于它的绝对值,a a =2. 3.开平方定义:求一个非负数的平方根的运算,叫做开平方. 二、立方根 1.立方根 (1)定义:如果一个数的立方等于a ,那么这个数叫做a 的立方根.(2)表示方法:3a . (3)性质:正数的立方根是正数,负数的立方根是负数,0的立方根是0.(4)运算性质:a a a ==3333)(. 三、实数 1.无理数定义:无限不循环小数叫做无理数. 2.实数有理数和无理数统称实数. 3.实数的分类 按定义分:⎪⎩⎪⎨⎧⎩⎨⎧无理数分数整数有理数实数按性质分:根,分别是a+3与2a -15,求a 的值,并求这个正数m.已知a a -=-22,求a 的取值范围.若0a 2=++c b ,求a 、b 、c 的值.已知实数a 、b 、c 在数轴上的位置如图所示,化简:222)(c a c b a a ---++一个数的立方根是它本身,则这个数是 .计算:=-33)2( .有下列各数:2π,0,9,32.0 ,2-1,722,⋅⋅⋅3030030003.0,其中无理数有 . 求一个无理数的整数部分和小数部分:已知a 是11的整数部分,b 是11的小数部分,求a 和b 的值.⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负无理数负有理数负实数零正无理数正有理数正实数实数 4.实数与数轴上点的关系 实数与数轴上的点一一对应. 5.实数大小比较常有方法平方法;做差法;倒数法;做商法比较大小:23____32 32____3-5+华东师大版初中数学八年级上册 第12章 整式的乘除 知识点典型例题一、幂的运算 1.同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加.已知32=x ,求32+x 的值.华东师大版初中数学八年级上册第13章全等三角形知识点典型例题一、命题、定理与证明1.命题(1)定义:表示判断的语句叫做命题.(2)组成:命题是由条件和结论两部分组成。
华东师大版八年级上册数学教学设计《定理与证明》

华东师大版八年级上册数学教学设计《定理与证明》一. 教材分析华东师大版八年级上册数学教材在《定理与证明》这一章节中,主要向学生介绍定理与证明的概念、方法和过程。
本章内容是学生继学习几何初步知识后,进一步深化对几何图形性质和规律的理解,培养学生逻辑思维和论证能力。
本章的主要内容包括定理的定义、定理的证明、公理化体系等。
通过本章的学习,使学生掌握定理与证明的基本概念和方法,提高学生分析问题和解决问题的能力。
二. 学情分析学生在学习本章内容前,已经掌握了基本的几何知识,具备一定的逻辑思维能力。
但部分学生对抽象的逻辑论证过程可能存在理解上的困难,因此,在教学过程中需要关注这部分学生的学习情况,加强对其逻辑思维和论证能力的培养。
同时,学生对于新知识的学习兴趣和积极性较高,可以通过引导和激励,激发学生学习本章内容的兴趣。
三. 教学目标1.知识与技能:使学生掌握定理与证明的基本概念和方法,学会阅读和理解几何论证过程。
2.过程与方法:培养学生逻辑思维和论证能力,提高学生分析问题和解决问题的能力。
3.情感态度与价值观:激发学生学习几何的兴趣,培养学生的抽象思维和创新意识。
四. 教学重难点1.教学重点:定理与证明的基本概念和方法,几何论证过程的阅读和理解。
2.教学难点:定理证明的逻辑推理过程,学生逻辑思维和论证能力的培养。
五. 教学方法1.引导法:通过问题引导,激发学生思考,培养学生逻辑思维和论证能力。
2.案例分析法:分析典型几何论证案例,使学生掌握定理与证明的方法。
3.小组合作学习法:引导学生进行合作交流,共同探讨几何论证问题,提高学生分析问题和解决问题的能力。
六. 教学准备1.教学课件:制作多媒体课件,帮助学生直观地理解定理与证明的概念和方法。
2.教学案例:准备一些典型的几何论证案例,用于分析和讲解。
3.练习题:设计一些有关定理与证明的练习题,巩固所学知识。
七. 教学过程1.导入(5分钟)通过复习几何基本知识,引导学生思考几何论证的过程,引出本章内容——定理与证明。
华师大版八年级上册1命题、定理与证明课件

∵ DF 平分∠ CDO,BE 平分∠ ABO(已知),
∴∠ 1= 1 ∠ CDO,∠ 2= 1 ∠ ABO(_角__平__分__线__的__定__义_ ).
2
2
∴∠ 1= ∠ 2(等量代换).
解题秘方:根据上一步的因为条件填写下一步的根据.
感悟新知
4-1. 如图, 已知: 点A,B,C 在同一条直线上.
感悟新知
知1-练
解:条件:两个角互为补角;结论:这两个角相等. 假命题. 条件:a=b;结论:a+c=b+c. 真命题. 条件:两个长方形的周长相等;结论:这两个长方
形的面积相等. 假命题.
感悟新知
知1-练
2-1. 下列命题是真命题的是( A ) A. 如果两个角不相等,那么这两个角不是对顶角 B. 如果a2=b2, 那么a=b C. 两个互补的角一定是邻补角 D. 如果两个角是同位角,那么这两个角一定相等
知2-练
感悟新知
知识点 3 命题证明的一般步骤
知3-讲
1. 证明 根据条件、定义以及基本事实、定理等,经过演绎 推理,来判断一个命题是否正确,这样的推理过程叫做 证明.
感悟新知
知3-讲
2. 命题证明的一般步骤 第一步:分清命题的条件和结论,若命题与图形有关,则
根据题意,画出图形,并在图形上标出相关的字母和符号; 第二步:根据条件、结论,结合图形,写出已知、求证; 第三步:视察图形,分析证明思路,找出证明方法; 第四步:写出证明的过程,并注明根据.
结论不成立,像这样的命题,称为假命题.
感悟新知
知1-练
例 1 把下列命题改写成“如果……,那么……”的情势: 对顶角相等; 平行于同一条直线的两条直线平行; 同角或等角的余角相等. 解题秘方:紧扣命题的结构情势进行改写.
华师大八年级数学上册《定理与证明》课件(共15张PPT)

这个结论正确吗?是否有一个多边形 的内角Fra bibliotek不满足这 一规律?
正确
通过上面几个例子说明: 通过特殊的事例得到的结论可能正确,也可 能不正确。
因此: 通过这种方式得到的结论,还需进一步加以 证实。
证明的定义
根据条件、定义及基本事实、定理等,经过演绎 推理,来判断一个命题是否正确,这样的推理过 程叫做证明。
•3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/4/212022/4/21April 21, 2022
谢谢观赏
You made my day!
倍
速
课
时
学
练
我们,还在路上……
公理、定理、命题的关系
真命题
命题
假命题
公理(正确性由实践总结) 定理(正确性通过推理证实)
练习
1.把下列定理改写成“如果……,那么……”的形式,指出 它的条件和结论,并用逻辑推理的方法证明题(1):
(1)同旁内角互补,两直线平行;
如果两直线被第三条直线所截,同旁内角互补, 那么这两直线平行。
(2)三角形的外角和等于360°.
13.1 命题、定理与证明
复习回顾
1、什么叫命题? 表示判断的语句叫做命题。
2、命题的结构 命题由条件和结论两部分构成,常可写成“如 果……那么……”的形式
3、命题的分类 正确的命题称为真命题,错误的命题称为假命题。
4、真、假命题的判断
判断一个命题是真命题,可以用逻辑推理的方 法证明
判断一个命题是假命题,只要举出一个例子,说 明该命题不成立就可以了,这种方法称为举反例;
如果三个角分别是三角形的三个外角,那么这三 个角的和等于360°。
八年级数学上册 第13章 全等三角形13.1 命题、定理与证明 2定理与证明课件

3.经过分析,找出由已知推出求证的
途径,写出证明过程.
第十一页,共二十二页。
根据下列命题,画出图形,并结合
图形写出已知、求证(不写证明过程):
1)垂直于同一直线的两直线平行;
2)内错角相等,两直线平行;
3)一个角的平分线上的点到这个角的两边
的距离相等; 4)两条平行线的一对(yī duì)内错角的平分线互相
∴ OE⊥OF 2 第十七页,共二十二页。
如何(rúhé)判断一个命题是假命题?
只要举出一个例子(反例),
它符合(fúhé)命题的题设,但不满足 结论就可以了.
第十八页,共二十二页。
判断下列(xiàliè)命题是真命题还是假命题.
如果是假命题,举出一个反例:
1)相等的角是对顶角; 2)同位角相等;
4)两条平行线的一对(yī duì)内错角的平分线互相 平行.
已知:如图,AB、CD被直线EF所截,且
AB∥CD,EG、FH分别(fēnbié)是∠AEF和
∠EFD的平分线
求证:EG∥FH
A
E
B
G CF
第十六页,共二十二页。
H D
例2.证明(zhèngmíng):邻补角的平分线互相垂直.
已知:如图,∠AOB、∠BOC互为邻补角(bǔ , jiǎo)
c
3a
1
2
b
第九页,共二十二页。
c
证明 :∵a∥已b 知( (zhèngmíng)
∴∠3=∠2
3a
1
)2
b
(两直线平行(píngxíng),同位角相) 等
∵ ∠3=∠1 ( 对顶角相等)(xiāngděng)
∴∠1=∠2 ( 等量代换)
四川省内江市资中县板栗中心学校八年级数学上册 勾股定理的综合应用课件 华东师大版

在Rt△ABC中,
B
D
C
A D A2 B B2D 6 2 3 22 7 5 .196
∴ S C 1 2 BA C D 1 2 6 5 .1 9 1.5 6 5 1 8.6 5
例2:在等腰△ABC中,AB=AC= 13cm ,BC=10cm,求△ABC的面
积及AC边A上的高。
13
13
15
13
B
14-x
xC
14 D
及时练
如图,盒内长,宽,高分别是30米,24米和18米, 盒内可放的棍子最长是多少米?
18
24
30
及时练
如图,在△ABC中,AB=AC,D点在CB延长线上,求证:
AD2-AB2=BD·CD
A
证明: 过A作AE⊥BC于E
∵AB=AC,∴BE=CE
D
在Rt △ADE中, AD2=AE2+DE2 在Rt △ABE中, AB2=AE2+BE2 ∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)
B
AC =6–1=5 ,BC =24× =112,
A
2
由勾股定理得 AB²= AC²+ BC²=169, C
B
∴AB=13(m) .
A
即最短路线AB为13m
如图,边长为1的正方体中,一只蚂 蚁从顶点A出发沿着正方体的外表面爬到 顶点B的最短距离是_____
B
B
B
A
A
A
如图所示,现在已测得长方体木块的 长2,宽1,高3.一只蜘蛛潜伏在木块的一 个顶点A处,一只苍蝇在这个长方体上和 蜘蛛相对的顶点B处。
C
2m
D
如图,现要在此楼梯旁建造无障碍通道,经测量 每格楼梯的高为11.25cm,宽20cm,你能求出通道的 长度吗?
1勾股定理(第1课时)(教学PPT课件(华师大版))28张
1955年希腊发行的一枚纪念邮票.
讲授新课
知识点一 直角三角形三边的关系
视察正方形瓷砖铺成的地面.
(1)正方形P的面积是
1
(2)正方形Q的面积是
1
平方厘米;
(3)正方形R的面积是
2
平方厘米.
平方厘米;
上面三个正方形的面积之间有什么关系?
等腰直角三角形ABC三边长度之间存在什么关系吗?
程.
b
a
b
a
c
c
b
c
c
a
a
b
讲授新课
证明:大正方形的面积=(a+b)2.
四个个全等的直角三角形和小正方形的面积
1
2
2
之和= 4 ab c 2ab c .
2
b
由题可知(a+b)2=2ab+c2,
a
c
化简可得a2+b2=c2.
我们利用拼图的方法,将形的问题
与数的问题结合起来,再进行整式
A的面积
B的面积
C的面积
左图
4
9
13
右图
16
9
25
结论:以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.
SA+SB=SC
讲授新课
猜想:两直角边a、b与斜边 c 之间的关系?
A
a
B b
c
a2+b2=c2
C
讲授新课
概念总结
由上面的探索可以发现:对于任意的直角三角形,如果它的两
数学(华东师大版)
八年级 上册
第14章 勾股定理
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.定理:
用推理的方法得到的真命题. 3.证明:
除公理外,一个命题的正确性 需要经过推理,才能作出判断,这 个推理的过程叫做证明.
【根据最新版数学教材编写】 5
举例:
1. 公理:
1) 直线公理:过两点有且只有一条直线.
2) 线段公理:两点之间,线段最短.
3) 平行公理:
经过直线外一点,有且只有一条
已知:如图,AB、CD被直线EF所截,且
AB∥CD,EG、FH分别是∠AEF和
∠EFD的平分线
求证:EG∥FH
A
E
B
G
H
C F 【根据最新版数学教材编写】
D 16
例2.证明:邻补角的平分线互相垂直.
已知:如图,∠AOB、∠BOC互为邻补角,
OE平分∠AOB, OF平分∠BOC
求证:OE⊥OF
E
B
证明:∵OE平分∠AOB,
②垂线段最短.
5) 平行公理的推论:
如果两条直线都和第三条直线平行,
那么这两条直线【也根据互最新相版数平学行教材.编写】 7
举例:
定理:
6) 平行线的判定定理:
内错角相等,两直线平行. 同旁内角互补,两直线平行.
7) 平行线的性质定理:
两直线平行,内错角相等. 两直线平行,同旁内角互补.
【根据最新版数学教材编写】 8
典例分析
3. 证明:
例1.已知:如图,a∥b, c是截线 .
求证:∠1=∠2
c
3a 1
2b
【根据最新版数学教材编写】 9
c
证明:∵a∥b ( 已知 ) ∴∠3=∠2
1 3a 2b
(两直线平行,同位角相等)
∵ ∠3=∠1 ( 对顶角相等 )
∴∠1=∠2 ( 等量代换 )
【根据最新版数学教材编写】 10
6)不等式的两边都乘以同一个数,不 等号的方向不变;
7)在平面内,经过一点有且只有一条 直线与已知直线垂直;
8)两个锐角的和是锐角.
【根据最新版数学教材编写】 20
课后小结 (1)画图;
定 1.命题证明的 (2)写已知、求证; 理 一般步骤 (3)写推理过程. 与 证 2.命题的证明 明
3.判断假命题的方法:举反例
命题证明的步骤: 1.根据题意,画出图形; 2.根据题设、结论,结合图形,写出
已知、求证; 3.经过分析,找出由已知推出求证的
途径,写出证明过程.
【根据最新版数学教材编写】 11
根据下列命题,画出图形,并结合
图形写出已知、求证(不写证明过程):
1)垂直于同一直线的两直线平行;
2)内错角相等,两直线平行;
∴∠1=
1OF平分∠BOC 2∠AOB, ∠2=
1 2
A ∠BOC
又∠AOB、∠BOC互为邻补角
12 F OC
∵ ∠AOB+∠BOC=180°
∴∠1+∠2= 1 (∠AOB+∠BOC)=90°
∴ OE⊥OF 2
【根据最新版数学教材编写】 17
如何判断一个命题是假命题?
只要举出一个例子(反例), 它符合命题的题设,但不满足 结论就可以了.
且∠1=∠2 求证:a∥b
c
1
a
2b
【根据最新版数学教材编写】 14
3)一个角的平分线上的点到这个角的两边 的距离相等;
已知:如图,OC是∠AOB的平分线,
EF⊥OA于F ,
A F
EG⊥OB于G O
EC
求证:EF=EG
G B 【根据最新版数学教材编写】 15
4)两条平行线的一对内错角的平分线互相 平行.
【根据最新版数学教材编写】 18
判断下列命题是真命题还是假命题. 如果是假命题,举出一个反例:
1)相等的角是对顶角; 2)同位角相等; 3)邻补角是互补的角; 4)互补的角是邻补角; 5)如果一个数能被2整除,那么这个数
也能被4整除; 【根据最新版数学教材编写】 19
判断下列命题是真命题还是假命题. 如果是假命题,举出一个反例:
2.如果两个角是同位角,那么这两个
角相等;×
3.两条直线被第三条直线所截,如果 同旁内角互补,那么这两条直线平
行;√
4.如果两个角互补,那么它们是邻补
角;× √ 5.垂直于同一条直【根线据的最新两版数直学教线材编平写】行. 4
1.公理:
推进新课
人们在长期实践中总结出来的,
并作为判定其他命题真假的根据.
【根据最新版数学教材编写】 2
命题
1.定义: 判断一件事情的语句.
2.构成:
1)每个命题都是由题设、结论两部分组成.
2)命题常写成“如果······那么······”的形 式3.分. 类: 1)真命题:正确的命题; 2)假命题:错误的命题.
【根据最新版数学教材编写】 3
判断下列命题的真假:
1.过两点有且只有一条直线;√
【根据最新版数学教材编写】 21
课后作业
• 完成练习册本课时对应习题
【根据最新版数学教材编写】 22
学习要注意到细处,不是粗枝大叶的, 以逐步学习摸索,找到客观规律。 — 立
【根据最新版数学教材编写】 23
同学们下课啦
授课老师:xxx
同学们下课啦
授课老师:xxx
直线与已知直线平行.
4) 平行线判定公理:
同位角相等,两直线平行.
5) 平行线性质公理:
两直线平行,同【根位据最角新版相数等学教.材编写】 6
举例:
2. 定理:
1) 补角的性质:同角或等角的补角相等.
2) 余角的性质:同角或等角的余角相等. 3) 对顶角的性质:对顶角相等
4) 垂线的性质:
①过一点有且只有一条直线与已知直线垂直;
2.定理与证明
【根据最新版数学教材编写】 1
新课导入
在现代哲学、数学、逻辑学、语言学中,命题是 指一个判断(陈述)的语义(实际表达的概念),这 个概念是可以被定义并观察的现象。命题不是指判断 (陈述)本身,而是指所表达的语义。当相异判断 (陈述)具有相同语义的时候,他们表达相同的命题。 在数学中,一般把判断某一件事情的陈述句叫做命题。
3)一个角的平分线上的点到这个角的两边
的距离相等;
4)两条平行线的一对内错角的平分线互相
平行.
【根据最新版数学教材编写】 12
1)垂直于同一直线的两直线平行;
已知:直线b⊥a , c⊥a
求证:b∥c
bc
a
【根据最新版数学教材编写】 13
2)内错角相等,两直线平行;
已知:如图,直线a、b被直线 c所截,
