五年级奥数课件-数的整除全国通用
数的整除课件
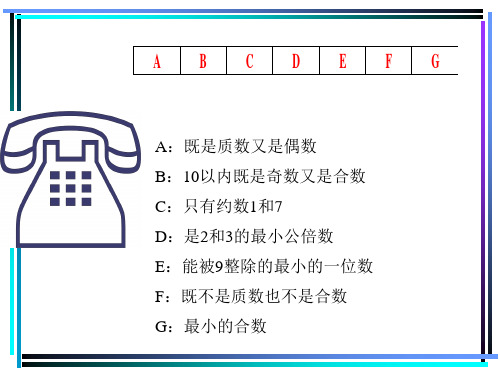
最少有3个约数
公约数只有1的两个数，叫做互质数
互质数和质数之间有什么区别?
互质数讲的是两个数的关系,这两个数的 公约数只有1.
公约数只有1的两个数，叫做互质数
互质数和质数之间有什么区别?
互质数讲的是两个数的关系,这两个数的 公约数只有1. 质数是对一个自然数而言的,它只有1和它 本身两个约数.
整除
倍数 约数
公倍数 最小公倍数 公约数 最大公约数
质数
互质数 合数
质因数 分解质因数 能被2整除数的特征 能被5整除数的特征 能被3整除数的特征
奇数 偶数
整数a除以整数b（b≠ 0），除得的商正好 是整数而没有余数，我们就说a 能被b整除（也 可以说b 能整除a ）
填空：在12÷ 3＝ 4 4 ÷ 8＝ 0.5 2÷ 0.1＝ 20 3.2 ÷ 0.8＝ 4中，被除数能除尽除数的有（ 4 ）个， 被除数能整除除数的有（ 1 ）个，是（12÷ 3＝ 4 ）．
两个数是互质数,最小公倍数 就是它们的乘积.
几个数公有的倍数，叫做这几个数的公倍数； 其中最小的一个叫做最小公倍数．
特殊情况
两个数是互质数,最小公倍数 就是它们的乘积.
几个数公有的倍数，叫做这几个数的公倍数； 其中最小的一个叫做最小公倍数．
特殊情况
两个数是互质数,最小公倍数 就是它们的乘积.
两个数具有约倍关系,最小公倍数 就是较大的数.
个位上是0、2、4、6、8的数，都能被2整除.
个位上是0或者5的数，都能被5整除.
一个数的各位上的数的和能被3整除,这个数就 能被3整除.
个位上是0、2、4、6、8的数，都能被2整除.
数的整除课件
如果一个数能被另一个数整除，则它们的最大公约数等于被除数与 商的最大公约数。
最大公约数的整除应用
在数学、计算机科学等领域中，最大公约数的整除性质有着广泛的 应用。
最小公倍数的整除
01
最小公倍数的定义
两个或多个整数的最小正整数倍数。
02
最小公倍数的整除性质
如果一个数能被另一个数整除，则它们的最小公倍数等于被除数与商的
在计算机科学中的应用
在计算机科学中，整除的概念也具有广 泛的应用。例如，在计算机算法中，整 除的概念可以帮助我们快速准确地完成
各种计算和数据处理任务。
在计算机图形学中，整除的概念也经常 被用到。例如，当我们需要将图像分成 若干等份时，整除的概念可以帮助我们 确保每个图像的像素和比例都是相同的
。
在网络安全领域，整除的概念也具有广 泛的应用。例如，在加密算法中，整除 的概念可以帮助我们快速准确地完成各
者进行练习。
1. 题目
2. 题目
3. 题目
判断以下哪个数字可以 被7整除：14、28、35
、42。
一个数被12整除，那么 这个数的个位数字是多
少？
如果一个数除以8的余数 是5，那么这个数是多少
？
进阶练习题
总结词
这些题目难度稍有提升，需要 掌握一些整除的性质和规律。
1. 题目
求出以下数字的最大互质数的整除
互质数的整除
如果两个数的最大公约数为1，则它 们互质，互质数的两数相除，商为1 。
互质数的整除性质
互质数的整除应用
在数学、计算机科学、密码学等领域 中，互质数的整除性质有着广泛的应 用。
互质的两个数相乘，其积能被这两个 数整除。
小学五级奥数数的整除特征 ppt课件
• 回忆：能被3（或9）整除的数的特征：
• 各个数位数字的和能被3（或9）整除。
• 解：1＋2＋3＋4＋5＋6＋7＋8＋9＋1＋0＋1 ＋1＋1＋2＋1＋3＋1＋4＝60
•
因为 3 60 9 60
• 所以这个数∣ 能被3整除而不能被9整除。
• 答：这个数能被3整除而不能被9整除。
ppt课件
16
应用举例（二）根据规律填空
8
数的整除性质4
• 4、我们最后再看一个问题：
• 如果c能整除b，b能整除a，那么c一定
能整除a吗？
• 自己出几个题目试试？
• 7能整除14，14能整除140，那么，7能 整除140吗？ 能
•
9能整除18，18能整除54，那么，9能
整除54吗？ 能
pptቤተ መጻሕፍቲ ባይዱ件
9
数的整除性质4
• 性质4： • 如果c能整除b，b能整除a，那么c能整除a。 • 即：如果c︱b ， b︱a 那么 c︱a。
答：满足条件的六位数是 519930或
。 919935
ppt课件
17
• （2）李老师为学校一共买了28支价格相同 的钢笔，共付人民币9□.2□元，已知□处 数字相同，请问：每支钢笔多少元？
ppt课件
3
数的整除性质1
• 性质1：
•
如果a、b都能被c整除，那么他们的
和或差也能被c整除。
• 即：如果c︱a ， c︱b 那么 c︱（a±b ）
• 你能再举出一个例子吗？
ppt课件
4
数的整除性质2
• 2、我们再来看一组例子：
• ① 15能整除45，3×5＝15，3和5都能整除 45吗？
• ② 3×7＝21，21能整除84，3和7都能整除 84吗？
小学五年奥数-数的整除
数的整除【知能大展台】1. 整除的概念对于整数a和不为零的整数b,如果数a除以数b的商是整数且没有余数，我们就说a能被b整除，b能整除a,记作b|a;a叫做b的倍数，b叫做a 的约数。
2. 数的整除性质①如果数a能被数C整除，数b也能被数C整除，那么它们的和(a+b)或差(a-b)也能被C整除c∣a,c∣b ,贝U CIa ±bo②几个整数相乘，如果其中有一个因数能被某一个数整除，则这几个数的积也能被这个数整除。
③数a能被数b整除，数a也能被数C整除，如果b,c互质，那么数a能被b与C的积整除。
3. 数的整除特征①一个整数的末一位数能被2或5整除，那么这个数就能被2或5整除②一个整数的末两位数能被4或25整除，那么这个数就能被4或25整除③一个整数的末三位数能被8或125整除，那么这个是就能被8或125整除④一个整数的各数位上数字的和能被3或9整除，那么这个数就能被3或9整除⑤一个整数的奇数位（指个位，百位，万位……）上的数字之和与偶数位（指十位，千位，十万位……）上的数字之和的差能被11整除，那么这个数就能被“整除⑥一个整数的末三位数与末三位数以前的数字组成的数的差能被7,"或13整除，那么这个数就能被7,"或13整除【试金石】例1 •小马虎在一张纸上写了一个无重复数字的五位数；3□6□5,其中十位数字和千位数字看不清楚了，但是已知这个数是75的倍数，那么满足上述条件的五位数中，最大的一个是多少？【分析】因为五位数3□6□5能被75整除，而75=3×25, 3与25互质。
所以3□6□ 5能同时被3和25整除。
3□6□5能被25整除，由于末尾是5,所以十位数字只能是2或7,即末两位数只能是25或75o当末两位数是25时，3□625呢功能被3整除，起各位数字之和必须能被 3 整除，则千位数字只能是2, 5, 8,而这些五位数中最大的一个是38625,且无重复数字。
五年级秋学期奥数 第5讲：数的整除性
第5讲：数的整除性灵活地运用整除性质，可以解决许多有关整除方面的问题。
一些特殊数整除的特征：1．个位是0、2、4、6、8的数能被2整除。
2．个位是0或5的数能被5整除。
3．各位数字之和能被3或9整除的数就能被3或9整除。
4．如果一个数的末两位数能被4或25整除，那么这个数就能被4或25整除。
5．如果一个数的末三位数能被8或125整除，那么这个数就能被8或125整除。
6．被11整除的数的特征：如果一个自然数的奇数位上数字和与偶数位上数字和的差（大数减小数）能被11整除，那么这个自然数就能被11整除，否则就不能。
7．能被7、11、13整除的数的特征：这个数的末三位数与末三位以前的数字所组成的数的差，如果这个差能被7、11、13整除，那么这个数就能被7、11、13整除。
学习例题：例1：在五位数15□8□的方框里填上什么数字，才能使它既能被3整除，又含有约数5？3是6的倍数，这样的六位数共有多少个？例2：六位数ABABA例3：在568后面补上三个数字，组成一个六位数，使它分别能被3、4、5整除。
符合这些条件的六位数中，最小的一个是多少？例4：五位数B A 329能被72整除。
问A 和B 各代表什么数字？例5：六位数B A 3412是88的倍数，这个数除以88所得的商是什么？例6．在五位数中，数字和等于43且能被11整除的数有哪些？思考与练习：1． 有一个四位数13AA ，它能被9整除。
A 所代表的数字是多少？2． 在2008后面填上三个数字，组成一个新七位数，使它分别能被除3、4、5整除，这个七位数最大是多少？3．173□是一个四位数，王老师说：“我在这个数的方框里分别填上3个数字，所得的四位数依次能被7、11、6整除。
”王老师填入的3个数字的和是多少？4．已知87654321□□这个十位数能被36整除，那么这个数个位上的数字最小是多少？5．用0、1、3、5、7这五个数字中的四个，可以组成许多能被11整除的四位数，其中最小的一个四位数是多少？6.将一个四位数减去各数位上数字的和后仍得一个四位数，19□2，那么□中应该填多少？7.六位数□1991□能被33整除，这样的六位数是多少？8.有0、1、4、7、9五个数字，从中选出四个数字组成不同的四位数，如果把其中能被3整除的四位数从小到大排列起来，第五个数的是多少?9.在一个两位数的数字之间加一个0，所得的三位数比原数大8倍，求这个数。
5奥 第5讲 数的整除
第五讲 数的整除例1， 有0，1，4，7，9五个数字，从中选出四个数字组成不同的四位数，如果把其中能被3整除的三位数从小到大排列起来，第五个数的末位数字是几？例2， 在五位数15□8□的□内填什么数字，才能使它既能被3整除，又含有约数5？例3， 有一个首位数字为8的五位数，它能被9整除，且各位数字均不相同，问这样的五位数最小是几？例4， 已知整数1X2X3X4X5能被11整除，求所有满足这个条件的整数。
例5， 在算式abcde 1×3=1abcde 中，不同的字母表示不同的数字，相同的字母表示相同的数字，求abcde .例6， 某小学五年级学生张明做数学题时发现“任意一个三位数，连着写两次得到一个六位数，这个六位数一定同时能被7、11、13整除”。
这个结论你会证明吗？例7， 将三位数3ab 接连重复地写下去，共写1993个3ab ，所得的数3ab3ab3ab ….3ab(1993个3ab)正好是91的倍数，试求ab=？例8， 下面这个四十一位数55……5□99……9(其中5和9各有20个)能被7整除。
那么中间方格内的数字是几？例9， 如果六位数1993□□能被105整除，那么，它的最后两位数是多少？例10， 在下面的方框中各填入一个数字，使这个六位数能被17和19整除。
那么，方框中的两位数“□□”是多少？ 11□□11练习1.一个六位数586□□□能同时被3、4、5整除，求这样的六位数中最小的一个。
2.在□内填上合适的数字，使□679□能同时被8、9整除。
3.有一个四位数是45ab，同时能被2、3、4、5、9整除，求出这个四位数。
4.李老师为学校一共买了28支价格相同的钢笔，共付人民币9□.2□元。
已知□处数字相同，请问每支钢笔多少元？5.求出所有能被3整除的两位数的和。
6.已知六位数□8919□能被33整除，那么这个六位数是多少？7.小马虎在一张纸上写了一个无重复数字的五位数9□4□5，其中十位数字和千位数字都看不清了，但是已知这个数能被75整除，那么满足上述条件的五位数中，最大的一个是多少？8.在25□79这个数的□内填上一个数字，使这个数能被11整除，方格内应填多少？。
五年级下册数学奥数讲义—第十三讲数的整除通用版
数的整除一、常见数字的整除判定方法1. 一个数的末位能被2或5整除，这个数就能被2或5整除；一个数的末两位能被4或25整除，这个数就能被4或25整除；一个数的末三位能被8或125整除，这个数就能被8或125整除；2. 一个位数数字和能被3整除，这个数就能被3整除；一个数各位数数字和能被9整除，这个数就能被9整除；3. 如果一个整数的奇数位上的数字之和与偶数位上的数字之和的差能被11整除，那么这个数能被11整除.4. 如果一个整数的末三位与末三位以前的数字组成的数之差能被7、11或13整除，那么这个数能被7、11或13整除.5.如果一个数能被99整除，这个数从后两位开始两位一截所得的所有数（如果有偶数位则拆出的数都有两个数字，如果是奇数位则拆出的数中若干个有两个数字还有一个是一位数）的和是99的倍数，这个数一定是99的倍数。
【备注】（以上规律仅在十进制数中成立.）二、整除性质性质1 如果数a和数b都能被数c整除，那么它们的和或差也能被c整除．即如果c︱a，c︱b，那么c︱(a±b)．性质2 如果数a能被数b整除，b又能被数c整除，那么a也能被c整除．即如果b∣a，c∣b，那么c∣a．用同样的方法，我们还可以得出：性质3 如果数a能被数b与数c的积整除，那么a也能被b或c整除．即如果bc∣a，那么b∣a，c∣a．性质4 如果数a能被数b整除，也能被数c整除，且数b和数c互质，那么a一定能被b与c的乘积整除．即如果b∣a，c∣a，且(b，c)=1，那么bc∣a．例如：如果3∣12，4∣12，且(3，4)=1，那么(3×4) ∣12．性质5 如果数a能被数b整除，那么am也能被bm整除．如果b｜a，那么bm｜am（m为非0整数）；性质6 如果数a能被数b整除，且数c能被数d整除，那么ac也能被bd整除．如果b｜a ，且d｜c ，那么bd｜ac；1. 2和5例：把若干个自然数1、2、3、……连乘到一起，如果已知这个乘积的最末十三位恰好都是零，那么最后出现的自然数最小应该是多少？解：乘积末尾的零的个数是由乘数中因数2和5的个数决定的，有一对2和5乘积末尾就有一个零．由于相邻两个自然数中必定有一个是2的倍数，而相邻5个数中才有一个5的倍数，所以我们只要观察因数5的个数就可以了．，，发现只有25、50、75、100、……这样的数中才会出现多个因数5，乘到55时共出现个因数5，所以至少应当写到55。
《数的整除总复习》课件
整除与分治策略在数学中有着广泛的应用。例如，在求解最大公约数和最小公倍数时，常常采用分治 策略，将问题分解为更小的部分，分别求解后再合并结果。这种方法能够简化问题，提高解题效率。
整除与数论的关系
总结词
数论是研究整数的性质和结构的数学分 支，整除是数论中的一个基本概念。
VS
详细描述
整除是数论中的一个核心概念，它是整数 的一个基本性质。通过研究整除的性质和 规律，可以深入了解整数的结构，进一步 探索数论中的其他问题。同时，整除也为 密码学、计算机科学等领域提供了重要的 理论基础和应用价值。
05
数的整除拓展
整除与同余式
总结词
同余式是整除的一种扩展，它描述了整数在模运算下的等价关系。
详细描述
同余式是数论中的一个重要概念，它表示两个或多个整数在模运算下具有相同 的余数。整除是同余式的一个特例，即当模数为1时，如果一个数a能被另一个 数b整除，则a与b模1同余。
整除与分治策略
总结词
分治策略是将复杂问题分解为若干个简单子问题，通过解决子问题来达到解决原问题的目的。
逻辑推理
03
利用整除性质进行逻辑推理是解决一些数学竞赛问题的重要方
法。
在日常生活中的应用
购物优惠
商家经常使用整除点来设置商品价格，以提供优 惠或促销活动。
时间计算
在日程安排和时间管理中，整除常用于计算时间 间隔或确定特定时间点。
金融计算
在投资和理财方面，整除在计算复利、评估风险 和制定预算时非常有用。
整除的唯一分解定理
总结词
整除的唯一分解定理是指，一个正整数可以表示为若干个质数的乘积，并且这种 表示方法是唯一的。
详细描述
这是整除的一个重要定理，它告诉我们一个正整数可以分解为若干个质数的乘积 ，而且这种分解方式是唯一的。这个定理在数学中有着广泛的应用，因为它可以 帮助我们更好地理解整数的结构，并解决与整数有关的数学问题。
五年级奥数-数的整除
数的整除如果整除a除以不为零数b，所得的商为整数而余数为0，我们就说a能被b整除，或叫b能整除a。
如果a能被b整除，那么，b叫做a的约数，a叫做b的倍数。
数的整除的特征：（1）能被2整除的数的特征：如果一个整数的个位数字是2、4、6、8、0，那么这个整数一定能被2整除。
（2）能被3（或9）整除的数的特征：如果一个整数的各个数字之和能被3（或9）整除，那么这个整数一定能被3（或9）整除。
（3）能被4（或25）整除的数的特征：如果一个整数的末两位数能被4（或25）整除，那么这个数就一定能被4（或25）整除。
（4）能被5整除的数的特征：如果一个整数的个位数字是0或5，那么这个整数一定能被5整除。
（5）能被6整除的数的特征：如果一个整数能被2整除，又能被3整除，那么这个数就一定能被6整除。
（6）能被7（或11或13）整除的数的特征：一个整数分成两个数，末三位为一个数，其余各位为另一个数，如果这两个数之差是0或是7（或11或13）的倍数，这个数就能被7（或11或13）整除。
（7）能被8（或125）整除的数的特征：如果一个整数的末三位数能被8（或125）整除，那么这个数就一定能被8（或125）整除。
（8）能被11整除的数的特征：如果一个整数的奇数位数字之和与偶数位数字之和的差（大减小）能被11整除，那么它必能被11整除。
一、例题与方法指导例1. 一个六位数23□56□是88的倍数,这个数除以88所得的商是_____或_____.思路导航：一个数如果是88的倍数,这个数必然既是8的倍数,又是11的倍数.根据8的倍数,它的末三位数肯定也是8的倍数,从而可知这个六位数个位上的数是0或8.而11的倍数奇偶位上数字和的差应是0或11的倍数,从已知的四个数看,这个六位数奇偶位上数字的和是相等的,要使奇偶位上数字和差为0,两个方框内填入的数字是相同的,因此这个六位数有两种可能或又 23056088=2620238568÷88=2711所以,本题的答案是2620或2711.例2. 123456789□□,这个十一位数能被36整除,那么这个数的个位上的数最小是_____.思路导航：因为36=9⨯4,所以这个十一位数既能被9整除,又能被4整除.因为1+2+…+9=45，由能被9整除的数的特征，（可知□+□之和是0（0+0）、9（1+8，8+1，2+7，7+2，3+6，6+3，4+5，5+4）和18（9+9）.再由能被4整除的数的特征:这个数的末尾两位数是4的倍数,可知□□是00,04,…，36，…，72，…96.这样,这个十一位数个位上有0,2,6三种可能性.所以,这个数的个位上的数最小是0.例3. 下面一个1983位数33…3□…4中间漏写了一个数字(方框),已 991个 991个知这个多位数被7整除，那么中间方框内的数字是_____.思路导航：33...3□44 (4)991个个=33...3⨯10993+3□4⨯10990+44 (4)990个 990个因为111111能被7整除，所以33…3和44…4都能被7整除,所以只要个个3□4能被7整除，原数即可被7整除.故得中间方框内的数字是6.例4. 有三个连续的两位数,它们的和也是两位数,并且是11的倍数.这三个数是_____.思路导航：三个连续的两位数其和必是3的倍数,已知其和是11的倍数,而3与11互质,所以和是33的倍数,能被33整除的两位数只有3个,它们是33、66、99.所以有当和为33时,三个数是10,11,12；当和为66时,三个数是21,22,23；当和为99时,三个数是32,33,34.所以，答案为 10,11,12或21,22,23或32,33,34。
数的整除PPT课件.ppt
特殊情况
两个数是互质数,最小公倍数 就是它们的乘积.
பைடு நூலகம்
两个数具有约倍关系,最小公倍数 就是较大的数.
一个数，如果只有1和它本身两个约数，这样的 数叫做质数（或素数）．
只有两个约数
一个数，如果除了1和它本身还有别的约数，这 样的数叫做合数．
一个数，如果只有1和它本身两个约数，这样的 数叫做质数（或素数）．
如果数a能被数b（b≠ 0）整除， a就叫做b的 倍数， b就叫做a的约数（或a 的约数）
因为15 ÷ 5＝ 3，所以15是倍数，5是约数（×）
约数和倍数是相互依存的
因为4.6 ÷ 2＝ 2.3，所以4.6是2的倍数，2是4.6 的约数（×）
如果数a能被数b（b≠ 0）整除， a就叫做b的 倍数， b就叫做a的约数（或a 的约数）
几个数公有的倍数，叫做这几个数的公倍数； 其中最小的一个叫做最小公倍数．
特殊情况
两个数是互质数,最小公倍数 就是它们的乘积.
几个数公有的倍数，叫做这几个数的公倍数； 其中最小的一个叫做最小公倍数．
特殊情况
两个数是互质数,最小公倍数 就是它们的乘积.
几个数公有的倍数，叫做这几个数的公倍数； 其中最小的一个叫做最小公倍数．
数的整除
整除
倍数 约数
公倍数 最小公倍数 公约数 最大公约数
质数 合数 互质数
质因数 分解质因数 能被2整除数的特征
能被5整除数的特征 能被3整除数的特征
奇数
整除
倍数 约数
公倍数 最小公倍数 公约数 最大公约数
质数 合数 互质数
质因数 分解质因数 能被2整除数的特征 能被5整除数的特征 能被3整除数的特征
一个数的各位上的数的和能被3整除,这个数就 能被3整除.
小学五年级奥数-数的整除特征课件
数的整除性质3
我们看下面的例子： 4能够整除36，6也能整除36，4与6的积能整除36吗？ 4能够整除80，5也能整除80，4与5的积能整除80吗？ 5能够整除80，8也能整除80，5与8的积能整除80吗？ 这说明这两个数需要满足一定的条件！
数的整除性质1
性质1： 如果a、b都能被c整除，那么他们的和或差也能被c整除。 即：如果c︱a ， c︱b 那么 c︱（a±b） 你能再举出一个例子吗？
数的整除性质2
我们再来看一组例子：
添加标题
01
3×7＝21，21能整除84，3和7都能整除84吗？
添加标题
03
上面的3个例子有什么共同点？
添加标题
∣
01
02
应用举例（二）根据规律填空
例2、⑴ 已知45︱ 求所有满足条件的六位数。
5
9
519930
李老师为学校一共买了28支价格相同的钢笔，共付人民币9□.2□元，已知□处数字相同，请问：每支钢笔多少元？
分析：由28支钢笔的价格相同可知，总钱数9□.2□是28 的倍数，同上面的解题思路类似，可以用数的整除性质和数的整除特征结合起来解答。
分别能被2 3、5、11整除，这个七位数最小值是多少？
6、在1992后面补上三个数字，组成一个七位数，使它们
02
能被11整除, 方格内应填_____。
5、“25□79这个数的□内填上一个数字,使这个数
01
∣
∣
33333333468375能不能被125整除 回忆：能被125整除的数的特征： 末三位数字能被125整除。 解： 因为这个数的末三位数字375能被125整除，所以33333333468375能被125整除。
五年级(奥数) 数的整除
五年级数的整除
1、有三根铁丝，分别长12厘米、18厘米、54厘米。
要把它们都截成同样长的小段不许剩余，每段最长是多少厘米？一共能截多少段？
2、五年级三个班分别有24人、36人、42人参加体育锻炼，要把它们分成人数相等的小组，但各班同学不能打乱。
最多每组多少人？每班各分多少组？
3、一张长方形纸长112厘米，宽80厘米，把它剪成若干个同样大小的正方形，使边长是
整厘米且不能有剩余，最少能剪多少个？
4、用长16厘米，宽14厘米的长方形木板来拼成一个正方形，最少需要用这样的木板多
少块？
5、张妮有若干张画片，7张一数还余4张，5张一数又少3张，3张一数正好。
问：张妮
至少有多少张画片？
6、五年级两个班的学生一起排队去做操，如果9人排一队，多出一人；如果10人排一队，同样多出一个人。
这两个班最少共有多少人？
7、有一篮鸡蛋，每按4个一堆分多一个；按5个一堆分多1个；按每6个一堆分也多1个。
这篮鸡蛋至少有多少个？
8、一个四位数9□2□既有约数2，又是3的倍数，同时又能被5整除。
这个四位数最大是什么？
9、六位数“568□□□”能同时被2、3、5整除。
求这样的六位数中最小的一个是多少？。
《数的整除》PPT课件
公倍数,最小公倍数: 几个数公有的倍数,叫做这几个数的公倍数, 其中最小的一个叫做这几个数的最小公倍 数.
例:(12,24,36 …)都是4和6的公倍数,(12 )是4和6的最小公倍数.
互质数: 公约数只有1的两个数叫做互质数.
2.因数和倍数
如果数a能被数b整除(b≠0),a就叫做b的倍 数,b就叫做a的因数.
因数
一个数的因数的个数是有 限的,其中最小的因数是1, 最大的因数是它本身.
倍数
一个数的倍数的个数是无 限的,其中最小的倍数是它 本身,没有最大的倍数.
因数和 倍数是 相互依 存的
.
3
3. 能被2.3.5整除的数的特征
合数。
()
×
⒑质数的全部约数之和一定是这个质数的
后继数。
()
√
.
13
二、巩固概念
1. 最小自然数是（ ） 2. 最小质数是（ ） 3. 最小合数是（ ） 4. 10以内的最大奇数是（ ） 5. 5的最小倍数是（ ） 6. 3的最大约数是（ ） 7. 7与3的最小公倍数是( ) 8.一个合数的约数有（ ）
.
10
奇数
偶数 能被2、3、5整除数的特征
互质 数
因数
整除
倍数
公因数 质数 合数
1 公倍数
最大公因数 质因数 分解质因数
最小公倍数
自然数（不包括0）
.
11
综合练习
一、判断题:(并将错题改正)
⒈因为3.2÷0.8=4,所以3.2能被0.8整除。
()
×
⒉把30分解质因数是30=2×3×5×1。×( )
奥数专题——数的整除特性PPT课件
能被整除的数的特征
2或5 4或25 8或125
末位数能被2或5整除 末两位数能被4或25整除 末三位数能被8或125整除
7、11、13 一个整数的末三位与末三位以前 的数字组成的数的差能被7，11或 13整除
.
14
.
15
数的整除特征
奥数专题
下列数字哪些能被2整除，哪些能被5 整除？
① 125，②756， ③1011， ④2450， ⑤7855 ,⑥8104，⑦9152，⑧70975
能被2整除：②、④、⑥、⑦ 能被5整除：①、④、⑤、⑧
.
2
（一）数的整除特性：
如果具有某个条件的数，都能被 整数b整除，反过来，能被b整除的 数，都具有这个条件，那么这个条 件就叫做被b整除的数的特征.
.
3
（二）数的整除特征 1.能被2或5整除的数的特征是： 这个数的末 一位能被2或5整除. 2.能被4或25整除的数的特征是： 这个数的末两位能被4或25整除. 3. 能被8或125整除的数的特征是： 这个数的末三位能被8列整数 ①53728， ②375， ③1011， ④328925，⑤8421862，⑥8150， ⑦73600，⑧309108.
（3）能被8整除的最小四位数是
，
最大三位数
..
.
7
练习1
（2）当m＝ 7 时，能被25整除.
（3）能被4整除的最大四位数___9996__.
（4）能被8整除的最小四位数是 1000 ，
最大三位数 992
..
.
8
（二）数的整除特征
1.能被2或5整除的数的特征是：
这个数的末 一位能被2或5整除.
2.能被4或25整除的数的特征是：
五年级奥数-数的整除问题
五年级奥数-数的整除问题介绍本文档将涵盖五年级奥数中与数的整除问题相关的内容。
数的整除是数学中的一项基本概念，它在解决实际问题和数学推理中起着重要的作用。
数的整除定义两个整数a和b，若存在整数c，使得c * b = a，则称a能被b 整除，记作b|a。
其中a称为被除数，b称为除数，c称为商。
整除的特性1. 如果a能被b整除，那么a的所有倍数也能被b整除。
2. 如果a能被b整除，b能被c整除，那么a也能被c整除。
3. 如果a能被b整除，b能被a整除，那么a和b相等。
判断一个数能否被另一个数整除的方法1. 试除法：从除数的最小可能取值开始逐步增加，直到找到一个能整除被除数的除数或者超过了被除数的一半。
如果找到了能整除的除数，则其为被除数的因数；否则，被除数为质数。
试除法：从除数的最小可能取值开始逐步增加，直到找到一个能整除被除数的除数或者超过了被除数的一半。
如果找到了能整除的除数，则其为被除数的因数；否则，被除数为质数。
2. 质因数分解法：将被除数和除数都进行质因数分解，然后比较它们的质因数是否相同。
如果除法相同，则说明除数能够整除被除数；否则，不可整除。
质因数分解法：将被除数和除数都进行质因数分解，然后比较它们的质因数是否相同。
如果除法相同，则说明除数能够整除被除数；否则，不可整除。
数的整除问题的应用数的整除问题在实际生活和数学中都有广泛的应用，例如：1. 分配问题：将一定数量的物品平均分给每个人，需要确定每个人能够得到多少个物品，就需要解决数的整除问题。
2. 判断质数：质数是只能被1和自身整除的数，通过判断能否被其他数整除，可以检验一个数是否为质数。
3. 数论问题：在数论研究中，数的整除问题是一个重要的主题，涉及到数的性质和结构等方面。
总结数的整除是五年级奥数中的基本概念之一，通过研究整除的定义、特性和判断方法，可以解决实际问题和进行数学推理。
在实际生活和数学领域中，数的整除问题有着广泛的应用，我们应该加强对该概念的理解和掌握。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
五年级奥数课件-数的整除 全国通用
五位数A691B能被55整除，符合要求的五位数 有哪些?
分析与解答: A691B 能被55整除，也就是A691B能分别被5 和11整除，这个数可能是A46910和A6915,依据能被11整除的 数的特征，当B=0时，(A+9+0)与(6+1)的差应是11的倍数， 从而确定A=9，那么这个五位数就是96910;当B=5时， (A+9+5)与(6+1)的差也应是11的倍数，从而确定A=4，这个 五位数是46915。 答:符合要求的五位数是96910和46915。
数的整除是整数内容最基本的问题。本讲内容较为抽象， 同学们可以通过型例题的学习和练习的变式训练提高数感， 做到有条理பைடு நூலகம்有根据地思考。
解题时应掌握以下 整除的性质和特征
数的整除性质
性质1:如果a、b都能被c整除，那么它们的和与差也 能被 c整除。{a÷c;b ÷c;(a+b) ÷c} 性质2:如果b与c的积能整除a,那么b与c都能整除a。 性质3:如果b、c都能整除a,且b与c互质，那么b与c的 积也能整除a。
=abc x1001 =abcx7x11x13 所以，这个六位数一定能同时被7、11、13整除的说法 是正确的。
4、一个五位数能被72整除，首尾两个数字不知道， 千、百、十位上的数字分别是6、7、9，这个五位数 是多少?
能被72整除的数一定可以被9整除，所以这五个数的和能被9整除。 设首位数为x，末位数为y, 6+7+9=22，所以x+y的和只能是5或14， 能被72整除的数也一定能被4整除所以末两位能被4整除，末位数 只能是2或者6，代入验算，这个五位数只能是36792
五年级奥数课件-数的整除 全国通用
性质4:如果c能整除b,b能整除a,那么c也能 整除a。 性质5:a个连续的自然数中必然有一个数 能被a整除。
五年级奥数课件-数的整除 全国通用
五年级奥数课件-数的整除 全国通用
数的整除特征
(1)一个整数的个位上的数能被2 (或5)整除，这个数 就能被2 (或5)整除。 (2)一个整数的末两位数能被4(或25)整除，这个数 就能被4(或25)整除。 (3)一个整数的末三位数能被8(或125)整除， 这个数 就能被8(或125)整除。
五年级奥数课件-数的整除 全国通用
五年级奥数课件-数的整除 全国通用
2、有一个四位数7A2B能被2、3、5整除，这个 四位数是多少?
如果7A2B能被2和5整除，可知它的个位一定是0，即B=0。 要使7A20能被3整除，7+A +2 +0的和应能被3整除， 当A取0、3、6、9时，7A20各位数字的和能被3整除。 这样的四位数有7020、7320、7620、7920。
( 100000 +x) x3=10x+ 1 300000 +3x= 10x + 1 7x = 299999 x =42857
五年级奥数课件-数的整除 全国通用
五年级奥数课件-数的整除 全国通用
一个六位数2356ab是22的倍数，那么这个六位数可 能是多少?
五年级奥数课件-数的整除 全国通用
五年级奥数课件-数的整除 全国通用 五年级奥数课件-数的整除 全国通用
5、有0、1、4、7、9五个数字，从中选出四个数字，组 成不同的四位数，如果把其中能被3整除的四位数从小 到大排列起来，第五个数是几?
根据能被3整除的数的特征，选出的四个数字之和应是3的倍 数。这样共有两种选法: 0、1、4、7和1、4、7、9。 第一种选法组成的四位数从小到大依次为: 1047、1074、1407、1470、1700..... 第二种选法组成的四位数从小到大依次为: 1479、14971749、1 794、1947.. 所以第五个数是1479。
6、在算式1abcde X 3 =abcde1中不同的字母表示不同 的数字，相同字母表示相同的数字，求abcde。
五年级奥数课件-数的整除 全国通用
方法一: 用逐步推理的方法，利用末位数字的特点得出结论。 由于ex3的末位数字为1，所以e=7; dx3 +2=? 7,于是dx 3=? 5，确定d=5; (cx3+1=? 5,确定c=8; bx3+2=? 8,确定b=2;i x3=? 2，确定a=4。所以abcde = 42857。 方法二:用置换法(前面计算题中讲过)。 设: abcde=X 那么1abcde = 100000 +x，abcdel1=10x +1，可得到方程:
五年级奥数课件-数的整除 全国通用
3、 有一位同学说，任意一个三位数连着写两次得到的 六位数，一定能同时被7、11、13整除。这个说法对么?
设这个三位数为abc,连着写两次组成的六位数是abcabc， 只需确定abcabc是否能被7、11、13整除就可以了。 因为: abcabc = abc x 1000 + abc
有一个四位数7AA1能被9整除，A代表什么数字? 这个四位数是几？
分析与解答: 要使7AA1能被9整除，根据能被9整 除的数的特征，可知7+A+A+1的和一定能被9整 除。和可能是9的1倍或2倍，即和是9或18。 如果7+A+A+1=9, A=0.5, A不可能是小数，所以不 符合题意。如果7+A+A+1=18, A=5。可见这个四 位数是7551。
五年级奥数课件-数的整除 全国通用
五年级奥数课件-数的整除 全国通用
(4)一个数的各位上的数字之和能被3(或9)整 除，这个数就能被3(或9)整除。 (5)一个数的奇数位上数字的和与偶数位上 的数字和的差能被11整除，这个数就能被 11整除。
五年级奥数课件-数的整除 全国通用
五年级奥数课件-数的整除 全国通用
五年级奥数课件-数的整除 全国通用
五年级奥数课件-数的整除 全国通用
1、四位数3AA1能被9整除，求A的值。
四位数3AA1要是9的倍数，它的各个数位之和就必 须是9的倍数，3 +A+A+1的和可能是9或18 当3 +A+A+1 =9时，A=2.5，2.5不是自然数，不符 合题目要求。 当3+A+A+1=18时，A=7，符合题目要求