池塘养鱼最大利润优化模型
养鱼方案的数学模型
养鱼方案的数学模型2011年5月5日【问题背景】“养鱼方案”是想通过建立数学模型来探讨实际养鱼的最优方法，化实际问题为理论的探究池塘养鱼获取最大利润的养鱼方案。
从中会忽略很多实际中存在的问题在实际采用中就需要变化的应对。
从实际问题出发寻找数学约束条件，通过数学建模、计算机运筹学模拟计算得到最佳模型求解。
【关键词】池塘养鱼、非线性规划、最大利润、lingo 软件求解一、问题重述在一个水面面积为2100100m 的池塘里养殖某种鱼，并有假设如下： 1、鱼的存活空间为2/1m kg ； 2、每kg 1鱼每天需要的饲料为kg 05.0，市场上鱼饲料的价格为kg /2.1元；3、鱼苗的价格忽略不计，每kg 1鱼苗大约有500条鱼；4、鱼可四季生长，每天的生长重量与鱼的自重成正比，365天长为成鱼，成鱼的重量为kg 2；5、池塘内与的繁殖与死亡均忽略；6、若q 为鱼重，则此种鱼的售价为：⎪⎪⎩⎪⎪⎨⎧<≤<≤<≤<=25.1/105.175.0/875.02.0/62.0/0q kgq kg q kg q kg q 元元元元 7、该池内只能投放鱼苗。
试建立适当的数学模型来得到一个能获得较大利润的三年养鱼方案。
二、模型假设与符号说明（一）、模型假设：1、假设每年都只有365天；2、只要有符合要求的鱼，都能顺利卖掉，且需要鱼苗时都能买到；3、中途捕捞时对池塘里剩余的鱼不会造成损伤，且利用有不同大小网眼的 网能够捕捞到想要的鱼；（二）、符号说明：)3,2,1,0,(=j i s ij —各个阶段鱼体重增长过程中鱼吃饲料的增长和；（ij s 05.0为饲料的总和） )3,2,1(=i q i ——各个阶段的鱼的重量；)3,2,1(=i n i ——各重量段捕鱼的数量；三、模型建立与求解充分利用池塘空间：尽最大程度放养的养鱼方案，空间饱和就捕鱼。
具体为：在开始一次性放入足够多的鱼苗数（确保空间足够都能长到kg 2.0），到鱼长到能卖6元时捕捞部分卖出，在这些鱼长到能卖8元和能卖10元时，各个阶段也有适当的捕捞，并在长到kg 2时全部捕出出售。
池塘养鱼的最优方案模型
池塘养鱼的最优方案模型摘要：根据题目给出的七个已知条件和问题，我们判断这是一个关于如何在有限的资源和条件下获得最大利润的养鱼问题。
本文分别考虑了年初一次性投放鱼苗年后一次性卖出和边投边卖尽可能利用鱼塘资源两种情况，并且在建模过程中运用了常微分方程，计算出鱼的重量关于时间的函数表达式，又运用等比数列求和公式来最终确定最优的年初投放鱼苗的方案。
在模型Ⅱ收益函数的计算中，本文不仅考虑了不同质量范围的鱼所用的饲料费和收入的不同，而且还考虑了不同质量的鱼所占的存活空间的不同，提出了鱼塘的单位面积的收益率的概念来作为衡量标准，以此来进行资源的最优化利用，并结合相关图像最终确定最优养鱼方案。
文中所提出的数学方法及手段均用软件进行了实现。
关键词养鱼方案微分方程等比数列matlab空间利用效用最大化一、问题提出设某地有一池塘，其水面面积约为100⨯1002m ，用来养殖某种鱼类。
在如下的假设下，设计能获取较大利润的三年的养鱼方案。
(1)鱼的存活空间为12kg m ；(2)每1kg 鱼每天需要的饲料为0.05kg ，市场上鱼饲料的价格为2.5元/kg ；(3)鱼苗的价格忽略不计，每1kg 鱼苗大约有500条鱼；(4)鱼可四季生长，每天的生长重量与鱼的自重成正比，365天长为成鱼，成鱼的重量为2kg ；(5)池内鱼的繁殖与死亡均忽略；(6)q 为鱼重，则此种鱼的售价为：⎪⎪⎩⎪⎪⎨⎧≤≤<≤<≤<=25.1/元155.11/元1012.0/元62.0/元0q kg q kg q kg q kg Q(7)池内只能投放鱼苗。
二 、问题分析养殖户为了获取较大的利润，必然会面对确定养殖方案的问题。
因此如何在限定的条件下找出最佳的出售时机以制定最优的养鱼方案成为了解决此问题的关键。
在这里，由于各种无法预测的不确定因素带来的影响，使得养鱼者的实际收益与预期收益会发生一定的偏差，从而有蒙受损失和获得额外收益的机会[1]。
年亩产纯利超十万元生态渔塘设计
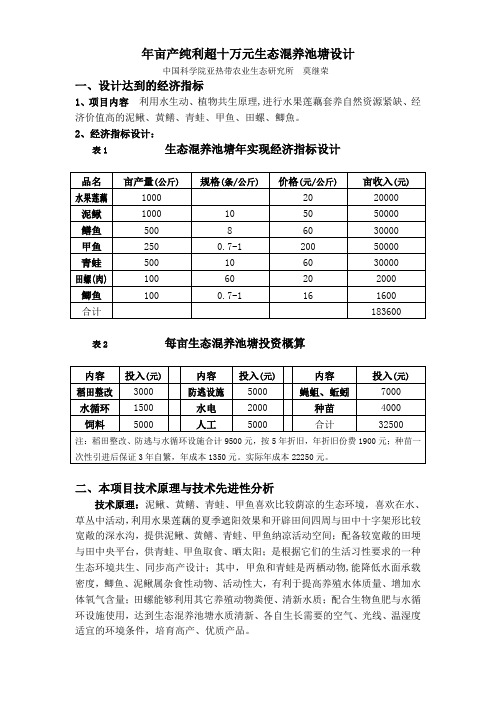
年亩产纯利超十万元生态混养池塘设计中国科学院亚热带农业生态研究所莫继荣一、设计达到的经济指标1、项目内容利用水生动、植物共生原理,进行水果莲藕套养自然资源紧缺、经济价值高的泥鳅、黄鳝、青蛙、甲鱼、田螺、鲫魚。
2、经济指标设计：表1 生态混养池塘年实现经济指标设计表2 每亩生态混养池塘投资概算二、本项目技术原理与技术先进性分析技术原理：泥鳅、黄鳝、青蛙、甲鱼喜欢比较荫凉的生态环境，喜欢在水、草丛中活动，利用水果莲藕的夏季遮阳效果和开辟田间四周与田中十字架形比较宽敞的深水沟，提供泥鳅、黄鳝、青蛙、甲鱼纳凉活动空间；配备较宽敞的田埂与田中央平台，供青蛙、甲鱼取食、晒太阳；是根据它们的生活习性要求的一种生态环境共生、同步高产设计；其中，甲魚和青蛙是两栖动物,能降低水面承载密度，鲫鱼、泥鳅属杂食性动物、活动性大，有利于提高养殖水体质量、增加水体氧气含量；田螺能够利用其它养殖动物粪便、清新水质；配合生物鱼肥与水循环设施使用，达到生态混养池塘水质清新、各自生长需要的空气、光线、温湿度适宜的环境条件，培育高产、优质产品。
技术先进性分析：目前，黄鳝、泥鳅、青蛙、甲鱼大多采用高密度设施养殖，普遍存在养殖密度大，养殖水体质量不能保证，容易发生病害，使用抗生素，产品肉质、鲜味达不到野生水平的难题。
本项目技术，采取品种间合理搭配，共生互利，营造天然环境养殖法是实现生态高效益、高品质混养技术的突破。
本项目中黄鳝、青蛙属于肉食性动物，采取猪、鸡粪发酵养殖蝇蛆，残料加草料发酵养殖蚯蚓，提供其饵料的养殖法，是物质循环利用、高效益转化的技术创新。
其中，采用蝇蛆/蚯蚓=4/1的混合搭配养殖，4斤蝇蛆+1斤蚯蚓能够生产出1斤黄鳝或青蛙，蝇蛆的生产成本0.5元/斤、蚯蚓2元/斤，黄鳝或青蛙的饵料成本才4元/斤，是一种高效农业模式。
泥鳅、甲鱼、鲫鱼是杂食性动物，利用豆粕、玉米、牧草发酵，降低粗纤维总含量的35%，加入适量蝇蛆、蚯蚓作生物促生长剂，自配不含化学添加剂饲料，能够加速生长、提高饵料系数、降低成本，而不降低其肉类品质、鲜味，是当前最为先进的养殖技术。
渔场鱼量的最优化模型
渔场鱼量的最优化模型摘要本文通过建立Gompertz模型和优化模型确定了渔场鱼量的最优解，并由此得到最大持续产量mh和获得最大产量的捕捞强度m E。
问题一中，对渔场鱼量的自然增长建立了Gompertz模型，进而表示出自然条件下单位时间的渔场鱼量，然后分析得到单位时间的捕捞量，从而可得出在捕捞情况下的渔场鱼量，根据平衡点的分析方法，确定出了鱼量的平衡点/E r Nx e，并分析出该点是稳定的。
对问题二，根据捕捞量和在稳定条件下满足的条件，建立优化模型，通过对模型进行求解得到最优解；然后利用图解法，对渔场鱼量和捕捞量的图形进行分析，得到的结果与优化模型的最优值相吻合，进一步验证了最优值的正确性。
关键字:Gompertz模型平衡点稳定性分析优化模型图解法1.问题的重述可持续发展是一项基本国策,对于像渔业、林业这样的再生资源,一定要注意适度开发,不能为了一时的高产去“竭泽而渔”,应该使渔场鱼量保持持续稳产,实现生物资源的可持续开发与利用。
这一问题是生物学家、数学家和经济管理学家都在关心的问题。
对于这方面的工作许多学者进行了广泛而深入的研究。
设渔场鱼量的自然增长服从Gompertz 模型：()ln Nx t rx x=，其中r 是固有增长率，N 是环境容许的最大鱼量；单位时间捕捞量为h Ex =。
（1） 讨论渔场鱼量的平衡点及其稳定性；（2）求最大持续产量m h 及获得最大产量的捕捞强度m E 和渔场鱼量水平*0x .2.问题的分析问题一分析问题一需确定渔场鱼量的平衡点及稳定性，首先根据Gompertz 模型可得到在无捕捞情况下单位时间渔场鱼量，由题中的已知条件也可表示出单位时间的捕捞量，从而可得到在捕捞情况下渔场鱼量满足的方程，进而可根据得到的方程求出渔场鱼量的平衡点，并由此分析其稳定性。
问题二分析在问题二中，采用了两种方法进行求解。
第一种方法是根据捕捞量()h x 的表达式及在()h x 达到最大时渔场鱼量()f x 与()h x 应满足的条件，将其转化为通过建立优化模型，并对模型进行求解来得到最优值，即确定出最大的持续产量m h ，渔场鱼量水平*0x 和获得最大产量的捕捞强度m E ；第二种方法是利用图解法，在同一坐标系中分别作出()f x 和()h x 的图形，而它们的交点即为平衡点，由图形可确定()h x 达到最大时对应的*0x ，由此可求得m h 和m E 。
鱼塘饲养鱼的数学模型
鱼塘饲养鱼的求解数学模型王波沈文平田平摘要本篇论文主要针对在鱼塘饲养鱼的过程中伴随着各种人为因素以及无可避免的环境因素的影响而分别建立的对鱼的尾数甚至每尾鱼重微分方程模型进而求解的问题。
首先在求解鱼的尾数这个相对简单的问题的时候，我们不再考虑出时间以外的变量对方程或者结果造成的影响，因为从题中我们已经获得了一个固定已知量即相对减少率，而它正是由于鱼在成长过程中受各方面约束所产生的，所以我们只需要根据鱼的尾数随时间的增加而减少的关系建立微分方程，然后根据简单的数学知识即可对此微分方程求解。
当然在对每尾鱼重求解时，我们依然像上个问题一样着重从鱼成长的关键因素“净增长率”出发，与之不同的是鱼重的改变是受到了人为因素和自身因素的综合影响，而鱼本身的增长率与自身的表面积存在正比关系，这也是鱼本身由于损耗而不可忽视的减少率鱼本身重量存在的关系，最后我们融入最关键的时间变量，就建立出了表面积和每尾鱼重分别与时间的函数关系，而这三者之间有共同有一个函数关系，即随着时间的加大，表面积增加，重量增加，所以于表面积有关的减少率增大，这就引起了净增长率的减小，于是这一大串的函数关系便共同联合成了微分方程，便得到这个模型的结果。
求解完成，我们根据题意与现实中综合因素的结合可分析出此模型切实可行。
问题重述在鱼塘中投放0n 尾鱼苗，随着时间的增大，尾数将减少，而每尾的重量将增加，设尾数)(t n 的相对减少率n n 为常数；由于喂养引起的每尾鱼量的增加率与鱼的表面积成正比，由于消耗引起的每尾鱼量的减少率与鱼重量成正比，分别建立尾数和每尾鱼重的微分方程，并求解。
符号说明t ：为所有模型中的通用变量时间变量表示投入鱼苗过后的天数 n0：为模型中的已知量表示投入的鱼苗尾数t0：表示刚投入鱼苗的当天n ：投入鱼苗后第t 天鱼的尾数的相对减少率为一常数n （t ）：表示投入育苗后第t 天鱼的尾数g （t ）：投入鱼苗后第t 天每尾鱼的重量s （t ）：投入鱼苗后第t 天每尾鱼的表面积p （t ）：投入鱼苗后第t 天由于喂养引起的每尾鱼量的增加率 q （t ）：投入鱼苗后第t 天由于消耗引起的减少率r （t ）：投入鱼苗后第t 天的每尾鱼量的净增加率k1：p(t)与s （t ）由于正比例函数的系数k2：q （t ）与g （t ）由于正比例函数的系数△ t ：某段时间的变化量dn（t）：表示鱼的尾数在某段时间的变化量dt：即为△t模型的基本假设1、鱼的尾数的相对减少率已经将各方面可能对其造成影响的因素考虑在内2、鱼量的增加率与减少率均是在考虑所有因素后所得出的函数关系3、模型中所涉及到的比例系数均为已知固定量4、鱼的尾数与每尾鱼量并无较大的影响关系5、变量n（t）、g（t）、s(t)、p(t)、q(t)、r(t)均为随时间变化的连续性变量问题一的数学模型一、对问题一的分析此题是根据已知最初鱼苗的尾数和鱼的尾数的相对减少率对未来某一天鱼的尾数用相应的微分方程表示出来并作出求解进而实现鱼的尾数变化的相关预测，而应此得到它的变化规律。
渔业经营与利润分析
市场比较法
选取可比公司： 选择与目标公司 业务相似、规模 相当的公司进行 对比
确定可比指标： 选取反映公司盈 利能力的关键指 标，如净利润、 毛利率等
计算可比公司平 均水平：计算可 比公司在选定指 标上的平均水平
评估目标公司利 润：将目标公司 在选定指标上的 表现与可比公司 平均水平进行比 较，评估其盈利 能力
虾类：如小龙虾、对虾等， 市场需求大，但养殖技术要 求较高
鱼类：如草鱼、鲤鱼、鲫鱼 等，市场需求大，但养殖成 本较高
贝类：如牡蛎、扇贝等，市 场需求稳定，但养殖周期较
长
蟹类：如大闸蟹、青蟹等， 市场需求大，但养殖技术要
求较高
捕捞量与品质
品质：影响渔业利润的另一 个重要因素，品质越好，价 格越高，利润也越高
等
运输成本：运输 费用、燃油费用
等
管理成本：行政 费用、财务费用
等
风险成本：自然 灾害、市场波动
等
渔业利润影响因 素
章节副标题
市场需求
消费者对海鲜 的需求：消费 者对海鲜的需 求量直接影响
渔业的利润
市场价格：市 场价格是影响 渔业利润的重 要因素，价格 波动会影响渔
业的利润
市场竞争：市 场竞争程度会 影响渔业的利 润，竞争激烈 会导致利润下
优点：简单易行，便于理解 和操作
缺点：没有考虑间接成本和 利润，可能无法准确反映真
实利润情况
间接成本法
概念：将渔业经营活动中的间接 成本分配到各个生产环节，从而 评估渔业利润的方法。
优点：简单易行，便于理解和操 作。
添加标题
添加标题
添加标题
添加标题
计算公式：间接成本=总间接成本 /总产量
数学建模 养鱼问题的最优模型
养鱼问题的最优模型摘 要：本文是根据鱼本身的生长情况，求利润最大化的养鱼规划及解决养鱼问题的数学模型，并利用相关分析解决我们的养鱼问题。
利用线性回归、微分方程分析研究鱼苗的产值，来获取最佳综合效益。
关键词：养鱼模型 线性规划 最大利润 微分方程一、问题重述在某地有一个池塘，其水面面积约为100×1002m ，用来养殖某种鱼类。
在如下的假设下，设计能获取较大利润的三年的养鱼方案。
①鱼的存活空间为1kg /2m ；②每1kg 鱼每天需要的饲料为0.05kg ，市场上鱼饲料的价格为0.2元/kg ；③鱼苗的价格忽略不计，每1kg 鱼苗大约有500条鱼；④鱼可四季生长，每天的生长重量与鱼的自重成正比，365天长为成鱼，成鱼的重量为2kg ；⑤池内鱼的繁殖与死亡均忽略；⑥若q 为鱼重，则此种鱼的售价为：⎪⎪⎩⎪⎪⎨⎧≤≤<≤<≤<=25.1/105.175.0/875.02.0/62.0/0q kg q kg q kg q kgQ 元元元元⑦该池内只能投放鱼苗。
二、问题分析要设计获得最大利润的养鱼方案，首先不考虑鱼的制约条件，如环境，由各种竞争导致的灭亡。
由鱼塘的面积、鱼的存活空间，每1kg 鱼每天需要的饲料，以及鱼饲料的价格，分析鱼的价值取向来考虑和设计一个最佳的养鱼方案。
但是由于养鱼的复杂性，忽略部分影响养鱼的因素，并应用线性规划模型解决养鱼问题。
三、 模型假设1、鱼塘只有鱼苗；2、不考虑鱼的繁殖以及由生存环境、不受时间、季节的限制来构成的死亡因素；3、鱼苗成鱼的过程服从生长系数。
4、放入的鱼苗不受个体差异的影响，都能按照题目所给的条件生长，同时放入的 鱼苗在相同的时间内都能长到同样大。
5、鱼可四季生长，每天的生长重量与鱼的自重成正比，365天长为成鱼，成鱼的重量为2kg ；四、符号说明以下为本文中使用的符号：1 0q 最初放入的鱼的数量2 k 鱼每天增重的比例3 t 时间（第t 天）4 )(t q 每条鱼在t 天下的重量5 )(t C 每条鱼在养殖t 天的条件下需要的饲料费用6 M 三年的收益总额五、模型求解根据池塘的容量，由鱼苗长成成鱼时的质量为2kg ，每条鱼的存活空间为1kg/m 2,则最初放入的鱼的数量为0q ，可由已知条件得到以下微分方程：kq dtt dq )( （1）kte q t q 0)(= （2） 50010=q （3） 2)365(=q （4） 通过计算可以得出： 01983.0=k故 ：养殖t 天的条件下每条鱼的重量为)(t q ，则01983.05001)(e t q = （5）根据已知条件计算出：;2)365(;5.1)334(;75.0)313(;2.0)243(====q q q q每天每公斤鱼的成本：.01.02.005.0元=⨯鱼的重量和养殖时间的关系表我们知道，01983.0=k ，养殖t 天的条件下每条鱼的重量为)(t q ：⎪⎪⎩⎪⎪⎨⎧≤≤<≤<≤<=25.1/105.175.0/875.02.0/62.0/0q kg q kg q kg q kgQ 元元元元设养殖t 天的条件下每条鱼需要的饲料费用为)(t C∑∑==+=⨯⨯+=ti i ti ik k t C 11)1(5000/12.005.0)1(500/1)( （6）三种鱼的情况分析：计算可得：每条鱼的平均利润为24.506667元。
海洋渔业资源管理中的最优解模型建模分析
海洋渔业资源管理中的最优解模型建模分析海洋资源是人类生存和发展的重要基础，而渔业资源作为海洋资源的重要组成部分，在人类社会中具有重要的经济和生态价值。
然而，由于过度开发和不合理管理，海洋渔业资源面临着持续减少和生态破坏的风险。
因此，在海洋渔业资源管理中，寻求最优解的模型建模分析成为一项重要任务。
1. 问题定义在进行最优解模型建模分析之前，首先需要明确问题的定义。
问题的定义包括但不限于以下几个方面：- 渔业资源管理的目标：例如，保护渔业资源、提高渔业的可持续发展等。
- 目标变量和约束条件：例如，渔获量、捕捞成本、生态环境影响等。
- 决策变量：例如，渔业开发强度、禁渔期设置等。
2. 数据采集与处理为了进行最优解模型建模分析，需要收集相关的数据。
数据的采集包括但不限于以下几种方式：- 实地调查：通过对渔业资源的实地调查，获取相关的渔业资源分布、渔获量、捕捞方式等数据。
- 统计数据：通过研究历史统计数据，获取渔业资源的变化趋势、捕捞成本等数据。
- 模型模拟：通过建立数值模型，模拟渔业资源的变化过程，获取渔业资源的未来预测数据。
对采集到的数据进行处理，包括但不限于以下几种方式：- 数据清洗：清除采集到的数据中的错误、异常值。
- 数据整合：将来自不同来源的数据进行整合，形成一个完整的数据集。
- 数据转换：根据问题的需要，对数据进行转换，例如将文本数据转化为数值数据、进行数据标准化等。
3. 模型建立根据问题的定义和数据的情况，选择合适的模型进行建立。
在海洋渔业资源管理中，常见的模型包括但不限于以下几种：- 渔业资源评估模型：通过建立数学模型，对渔业资源的状况进行评估，如渔获量的估计模型、渔船数量的影响模型等。
- 渔业开发强度优化模型：通过建立数学模型，对渔业开发强度进行优化，使得资源利用最大化，如最优开发区位选择模型、最优捕捞量决策模型等。
- 生态影响评估模型：通过建立数学模型，评估渔业活动对生态环境的影响，如捕撒率模型、生态适应性评估模型等。
数学建模论文 捕鱼效益最大化模型
北京理工大学数学学院《常微分方程》小论文捕鱼业效益最大化的微分方程模型2012/12/18捕鱼业效益最大化常微分方程模型摘要在将可持续发展作为基本国策的大背景下，像渔业这样的再生资源应该在持续稳产的前提下追求效益的最大化。
本文考察一个渔场，首先建立在捕捞情况下渔场鱼量遵从的方程，分析鱼量稳定的条件，并且在稳定的前提下讨论渔场的效益最大化问题，最后提出相应的优化方案及建议。
关键字:渔场鱼量捕捞强度平衡点稳定条件效益一、问题分析如今人们大范围过度捕捞导致了渔业的日渐枯竭，近海资源已经被严重透支，到远洋争议海域捕鱼又充满了危险，近年不断有渔船被日韩海监船扣压，更有甚者，去年3月份与韩国海警爆发冲突，导致一人死亡，引发各种问题。
然而怎样才能实现捕鱼业效益的最大化呢？应该如何控制捕捞强度才能实现效益的最大化？本文就这些问题进行了以下分析：①建立渔场鱼量x，捕捞强度E关于t的微分方程；②由上述微分方程组求出平衡点并分析其稳定性；③在稳定条件下求出渔场效益；④对其效益进行分析提出优化方案.二、模型假设：（1）在无捕捞条件下，渔场中的余量x(t)的增长服从logistic规律（即阻滞增长模型）；（2）单位时间的捕捞量（即产量）与渔场鱼量x(t)成正比，比例系数为E；（3）捕捞强度E(t)的变化率与利润成正比；（4）鱼的销售单价为常数p，单位捕捞率的费用为常数c；三、模型建立与求解1.在无捕捞条件下x(t)关于时间的微分方程) (1)ẋ(t)=f(x)=rx(1−xNr为固有增长率，N是环境容许的最大鱼量，用f(x)表示单位时间的增长量.2.捕捞情况下渔场鱼量满足的方程单位时间的捕捞量（即产量）与渔场鱼量x(t)成正比，比例系数为捕捞强度，于是单位时间的捕捞量为：h(x)=Ex (2)根据以上假设并记F(x)=f(x)-h(x)得到捕捞情况下渔场鱼量满足的方程为：)−Ex (3)x(t)=F(x)=rx(1−xN3.捕捞强度E(t)关于时间的微分方程E(t)=k(T−S) (4)k为比例常数，T为单位时间的收入，S为单位时间的支出.其中T=ph(x)=pEx, S=cE (5)4.求平衡点并分析其稳定性我们并不需要解方程(3)和(4)以得到x(t)，E(t)的动态变化过程，只希望知道渔场的稳定鱼量和保持稳定的条件，即时间t足够长以后渔场鱼量x(t)的趋向，并由此确定此时的效益.接下来我们将求解方程(3)和(4)的平衡点并分析其稳定性.{ẋ(t )=u (x,E )=rx (1−x N )−Ex E (t )=v (x,E )=k (T −S )……（6） 将（5）式带入下面的代数方程组，{u (x,E )=0v(x,E)=0, 解出平衡点为，（0,0），（N ，0），（c p ,r(1−c Np )）.稳定性分析：当x=0,E=0时，即渔场鱼量为0且捕捞强度为0，此种情况不具有分析意义；当x=N ，E=0时，即渔场鱼量为环境最大容纳量，没有捕捞，同样，这种情况也不具有分析意义；当x=c p ，E=r(1−c Np )时，由于（6）为非线性方程组，所以我们将采用线性近似的方法讨论此时的稳定性。
渔业养殖中的养殖效益评估与优化
渔业养殖中的养殖效益评估与优化渔业养殖作为一种重要的经济活动，对于满足人们日益增长的鱼类需求、促进区域经济发展以及维护水生态平衡都起着至关重要的作用。
然而，在渔业养殖过程中，如何对养殖效益进行评估和优化，以确保养殖活动的可持续发展和经济效益的最大化，成为了较为紧迫的问题。
本文将对渔业养殖中的养殖效益评估与优化进行探讨。
一、养殖效益评估的方法和指标1. 养殖效益评估的方法（1）收益成本比法：通过比较养殖项目的总收益与总成本之间的比值，评估养殖效益的高低程度。
（2）投资回收期法：通过计算养殖项目的投资回收期，评估养殖效益的快慢程度。
（3）净利润法：通过计算养殖项目的净利润，评估养殖效益的经济效果。
2. 养殖效益评估的指标（1）投资效益：包括投资回收期、净现值和内部收益率等指标。
（2）规模效益：包括单位面积的产量、单位投入的产出等指标。
（3）经济效益：包括净利润、生产效益和劳动生产率等指标。
二、养殖效益优化的途径和方法1. 科学合理的养殖技术选择（1）根据养殖场地的环境条件和水质状况，选择适宜的养殖品种和养殖方式。
（2）优化养殖环境，确保鱼类的健康生长和高效利用饲料。
2. 合理安排养殖生产经营管理（1）制定合理的养殖生产计划，科学配备养殖设备和技术人员。
（2）控制养殖成本，合理利用养殖投入，降低经营成本。
3. 建立健全的市场销售渠道（1）与周边城市或贸易商建立合作关系，拓展销售渠道。
（2）加强品牌建设，提高产品附加值，增加销售利润。
三、养殖效益评估与优化的案例分析以某渔业养殖公司为例，该公司专注于高品质海水养殖鱼类的培育与销售。
为评估和优化其养殖效益，公司采用了收益成本比法、投资回收期法和净利润法等评估方法，以及投资效益、规模效益和经济效益等指标。
在评估过程中，公司发现投资回收期较长，净利润率偏低，说明目前养殖效益有待提升。
为了优化养殖效益，公司采取了以下措施：首先，公司加大了技术研发和改进力度，引进先进的养殖技术和设备，提高养殖效率和产品质量。
640立方推水池养的鱼高于18亩鱼塘收益-佛山三水池塘生态推水养殖模式
巾 边 农、 发腱仃 公 （ 以下 简称 “ 边 农业” ）， ｊ 水 入池塘 ，圳有 良好 的养
环境一最近 ， 项， 卜 念环保的推水养嫡项 Ｆ ｉ ¨十余米 ・ ¨池 塘 ， 《 海洋 渔业 》
针刈 的ｆ 止Ｊ Ｉ 川 的 实
存这 落地
．成 为 ｒ Ｊ 尔省佛 山市 ｉ 水 就 看到 ｒ 靠 常 处Ｊ 排 建 了 ４条 养殖水 “ 这 就是 整套项 ｆ ｛ 的精华 ”李 啭华 介 同样 ． 说 ．水惜 最 前端 装 仃增氧 推水 机 ．水惜艰
的 候 条 件 干 ¨ 养 ｒ Ｉ 『 】 种 “没 汁心 虑 Ｊ ｛ ＿ ． 『 』 匕 蚌相 １ ｔ 种
．
化
渺北 汀畔车沿荇 ｋ Ｋ 的汀 畔 大堤 ，经 过 ・
小段 密林 ，汀 畔， 念 农庄跃 然 眼前 离 ＿ 人
约成 ｌ ０ 。斜ｆ ｆ ｊ ， 水槽 两边 均 没 仃 一
验 ’ 法 ，Ｊ １ 总 …卡 ¨埘 心 的 技
卣 ‘ 个池塘乍态推水芥 ｝ Ｉ 【 ， Ｊ 范基地
术 嘤点 ，地 力 标 准 、行 、 Ｉ ｌ ， 标 准
和 家 准 Ｊ 、 怏迎 ● 水 究 熊 远 爪 ” 广 东 省农 、 ｉ 机 械 试验 定 站 研 ． 家仃 Ｊ 还 崽 刮 火 ． ｒ 集 装 箱的成 果 利 干 ¨ ： 作 沦 义较 少 的
ｌ ６ ２万 冗
宽 ４米 ．这 ６ ４ ０ 方 的水怵 就是 鱼生 Ｋ
然 ．这 个数 字 还 有 部 分 停 留在 养殖 对环境 的压 力 “ 该模 式主要 心川 殖＿ Ｅ ｝ ＿ Ｊ 水可 以循环利 用 ， 以减少环 境污 染 ． 实现零 排放 ，或者说 至少达 标排放 ”
按 照 目前 的养殖情 况来 看 ， 水中 植物 、微牛物 等净 化池 塘水 质 ，养 的空 问； 而 ｊ 之 相连 的水域 就是 集 污池 ： 理 论 ．不过 ，
池塘养鱼高产秘笈：立体混养模式“八”字精养法，产出高品质鱼
池塘养鱼高产秘笈：立体混养模式“八”字精养法，产出高品质鱼前言：池塘养鱼是利用无公害池塘淡水把鱼苗育成达到食用或商品成鱼标准的最后阶段与最终目的的整个过程。
通过先进的水产养殖技术，促进鱼类快速、健壮地成长，以达到肉质鲜美、产量高、成本低、经济效益显著的总体目标。
乡民锋哥所在的广东河源地区属亚热带气候，全年气候温和湿润，雨水充沛，多雨季节与高温季节同步，土壤肥沃，而且大部分区域仍保持着原始生态的状态，水系河网山溪密集，溪水清澈见底，良好的天然水利条件与优良的水质为建设无公害商品鱼的养殖鱼塘及发展提供了重要的水资源及自然的地理优势。
下面锋哥就借本文与大家聊聊无公害商品鱼鱼塘养殖的一些心得体会与技巧，希望可为水产养殖朋友们带来参考建议。
池塘养鱼的特性为水体面积小，容易改善水质、把握放养密度，管理和起捕也比较方便，投资少、见效快，很适用于农村家庭户承包养殖。
在我国池塘养鱼早已有悠久的生产历史，并且经验丰富，行间总结有一套行之有效的“八字精养法”，可以概括为水（水深水活）、种（良种体健）、饵（精饵量足）、密（合理密放）、混（多种混养）、轮（轮捕轮放）、防（防病除害）、管（精心管理）。
这套精养法的要点为相互依存、相互制约、相互促进，是养鱼高产稳产的综合技术措施。
池塘养鱼高产秘笈：立体混养模式+“八”字精养法，产出高品质鱼一、高产池塘的基本条件淡水鱼类对各种水域环境适应性较强，除污染严重的水域外，有水就有鱼。
但真正要把养鱼作为一种生产门路来经营的话，就必须按照水产养殖的要求，对现有老旧池塘进行改建或新建养鱼池塘，实现科学产出优质鱼品。
（一）、高产池塘的基本条件1、水源充足、水质好这是池塘养鱼的一个基本条件。
水源充足，可以经常加注新水、改善水质，有利于鱼类的生长和浮游生物的繁殖；水源充足，注、排水方便，鱼类浮头时，有利于急救。
无污染的江河、水库、溪流都是比较理想的水源。
2、水深适度鱼谚有“一寸水，一寸鱼”的说法，说明水深与增产有着密切的关系。
四种新型现代水产生态养殖模式详解
四种新型现代水产生态养殖模式详解随着我国经济技术的发展和全面建成小康社会的不断深入，国内渔业发展也面临着重大挑战，渔业转方式调结构任务日益紧迫，现代渔业发展必须由注重产量增长转到更加注重质量效益，由注重资源利用转到更加注重生态环境保护上来，走产出高效、产品安全、资源节约、环境友好的农业现代化道路。
“十三五”期间，国家将通过促进渔业绿色发展、循环发展、低碳发展来实现渔业生态文明建设的目标。
下面将为您介绍几种新型现代水产生态养殖模式。
养鱼：四大家鱼罗非鱼混养比例调整好，每亩多赚6000元一、池塘循环流水养殖模式池塘循环流水养殖模式借鉴了工厂化循环水养殖理念，将传统池塘的“开放式散养”变为“集约化圈养”，使“静水”池塘实现了“流水”养鱼。
该种养殖模式是在池塘中的固定位置建设一套面积不超过养殖池塘总面积5%的养殖系统，主养鱼类全部圈养于系统内，系统外的池塘面积用于净化水质，以供主养鱼类所需。
养殖系统前端的推水装置可产生由前向后的水流，结合池塘中间建设的两端开放式隔水导流墙，使整个池塘的水体流动起来，达到流水养殖的效果。
主养鱼类产生的残饵、粪便随着系统内水体流动，通过废弃物收集装置，将残饵粪便从系统中移出，转移至池塘之外的沉淀池并循环利用。
此外，池塘其它区域用于套养滤食性鱼类（鲢、鳙、匙吻鲟等），达到增产和净化水质的目的。
该技术符合我国渔业对节水、节能、生态、高效的发展要求，在资源节约、生态环境保护及渔业增效等方面具有明显优势，并且能够解决国内渔业养殖模式在转型方面遇到的诸多问题。
技术优势1、池塘循环流水养殖技术通过气提水装置，在增加水体溶氧的同时带动水体循环流动，养殖废弃物随着水流不断沉积在系统末端并及时排出，使养殖水体得到了净化，大大降低了池塘养殖的药物使用率，在保护水环境的同时提高了水产品的质量安全。
2、在增加产量、提高效益的同时，可将水产养殖中大部分的残饵粪便及时收集并排出，被植物再次利用，实现了池塘的低碳生态养殖。
对三年养鱼如何获取最大利润的分析与量化模型分析00
对三年养鱼如何获取最大利润的量化模型建立与分析杨凤坤张文彬摘要：本文主要阐述日常生活中关于养鱼获取利润最大化问题的分析，由于影响鱼生长的因素很多，并且各种因素对鱼生长的影响程度不同，我们结合现实生活中的实际情况，考虑到现实环境的多变性与复杂性，我们忽略部分次要因素，建立解决养鱼获取利润最大化问题的数学模型，并借助MATLAB软件编程计算。
通过各种模型的动态规划与线性规划分析比较来得出最优解，确定三年获得较大利润的最优养鱼方案。
以下为四个基本的养育模型：模型Ⅰ：一次性养殖模型，一年卖一次，投放一定数量的鱼让鱼长成成鱼；模型Ⅱ：养卖结合模型，考虑到中间资金回收与正常运转；关键词：利润最大化养鱼模型MA TLAB软件动态规划线性规划一、问题重述m，用来养殖某种鱼类。
在如下的假设设某地有一池塘，其水面面积约为100×1002设计能获取较大利润的三年的养鱼方案。
m；①鱼的存活空间为1kg /2②每1kg鱼每天需要的饲料为0.05kg，市场上鱼饲料的价格为0.2元/kg；③鱼苗的价格忽略不计，每1kg鱼苗大约有500条鱼；④鱼可四季生长，每天的生长重量与鱼的自重成正比，365天长为成鱼，成鱼的重量为2kg；⑤池内鱼的繁殖与死亡均忽略；⑥若q为鱼重，则此种鱼的售价为：⎪⎪⎩⎪⎪⎨⎧≤≤<≤<≤<=25.1/105.175.0/875.02.0/62.0/0q kgq kg q kg q kgQ 元元元元 ⑦该池内只能投放鱼苗。
二、问题分析本文主要是设计一个在一定时间和一定的空间内养鱼可以获得最大利益方案，从题目中我们知道池塘的面积，鱼的生活空间，池内鱼的繁殖于死亡均忽略，每1kg 鱼每天需要的饲料和鱼长成成鱼的时间以及不同重量的鱼的售价，因此可以将鱼的价格和鱼的繁殖时间联系起来，构建一个价格体系，考虑在不同时间段鱼的售价与饲料成本，绘制鱼的增长图和饲料成本图，但由于养鱼的复杂性，我们忽略部分影响养鱼的因素，应用线性规划和动态线性模型来分析鱼在不同时段的价值来考虑设计最佳的养鱼方案，从而为部分渔民提供一个参考。
池塘养殖鱼的养殖利润模式
使用高档饲料才更有利。 3、 若不同品位饲料的增重饲料成本相等，则鱼价只需高于增重饲料成本，使用高档饲料就
更有利。 4、 若高品位饲料的增重饲料成本更低，则鱼价即使低于增重饲料成本，使用高档饲料也更
鱼的养殖利润模式
名词:品位______饲料的品质在市场上的定位。
设：一农户在单位面积池塘（或网箱）内使用的是售价为 Ps（元/Kg）、饲料系数为
FCR 的饲料，在养殖期 T 时间内，投饲量为 Fi（kg）时、鱼体达上市规格后，成鱼售
价为 Py（元/kg），全期的非饲料成本（含苗种、塘租、水电、人工、设备等成本）为 C
利润（元） 鱼价 4.12 元/kg
-1000
-940
-881
-821
4.61
-384
-384
-384
-384
4.92
0
-37
-74
-111
4.95
41
0
-41
-82
4.99
92
46
0
-46
5.05
157
105
52
0
例 2）、不同品位饲料的增重饲料成本相等时
见表 2 ⑴ 1~4 号饲料的赢亏鱼价 Py1 分别为：4.92、5.05、5.21 和 5.41 元/kg，依次升高。
⑴ 1~4 号饲料的赢亏平衡点鱼价 Py1 分别为：4.92、5.32、5.78 和 6.30 元/kg，依次增 加。
⑵ 1 与 4 号饲料的品位选择点鱼价 Py2 为 2.76 元/kg，比最低的增重饲料成本 3.72 元/kg 还低。
数学建模养鱼问题
研究获得三年养鱼利润最优模型摘要在我们日常生活中，都有这么些相关的例子。
那么这里我们将基于求利润最优化的养鱼规划问题，根据鱼的存活空间有限，以及鱼本身的生长情况，可以假设鱼在长成成鱼后生长非常缓慢，近似为不生长，未成年鱼的生长模型为指数增长模型,得出鱼的增长函数，对于的价格进行预知，将利润的最大化问题着手于研究养鱼周期、捕鱼次数及每次捕鱼的重量，结合鱼的生长模型充分利用池塘空间，在合理假设条件下建立数学模型，并借助MATLAB软件编程计算，通过比较分析各模型的最优解，确定出三年获得较大利润的最优养鱼方案，为养殖户提供有用的参考。
关键字：Matlab 指数增长模型养鱼周期捕鱼次数捕鱼重量较大利润一、 问题重述设某地有一池塘，其水面面积约为100×1002m ，用来养殖某种鱼类。
在如下的假设下，设计能获取较大利润的三年的养鱼方案。
① 鱼的存活空间为1kg /2m ；② 每1kg 鱼每天需要的饲料为0.05kg ，市场上鱼饲料的价格为0.2元/kg ； ③ 鱼苗的价格忽略不计，每1kg 鱼苗大约有500条鱼；④ 鱼可四季生长，每天的生长重量与鱼的自重成正比，365天长为成鱼，成鱼的重量为2kg ；⑤池内鱼的繁殖与死亡均忽略； ⑥若q 为鱼重，则此种鱼的售价为：⎪⎪⎩⎪⎪⎨⎧≤≤<≤<≤<=25.1/105.175.0/875.02.0/62.0/0q kg q kg q kg q kgQ 元元元元⑦该池内只能投放鱼苗。
二、 模型假设（1）、养鱼者的经营模式为“放鱼苗喂饲料捕捞，销售全部捕捞”周期循环，每个周期只投放一次鱼苗。
（2）、在饲养过程中，不考虑意外灾害，如洪灾、旱灾，台风等等。
（3）、鱼可以一年四季生长，未成年鱼每天生长的重量与鱼的自重成正比。
（4）、鱼的繁殖和死亡均可以忽略。
（5）、捕捞鱼时采取承包不放水的方式。
（6）、每个周期分n 次捕捞销售，每相隔两次捕捞时间间隔相同，n>=2；且在捕捞时，部分鱼对其它鱼的生长不造成影响，捕出的鱼能全部按预定价格销售。
高塘租下,全年亩利润3000元以上,花鲢(大头)主养模式探索成果
高塘租下，全年亩利润3000元以上，花鲢（大头）主养模式探索成果近些年来，经历了拆网箱后，华中和华西南地区养殖草鱼的增长，全国水产养殖的增长和养殖技术的增长，草鱼的养殖量不降返增，草鱼价格逐步走低，养殖草鱼的利润越来越低了，部分养鱼户发觉花鲢鱼也是混养鱼塘里的主要利润来源，这在以草鱼为主的养殖模式下是一种机会出路，也是常规鱼的选择。
根据自己多年水产从业经历，结合比较优质的养殖户的养殖模式优化总结出花鲢鱼增产增效养殖模式。
养殖目标：花鲢亩产达到1000斤。
养殖面积：以1亩计，水深约1.5-2米。
放养规格：花鲢0.1-1.5斤，鲫鱼≤1两，草鱼≤1斤，白鲢≤0.5斤放养模式：花鲢1（≤0.5斤）100尾，花鲢2（0.5-1斤）100尾，花鲢3（1 -1.5斤）150尾，鲫鱼100尾，草鱼50尾，白鲢50尾，共计550尾，其中主养品种花鲢占63.6%，套养鲫鱼占18.2%，草鱼占9.1%，白鲢占9.1%放养密度：花鲢350尾/亩，鲫鱼100尾/亩，草鱼50尾/亩，白鲢50尾/亩该放养模式属于以花鲢为主的高密度精养，充分利用了池塘的空间载鱼量，养殖产量会较高，可获得较高的经济效益；但是也对养殖硬件和软件有很高的要求，下面从水源水质、养殖设施设备、饲料、疾病防治、池塘水质调控、投喂管理、市场行情等方面一一分析，如何做到花鲢的高产。
一、水源水质：实际生产中对鱼的长势影响较大的水质因素主要有：PH值、溶解氧、分子氨和亚硝酸盐。
要将这几个因素调控在较好的范围，需要较高的技术水平，比如看水色，观天象，正确施肥，适时开启增氧设施，定期测水质，正确的使用调水产品等等。
二、养殖设施和设备：高产鱼塘需增加的设备包括：净水池、、自动投饵机、高效增氧机等等。
三、饲料：饲料的主要作用是促进吃食鱼快速生长，并达到体质健壮。
实践证明花鲢也是可以通过投喂饲料来获得快速增长的。
好的饲料需要从两个方面来衡量：一是饵料系数（长一斤鱼所需要的饲料斤数），二是饲料价格。
基于养鱼最大利润的模型探究
项目
捕捞次数
捕捞时间
捕捞条数
放入鱼苗条数
捞出鱼自重
捞出鱼总重
鱼塘里余鱼的数量
第五次捕捞
第593天
36667条
0条
0.2kg/条
7333.4kg
13333条
第六次捕捞
第633天
8333条
0条
0.75kg/条
6249.75kg
5000条
第七次捕捞
第715天
5000条
50000条
2kg/条
10000kg
5.1.4方案四：365天型。
在此方案下，把鱼养到2kg即成鱼才全部捞出，投放于苗数为：10000/2=5000条，在365天时打捞出全部鱼可卖得： 100000元。消耗的饲养费为： =5319.7元。故可获利为：94680.3元。而3年共1095天，即刚好可养养三期鱼。则可得在此方案下三年总获利为：94680.3×3=284040.9元。
鱼类型
243天型
313天型
350天型
365天型
捕捞总条数
投入鱼苗条数
根据条件我们得到相应一年的目标函数及约束条件。
目标函数为：
约束条件为：
+ + + =50000;
+ + + 50000 （50000- ） + ;
（50000- + ;
（50000- - - ） + ;
四、符号说明
:鱼售出时的单价。
:每条鱼养殖t天的重量。
r：鱼每天的生长重量与鱼的自重的比例系数。
:每条鱼养殖t天所消耗的饲养费。
:捞出鱼卖得的总价钱
五、模型建立
渔场鱼量最优化模型
景德镇陶瓷学院数学模型课程设计学院：信息工程学院班级：信息小组成员：捕鱼业的持续收获摘要 运用微分方程稳定性理论，建立渔场鱼量的自然生长服从种族增长规律Gompertz 模型的情况下，分析了鱼量稳定的条件，并且在稳定的前提下，使用图解法和微分法讨论如何控制捕捞使持续产量达到最大和经济效率达到最大并且研究捕捞过度问题。
最后，对模型的优缺点进行了讨论。
关键词：Gompertz 模型 稳定性 微分法 捕捞过度正文问题复述可持续发展是一项基本国策，对于像渔业、林业这样的再生资源，一定要适度开发，不能为了一时的高产去“涸泽而渔”，应该在持续稳产的前提下追求产量或利益最优化。
已知某渔场鱼量的自然生长服从种族增长规律Gompertz 模型：rxln xN，其中r 是固有增长率，N 是环境容许的最大鱼量。
产量模型一．模型假设1.假设鱼群的数量随时间连续地，甚至是可微地变化；2.假设鱼群生活在一个稳定的环境中，即其增长率与时间无关；3.种群的增长是种群个体死亡与繁殖共同作用的结果；4.资源有限的生存环境对种群的繁衍，生长有抑制作用，而且这一作用与鱼群的数量是成正比的；5.渔场鱼量的自然增长服从Gompertz 模型。
二．符号说明符号 含义X(t) 时刻t 渔场中的鱼量 r 固有增长率 N 坏境容许的最大鱼量 f(x) 单位时间的增长量 E 单位时间捕捞率 h(x) 单位时间的捕捞量 X 0 平衡点 X 1 平衡点 h m 最大持续产量E M 获得最大产量的捕捞强度 X 0*最大的持续产量此时的稳定平衡点三.模型建立1.在无捕捞条件下x(t)的增长服从Gompertz 规律，即x.(t)=f(x)=rxln x N(1)2.单位时间的捕捞量（即产量）与渔场鱼量x(t)成正比，捕捞强度为E ，可以用比如捕鱼肉眼的大小或出海渔船数量来控制其大小，于是单位时间的捕捞量为：h(x)=Ex. (2) 根据以上假设并记F(X)=f(x)-h(x) 得到捕捞情况下渔场鱼量满足x.(t)=F(X)= rxln x N- Ex (3)四．模型的求解令F(x)=0 得到两个平衡点Ｘ０=NeE r-,Ｘ１=0 (4)不难算出F ＇（x ）=rln x N-r-E,所以F ＇（Ｘ０）=-r, F ＇（Ｘ１)=∞若Ne Er -（Ｘ０）=-r<0,即r>0 (5) 时Ｘ０点稳定，Ｘ１点不稳定 。
做账实操-养鱼利润和成本计算.pptx
3、饲料、肥料费用：约需1500元左右。
4、水电、医药：约需500元左右。
综上，养鱼的成本约需鱼塘建设800元+引进鱼种500元+饲料肥料1500元+水电医药500元=3300元。
养鱼的利润
一般一亩鱼塘的产量在100。斤左右若按亩产800斤计算,花白鲤亩产400斤，白鲤350斤，花鲤50斤，目前市面 上花白鲤的售价为8元/斤左右，白鲤售价为6.5元/斤左右，花鲤售价约在10元/斤左右，总收入约为花白鲤8元;400斤 +白鲤6.5元;350斤+花鲤10元50斤=5975元左右。养鱼的利润约为收入5975-成本3300元=2675元。
3、换水：定期换水，确保水中含氧量充足，每次换水时只需换掉1/3-1/4即可，换水时水温温差不能太快，换 水时间根据水质决定，若水质浑浊则勤换，水质清澈则可少换。
4、放养密度：家庭水族箱一般较小，因此放养密度不能过大，具体数量根据水族箱的大小进行调整，若水族箱 长约40cm,宽约25cm,高约30cm,则可以饲养6-8条规格在5-7cm的小鱼。投放密度与鱼缸大小、鱼只规格、水温、水 质都有一定关系，一般鱼体较大则投放少；冬季多养，夏季少养；水温较低时多养，水温高时则少养。
家庭养鱼技术
1、饲料投喂：给鱼投喂富含营养的水蚤、蚯蚓、黄粉虫等动物性饲料和白芝麻；最好不要投喂劣质金鱼饲料， 营养较差，不易被吸收且容易污染水质。投喂饲料一般在上午、下午各一次，投喂数量不要太多，以鱼能吃完为宜 ，以免影响水质。
2、光照：将鱼缸放在有阳光照射1-2小时的地方，以利用阳光中的紫外线杀菌，减少鱼群患病，且在光合作用 下，鱼体的颜色会更加鲜艳美观。
养鱼的成本
鱼塘养鱼一般选择混合喂养，养，下面我 们主要用鲤鱼的混养来做个简单的利润和成本计算，仅供大家参考：
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
池塘养鱼最大利润优化模型【摘要】：随着社会的发展，数学模型在社会领域占据了比较重要的地位。
本文以某池塘养殖鱼类为背景而提出的，养殖户为了获取较大的利润，确定限定的条件下找出最佳的出售时机以制定最优的养鱼方案解决此养殖最优化方案的问题。
对于该建模题中对于目标函数的求解，运用了lingo软件进行求解，使得问题的求解更加快捷和准确。
该模型可应用于最大利润的求解，并且简单清晰，为生产者提供最优化的投资方案。
【关键字】：最大利润成本费用最优问题最优解 lingo一、问题重述某地有一池塘，其水面面积约为2100100m ⨯，用来养殖某种鱼类。
在如下的假设下，设计能获取较大利润的三年的养鱼方案。
（1）鱼的存活空间为2/1m kg ；（2）每kg 1鱼每需要的饲料为kg 05.0，市场上鱼饲料的价格为kg /2.1元； （3）鱼苗的价格忽略不计，每kg 1鱼苗大约有500条鱼；（4）鱼可四季生长，每天的生长重量与鱼的自重成正比，365天长成为鱼，成鱼的重量为kg 2；（5）池内鱼的繁殖与死亡均忽略；（6）若q 为鱼重，则此种鱼的售价为??<?<?<=25.1/105.175.0/875.02.0/62.0/0q kg q kg q kg q kg Q 元 元 元 元（7）该池内只能投放鱼苗。
二、问题分析在池塘养殖鱼类，我们如何在众多的养殖方案中选择可获取较大利润的时效三年的养鱼方案，这是我们要解决的核心问题。
针对此问题，在假设同批生长鱼苗在同时间出售的前提下，我们便考虑从出售时机的角度来寻求最优方案，也就可以先从研究一条鱼的角度来求解问题。
首先算出养殖d 天的每条鱼的平均每天产生的利润，即售出价格减去消耗饲料的费用，由此可求出d 的最佳解使得在该模型中此利润最大，以及养殖一批鱼的最大利润。
进而我们可以求得三年内可养殖该鱼种的批数和获取的利润值。
三、模型假设（1）池塘的水面面积都是且只是鱼的存活空间，不会被其他生物所占据； （2）鱼的食物只来源于市场上销售的鱼饲料，且鱼苗仅在每天喂养饲料的情况下生长直至长为成鱼；（3）饲料供给时，池塘里的鱼均只吃每天所需的饲料；（4）鱼可四季生长，不考虑气候的影响，每天鱼的生长重量与鱼的自重成正比；（5）池塘中该池内只能投放鱼苗且鱼种未全部捕捞前不投放鱼苗；（6）不考虑池内鱼的繁殖与死亡。
四、符号假设q 0：一只鱼苗的初始重量，单位：kg，即：5001q= (kg)；q: 一条鱼在任一时刻的重量,单位：kg;q1:饲养 d天的一条鱼重量，单位：kg；k:鱼每天的生长重量与鱼的自重所成的比例；d: 养殖天数；C: 每条鱼饲养成本，单位：元；C0：每Kg鱼每天消耗饲料费用Q: 鱼的价格，单位：元/kg。
五、模型建立题目要求设计的是池塘能获取较大利润的三年的养鱼方案，根据设定的假设同批生长鱼苗在同时间出售，就可以将研究的范围缩小至先考虑一条鱼的利润的优化求解。
我们可以通过求解的一条鱼的利润的作为目标函数来求整个池塘的基础:1、每鱼的利润=每条鱼的重量*价格—每条鱼饲养成本，即：W=q*Q—C2、当d=365时成鱼重为：q*(1+k)^365=2 (Kg)；故：k=1000^(1/365)-1；3、养殖d天每条鱼的重量：q1=q*(1000^(1/365))^d（Kg）；4、由已知每Kg鱼每天消耗饲料费用：C0=1.2*0.05= 0.06（元），则有养殖d 天每条鱼消耗的饲料价格（元）其中j=0,1,2, (365)根据上面的条件从而我们就可以建立一条鱼的利润最大模型为：Max W=q*Q—C;s.t.0<=Q;Q<=10;q=2;k=1000^(1/365)-1;C= C 0*∑q j=∑0.06*1/500*(1+k)^d;六、模型求解1、我们直接运用lingo 程序，求解得到模型的最优解，程序及运行结果如下： model :max =q*Q-(0.06*0.002*(1-(1+x)^365))/x; 0<=Q;Q<=10;q=2;x=1000^(1/365)-1; end通过lingo 软件可以运行得到最优解如下：Global optimal solution found.Objective value: 10.27461 Infeasibilities: 0.000000 Total solver iterations: 0Variable Value Reduced Cost Q 2.000000 0.000000 X 0.1910558E-01 0.000000 Row Slack or Surplus Dual Price 1 10.27461 1.000000 2 2.000000 0.000000 3 8.000000 0.000000 4 0.000000 4.000244 5 0.000000 1996.602由通过lingo 软件计算结果可知养殖365天完全成鱼后出售的每条鱼平均每天产生的利润最高，所以应将每条鱼完全养到成鱼，故每条鱼的利润为w=10*2-∑0.06*1/500*(1+x)^d （元）其中d=0,1,2,...,365约等于10.27461元。
在这个结果的基础上，我们就可以得到一批鱼的利润W=NW 0 . 2、约束的假设条件：（1） 池塘水面面积约为2100100m ，鱼的存活空间为2/1m kg ，可知池塘最大能容鱼的重量为10000;而每条成鱼的重量为2 kg/条；则池塘内所饲养的鱼的数量最多只能为N=10000/2=5000 条。
（2） 365天为一批鱼的生长至销售的周期，因此三年共可以养殖三批此种鱼类。
综上，我们可以得到1541192746.10500033W 301=⨯⨯===nW Z Max在这个模型的基础上，我们就设计出了能获取较大利润的三年的养鱼方案，即三年池塘共养殖三批该种鱼类，每批投放鱼苗10kg 即5000条，将鱼养殖365天长至成鱼，变可获得较大的利润，且该利润为154119元。
七、模型评价 一、优点：1、该模型把一个池塘的鱼利润最优的问题简单化，分析到具体每条鱼最优问题，通过考虑到养殖天数与利润的关系得出了一套获取较大利润的养鱼方案从而得出总体最优问题。
2、充分运用LINGO 软件来编程求解，求解过程简便，所得数据合理。
3、该模型实用性较强，对现实有一定的指导意义。
二、缺点：1、没有完全解决捕捞的时间问题，只解决同批鱼同时全部捕捞的情况，但可将这个模型运用到同批鱼不同时捕捞的情况中, 不同时捕捞时的利润会更大一些。
2、该模型没有充分考虑鱼生长的很多影响因素（如温度、光照等）；只能做一定参考，不能把它完全运用实际中。
八、模型的改进与推广我们可以将该模型推广到同批鱼不同时打捞的情况中，按照该模型的基本思想进行解答，可将这种更复杂的情况分阶段考虑。
由于鱼可四季生长，每天的生长重量与鱼的自重成正比，365天长成为鱼，成鱼的重量为kg 2；可以如下方程求出鱼在不同阶段的质量，所需的天数。
2k)(1q 3650=+；2.0k)(1q n10=+；75.0k)(1q n20=+；5.1k)(1q n30=+；易得：k=0.0191；n1=243；n2=313；n3=349。
从而我们可以知道每条鱼苗经过243天长成0.2kg ；经过313天长成0.75kg ；经过349天长成1.5kg ；经过365天长成2.0kg 。
我们就可以制定多阶段的捕鱼优化模型：设开始放入鱼苗为x0kg ；在0.2—0.75kg 每天卖鱼xi kg ；在0.75—1.5kg 每天卖鱼xj kg ；在1.5—2kg 每天卖鱼xk kg ；可以建立如下模型： max=6∑=7011i i x +8∑=3712j j x +10{∑=15153k k x -[=+∑=+++2431ki m k)x 0(1m j -∑=15153k k x ]-0.2*0.05*{∑+243mk)x 0(1m+[∑++243im k)x 0(1m-∑=7011i i x ]+[∑+++243j i m k)x 0(1m-∑=3712j j x ]+[∑++++243ki m k)x 0(1mj -∑=15153k k x ]}st1/500(1+k)365=2；10000)1(0x 243≥+k ；10000k)x 0(1243m≤+∑m;∑++243im k)x 0(1m-∑=7011i i x 10000≤;∑+++243ji m k)x 0(1m-∑=3712j j x 10000≤;∑++++243kj m k)x 0(1mj -∑=15153k k x 10000≤;m+j+k+l=365.由于该模型在用lingo 软件中，求解程序比较复杂，所以我们在这就不求解了。
此外，我们的模型还需要从实际问题的更复杂性来进行调整，这个模型才会比较接近现实，有较强的实用价值。
参考文献[1] 姜启源，谢金星，叶俊. 数学模型（第三版）[M]. 北京.高等教育出版社，2003.8[2] 蔡锁章. 数学建模原理与方法[M]. 北京：海洋出版社，2000[3] 张杰，周硕，郭丽解. 运筹学模型与实验[M].北京:中国电力出版社,2007[4] 施光燕，董加礼.最优化方法.高等教育出版社[M]，1999.9。