GPS 1-卫星伪距定位原理
GPS理论与应用--伪随机码测距原理 ppt课件

GPS理论与应用
5.伪随机码测距原理
When a radio transmits a signal, it is in the form of a simple sine wave that has a particular frequency (the number of “humps” on the sine wave that pass a fixed point per unit of time-usually given as Hertz, or times per second), wavelength (the distance between “humps” or any matching successive point on the sine wave), and amplitude (the “height” of the “humps”).
This simply means that the carrier signal is modulated (varied) by changing its phase (updown position of the waves) back and forth (biphase) at a regular and programmed rate and interval.
载频作载波,分别被称作L1的主频率和 L2的次频率。
这些载波频率由扩频码(每一颗卫星均 有专门的伪随机序列)和导航电文所调
制。所有卫星均在这两个相同的载波频 率上发射,但由于伪随机码调制不同, 因此无明显的相互干扰。
伪距测距原理
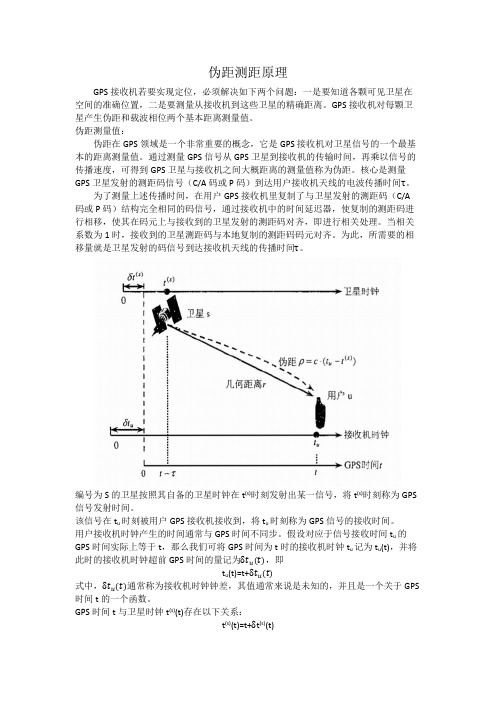
伪距测距原理GPS接收机若要实现定位,必须解决如下两个问题:一是要知道各颗可见卫星在空间的准确位置,二是要测量从接收机到这些卫星的精确距离。
GPS接收机对每颗卫星产生伪距和载波相位两个基本距离测量值。
伪距测量值:伪距在GPS领域是一个非常重要的概念,它是GPS接收机对卫星信号的一个最基本的距离测量值。
通过测量GPS信号从GPS卫星到接收机的传输时间,再乘以信号的传播速度,可得到GPS卫星与接收机之间大概距离的测量值称为伪距。
核心是测量GPS卫星发射的测距码信号(C/A码或P码)到达用户接收机天线的电波传播时间τ。
为了测量上述传播时间,在用户GPS接收机里复制了与卫星发射的测距码(C/A码或P码)结构完全相同的码信号,通过接收机中的时间延迟器,使复制的测距码进行相移,使其在码元上与接收到的卫星发射的测距码对齐,即进行相关处理。
当相关系数为1时,接收到的卫星测距码与本地复制的测距码码元对齐。
为此,所需要的相移量就是卫星发射的码信号到达接收机天线的传播时间τ。
编号为S的卫星按照其自备的卫星时钟在t(s)时刻发射出某一信号,将t(s)时刻称为GPS 信号发射时间。
该信号在t u时刻被用户GPS接收机接收到,将t u时刻称为GPS信号的接收时间。
用户接收机时钟产生的时间通常与GPS时间不同步。
假设对应于信号接收时间t u的GPS 时间实际上等于t,那么我们可将GPS时间为t时的接收机时钟t u记为t u(t),并将此时的接收机时钟超前GPS时间的量记为δt u(t),即t u(t)=t+δt u(t)式中,δt u(t)通常称为接收机时钟钟差,其值通常来说是未知的,并且是一个关于GPS 时间t的一个函数。
GPS时间t与卫星时钟t(s)(t)存在以下关系:t(s)(t)=t+δt(s)(t)其中卫星时钟钟差δt(s)(t)可以视为已知的,根据此式GPS时间与卫星时钟在信号发射时刻(t-τ)时的关系可表达成t(s)(t-τ)=t-τ+δt(s)(t-τ)GPS接收机根据接收机时钟在t u(t)时刻对GPS信号进行采样,然后对采样信号进行处理,可得到标记在GPS信号上的发射时间t(s)(t-τ)。
伪距定位的基本原理

伪距定位的基本原理
伪距定位技术是一种基于卫星信号的定位方法,主要使用在全球定位系统(GPS)中。
其原理是通过接收卫星信号并测量信号传输时间,从而得到接收器与卫星之间的距离差。
通过多个卫星的信号测量,可以计算出接收器的位置。
伪距定位技术的基本原理是利用卫星发射的信号,接收器接收到信号后记录下信号的到达时间。
因为信号传输时速度是已知的,通过记录到达时间,就可以计算出信号传播的距离。
而通过接收多颗卫星的信号并计算距离,就可以确定接收器的位置。
在伪距定位技术中,卫星发射的信号包含有精确的时间信息。
接收器通过接收这个信号,可以知道卫星在发送信号时的精确时间。
而当信号到达接收器时,接收器也可以记录下接收信号的时间。
通过计算信号传播时的时间差,就可以计算出信号传播的距离。
然而,在实际应用中,由于卫星与接收器之间的距离相差较远,信号传播的路径存在多种可能。
因此,要精确地计算信号的传播距离,需要考虑多种因素,如信号传播的时间、信号传播的路径、信号传播过程中遇到的障碍物等。
为了提高伪距定位的精度,需要使用更为复杂的算法,如差分GPS等。
总的来说,伪距定位技术是一种基于卫星信号的定位方法,其原理是通过接收卫星信号并测量信号传输时间,从而得到接收器与卫星
之间的距离差。
通过多个卫星的信号测量,可以计算出接收器的位置。
在实际应用中,为了提高精度,需要考虑多种因素,并使用更为复杂的算法。
GPS定位原理和简单公式

GPS定位原理和简单公式GPS是全球定位系统的缩写,是一种通过卫星系统来测量和确定地球上的物体位置的技术。
它利用一组卫星围绕地球轨道运行,通过接收来自卫星的信号来确定接收器(GPS设备)的位置、速度和时间等信息。
GPS定位原理基于三角测量原理和时间测量原理。
1.三角测量原理:GPS定位主要是通过测量接收器与卫星之间的距离来确定接收器的位置。
GPS接收器接收到至少4颗卫星的信号,通过测量信号的传播时间得知信号的传播距离,进而利用三角测量原理计算出接收器的位置。
2.时间测量原理:GPS系统中的每颗卫星都具有一个高精度的原子钟,接收器通过接收卫星信号中的时间信息,利用接收时间和发送时间之间的差值,计算出信号传播的时间,从而进一步计算出接收器与卫星之间的距离。
简单的GPS定位公式:1.距离计算公式:GPS接收器与卫星之间的距离可以通过测量信号传播时间得到。
假设接收器与卫星之间的距离为r,光速为c,传播时间为t,则有r=c×t。
2.三角测量公式:GPS定位是通过测量与至少4颗卫星的距离,来计算接收器的位置。
设接收器的位置为(x,y,z),卫星的位置为(x_i,y_i,z_i),与卫星的距离为r_i,根据三角测量原理,可得到以下方程:(x-x_1)^2+(y-y_1)^2+(z-z_1)^2=r_1^2(x-x_2)^2+(y-y_2)^2+(z-z_2)^2=r_2^2...(x-x_n)^2+(y-y_n)^2+(z-z_n)^2=r_n^2这是一个非线性方程组,可以通过迭代方法求解,求得接收器的位置。
3.定位算法:GPS定位一般使用最小二乘法来进行计算。
最小二乘法是一种数学优化方法,用于最小化误差的平方和。
在GPS定位中,通过最小化测量距离与计算距离之间的差值的平方和,来确定接收器的位置。
总结:GPS定位原理基于三角测量和时间测量原理,通过测量接收器与卫星之间的距离,利用三角测量公式和最小二乘法来计算接收器的位置。
GPS 1-卫星伪距定位原理
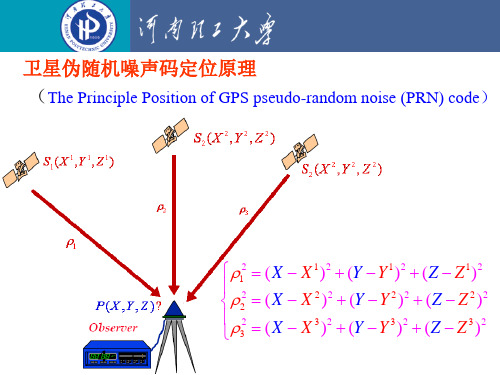
卫星伪随机噪声码定位原理 (The Principle Position of GPS pseudo-random noise (PRN) code)
12 ( X X 1 )2 (Y Y 1 )2 ( Z Z 1 )2 2 2 ( X X 2 )2 (Y Y 2 )2 ( Z Z 2 )2 2 3 ( X X 3 )2 (Y Y 3 )2 ( Z Z 3 )2
n j 1 n j 4 41 n j 1
j
Gi ( Ai (t )T Ai (t ))1 Ai (t )T Li (t ) 最小二乘解 41
4n j n j 4 4n j n j 1
现假定共观测了 nt 个历元,则可形成 nt 组误差方程组:
vi (t1 ) Ai (t1 ) Li (t1 ) n j 1 n j 1 j vi (t2 ) Ai (t2 ) X i n 1 n j 1 n j 1 Y Li (t2 ) i Zi D i Li (tni ) vi (jtni ) Ai (j tni ) n 1 n 1
线性化以后的伪距观测方程:
Dij (t ) (Dij (t ))0 - ki j (t )Xi - li j (t )Yi - mij (t )Zi ctij (t ) Ii j (t ) Ti j (t )
(-2)
式(1-2)中有三个测站未知数 X i , Yi , Zi 以及一个钟差 未知数 tij (t ),电离层和对流层改正一般通过专门的数学模 型另行处理。这样,接收机至少需要跟踪4颗卫星,才能 求解。
伪距测量及定位原理

伪距测量及定位原理伪距测量及定位原理是一种基于卫星信号的测距技术,可以用来确定接收器的位置。
这种技术是现代导航系统中最常用的定位技术之一。
伪距测量是通过测量卫星信号从发射到接收器的时间来计算距离,再结合卫星的位置信息,最终确定接收器的位置。
伪距测量的原理是基于卫星导航系统发射的信号在空间中传播的速度是已知的。
当卫星信号到达接收器时,可以通过测量信号从发射到接收器的时间来计算距离。
由于卫星的位置信息是已知的,通过多个卫星的信号测距,可以得到接收器相对于这些卫星的距离。
进一步,通过三个或以上的卫星信号测距,可以利用三边定位原理来确定接收器的位置。
伪距测量及定位原理的关键在于准确测量信号的传播时间。
接收器会接收到多个卫星的信号,每个信号都会有一个不同的传播时间。
为了准确测量传播时间,接收器需要和卫星进行时间同步。
卫星会通过导航信号发送时间信息,接收器通过接收这些信息来进行时间同步。
一旦接收器和卫星的时间同步完成,接收器就可以通过测量信号的传播时间来计算距离。
伪距测量及定位原理的精度受到多种因素的影响。
首先,信号的传播速度在大气中会发生变化,这会导致距离的测量误差。
其次,卫星的位置信息也会存在一定的误差。
此外,接收器本身的误差也会对定位精度产生影响。
为了提高定位的精度,可以使用差分定位技术,通过与参考站的信号进行比较,消除误差。
伪距测量及定位原理在现代导航系统中得到了广泛应用。
全球定位系统(GPS)就是一种基于伪距测量及定位原理的导航系统。
通过接收多颗卫星的信号,GPS可以实现准确的定位和导航。
除了导航系统,伪距测量及定位原理还可以应用于地震监测、航空航天等领域。
总结一下,伪距测量及定位原理是一种基于卫星信号的测距技术,通过测量信号的传播时间来计算距离,再结合卫星的位置信息,最终确定接收器的位置。
这种技术在现代导航系统中得到了广泛应用,提供了准确的定位和导航功能。
尽管伪距测量及定位原理存在一定的误差,但通过差分定位等技术,可以提高定位的精度。
GPS伪距单点定位

GPS伪距单点定位⼀计算流程GPS单点定位的原理⽐较简单,主要就是空间距离的后⽅交会,⽤⼀台接收机同时接受四个或者以上卫星的信号得出卫星的位置坐标和卫星与接收机的距离,运⽤后⽅交会解算出接收机的三维坐标。
其中,接收机钟误差作为⼀个参数参与解算。
如果观测的卫星数⽬多于四颗,则采⽤最⼩⼆乘法进⾏平差求解。
1,读取数据包括读取O⽂件和N⽂件⾥的数据O⽂件⾥包括头⽂件和观测数据⽂件。
头⽂件⾥要读取出观测⽇期、接收机近似坐标,观测间隔,观测数据类型等。
观测数据⽂件包括观测时间,卫星数量,卫星质量标记,卫星的伪随机编号,之后分每个历元有对各颗卫星的观测数据,例如,P1、P2、L1、L2,要将这些数据读取出来。
N⽂件⾥包含的数据种类⽐较多,主要包括卫星的星历数据,通过这些数据可以求解出卫星的位置坐标。
数据包括卫星钟差参考时刻、卫星星历参考时刻,以及参考时刻升交点⾚径、参考时刻轨道倾⾓等好多参数信息。
2,计算卫星位置卫星计算位置⾥⾯采⽤模块函数的⽅式,可以直接调⽤。
在读取N⽂件中的数据之后,可以调⽤这些已经读出来的数据进⾏使⽤,函数提供两个形参,⼀个是星历数据的编号,另外⼀个是卫星信号发射时刻。
计算过程⽐较繁琐,⼀步⼀步的算就⾏。
3,交会定位计算⼀般每个历元的卫星数⽬不⽌四颗,通常采⽤最⼩⼆乘法进⾏平差求解。
公式为:V=AδX-L。
在具体计算的时候,⾸先要对(1)式进⾏线性化,得到矩阵A,L,这中间要⽤到很多矩阵的运算。
在求得卫星位置之后,要对O⽂件中每个历元⾥的卫星编号与N⽂件中的卫星编号进⾏匹配,如果匹配成功,再对时间进⾏匹配,如果时间差⼩于两个⼩时,那么该数据可以⽤于运算。
就这样,⼀个历元⾥匹配出的卫星数⽬超过4个的话,就可以通过平差计算出接收机的坐标了。
4,GPS时间的计算GPS时间的计算⽐较简单,计算出参考1980年1⽉6⽇0时0分0秒的不⾜⼀周的秒数。
主要在于判断所在的年是否为闰年,是否超过2⽉份,其他的问题就⽐较简单,采⽤⼀个Select Case的条件语句就可以了,函数最后得到不⾜⼀周的秒数就⾏。
GPS 伪距单点被动式定位的原理

GPS 伪距单点被动式定位的原理天工研发和生产的GB10,GM10 GPS 接收模块,其定位的原理就是典型的伪距单点被动式定位。
关于GPS伪距单点被动式定位,先谈一谈在伪距单点被动式定位中的三种时间标准:(1) 每颗GPS卫星的时间标准。
(2) 用户接收机的时间标准(3) 统一上述两种时间标准的GPS时间系统(简称GPS时系)以GPS时系时间为标准,做如下的假设:(1) 假设卫星时钟和标准GPS时系的误差为dt。
(2) 假设用户接收机的时钟和标准GPS时系的误差为DT。
显然,在以上的假设基础上,以GPS标准时系时间为标准时间的传输时间误差为:△T=dt-DT (1)我们知道,从卫星到用户接收机的距离为:S1=C(T2-T1) (2)C:光速,也就是电磁波在真空中的传输速度;T1:GPS导航信号从卫星上开始传输的时间;T2:电磁波到达用户接收机的时间。
和标准的GPS时系相比,无论是卫星还是用户接收机都存在着时间误差,根据(1)式可知道,这个时间误差为△T,所以,根据(2)式算出卫星和用户接收机的瞬时距离S1并不是两者间的出真实距离瞬,所以叫做出伪距瞬(Pseudorrange)。
而且,导航信号从GPS卫星到用户接收机之间的瞬传输路径瞬也并非是瞬真空瞬环境,若考虑到电离层和对流层对导航信号传输的影响,则卫星到用户接收机之间更为准确的距离为:S2=C(T4-T3) (3)S3=S2+C(dt-DT)+D1+D2 (4)S2:卫星到用户接收机的瞬真实瞬距离,显然,T4,T3是以GPS系统时间为基础的导航信号的出发时间和到达用户接收机的时间。
S3:考虑了电离层及对流层对导航信号传输影响以及时间误差影响后的伪距。
D1:电离层效应引起的距离偏差,不同的载频影响不一样。
D2:对流层效应引起的距离偏差,不同的气象条件影响不一样。
请看下图:上图中,P1,P2,P3,P4为在轨卫星到用户接收机的几何距离,假设在轨卫星1的三维坐标为(X1,Y1,Z1),用户接收机的三维坐标为(Xu ,Yu ,Zu ),很明显:P1= Zu)-(Z1+Yu)-(Y1+ Xu)-(X1222 (5)P2= Zu)-(Z2+Yu)-(Y2+ Xu)-(X2222 (6)P3= Zu)-(Z3+Yu)-(Y3+ Xu)-(X3222 (7)P4= Zu)-(Z4+Yu)-(Y4+ Xu)-(X4222 (8)根据(4)式,我们可以知道,根据导航信号传输时间算出的伪距S3是用户三维坐标和在轨卫星三维坐标的函数,则我们有:S3=Pn+ C(dt-DT)+D1+D2 (n=1,2,3,4比。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
X i X i0 X i Yi Yi 0 Yi Z i Z i0 Z i
Di j (t ) 1 ( )0 j ( X j (t ) X i0 ) ki j (t ) X i ( Di (t ))0
Di j (t ) 1 ( )0 j (Y j (t ) Yi 0 ) li j (t ) Yi ( Di (t ))0 Di j (t ) 1 ( )0 j (Z j (t ) Zi0 ) mij (t ) Zi ( Di (t ))0
j j j j
(1-1)
Di j c (ti (GPS ) t j (GPS ))
其中:
理想距离
I i j (t ) : 电离层延迟改正; Ti j (t ) : 对流层延迟改正。
j 显然,伪距观测方程(1-1)中 Di (t )是非线性项,表示测站与 卫星之间的几何距离:
Di j (t ) [( X j (t ) X i )2 (Y j (t ) Yi )2 (Z j (t ) Zi )2 ]1 2
简化的误差方程: 最小二乘解: 精度评定: 其中 (QT )kk 为 i
( n j ni )1
Vi
( n j ni )4
Ai
Ti
41
( n j ni )1
Li
Ti ( AiT Ai )1 AiT Li
41 44 41
( mTi ) k 0
QT
现假定电离层和对流层延迟等效距离误差已通过 适当的数学模型求出,据此, 结合式(1-2),令:
Ri j (t ) Di j (t ) I i j (t ) Ti j (t ) Di c ti j (t )
于是,伪距观测方程可以改写为:
Ri j (t ) ( Di j (t ))0 ki j (t ) X i li j (t ) Yi mij (t ) Zi Di
(1-3)
式中j=1,2,3,4。采用矩阵形式,则有:
ki1 (t ) 2 ki (t ) ki3 (t ) 4 ki (t ) 1 X i ( Di1 (t ))0 Ri1 (t ) li2 (t ) mi2 (t ) 1 Yi ( Di2 (t ))0 Ri2 (t ) 3 3 Z i ( Di3 (t ))0 Ri3 (t ) li (t ) mi (t ) 1 li4 (t ) mi4 (t ) 1 Di ( Di4 (t ))0 Ri4 (t ) li1 (t ) mi1 (t )
线性化以后的伪距观测方程:
Dij (t ) (Dij (t ))0 - ki j (t )Xi - li j (t )Yi - mij (t )Zi ctij (t ) Ii j (t ) Ti j (t )
(1-2)
式(1-2)中有三个测站未知数 X i , Yi , Zi 以及一个钟差 未知数 tij (t ),电离层和对流层改正一般通过专门的数学模 型另行处理。这样,接收机至少需要跟踪4颗卫星,才能 求解。
(1) GPS卫星的测距码信号与伪距测量 原理
(a)概念(码、随机噪声码、伪随机噪声码、GPS测距码) (b) GPS测距码测距原理
(2)伪距导航定位的观测方程及其求解
(a)观测方程 (b)求解过程 (c)精度评定
(1)GPS卫星的测距码信号与伪距测量 原理
(a)基本概念 (i)码:表达信息的二进制数及其组合。 (ii)随机噪声码:每一时刻,码元是0或是1完全 是随机的一组码序列,这种码元幅值是完全无规律 的码序列,称为随机噪声码序列。 特性:它是一种非周期序列,无法复制。但是, 随机噪声码序列却有良好的自相关性,GPS测距码 测距就是利用了为随机噪声码良好的自相关性才获 得成功。
卫星伪随机噪声码定位原理 (The Principle Position of GPS pseudo-random noise (PRN) code)
12 ( X X 1 )2 (Y Y 1 )2 ( Z Z 1 )2 2 2 ( X X 2 )2 (Y Y 2 )2 ( Z Z 2 )2 2 3 ( X X 3 )2 (Y Y 3 )2 ( Z Z 3 )2
何谓自相关性? 自相关性是指两个结构相同的码序列的相关程 度,它由自相关函数描述。
自相关函数:
( iii ) 伪 随 机 噪 声 码 (Pseudo Random Noise-PRN Code)
(ⅳ) GPS测距码
(b)GPS伪随机码的测距原理
(i)卫星依据自己时钟(钟脉冲)发出 某一结构的测距码,经过△t时的传播到 达GPS接收机。 (ii)接收机在自己钟脉冲驱动下,产生 一组结构完全相同的复制码。 (iii)通过时延器使之延迟时间τ,对两 码进相关比较。
(ⅳ)直至两码完全对齐,相关系数R (t)=max=1,则该时间延迟τ即为传播 时间△t(τ=△t)。
(ⅴ)距离ρ=c·△t=c·τ。
(2)伪距导航定位的观测方程及其 求解
(a)观测方程 (b)求解过程 (c)精度评定
(a)伪距观测方程的建立 t j t j (GPS ) t j (t )
简化:
Ai (t ) Gi Li (t )
44 41 41
由此,伪距法绝对定位解可表示为:
Gi Ai (t )1 Li (t )
41 44 41
当跟踪卫星颗数 n >4 时,则可应用最小二乘法 求解,这时有误差方程:
vi (t ) Ai (t ) Gi Li (t )
Di j (t ) ct c[ti (GPS ) t j (GPS )] c( ti (t ) t j (t )) Di j (t ) c tij (t )
现顾及大气折射影响
伪距观测方程:
j (t ) D j (t ) I j (t ) T j (t ) c t (t ) c t j (t ) Di i i i i Di (t ) Ii (t ) Ti (t ) c t i (t )
ti ti (GPS ) ti (t )
t j (GPS ) 信号发射时卫星钟的GPS标准时间(理想时刻)
ti (GPS ) 信号接收时接收机钟的GPS标准时间(理想时刻)
t j 信号发射时卫星钟的钟面时
ti 信号接收时接收机的钟面时
tபைடு நூலகம்j (t ) 卫星钟在t观测历元的改正数(卫星钟差)
ti (t ) 接收机钟在t观测历元的改正数(接收机钟差)
(a)伪距观测方程的建立(续)
卫星信号由卫星到达测站的钟面传播时间:
ti ti t ti (GPS ) t (GPS ) ti (t ) t (t )
j j j j
在不顾及大气折射等误差影响的情况下,由钟面 传播时间乘以光速,就得到卫星至测站的伪距。
i ( AiT Ai ) 1
4 4
(QTi ) kk
阵主对角线上第k个元素。
4 4 Ti
0
v Tpv f
n j 1 n j 4 41 n j 1
j
Gi ( Ai (t )T Ai (t ))1 Ai (t )T Li (t ) 最小二乘解 41
4n j n j 4 4n j n j 1
现假定共观测了 nt 个历元,则可形成 nt 组误差方程组:
vi (t1 ) Ai (t1 ) Li (t1 ) n j 1 n j 1 j vi (t2 ) Ai (t2 ) X i n 1 n j 1 n j 1 Y Li (t2 ) i Zi D i Li (tni ) vi (jtni ) Ai (j tni ) n 1 n 1
