§4.5法布里—泊罗(Fabry—Perot)干涉仪与干涉滤光片
法布里珀罗干涉仪多光束干涉

i ( N −1)ϕ
]
Ae
2
iϕ 0
e −1 = A0 iϕ , e −1
2 iϕ 0 − iϕ 0 −iNϕ
iNϕ
a 1 (1 − q ) Sn = 1− q
n
A =Ae e
iNϕ
−1 e −1 e = A0 iϕ ⋅ − iϕ e −1 e −1
1 sin ( Nϕ) iNϕ −iNϕ +e ) 2 2 − (e 2 1− cosNϕ 2 2 = A0 = A0 = A0 1− cosϕ 2 1 2 − (eiϕ + e−iϕ ) sin ( ϕ) 2
2
A
2
= A 02
sin
1 Nϕ 2 1 sin 2 ϕ 2
2
ϕ A0为每束光的振幅,N为光束的总数, 则为各相邻 光束之间的位相差。
由上式可知,当 ϕ = 2 jπ ( j = 0,±1,±2,±3, L) 得到最大值 时,
2 A最大
1 sin Nϕ 2 = lin A02 = N 2 A02 ϕ → 2 jπ 2 1 sin ϕ 2
利有无穷等比级数求和公式:
[
]
S = ∑ a1 q
n =1
∞
n −1
a1 = 1− q
iωt
Al
i [ωt +ϕ0 ]
⎡ ⎤ 1 = (1 − ρ ) A0 l ⎢ ⎥ 1 − ρl −uϕ ⎦ ⎣
合振动的强度为:
A 2 = (1 − ρ ) 2 A02 1 1 ⋅ 1 − ρl −iϕ 1 − ρl iϕ 1 = (1 − ρ ) 2 A02 1 + ρ 2 − 2 ρ cos ϕ 1 = (1 − ρ ) 2 A02 1 + ρ 2 − 2 ρ + 2 ρ (1 − cos ϕ ) 1 = (1 − ρ ) 2 A02 ϕ (1 − ρ ) 2 + 4 ρ sin 2 2
第五节 法布里-珀罗干涉仪多光束干涉精选版演示课件.ppt

yjyuuy
10
Aei0
A0
eiN 1 ei 1 ,
Sn
a1 (1 q n ) 1 q
A2 A2ei0 ei0
A0
eiN ei
1 1
eiN 1 ei 1
A02
2 (eiN 2 (ei
eiN ) ei )
A02
1 cos N 1 cos
第五节 法布里—珀罗干涉仪多光束干涉
yjyuuy
1
• 迈克耳孙干涉仪是应用分振幅原理的干涉仪,波幅分解后成为一个双 光束系统,如果两束光的强度相同即振幅都等有A1,则光强为
2 A12 (1
cos )
4 A12
cos 2
2
图1-15
yjyuuy
2
• 它不介易乎测最定大最值大值4 A或12和最最小小值值的0精之确间位,置随。位对相实差际应连用续来改说变,,干用涉实花验样方最法
图1-16
yjyuuy
3
图1-17
• 这些透射光束都是相互平行的,如果一起通过透镜L2,则在焦平面上
形成薄膜干涉条纹,每相邻两光束在到达透镜L2的焦平面上的同一点
时,彼此的光程差值都一样:
yjyuuy
2n2h cos i2
4
位相差为
4
n2 h cos i2
• 若第一束透射光的初位相为零,则各光束的位相依次为
多光束干涉。计算这些光束的叠加结果,
A1eit , A2ei(t), A3ei(t2), A4ei(t3) , ANeit(N1)
设
A1 A2 A3 Av A0
法布里-珀罗干涉仪PPT课件

R' P dn d
光栅,600线/mm,宽10cm,一级 主极大处:
R’=60000
R' mN
19
E( 照度) LT
AF f2
L:照射在干涉仪上的像的亮度。
T:干涉仪的透射率。 AF:干涉仪的面积。 f:成像透镜的焦距。
L 2P A
E P A
20
21
需要预色散。 注意色散范围。
R
m
2nd cos
2
2nd
R c
2nd 14
原理方程:
IT
1
I0 F sin2
2
其中
单色条纹的半值宽度:
F
4R (1 R)2
2nd cos m
4nd cos /
IT
I0 2
F sin2 1
2
2m
2
F sin2 F ( )2 1
44
2(1 R)
R
半值宽度
15
2
2f
cos 1 2
2
1
D 8f
2 2
零点处展开
24
激光 谐振腔
两个高反射率表面是具有相同曲率半径r的凹球 面镜,并且两个表面的间隔d等于其曲率半径, 因此两个凹球面镜的焦点是位于轴上的同一点。
25
共焦式干涉仪的径向色散率随两镜面的间隔
增加而增大,平面式干涉仪的色散率与镜面
间隔距离无关,但两者都是在中心处的色散
D d 1 d
R 2
m 2nd
R
m
1
R R
mN e
共焦法布里-珀罗干涉仪.
27
28
5
Snell定律
法布里珀罗滤波器原理

法布里珀罗滤波器原理法布里珀罗滤波器(Faber-Perot Interferometer)是一种利用多次反射和透射现象实现滤波的光学仪器。
它由两个平行的反射镜构成,之间的空间被称为皮尔斯堡夫透射腔(Fabry-Perot Etalon),其中一个镜子可调节距离,以改变滤波器的特性。
法布里珀罗滤波器的原理基于干涉现象。
当一束光射入法布里珀罗滤波器时,部分光线被反射,经过多次反射和透射后形成干涉图案。
这些干涉图案会导致特定波长的光被增强或抑制,从而实现滤波的效果。
在法布里珀罗滤波器中,光线在两个反射镜之间多次来回反射,形成了一系列的干涉光束。
这些干涉光束会叠加在一起,形成干涉图案。
干涉图案的形状取决于入射光的波长和反射镜之间的距离。
当入射光的波长与干涉图案的峰值或谷值对齐时,干涉图案会增强或抑制该波长的光,实现滤波效果。
调节法布里珀罗滤波器的滤波特性可以通过改变反射镜之间的距离来实现。
当反射镜之间的距离为整数倍的波长时,滤波器将增强该波长的光,形成共振现象。
而当反射镜之间的距离为半波长时,滤波器将抑制该波长的光。
通过调节反射镜的距离,可以选择性地增强或抑制特定波长的光。
法布里珀罗滤波器的应用非常广泛。
它可以用于光谱分析、激光调谐、光纤通信等领域。
在光谱分析中,法布里珀罗滤波器可以选择特定波长的光进行测量,提高测量的准确性和分辨率。
在激光调谐中,法布里珀罗滤波器可以通过调节反射镜的距离来选择性地调谐激光的波长。
在光纤通信中,法布里珀罗滤波器可以用于选择特定波长的光进行传输,提高通信的速率和可靠性。
尽管法布里珀罗滤波器在光学领域有许多应用,但也存在一些局限性。
首先,法布里珀罗滤波器的滤波特性受到入射光的角度和偏振状态的影响。
其次,法布里珀罗滤波器的制造和调节相对复杂,需要高精度的光学元件和精密的调节装置。
此外,法布里珀罗滤波器对入射光的强度非常敏感,需要进行精确的功率控制。
法布里珀罗滤波器是一种基于干涉现象实现滤波的光学仪器。
法布里—珀罗干涉仪
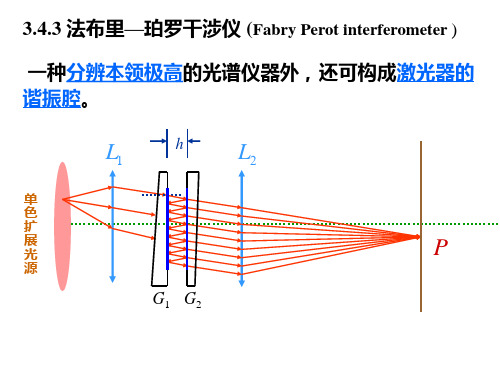
IM
0.81IM
G F
(2)分辨本领
如果不考虑标准具的吸收损耗,1 和 2 的透射光合
强度为
I
1
I1i F sin2
1
2
I2i
1 F sin2 2
2
(101)
式中,1 和 2 是在干涉场上同一点的两个波长条纹
所对应的相位差。
(2)分辨本领
设 I1i= I2i= Ii,1-2 = ,则在合强度极小处(F点), 1= 2m+ / 2, 2=2m- / 2,因此极小值强度为
许的最大分光波长差,称为自由光谱范围(Δ)f。
(1)自由光谱范围——标准具常数
对于靠近条纹中心的某一点( 0)处,2 的第 m 级 条纹与 1 的第 m+1 级条纹发生重叠时,其光程差相
等,有
(m 1)1 m2 =m[1 +()f ]
因此,
( )f
=
1
m
12
2nh
(1)自由光谱范围——标准具常数
2nhcos m
不计平行板材料的色散,两边进行微分,可得
d m d 2nh sin
(109)
(3)角色散 或
d c ot d
(110)
角度 愈小,仪器的角色散愈大。因此,在法—珀干
涉仪的干涉环中心处光谱最纯。
2)用作激光器的谐振腔
如图所示,一台激光器主要由两个核心部件组成:激
光工作物质(激活介质)和由 M1、M2 构成的谐振腔。
2(1 R)
R
(115)
而由(39)式有
4πnL 2
k 4π nh cos (39)
(3)单模线宽
因此,当光波包含有许多波长时,与相位差半宽度 相应的波长差为
法布里珀罗腔fp腔的原理及应用

法布里珀罗腔(fp腔)的原理及应用1. 简介法布里珀罗腔(Fabry-Perot cavity)是一种光学腔,由两个高反射率的光学镜片夹持而成。
它是一种基于干涉效应的光学器件,可以用于光谱分析、激光器和光纤通信等领域。
本文将介绍法布里珀罗腔的原理及其应用。
2. 原理法布里珀罗腔的原理基于光的干涉现象,两个平行的高反射率光学镜片之间形成一个干涉空腔。
当光线从一个镜片入射后,一部分光会被反射回来,而另一部分光会透过镜片进入腔内。
在腔内,光线来回多次反射,形成了干涉现象。
具体的原理可以用以下步骤来说明:•光线从入射面射入法布里珀罗腔,一部分光被反射回来,一部分光透过进入腔内。
•光线在腔内来回反射,形成了构成干涉的光束。
•反射光与透射光相互干涉,形成干涉图样。
法布里珀罗腔的干涉图样取决于入射光的频率和反射镜的特性。
当入射光的频率与腔内干涉频率相匹配时,干涉峰会出现,从而形成谐振。
由于一系列干涉峰的出现,法布里珀罗腔可以实现对特定频率的光的增强。
3. 应用法布里珀罗腔在光学领域有广泛的应用,下面将介绍几个常见的应用领域。
3.1 光谱分析法布里珀罗腔可以用于光谱分析,通过改变入射光的频率,可以得到不同频率的干涉峰,从而实现对光的频谱分析。
光谱分析在物质分析和光学研究中具有重要意义,法布里珀罗腔的高分辨率和灵敏度使其成为一种常见的光谱分析工具。
3.2 激光器法布里珀罗腔也可以作为激光器的腔体。
当激发介质位于法布里珀罗腔中时,光在腔内来回反射增强,从而形成激光输出。
法布里珀罗腔激光器具有窄谱线宽、较高的功率和较长的寿命等优点,被广泛应用于激光技术领域。
3.3 光纤通信法布里珀罗腔还可以用于光纤通信系统中。
在光纤通信中,法布里珀罗腔可以作为滤波器或反射器件,实现对特定波长光的选择性传输和控制。
通过调节法布里珀罗腔的参数,可以实现光纤通信的波长调制和调制多路复用等功能。
4. 总结法布里珀罗腔是一种基于光的干涉现象的光学器件,具有广泛的应用领域。
法布里-珀罗干涉仪

m
2nd sin
2nd sin
• 干涉条纹之间靠得很近。 • 中心干涉条纹距离较大且条纹本身较粗。
法布里-珀罗干涉仪
自由光谱范围(色散范围)
• 各色光干涉极大不发生级次交叠的最大波
长范围。
2nd cos m
m
重叠
m 1
d m d
dm
d
m 1 (相邻条纹)
法布里-珀罗干涉仪
法布里-珀罗干涉仪
F-P干涉仪与F-P标准具
两块镀有高反膜的平行玻璃板,若 间隔可以改变,则称为F-P干涉仪; 如果间隔固定,则称为F-P标准具。
法布里-珀罗干涉仪
法布里-珀罗干涉仪的原理 与基本方程
Snell定律
法布里-珀罗干涉仪
法布里-珀罗干涉仪的原理
• 透射光振幅为:
• 透射光强为:
由Stokes定律:
性能产生影响。
法布里-珀罗干涉仪
F-P干涉仪的分辨本领优于棱镜、光栅
F-P干涉仪,1cm长度,波长500nm , m=40000 , 反 射 率 90 % , Ne≈28 :
R>1×106
R mNe
重火石棱镜,边长10 cm ,在波 长 4358.6Ǻ 处 , dn/dl = 2.7×10 - 5/Ǻ:
d
4nd
cos
d 2
2m d
法布里-珀罗干涉仪
分辨本领
• 由Rayleigh判据: 单色条纹的半值宽度=不同波长条纹峰值角间距
2(1 R) d 2m d
R
R
m R
1 R
mNe
Ne
1
R R
有效光 束数 法布里-珀罗干涉仪
法布里-珀罗干涉仪的分辨本领
塞曼效应实验中关于法布里-珀罗(Fabry-Perot)标准具的几个问题论文

塞曼效应实验中关于法布里-珀罗(Fabry-Perot )标准具的几个问题摘要:对塞曼效应试验过程中F-P 标准具平行度调整方法的原理,以及仪器自由光谱范围、平整度与得到谱线的部分关系做出了简要的分析。
关键词:塞曼分裂 ; F-P 标准具 ; 自由光谱范围0引言:法布里-珀罗(简称F —P )干涉仪是一种重要的高分辨率光谱仪,在石英紫外至近红外光谱范围内有极高的分辨本领,用于一般塞曼效应,可以得到较好的谱线。
在实验中,如何准确的调整F-P 标准具平行度是关键点。
实验步骤(实验室里的方法步骤单)中给出了仪器调整的方法,有两种方法我们选取常用而且效果较好的方法,气压扫描法。
将针孔观察器具置于干涉图中心(已校准光路末端),改变标准具内气压,从针孔后看等厚干涉条纹。
气压增高时,条纹移动方向是镜面间距减小的方向,调节相应的旋钮改变镜面间距。
调到接近平行时,条纹间距最大,直线性变差,条纹宽度变大,气压扫描时,变为大片的亮斑和暗区。
那么,气压增高时,条纹移动方向为何是镜面间距减小的方向,为何接近平行时会观察到大片的亮斑和暗区? 实验未加磁场时,汞546.1nm 的透射光谱图,实验步骤中指出两峰a,b 之间所对应得波数Δv 即为自由光谱区,也应该做出解释。
1 原理F-P 标准具工作的简单原理:由两块精确平行的玻璃板或石英板组成,直径在2-15厘米之间.两板之间安放热膨胀系数极小的石英垫圈,标准具的垫圈厚度固定,一般在零点几毫米至几厘米之间。
两块板的表面平整度高达波长的1/20至1/200,反射率一般在90%以上。
如图(1—1),以θ角入射的光线在两板之间多次反射,相邻两透射光束的光程差Δ为2cos nt θ∆= (1)输出光强的极大条件为2cos nt N θλ=(2),N 为干涉序,n 为镜面间介质折射率,t 为两镜面间距。
若采用面光源,所有以i 角入射到FP 标准具的光线,均有相同的光程差,在焦面上形成一个以O 为原点,OP 为半径的圆。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2d cosθ = mλ
m为整数
F—P干涉仪是用F—P标准具代替光谱仪中的棱镜或光栅 作分光元件,但直接得到的是等倾干涉条纹,要经过付里 叶变换后,才能得到谱线。下面介绍的是干涉条纹的特 性,它直接决定了谱线的性质。
4.5.2 法布里—泊罗干涉仪的特性 (1)F—P标准仪器的强度分布: 假设玻璃介质无吸收,透射率t =1-r,r为反射率, 强度分布可用爱里(Airy)函数表示
§4.5 法布里—泊罗(Fabry—Perot)干涉仪与干涉 滤光片 提高光谱仪分辨本领的方法,除了采用大块光栅 和阶梯光栅外,还可以利用干涉仪。现代天文观测 从射电到红外、光学都普遍采用干涉技术,有在两 个望远镜之间进行干涉,也有利用干涉原理制成的 分光仪器。最常用的干涉仪有: • 法布里—泊罗(F—P)干涉仪(光谱仪) • 干涉滤光片 • 傅里叶变换光谱仪(用扫描迈克尔逊干涉仪对 光谱进行分光测量的仪器)
2d ≈λ 2d cos θ = mλ m
7.6)有错
(3)自由光谱范围:
相邻两干涉级间的波长间隔 • (4)理论分辨本领:
λ 2πd r r R= = = mπ = Nrm Δλ λ (1 − r ) 1− r
Δλ m =
λ2
2nd
(1) 干涉滤光片的结构、原理与标准具一样,在一块玻璃 两面镀部分反射膜的方法,也可以用折射率不同的两种 介质交替组成等厚(1/4λ)的多层膜,可达10层以上。
玻璃内部反射可忽略
金属膜
干涉亮条纹:2nd=mλ 即: λm = 2nd/ m 透明介质, 折射率为n, 厚度为d ( 正入射时θ=0)
透明介质层
A= 1 1 + 4r (1 − r ) − 2 sin 2 ( 2πd
λ
cosθ )
I (θ ) = I 0 ⋅ A
A为爱里函数,I0为入射光强度
(2)角色散度: 由亮条纹极大条件,可得: dθ m =− θ 通常很小,则有 sin θ ≈ θ , cos θ ≈ 1 dλ 2d sin θ 则由
优点是分辨率较高(103~104) ,没有光谱级次(用干涉 膜实现,与光栅不同),自由光谱范围宽,且没有狭缝。 可在近紫外~中红外实现分光光谱,一般是窄带滤光 片,天文专用的带宽0.5nm左右,中心波长为感兴趣 的λm, 如:Hβ,则λm =486nm。普通带宽为10-20nm 较容易做。也可通过加滤光片实现。 (2) 使用干涉滤光片要注意的几个问题: 垂直入射:要求使用时是正入射的准平行光 (θ=0) , 若角度变大,中心波长向短波移动,背景光增加。 防潮 — 湿度可导致透射率下降 恒温— 温度变化也会导致中心波长变化
照相透镜将干涉图 样聚焦于探测器, 干涉光强随δ改变 作正弦变化,当δ λ 为λ和 的整数倍 2 时,光强相应的极 大和极小。 再用付里叶变换将 以上干涉图样变换 为频率ν随强度的 变化,即为光谱。
设B(ν)为光源的光谱,b(δ)为探测器记录的干涉信号。 假设B(ν)和b(δ)对称且为实数,则对混合光有: 2πiδν +∞ +∞ 2πδν c b(δ ) = ∫ B (ν )e dν = ∫ B (ν ) cos dν −∞ −∞ c
Canada-France-Hawaii Telescope 3.6m Fabry-Perot Spectrograp
单色器,控制入射的光谱范围
4.5.3 光学干涉滤光片 Interference film
• 光学干涉滤光片是建立在光学薄膜干涉原理 上的精密光学滤光器件。通过设计和改变膜 系的结构和膜层的光学参数,可以获得各种 光谱特性,用于控制、调整和改变光波的透 射、反射、吸收、偏振或相位状态。
λ
• Michelson's plan was to detect the phase shift shown on the left. • However, Lorentz was right: there is no phase shift because the interferometer contracts.
§4.6 傅里叶变换光谱仪(Fourier Transform Spectrometer) 4.6.1. FTS的结构: 也称扫描迈克尔逊干涉仪(Michelson interferometer), 核心是迈克尔逊干涉仪。 望远镜来的光,经准直镜 后,平行光射到迈克尔逊 干涉仪的光束分离器,形 成两束光,改变移动镜位 置,可改变水平光束的光 程和位相。光程差用δ表 示,单色光用频率表示 ν = c ,δ的改变引入一个相位 2πiδν 项e c 。
=
λ
m
(n = 1)
•
r 为平面镜的反射系数; Nr 为有效干涉光线数(精细度)
•
• 判断两干涉条纹能否分开,一般用泰勒(阿贝)判据:
两条强度曲线在半强度点处交叉,交叉点强度等于任一条曲线 的最大强度,认为可以分开。
可见,R与m和r有关,加大m,就要加大d,但自由光谱范 围要缩小,可提高r来改善分辨本领,但r大会降低干涉条纹 的辐照度。现r可达85~90%,若取d=0.1m,r =0.9, λ在可见 光范围内,R~107,比普通光栅光谱仪高100倍,且体积较 小,但制作较难,且数据处理要经付里叶变换。
b(δ)为干涉图谱,为探测器的 输出,是程差δ的函数,光源的 光谱B(ν)则为干涉图谱的付里 叶变换,所以称付里叶变换光谱 仪。 干涉仪得到的是各种波长光的叠 加,它较之狭缝色散仪,增加了 光子流量,提高了信噪比,所以 在红外波段得到广泛应用。因红 外噪音主要来自背景辐射。
4.6.2. FTS的原理及分辨本领: 其光谱分辨本领由光程差改变获取频 谱,由干涉仪最大的程差决定。若移 动镜最大可移动L,则最大移动度为 2L,则理论分辨本领
4.5.1 F—P干涉仪的结构与原理 结构如图 核 心 器 件 是 F—P 标 准 具,两块玻璃距离不 变。 表面光洁度要求高, λ 2λ 达100 ~ 100 ,由玻 璃和石英镜面组成。
光程差: 是一条光线产生的光程差,认为n=1,θ为入射角,d为 两块玻璃间的距离, 在焦平面上条纹极大亮度的条件为:
