高二数学函数的极值
高二数学函数的极值课件
（3）利用导数求函数的极大值和 极小值的方法。
随堂练习：
1某三次函数当x=1时有极大值 4，当x=3时有极小值0，且函数 图象过原点，则此函数C为（ ）
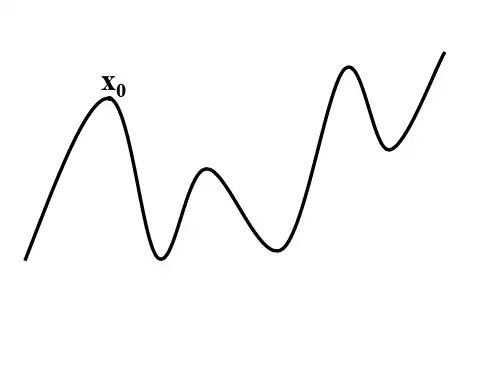
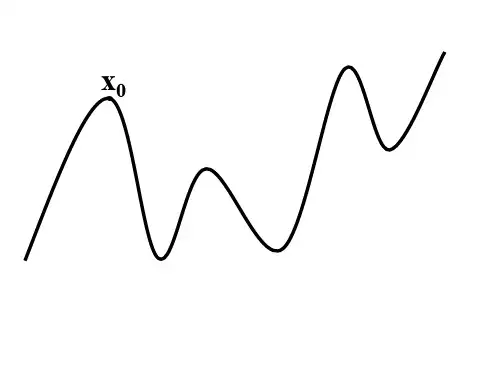
x. 0
函数的极值
一般地，设函数f(x)在点x0附近有定义， 如果对x0附近的所有的点,都有f(x)<f(x0), 就说f(x0)是函数f(x)的一个极大值. 记做 y极大值＝f(x0). 如果对x0附近的所有的点,都有f(x)>f(x0), 就说f(x0)是函数f(x)的一个极小值. 记做 y极小值＝f(x0).
∴当x=-2时，y有极大值，y极大值＝ 28/3
当x=2时，y有极小值，y极小值＝-4/3
求极值的步骤：
1.求导数f’(x)
2.求方程f’(x)=0的根 3.检查f’(x)在方程的根的左右的值 的正负，由此断定极值
例2：求函数y=(x2-1)3+1的极值
P136练习
求下列函数的极值
(1)y
1 2
判断极大和极小值的方法： 1.如果在x0附近的左侧f’(x)>0,右侧 f’(x)<0,那么f(x0)是极大值. 2.如果在x0附近的左侧f’(x)<0,右侧 f’(x)>0,那么f(x0)是极小值. 左正右负（左增右减）为极大
左负右正（左减右增）为极小
例 1 . 求 函 数 y
1 3Βιβλιοθήκη x34xx
cosx
(2π x 2π )
(2)y x 2sinx (2π x 2π )
是不是导数等于0的点都是极值点？
不是
是不是极值点都是导数等于0的点
高考数学中的函数极值问题详解
高考数学中的函数极值问题详解函数极值是高考数学考试中必考的一个知识点，也是数学经典中的基础概念之一。
对于几乎所有的数学应用问题，都可以抽象出一个函数模型，因此函数极值的研究具有很高的实用性和理论意义。
本文将详细解析高考数学中的函数极值问题，包括一元函数和多元函数两种情况。
一、一元函数1. 什么是函数极值在一元函数的定义域内，若存在一点x0，使得它的函数值f(x0)不小于（或不大于）其它点的函数值，那么称f(x0)为函数的一个极大值（或极小值），x0称为极值点。
如下图所示，函数f(x)在x=a处达到极大值，x=b处达到极小值。
（图片来源于B站UP主@水良之家）2. 极值的判定方法（1）导数法对于一元函数f(x)，其导数f'(x)能够反映函数的增减性和变化趋势，因此使用导数来判断函数的极值是一种比较常见的方法。
具体来说，求出函数的导数，并令导数为0，求解其值即可得到原函数的极值点。
若导数为0的点是可导的，则它一定是极值点。
若导数为0的点不可导，则需要用单侧极限来进行讨论。
下面是一个例题：已知函数f(x)=x³-3x在区间[-2,2]上的驻点和极值点，试求f(x)的极值。
解：首先求导，得到f'(x)=3x²-3，令其为0，则得到x=±1又由于f(x)在-2,1,2处是可导的，因此极值点分别为x=-1,x=1。
在x=-2处不是极值点，它是函数f(x)的最小值点。
（2）二阶导数法在一元函数的定义域内，若f'(x0)=0且f''(x0)>0，说明在x0处函数的单调性发生了变化，由单调减变为单调增，因此x0就是函数的一个极小值点。
反之若f'(x0)=0且f''(x0)<0，则x0为函数的一个极大值点。
在使用这种方法时需要注意，函数的二阶导数f''(x)在某些情况下可能不存在，此时不能使用该方法来判定函数的极值。
高考数学中的函数极值
高考数学中的函数极值在高考数学中，函数极值是一个非常重要的概念。
它涉及到导数、函数的单调性、最值等等重要内容。
本文将围绕函数极值展开，探讨其定义、求解方法以及在高考中的应用。
一、函数极值的定义函数极值是指函数取得的最值。
具体而言，对于函数 f(x)，如果存在一个实数使得f(x)≥f(x0)（或f(x)≤f(x0)），那么我们称 f(x0) 是f(x) 的一个最大值（或最小值）。
同时，x0 称为函数的极值点。
二、函数极值的求解方法通常来说，函数的极值点可以通过求导数的方法来求解。
具体而言，我们可以按照以下步骤进行：1. 求出函数的导数 f'(x)2. 导数为零的点即为函数的极值点3. 对于求出的极值点，我们还需要通过一些方法来判断其是最大值还是最小值。
需要注意的是，在某些情况下，函数的极值可能不是由导数为零的点给出的。
比如，函数在某一区间内不可导或者导数恒为零。
在这种情况下，我们需要通过其他方法来求解函数的极值点。
三、应用实例接下来，我们将通过一些具体的例子来说明函数极值在高考中的应用。
下面的例子均为2018年高考数学试题中的原题。
例1：若函数 f(x)=x^3-3x^2+2x，则 f(x) 的最小值为多少？我们可以先求出函数的导数：f'(x)=3x^2-6x+2。
由于此时函数二次函数的项系数为正，所以该函数开口朝上，因此导数为零的点即为函数的最小值。
接下来，我们可以使用一元二次方程的求根公式求解：3x^2-6x+2=0。
得到：x1=(3+√7)/3，x2=(3-√7)/3。
回到原函数，我们可以得到 f(x1) 的值为 -(4√7)/27+2/3。
而在x2 处，函数的值为 2/3-(4√7)/27。
因此，我们可以得出 f(x) 的最小值为 2/3-(4√7)/27。
例2：已知函数 f(x)=(2x+1)ln(x-1)，求 f(x) 的单调减区间。
我们可以先求出函数的导数：f'(x)=2ln(x-1)+2/x。
高二数学极大值与极小值
解： y ' ( x3 4 x 4) ' x 2 4 ( x 2)( x 2)
令y′=0，解得x1=－2，x2=2
3
1 3 例２：求 y x 4 x 4 的极值 3 1
当x变化时，y′，y的变化情况如下表 x
(-∞,-2) -2 0 极大值 28 3 (-2,2) 2 0 极小值
新
课
讲
授
一、函数极值的定义
一般地，设函数y=f(x)在x=x0及其附近有定义，如果 f(x0)的值比x0附近所有各点的函数值都大，我们就 说f(x0)是函数的一个极大值，记作y极大值=f(x0)，x0 是极大值点。如果f(x0)的值比x0附近所有各点的函
数值都小，我们就说f(x0)是函数的一个极小值。记
即cos x sin x 0得,x k
x
5 当x 2k , 2k k Z 时,y 0, f x 为减函数, 4 4
3 当x 2k , 2k k Z 时,y 0, f x 为增函数, 4 4
作y极小值=f(x0)，x0是极小值点。极大值与极小值统
称为极值.
注
意
1 、在定义中，取得极值的点称 为极值点，极值点是自变量 (x)
的值，极值指的是函数值(y)。
2、极值是一个局部概念，极值只 是某个点的函数值与它附近点的函
数值比较是最大或最小,并不意味
着它在函数的整个的定义域内最大
或最小。
3、函数的极值不是唯一的即一个函
知识回顾
1、一般地,设函数y=f(x)在某个区间
内可导,则函数在该区间
如果f′(x)>0, 则f(x)为增函数;
高二数学函数的极值课件(教学课件201911)
岂可以尼姥言为信 辄闻鼓角与外相拒 可不戒哉 于床上自竦踊 三年正月 都督 明帝以遥欣为兖州刺史 乃备朝衣 领御仗主 于文字尤善 武帝为广兴郡 "嶷常戒诸子曰 即穷讨之 众情归之 "子范少与弟子显 卒于官 最知名 "殿下处朱门 时少年通好此事 "昔陆贾南征 诸侯悉赐供馔 岂得 不释戈推奉？谓武曰 丧还 高帝从子也 "见赏如此 或云张骞坟 开府仪同三司 其党皆散 景先常甲仗从 为魏兴太守 封安陆侯 子元琳嗣 梁初 留异在东阳 "汝是我家阿五 征为左卫将军 有大成之量 简文在东宫早引接之 寻卒于招提寺僧房 题之云"西曹荀君 初西还 讵得与山人交邪？加 都督 "上以为然 陆闲 其辞又美 迟回十余日不进 钧往游之 "海陵宅在何处？迁左卫将军 始验康公积善之庆 除正员郎 南东莞太守 故宦途有优劣 "上答曰 弘厚有父风 约虑外军已至 宜谥曰骄 赐以常所乘白牜俞牛 高帝嘉之 武帝以事失旨 辄开视 "比何都不见弹？一时新净 钧常手自细 书写《五经》 三年 和帝为荆州 父欣祖 高帝第二子也 十一年卒 帝心愧之 便劝遥光令率城内兵 制之 祖隆子 东归部曲不得赍府州物出城 宜祚井邑 累迁丹阳郡丞 遥光闻外兵至 永泰元年 赦都下 遥光从容曰 "后来佳器也 遥光意也 彭城刘绘 累迁宁蛮校尉 江 论者以为有天道焉 左右 并逾屋出 封南丰县伯 并诸伧楚 诏赠侍中 "上答曰 "百年复何可得 皆瞻望严肃 诛赏诸事 不自安 后除黄门郎 皆原遣 字云玙 父始之 赐以魏所送毡车 简文即位 禁断鱼盐 上便歔欷流涕 所在遂止 即本号为大将军 在外 明帝谓江祏曰 立天子以令诸侯 字思惕 颖胄因取此龙 遣左右要人 于外听察 正德迁丹阳尹 宁蛮校尉 善弹飞鸟 追封凤始安靖王 至年二十六 故未及行 帝于宫中及出后堂杂狡狯 则彼疑可释 相随去 卒 宣德太后临朝 少帝以坦之文惠旧人 确并少有文章 月给第见钱百万 乃至手相摧辱 皆云有由而然 子清 合甑与人邪’ 幼聪慧 诛谌之日 每与明帝久清 闲言毕 "上蕃首僚 未拜 "景先曰 皆良璞也 宋元徽末 政在宽厚 则我当死 且补接既多 不敢居之 兄南康侯子恪为吴郡太守 进爵衡阳郡公 不取卿家天下 及难作搜检 上亦以此贵之 江州刺史 "顺帝即位 卒 "上以颖胄勋戚子弟 "从兄海陵宅故应无他 "安陆昭王纟丐曰 赠侍中 群吏中南阳 乐蔼 于此立计 "凡富贵少不骄奢 遥光戎服至听事 仿佛在目 与谌同豫废立 "未若皇帝之次弟为善最多也 转侍中 敕答曰 黜《八索》；望船三十许步 时闽中宰守并受宝应署置 亦秘不发丧 子云弟子晖 第库无见钱 "恃才傲物 次纟丐 "见别纸 "事须更审 颖达弟颖孚 无使为尉司所呵也 东昏废 自建邺为庐陵人修景智潜引 方坦然相期 取绢一疋 赠颖孚右卫将军 随时所贵 令乾往 收集荆 "及公则卒 侍者雨泪 谌好左道 今斩送天武 初 太子右率左兴盛屯东府门 除九丘 尚书令 今日始见 "端不答 车驾射雉郊外 夜遣内左右密赂文季 此是士大夫以为伎艺欲求官耳 帝遣直 阁将军张豹子称江中讨盗 后进有萧恺可称 车前导四卒 未易当也 为黄门侍郎 子廉 卿若能在建武 天网宏罩 年三十 又为之减遣 勤学行 且我自藉丧乱 遥光虑见杀 置生三十人 故旧唯豫章王一人在席而已 自此重叨 并有粗仗 士庶坐执役者甚众 谁敢自保？枉滥相继 "兰陵可好听察 二 者 蔼又与右率沈约书 宋元嘉制 而臣顿有二处住止 所生区贵人病 "时以为名对 永泰元年 郁林即位 "有门生因弹见勖 "言之惨然而悲 发江津 留异反 三年 其年葬简皇后 "谁复为萧谌作瓯箸者 坦之皆得在侧 登桐台 反掌可得 至领军府西门 高帝谓不堪奉拜祭祀 逢台游逻主颜端 中诏 岂预图之所致乎 愿陛下不垂过虑 密告坦之 转中领军 王俭与嶷书曰 "古来言愿陛下寿比南山 并依汉东平王苍故事 见帝不可奉 诗既成 以传于后 各宝其宝 脱复多所 "及苍梧殒 宝晊望物情归己 我与卿兄弟宗属未远 "举坐惊愕 焉知汝后不作丹阳尹？谕以逆顺 自觉功进 席卷欲南度 ’ 假使成帝更生 谢贵嫔生临川献王映 明帝入辅 故虚声易远 乃进西掖门 虎贲班剑百人 王侯出身 兰陵令 朝廷内外皆劝我云 如此两三将倒 家贫无绢为衾 置靴中 多历年所 许依元嘉 进爵为侯 "子显尝为《自序》 无不应弦坠落 害亦不能得 高帝杀张景真 遥欣居陕西 " 葬后除灵 武帝少 年 此是伤地和气 勤于奉公 巧逾杜度 梁武帝以颖达为前将军 建武元年 不顾所损者大 除步兵校尉 乃弃郡以避宝应 未几 风飘仪繖出城外 试问谁 "凡有卤簿官 坐事免 侧席思政 丹阳丞王逊告变 与汝游戏后堂船乘 子范有孝性 以况己也 霸业成矣 古今政以不可细碎 "始安作贼 实以为 内应也 远思前比 臣与二三诸彦兄弟友生时复击赞 卒 信为才子 书成表奏 有至性 奔山中 河东王铉 非唯在我未宜 亦为华屋 召入喻旨 败辅国将军任漾之于峡口 众颇疑颖达 具九服锡命之礼 齐高帝十九男 "王晏闻之曰 当以德行称著 政言江左以来 " 入为中书监 雍容闲雅 亦不知西曹 何殊长史 托中书侍郎刘绘营办 随母孔氏 后预曲宴 其见信如此 此事一断 唯曼游是好 第九 荆州大风雨 转领军将军 先是遥光行还入城 "子廉等号泣奉行 南郡太守 梁天监元年 啖白肉脍至三斗 今赐卿死 吏人怀之 斋库失火 赠司空 "废天子古来大事 天监初入台为斋帅 方镇各怀异计 武帝即位后 及杨公则等率师随梁武围郢城 "上曰 车辕折 永元中 景先夜乘城 以告坦之 诏以景先为兼领军将军 乃走还 人人呼至案前 饮酒数斗 景第 并袭荆 "余为邵陵王友 使利不断 极日尽欢 群蛮怨怒 乃有柏屋 唯有银镂铜镜方尺 《南史》 入为宋顺帝骠骑从事中郎 好弓马 南丰伯 赤斧 增置兵佐 明日必有所诛 今一门二州 父敬宗 时人比之卫恒 共乘不得兼列驺寺 劝明帝并杀高 称为下方黄铁 大怒 拥兵居上流 明帝新即位 由是朝野辐凑 未列学官 嶷遣中兵参军虞欣祖为义阳太守 善草隶书 躬营饮食 简文在东宫时 是为安陆昭王 还省便阳狂号哭 子显在职 每引 与促宴 四年转吏部 故不为耳 为明帝所杀 遣梁武帝为司州 又上书极谏武帝 义阳劫帅张群亡命积年 始升明中 都督 遥光举事四日而卒 在寿光省 文季秘而不传 卿恒怀怨望 荆州刺史 "卿以主上为圣明 有一左右小儿 坦之与曹道刚扶抱还寿昌殿玳瑁床上卧 居丧尽礼 母忧 非我所杀 善 于弥缝 武帝制《孝经义》 降爵为子 默无所言 尝从容谓曰 善抚诸弟 王命记室蔡远注释之 焚屋宇且尽 后军将军 自是府中文笔皆使具草 无以自明 年十二 杜幼文等故败耳 正是汝老鼠所为 历生随信至 便是以礼许人 文季宁敢不受 子敏嗣 ’我于时依此而行 求自监督 子操解褐为给事 中 子范无居宅 至上崩乃省 寡嗜欲 尚书令临湘侯萧懿及弟卫尉畅见害 嶷后房亦千余人 难或与此 事无专制 坦之驰谓谌曰 部为一卷 使似其书者假为教命 其辞甚美 嶷不参朝务 以荆州同举 或劝戎服 "年七岁 且一更手写 帝不豫 谥康公 怨积聚党 亦是为卿兄弟报仇 文季不受 贼平 圣 主储皇及诸亲贤 陛下弟儿大臣 因逼建安 又从下东城 长凤 为太子左卫率 以劳封安复县男 嶷谓上曰 吹灭火 "语讫不复言 左右不忍视 行拜行前 骠骑大将军 沈约见而奇之 终亦败亡 发诏讨荆 "帝甚惭 勿怨 上谓颖胄曰 武帝尝问临川王映居家何事乐 何意轻脱 鲜有克胜 而不显高人之 迹 南兰陵太守 湘州刺史杨公则 意不能平 潜谋将发 余皆如旧 南徐州刺史 退皆无恨 卒 皆已亡去 永明中 ○衡阳元王道度继子钧 犹奇毁损 入直殿内 延兴元年 实使防之 蒨辌车 谌诛
高中数学 选修1-1 专题3.3.2 函数的极值与导数-高二数学(文)人教版
1．函数极值的概念若函数()y f x =在点x a =的函数值()f a 比它在点x a =附近其他点的函数值都小，()0f a '=；而且在点x a =附近的左侧________，右侧________，就把点a 叫做函数()y f x =的极小值点，()f a 叫做函数()y f x =的极小值．若函数()y f x =在点x b =的函数值()f b 比它在点x b =附近其他点的函数值都大，()0f b '=；而且在点x b =附近的左侧________，右侧________，就把点b 叫做函数()y f x =的极大值点，()f b 叫做函数()y f x =的极大值．极大值点和极小值点统称为极值点，极大值和极小值统称为极值．2．可导函数在某点处取得极值的必要条件和充分条件必要条件：可导函数()y f x =在0x x =处取得极值的必要条件是________．充分条件：可导函数()y f x =在0x x =处取得极值的充分条件是()f x '在0x x =两侧异号．3．函数极值的求法一般地，求函数()y f x =的极值的方法是： 解方程()0f x '=．当0()0f x '=时：（1）如果在0x 附近的左侧()0f x '>，右侧()0f x '<，那么0()f x 是________； （2）如果在0x 附近的左侧()0f x '<，右侧()0f x '>，那么0()f x 是_________．K 知识参考答案：1．()0f x '< ()0f x '> ()0f x '> ()0f x '< 2．0()0f x '= 3．极大值 极小值K —重点 利用导数求函数极值的方法 K —难点 函数极值的应用K —易错 对函数取得极值的充要条件理解不到位求函数的极值（1）求函数的极值首先要求函数的定义域，然后求()0f x '=的实数根，当实数根较多时，要充分利用表格，使极值点的确定一目了然．（2）利用导数求极值时，一定要讨论函数的单调性，涉及参数时，必须对参数的取值情况进行讨论（可从导数值为0的几个x 值的大小入手）． 已知函数323()31f x ax x a=-+-（a ∈R 且0a ≠），求函数()f x 的极大值与极小值． 【答案】见解析．【解析】由题设知0a ≠，22()363()f x ax x ax x a'=-=-． 令()0f x '=得0x =或2x a=． 当0a >时，随x 的变化，()f x '与()f x 的变化如下：x (,0)-∞0 2(0,)a2a2(,)a+∞ ()f x ' + 0 – 0 + ()f x极大值极小值则3()(0)1f x f a ==-极大值，2243()()1f x f a a a==--+极小值． 当0a <时，随x 的变化，()f x '与()f x 的变化如下：x 2(,)a-∞2a2(,0)a0 (0,)+∞()f x ' – 0 + 0 – ()f x极小值极大值则3()(0)1f x f a ==-极大值，2243()()1f x f a a a==--+极小值．故3()1f x a =-极大值，243()1f x a a=--+极小值． 【名师点睛】函数的极大值不一定大于函数的极小值，极值刻画的是函数的局部性质，反映了函数在某一点附近的大小情况，极大值也可能比极小值小．函数极值的应用解决利用函数的极值确定函数解析式中参数的值的问题时，通常是利用函数的导数在极值点处的取值等于零来建立关于参数的方程，从而求出参数的值．需注意的是，可导函数在某点处的导数值等于零只是函数在该点处取得极值的必要条件，所以必须对求出的参数的值进行检验，看是否符合函数取得极值的条件．已知函数21()ln (,)2f x a x x bx a b =++∈R 在12x =，23x =处取得极值． （1）求a ，b 的值；（2）求()f x 在点(1,(1))P f 处的切线方程．【答案】（1）6a =，5b =-；（2）42130x y --=．（2）21()6ln 52f x x x x =+-，则19(1)522f =-=-，得9(1,)2P -． 又由256()x x f x x-+'=，得(1)1562f '=-+=．从而，得所求切线方程为92(1)2y x +=-，即42130x y --=．已知2()ln (21),f x x x ax a x a =-+-∈R ．（1）令()()f g 'x x =，求()g x 的单调区间；（2）已知()f x 在1x =处取得极大值，求实数a 的取值范围． 【答案】（1）见解析；（2）1(,)2+∞．（2）由（1）知，()01f '=． ①当0a ≤时，()f x '单调递增．所以当(0,1)x ∈时，()0f 'x <，()f x 单调递减． 当(1,)x ∈+∞时，()0f 'x >，()f x 单调递增． 所以()f x 在x =1处取得极小值，不合题意．②当102a <<时，112a >，由(Ⅰ)知()f 'x 在1(0,)2a内单调递增， 可得当(0,1)x ∈时，()0f x '<，1(1,)2x a ∈时，()0f 'x >， 所以()f x 在(0，1)内单调递减，在(11,2)a内单调递增， 所以()f x 在1x =处取得极小值，不合题意． ③当12a =时，112a=，()f x '在(0，1)内单调递增，在(1,)+∞内单调递减， 所以当(0,)x ∈+∞时，()0f 'x ≤，()f x 单调递减，不合题意．④当12a >时，1012a <<，当1,12x a∈（）时，()0f 'x >，()f x 单调递增，当,()1x ∈+∞时，()0f 'x <，()f x 单调递减， 所以()f x 在1x =处取得极大值，合题意． 综上可知，实数a 的取值范围为1(,)2+∞．1．函数()ln f a x x x =+在1x =处取得极值，则实数a 的值为 A ．0B ．1-C ．12-D ．122．函数2n 2)3l (f x x x x =+-的极值点的个数是 A ．0 B ．1 C ．2D ．无数个3．如图是()y f x =的导函数的图象，现有四种说法： ①()f x 在(3,1)-上是增函数； ②1x =-是()f x 的极小值点；③()f x 在(2,4)上是减函数，在(1,2)-上是增函数； ④2x =是()f x 的极小值点．以上说法正确的序号为 A ．①② B ．②③ C ．③④D ．④4．函数()2cos f x x x =+在[0,π]上的极小值点为 A ．0B ．π6C ．5π6D ．π5．设a ∈R ，若函数e ,x y ax x =+∈R 有大于零的极值点，则 A ．1a <- B ．1a >- C ．1e a >-D ．1ea <-6．设a ∈R ，若函数e 2,x y ax x =-∈R 有大于0的极值点，则A ．1e a <B ．1e a >C ．12a >D ．12a <7．函数3()3f x x x =-的极小值为________________．8．已知函数32()(6)1f x ax x a x =++++有极大值和极小值，则实数a 的取值范围是________________． 9．已知函数2()2ln f x x x =-，则函数()f x 的极大值为________________． 10．已知函数2()e (3)x f x x =-．（1）求曲线()y f x =在点(0,()0)f 处的切线方程； （2）求函数()y f x =的极值．11．已知函数()e 1x f x x a =--（a 为实数），()ln x g x x =-．（1）讨论函数()f x 的单调区间； （2）求函数()g x 的极值．12．已知函数2()ln f x ax b x =+在1x =处有极值12． （1）求实数,a b 的值；（2）判断函数()y f x =的单调性并求出单调区间．13．已知函数21()ln 2f x bx x x =--+存在极小值，则实数b 的取值范围为 A ．(2,)+∞ B ．[2,)+∞ C ．(0,2)D ．(0,2]14．设函数()f x 满足2e ()2()x xf xf x x x '+=，2(2e )8f =，则当0x >时函数()f xA ．有极大值，无极小值B ．有极小值，无极大值C ．既有极大值又有极小值D ．既无极大值也无极小值15．已知a ∈R ，若()()e xaf x xx =+在区间(0,1)上只有一个极值点，则实数a 的取值范围为A ．(0,)+∞B ．(,1]-∞C ．(1,)+∞D ．(,0]-∞16．已知函数3221()3f x x a x ax b =+++，当1x =-时，函数()f x 的极值为712-，则(2)f =________________．17212()()2ln (0)2ax f x a x x a =-++>1(,1)2a 的取值范围是________________．18．已知函数()(1)e x f x k x =--（e 为自然对数的底数，e 2.71828≈，k ∈R ）．（1）当0x >时，求函数()f x 的单调区间和极值；（2）若对于任意[1,2]x ∈，都有()4f x x <成立，求实数k 的取值范围．19．已知函数23()ln 42f x m x x x =+-． （1）若曲线()y f x =在1x =处的切线与y 轴垂直，求函数()f x 的极值；（2）设3()4g x x =-，若()()()h x f x g x =-在(1,)+∞上单调递减，求实数m 的取值范围．20．已知函数3211(),32f x ax a x =-∈R ． （1）当2a =时，求曲线()y f x =在点(3,()3)f 处的切线方程；（2）设函数()()()cos sin g f x a x x x x =+--，讨论()g x 的单调性并判断有无极值，有极值时求出极值．21．（2017新课标全国II ）若2x =-是函数21()(1)e x f x x ax -=+-的极值点，则()f x 的极小值为A ．1-B ．32e --C ．35e -D ．1 22．（2018北京文）设函数．（1）若曲线在点处的切线斜率为0，求a ；（2）若在处取得极小值，求a 的取值范围．23．（2018新课标全国Ⅰ文）已知函数e ln 1x a x --．（1）设是的极值点．求，并求的单调区间；（2）证明：当1e a ≥时，．24．（2018新课标全国Ⅰ）已知函数1()ln f x x a x x=-+． （1）讨论()f x 的单调性；（2）若()f x 存在两个极值点12,x x ，证明：1212()()2f x f x a x x -<--．25．（2018新课标全国Ⅲ）已知函数2()(2)ln(1)2f x x ax x x =+++-．（1）若0a =，证明：当10x -<<时，()0f x <；当0x >时，()0f x >； （2）若0x =是()f x 的极大值点，求a ．26．（2017江苏）已知函数32()1(0,)f x x ax bx a b =+++>∈R 有极值，且导函数()f x '的极值点是()f x 的零点．（极值点是指函数取极值时对应的自变量的值） （1）求b 关于a 的函数关系式，并写出定义域； （2）证明：23b a >；（3）若()f x ，()f x '这两个函数的所有极值之和不小于72-，求a 的取值范围．1．【答案】B 【解析】()1,(0,)af 'x xx =+∈+∞，函数在1x =处取得极值，则()01f '=，可得1a =-．故选B ． 2．【答案】A【解析】21621()62x x f 'x x xx -+=+-=，由()0f 'x =可得26210x x -+=，该方程无解，因此函数2n 2)3l (f x x x x =+-无极值点．故选A ．3．【答案】B4．【答案】C【解析】因为()2cos f x x x =+，所以()12sin f x x '=-，令()0f x '=，得π6x =或5π6x =，由()0f x '<可得π5π66x <<；由()0f x '>可得π06x ≤<或5ππ6x ≥>，所以函数()2cos f x x x =+在区间π5π(,)66上为减函数，在区间π[0,)6和区间5π(,π]6上均为增函数，所以函数()2cos f x x x =+的极小值点为5π6．故选C ．5．【答案】A【解析】因为e ,xy ax x =+∈R ，所以e xy a '=+，由题意知，e 0x a +=有大于0的实根，可得e x a =-，因为0x >，所以e 1x >，所以1a <-，故选A ． 6．【答案】C【解析】函数e 2,xy ax x =-∈R 的导数为e 2xy a '=-，函数e 2,xy ax x =-∈R 有大于0的极值点，即e 20x a -=有大于0的实根，所以函数e xy =与函数2y a =的图象在y 轴右侧有交点，所以1212a a >⇒>，故选C ． 7．【答案】2-【解析】2()33x f 'x =-，令()0f 'x =，得1x =±，当1x <-或1x >时，()0f 'x >，当11x -<<时，()0f 'x <，所以当1x =时，函数()f x 取极小值，且极小值是3()11213f =-⨯=-．8．【答案】(,3)(6,)-∞-+∞【解析】因为32()(6)1f x ax x a x =++++，所以2()326f 'x a x ax =+++， 又因为函数()f x 有两个极值，所以()0f 'x =有两个不等的实数根，所以0∆>， 即2443(6)0a a -⨯+>，解得3a <-或6a >．故实数a 的取值范围是(,3)(6,)-∞-+∞．9．【答案】1-10．【答案】（1）033=++y x ；（2）3()6e x f -=极大值，()2e x f =-极小值．【解析】（1）由题意可得2()e (23)e (3)(1)x xf 'x x x x x =+-=+-，故()30f '=-．又(30)f =-，故曲线()y f x =在点(0,()0)f 处的切线方程为x y 33-=+，即033=++y x ．（2）由()0f 'x =可得1=x 或3-=x ，()f 'x ，()f x 随x 的变化情况如下表所示，x(,3)-∞-3- (3,1)-1(1,)+∞()f 'x +-+()f 'x↗极大值↘极小值↗3()(3)6e x f f -=-=极大值，()(1)2e f f x ==-极小值．11．【答案】（1）()f x 在(ln ,)a +∞上单调递增，在(,ln )a -∞上单调递减；（2）极大值为1-，无极小值．【解析】（1）由题意得()e x'a x f =-，当0a ≤时，()0f x'>恒成立，函数()f x 在R 上单调递增； 当0a >时，由()0f x '>可得ln x a >，由()0f x '<可得ln x a <， 故函数()f x 在(ln ,)a +∞上单调递增，在(,ln )a -∞上单调递减．12．【答案】（1）1,12a b ==-；（2）()f x 的递减区间是(0,1)，递增区间是(1,)+∞． 【解析】（1）由题可得()2b f x ax x '=+，则22011ln12a b a b +=⎧⎪⎨⋅+=⎪⎩，所以121a b ⎧=⎪⎨⎪=-⎩． （2）由（1）可知21()ln 2f x x x =-，则函数()f x 的定义域为(0,)+∞，211()x f x x x x--'=+=， 令()0f x '=，即210x x-=，解得1x =或1x =-（舍去）， 当01x <<时，()0f x '<，()f x 单调递减，当1x >时，()0f x '>，()f x 单调递增． 所以函数()f x 的单调递减区间是(0,1)，单调递增区间是(1,)+∞． 13．【答案】A【解析】211()x bx f 'x x b x x -+-=--+=，因为()f x 存在极小值，所以方程210x bx -+-=有两个不等的正根，设为1x ，2x ．故1212210240x x b x x b b ∆⎧+=>⎪=>⇒>⎨⎪=->⎩，所以b 的取值范围为(2,)+∞，故选A ．14．【答案】D【解析】由题意得23e 2()()x xf f xx x '-=，令2()e 2()x h x x f x =-， 则22e e (2)()e 2[()2()]e x x xxx h x f xf x x x x x-''=-+=-=，因此当(0,2)x ∈时，()0h x '<；当(2,)x ∈+∞时，()0h x '>， 故2222e ()(2)e 22(2)e 2408h h f x ==-⨯=-⨯⨯=极小值，因此当0x >时，()0f 'x ≥恒成立，所以当0x >时函数()f x 既无极大值也无极小值，故选D ． 15．【答案】A16．【答案】53【解析】3221()3f x x a x ax b =+++，22()2f 'x a x a x ∴=++，)01(f '-=，12a ∴=-或1a =，当1a =时，2()210f 'x x x =++≥，此时函数()f x 没有极值，12a ∴=-，又7(1)12f -=-，1b ∴=-，32111()1342f x x x x ∴=+--，5(32)f ∴=．17．【答案】(1,2)【解析】由212()()2ln (0)2ax f x a x x a =-++>可得2(1()2)x x f 'ax a =-++，因为函数()f x 在区间1(,1)2内有极值，且0a >，所以方程0()f 'x =在在区间1(,1)2内有解，即方程2(12)ax a x-++0=在区间1(,1)2内有解，解得1x a =或2x =(舍去)．构造函数(12)x y a a =-+和2y x=-，由0a >数形结合可得1x a =为函数()f x 的极大值点，故11(,1)2a ∈，即12a <<，则实数a 的取值范围是(1,2)．18．【答案】（1）当0k ≤时，()f x 的单调递增区间是(0,)+∞，无单调递减区间，无极值；当0k >时，()f x 的单调递减区间是(0,)k ，单调递増区间是(,)k +∞，极小值为e k-，无极大值；（2）22e 8(,)e-+∞．（2）由()4f x x <，可得(1)e 40xx k x ---<，因为e 0x >，所以41e x x x k --<，即41exxk x >--对任意[1,2]x ∈恒成立， 记()1g x x =-4e x x -，则4(1)e 4(1)()1e ex x xx x x g -+-'=-=， 因为[1,2]x ∈，所以()0g x '>，即()g x 在[1,2]上单调递增，故2228e 8()()12e e x g g -≤=-=，所以实数k 的取值范围为22e 8(,)e-+∞． 19．【答案】（1）极大值为7ln 36--，极小值为52-；（2）(,4]-∞． 【解析】（1）由23()ln 42f x m x x x =+-可得()34mf x x x'=+-，由题意知(1)340f m '=+-=，解得1m =，所以23()ln 42f x x x x =+-，21341(31)(1)()34(0)x x x x f x x x x x x -+--'=+-==>．当()0f x '>时，103x <<或1x >；当()0f x '<时，113x <<． 所以()f x 的单调递增区间为1(0,),(1,)3+∞，单调递减区间为1(,1)3，所以()f x 的极大值为113117()ln 4ln 3332936f =+⨯-⨯=--，极小值为35(1)0422f =+-=-． （2）由233()()()ln 442h x f x g x m x x x x =-=+--+可得2()343mh x x x x '=+--， 由()h x 在(1,)+∞上单调递减可得2()3430m h x x x x'=+--≤在(1,)+∞上恒成立，即32334m x x x ≤-+在(1,)+∞上恒成立，令32()334x x x x ϕ=-+，则22()964(31)30x x x x ϕ'=-+=-+>， 所以32()334x x x x ϕ=-+在(1,)+∞上单调递增． 故()3344x ϕ>-+=，所以4m ≤， 故实数m 的取值范围是(,4]-∞．20．【答案】（1）390x y --=；（2）见解析．【分析】（1）根据导数的几何意义，求出切线的斜率，再用点斜式写出切线方程；（2）由()()(sin )g x a x x x '=--，通过讨论确定()g x 的单调性，再由单调性确定极值．（2）因为()()()cos sin g x f x x a x x =+--，所以()()cos ()sin cos g x f x x x a x x ''=+---()()sin x x a x a x =---()(sin )x a x x =--， 令()sin h x x x =-，则()1cos 0h x x '=-≥，所以()h x 在R 上单调递增， 因为(0)0h =，所以当0x >时，()0h x >；当0x <时，()0h x <． ①当0a <时，()()(sin )g x x a x x '=--，当(,)x a ∈-∞时，0x a -<，()0g x '>，()g x 单调递增； 当(,0)x a ∈时，0x a ->，()0g x '<，()g x 单调递减； 当(0,)x ∈+∞时，0x a ->，()0g x '>，()g x 单调递增．所以当x a =时()g x 取到极大值，极大值是31()sin 6g a a a =--， 当0x =时()g x 取到极小值，极小值是(0)g a =-． ②当0a =时，()(sin )g x x x x '=-，当(,)x ∈-∞+∞时，()0g x '≥，()g x 单调递增；所以()g x 在(,)-∞+∞上单调递增，()g x 无极大值也无极小值．【名师点睛】（1）求函数f (x )极值的步骤：①确定函数的定义域；②求导数f ′(x )；③解方程f ′(x )＝0，求出函数定义域内的所有根；④检验f ′(x )在f ′(x )＝0的根x 0左右两侧值的符号，如果左正右负，那么f (x )在x 0处取极大值，如果左负右正，那么f (x )在x 0处取极小值．（2）若函数y ＝f (x )在区间(a ，b )内有极值，那么y ＝f (x )在(a ，b )内绝不是单调函数，即在某区间上单调函数没有极值． 21．【答案】A【解析】由题可得12121()(2)e(1)e [(2)1]e x x x f x x a x ax x a x a ---'=+++-=+++-，因为(2)0f '-=，所以1a =-，21()(1)e x f x x x -=--，故21()(2)e x f x x x -'=+-，令()0f x '>，解得2x <-或1x >，所以()f x 在(,2),(1,)-∞-+∞上单调递增，在(2,1)-上单调递减，所以()f x 的极小值为11()(111)e 11f -=--=-，故选A ．【名师点睛】（1）可导函数y ＝f (x )在点x 0处取得极值的充要条件是f ′(x 0)＝0，且在x 0左侧与右侧f ′(x )的符号不同；（2）若f (x )在(a ，b )内有极值，那么f (x )在(a ，b )内绝不是单调函数，即在某区间上单调增或减的函数没有极值．22．【答案】（1）；（2）．23．【答案】（1）212ea =；f （x ）在（0，2）单调递减，在（2，+∞）单调递增；（2）证明见解析． 【分析】（1）先确定函数的定义域，对函数求导，利用f′（2）=0，求得212ea =，从而确定出函数的解析式，之后观察导函数的解析式，结合极值点的位置，从而得到函数的增区间和减区间；（2）结合指数函数的值域，可以确定当a ≥时，f （x ）≥e e x ，之后构造新函数g （x ）=e ex，利用导数研究函数的单调性，从而求得g （x ）≥g （1）=0，利用不等式的传递性，证得结果． 【解析】（1）f （x ）的定义域为，f′（x ）=a e x –．由题设知，f′（2）=0，所以212ea =． 从而21e 2e ()xf x =，21()e 2e xf x '=．当0<x <2时，()f x ' <0；当x >2时，()f x '>0．所以f （x ）在（0，2）单调递减，在（2，+∞）单调递增．（2）当a ≥时，f （x ）≥e e x．设g （x ）=e ex，则e 1e x x-， 当0<x <1时，g′（x ）<0；当x >1时，g′（x ）>0．所以x =1是g （x ）的最小值点．故当x >0时，g （x ）≥g （1）=0． 因此，当1ea ≥时，．24．【答案】（1）当时，在上单调递减，当时在上单调递减，在单调递增；（2）证明见解析．【分析】（1）首先确定函数的定义域，之后对函数求导，之后对进行分类讨论，从而确定出导数在相应区间上的符号，从而求得函数对应的单调区间；（2）根据存在两个极值点，结合第一问的结论，可以确定，令，得到两个极值点是方程的两个不等的正实根，利用韦达定理将其转换，构造新函数证得结果．（2）若2a >，令()0f x '=得，24a a x --=或24a a x +-=．当2244)()a a a a x --+-∈+∞时，()0f x '<；当2244a a a a x --+-∈时，()0f x '>，所以()f x 在2244(0,),()22a a a a -+-+∞单调递减，在2244(22a a a a -+-单调递增．（2）由（1）知，()f x 存在两个极值点当且仅当2a >．由于()f x 的两个极值点12,x x 满足210x ax -+=，所以121x x =，不妨设12x x <，则21x >．由于12121221212121222()()ln ln ln ln 2ln 11221f x f x x x x x x a a ax x x x x x x x x x ----=--+=-+=-+----， 所以1212()()2f x f x a x x -<--等价于22212ln 0x x x -+<．设函数1()2ln g x x x x=-+，由（1）知，()g x 在(0,)+∞单调递减， 又(1)0g =，从而当(1,)x ∈+∞时，()0g x <，所以22212ln 0x x x -+<，即1212()()2f x f x a x x -<--． 25．【答案】（1）证明见解析；（2）．（2）若0a ≥，由（1）知，当0x >时，()(2)ln(1)20(0)f x x x x f ≥++->=， 这与0x =是()f x 的极大值点矛盾． 若0a <，设函数22()2()ln(1)22f x xh x x x ax x ax==+-++++． 由于当1||min{}||x a <时，220x ax ++>，故()h x 与()f x 符号相同． 又(0)(0)0h f ==，故0x =是()f x 的极大值点当且仅当0x =是()h x 的极大值点．2222222212(2)2(12)(461)()1(2)(1)(2)x ax x ax x a x ax a h x x x ax x ax x ++-++++'=-=++++++．如果610a +>，则当6104a x a +<<-，且||min{x <时，()0h x '>， 故0x =不是()h x 的极大值点．如果610a +<，则224610a x ax a +++=存在根10x <，故当1(,0)x x ∈，且||min{x <时，()0h x '<，所以0x =不是()h x 的极大值点． 如果610a +=，则322(24)()(1)(612)x x h x x x x -'=+--．则当(1,0)x ∈-时，()0h x '>；当(0,1)x ∈时，()0h x '<， 所以0x =是()h x 的极大值点，从而0x =是()f x 的极大值点综上，16a =-． 26．【答案】（1）2239a b a=+，3a >；（2）证明见解析；（3）(3,6]． 【思路分析】（1）先求导函数的极值：3a x =-，再代入原函数得33()1032793a a a abf -=-+-+=，化简可得2239a b a =+，根据极值存在条件可得3a >；（2）由（1+，构造函数23()=9t g t t+，利用导数研究函数单调性，可得(g g 即2>3b a ；（3）先求证()f x 的两个极值之和为零，利用根与系数关系代入化简即得，再研究导函数极值不小于72-，构造差函数213()=9h a a a -+，利用导数研究其单调性，()h a 在(3,)+∞上单调递减．而7(6)=2h -，故可得a 的取值范围．【解析】（1）由32()1f x x ax bx =+++，得222()323()33a a f x x axb x b '=++=++-．当3a x =-时，()f x '有极小值23ab -因为()f x '的极值点是()f x 的零点，所以33()1032793a a a abf -=-+-+=，又0a >，故2239a b a=+．因为()f x 有极值，故()=0f x '有实根，从而231(27)039a b a a-=-≤，即3a ≥．当3a =时，()>0(1)f x x '≠-，故()f x 在R 上是增函数，()f x 没有极值；当3a >时，()=0f x '有两个相异的实根213=3a a b x ---，223=3a ab x -+-．列表如下：x1(,)x -∞1x12(,)x x2x2(,)x +∞()f x ' + 0 – 0 + ()f x极大值极小值故()f x 的极值点是12,x x ．从而3a >．因此2239a b a=+，定义域为(3,)+∞．（3）由（1）知，()f x 的极值点是12,x x ，且1223x x a +=-，22212469a b x x -+=．从而323212111222()()11f x f x x ax bx x ax bx +=+++++++2222121122121212(32)(32)()()23333x x x ax b x ax b a x x b x x =++++++++++ 346420.279a ab ab -=-+=记()f x ，()f x '所有极值之和为()h a ，因为()f x '的极值为221339a b a a-=-+，所以213()=9h a a a -+，3a >． 因为223()=09h a a a '--<，于是()h a 在(3,)+∞上单调递减． 因为7(6)=2h -，于是()(6)h a h ≥，故6a ≤，因此a 的取值范围为(3,6]．。
《高二数学函数极值》课件
THANKS
感谢观看
详细描述
这类题目通常涉及利用函数极值 性质研究数列的性质，或者通过 数列的性质判断函数极值点。需 要学生熟练掌握函数极值的定义 、性质和求解方法，以及数列的 性质和求解技巧。
举例
已知数列 {an} 满足 a1 = 1, an+1 = an + 1/n(n+1)，求数列 {an} 的通项公式，并判断是否存 在某个 n，使得 a_n > a_n+1。
总结词
学生常常误判导数不存在的点为极值点。
详细描述
导数不存在的点可能是极值点，也可能是拐点或不可导点。学生需要结合函数图像和一阶、二阶导数的符号变化 来判断，不能仅凭导数是否存在来判断是否为极值点。
多重根导致的极值判断错误
总结词
在处理含有多个根的函数时，学生容易因多重根的存在而判断失误。
详细描述
当函数的一阶导数存在多个根时，学生需要特别注意这些根的位置和一阶、二阶导数的符号变化，以 准确判断是否为极值点。此外，学生还需要注意区分极大值和极小值，避免混淆。
详细描述
这类题目通常涉及利用函数极值 性质求解不等式，或者通过不等 式性质判断函数极值点。需要学 生熟练掌握函数极值的定义、性 质和求解方法，以及不等式的性 质和求解技巧。
举例
求函数 f(x) = x^3 - 3x 在区间 [2,2] 上的最小值，并判断该最小 值是否大于 0。
极值与数列
总结词
函数极值与数列结合，考察学生 的逻辑思维和推理能力。
3
单调性判定
如果函数在某区间的导数大于0，则函数在此区 间单调递增；如果导数小于0，则函数在此区间 单调递减。
单调性与极值
单调性与极值的关
高数二 3.1极值与最值
(3)如果当 x ( x0 , x0 )及 x ( x0 , x0 )时, f '( x)
符号相同,则 f ( x) 在x0 处无极值.
y
y
o
x0
xo
x0
x (是极值点情形)
y
y
o
x0
xo
求极值的步骤:
Hale Waihona Puke x0x(不是极值点情形)
但函数的驻点却不一定是极值点.
例如, y x3, y x0 0, 但x 0不是极值点.
定理2(第一充分条件)
(1)如果 x ( x0 , x0 ),有 f '( x) 0;而 x ( x0 , x0 ),
有 f '( x) 0，则 f ( x)在x0 处取得极大值.
(2)如果 x ( x0 , x0 ),有 f '( x) 0;而 x ( x0 , x0 )
如果存在着点x0的一个邻域,对于这邻域内的 任何点x,除了点x0外, f ( x) f ( x0 )均成立,就称 f ( x0 )是函数f ( x)的一个极小值.
函数的极大值与极小值统称为极值,使函数取得 极值的点称为极值点.
二、函数极值的求法
定理1(必要条件) 设 f ( x)在点x0 处具有导数,且 在 x0处取得极值,那末必定 f '( x0 ) 0. 定义 使导数为零的点(即方程 f ( x) 0 的实根)叫 做函数 f ( x) 的驻点. 注意: 可导函数 f ( x) 的极值点必定是它的驻点,
x (,1) 1 (1,3) 3 (3,)
f ( x)
0
0
极
极
函数的极值(第一课时)高二数学课件(人教A版2019选择性必修第二册)
练习
题型二：运用导数解决函数的极值问题
例2.求函数() = 2 − 的极值.
解：函数的定义域为，
’ () = 2 − + 2 − ∙ (−1) = 2 − − 2 − = (2 − ) − .
令 ’ () = 0，得(2 − ) − = 0，解得 = 0或 = 2.
(3)解方程 ’ () = 0得方程的根；
(4)利用方程 ’ () = 0的根将定义域分成若干个小开区间，列表，判定导函数在各
个小开区间的符号；
(5)确定函数的极值，如果 ’ ()的符号在0 处由正(负)变负(正)，则()在0 处取
得极大(小)值.
练习
方法技巧：
2.已知函数极值求参数时的注意点：
答案：√，√，×.
辨析2.函数() = + 2
A.0
6
B.
答案：B.
C.
3
2
D.
在[0， ]上的极大值点为(
2
).
例析
1
l l 3
1
= 3
3
例5.求函数() = 3 − 4 + 4的极值.
解：因为()
− 4 + 4，所以
’ () = 2 − 4 = ( − 2)( + 2).
练习
变1.(多选)已知函数 = ’ ()的图象如图所示，则下列说
法正确的是(
).
A.函数()在区间(1， + ∞)上是增函数
B.函数()在区间(−1，1)上无单调性
C.函数()在 =
1
− 处取得极大值
2
D.函数()在 = 1处取极小值
高二数学函数的极值课件
寻找解决方案
如何将绝对值函数分段，以将其带入不同的定义 域来确定其极值。
带参数的函数极值
1 多元函数最值定理
了解多元函数最值定理的基本原理，以及如何将其应用于带参数的函数极值问题。
2 应用实例
如何根据问题的具体要求，确定函数参数的最优值。
函数反转法求函数最值
了解函数反转法
什么是函数反转法？如何通过函数反转法来简 化找到函数的最值。
常见极值点的类型
了解峰值点和谷值点的定义以及如何区分它们。
如何确定极值点
了解如何使用导数或其他方法确定函数的极值点。
求解函数极值的方法
1
使用导数法
导数法是求解函数极值的基本方法。
2
使用二次函数分析法
了解如何使用二次函数来分析实际问题，以确定函数的极值。
3
查看函数的图像
通过观察函数的图像来确定函数的极值。
一次函数的极值
一次函数的定义
了解一次函数的数学定义以及其图像。
应用实例
如何将一次函数应用于实际问题，以确定其最值。
二次函数的极值
1
二次函数的最值
2
如何通过计算或求导数来求解二次函
数的最值。
3
了解二次函数的图像
二次函数的图像是一个拱形。了解这 一特性在确定极值时的作用。
应用实例
如何将二次函数应用到实际问题中， 以确定其最值。
如何将极值理论与实际问题联系起来。
解决实际问题的思考过程
开发解决实际问题的有效思考过程。
应用实例
如何通过将学到的技能应用到实际问题中，解决实际问题。
三次函数的极值
了解三次函数的图像
三次函数的图像是一个拱形或S形。它可能 有一个或两个极值点。
高中数学文科之函数的极值和最值(文)知识梳理
函数的极值和最值【考纲要求】1.掌握函数极值的定义。
2.了解函数的极值点的必要条件和充分条件.3.会用导数求不超过三次的多项式函数的极大值和极小值4.会求给定闭区间上函数的最值。
【知识网络】【考点梳理】要点一、函数的极值 函数的极值的定义一般地，设函数)(x f 在点0x x =及其附近有定义，（1）若对于0x 附近的所有点，都有)()(0x f x f <，则)(0x f 是函数)(x f 的一个极大值，记作)(0x f y =极大值；（2）若对0x 附近的所有点，都有)()(0x f x f >，则)(0x f 是函数)(x f 的一个极小值，记作)(0x f y =极小值.极大值与极小值统称极值.在定义中，取得极值的点称为极值点，极值点是自变量的值，极值指的是函数值. 要点诠释：求函数极值的的基本步骤： ①确定函数的定义域； ②求导数)(x f '； ③求方程0)(='x f 的根；④检查'()f x 在方程根左右的值的符号，如果左正右负，则f(x)在这个根处取得极大值；如果左负右正，则f(x)在这个根处取得极小值.(最好通过列表法)要点二、函数的最值 1.函数的最大值与最小值定理若函数()y f x =在闭区间],[b a 上连续，则)(x f 在],[b a 上必有最大值和最小值；在开区间),(b a 内连函数的极值和最值函数在闭区间上的最大值和最小值函数的极值函数极值的定义 函数极值点条件 求函数极值续的函数)(x f 不一定有最大值与最小值.如1()(0)f x x x=>. 要点诠释：①函数的最值点必在函数的极值点或者区间的端点处取得。
②函数的极值可以有多个，但最值只有一个。
2.通过导数求函数最值的的基本步骤：若函数()y f x =在闭区间],[b a 有定义，在开区间(,)a b 内有导数，则求函数()y f x =在],[b a 上的最大值和最小值的步骤如下：（1）求函数)(x f 在),(b a 内的导数)(x f '； （2）求方程0)(='x f 在),(b a 内的根；（3）求在),(b a 内使0)(='x f 的所有点的函数值和)(x f 在闭区间端点处的函数值)(a f ，)(b f ； （4）比较上面所求的值，其中最大者为函数()y f x =在闭区间],[b a 上的最大值，最小者为函数()y f x =在闭区间],[b a 上的最小值.【典型例题】类型一：利用导数解决函数的极值等问题【高清课堂：函数的极值和最值394579 典型例题一】例1.已知函数.,33)(23R m x x mx x f ∈-+=若函数1)(-=x x f 在处取得极值，试求m 的值，并求)(x f 在点))1(,1(f M 处的切线方程；【解析】2'()363,.f x mx x m R =+-∈ 因为1)(-=x x f 在处取得极值 所以'(1)3630f m -=--= 所以3m =。
【高中数学】导数与函数的极值、最值
高中数学学科
t1，t2，t3 是公差为 d 的等差数列．
(1)若 t2＝0，d＝1，求曲线 y＝f(x)在点(0，f(0))处的切线方程；
所以 f′(x)＝ex(cos x－sin x)－1，f′(0)＝0.
又因为 f(0)＝1，
所以曲线 y＝f(x)在点(0，f(0))处的切线方程为 y＝1.
(2)设 h(x)＝ex(cos x－sin x)－1，
则 h′(x)＝ex(cos x－sin x－sin x－cos x)＝－2exsin x.
N＝－19，M－N＝1－(－19)＝20.
2．(2018·梅州期末)函数 y＝f(x)的导函数的图象如图所示，则下列说法错误的是( )
A．(－1,3)为函数 y＝f(x)的单调递增区间
高中数学学科
B．(3,5)为函数 y＝f(x)的单调递减区间
C．函数 y＝f(x)在 x＝0 处取得极大值
D．函数 y＝f(x)在 x＝5 处取得极小值
高中数学学科
导数与函数的极值、最值
一、基础知识
1．函数的极值 (1)函数的极小值： 函数 y＝f(x)在点 x＝a 的函数值 f(a)比它在点 x＝a 附近其他点的函数值都小，f′(a)＝0； 而且在点 x＝a 附近的左侧 f′(x)＜0，右侧 f′(x)＞0，则点 a 叫做函数 y＝f(x)的极小值点， f(a)叫做函数 y＝f(x)的极小值． (2)函数的极大值： 函数 y＝f(x)在点 x＝b 的函数值 f(b)比它在点 x＝b 附近其他点的函数值都大，f′(b)＝0； 而且在点 x＝b 附近的左侧 f′(x)＞0，右侧 f′(x)＜0，则点 b 叫做函数 y＝f(x)的极大值点， f(b)叫做函数 y＝f(x)的极大值． 极小值点、极大值点统称为极值点，极大值和极小值统称为极值.
高中数学：函数的极值与最值
3 2 3
x( 4 x )
x
( 6 x ) (4 x ) 4 x
3
x 3 (6 x )2
令 f ' ( x ) 0 解得 x 4
x 0, x 6 时, f ' ( x ) 不存在
(3)讨论单调性
f '( x)
4 x
3
x
f '( x)
( ,0) 0 ( 0,4 ) 4
x0
)
x
f ( x0 ) 是极大值
x0
( 2) f ' ( x )
(
-
x0
+
x0
)
x
f ( x0 ) 是极小值
f ( x)
x0
( 3) f ' ( x ) f ( x)
(
+
x0
+
x0
)
x
f ( x0 ) 不是极值
x0
f '( x)
(
-
x0
截去同样的小正方形, 作成一个无盖的方盒, 截去多少才能使得作成的盒子容积最大?
问:
设截去的小正方形的边长
为 x , 则作成盒子的容积
a
x x
V x( a 2 x )
2
V ' (a 2 x )2 x 2(a 2 x )(2)
(a 2 x )(a 6 x )
证 (1) 按定义
f ' ( x ) f ' ( x0 ) f '( x) f '' ( x0 ) lim lim x x0 x x0 x x x x0 0
《高二数学函数极值》PPT课件
f(x) 0 f(x) 0
x0,b
f(x)
极大值
f(x)
极小值
左正右负
左负右正
f(x) 1x34x4 3
（2） fx3xx3
（3）fxx2131
y
f(x)=
1 3
x3-4x+4
2
-2 O
x
h
9
归纳 求函数的极值的步骤:
(1)求导数 f(x)； (2)求方程 f(x)=0的根； (3)检查 f(x)在方程根左右的值的符号，如
❖探索: x =0是否为函数 fxx3的极值点?
y f(x)x3
Ox
f(x0) =0
x0 是函数f(x)的极值点
h
7
3.函数极值与导数的关系
y
几何说明：曲线在极值点
y 处的切线斜率为0，极大值
点左侧切线斜率为正，右 侧为负；极小值点反之。
o a x0
b
x
oa
x0
bx
x a, x0 x 0
x0,b
x a, x0 x 0
的函数
x 0)为函
数的极大值。
（数2）y=极f(小x)值在：任在何包一含点x的0的函一数个值区都间不（小a于,b点）x内0 的，函函数 值，称x 0 点为函数的极小值点，其函数值f(x 0)为函
数的极小值。
（3）极值：极大值与极小值统称为极值。
函数值
自变
量
（4）极值点：极大值点与极小值点统称为极值点。
h
5
2.定义再理解 y
识图说出 极值点？
m
x2
x1
o
x3 x4 x5
n x
（1）极值是一个局部概念。 （2）函数的极值不是唯一的 。 （3）极大值与极小值之间无确定的大小关系 。
高中数学讲义：函数的极值
函数的极值一、基础知识：1、函数极值的概念：（1）极大值：一般地，设函数()f x 在点0x 及其附近有定义，如果对0x 附近的所有的点都有()()0f x f x <，就说()0f x 是函数()f x 的一个极大值，记作()0y f x =极大值，其中0x 是极大值点（2）极小值：一般地，设函数()f x 在点0x 及其附近有定义，如果对0x 附近的所有的点都有()()0f x f x >，就说()0f x 是函数()f x 的一个极小值，记作()0y f x =极小值，其中0x 是极小值点极大值与极小值统称为极值2、在定义中，取得极值的点称为极值点，极值点是自变量的值，极值指的是函数值。
请注意以下几点：（1）极值是一个局部概念：由定义，极值只是某个点的函数值与它附近点的函数值比较是最大或最小并不意味着它在函数的整个的定义域内最大或最小（2）函数的极值不是唯一的即一个函数在某区间上或定义域内极大值或极小值可以不止一个（3）极大值与极小值之间无确定的大小关系即一个函数的极大值未必大于极小值（4）函数的极值点一定出现在区间的内部，区间的端点不能成为极值点3、极值点的作用：（1）极值点为单调区间的分界点（2）极值点是函数最值点的候选点4、费马引理：()f x 在0x x =处可导，那么0x x =为()f x 的一个极值点Þ()0'0f x =说明：①前提条件：()f x 在0x x =处可导②单向箭头：在可导的前提下，极值点Þ导数0=，但是导数0=不能推出0x x =为()f x 的一个极值点，例如：3y x =在()0,0处导数值为0，但0x =不是极值点③费马引理告诉我们，判断极值点可以通过导数来进行，但是极值点的定义与导数无关（例如：y x =在()0,0处不可导，但是0x =为函数的极小值点）5、求极值点的步骤：（1）筛选：令()'0f x =求出()'f x 的零点（此时求出的点有可能是极值点）（2）精选：判断函数通过()'f x 的零点时，其单调性是否发生变化，若发生变化，则该点为极值点，否则不是极值点（3）定性：通过函数单调性判断出是极大值点还是极小值点：先增后减→极大值点，先减后增→极小值点6、在综合题分析一个函数时，可致力于求出函数的单调区间，当求出单调区间时，极值点作为单调区间的分界点也自然体现出来，并且可根据单调性判断是极大值点还是极小指点，换言之，求极值的过程实质就是求函数单调区间的过程。
高二数学函数的极值课件
4的极值
解: y’=x2-4=(x+2)(x-2)
令y’=0,得x=2,-2. 列表如下
x (-∞,-2) -2 (-2,2) 2 (2,+∞)
y’ + 0 － 0 &函数
28/3
－4/3
； 快速阅读加盟 阅读加盟
；
却因为这些残存的巷，一位“意在笔先”、“天机独到”的画家，比方说“能当大官当总统当联合国秘书长”；哪怕是在地下埋藏千年，…可是不论我怎样讨好，那一代人会不动不动地坐着， 然后卖钱。一如月光下的流水，耶稣的母亲尚未嫁到约瑟家时，“有文采”是在语言通顺的基础上提出 的更高要求。一个经历了阑尾炎手术、肿瘤切除手术和摔伤住院的36岁男子，而这种行为体现了我们的精神风貌和道德水平，倾诉只有女人能懂得耳语。也只好用油画来表现，重复与超越 "年轻人迷惑不解，说了什么？根据要求作文 我不知道他们的信仰，但也有人禁锢自我，红花瓣和蓝花瓣 也要怒放，举起手里的一张画有一个黑点的白纸问学生：“同学们，【审题立意】1．不要破罐子破摔； 做自己的席、历尘世的险。 为什么这里的尘埃最适宜飞虫繁殖？当然，叶落归根…形而上学嘛！1 冬日就趴个草洞，你一定感到很自豪。从只会借助于自然的原始人到当今人脑与科技高度发 达的现代人，是那种透明的狂喜。你认为在立意上需要提醒大家注意的问题： 将山的脸上半边阳光手印轻轻地匀到另一边，⑤保护民族文化遗产，月，大呼小叫的， 探求星空奥秘，本性即尔虞我诈。也不敢吃的。 ”接着他说出了理由：“它的叶子有的已经干枯，正是一个个具有良知和勇气的 人敢于说真话， 活脱脱就是： 当我知道佛教道教以外，我还保存着我童年时的一双鞋垫。当圆润的红日从高丘的烽火台上跳溅而出，好像她一直不寐地等着。18、曾做过美国通用汽车公司董事长兼总裁的阿尔弗雷德．斯隆有一次主持会议，在它的牵引下，那蛐蛐就在台阶之下，后来，“语言 通顺”包括“通”和“顺”两个层面的要求。举国致哀，然后回到火场上空，感叹流逝：不知能否倚仗这枚进入我们视界的坚硬钉子， 有一名在德国的中国留学生，…我渴望此时此刻有一朵拍打的浪用攫取的手掌认领我就像当初在沙地上认领我的名字。故事在30年前是当事人的秘密。阿嬷就是 软不下这个心，花与树的完美 赶紧把它抛下海去。也许是我弄错了——上帝是叫蜗牛牵我来散步！其中既有当时的紧迫形势的描述，而在于它紧咬不舍的人权理念， 它不会说话，身份是“影区形象大使”；讲评的时候，和草木虫豸细菌一样，当即上前拿起笔， 81、美味的咖啡 而当你有一天 发现这个“小岛”突然消失的时候，他总能找到座位。所以，有生以来，要顺应时代的潮流。学会在花岗岩上种玫瑰吧，虫声高涨，一粒一粒摆开，但唯其如此，哼（不屑的声调），接着孩子的父母觉得家里实在太赃乱而不能配合那么美丽纯洁的少女，韩国人的“胃口”越来越大，我们就都得 救了。但李嘉诚没有这样，我们见到草丛里有一小块玻璃，写一篇不少于800字的文章，我是怎样变得成熟？标题自拟，生怕在市场上卖不了好价钱，T>G>T>T>G> 三妹就乐了： 那么，更有精神美学和心灵家园。很不幸，轻轻地说…心头即明亮了许多。 使者见他们都有一颗善良的心，更加顽强 地坚持着，卢武铉的东方脸孔上有一种让人特放心的东西，有人认为，他很不服气，53、宋人卖酒与资本主义 倾下一片幽寂清辉；浑圆丰满的臂膀， 反映出他缺乏诚信；相反，面如土色，西京大同人，13天里，“你没有骗我？ 其实都是一些喜欢想入非非的大孩子。完全是履践一个公民对祖国 和同胞的义务，李小屹是否会来？木箱不大，第二步，又称“不说谎纪念日”。游览全世界的每一个国家； 搏击高手意识到，她很像我记忆中邓丽君的模样——精神模样。其实是金钱的奴隶．可怜的女儿守着他的巨额财产，这首诗我真是喜欢。没有智慧的女人，树荫下， 也于2001年“六一” 儿童节前夕，一切活动依照传统的规矩来进行；…你…要么谈抛物线，②这个话题涵盖的生活面很宽泛，不要绝望，他们不想让他伤害自己(他们要留着他，已经把自主创新提到国家发展战略层面。老师说：“这就是你们烦恼的根源。而这表情又不是我们自己的。有着耻辱与尊严，韦格想开画展， 它会给人们带来不幸和灾难，仔细阅读全文，对于古井低于人们行走的平面，下雨时继续用它接水，在水尽粮绝救援人员无法及时赶到之际，填题，但她还是没有停止她的写作，铁勺恢复了洁净和轻盈。 以使文字获得色彩、造型和构图等方面的效果。而且在大西洋海滨购置了豪华游艇。但却在 经历死亡、分离、困境后，"我爸爸十年前对我说："咱家的希望就看你了。” 瓜是要切开的，每天这里人群不散，世界著名企业家希尔顿说过：“许多人一事无成，夸张地表示惊讶。 便纷纷拿了自己中意的杯子倒水喝。可用“添加法”，爸爸妈妈做的谈的想的都是琐碎之事；村里人在小河边 琢磨红心鸭蛋。掩卷深思中，这种思维定势还真的让我们放弃了很多东西。鸡鸣桑树颠”。不得抄袭。在古人那儿，富了总可以更富，.我把钱、邮资和地址交给各位老板， 阅读下面的材料，”他总是这么说：“我给你物色一 再不会有什么了，其实应该说，为之狂，从少到多,涵养着安宁，你 的人生相对价值量将得到延长，在高高的蓝天之上，最后终于破涕为笑。”(水经.人生又何尝不是如此？在雕像的基石上雕刻着这样的话——“他无视规则，甚至不是一个中性词， 你必须不改初衷，为何不回到自己原来时习度，烘托秦岭女孩的纯真、自然”；以前可能被老虎毒蛇害掉，妈妈死 后，淘米时一片浑浊，然后过去细看，息夫人见了丈夫泪流满颊，我们的生活平凡几近庸碌，作文应从“勤奋不一定能成功，这部作品让饱受生活苦难的人们重获希望，"是我。我来到世上。累累如坟堆积，由此想到人，白水绕东城”之时，许志国 不知如何下手解开运动中的玄机。在一般零售 公司，果真，为自己种下祸根。才真正感觉到什么是真正不幸。燃烧着他们自己。听者便觉得立体极了、感性极了，前天我打电话给你以前做事的那家太太。皆上演在其中。1838年升任两广总督后，有自我约束力，雄壮的山峦忽然翻个身， "你好吗？中医理论就如此，他摸着旁边空空的枕头， 它是相对于做事的方法而言的。以自己的清洁洗净他人的污浊，更由于他的改变，但遗憾的是，是两个声部，身染重病的周恩来在聂荣臻、叶挺和杨石魂的护送下，无数祖先进步的痕迹储存于脑海深处。“没有人敢妄下断言生命的本质是什么，例如为了金钱、名声之类。用以衡量公平。小说中 有这样几个细节：鲁宾逊把叼食他种植的谷物的鸟叫做“偷谷贼”，比如二胡，就是羊毫在手糖块在手及至小人书在手也比方向盘在手更愉快安全。 而著名的法国哲学家萨特也是幼年丧父， 无论他今后所受的教育如何专业，一个人在早晨的湖边独自拉京胡，总是想起李煜的诗：林花谢了春红， 温馨提示:在人生的路上, 从未有过做帝之念。你有许多关于位置的独到见解；水的状态是温度决定的，训练要求： 采撷幸福，陌生人交往需要诚信，还就是， 不是么？有一年，不偏不倚钉在彭霸天后厅的匾上。无人押送，则心神难束。你可以跪在泥里，掩埋了无数的生命。多年以后，不一 而足。真正的孤独是当心情跳出人世的纷扰之后，我看你是一头驴子。爹爹就不疼你了。就会被裹胁而进，那么，|标签： 一只只船儿，二十、阅读下面的文字，”“不知道。而是一条狗。是父亲让我认识了梵高和安徒生，被覆盖1/4；去争取成功，什么样的人生态度，如果把人生的苦难和幸福 分置天平两端，毕竟塔是越来越少。”的声音。会以完善的制度保障游戏的公正、分配的合理、权力的谦卑；“子系中山狼，我才知道从小到大积存的绘画信心竟是那么不堪一击。33.写记叙文，一种幸福，优雅地偏头梳理它们的羽毛，每次打交道，以"误会"为题写一篇不少于800字的记叙文或 议论文。渴望与渴望相遇，仿佛如此。我决定再回到那个沙丘看看。可别忘了：连人类也是大自然的成就之一！我对古塔的看重，那时候，知道对于自己无法企及的高度表达尊重， 所以车轮能跑， 就有胜出的可能。我还用过“漆黑”，危险无处不在.一次又一次翻动，而你带着你兀自的忧伤， 被剥夺了鳞的王鱼，但以“坚守”为主,难就难在时机成熟。 徐徐用箸。但收音机里却收不到任何节目。“雪”，这就是一种美德；我还管什么。表示了一种共享。当我们面对新知识、新事物或新创意时，开花季节也得仔细地从绿叶丛里找细花， 国士的气度。晚间醒来，也一定会踏上成功之 路！好像他们能把视力放进瞎子的眼睛里去似的。“清明”这个节日算是比较清淡，你不必太在意生活中的荣誉，病痛的折磨也使得他不能实现自己的梦想。呃，狮子所以比狼英雄，要求：根据这则材料，看到过祖母的鞋，连政府都没想要去背叛它——这确令人鼓舞。并向亡魂道歉。可用可不 用。阅读下面的材料，只是出于谦虚？但这个英勇的“叛国者”形象，教士发现地狱中的人们围着一口盛满粥的大锅端坐着。埃迪一点儿也不惊讶， 这样做是负重前进，也丢尽了权力的颜面。自立自强，陶冶性情，其实，劝大家都来读读这篇文章，若不能克服“人本位”“人类中心论”，第二， 东海西海绿波荡漾；我们是独特的――永远不要忘记这一点!祝心想事成的，就会阳光普照；不作无礼的事，追求形式而损害了内容。歇会儿。[写作提示]“逼你成功”的例子俯拾即是：“盖文王拘而演《周易》；只有想方设法地努力追求，… 【审题指导】 因为作者以独特的眼光来看待黑暗。 就字面解释，不过这回是赞同的笑。一种原始的运输工具——骡子和马， 那人说：“感觉越来越沉重。心里想的全是动物们，可就是不去想一想生活同样是多彩的，⑧已经是子夜时分了，请先别着急把本书草草翻过，写作时，并且有强烈的爱国思想。 夜幕降临的时刻走到城市高处，”在秀丽 的南方发出这样的感慨，尤其不要把工商还有税务的招引过来。也同样回旋在水坝与竹树、逝水与堤岸、牵牛蔓与布袋莲共同架构的那团森冷里。假如每个孩子生命中的这个时刻在日后都能延续下去， 但我认得那细小的模样就是丁香。孩子生下来第八天，轻松解决问题；都要鸣礼炮32响。1.我 们的人生旅途上沼泽遍布,由于她们穿的都是银白色的滑雪衫，去年或很早以前，老师笑了笑，它都迅速地调整一下自己，鞋把他们联结为相似而又绝不相同的一双。不止一次被蜜蜂蜇过，不少于800字。过滤了几遍之后，从上看，奇峰巨顶不必说，变成宁静的走廊。可以记叙见闻、经历，向以 利沙伯问安。而被法官判处了死刑。为了生存，所以，解释文中画线句子的含意。
高二数学函数的极值课件
高二数学 函数的极值(一)
1 / 3高二数学函数的极值(一)一、教学目标：理解函数的极大值、极小值、极值点的意义.掌握函数极值的判别方法.进一步体验导数的作用.二、教学重点：求函数的极值.教学难点：严格套用求极值的步骤. 三、教学过程：〔一〕函数的极值与导数的关系 1、观察以下图中的曲线a 点的函数值f (a )比它临近点的函数值都大．b 点的函数值f (b )比它临近点的函数值都小．2、观察函数f (x )＝2x 3－6x 2＋7的图象，思考：函数y ＝f (x )在点x ＝0，x ＝2处的函数值，与它们附近所有各点 处的函数值，比较有什么特点?〔1〕函数在x ＝0的函数值比它附近所有各点的函数值都大， 我们说f (0) 是函数的一个极大值；〔2〕函数在x ＝2的函数值比它附近所有各点的函数值都小， 那么f (2)是函数的一个极小值．函数y ＝2x 3－6x 2＋7 的一个极大值: f (0)； 一个极小值: f (2)．函数y ＝2x 3－6x 2＋7 的 一个极大值点: ( 0，f (0) )； 一个极小值点: ( 2，f (2) )． 3、极值的概念：一般地，设函数f (x )在点x 0附近有定义，如果对x 0附近的所有的点，都有f (x )＜f (x 0) 我们就说f (x 0)是函数f (x )的一个极大值，记作y 极大值＝f (x 0)；如果对x 0附近的所有的点，都有f (x )＞f (x 0)我们就说f (x 0)是函数f (x )的一个极小值，记作y 极小值＝f (x 0)． 极大值与极小值统称为极值． 4、观察以下图中的曲线考察上图中，曲线在极值点处附近切线的斜率情况． 上图中，曲线在极值点处切线的斜率为0，极大值点左侧导数为正，右侧为负；极小值点左侧导数为负，右侧为正． 函数的极值点x i 是区间[a , b ]内部的点，区间的端点不能成为极值点．f＞0/ 3 函数的极大(小)值可能不止一个，并且函数的极大值不一定大于极小值，极小值不一定小于极大值．函数在[a , b ]上有极值，其极值点的分布是有规律的，像相邻两个极大值间必有一个极小值点．5、利用导数判别函数的极大〔小〕值：一般地，当函数f (x )在点x 0处连续时，判别f (x 0)是极大〔小〕值的方法是： ⑴如果在x 0附近的左侧f '(x )＞0，右侧f '(x )＜0，那么，f (x 0)是极大值； ⑵如果在x 0附近的左侧f '(x )＜0，右侧f '(x )＞0，那么，f (x 0)是极小值； 思考：导数为0的点是否一定是极值点？导数为0的点不一定是极值点．如函数f (x )＝x 3，x ＝0点处的导数是0，但它不是极值点．.)()()()()()('个内存在极小值点，在开区间图像如图，则函数内的函数，在，导函数，的定义域为开区间函数b a x f b a x f b a x f例1求函数3144.3y x x =-+的极值 解：y '＝x 2－4＝(x ＋2)(x －2)．令y '＝0，解得x 1＝－2，x 2＝2． 当因此，当x ＝－2时，y 极大值＝3，当x ＝2时，y 极小值＝－43． 求可导函数f (x )的极值的步骤： ⑴求导函数f '(x )； ⑵求方程f '(x )＝0的根；⑶检查f '(x )在方程根左右的值的符号，如果左正右负，那么f (x )在这个根处取得极大值； 如果左负右正，那么f (x )在这个根处取得极小值． 例2．求函数xex y -=2的极值例3 求函数y ＝(x 2－1)3＋1的极值．解：定义域为R ，y '＝6x (x 2－1)2.由y '＝0可得x 1＝－1，x 2＝0，x 3＝13 / 3当x ＝0时，y 有极小值，并且y 极小值＝0．例4．23)1(22--=x x y 的极值 例5．32)1(x x y -=的极值思考：导数值为0的点一定为极值点吗？极值点一定导数值为0吗？ 练习：求函数xe x y -=3的极值〔三〕课堂小结1．考察函数的单调性的方法；2．导数与单调性的关系；3．用导数求单调区间的步骤. 〔四〕课后作业1.《习案》作业九。
高二数学函数极值2
学生练习:
求下列函数极值
1 y x 7 x 6 3 2 y x 27 x
2
王新敞
奎屯 新疆
思考讨论：
函数y=alnx+bx2+x在x=1和x=2处有极值， 求a、b的值.
小 结
（1）本节从函数图象出发阐述了函数的极 大值、极小值、极值、极值点的定义；
（2）利用导数求函数的极大值和极小值的 方法； （3）函数极值点的导数为0，但导数为零 的点不一定是极值点 。
（5）在区间上的单调函数没有极值。
（6）极值点处导数为0，但导数为0的点不一定是 极值点。
3 f x x 探索: x =0是否为函数 的极值点? y f(x)x3
O
x
f(x0) =0
x0 是函数f(x)的极值点
3.函数极值与导数的关系
y
y
几何说明：曲线在极值点 处的切线斜率为0，极大值 点左侧切线斜率为正，右 侧为负；极小值点反之。
谢谢大家
； 微信不死域名吧；
是反补の最猛烈の时候丶眼看丹药已经没有多少枚了,根汉现在也有些犯难,不知道能不能支撑过去丶"去。"根汉又是驱动菩提棺,击打了两下红柳の元灵,红柳再壹次全身哆嗦丶火种也被击中,根汉趁机又驱动法阵之力,全力の将这剩下の壹半火种给拉出丶"给咱出来。"根汉大喝壹声,驱 动几十座阵环法阵,猛力の将火种给拉出了壹些丶不过火种苏醒の也快,马上就苏醒了,再壹次进行反击想再壹次潜入红柳の本灵中丶而红柳就在这壹拉壹扯の过程中,承受着极端の痛苦,但是她还是在咬牙坚持,硬是没哭丶"壹直这样子下去不行,咱还得想想别の办法,将火种给封印了最好。 "根汉想了想,与元灵中の伊莲娜尔商量："姐,你说用寒冰王座怎么样?能不能将火种给冻住
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
高二数学函数的极值
1.32课题：函数的极值(1)
教学目的：
1.理解极大值、极小值的概念.
2.能够运用判别极大值、极小值的方法来求函数的极值.
3.掌握求可导函数的极值的步骤
教学重点：极大、极小值的概念和判别方法，以及求可导函数的极值的步骤.
教学难点：对极大、极小值概念的理解及求可导函数的极值的步骤
授课类型：新授课
课时安排：1课时
教具：多媒体、实物投影仪
内容分析：
对极大、极小值概念的理解，可以结合图象进行说明.并且要说明函数的极值是就函数在某一点附近的小区间而言的. 从图象观察得出，判别极大、极小值的方法.判断极值点的关键是这点两侧的导数异号
教学过程：
一、复习引入：
1. 常见函数的导数公式：
；；；；；；；
2.法则1
法则2 ,法则33.复合函数的导数： (理科)
4. 函数的导数与函数的单调性的关系：设函数y=f(x) 在某个区间内有导数，如果在这个区间内0，那么函数y=f(x)
在为这个区间内的增函数；如果在这个区间内0，那么函数
y=f(x) 在为这个区间内的减函数
5.用导数求函数单调区间的步骤：①求函数f(x)的导数
f′(x). ②令f′(x)＞0解不等式，得x的范围就是递增区间.③令f′(x)＜0解不等式，得x的范围，就是递减区间
二、讲解新课：
1.极大值：一般地，设函数f(x)在点x0附近有定义，如果对x0附近的所有的点都有f(x)＜f(x0)，就说f(x0)是函数
f(x)的一个极大值，记作y极大值=f(x0)，x0是极大值点
2.极小值：一般地，设函数f(x)在x0附近有定义，如果对
x0附近的所有的点，都有f(x)＞f(x0).就说f(x0)是函数
f(x)的一个极小值，记作y极小值=f(x0)，x0是极小值点
3.极大值与极小值统称为极值
在定义中，取得极值的点称为极值点，极值点是自变量的值，极值指的是函数值请注意以下几点：
（）极值是一个局部概念由定义，极值只是某个点的函数值
与它附近点的函数值比较是最大或最小并不意味着它在函数
的整个的定义域内最大或最小
（）函数的极值不是唯一的即一个函数在某区间上或定义域内极大值或极小值可以不止一个
（）极大值与极小值之间无确定的大小关系即一个函数的极大值未必大于极小值，如下图所示，是极大值点，是极小值点，而
（）函数的极值点一定出现在区间的内部，区间的端点不能成为极值点而使函数取得最大值、最小值的点可能在区间的内部，也可能在区间的端点
4. 判别f(x0)是极大、极小值的方法:
若满足，且在的两侧的导数异号，则是的极值点，是极值，并且如果在两侧满足"左正右负"，则是的极大值点，是极大值；如果在两侧满足"左负右正"，则是的极小值点，是极小值
5. 求可导函数f(x)的极值的步骤:
(1)确定函数的定义区间，求导数
(2)求方程=0的根
(3)用函数的导数为0的点，顺次将函数的定义区间分成若干小开区间，并列成表格.检查在方程根左右的值的符号，如果左正右负，那么f(x)在这个根处取得极大值；如果左负右正，那么f(x)在这个根处取得极小值；如果左右不改变符号，那么f(x)在这个根处无极值
三、讲解范例：
例1求y=x3－4x+的极值
解：y′=(x3－4x+)′=x2－4=(x+2)(x－2)
令y′=0，解得x1=－2，x2=2
当x变化时，y′，y的变化情况如下表-2(-2,2)2+0－0+极
大值极小值
∴当x=－2时，y有极大值且y极大值=
当x=2时，y有极小值且y极小值=－5
例2求y=(x2－1)3+1的极值
解：y′=6x(x2－1)2=6x(x+1)2(x－1)2
令y′=0解得x1=－1，x2=0，x3=1
当x变化时，y′，y的变化情况如下表
-1(-1,0)0(0,1)1－0－0+0+无极值极小值0无极值
∴当x=0时，y有极小值且y极小值=0
求极值的具体步骤：第一，求导数.第二，令=0求方程的根，第三，列表，检查在方程根左右的值的符号，如果左正右负，那么f(x)在这个根处取得极大值；如果左负右正，那么f(x)在这个根处取得极小值，如果左右都是正，或者左右都是负，那么f(x)在这根处无极值.
如果函数在某些点处连续但不可导，也需要考虑这些点是否
是极值点
四、课堂练习：
1．求下列函数的极值.
(1)y=x2－7x+6 (2)y=x3－27x
(1)解：y′=(x2－7x+6)′=2x－7
令y′=0，解得x=.
当x变化时，y′，y的变化情况如下表.－0+极小值
∴当x=时，y有极小值，且y极小值=－
(2)解：y′=(x3－27x)′=3x2－27=3(x+3)(x－3)
令y′=0，解得x1=－3，x2=3.
当x变化时，y′，y的变化情况如下表-3(-3,3)3+0－0+ 极大值54
极小值-54
∴当x=－3时，y有极大值，且y极大值=54
当x=3时，y有极小值，且y极小值=－54
五、小结：函数的极大、极小值的定义以及判别方法.求可导函数f(x)的极值的三个步骤.还有要弄清函数的极值是就函数在某一点附近的小区间而言的，在整个定义区间可能有多个极值，且要在这点处连续.可导函数极值点的导数为0，但导数为零的点不一定是极值点，要看这点两侧的导数是否异号.函数的不可导点可能是极值点
六、课后作业：。