《经济预测与决策》课后习题
经济预测与决策技术及MATLAB实现第14章 熵权法与逼近理想解排序法

0.595
0.43
40443
碳排放强度 (吨/万元)
1338.39 1285.47 1192.46 1047.06 984.61 928.95 779.64 730.29 689.98 680.55
(1)输入指标数据,确定对象个数和指标个数 %压力因素(P) clear X=[…]; %数据见表14-2 [m,n]=size(X); % m为对象个数,n为指标个数 (2)初始数据矩阵标准化 %全是负向指标 X1=[]; for j=1:n X2=(max(X(:,j))-X(:,j))./(max(X(:,j))-min(X(:,j))); X1=[X1,X2]; end
14.1 熵权法
14.1.2 熵的计算步骤
熵权法是通过计算指标的信息熵,利用指标的差异程度 来度量已知数据中包含的有效信息和指标权重。指标的 离散程度越大,其熵值越小,表明其信息的有效价值越 大,该指标在综合评价中对目标的影响也就越大。其基 本计算步骤如下:
14.1.3 熵权的性质与意义
1. 熵权的性质 (1)若某列元素数值都相同,则熵最大值为1,熵权为0。 表明在某指标上各评价对象的数值相同时,该指标未包含任 何有价值的信息。 (2)若某列元素数值相差越大,则熵值就越小,熵权就越 大。表明该指标包含有价值的信息。 (3)若指标的熵值越大,则其熵权越小,表明该指标越不 重要。
4. 求第二指标层影响因素指标的权重
年份
2005 2006 2007 2008 2009 2010 2011 2012 2013 2014
城镇登记失业率 (%) 3.3 3.3 3.2 3.5 3.4 3.4 3.4 3.3 3.2 3.3
城镇恩格尔系数 (%) 33.69 32.02 32.90 33.61 32.92 32.06 33.15 32.97 29.18 28.92
经济预测与决策试题及答案

经济预测与决策一、单项选择题1. 经济预测是编制计划的A. 依据B.结果C.目的D.方法2. 各种可能结果发生概率P(Ei)的总和∑P(Ei)=A.1B.0C. ≤1D. 0≤3. 专家评估法包括()等方法。
A.市场调查法B.主观概率加权法C.专家会议法D.三点法4. 完全拟合时,可决系数r2的值是:A. -1B. 0C. 1D. 0r215. 样本回归直线对数据拟合程度的综合度量指标有:。
A.拟合优度B.可决系数C.季节指数D.平滑系数6. 当时间序列出现线性变动趋势时,可以采用()进行预测。
A. 一次移动平均法B. 二次移动平均法C. 一次指数平滑法D. 三次指数平滑法7. 二次指数平滑法中,计算斜率系数的估计式是()。
8. 最小平方法中,对于自变量t,有()。
9. 当时间序列的二阶差分2Yt近似为常数时,可建立()模型进行预测。
A..线性回归B.直线趋势C.二次曲线D.指数曲线10. ()是用百分数或系数形式表示的季节变动指标。
A.同期平均数B.连锁系数C.季节变差D. 季节指数11. 若时间序列呈水平型季节变动,则意味着时间序列中不存在明显的()A. 长期趋势变动B. 季节变动C.循环变动D.不规则变动12. 若概率矩阵P的有限次方幂Pm的所有元素Pij为(),则P为正规概率矩阵。
A. -∞<Pij<∞B. -∞<Pij≤0C. 0≤Pij<∞D. 0<Pij<∞13. 转移概率,这种转移概率可以依据其前一种状态推算出来,而与该系统的原始状态和此次转移以前的有限次或无限次转移()。
A. 无关B. 有关C. 正相关D. 负相关14. 经济决策是指经济管理部门和企业为了达到某种经济目标,在经济调查、经济预测和对经济发展、管理活动等规律性认识的基础上,运用科学的方法,根据对经济效果或效益的评价,从几种可供选择的行动方案中,选出一个()的方案,作为经济行动的指导。
A.可行B. 令人满意C.经济D.最优15. ()原则是指,从几种可供选择的方案中,择优选取可行的令人满意的方案。
(整理)经济预测与决策练习题

第一章统计预测概述一、单项选择题8、统计预测的研究对象是()A、经济现象的数值B、宏观市场C、微观市场D、经济未来变化趋势答:A二、多项选择题4、定量预测方法大致可以分为()A、回归预测法B、相互影响分析法C、时间序列预测法D、情景预测法E、领先指标法答:AC三、名词解释2、统计预测答:即如何利用科学的统计方法对事物的未来发展进行定量推测,并计算概率置信区间。
四、简答题1、试述统计预测与经济预测的联系和区别。
答:两者的主要联系是:①它们都以经济现象的数值作为其研究的对象;②它们都直接或间接地为宏观和微观的市场预测、管理决策、制定政策和检查政策等提供信息;③统计预测为经济定量预测提供所需的统计方法论。
两者的主要区别是:①从研究的角度看,统计预测和经济预测都以经济现象的数值作为其研究对象,但着眼点不同。
前者属于方法论研究,其研究的结果表现为预测方法的完善程度;后者则是对实际经济现象进行预测,是一种实质性预测,其结果表现为对某种经济现象的未来发展做出判断;②从研究的领域来看,经济预测是研究经济领域中的问题,而统计预测则被广泛的应用于人类活动的各个领域。
第二章定性预测法一、单项选择题3、()需要人们根据经验或预感对所预测的事件事先估算一个主观概率。
A 德尔菲法B 主观概率法C 情景分析法D 销售人员预测法答:B二、多项选择题2、主观概率法的预测步骤有:A 准备相关资料B 编制主观概率表C 确定专家人选D 汇总整理E 判断预测答:A B D E三、名词解释2、主观概率答:是人们对根据某几次经验结果所作的主观判断的量度。
四、简答题1、定型预测有什么特点?它和定量预测有什么区别和联系?答:定型预测的特点在于:(1)着重对事物发展的性质进行预测,主要凭借人的经验以及分析能力;(2)着重对事物发展的趋势、方向和重大转折点进行预测。
定型预测和定量预测的区别和联系在于:定性预测的优点在于:注重于事物发展在性质方面的预测,具有较大的灵活性,易于充分发挥人的主观能动作用,且简单的迅速,省时省费用。
经济分析与预测练习题答案

经济分析与预测练习题答案经济分析与预测练习题答案经济分析与预测是经济学中的重要内容,通过对经济现象的观察和数据的分析,可以帮助我们了解经济的运行规律和趋势。
在这篇文章中,我们将回答一些关于经济分析与预测的练习题。
1. 什么是经济分析?经济分析是指对经济现象进行系统研究和分析的过程。
它包括对经济数据的收集、整理和分析,以及对经济问题的解释和预测。
经济分析可以帮助我们了解经济的运行机制和规律,为决策提供依据。
2. 经济数据有哪些类型?经济数据可以分为宏观经济数据和微观经济数据。
宏观经济数据是指反映整个经济体系运行状况的数据,如国内生产总值(GDP)、通货膨胀率、失业率等。
微观经济数据是指反映个体经济行为和市场状况的数据,如个人收入、消费支出、企业利润等。
3. 什么是经济预测?经济预测是指对未来经济发展趋势和变化进行预测的过程。
通过对已有的经济数据和经济理论的分析,可以预测未来经济的增长率、通货膨胀率、利率等。
经济预测可以帮助政府、企业和个人做出合理的决策,降低风险和损失。
4. 经济预测的方法有哪些?经济预测的方法包括定性分析和定量分析。
定性分析是基于经验和专业知识对经济问题进行判断和预测,如通过对政策变化和市场环境的分析来预测经济走势。
定量分析是基于经济模型和统计方法对经济数据进行预测,如使用时间序列分析和回归分析来预测经济变量的未来走势。
5. 经济预测的局限性是什么?经济预测存在一定的局限性。
首先,经济预测是基于已有的经济数据和经济理论进行的,如果数据不准确或者理论有误,预测结果可能不准确。
其次,经济预测受到外部环境的影响,如政策变化、自然灾害等因素都可能导致预测结果的偏差。
最后,经济系统的复杂性和不确定性也增加了预测的难度。
6. 经济分析和预测在实际中的应用有哪些?经济分析和预测在实际中有广泛的应用。
政府可以通过对经济数据的分析和预测来制定宏观经济政策,促进经济的稳定和增长。
企业可以通过对市场需求和竞争环境的分析和预测来制定市场营销策略和生产计划。
经济预测与决策课程设计

经济预测与决策 课程设计一、课程目标知识目标:1. 学生能够理解并掌握经济预测的基本概念、原理和方法。
2. 学生能够了解经济决策的类型、过程及其在实际中的应用。
3. 学生能够掌握并运用数据分析技能,对经济数据进行分析,为预测和决策提供依据。
技能目标:1. 学生能够运用所学经济预测方法,对实际问题进行预测分析,并提出合理的预测结果。
2. 学生能够结合实际案例,设计简单的经济决策模型,并运用到实际问题的解决中。
3. 学生能够通过小组合作,进行数据分析,提高团队协作和沟通能力。
情感态度价值观目标:1. 学生能够认识到经济预测与决策在国家和企业经济发展中的重要性,增强对经济学的兴趣和热爱。
2. 学生在学习过程中,培养批判性思维和问题解决能力,形成积极主动探索知识的良好习惯。
3. 学生能够树立正确的价值观,关注国家经济发展,提高社会责任感和使命感。
课程性质:本课程为高中年级经济学选修课程,旨在通过实际案例分析,使学生掌握经济预测与决策的基本知识和技能。
学生特点:高中年级学生具有一定的逻辑思维能力和数学基础,对实际经济问题充满好奇心,喜欢探索和解决问题。
教学要求:教师应注重理论与实践相结合,引导学生运用所学知识解决实际问题,提高学生的分析、预测和决策能力。
通过小组讨论、案例分析等教学手段,培养学生的团队协作和沟通能力。
在教学过程中,关注学生的情感态度价值观的培养,使学生在掌握知识技能的同时,形成正确的价值观。
二、教学内容1. 经济预测基本概念:介绍预测的定义、作用和类型,结合教材第3章相关内容,分析不同预测方法的适用场景。
教学安排:2课时2. 经济预测方法:讲解趋势预测、季节性预测、周期性预测等常用预测方法,结合教材第4章进行案例分析。
教学安排:4课时3. 经济决策类型与过程:介绍个体决策、集体决策等类型,分析决策过程,结合教材第5章实际案例进行讲解。
教学安排:3课时4. 数据分析方法:讲解描述性统计、概率分布、回归分析等数据分析方法,结合教材第6章进行实际操作。
经济预测与决策_习题
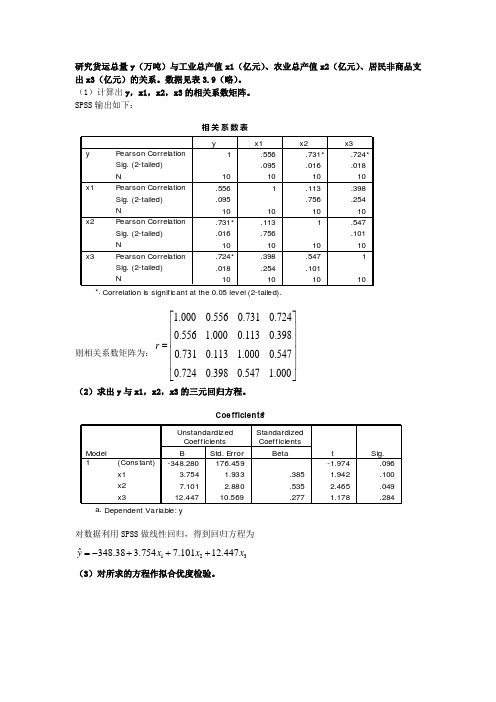
研究货运总量y (万吨)与工业总产值x1(亿元)、农业总产值x2(亿元)、居民非商品支出x3(亿元)的关系。
数据见表3.9(略)。
(1)计算出y ,x1,x2,x3的相关系数矩阵。
SPSS 输出如下:则相关系数矩阵为: 1.0000.5560.7310.7240.556 1.0000.1130.3980.7310.113 1.0000.5470.7240.3980.547 1.000r ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦(2)求出y 与x1,x2,x3的三元回归方程。
对数据利用SPSS 做线性回归,得到回归方程为123ˆ348.38 3.7547.10112.447yx x x =-+++ (3)对所求的方程作拟合优度检验。
由上表可知,调整后的决定系数为0.708,说明回归方程对样本观测值的拟合程度较好。
(4)对回归方程作显著性检验;原假设::3210===βββHF 统计量服从自由度为(3,6)的F 分布,给定显著性水平α=0.05,查表得76.4)6.3(05.0=F ,由方查分析表得,F 值=8.283>4.76,p 值=0.015,拒绝原假设H ,由方差分析表可以得到8.283,0.0150.05F P ==<,说明在置信水平为95%下,回归方程显著。
(5)对每一个回归系数作显著性检验;做t 检验:设原假设为:0=i H β,it 统计量服从自由度为n-p-1=6的t 分布,给定显著性水平0.05,查得单侧检验临界值为1.943,X1的t 值=1.942<1.943,处在否定域边缘。
X2的t 值=2.465>1.943。
拒绝原假设。
由上表可得,在显著性水平0.05α=时,只有2x的P 值<0.05,通过检验,即只有2x 的回归系数较为显著 ;其余自变量的P 值均大于0.05,即x1,x2的系数均不显著。
(6)如果有的回归系数没有通过显著性检验,将其剔除,重新建立回归方程,并作回归方程的显著性检验和回归系数的显著性检验。
《经济预测与决策》习题答案 第十六章

16.1 单项选择题(在每小题的4个备选答案中选出1个正确答案,并将其字母填在题干后面的括号内。
)
16.2 多项选择题(在下列5个备选答案中,至少有2个是正确的,请将其全部选出,并把字母填在题干后面的括号内。
)
16.3 基本概念与简答题
16.3.1 简述不确定型决策的条件。
16.3.2 简述不确定型决策的常用准则(原理)。
16.3.3 何谓“最小的最大后悔值”决策准则?它与“好中求好”决策准则有何不同?
16.3.4 简述α系数决策方法(赫威兹决策准则)及其特点。
16.3.5 简要比较五种不确定型决策准则的特点。
16.4 计算与分析题
16.4.1 已知某产品有三种生产方案可供选择,未来可能面临三种销售状态,其条件损益值见表16.4.1所示。
表16.4.1 损益值表单位:万元
(1)运用“好中求好”决策准则作出决策;
(2)运用“坏中求好”决策准则作出决策;
(3)运用α系数决策方法作出决策(α=0.4);
(4)运用“最小的最大后悔值”决策准则作出决策。
经济预测与决策练习题

经济预测与决策练习题随着社会的不断进步,经济预测与决策变得越来越重要。
无论是个人还是组织,都需要通过合理的经济预测来做出明智的决策。
然而,对于大部分人来说,经济预测和决策并不是一件容易的事情。
因此,我准备了以下几个经济预测与决策的练习题,希望能帮助大家更好地理解和应用这一重要概念。
1. 假设你是一家制造业公司的财务主管,在当前市场环境下,你需要预测明年的销售收入。
你可以利用过去的销售数据和市场趋势来进行预测。
请问,你会选择使用哪种经济预测方法?请列举并解释其优缺点。
2. 假设你是一家零售企业的业务经理,你需要预测下个季度的销售额。
你已经收集了过去几个季度的销售数据和相关的市场因素,并运用回归分析得到了一个预测模型。
然而,在应用模型之前,你还需要对数据进行一些预处理。
请列举并解释三种常见的数据预处理方法。
3. 假设你是一家初创公司的创始人,你需要为公司筹集资金,因此你需要制定一个详细的财务计划。
请列举并解释一个完整的财务计划应包含的内容。
此外,你认为在制定财务计划时应考虑哪些重要因素?4. 假设你是一个普通投资者,你希望通过投资股票来获得回报。
在选择要投资的股票时,你可以运用一些技术指标来辅助决策。
请列举并解释三种常见的技术指标,并解释它们如何帮助你做出投资决策。
5. 假设你是一家跨国公司的市场部经理,你需要为公司开展市场调研,以了解目标市场的情况,并做出相应的决策。
请列举并解释三种常见的市场调研方法,并解释它们各自的优势和劣势。
经济预测与决策是一门综合性的学科,涉及到多个领域和技术。
通过以上练习题,我们可以更好地了解经济预测与决策的方法和工具,以及它们在实际情境中的应用。
无论是在个人生活还是工作中,我们都需要运用这些知识,做出明智的经济决策。
然而,值得注意的是,经济预测与决策并非一成不变的。
我们所做的预测和决策可能会受到外部环境的变化影响,因此需要不断进行修正和调整。
此外,经济预测与决策也需要结合实践和经验,才能更加准确和有效。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章经济预测的基本原理1.什么叫经济预测?经济预测是一门研究经济发展过程及其变动趋势的学科。
2.经济预测与决策有什么关系?经济计划是为实现经济决策目标而编制的一种经济活动方案,而经济决策的目标又是依据经济预测的结果而确定的。
3.什么叫宏观经济预测?宏观经济预测是指对整个国民经济或一个地区、一个部门的经济发展前景的预测,它以整个社会(或地区、部门)的经济发展的总图景作为考察对象。
4.什么叫微观经济预测?微观经济预测是指对一个企业的经济发展前景或家庭、个人的经济活动的预测,它以单个经济单位的经济活动前景作为考察的对象。
5.什么叫定性经济预测?定性经济预测是对某一经济现象的未来状态所作的一种描述,也就是对未来的经济状态提供可能变动的方向而非数量的大小所作出的预测。
6.什么叫定量经济预测?定量经济预测是运用经济统计的数据资料,根据预测目标中的经济变量之间的关系,建立起预测模型以推导出预测值。
7.预测的基本要素有哪些?信息要素,方法要素,分析要素,判断要素。
第四章判断预测技术1.直接头脑风暴法与质疑头脑风暴法的主要区别是什么?在专家选择上有何异同?直接头脑风暴法是组织专家对所要解决的问题,开会讨论,各持己见地、自由地发表意见,集思广益,提出所要解决问题的具体方案。
质疑头脑风暴法是对已制定的某种计划方案或工作文件,召开专家会议,由专家提出质疑,去掉不合理的或不科学的部分,补充不具体或不全面的部分,使报告或计划趋于完善。
P1-P3=0.11>0故该公司各厂明年投资的总趋势增加。
5.甲的平均销售量=(800+4*700+600)/6=700甲预测的销售量的方差为2=[(800-600)/6 ]2=1111.11δ甲=33.33δ甲乙的平均销售量=(750+4*640+550)/6=643乙预测的销售量的方差为2=[(750-550)/6]2=1111.11δ乙δ=33.33乙丙的平均销售量=(850+4*700+600)/6=708=41.67丙预测的销售量的方差为δ丙推销员的销路预测是(700+643+708)/3=684其预测值的方差为δ2=(δ甲2+δ乙2+δ丙2)/9=439.85δ=20.97故,预测值在439.85-2*20.97至439.85+2*20.97之间的可能性为95.4% 6.柜台A,2Φ[(450-400)/δA]-1=90%)=0.95所以,Φ(50/δA50/δA =1.65=50/1.65=30.30所以,δA由此得,专柜A的预测值的均值为400,标准差为30.30同理,专柜B的预测值的均值为450,标准差为25.51专柜C的预测值的均值为350,标准差为34.72(400+450+250)/3=400δ=17.56故其均值是400,标准差是17.56 总销售量预测值在[400-17.56,400+17.56]之间的可能性为68.3%,在[400-2*17.56,400+2*17.56]之间的可能性为98.4%第五章一元回归预测技术x1=22.7/8=2.84 y1=6030/8=753.75b=(17569-(22.7/8)*6030)/(67.15-(22.7/8)*22.7=167.5490644a=6030/8-167.55*22.7/8=278.3295299y=278.33+167.55xr=(17569-8*2.84*753.75)/√(67.15-8*2.84^2)√(4627700-8*753.75^2)=0.95 若增加广告费支出,有望增加销售额。
将x=4.5带入原方程得,y=1032.32.由表中月份和销售额之间的关系易知,十一月份的销售额为10.2,十二月的为10.6.b=(255730-518.75*476)/(2243300-518.75*4150)=0.097a=59.5-518.75*0.097=9.02y=9.02+0.097x将x=700带入方程得,y=77故该商品的需求量是77万元。
4.b=(617.49-4.4*132.1)/(296.8-4.4*61.8)=1.43a=9.4-1.43*4.4=3.11故得,y=3.11+1.43x将x=9.2带入该方程,得y=16.27nyi-yi^ (yi-yi^)2-0.414 0.171396-0.214 0.045796-0.2 0.040.043 0.0018490.428 0.1831840.113 0.0127690.27 0.0729-0.174 0.030276-0.317 0.1004890.154 0.0237160.268 0.0718240.825 0.6806250.124 0.015376-0.72 0.51841.9686δ2=Q/(n-2)=0.16由P(y^-2δ<y<y^+2δ)=95%,故得P=(15.47,17.07)5.年份x 财政收入(亿元)y1989 724.71990 773.71991 786.51992 802.81993 791.81994 822.21995 924.11996 10331997 1103.21998 1092.75a+9955b=3879.55a+9980=4875.2a=-86485.6b=43.8y=-86485.6+43.8x把x1=1999,x2=2000分别带入,得y1=1070.6 ,y2=1114.46.价格x 需求量y x2 y2 x*y yi-yi^ (yi-yi^)21.5 352.25 1225 52.5 -0.295 0.0870251.8 32 3.24 1024 57.6 -0.028 0.0007842 30 4 900 60 0.15 0.02252.1 29 4.41 841 60.9 0.239 0.0571212.3 27 5.29 729 62.1 0.417 0.1738892.5 24 6.25 576 60 -0.405 0.1640252.8 21 7.84 441 58.8 -0.138 0.019044 ∑15 198 33.28 411.9 0.524388 均值 2.142857 28.28571429a 51.62563b -10.892故y=51.63-10.89xδ2= Q/(n-2)=0.1118=51.63-10.89x1-2*0.3320=51.63-10.98x2+2*0.33得x1=3.02,x2=2.96故价格范围是(3.02,2.96)第六章 多元回归预测技术1.求多元线性回归方程 设多元线性回顾模型为: ^22^11^0^x b x b b y ++=,还是像一元线性回归一样用最小二乘方的方法求解参数,残差平方和=∑=ni 1(i iy y ^-)2=∑=n i 12^2^211^0)(x b x b b y i i i---= Q ,由多元微分学可知)^^^(20)^^^(20)^^(221211^2^^112211^1^^1221^10^0^^=----=∂∂=----=∂∂=----=∂∂∑∑∑===x x bx bb y b xx b x bb y b xb x b by b ini iii iini ii ini ii iQ Q Q ;将数据代入整理后的方程组当中,就可以得到要求的参数^b=12.2516415,^1b=0.096356147,^2b=-0.249406279,故回归方程为:^y =12.2516415+0.096356147*x1-0.249406279*x2; 当x1=460,x2=100时, 标准差:s y ==1)(112^---=--∑=p n p n Qni iiy y =sqrt(42.48429154/(14-2-1))=1.965250193点预测值:^y= 31.63484119,又由于p(^y-2*s y <yo<^y+2*s y )=95.4%,可算出置信区间(27.7043408,35.56534157)2.设多元线性回顾模型为:^22^11^0^x b x b b y ++=,还是像一元线性回归一样用最小二乘方的方法求解参数,残差平方和=∑=ni 1(i iy y ^-)2=∑=n i 12^2^211^0)(x b x b b y i i i---= Q ,由多元微分学可知)^^^(20)^^^(20)^^(221211^2^^112211^1^^1221^10^0^^=----=∂∂=----=∂∂=----=∂∂∑∑∑===x x bx bb y b x x bx bb y b xb x b by b ini iii iini ii ini ii iQ Q Q ;将数据代入整理后的方程组当中,就可以得到要求的参数^b=108.2184312,^1b=-8.522687302,^2b=0.029097784,故回归方程为:^y =108.2184312-8.522687302*x1+0.029097784*x2; 当x1=10,x2=1500时, 点预测值:^0y =66.63823426标准差:s y =sqrt(592.8640521/7)=9.202981288 区间预测:p(^y -2*s y <yo<^y +2*s y )=95.4%,=(48.23227168,85.04419683)3.x a a a x y 2210**++=要将非线性方程转化成线性方程, 令x=x1,x 2=x2得到方程为:y=a0+a1*x1+a2*x2然后就用多元线性回归的方法进行计算参数a0,a1,a2 即用最小二乘方的办法残差平方和=∑=ni 1(i iy y ^-)2=∑=n i 12^2^211^0)(x a x a a y i i i---= Q ,由多元微分学可知)^^^(20)^^^(20)^^(221211^2^^112211^1^^1221^10^0^^=----=∂∂=----=∂∂=----=∂∂∑∑∑===x x ax aa y a x x ax aa y a xa x a ay a ini iii iini ii ini ii iQ Q Q ;将数据代入整理后的方程组当中,就可以得到要求的参数a0= 2.587786,a1= 2.064922,a2= -0.211, 得到线性方程为:y =2.587786+ 2.064922*x1-0.211*x2;有方程分析可得,要想制止销售量的下降趋势,应该增加价格 5.由题意可知,y=βαx,对该方程取对数得到:lny=ln α+x*ln β 令 lny=y,ln α=a,ln β=b,得到方程为:y=a+bx然后就用一元线性回归的方法进行计算参数a,b, 用平均值法来计算:X y x y1998 0 2002 0.556302501 1999 0.079181246 2003 0.672097858 2000 0.255272505 2004 0.819543936 2001 0.397940009 2005 0.959041392 分别求和的7998b+4a=0.732394 (1) 8014b+4a=3.006985687 (2) 由(1)(2)方程的:a=-284.07,b=0.142162 得到线性方程为:y=-284.07+0.142162*x当X=2006时,y= 1.107151 6.由题意可知,y=βαx ,对该方程取对数得到:lny=ln α+x*ln β 令 lny=y,ln α=a,ln β=b, 得到方程为:y=a+bx然后就用多元线性回归的方法进行计算参数a,b用平均值法来计算:X y x y1997 15810 2001 250141998 17618 2002 357211999 20824 2003 440682000 22342 2004 639202001 25014 2005 75763分别求和的9995b+5a=21.51075782 (1) 10015b+5a=23.28032402 (2) 由(1)(2)方程的:a=-172.566,b=0.088478得到线性方程为:y= -172.566+0.088478x当X=2006时,y= 4.9215第七章序列相关和异方差的处理技术1.解:年份 c y c的预测值c的预测值-c平方1995 11378 11617 16077.05 -4699.05 22081070.9 1996 13012 13297 17169.05 -4157.05 17281064.7 1997 15263 15790 18789.5 -3526.5 12436202.25 1998 16873 18017 20237.05 -3364.05 11316832.4 1999 17764 19214 21015.1 -3251.1 10569651.21 2000 18857 20198 21654.7 -2797.7 7827125.29 2001 20074 21512 22508.8 -2434.8 5928251.04 2002 21439 23124 23556.6 -2117.6 4484229.76 2003 22833 24724 24596.6 -1763.6 3110284.96 2004 24205 26175 25539.75 -1334.75 1781557.563 2005 25307 27219 26218.35 -911.35 830558.822597646828.9 (1)残差平方和=97646828.9Et Et-1 Et*Et-1 Et*Et-4699.05 -4157.05-4157.05 -3526.5-3526.5 -3364.05-3364.05 -3251.1-3251.1 -2797.7-2797.7 -2434.8-2434.8 -2117.6-2117.6 -1763.6-1763.6 -1334.75-1334.75 -911.35 -911.35 0 830558.8 0.874197 存在某种正自相关,p=0.87 (2)P=0.87,存在一阶自相关 (3)将方程改写为则此方程不存在相关性。
