班级考试成绩自动统计分析
第1次八年级体育段考成绩自动分析统计表2

全班 排名
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 班级 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 八(1) 姓名 罗文杰 林俊宏 雷林宏 陈家健 欧阳思怡 欧诗敏 吕乐敏 练思贤 胡思晴 吴海怡 杨妮娜 陈依欣 田满园 沙思煜 宋依霖 林志鸿 邱伟松 邱俊楠 罗丽雯 李向题 欧阳冬如 朱景龙 王敬友 田木贵 张熙媛 陈凯涛 冯超 曹艺馨 周奕燊 罗祖欣 练吉香 陈咏玲 吴仕彬 周文慧 陈淑婷 黄思琪 张文城 巫健安 性别 男 男 男 男 女 女 女 男 女 女 女 女 女 男 女 男 男 男 女 男 女 男 男 男 女 男 男 男 女 男 女 女 男 女 女 女 男 男 1000/800 (分.秒) 3.25 3.41 3.32 3.45 3.27 3.3 3.22 3.49 3.25 3.36 3.36 3.26 3.38 3.33 3.26 3.37 3.52 3.45 3.5 4.05 3.38 4.05 3.57 4.01 3.43 3.41 4.08 3.42 3.32 4.07 3.49 4.14 3.42 3.39 3.37 3.42 5.08 4.03 分数 100 100 100 100 100 100 100 98 100 97 97 100 96 100 100 100 96 100 90 90 96 90 94 92 93 100 88 100 99 89 91 70 100 96 96 94 37 91 2.3 2.35 2.4 2.45 2.6 立定跳远 (米) 2.6 分数 100 0 0 0 0 0 0 100 0 0 0 0 0 95 0 93 0 90 0 0 0 0 0 0 0 82 0 0 0 0 0 0 0 0 0 0 0 0 实心球 (米) 分数 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 164 141 138 149 141 158 113 117 101 104 144 44 180 188 157 167 159 160 156 167 165 170 177 178 167 176 176 177 181 184 174 175 跳绳 (次) 分数 0 100 100 100 100 99 99 0 97 100 100 96 100 0 94 0 96 0 100 100 91 96 91 92 90 0 94 78 75 84 78 91 56 58 48 50 80 13 总分 50 50 50 50 50 49.75 49.75 49.5 49.25 49.25 49.25 49 49 48.75 48.5 48.25 48 47.5 47.5 47.5 46.75 46.5 46.25 46 45.75 45.5 45.5 44.5 43.5 43.25 42.25 40.25 39 38.5 36 36 29.25 26
学期期末考试学业成绩分析报告

2020级XX管理专业2020-2021学年第一学期学业成绩分析报告为了掌握XX管理专业学生的学习情况和上学期期末考试成绩,充分发挥学生、家长、学校三位一体的教育功能,提高学生的学习自信心、主动性和目的性,针对性做好学风建设和促进工作,根据学校进一步加强学风建设的总体要求,在学院的统筹和部署下,对2020级XX管理专业一、二班2020-2021学年第一学期期末考试成绩进行了学业分析。
以此为契机,分析学生考试不及格的主、客观原因,自身及环境因素,探寻提高班级学习成绩的对策,制定卓有成效的实施方案,着力加强班级及专业学风建设。
XX管理专业两个班级就2020-2021学年第一学期期末考试成绩分析开展了学业分析报告主题班会,针对考试成绩侧面反映出的班级学风风貌进行了深刻剖析,并制订了本学年第二学期班级学风建设议案。
现将2020级XX管理专业一、二班2020-2021学年第一学期期末考试成绩各方面情况进行如下分析总结:一、2020-2021学年第一学期期末考试成绩统计分析1.不及格人数及不及格率分析2020级XX专业一、二班共有学生83人,2020-2021学年第一学期期末考试,专业不及格率为31.33%。
不及格学生总人数为26人,占比将近总人数的三分之一,其中,女生不及格人数为20人,男生不及格人数为6人。
2020级XX 一班有学生41人,其中27人通过全部课程考试,不及格人数为14人,11名女生,3名男生,班级不及格率为34.15%,该班级不及格率高于专业不及格率;2020级XX二班有学生42人,30人通过全部课程考试,不及格人数为12人,3名男生,9名女生,班级不及格率为28.57%,该不及格率低于XX专业不及格率。
通过对比XX一、二两个班级的考试成绩,我们可以发现,XX一班班级总人数比XX二班少一人,但是不及格人数却比XX二班多两人,不及格率比XX二班高出近六个百分点。
XX一、二班不及格人数占XX专业总不及格人数的比例分别是54%和46%。
学生成绩的统计分析

学生成绩的统计分析一、考试试卷的统计分析(一)试卷难度的分析所谓难度是指考试中试题或者试卷的难易程度,是考试题目对学生知识和能力水平适合程度的指标。
1、难度的计算以往教师在考试中对试题难度的测定大部分是凭感觉。
这种方法本身比较模糊,对有经验的教师也并不是非常有效。
根据难度的概念,得到如下公式。
以、x、a表示第i题的成绩均值和满分值,则:第i题的难度:d=1-x/a若第i题全部答对,则d=0;若第/题全部答错,则d=1;当d=0、5,说明此题难度适中。
试卷难度:试卷难度的测定建立在试题难度的基础上,以试题难度为变量,以试题满分值为权数的加权算数平均数。
一般而言,试卷都是以#$$分为满分,于是对于学校的常规考试,目的在于测量个体差异。
当d=0或1时,即试题全部答对或答错,该题便无法提供个体差异的信息。
而只有当d=0、5时,题目才能做最大程度的区分度。
但在实际工作中要使每题难度均达到0、5有一定的困难。
因此,一般要求试卷平均难度为0、5左右,各试题的难度控制在0、50、2之间。
2、难度的比较按以上公式计算的试题及试卷难度,只能看出不同试题或不同试卷的难易程度,但却不能分析题目或试卷之间的相对难度。
如某试卷中,第一,第二,第三题的难度分别是0、3,0、4,0、5。
从难度数据中可以看出,第一题相对较容易,第三题较难。
但第二题与第一题的难度差和第三题与第二题的难度差是否相等?这却不一定。
原因是不同试题的难度位于不同的等距量表,因而不具有可比性。
为解决试题及试卷之间难度的相互对比,需要将以上公式计算的难度,通过正态分布表,转化为标准分。
如:12$(",42,#(&&;12$(!,42,#()*;12$(*,42$。
显然,第二题与第一题的难度差为$(#",第三题与第二题的难度差为#()*,难度差并不相等。
(二)试卷区分度的分析区分度也叫鉴别力,就是通过一次考试将不同程度,不同能力的学生区分开来的重要指标。
班级期中考试成绩统计分析表
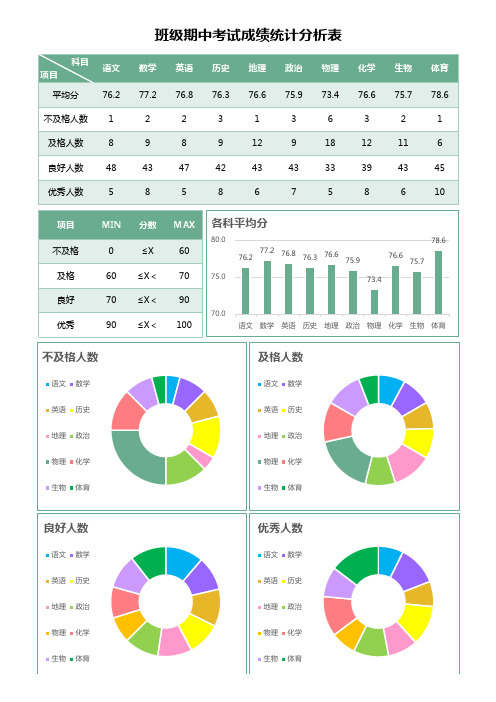
不及格人数
语文 数学 英语 历史 地理 政治 物理 化学 生物 体育
及格人数
语文 数学 英语 历史 地理 政治 物理 化学 生物 体育
良好人数
语文 数学 英语 历史 地理 政治 物理 化学 生物 体育
优秀人数
语文 数学 英语 历史 地理 政治 物理 化学 生物 体育
5
8
5
8
6
7
5
8
6
10
项目 不及格
及格 良好 优秀
MIN 0 60 70 90
分数 ≤X ≤X< ≤X< ≤X<
MAX 60 70 90 100
各科平均分
80.0
76.2 77.2 76.8 76.3 76.6 75.9
78.6 76.6
75.7
75.0
73.4
70.0
语文 数学 英语 历史 地理 政治 物理 化学 生物 体育
班级期中考试成绩统计分析表
项目 科目 语文
平均分
76.2
数学 77.2
英语 76.8
历史 76.3
地理 76.6
政治 75.9
物理 73.4
化学 76.6
生物 75.7
体育 78.6
不及格人数 1
2
2
3
1
3
6
3
2
1
及格人数
8
9
8
9
12
9
18
12
11
6
良好人数
48
43
47
42
43
43
33
39
43
45Biblioteka 优秀人数
如何对学生考试成绩进行数据分析范文

专业整理一、原始分和标准分的定义原始分是考试后直接从卷面上得到的分数。
标准分是指通过原始分转化而得到的一种地位量数,它反映考生成绩在全体考生成绩中的位置。
因此,无论试题难或易,无论整体原始分偏高或偏低,整体标准分都没有什么变化。
二、标准分的计算根据教育统计学的原理,标准分Z是原始分与平均分的离差以标准差为单位的分数,用公式表示为:Z=(X-A)/S其中:X为该次考试中考生个人所得的原始分;A为该次考试中全体考生的平均分;S为该次考试分数的标准差。
通过转换后得到的标准分Z在一般情况下都带小数,而且会出现负值,实际使用时不太方便,所以还要对Z分数进行线性变换(T变换):T=500+100Z这就是我们通常所说的标准分。
这种标准分的平均值为500,也就是说,如果某考生的标准分为500,则该生的成绩处于此次考试的中间位置。
标准分有如下性质:⑴平均值为0,标准差为1;⑵分数之间等距,可以作加减运算;⑶原始分转换为标准分是线性转换,不会改变原始分的分布形状,也不改变原来分数的位置次序。
三、使用标准分比使用原始分有什么好处?根据教育统计学的原理,原始分转换成标准分的意义可以从下面的比较中反映出来:⑴单个标准分能够反映考生成绩在全体考生成绩中的位置,而单个原始分则不能。
例如,某考生某科的原始成绩为85分,无法说明其这科成绩究竟如何,因为这与试题的难度有关,与总体考生的分数有关。
如果某考生某科的标准分为650,即Z分数为1.5,则通过查正态分布表,查得对应的百分比为0.9332,于是我们知道,该考生的成绩超过了93.32%的考生的成绩,这就是分数解释的标准化。
⑵不同学科的原始分不可比,而不同学科的标准分是可比的。
不同的学科,由于试题的难易程度不同,各学科的分数价值也就不同。
例如某考生的语文原始成绩为80分,数学原始成绩为70分,从原始分看,其语文成绩优于数学成绩。
但如果这次考试全体考生的语文原始分平均为86分,而数学原始分平均为60分,则该考生的语文成绩处于全体考生的平均水平之下,而数学成绩处于全体考生的平均水平之上,即该生的数学成绩实质上优于语文成绩。
Excel 进行学生成绩统计分析

Excel 进行学生成绩统计分析处理学生成绩时所分析的项目包括参考班级,参考人数、平均分,及格人数、及格率、优秀人数、优秀率,最高分、最低分以及各分数段所占的人数:600分以上人数、500~599 分人数、400~499 人数、300~399 人数、300 分以下人数。
这个统计比较复杂,且工作量大,如果用人工计算,不但效率低,且出错机率大,而用EXCEL函数可以很好解决这个问题。
新建空白Excel工作簿,将自动建立的Sheet1、Sheet2、Sheet3工作表重命名为成绩表、分析表、分数段统计表。
其中各科考试成绩表用于输入各科成绩。
(一)设计各科成绩表在各科考试成绩表第一行中输入分析名称,如“** 中学2007~2008 学年度第一学期高一月考成绩表”,在第二行从A1单元格开始顺序输入记录字段名:考号、姓名、班级、语文、数学、英语、物理、化学等。
假设全级学生有674 人,10个班,所以从第3行到第676 行用来输入所有学生各科的成绩。
1. 求总分:主要用SUM函数,其语法格式为SUM(Ref),此处Ref为参与计算的单元格区域。
例如:SUM(B2:E2)是表示求B2、C2、D2、E2四个单元格内数字的和。
另外还用到SUMIF函数,语法格式为SUMIF(Range,Criteria,Sum_range),其功能是根据指定条件对若干单元格求和,参数Range表示引用,用于条件判断的单元格区域。
Criteria表示数字、表达式或文本,指出哪些单元格符合被相加求和的条件。
Sum_range表示引用,需要求和的实际单元格。
注意:Criteria如果是文本,那么引号应该是半角的,而不是全角的,否则会出错!在O3单元格中输入=sum(F3:N3),便可求出第一个同学韩威的总分,然后选中O3单元格,当右下角出现小”+”字图标时时使用拖拉大法往下自动填充,或左键双击即可.2.排名次:Microsoft Excel中用RANK函数求名次(排序),它的语法为:RANK(Number,Ref,Order) 返回一个数字在数字列表中的排位。
学生成绩统计分析表模板(平时成绩占20%或0%)

据。
所有班级考试人数合计
பைடு நூலகம்
所有班级总评平均分
所有班级标准差
70-79
60-69 不及格 总计
0 70-79
0 60-69
0 不及格
序号 平时成绩 期末成绩 总评
人数统计
本班平时成绩人 数
本班考试人数
平均分
本班总评平均 分
标准差
S
n
1 1
n
(X 1
i
X)2
S
1 n
n
1
(X
i
X
)2
本班标准差
本班分数段
90以上
80-89
1
0.8
0.6
0.4
0.2 0
0 90以上
0 80-89
0%,期末成绩占80%;平时成绩满分100分制或20分制 等于期末成绩)及其它相关数据,并绘制本班成绩分
用Excel表作班级成绩分析

用Excel表作班级成绩分析(每次考试,我们都要对考试情况作分析,所分析的项目包括有参考班级,参考人数、平均分,合格人数、合格率、优秀人数、优秀率,最高分、最低分以及各分数段所占的人数:100分人数、80~99 分人数、60~79 人数、30~59 人数、30 分以下人数。
这个统计比较复杂,且工作量大,假如用人工计算,不但效率低,且出错机率大,而用EXCEL 函数能够很好解决这个问题。
我们可采用以下方法:新建空白Excel 工作簿,将自动建立的Sheet1、Sheet2工作表重命名为成绩分析表、各科考试成绩。
其中各科考试成绩工作表用于输入各科成绩。
(一)设计各科成绩工作表序输入记录字段名:班级、学号、姓名、政治、计算机、数学、英语、操作基础、电子技术。
假设全级学生有695 人,所以从第3行到第698 行用来输入所有学生各科的成绩。
(二)设计成绩分析工作表下面就以计算机科分析表设计为例实行描绘,其他科的分析相似操作。
1.设计分析表将A1:I1 合并并居中,输入“** 中学2004~2005 学年第一学期成绩分析表”。
用同样的方法将A2:I2 合并并居中,输入“科目:计算机”其他文字按表格内容输入即可。
2.求科各班参考人数我们在这里可采用COUNTIF函数,COUNTIF 函数用于计算给定区域内满足特定条件的单元格的数目,所以在C4单元格中输入“=COUNTIF(各科考试成绩!$A$3: 各科考试成绩!$A$698,"=A4”)”,即可求出107班的参考人数。
然后选中C4 单元格,拖动C4 单元格右下角的小“十”字图标至C7 单元格(复制公式),这样,就能自动得到C4 至C7 单元格的公式。
最后在C8 单元格中输入“=SUM(C4:C7)”,用于分析全年级参考总人数。
3.求科各班总分我们在这里可采用SUMIF 函数,SUMIF 函数功能是根据指定条件对若干单元格求和,在D 4 单元格中输入“=SUMIF(各科考试成绩!$A$3: 各科考试成绩!$A$698,"= A4", 各科考试成绩!$H$3:各科考试成绩!$H$698) ”,该单元格公式作用为:计算107 班计算机科总分。
