七年级数学下册 6.1 平方根(第2课时)课件 (新版)新人教版.pptx
合集下载
人教版初中数学七年级下册6.1.3《平方根》课件(共15张PPT)_2

0的平方根是( 0 );
负数有平方根吗?
负数( 没有 )平方根.
探究二、平方根的表示方法
ɑ(ɑ≥0)的平方根表示为:
a
aa0
根号 被开方数
读作正、负根号ɑ
则:16的平方根可以写作: 16=±4
3 表示:__3_的__平__方__根_____
请你区别:( ɑ ≥0 )
α, α
aa0
, α分别表示什么意义?
(1)100 (2) 9
16
(3)0.25
解 (1)10210,0100的平方根是10 ;
(2)
3
2
9
,
4 16
9 16
的平方根是
3 4
;
(3)0.520.25, 0.25的平方根是 0.5.
归纳平方根的性质
aa0
正数的平方根有什么特点?
正数的平方根有( 两 )个,它们互为相反数;
0的平方根是多少?
x2
aa0
a
输出入x
输出入a
平方根的定义:
aa0
一般地,如果一个数的平方等于a,那么这 个数叫做a的平方根或二次方根.这就是说,
如果 x2 a,那么x 叫做a的平方根
探究一、平方根与开平方
x2
a
aa0
x2
a
输入x
输出a 输出x
输入a
平方
互为逆 运算
开平方
例题解析
aa0
例4 求下列各数的平方根
aa0
6.1 平方根
(第二课时)
学习目标
aa0
1、掌握平方根的概念与性质. 2、会通过开平方运算求一个非负数的平方根. 3、理解平方与开平方互为逆运算.
负数有平方根吗?
负数( 没有 )平方根.
探究二、平方根的表示方法
ɑ(ɑ≥0)的平方根表示为:
a
aa0
根号 被开方数
读作正、负根号ɑ
则:16的平方根可以写作: 16=±4
3 表示:__3_的__平__方__根_____
请你区别:( ɑ ≥0 )
α, α
aa0
, α分别表示什么意义?
(1)100 (2) 9
16
(3)0.25
解 (1)10210,0100的平方根是10 ;
(2)
3
2
9
,
4 16
9 16
的平方根是
3 4
;
(3)0.520.25, 0.25的平方根是 0.5.
归纳平方根的性质
aa0
正数的平方根有什么特点?
正数的平方根有( 两 )个,它们互为相反数;
0的平方根是多少?
x2
aa0
a
输出入x
输出入a
平方根的定义:
aa0
一般地,如果一个数的平方等于a,那么这 个数叫做a的平方根或二次方根.这就是说,
如果 x2 a,那么x 叫做a的平方根
探究一、平方根与开平方
x2
a
aa0
x2
a
输入x
输出a 输出x
输入a
平方
互为逆 运算
开平方
例题解析
aa0
例4 求下列各数的平方根
aa0
6.1 平方根
(第二课时)
学习目标
aa0
1、掌握平方根的概念与性质. 2、会通过开平方运算求一个非负数的平方根. 3、理解平方与开平方互为逆运算.
七年级数学下册第六章实数:平方根第2课时平方根课件ppt新版新人教版

4.(2019·台州)若一个数的平方等于5,则这个数等于_____5___. 5.若-2 是m的一个平方根,则m+7的平方根是__±__3____.
知识点二 平方根与算术平方根的关系
8.若正方形的边长为a,面积为S,则(B )
A.S的平方根是a
B.a是S的算术平方根
C.a=± S
D.S= a
9.若一个数的算术平方根是5,则这个数的平方根为( D )
A.25
B.±25
C.-5
D.±5
10.若一个数的算术平方根是6,则比它大2的数的平方根是_____3_8__.
11.已知25x2-144=0,且x是正数,求5x+13的平方根.
解:由25x2-144=0,得x=± 12 .
5
∵x是正数,∴x= 12 ,∴5x+13=5× 12 +13=25,
5
解:∵2a-1的平方根为± 3 ,∴2a-1=3,解得a=2. ∵3a-2b+1的平方根为±3,∴3×2-2b+1=9,解得b=-1, ∴4a-b=4×2-(-1)=9,∴4a-b的平方根为±3.
17.若x2=9,y2=16,且x>y,求x-y的平方根. 解:依题意,得x=3,y=-4或x=-3,y=-4, ∴x-y=7或1,∴x-y的平方根为± 7 或±1.
18.已知a,b,c满足b= (a 3)2 +4,c的平方根等于它本身,求 a b c 的值. 解:由题意,得-(a-3)2≥0,∴a=3,∴ b (a 3)2 4 4. ∵c的平方根等于它本身,∴c=0,∴ a b c 3 4 0 5.
19.(1)一个非负数的平方根是2a-1和a-5,这个非负数是多少? 解:(1)根据题意,得(2a-1)+(a-5)=0,解得a=2, ∴这个非负数是(2a-1)2=(2×2-1)2=9.
人教版七年级下册数学课件 :6.1平方根(共84张PPT)

6.1 平方根/
算术平方根估算数值
例1 估算 19 -3的值 ( A )
A.在1和2之间
B.在2和3之间
C.在3和4之间
D.在4和5之间
解析:因为42<19<52,所以4< 19 <5,所以1< 19 -3<2. 故选A.
总结:估计一个有理数的算术平方根的近似值,必须先判断 这个有理数位于哪两个数的平方之间.
总结:几个非负数的和为0,则每个数均为0,初中阶段学过 的非负数有绝对值、偶次幂及一个数的算术平方根.
巩固练习
6.1 平方根/
4.求下列各式中字母的值. (1)若|a+3|=0 ,则a= -3 ;
(2)若 (m-7)2=0 ,则m= 7 ; (3)若 a 5 0,则a= 5 ;
(4)若 a 3 b 4 0 ,则代数式(a b)2019 =_-
x2
1
4
x 1 1 0.5 42
故每块地板砖的边长是0.5 m.
课堂检测
拓广探索题
6.1 平方根/
已知:|x+2y|+ 求x-3y+4z的值. 解:由题意得:
3x - 7 +(5y + z )2 = 0
3x 7 0, x 2 y 0,5y z 0,
解得 x 7 , y 7 , z 35 ,
素养目标
6.1 平方根/
3. 了解开方与乘方互为逆运算,会用平方运算求 某些非负数的算术平方根.
2. 会求一些数的算术平方根,并用算术平方根符 号表示.
1. 了解算术平方根的概念,会表示正数的算术 平方根,并了解算术平方根的非负性.
探究新知 知识点1
人教版七年级数学下册6.1 平方根(2)

9
练习:国际比赛的足球场的长在100m到 110m之间,宽在64m到75m之间,现有 一个长方形的足球场其长是宽的1.5倍, 面积为7560m2,问:这个足球场能用作 国际比赛吗?
10
补充练习;
1. 16的算术平方根是 2 ; 52 122 1 3 。
2.若 2x 5 4,则(2x 5)2 25 6 。
例:已知 x y 4 x 2y 5 0,求x、y的值。
解
:由题意得xx
y 4 0 2y 5 0
解方
程组
得yx
3 1
我们已学习了3种非负数,即绝对值、 偶数次方、算术平方根。几个非负数 的和为零,它们就同时为零,然后转 化为方程(或方程组)来解。
7
探究: (1) 求 22,( 3)2,52,( 6)2,72,
02的 值 , 对 于 任 意 数a,a2 ?
练习:1. (m 1)2 3,则m 4或 -2 。 2.若 (a 2)2 2 a,则a的取值范围是a ≤ 2 。
(2)求( 4)2,( 9)2,( 25)2,( 49)2, ( 0)2的值,对于任意非负数a,( a)2 ?
8
小丽想用一块面积为 400cm2 正方形纸片,沿着边的方向裁出一块 面积为300cm2的长方形纸片用来绘 画,使它的长宽之比为3:2, 不知能否裁出来,正在发愁。小明见 了说“别发愁,一定能用一块面积大 的纸片裁出一块面积小的纸片”,你 同意小明的说法吗? 小丽能用这块 纸片裁出符合要求的纸片吗?
3.当a ≥0 时 ,9a2的算术平方根为3a。
4. 5 a b的最大值为 - 5 , 此时a与b的关系为 互 为 相 反 数 。
5.已知(x1)2 y 2 z 3 0
求x y z的算术平方根。
练习:国际比赛的足球场的长在100m到 110m之间,宽在64m到75m之间,现有 一个长方形的足球场其长是宽的1.5倍, 面积为7560m2,问:这个足球场能用作 国际比赛吗?
10
补充练习;
1. 16的算术平方根是 2 ; 52 122 1 3 。
2.若 2x 5 4,则(2x 5)2 25 6 。
例:已知 x y 4 x 2y 5 0,求x、y的值。
解
:由题意得xx
y 4 0 2y 5 0
解方
程组
得yx
3 1
我们已学习了3种非负数,即绝对值、 偶数次方、算术平方根。几个非负数 的和为零,它们就同时为零,然后转 化为方程(或方程组)来解。
7
探究: (1) 求 22,( 3)2,52,( 6)2,72,
02的 值 , 对 于 任 意 数a,a2 ?
练习:1. (m 1)2 3,则m 4或 -2 。 2.若 (a 2)2 2 a,则a的取值范围是a ≤ 2 。
(2)求( 4)2,( 9)2,( 25)2,( 49)2, ( 0)2的值,对于任意非负数a,( a)2 ?
8
小丽想用一块面积为 400cm2 正方形纸片,沿着边的方向裁出一块 面积为300cm2的长方形纸片用来绘 画,使它的长宽之比为3:2, 不知能否裁出来,正在发愁。小明见 了说“别发愁,一定能用一块面积大 的纸片裁出一块面积小的纸片”,你 同意小明的说法吗? 小丽能用这块 纸片裁出符合要求的纸片吗?
3.当a ≥0 时 ,9a2的算术平方根为3a。
4. 5 a b的最大值为 - 5 , 此时a与b的关系为 互 为 相 反 数 。
5.已知(x1)2 y 2 z 3 0
求x y z的算术平方根。
(新人教版)七年级数学下册:6.1《平方根》PPT课件
a 与- a 互为相反数; (3) 在± a 中,a≥0.
(4)( a )2=a (a≥0),
a2
| a |
a,a≥0 a. a<0
(5)一个正数有两个平方根,它们互为 相反数.
零的平方根是零.
负数没有平方根.
平方根与算术平方根的 联系与区别:
联系:
1.算术平方根是平方根的一种; 2.只有非负数才有算术平方根和平方根; 3.0的算术平方根和平方根都是0.
所以7900 <v <11200
答: 要使宇宙飞船离开地球进入轨道正常 运行,必须使它的速度大于7900米/秒,小于 11200米/秒.
想一想
要做一张边长是4cm 的方桌面,它的面积是多 少?
这个问题实际上就是 求:42=?的问题.
根据乘方运算,可知 42=16cm2.
4cm
反过来,要做一张面积是16cm2的 桌面,它的边长是多少cm?
新课导入
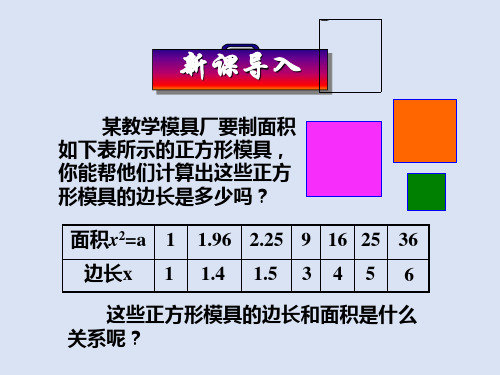
某教学模具厂要制面积 如下表所示的正方形模具, 你能帮他们计算出这些正方 形模具的边长是多少吗?
面积x2=a 1 1.96 2.25 9 16 25 36 边长x 1 1.4 1.5 3 4 5 6
这些正方形模具的边长和面积是什么 关系呢?
教学目标
知识与能力
1.理解平方根和算术平方根的概念,了解平方 与开平方的关系;
毕达哥拉斯认为“宇宙间的一切现象都能 归结为整数或整数之比,即都可用有理数来描 述.
但后来,这学派的一位年轻成员希伯索斯 发现边长为1的正方形的对角线的长不能用有理 数来表示,这就动摇了毕达哥拉斯学派的信条, 引起了信徒们的恐慌,他们试图封锁这一发现, 然而希伯索斯偷偷将这一发现传播出去,这为 他招来了杀身之祸,在他逃回家的路上,遭到 毕氏成员的围捕,被投入大海.
(4)( a )2=a (a≥0),
a2
| a |
a,a≥0 a. a<0
(5)一个正数有两个平方根,它们互为 相反数.
零的平方根是零.
负数没有平方根.
平方根与算术平方根的 联系与区别:
联系:
1.算术平方根是平方根的一种; 2.只有非负数才有算术平方根和平方根; 3.0的算术平方根和平方根都是0.
所以7900 <v <11200
答: 要使宇宙飞船离开地球进入轨道正常 运行,必须使它的速度大于7900米/秒,小于 11200米/秒.
想一想
要做一张边长是4cm 的方桌面,它的面积是多 少?
这个问题实际上就是 求:42=?的问题.
根据乘方运算,可知 42=16cm2.
4cm
反过来,要做一张面积是16cm2的 桌面,它的边长是多少cm?
新课导入
某教学模具厂要制面积 如下表所示的正方形模具, 你能帮他们计算出这些正方 形模具的边长是多少吗?
面积x2=a 1 1.96 2.25 9 16 25 36 边长x 1 1.4 1.5 3 4 5 6
这些正方形模具的边长和面积是什么 关系呢?
教学目标
知识与能力
1.理解平方根和算术平方根的概念,了解平方 与开平方的关系;
毕达哥拉斯认为“宇宙间的一切现象都能 归结为整数或整数之比,即都可用有理数来描 述.
但后来,这学派的一位年轻成员希伯索斯 发现边长为1的正方形的对角线的长不能用有理 数来表示,这就动摇了毕达哥拉斯学派的信条, 引起了信徒们的恐慌,他们试图封锁这一发现, 然而希伯索斯偷偷将这一发现传播出去,这为 他招来了杀身之祸,在他逃回家的路上,遭到 毕氏成员的围捕,被投入大海.
6.1平方根(课时2)课件(新人教版七年级数学下)

2 7 和27的大小.
【学习体会】
1.本节课你独立思考了那些知识?参与讨论了哪些知识? 还有那些疑惑? 2.本节课你最成功的地方是什么?说给你小组成员听听.
【当堂达标】 1. 比较下列各数的大小: (1)
65与8 ;(2)
5-1 与1 . 2
2.已知
2.3409 =1.53,求 23409 的值
6.2平方根(第二课时)
பைடு நூலகம்
【学习目标】
1.能用“夹值法”求一个数的平方根的近似值. 2.会用计算器求一个数的算术平方根. 3.理解被开方数扩大(缩小)与它的算数平方根扩大(缩小)的规律.
【重点难点】
重点:利用“夹值法”求一个数的算术平方根. 难点:理解被开方数扩大(缩小)与它的算术平方根扩大(缩小)的规律.
创设情景
怎样用两个面积为1的小正方形拼成一个面积为2的大正方形? 大正方形的边长是多少?
2 到底有多大?
【课中探究】
数学活动一:估值 根据自己的经验,你估计一下
2
大约有多大?
数学活动二:探究 ∵1² =1 2² =4 ∴1< 2 <2 ∵1.4² =1.96 1.5² =2.25 ∴1.4< 2 <1.5 ∵1.41² =1.9881 1.42² =2.0164 ∴1.41< 2 <1.42 ∵1.414² =1.999396 1.415² =2.002225 ∴1.414< 2 <1.415…… 事实上,越往下进行,得到的值就越准确。 2 =1.41421356…
3.用计算器计算:(如需取近似值,则精确到0.01) ( 1)
1369
;(2) 101.2036 ;(3) 5
.
它是一个无限不循环小数,像这样的数还有很多,如: 3、 5 …….
新人教版七年级数学初一下册6.1平方根2PPT课件
③ (
)2=0
④ ( )2 = 0.49
平方根的概念
如果一个数的平方等于 a ,这个数 叫a的平方根或二次方根。 2 若 x = a,则 x 叫做 a 的平方根。 记作: 读作:正负根号a a
如(±5)2=25,则±5是25的平方根, 记作
25= 5
求一个数的平方根的运算,叫做开平方。
( 3) 0
(2)-81
(4)0.0001
2
(5)(7)
(6) 7
2
练习2:判断下列各式计算是否正确,并说明理由
(1) 4= 2 (3)- 4= 2
a
- a
a 2 x =a
(×) (×)
(2) 4= 2( √ )
读作:正,负根号a
a的平方根表示为
a
表示 a的算术平方根
a (a 0)
(a叫被开方数)
算术平方根的表示法: a (a≥0)
(平方根与算术平方根的概念的区别与联系)
辨析概念
平方根与算术平方根的联系与区别:
联系:1.包含关系:平方根包含算术平方根, 算术平方根是平方根的一种.
2.只有非负数才有平方根和算术平方根. 3. 0的平方根是0,算术平方根也是0 . 区别: 1.个数不同:一个正数有两个平方根,但只有 一个算术平方根. 2.表示法不同:平方根表示为 a ,而算 术平方根表示为 a .
( 2) 3
1 (3) 2 10
学习目标 1、掌握平方根和开平方的概念。
2、掌握平方根的性质。
3、能够通过平方运算求一个非负数 的平方根及算术平方根。
思考与探索
1.一个数的平方是9,这个数是什么数?
2. 一个数的平方是
6.1平方根(第2课时)课件ppt人教版七年级下
, (2) 依次按键 2 显示:1.414213562. ∴ 2 1.414 .
3.解决章引言中提出的问题 你知道宇宙飞船离开地球进入轨道正常运行的 速度在什么范围吗?这时它的速度要大于第一
v v v(单位:m/s ). 1 ,2的大小满足v12 gR, 2 2 v2 2 gR ,其中 g 9.8 m/s2 ,R是地球半 径, 6.4 106 m .怎样求 v1, 2 v 呢? R
„„ 1.414 < 2 < 1.415 2 = 1.4142135623730950 …
无限不循环小数
1.解决问题 你以前见过这种数吗?
2有多大呢?
2
2.用计算器求算术平方根 例1 用计算器求下列各式的值: (1) 3136 ; (2) 2 (精确到 0.001 ).
,
解:(1) 依次按键 3136 显示:ห้องสมุดไป่ตู้6. ∴ 3136 56 .
6.反馈练习
1.估计 56 的大小应在( C ). A.5~6 之间 B.6~7 之间 C.7~8 之间 D. 8~9 之间
2.利用规律计算:已知 2 1.414, 20 4.472 ,则 0.2 0.447.2 _____ 3. 用计算器计算下列各式的值(精确到 0.01).
0.462 54,
1.解决上节课提出的问题
拼成的这个面积为 2 的大正方形的 边长应该是多少呢?
?
边长= 2
2 有多大呢?
1.解决问题
2 有多大呢?
2 大于1而小于2
你是怎样判断出 2 大于1而小于2的?
12 1 ,22 4 , 因为 而1 < 2 <4 , 所以1 2 2 .
你能不能得到 2 的更精确的范围?
人教版七年级数学下册课件:6.1.2 平方根(共16张PPT)
平方根(例如_2___,_3___,_1_0__等)都是 无限不循环小数.
三、研学教材
知识点二 用计算器求算术平方根
例2 用计算器求下列各式的值: (1) 3136 (2) 2 (精确到0.001)
解:(1)依次按键 3136,显示56. ∴ 3136 =56.
(2)依次按键____2__,显示_1_.4_1_4_2_1_3…_ .… ∴ 2 ≈ 1.414.
0.625 =__0_._7_9____
6.25 =__2_.5__
62 .5 =__7_._9_____
625 =__2_5__
6250 =____7_9____
62500 =_2_5__0_ 625000 =___7_9_0____
规律: 当被开方数的小数点向右移动2位时, 算术平方根的小数点只向_右____移动_1___位;
因为 1.42= _1_._9_6,1.52=_2_.2_5_, 所以__1_.4_< 2 <__1_._5_;......
事实上, 2 =1.414 213 562 373..., 它是一个无限不循环小数.
三、研学教材
无限不循环小数是指小__数__点__后__有_无__限__个_ 数_位__,_但_没__有__周__期__性_的__重__复__,__或_者__说__没__有__规__ 律___的小数. 实际上,许多正有理数的算术
第六章 实数 6.1.2 平方根(2)
一、新课引入 1、若 X >0,且 X 2=25,则称 X 为
__2_5_的算术平方根,记作 X =___2_5_;
2、4是_1_6_的算术平方根.
二、学习目标
1、会用计算器求一个数的算术平方根, 能用夹值法求一个数的算术平方根的 近似值;
三、研学教材
知识点二 用计算器求算术平方根
例2 用计算器求下列各式的值: (1) 3136 (2) 2 (精确到0.001)
解:(1)依次按键 3136,显示56. ∴ 3136 =56.
(2)依次按键____2__,显示_1_.4_1_4_2_1_3…_ .… ∴ 2 ≈ 1.414.
0.625 =__0_._7_9____
6.25 =__2_.5__
62 .5 =__7_._9_____
625 =__2_5__
6250 =____7_9____
62500 =_2_5__0_ 625000 =___7_9_0____
规律: 当被开方数的小数点向右移动2位时, 算术平方根的小数点只向_右____移动_1___位;
因为 1.42= _1_._9_6,1.52=_2_.2_5_, 所以__1_.4_< 2 <__1_._5_;......
事实上, 2 =1.414 213 562 373..., 它是一个无限不循环小数.
三、研学教材
无限不循环小数是指小__数__点__后__有_无__限__个_ 数_位__,_但_没__有__周__期__性_的__重__复__,__或_者__说__没__有__规__ 律___的小数. 实际上,许多正有理数的算术
第六章 实数 6.1.2 平方根(2)
一、新课引入 1、若 X >0,且 X 2=25,则称 X 为
__2_5_的算术平方根,记作 X =___2_5_;
2、4是_1_6_的算术平方根.
二、学习目标
1、会用计算器求一个数的算术平方根, 能用夹值法求一个数的算术平方根的 近似值;
最新人教版初中七年级下册数学【第六章 6.1平方根(2)】教学课件
(1) 9;
(2) − 0.49;
(3) ±
64 . 81
解: (1)
9 =3;
(2) −
0.49 =− 0.7; (3) ±
64 =± 8 . 81 9
学以致用
练习3:求下列各式中�的
值 (1) x2 = 36;
(2) 25x2 − 81 = 0
解:x2 = 36, x =± 6,
解:
25x2 = 81, x2 = 8215,
25 _4_
9 1 0 0.0025
25 4
开平方
_+_3 _−_3
_+_1
_−_1 _0_ +_0._05
−_0._05 +5 _2_ −5 _2
开平方定义:求一个数�的平方根运算,叫做开平
方 . 平方运算
互逆
开平方运算
知识归纳
• 平方根的性质: 1. 正数的平方根有两个,它们互为相反数,其中正的
3. 我们已学过的运算有加、减、乘、除、乘方五 种,其中加与减,乘与除是互为逆运算的,那 么乘方有没有逆运算呢?
知识探究
提出问题:一个数的平方等于9,这个数是多少?
∵32=9, ∴这个数可以是3;
∵(− 3)2=9, ∴这个数可以是−3;
综上所述,一个数的平方等于9,这个数可以是3或−3.
x2
1
x ±1
∴x1 = 6,x2 =− 6;
x
=±
9 5
,
∴x1 =
95,x2
=− 9 5
.
学以致用
练习4:已知3a − 1与13 − 5a是�的两个不同的平方根,求� 的值. 解:∵3a − 1与13 − 5a是�两个平方根,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
◆知识导航
◆典例导学 ◆反馈演练( ◎第一 ◆反馈演练( ◎第一阶 ◎第二阶 ◎第三2阶 )
◆知识导航
◆典例导学 ◆反馈演练( ◎第一阶 ◎第二阶 ◎第三3阶 )
◆知识导航
◆典例导学 ◆反馈演练( ◎第一阶 ◎第二阶 ◎第三4阶 )
◆知识导航
◆典例导学 ◆反馈演练( ◎第一阶 ◎第二阶 ◎第三5阶 )
◆知识导航
◆典例导学 ◆反馈演练( ◎第一阶 ◎第二阶 ◎第三6阶 )
◆知识导航
◆典例导学 ◆反馈演练( ◎第一阶 ◎第二阶 ◎第三7阶 )
◆知识导航
◆典例导学 ◆反馈演练( ◎第一阶 ◎第二阶 ◎第三8阶 )
◆知识导航
◆典例导学 ◆反馈演练( ◎第一阶 ◎第二阶 ◎第三9阶 )
◆知识导航
◆知识导航
◆典例导学 ◆反馈演练( ◎第一阶 ◎第二阶 ◎第三15阶 )
◆典例导学 ◆反馈演练( ◎第一阶 ◎第二阶 ◎第三10阶 )
◆知识导航
◆典例导学 ◆反馈演练( ◎第一阶 ◎第二阶 ◎第三11阶 )
◆知识导航
◆典例导学 ◆反馈演练( ◎第一阶 ◎第二阶 ◎第三12阶 )
◆知识导航
◆典例导学 ◆反馈演练( ◎第一阶 ◎第二阶 ◎第三13阶 )
◆知识导航
◆典例导学 ◆反馈演练( ◎第一阶 ◎第二阶 ◎第三14阶 )
◆典例导学 ◆反馈演练( ◎第一 ◆反馈演练( ◎第一阶 ◎第二阶 ◎第三2阶 )
◆知识导航
◆典例导学 ◆反馈演练( ◎第一阶 ◎第二阶 ◎第三3阶 )
◆知识导航
◆典例导学 ◆反馈演练( ◎第一阶 ◎第二阶 ◎第三4阶 )
◆知识导航
◆典例导学 ◆反馈演练( ◎第一阶 ◎第二阶 ◎第三5阶 )
◆知识导航
◆典例导学 ◆反馈演练( ◎第一阶 ◎第二阶 ◎第三6阶 )
◆知识导航
◆典例导学 ◆反馈演练( ◎第一阶 ◎第二阶 ◎第三7阶 )
◆知识导航
◆典例导学 ◆反馈演练( ◎第一阶 ◎第二阶 ◎第三8阶 )
◆知识导航
◆典例导学 ◆反馈演练( ◎第一阶 ◎第二阶 ◎第三9阶 )
◆知识导航
◆知识导航
◆典例导学 ◆反馈演练( ◎第一阶 ◎第二阶 ◎第三15阶 )
◆典例导学 ◆反馈演练( ◎第一阶 ◎第二阶 ◎第三10阶 )
◆知识导航
◆典例导学 ◆反馈演练( ◎第一阶 ◎第二阶 ◎第三11阶 )
◆知识导航
◆典例导学 ◆反馈演练( ◎第一阶 ◎第二阶 ◎第三12阶 )
◆知识导航
◆典例导学 ◆反馈演练( ◎第一阶 ◎第二阶 ◎第三13阶 )
◆知识导航
◆典例导学 ◆反馈演练( ◎第一阶 ◎第二阶 ◎第三14阶 )
