Koch曲线
koch曲线 迭代函数

koch曲线迭代函数(实用版)目录1.引言:介绍 Koch 曲线和迭代函数的概念2.Koch 曲线的特点:描述 Koch 曲线的形状和性质3.迭代函数的应用:讲解迭代函数在 Koch 曲线生成过程中的作用4.Koch 曲线的生成方法:介绍使用迭代函数生成 Koch 曲线的具体步骤5.结论:总结 Koch 曲线和迭代函数的关系以及在数学领域的应用正文Koch 曲线是一种分形曲线,由瑞典数学家 Koch 在 20 世纪 60 年代提出。
它是一种无限长、无限细的曲线,具有自相似性、无标度性和不可压缩性等特性。
Koch 曲线的研究对分形理论、非线性科学等领域具有重要意义。
迭代函数是数学中的一种函数类型,通过将函数的输出作为输入,反复进行计算,可以得到一系列越来越接近于某个值或某个函数的数值。
迭代函数在数学、物理、计算机科学等领域有广泛的应用。
在 Koch 曲线的生成过程中,迭代函数发挥了关键作用。
Koch 曲线的生成方法是通过一个迭代函数来不断对曲线进行收缩和放大,经过无穷多次迭代后,可以得到一条越来越接近于 Koch 曲线的曲线。
这个过程充分体现了迭代函数在数学中的应用价值。
具体来说,Koch 曲线的生成过程可以分为以下几个步骤:1.初始化:设定一个初始曲线,作为迭代的起点。
2.迭代:将初始曲线按照一定的比例进行收缩,然后再按照同样的比例进行放大,形成一个新的曲线。
3.重复:将新的曲线作为下一次迭代的初始曲线,继续进行迭代。
4.终止:当迭代次数达到预设值或曲线满足某种条件时,迭代过程终止。
通过以上迭代过程,我们可以得到一条越来越接近于 Koch 曲线的曲线。
在这个过程中,迭代函数起到了关键的作用,它决定了曲线的变化规律,从而影响了 Koch 曲线的最终形态。
总之,Koch 曲线和迭代函数在数学领域具有重要意义。
Koch 曲线作为一种特殊的分形曲线,具有独特的形状和性质,而迭代函数则在 Koch 曲线的生成过程中发挥了关键作用。
Koch类方波曲线的解析表达式的开题报告

Koch类方波曲线的解析表达式的开题报告开题报告:题目:Koch类方波曲线的解析表达式研究背景:Koch曲线是由瑞典数学家Helge von Koch于1904年首次提出的。
Koch曲线是一种分形曲线,它可以通过每次迭代将直线的每个线段替换为一系列更小的线段来生成。
Koch曲线的变形还有Koch雪花,是一种结构简单但却充满美感的曲线,很受数学爱好者的喜爱。
Koch类方波曲线是一类特殊的Koch曲线,它是由一条直线分别向左和向右延伸形成的折线,并且其每一段线段的长度都相等。
与其他Koch曲线不同,Koch类方波曲线的曲线形状更加接近方波,具有更加显著的周期性和对称性,因此在信号处理、图像处理以及计算机图形学等领域都有很广泛的应用。
研究目的:本文旨在研究Koch类方波曲线的解析表达式,通过推导该曲线的解析表达式,可以更加直观地描述其特征和性质,并且为进一步的应用研究提供理论上的基础。
研究方法:本文将采用数学分析、计算机模拟等方法来研究Koch类方波曲线的解析表达式。
具体地,通过对Koch类方波曲线进行多次迭代,得到其逐渐逼近方波的形状,并且通过数学分析和计算机模拟的方法,得到该曲线的解析表达式。
研究意义:研究Koch类方波曲线的解析表达式,不仅可以帮助我们了解这种特殊类型的Koch曲线的特点和性质,还可以为信号处理、图像处理以及计算机图形学等领域的应用提供理论上的支持和参考。
此外,在数学教学中,Koch类方波曲线也是一种非常好的教学资源,可以帮助学生更加深入地理解分形几何的概念和原理,提高学生的数学素养和创新思维能力。
预期成果:本文预期能够推导出Koch类方波曲线的解析表达式,并且通过计算机模拟和图像处理的方法来验证其正确性和可靠性。
同时,本文还将探讨Koch类方波曲线的一些特征和性质,并且对其应用研究进行简要介绍,为相关领域的研究提供理论支持和参考。
研究计划:第一步:收集和整理Koch类方波曲线的相关研究资料,包括历史沿革、数学原理、应用研究等方面的内容。
科赫曲线

科赫曲线
简介
科赫曲线(Koch curve )是一种像雪花的几何曲线,所以又称为雪花曲线。
1904年瑞典数学家科赫第一次描述了这种不论由直段还是由曲段组成的始终保持连通的线,因此将这种曲线成为科赫曲线。
定义
设想一个边长为1的等边三角形,取每边中间的三分之一,接上去一个形状完全相似的但边长为其三分之一的三角形,结果是一个六角形。
现在取六角形的每个边做同样的变换,即在中间三分之一接上更小的三角形,以此重复,直至无穷。
外界的变得原来越细微曲折,形状接近理想化的雪花。
画法
1、任意画一个正三角形,并把每一边三等分;
2、取三等分后的一边中间一段为边向外作正三角形,并把这“中间一段”擦掉;
3、重复上述两步,画出更小的三角形。
4、一直重复,直到无穷,所画出的曲线叫做科赫曲线。
特性
1、它是一条连续的回线,永远不会自我相交。
2、曲线任何处不可导,即任何地点都是不平滑的。
3、曲线是无限长的,即在有限空间里的无限长度。
4、曲线上任意两点距离无穷大。
5、每次变化面积都会增加,但是总面积是有限的,不会超过初始三角形的外接圆。
思考
科赫曲线中产生一个匪夷所思的悖论:"无穷大"的边界,包围着有限的面积。
这让保守派数学大师们都很难相信。
科赫曲线是比较典型的分形图形,它具有严格的自相似特性。
提问:在有限面积里面,无穷的去选择无穷小的点来组成的"封闭"曲线.会包围着无穷大的面积吗?。
计算机图形学实验Koch曲线
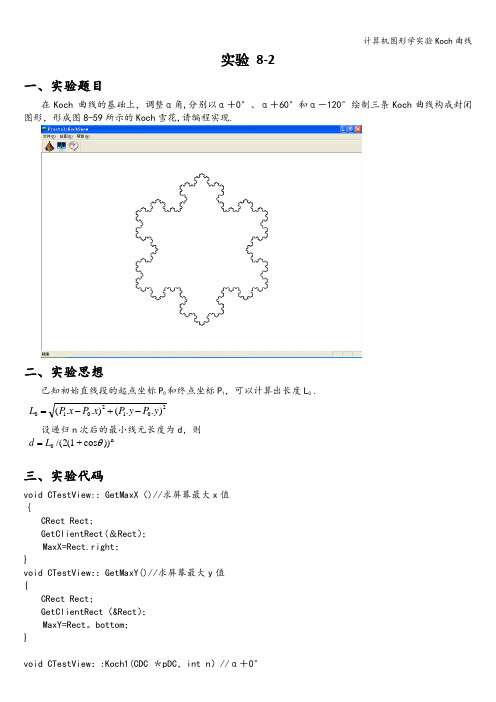
实验 8-2一、实验题目在Koch 曲线的基础上,调整α角,分别以α+0°、α+60°和α-120°绘制三条Koch 曲线构成封闭图形,形成图8-59所示的Koch 雪花,请编程实现.二、实验思想已知初始直线段的起点坐标P 0和终点坐标P 1,可以计算出长度L 0 .设递归n 次后的最小线元长度为d ,则三、实验代码void CTestView::GetMaxX ()//求屏幕最大x 值{CRect Rect;GetClientRect(&Rect );MaxX=Rect.right ;}void CTestView ::GetMaxY()//求屏幕最大y 值{CRect Rect ;GetClientRect (&Rect );MaxY=Rect 。
bottom ;}void CTestView ::Koch1(CDC *pDC ,int n )//α+0°2012010)..()..(y P y P x P x P L -+-=n0))cos +2(1/(θL d ={Position.x=MaxX/4;Position.y=MaxY/4;if(n==0){b.x+=d*cos(alpha*PI/180);b。
y+=d*sin(alpha*PI/180);pDC->MoveTo(ROUND(a.x+Position.x),ROUND(a。
y+MaxY-Position。
y));pDC->LineTo(ROUND(b。
x+Position。
x),ROUND(b。
y+MaxY—Position。
y));a=b;return;}Koch1(pDC,n-1);alpha+=60;Koch1(pDC,n—1);alpha—=120;Koch1(pDC,n—1);alpha+=60;Koch1(pDC,n-1);}void CTestView::Koch2(CDC *pDC,int n)//α+60°{Position.x=MaxX/4;Position.y=MaxY/4;if(n==0){b。
Koch曲线
一、问题提出:画出Koch 曲线,计算它的第n 级分形的周长L n 。
第一步:先以10cm 为边长,以原点为中心画出正三角形,计算周长L 0。
第二步:将每一边长三等分,在中间段向外突出作小一级正三角形,擦去中间段,计算周长L 1。
第n 步:重复第二步至n=10,50,100,计算周长L n 至极限。
演示过程。
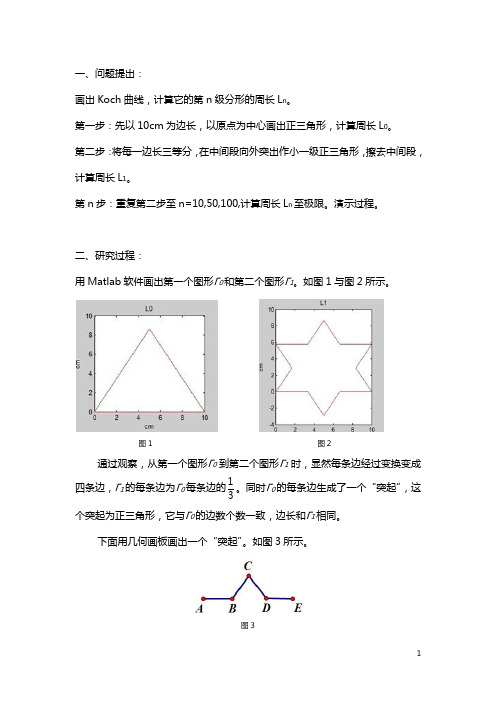
二、研究过程:用Matlab 软件画出第一个图形Γ0和第二个图形Γ1。
如图1与图2所示。
图1 图2通过观察,从第一个图形Γ0到第二个图形Γ1时,显然每条边经过变换变成四条边,Γ1的每条边为Γ0每条边的31。
同时Γ0的每条边生成了一个“突起”,这个突起为正三角形,它与Γ0的边数个数一致,边长和Γ1相同。
下面用几何画板画出一个“突起”。
如图3所示。
图3由图3可以看出:AE 为原来的边,取它的三分点B 、D ,在由BD 为边做出△BCD 。
C 点可以看成D 绕B 点逆时针旋转60°得到,此时B 、C 、D 确定。
设A (x 1,y ), E (x 2,y ),则B ⎪⎭⎫ ⎝⎛-+,y x x x 3121;D ⎪⎭⎫ ⎝⎛--,y x x x 3122;设()00,y x BC =→,而⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡032123232103cos sin sin cos 121200x x x x θθθθy x , 得到()⎪⎪⎩⎪⎪⎨⎧-=-=636120120x x y x x x ,即()⎪⎪⎭⎫ ⎝⎛--=→63,61212x x x x BC 。
故用Matlab 演示过程时,在正三角形三边均取两个三分点,然后通过转轴变换移动D 至C 点,最后连接BC 、CD 即可得到图像。
同理可得,从Γn-1到Γn 的过程中,每条边经过变换变成四条边,Γn 的每条边为Γn-1每条边的31。
同时Γn-1的每条边生成了一个正三角形,它与Γn-1的边数个数一致,边长和Γn 相同。
Koch曲线

Koch 分形曲线1.1 分形原理这是一类复杂的平面曲线,可用算法描述。
从一条直线段开始,将线段中间三分之一部分用等边三角形的两条边代替,形成具有5个结点的图形(图1);在新的图形中,又将图中每一直线段中间的三分之一部分都用一等边三角形的两条边代替,再次形成新的图形(图2),这时,图形中共有17个结点。
这种迭代继续进行下去可以形成Koch 分形曲线。
在迭代过程中,图形中的点将越来越多,而曲线最终显示细节的多少将取决于迭代次数和显示系统的分辩率。
1.2 算法分析算法分析:考虑由直线段(2个点)产生第一个图形(5个点)的过程。
设1P 和5P 分别为原始直线段的两个端点。
现在需要在直线段的中间依次插入三个点234,,P P P 产生第一次迭代的图形(图1)。
显然,2P位于1P 点右端直线段的三分之一处, 4P 位于1P 点右端直线段的三分之二处;而3P 点的位置可以看成是由4P 点绕2P 旋转60度(逆时针方向)而得到的,故可以处理为向量24P P 经正交变换而得到向量23P P 。
算法如下:(1) 2151()/3P P P P =+-;(2) 41512()/3P P P P =+-;(3) 3242()T P P P P A =+-⨯;图2 第二次迭代图1 第一次迭代在(3)中, A 为正交矩阵:c o s s i n 33sin cos 33A ππππ⎡⎤-⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦算法根据初始数据(1P 和5P 点的坐标),产生图1中5个结点的坐标。
结点的坐标数组形成一个5×2矩阵,矩阵的第一行为1P 的坐标,第二行为2P 的坐标,……,第五行为5P 的坐标。
矩阵的第一列元素分别为5个结点的X 坐标,第二列元素分别为5个结点的Y 坐标。
进一步考虑Koch 曲线形成过程中结点数目的变化规律。
设第k 次迭代产生结点数为k n ,第k+1次迭代产生结点数为1k n +,则k n 和1k n +之间的递推关系式为143k k n n +=-。
一些奇怪的可微函数曲线

一些奇怪的可微函数曲线可微函数是数学中非常重要的一类函数,它在数学分析、微积分和物理学等领域具有广泛的应用。
在这些函数中,有一些具有奇特的性质和曲线形状,下面我将介绍一些奇怪的可微函数曲线。
1. Koch曲线:Koch曲线是由瑞典数学家Helge von Koch在1904年引入的一条分形曲线。
该曲线以等边三角形为起点,然后通过迭代的方式,每一步将三角形的每条边分成三段,然后在中间的一段上添加一个等边三角形。
重复这个过程,曲线会越来越复杂,趋近于无穷长。
Koch曲线具有无限的长度和面积,但它的曲线却是平滑的。
2.蒙汉姆叶曲线:蒙汉姆叶曲线是由英国数学家蒙汉姆在1880年提出的一条具有奇特形状的曲线。
该曲线是通过一个参数方程定义的:x = sin(t), y = sin(4t) - sin(3t)。
当t从0到2π变化时,曲线会在平面上形成一条环状的曲线。
蒙汉姆叶曲线具有很多奇特的性质,例如,在t等于π/2和3π/2时,曲线上的点会出现奇点(即导数不存在),这给曲线带来了一些奇怪的行为。
3.希尔伯特曲线:希尔伯特曲线是由德国数学家David Hilbert在1891年引入的一条空间填充曲线。
该曲线的定义是通过迭代的方式,在每一步将曲线的每一段映射到一个正方形的内部,然后在正方形内部按照特定的规则连接起来。
通过不断迭代,希尔伯特曲线可以填满整个二维平面。
希尔伯特曲线具有无穷长和无穷面积,但它的曲率却处处为零。
4. Weierstrass函数:Weierstrass函数是由德国数学家Karl Weierstrass在19世纪提出的一类连续但处处不可微的函数。
该函数的定义是通过无穷级数展开的方式得到的:f(x) = Σ(a^n * cos(b^n * π * x)),其中n为自然数,a和b是满足一定条件的实数。
Weierstrass函数具有非常奇特的性质,例如,在任意小的区间上,曲线都会显示出多个频繁的震荡现象,这使得它的导数在几乎每个点处都不存在。
Koch曲线

Koch曲线
koch曲线
科赫曲线(de:Koch-Kurve)
Koch曲线是一个数学曲线,同时也是早期被描述的一种分形曲线。
它由瑞典数学家Helge von Koch在1904年发表的一篇题为“从初等几何构造的一条没有切线的连续曲线”(原来的法文题目:"Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire")的论文中提出。
有一种Koch曲线是象雪花一样,被称为Koch雪花(或Koch星),它是由三条Koch曲线围成的等边三角形。
设想从一个线段开始,根据下列规则构造一个Koch曲线:
1.三等分一条线段;
2.用一个等边三角形替代第一步划分三等分的中间部分;
3.在每一条直线上,重复第二步。
Koch曲线是以上步骤地无限重复的极限结果。
Koch曲线的长度为无穷大,因为以上的变换都是一条线段变四条线段,每一条线段的长度是上一级的1/3,因此操作n步的总长度是(4/3)n:若n→∞,则总长度趋于无穷。
Koch曲线的分形维数是log 4/log 3 ≈ 1.26,其维数大于线的维数(1),小于Peano填充曲线的维数(2)。
Koch曲线是连续的,但是处处不可导的。
Koch雪花的面积是2* √3 * s²/5 ,这里的s是最初三角形的边长,Koc h雪花的面积是原三角形面积的8/5,它成为一条无限长的边界围绕着一个有限的面积的几何对象。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Koch曲线
koch曲线
科赫曲线(de:Koch-Kurve)
Koch曲线是一个数学曲线,同时也是早期被描述的一种分形曲线。
它由瑞典数学家Helge von Koch在1904年发表的一篇题为“从初等几何构造的一条没有切线的连续曲线”(原来的法文题目:"Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire")的论文中提出。
有一种Koch曲线是象雪花一样,被称为Koch雪花(或Koch星),它是由三条Koch曲线围成的等边三角形。
设想从一个线段开始,根据下列规则构造一个Koch曲线:
1.三等分一条线段;
2.用一个等边三角形替代第一步划分三等分的中间部分;
3.在每一条直线上,重复第二步。
Koch曲线是以上步骤地无限重复的极限结果。
Koch曲线的长度为无穷大,因为以上的变换都是一条线段变四条线段,每一条线段的长度是上一级的1/3,因此操作n步的总长度是(4/3)n:若n→∞,则总长度趋于无穷。
Koch曲线的分形维数是log 4/log 3 ≈ 1.26,其维数大于线的维数(1),小于Peano填充曲线的维数(2)。
Koch曲线是连续的,但是处处不可导的。
Koch雪花的面积是2* √3 * s²/5 ,这里的s是最初三角形的边长,Koc h雪花的面积是原三角形面积的8/5,它成为一条无限长的边界围绕着一个有限的面积的几何对象。
