刚体的平面运动动力学课后答案
第7.5节刚体平面运动的动力学

第7.5节 刚体平面运动的动力学7.5.1 10m 搞得烟筒因底部损坏而倒下来,求其上端到达地面时的线速度。
设倾倒时底部未移动。
可近似认为烟筒为均质杆。
解:烟筒的长度l =10m 。
设烟筒上端到达地面的瞬间,烟筒绕其底部的转动角速度为ω。
在倾倒过程中,只受重力作用,做的功为:mg ⋅½l 。
由刚体定轴转动的动能定理:lgmlI I l mg 323122121=∴==⋅ωω烟筒上端到达地面时的线速度为:s m gl l v /2.17108.933≈⨯⨯===ω7.5.2 用四根质量各为m 长度各为l 的均质细杆制成正方形框架,可围绕其中一边的中点在竖直平面内转动,支点O 是光滑的.最初,框架处于静止且AB 边沿竖直方向,释放后向下摆动,求当AB 边达到水平时,框架质心的线速度C v。
以及框架作用于支点的压力N .解:先求正方形框架对通过其质心且与其垂直的转轴(质心轴)的转动惯量:框架的质心位于框架的中心,即两条对角线的交点上。
每根细杆对其本身的质心轴的转动惯量:21210ml I =,细杆的质心与框架的质心的距离为l 21,由平行轴定理:2342210])([4ml l m I I c =⋅+⋅=再由平行轴定理,得框架对通过0点的转轴的转动惯量:237221)(4ml l m I I c =⋅+=(1)求框架质心的线速度v c框架在下摆过程中,只有重力做功,机械能守恒。
选取杆AB 达到水平时框架质心位置位势能零点,得:gll v l h m M I Mgh c lgc c 7321712212214===∴===ωωω(2)求框架对支点的压力N以框架为研究对象,它受到重力M g 和支点的支撑力N 的作用,由质心运动定理:c a M g M N =+取自然坐标系,τ沿水平方向,n 铅直向上,得投影方程:βτττc n c c n n Mh Ma N mgmg mg N mg l gl m h v M Ma Mg N n===+=⇒=⋅===-7372472421732744:ˆ:ˆ在铅直位置时,外力矩为0,故角加速度β=0,==〉N τ = 07.5.3 由长为l ,质量各为m 的均质细杆组成正方形框架,其中一角连于光滑水平转轴O ,转轴与框架所在平面垂直.最初,对角线OP 处于水平,然后从静止开始向下自由摆动.求OP 对角线与水平成450时P 点的速度,并求此时框架对支点的作用力.解:先求正方形框架对通过其质心且与其垂直的转轴(质心轴)的转动惯量:框架的质心位于框架的中心,即两条对角线的交点上。
理论力学(哈工大版)第九章:刚体的平面运动

第五章 刚体的平面运动5-1 刚体的平面运动方程一.平面运动的定义二.平面运动的简化刚体的平面运动可以简化为平面图形S 在其自身平面内的运动.三、平面运动分解为平动和转动1.平面运动方程为了确定代表平面运动刚体的平面图形的位置,我们只需确定平面图形内任意一条线段的位置.平面运动方程)(1t f x A = )(2t f y A = )(3t f =ϕ2.平面运动分解为平动和转动刚体平面运动可以看成是平动和转动的合成运动.刚体的平面运动可以分解为随基点的平动和绕基点的转动.3.刚体平面运动的角速度和角加速度平面运动随基点平动的运动规律与基点的选择有关,而绕基点转动的规律与基点选取无关(即在同一瞬间,图形绕任一基点转动的ε ,ω都是相同的)5-2 平面图形内各点的速度一.基点法(合成法)BA A B v v v +=平面图形上任一点的速度等于基点的速度与该点随图形绕基点转动的速度的矢量和二.速度投影法(自:就是基点法的变式) 速度投影定理:[][]AB A AB B v v =平面图形上任意两点的速度在该两点连线上的投影彼此相等三.瞬时速度中心法(速度瞬心法)1. 问题的提出2.速度瞬心的概念即在某一瞬时必唯一存在一点速度等于零,该点称为平面图形在该瞬时的瞬时速度中心,简称速度瞬心.3.几种确定速度瞬心位置的方法 ①已知图形上一点的速度A v 和图形角速度ω,可以确定速度瞬心的位置.(P 点)②已知一平面图形在固定面上作无滑动的滚动, 则图形与固定面的接触点P 为速度瞬心.③已知某瞬间平面图形上A ,B 两点速度B A v v ,的方向,且B A v v 不平行过A , B 两点分别作速度B A v v ,的垂线,交点P 即为该瞬间的速度瞬心.④ 已知某瞬时图形上A ,B 两点速度B A v v ,大小,且AB v AB v B A ⊥⊥ ,⑤已知某瞬时图形上A ,B 两点的速度方向相同,且不与AB 连线垂直.瞬时平动注意:瞬时平动与平动不同瞬时平动构件上各点的速度都相等,但各点的加速度并不相等。
理论力学课后习题答案-第6章--刚体的平面运动分析
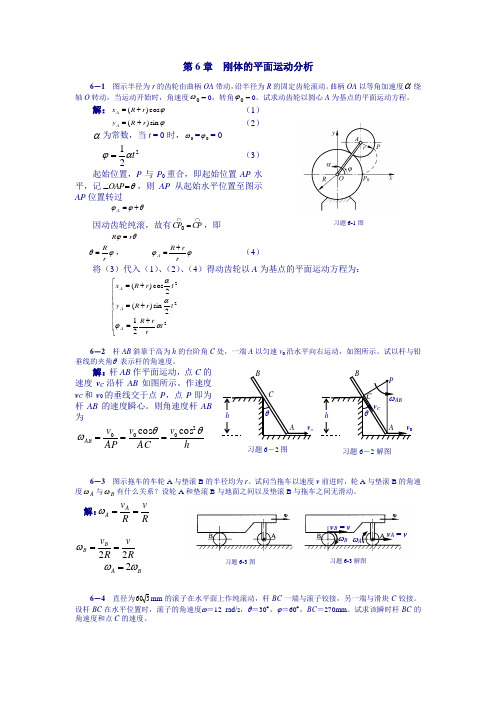
第6章 刚体的平面运动分析6-1 图示半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动。
曲柄OA 以等角加速度α绕轴O 转动,当运动开始时,角速度0ω= 0,转角0ϕ= 0。
试求动齿轮以圆心A 为基点的平面运动方程。
解:ϕcos )(r R x A += (1) ϕsin )(r R y A +=(2)α为常数,当t = 0时,0ω=0ϕ= 0 221t αϕ=(3)起始位置,P 与P 0重合,即起始位置AP 水平,记θ=∠OAP ,则AP 从起始水平位置至图示AP 位置转过θϕϕ+=A因动齿轮纯滚,故有⋂⋂=CP CP 0,即 θϕr R = ϕθr R =, ϕϕrr R A += (4)将(3)代入(1)、(2)、(4)得动齿轮以A 为基点的平面运动方程为:⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=222212sin )(2cos )(t r r R t r R y t r R x A A A αϕαα6-2 杆AB 斜靠于高为h 的台阶角C 处,一端A 以匀速v 0沿水平向右运动,如图所示。
试以杆与铅垂线的夹角θ 表示杆的角速度。
解:杆AB 作平面运动,点C 的速度v C 沿杆AB 如图所示。
作速度v C 和v 0的垂线交于点P ,点P 即为杆AB 的速度瞬心。
则角速度杆AB 为6-3 图示拖车的车轮A 与垫滚B 的半径均为r 。
试问当拖车以速度v 前进时,轮A 与垫滚B 的角速度A ω与B ω有什么关系?设轮A 和垫滚B 与地面之间以及垫滚B 与拖车之间无滑动。
解:RvR v A A ==ωR v R v B B 22==ωB A ωω2=6-4 直径为360mm 的滚子在水平面上作纯滚动,杆BC 一端与滚子铰接,另一端与滑块C 铰接。
设杆BC 在水平位置时,滚子的角速度ω=12 rad/s ,θ=30︒,ϕ=60︒,BC =270mm 。
试求该瞬时杆BC 的角速度和点C 的速度。
hv AC v AP v ABθθω2000cos cos ===习题6-1图ABCv 0hθ习题6-2图PωABv CABCv ohθ习题6-2解图习题6-3解图习题6-3图v A = vv B = v ωAωB习题6-6图习题6-6解图解:杆BC 的瞬心在点P ,滚子O 的瞬心在点D BDv B ⋅=ωBPBD BP v B BC ⋅==ωω ︒︒⨯=30sin 27030cos 36012 rad/s 8=PC v BC C ⋅=ωm/s 87.130cos 27.08=︒⨯=6-5 在下列机构中,那些构件做平面运动,画出它们图示位置的速度瞬心。
最新《力学》漆安慎(第二版)答案07章

力学(第二版)漆安慎习题解答第七章刚体力学第七章 刚体力学 一、基本知识小结⒈刚体的质心定义:∑⎰⎰==dm dm r r mr m r c i i c //求质心方法:对称分析法,分割法,积分法。
⒉刚体对轴的转动惯量定义:∑⎰==dm r I r m I ii 22平行轴定理 I o = I c +md 2 正交轴定理 I z = I x +I y.常见刚体的转动惯量:(略) ⒊刚体的动量和质心运动定理∑==c c a m F v m p⒋刚体对轴的角动量和转动定理∑==βτωI I L⒌刚体的转动动能和重力势能c p k mgy E I E ==221ω⒍刚体的平面运动=随质心坐标系的平动+绕质心坐标系的转动动力学方程:∑∑==c c c c I a m F βτ(不必考虑惯性力矩)动能:221221cc c k I mv E ω+= ⒎刚体的平衡方程∑=0F, 对任意轴∑=0τ二、思考题解答7.1 火车在拐弯时所作的运动是不是平动?答:刚体作平动时固联其上的任一一条直线,在各时刻的位置(方位)始终彼此平行。
若将火车的车厢看作一个刚体,当火车作直线运行时,车厢上各部分具有平行运动的轨迹、相同的运动速度和加速度,选取车厢上的任一点都可代替车厢整体的运动,这就是火车的平动。
但当火车拐弯时,车厢上各部分的速度和加速度都不相同,即固联在刚体上任一条直线,在各时刻的位置不能保持彼此平行,所以火车拐弯时的运动不是平动。
7.2 对静止的刚体施以外力作用,如果合外力为零,刚体会不会运动?答:对静止的刚体施以外力作用,当合外力为了零,即0i c F ma ==∑时,刚体的质心将保持静止,但合外力为零并不表明所有的外力都作用于刚体的同一点。
所以,对某一确定点刚体所受合外力的力矩i i iM M r F ==⨯∑∑不一定为零。
由刚体的转动定律M J α=可知,刚体将发生转动。
比如,置于光滑水平面上的匀质杆,对其两端施以大小相同、方向相反,沿水平面且垂直于杆的两个作用力时,杆所受的外力的合力为零,其质心虽然保持静止,但由于所受合外力矩不为零,将作绕质心轴的转动。
第6章刚体的平面运动习题解答080814

,(逆时针)、
,
杆OB得角速度为
,(逆时针)、
两齿轮啮合点M得速度为,则轮1得角速度为
,(逆时针)、
6-9如图所示,轮O在水平面上匀速滚动而不滑动,轮缘上固连销钉连接滑块B,此滑块在摇杆得槽内滑动,并带动摇杆绕轴转动。已知轮得半径m,在图示位置时,就是轮得切线,轮心得速度m/s,摇杆与水平面得夹角为。求摇杆得角速度与角加速度。
解:如图所示,对各构件进行速度分析、
1)杆作平面运动、因,所以杆为瞬时平移,得
、
2)杆作平面运动、由找得杆得速度瞬心为D点,所以,杆上得速度分布好像与三角板一起绕作定轴转动一样,得
,方向如图示、
3)杆作平面运动、由找得杆得速度瞬心为,故有
,(顺时针);
,(方向向上).
6—5图示四连杆机构中,连杆由一块三角板ABD构成。已知曲柄得角速度rad/s,mm,mm,mm。当mm铅直时,AB平行于,且、A、D在同一直线上,角。求三角板ABD得角速度与点D得速度.
解:1)速度分析、
动齿轮A在定齿轮O上作纯滚动,所以,动齿轮A上与定齿轮O接触得这点就就是动齿轮得A得速度瞬心,于就是有
,,(逆时针)、
、
选BE杆上得B点为动点,套筒C为动系,如图(a)。由速度合成定理
,
得
,
、
式中、从而杆BE得角速度为
,(顺时针)、
当选BE杆上得为动点时,牵连速度为零,又因为杆相对于套筒就是作平移,从而杆BE上得点得速度为
解出
,
,
于就是,杆得角速度为
,(逆时针);
杆得角速度为
,(顺时针)、
选取滑块上得销钉C为动点,摇杆为动系,则
刚体平面运动-习题解答

r1 r2 4 r2
1
(r r ) vC 2(r1 r2 ) r 4 1 3 4 (1 3 ) 4 12 4 r1 r1 r1 r1 ()
n1 12n4 10800r / min
6-6. 图示小型精压机的传动机构,OA=O1B=r=0.1m, EB=BD=AD=l=0.4m。
解: (1)求 aB 和AB
V A 常量, a A 0 V A || VB , 且AB不垂直于V A , AB杆作瞬时平动
AB 0, BC VB / BC 10 / 5 2
选A为基点, 则 a B a B a A a BA a BA 由图中几何关系得
杆 EF 的速度瞬心在点 P:
EF
vF vF v sin F 1.33 rad / s (顺) PF EF sin EF
6-4.在瓦特行星传动机构中,平衡杆 O1A 绕 O1 轴转动,并借连杆 AB 带动曲柄 OB;而曲柄 OB 活动地装置在 O 轴上,如图所示。在 O 轴上装有齿轮 I,齿轮
57.8m / s 2
杆 O1 B 的角加速度 @
2 1 a 逆时针 B / O1 B 57.8 / 0.3 192.7 rad / s
6-3.图示机构中,已知:OA=0.1m, DE=0.1m, EF 0.1 3 m ,D 距 OB 线为 h=0.1m; OA 4 rad s 。在图示位置时,曲柄 OA 与水平线 OB 垂直;且 B、D 和 F 在同一铅直线上。又 DE 垂直于 EF。求杆 EF 的角速度和点 F 的速度。
a A R 0 ,
n
选A为基点, 则
a B a A a BA a BA
刚体平面运动动力学

av)c
作用在刚体上的力矩使刚体旋转,绕质心轴的角加速度为 z'
P.236 图 r
r
将力F沿作用线大小方向不变地滑移到 ,F不' 影响两种效果
7.27
作用在刚体上的力是滑移矢量
刚体力的三要素:大小、方向、作用线
4 刚体平面运动
二、作用于刚体上的力
2.力偶和力偶矩
力偶:大小相等方向相反彼此平行的一对力
平面运动动能定理
A外ຫໍສະໝຸດ Ek(1 2
mvc2
1 2
Ic2 )
P.240 例题 3
刚体平面运动的基本动力学方程:
v Fi
mavc
M I Z'
z' z'
力偶作用效果:
力偶不改变质心的运动状态 只改变刚体的转动状态
4 刚体平面运动
二、作用于刚体上的力
2.力偶和力r偶矩
r
F' O1
C
O2
F
Od' MZ O"
F O"C F O'C F ( O"C O'C )
4 刚体平面运动
v Fi
mavc
MZ' Iz' z' 0
二维平动:刚体作平面运动又只作平动
P.239 例题 2
4 刚体平面运动
三、刚体平面运动的动能
平面运动 = 平动 + 定轴转动 平面运动动能 = 随质心平动动能 + 绕质心轴转动的动能
Ek
1 2
mvc2
1 2
I c 2
4 刚体平面运动
陈世民理论力学简明教程第二版答案第五张刚体力学

第五张 刚体力学平动中见彼此,转动中见分高低.运动美会让你感受到创造的乐趣.走过这遭,也许会有曾经沧海难为水的感叹.别忘了,坐标变换将为你迷津救渡,同时亦会略显身手.【要点分析与总结】1 刚体的运动(1)刚体内的任一点的速度、加速度(A 为基点) (2)刚体内的瞬心S :()21s A A r r ωυω=+⨯〈析〉ω为基点转动的矢量和,12ωωω=++值得注意的是:有转动时r '与r ω'⨯的微分,引入了r ω'⨯与()r ωω'⨯⨯项。
2 刚体的动量,角动量,动能 (1)动量:c P m υ=(2)角动量: x x xx xy xz i i i y yxyy yz y zx zyzz z z L J J J L r m L J J J J J J J L ωυωωω⎛⎫⎛⎫⎛⎫-- ⎪ ⎪⎪=⨯===-- ⎪ ⎪ ⎪ ⎪ ⎪⎪--⎝⎭⎝⎭⎝⎭∑式中:转动惯量()()()222222xx yy zz J y z dmJ z x dm J x y dm ⎧=+⎪⎪=+⎨⎪=+⎪⎩⎰⎰⎰惯量积xx yy zz J xydmJ yzdm J zxdm ⎧=⎪⎪=⎨⎪=⎪⎩⎰⎰⎰且c c cL r m L υ'=⨯+ * l e 方向(以l 为轴)的转动惯量: (,,αβγ分别为l e 与,,x y z 轴夹角的余弦) * 惯量主轴惯量主轴可以是对称轴或对称面的法线若X 轴为惯量主轴,则含X 的惯量积为0,即: 0==xy xz J J 若,,x y z 轴均为惯量主轴,则:xx yy zz L J i J j J k =++ 〈析〉建立的坐标轴轴应尽可能的是惯量主轴,这样会降低解题繁度。
(3) 动能:22211112222c i i c c iT m m m J υυυωω'=+=+∑* 定轴转动时: 212T J ω=* 平面平行运动: 221122c c T m J υω=+3刚体的动力学方程与质点动力学方程相同。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
刚体的平面运动 刚体的平面运动刚体的平面运动是刚体运动的一种特殊形式,可视为刚体的平移与转动的合成。
本章研究的主要内容是如何描述刚体的平面运动,以及如何计算刚体上点的速度和加速度。
一、 刚体的平移(平动) 刚体在运动过程中,如果其上任一直线始终保持与初始的方向平行,则称该刚体作平移或平动。
平移刚体上各点的速度相同,加速度相同,运动轨迹的形状也相同。
因此研究刚体的平移问题可简化成一个质点的运动问题来研究。
二、 刚体的定轴转动刚体在运动过程中,若其上(或刚体的延展体上)有一直线保持不动,且刚体绕此直线转动,则称该刚体作定轴转动。
(1)定轴转动刚体的运动方程: )(t f =ϕ(2)定轴转动刚体的角速度: )(t f ==ϕω(3)定轴转动刚体的角加速度: )(t f ===ϕωα (4)定轴转动刚体上一点P 的速度和加速度用矢量表示速度: r v ⨯=ω (7-1)加速度:v r a a a ⨯+⨯=+=ωαn t (7-2)其中:ωα,为定轴转动刚体的角速度和角加速度矢量,r 是由转轴上任一点引向P 点的矢径。
三、刚体的平面运动 刚体在运动过程中,若其上任一点到某一固定平面的距离保持不变,则称该刚体作平面运动。
研究刚体的平面运动可简化为研究一个平面图形在其所在平面内的运动。
1、 刚体平面运动的角速度和角加速度 在平面图形上任取两点A 、B ,过这两点的连线某一基准线的夹角为θ(如图7-2)。
当刚体运动时这个夹角将随时间变化)(t θ,刚体平面运动的角速度和角加速度分别定义为:θω =, (7-3) θωα == (7-4) 2、 刚体平面运动的运动方程平面运动刚体有三个自由度,其运动方程为:)(),(),(321t f t f y t f x A A ===ϕ (7-5)其中:A 点称为基点(如图7-3所示)。
因此刚体的平面运动可视为刚体随基点的平图7-1刚体的平面运动是刚体运动的一种特殊形式,可视为刚体的平移与转动的合成。
本章研究的主要内容是如何描述刚体的平面运动,以及如何计算刚体上点的速度和加速度。
一、 刚体的平移(平动)刚体在运动过程中,如果其上任一直线始终保持与初始的方向平行,则称该刚体作平移或平动。
平移刚体上各点的速度相同,加速度相同,运动轨迹的形状也相同。
因此研究刚体的平移问题可简化成一个质点的运动问题来研究。
二、 刚体的定轴转动刚体在运动过程中,若其上(或刚体的延展体上)有一直线保持不动,且刚体绕此直线转动,则称该刚体作定轴转动。
(1)定轴转动刚体的运动方程: )(t f =ϕ(2)定轴转动刚体的角速度: )(t f ==ϕω (3)定轴转动刚体的角加速度: )(t f===ϕωα (4)定轴转动刚体上一点P 的速度和加速度用矢量表示速度: r v ⨯=ω (7-1)加速度:v r a a a ⨯+⨯=+=ωαn t (7-2)其中:ωα,为定轴转动刚体的角速度和角加速度矢量,r 是由转轴上任一点引向P点的矢径。
三、刚体的平面运动刚体在运动过程中,若其上任一点到某一固定平面的距离保持不变,则称该刚体作平面运动。
研究刚体的平面运动可简化为研究一个平面图形在其所在平面内的运动。
1、 刚体平面运动的角速度和角加速度在平面图形上任取两点A 、B ,过这两点的连线某一基准线的夹角为θ(如图7-2)。
当刚体运动时这个夹角将随时间变化)(t θ,刚体平面运动的角速度和角加速度分别定义为:θω =, (7-3) θωα == (7-4) 2、 刚体平面运动的运动方程平面运动刚体有三个自由度,其运动方程为:)(),(),(321t f t f y t f x A A ===ϕ (7-5)其中:A 点称为基点(如图7-3所示)。
因此刚体的平面运动可视为刚体随基点的平移和绕基点转动的合成,而刚体的平面平移(c ≡ϕ,其中c 为常量)和定轴转动(,,21c y c x A A ==其中21,c c 为常量)又是刚体平面运动的特殊情况。
同一平面运动刚体,若选取得不同的基点,则基点的运动方程会有所不同,图7-1图7-2刚体绕不同基点转过的角度只相差一个常量,因此刚体的角速度和角加速度与基点的选取无关,根据平面运动刚体角速度、角加速度的定义(7-3)式和(7-4)式也可得到这一结论。
3、 平面图形上各点的速度基点法公式:BA A B v v v += (7-6)基点法公式建立了平面图形上任意两点的速度与平面图形角速度的关系。
速度投影定理:平面图形上任意两点的速度在这两点连线上的投影相等,即:[][]AB AB B A v v = (7-7)该定理反映了刚体上任意两点间距离保持不变的性质。
速度瞬心法:只要平面图形的角速度不为零,就必定存在唯一的一点,其速度在该瞬时为零,该点称为平面图形的速度瞬心,用v c 表示。
平面图形上任一点M 的速度可表示成Mv C M r v ⨯=ω (7-8)其中:M vC r 是从速度瞬心v c 引向M 点的矢径,ω为平面图形的角速度矢量。
4、平面图形上各点的加速度 基点法公式:nt BABA A B a a a a ++= (7-9)其中:)(,ntAB AB r a r a ⨯⨯=⨯=ωωαBA BA 。
基点法公式建立了平面图形上任意两点的加速度与平面图形的角速度和角加速度间的关系。
只要平面图形的角速度和角加速度不同时为零,则其上必存在唯一的一点,其加速度在该瞬时为零,该点称为平面图形的加速度瞬心,用a C 表示。
3-3 取套筒B 为动点,OA 杆为动系根据点的复合运动速度合成定理r e a v v v +=可得:l v v ω==e 0a 30cos ,l v v v BCB ω332a ===研究AD 杆,应用速度投影定理有:030cos D A v v =,l v D ω334=再取套筒D 为动点,BC 杆为动系,根据点的复合运动速度合成定理r D BC D v v v +=avevr vA vD vr D v将上式在x 轴上投影有:r D BC D v v v +-=-,l v v v BC D D ω332r -=+-=3- 4 AB 构件(灰色物体)作平面运动,已知A 点的速度s A O v A /0cm 4510==ωAB 的速度瞬心位于C ,应用速度瞬心法有:rad/s 23==AC v A AB ωBC v AB B ω=,设OB 杆的角速度为ω,则有rad/s415==OB v B ω设P 点是AB 构件上与齿轮I 的接触点,该点的速度:CP v AB P ω=齿轮I 的角速度为:rad/s 61==r v PI ω3-6 AB 杆作平面运动,取A 为基点 根据基点法公式有:BA A B v v v +=将上式在AB 连线上投影,可得,01==B O B v ω因此,041ωω==AB v A AB因为B 点作圆周运动,此时速度为零,因此只有切向加速度(方向如图)。
根据加速度基点法公式n t BA BAA B aaa a ++=将上式在AB 连线上投影,可得n60cos BA A B aa a +=-,r a B 25.2ω-= 201231ωα-==B O a B B O (瞬时针)3-7 齿轮II 作平面运动,取A 为基点有A vB vP vCAB ωI ωB vBA vA vA aB at BAan BAatnt BABA A B a a a a ++=nt 1BABA a a a a ++=将上式在x 投影有:n1cos BAa a a -=-β由此求得:212n 2cos 2r a a r a BAII βω+==再将基点法公式在y 轴上投影有: 2t2sin r a a II BA αβ==,由此求得22sin r a II βα=再研究齿轮II 上的圆心,取A 为基点n t n t 2222A O A O A O O a a a a a ++=+将上式在y 轴上投影有2sin 2t t 22βαa r a a II AO O ===,由此解得:)(2sin 2121t221r r a r r a OO O +=+=βα再将基点法公式在x 轴上投影有:n 1n 22A O O a a a -=- 由此解得:2cos 1n 2a a a O -=β, 又因为221n212)(O OO r r a ω+=由此可得:)(2cos 21121r r a a O O +-±=βω3-9 卷筒作平面运动,C 为速度瞬心,其上D 点的速度为v ,卷筒的角速度为:r R v DC v -==ω角加速度为:r R a r R v -=-== ωα卷筒O 点的速度为:r R vRR v O -==ωO 点作直线运动,其加速度为:r R aRr R R v va O O -=-==研究卷筒,取O 为基点,求B 点的加速度。
n0t B BO O B a a a a ++=将其分别在x,y 轴上投影n t BO By BOO Bx aa aa a -=+=422222)(4)(v r R a r R Ra a a By Bx B +--=+=同理,取O 为基点,求C 点的加速度。
n0t C CO O C a a a a ++=将其分别在x,y 轴上投影n t 0COCy CO O Cx a a a a a ==-=22)(r R Rv a a CyC -==3-10 图示瞬时,AB 杆瞬时平移,因此有:m /s 2===OA v v A B ωAB 杆的角速度:0=AB ω圆盘作平面运动,速度瞬心在P 点,圆盘的 的角速度为:m/s 4==r v BB ω圆盘上C 点的速度为:m/s 22==PC v B C ωAB 杆上的A 、B 两点均作圆周运动,取A 为基点根据基点法公式有t n t BA A BB B aa a a a +=+=将上式在x 轴上投影可得:0t =-Ba 因此:22nm/s 8===r v a a BBB由于任意瞬时,圆盘的角速度均为:r v B B =ω将其对时间求导有:r a r v B B B t== ω,Oan CO aOt COaCBt BOan BO aαB ωt BAatBaA an BaA vB vB ωPC vvaar aea K a由于0t=B a ,所以圆盘的角加速度0==B B ωα 。
圆盘作平面运动,取B 为基点,根据基点法公式有:n n t CBB CBCBB C a a aaa a +=++=22n2n m/s 28)()(=+=CB B C a a a3-13 滑块C 的速度及其加速度就是DC 杆的速度和加速度。
AB 杆作平面运动,其速度瞬心为P , AB 杆的角速度为:rad/s 1==AP v AAB ω杆上C 点的速度为:m /s 2.0==PC v AB C ω取AB 杆为动系,套筒C 为动点,根据点的复合运动速度合成定理有: r e a v v v +=其中:C v v =e ,根据几何关系可求得:m/s 153r a ==v vAB 杆作平面运动,其A 点加速度为零,B 点加速度铅垂,由加速度基点法公式可知nt n t BABA BA BA A B a a a a a a +=++=由该式可求得2nm/s 8.030sin ==BAB a a由于A 点的加速度为零,AB 杆上各点加速度的分布如同定轴转动的加速度分布,AB 杆中点的加速度为: 2m/s 4.05.0==B C a a再取AB 杆为动系,套筒C 为动点,根据复合运动加速度合成定理有:K r e a a a a a ++=其中:a K 表示科氏加速度;牵连加速度就是AB 杆上C 点的加速度,即:2e m/s 4.0=a将上述公式在垂直于AB 杆的轴上投影有:K 0e 0a 30cos 30cos a a a +=科氏加速度r K 2v a AB ω=,由上式可求得:2a m/s 32=aBCB an BC aevr vavB atBAan BAaCa3-14:取圆盘中心1O 为动点,半圆盘为动系,动点的绝对运动为直线运动;相对运动为圆周运动;牵连运动为直线平移。
