永春县2011年秋季八年级期末检测
福建省永春县汤城中学2011-2012学年八年级上学期期末考试数学试题(扫描版)
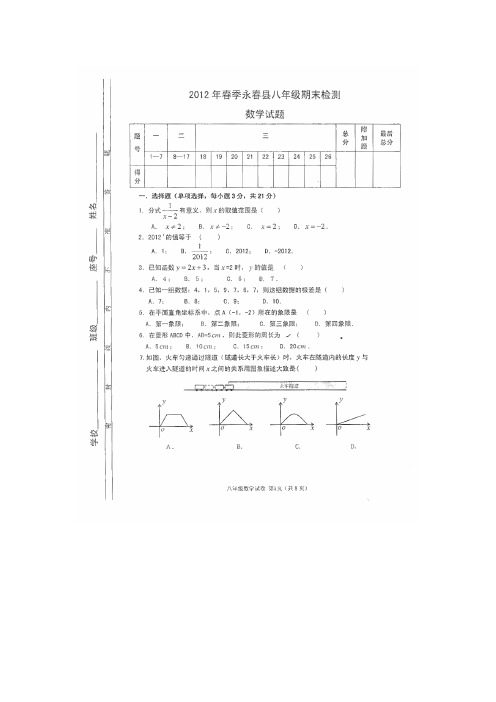
2012年春季八年级期末考数学科参考答案一.选择题(单项选择,每小题3分,共21分)1.A ;2.B ;3.D ;4.B ;5.C ;6.D ;7.A.二.填空题(每小题4分,共40分)8.1 ; 9. 3×10-5;10.3ab ;11. (-2,-3); 12. 略 ; 13.9.3; 14. 甲; 15.减小; 16. 33-=x y ; 17.(2,0);(0,23) 三、解答题(共89分) 18.①原式=yx y x --22 (4分)=y x + 8分 ②方程两边同乘以3)2(-x x ,2分 得8(x -2)=9x 5分 解得x =-16. 7分 检验: 8分19.证明 ∵ AD 平分∠BAC ,∴ ∠BAD =∠CAD . 3分在△ABD 与△ACD 中,∵ AB =AC , ∠BAD =∠CAD ,AD =AD , 6分∴ △ABD ≌△ACD (S.A.S.). 8分20.∵ 四边形ABCD 是平行四边形,∴ AB ∥CD AB=CD 4分即AE ∥FD . 5分点E 、F 分别是边AB 、DC 的中点 ∴ AE =FD , 6分∴ 四边形AEFD 为平行四边形. 8分21.正确画出一个图形得4分 共8分22.(1)李文的平均成绩为82分,刘明的平均成绩为3245 2分李文被录用 4分(2)李文的平均成绩为83.8分,刘明的平均成绩为84. 5 6分刘明被录用 8分23.:(1)k =2 =b 3 =n 1 6分(2)根据图象可得,当1<x <2时,2y >1y 8分24.(1)184cm 2 4分 (2)由题意, Q 点到B 点的时间为326秒. 四边形PQCD 为平行四边形,即CQ=PD , 6分即20-t =3t ; 8分 t =5秒. 9分25.(1)⎩⎨⎧-=+=+153b k b k 2分 ⎩⎨⎧=-=41b k 3分4+-=x y 4分(2)直线AB 与x 轴的交点P ,满足PA+PB 最小 6分4+-a =0 7分 a =4 8分(3)①连结AB,作线段AB 的垂直平分线与x 轴的交点P 满足│AP-BP │最小 9分过A 作AM ⊥x 轴,垂足为M,过B 作BN ⊥y 轴,垂足为N,AM 2+MP 2=BN 2+NP 2∴32+(a -1)2=12+(5-a )2 =a 2 10分 ②作B 点P 关于x 轴的对称点B ′,则B ′(5,1) 直线AB ′与x 轴的交点P 满足│AP-BP │最大11分直线AB ′ 2721+-=x y y =0 ∴a =7 12分 26.(1)O 180 4分 (2)由题意得EF 垂直平分BC ,故BB'=B'C , 5分由翻折可得, B'C =BC , 7分∴△BB'C 是等边三角形. 8分(2)分别取CE 、EG 、GI 的中点P 、Q 、R ,连接DP 、FQ 、HR 、AD 、AF 、AH , ∵△ABC 中,BA =BC ,根据平移变换的性质,△ CDE 、△EFG 和△GHI 都是等腰三角形,∴DP ⊥CE ,FQ ⊥EG ,HR ⊥GI .在Rt △AHR 中,AH =AI =4a ,AH 2=HR 2+AR 2,HR 2=154a 2,9分 则DP 2=FQ 2=HR 2=154a 2, AD 2=AP 2+DP 2=6a 2,AF 2=AQ 2+FQ 2=10a 2, 新三角形三边长为4a 、6a 、10a . 10分∵AH 2=AD 2+AF 2 ∴新三角形为直角三角形. 其面积为126a 10a =15a 2.∵15a 2<1515 ∴a 2<15 11分 ∴a 的最大整数值为3. 12分A B C I ED G F Ha P Q R。
福建省永春第一中学八年级下学期期末考试英语试题

永春一中八年级期末考英语科试卷()命题教师:学校组织命题考试时间120分钟,试卷总分150分温馨提示:请把所有答案填写(涂)在答题卡上,请不要错位、越界答题!第Ⅰ卷(选择题共105分)I. 听力部分(共三节,20小题,每小题分,满分30分)第一节. 听句子从A、B、C三幅图画中选出符合句子内容的图画。
(每个句子读两遍,每小题分,满分分)第二节.听对话理解听下面七段对话,从题中所给的A、B、C三个选项中选出最佳选项。
(每段对话读两遍,每小题分,满分15分)听第一段对话,完成第6小题。
( )6. What does Mike ask the girl to speak louderA. Because something is wrong with his ear.B. Because something is wrong with his line.C. Because they are talking in a noisy street .听第二段对话,完成第7小题。
( )7. What does Jack ask the girl to doA. Go to bed earlier.B. Not to be late again.C. Go to school right now.听第三段对话,完成第8小题。
( ) is Mr. Zhang talking withA. A guest.B. A friend.C. His workmate.听第四段对话,完成第9小题。
( ) can’t Tim sleep wellA. Because it is too hot.B. Because he hasn’t finished his work.C. Because he is afraid to sleep alone.听第五段对话,完成第10-11小题。
( ) will they get to ShanghaiA. In half an hour.B. In an hourC. In one and a half hours. ( ) will they do thenA. Play cards.B. Play chess.C. Play tennis.听第六段对话,完成第12-13小题。
泉州市永春县八年级下学期期末物理试卷

泉州市永春县八年级下学期期末物理试卷姓名:________ 班级:________ 成绩:________一、选择题 (共15题;共31分)1. (2分)如图的实验中,探究的物理问题是()A . 大气压强的测量B . 液体内部压强与方向的关系C . 液体内部压强与液体深度的关系D . 液体内部压强与液体密度的关系2. (2分) (2019八下·庆云期中) 如图所示,将一个瓶子,装入适量带色的水,再取一根两端开口的细玻璃管,使玻璃管穿过橡皮塞插入水中。
从管子上端吹入少量气体,使瓶内气体压强大于大气压,水沿玻璃管上升到瓶口以上。
当拿着它从山下的报国寺到金顶山上,玻璃管内水柱高度将()A . 升高B . 不变C . 降低D . 无法判断3. (2分) (2018八下·武威月考) 下列事例中,属于惯性造成危害的是()A . 拍打被子去掉灰尘B . 乘客在紧急刹车时摔倒C . 运动员采用助跑跳得更远D . 投出去的篮球飞向篮筐4. (2分)(2018·辽阳模拟) 在自由下落过程中物体运动速度会越来越快.一个物体由A点自由下落,相继经过B、C两点,已知AB=BC,如图所示,物体在AB段重力做功W1 ,做功功率P1;在BC段重力做功W2 ,做功功率P2 ,则下列关系正确的是()A . W1<W2 P1<P2B . W1=W2 P1>P2C . W1=W2 P1<P2D . W1>W2 P1>P25. (2分) 2015年,东营市以优异成绩入选第四届全国文明城市,清洁车在美化城市环境方而起着重要作用.如图所示,清洁车匀速行驶,将水不停地洒在地上.下列有关说法错误的是()A . 清洁车所受重力与地面对它的支持力是一对平衡力B . 路上行人感觉清凉,是因为水蒸发要吸收热量C . 洒水过程中清洁车的动能始终保持不变D . 以清洁车为参照物,路两旁的树是运动的6. (2分)足球是很多人的至爱,如图所示关于足球场上的一些现象,下列说法正确的是()A . 运动员将足球踢出后,足球在空中飞行的过程中受到运动员对足球的踢力B . 裁判员向上举起旗子的过程中,裁判员对旗子没有做功C . 进球时,球与网接触,球网网眼变大,说明力能使物体发生形变D . 运动员争顶头球向上跳起的过程中,动能和重力势能均减小7. (2分)(2019·琼海模拟) 目前,小汽车几乎普及了城市家庭。
2011年永春初中学业质量检查

2011年永春县初中学业质量检查生物试题(本卷共两大题,43小题,共6页。
满分:100分考试时间:60分钟)友情提示:所有答案必须填写到答题卡相应的位置上。
毕业学校_____________ 姓名 _______________考生号 __________________一、选择题(本大题共50分,1-20题每小题1分,21-35题每小题2分。
每小题的四个选项中只有一个是正确的。
错选、多选或不选均不得分。
请务必用2B铅笔将答案涂在答题卡上,否则无效。
)1.地球上最大的生态系统是A.海洋生态系统 B.森林生态系统 C.草原生态系统 D.生物圈2.下列分类单位中包含生物种类最多的是A.属 B.科 C.门 D.种3.以下不属于...威胁生物多样性的原因是A.土地沙漠化 B.环境污染 C.生物变异 D.生物入侵4.没有根、茎、叶等器官分化的植物类群是A.藻类植物 B.苔藓植物 C.蕨类植物 D.种子植物Array 5.手被针扎到立即缩回,该反射的神经中枢位于图中的A.① B.②C.③ D.④6.下列属于我国特有珍稀植物的是A.榕树 B.肾蕨 C.银杉 D.茉莉7.云南某地红豆杉因树皮被环剥致死,这是因为运输有机物的筛管位于A.韧皮部 B.木质部 C.根冠 D.形成层8.小林一到黄昏就看不清东西,经医生诊断他患了夜盲症。
医生建议他多吃A.动物肾脏、胡萝卜 B.蔬菜、水果C.动物肝脏、胡萝卜 D.薯条、玉米9.连绵阴雨导致玉米产量降低,主要是因为天气影响了下列哪个时期A.开花 B.传粉 C.受精 D.果实种子形成10.醉酒的人驾车时明显表现为反应慢、动作不协调,从而影响各项操作。
造成驾车人动作不协调的主要原因是酒精麻醉了人的A.小脑 B.大脑 C.脊髓 D.脑干11.吃剩的饭菜放在冰箱内不容易腐败变质的主要原因是冰箱内A.没有空气,细菌无法繁殖 B.温度低,把细菌都冻死了C.温度低,细菌繁殖速度慢 D.温度低,营养物质分解慢12.下列条件中属于种子萌发所必需的是①充分的光照②适宜的温度③充足的空气④适量的水分A.①②③ B.①②④ C.②③④ D.①③④13.做屈肘动作时,没有参与的人体结构是A.肱二头肌 B.肱三头肌C.肘关节 D.指关节14.与做馒头、制酸奶有关的微生物依次为A.酵母菌、乳酸菌 B.霉菌、酵母菌C.酵母菌、霉菌 D.乳酸菌、酵母菌、15.下列关于神经元说法错误..的是A.神经元包括细胞体和突起 B.神经元包括树突和轴突C.神经元受刺激后能产生冲动 D.神经元能传导冲动16.下列神经活动属于条件(复杂)反射的是A.眨眼反射 B.膝跳反射 C.吃梅止渴 D.望梅止渴17.右图是人体消化系统的模式图,图中表示人体消化和吸收的主要场所的结构是Array A.② B.③C.④ D.⑤18.上图中的结构①分泌的消化液不足,主要影响______的消化A.豆腐 B.肥肉C.土豆 D.鱼19.人体精子与卵细胞结合的场所是A.阴道 B.输卵管 C.子宫 D.卵巢20.下列有关人体结构层次的描述,错误..的是A.细胞是人体结构和功能的基本单位 B.细胞分化形成组织C.细胞→组织→器官→人体 D.脑、肝、心、肺等都是器官21.“春蚕到死丝方尽,蜡炬成灰泪始干”,诗中的“死”是指家蚕发育的哪个时期A.卵 B幼虫 C.蛹 D.蚕蛾22.我们用显微镜观察洋葱表皮细胞,若目镜不变,先用10×物镜,后转换为40×物镜,则视野中A.细胞变大、数目变多 B.细胞变小、数目变少C.细胞变大、数目变少 D.细胞变小、数目变多23.“人间四月芳菲尽,山寺桃花始盛开”,造成这一差异的主要生态因素是A.温度 B.光照 C.湿度 D.土壤24.在我们学到的成语中,很多与生物学有关系。
永春县2011年质检试卷

2011年永春县初中学业质量检查数 学 试 题(满分:150分;考试时间:120分钟)学校 姓名 考生号 友情提示:请认真作答,把答案准确地填写在答题卡上.一、选择题(每小题3分,共21分)每小题只有一个答案是正确的,请在答题卡上相应题目的答题区域内作答,答对的得3分,答错、不答或答案超过一个的一律得0分. 1.-3的倒数是( ) A .31; B .31-; C .-3; D .3.2.若2=x 是方程013=+-m x 的解,则m 的值是( )A .4;B .5 ;C .6;D .7. 3.不等式712>-x 的解集是( )A .4>x ;B .3>x ;C .4<x ;D .3<x . 4.以下列各组数为长度的三条线段能组成三角形的是( )A .5,5,8;B .4,5,9;C .3,5,8;D .4,4,9. 5.如图是由七个相同的小正方体堆成的物体,这个物体的俯视图( )6.已知⊙1O 与⊙2O 的半径分别为5和3,若两圆相交,则两圆的圆心距d 的范围是( ) A .2=d ; B .82<<d ; C . 8=d ; D .8>d .7.如图,某工厂有两个大小相同的蓄水池,且中间有管道连通.现要向甲池中注水, 若单位时间内的注水量不变,那么,从注水开始,水池乙...水面上升的高度h 与 注水时间t 之间的函数关系的图像可能是 ( )CBAD乙甲A .B .C .D .二、填空题(每小题4分,共40分)在答题卡上相应题目的答题区域内作答. 8.计算:43)(a = .9.分解因式:42-x = .10.2010年,我县共接待境内外旅游总人数达到1500000人次,用科学记数法表示为 人次. 11.使分式41-x 有意义的x 的取值范围是 . 12.某学习小组7个男同学的身高(单位:米)为:1.58、1.64、1.65、1.66、1.66、1.70、1.72,那么这组数据的中位数为________. 13.六边形的内角和等于 ° 14.梯形的上底长为5cm ,下底长为6cm ,则它的中位线长是 cm .15.如图,⊙O 是△ABC 的外接圆,AB 是直径.若∠OCB=50°,则∠B= °. 16.已知圆锥的底面半径是3,母线长是4,则圆锥的侧面积是 .17.如图,在平面直角坐标系中,点A 在x 轴上,OA =3,AB =4,OA ⊥AB. (1)△OAB 的面积为 ;(2)若点C 在线段OB 上,OC =2BC ,双曲 线xky =过点C ,则k = .三、解答题(共89分)在答题卡上相应题目的答题区域内作答. 18.(9分)计算:│-3│-12×3+20110-(41)-1第15题19.(9分)先化简,再求值:)3()2)(2(x x x x -+-+,其中12+=x .20.(9分)学校开设排球、篮球、羽毛球、体操四项课外活动.学生可根据自己的爱好任选其中一项,根据报名情况绘制了尚未完成的频数分布直方图,已知选 篮球的人数占报名总人数的10%,解答下列问题: (1)该校学生报名总人数有多少人?(2)选排球的人数占报名总人数的百分之几? (3)将频数分布直方图补充完整. 21.(9分)如图,点E 、F 分别是平行四边形ABCD 边上的点,BF=DE .求证:△ABF ≌△CDE.BCDEFA22.(9分)把分别写有2、3、4数字的三张卡片(卡片除数字外其他完全一样)搅匀后放在一个不透明的袋子中,先抽出一张记下数字后,放回袋中搅匀后再抽出一张. (1)请用树形图或列表把所有可能表示出来;(2)若把第一次抽出的数字记为十位上的数字,第二次抽出的数字记为个位上的数字,求组成的两位数是3的倍数的概率.23.(9分)如图,在⊙O 中,AB 为⊙O 的直径,AC 是弦,OC=4,∠OAC=60°.(1)求∠AOC 的度数;(2)P 为BA 延长线上的一点,当PC 与⊙O 相切时,求PO 的长.24.(9分)为打造“书香校园”,某学校计划用不超过1900本科技类书籍和1620本 人文类书籍,组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类 书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书 籍60本.(1)设组建中型图书角x 个,则组建小型图书角 个(用含的代数式表示); (2)求出符合题意的组建方案.A COPB25.(13分)已知:如图,抛物线)4(332a x x y +-=与x 轴交于A 、B 两点(A 在B 的左侧),与y 轴交于点C )3,0(. (1)直接写出a 的值;(2)在抛物线的对称轴上是否存在一点P ,使得⊙P 与y 轴和直线BC 同时相切,若存在,求出点P 的坐标,若不存在,请说明理由;(3)把抛物线沿x 轴向右平移)0(>m m 个单位,所得抛物线与x 轴交于A ′、B ′两点,与原抛物线交于点M ,当△MA ′B ′的面积为63时,求m 的值.O ABCXY26 .(13分)如图(1),将一个边长为1的正方形纸片ABCD 折叠,点B 落在边 AD 上的B ′处(不与A 、D 重合), MN 为折痕,折叠后B ′C ′与DN 交于P. (1)直接写出正方形纸片ABCD 的周长;(2)如图(2),过点N 作NR ⊥AB ,垂足为R.连结BB ′交MN 于点Q. ①求证:△ABB ′≌△RNM;②设AB ′=x ,求出四边形MNC ′B ′的面积S 与x 的函数关系式,并求S 的最小值.四、附加题(共10分)在答题卡上相应题目的答题区域内作答友情提示:请同学们做完上面考题后,再认真检查一遍,估计一下你的得分情况.如果你全卷得分低于90分(及格线),则本题的得分将计入全卷总分,但计入后全卷总分最多不超过90分;如果你全卷得分已经达到或超过90分,则本题的得分不计入全卷总分. 1.(5分)解方程:82 x .2.(5分)如图,在△ABC 中,∠B=25°,∠C =75°, 求∠A 的度数.ABCC'B'BCDMN PA图2图1R M B'C'2011年永春县初中学业质量检查数学科参考答案一、选择题(每小题3分,共21分)BDAA CBC二、填空题(每小题4分,共40分)8.12a ; 9. )2)(2(-+x x ; 10. 1.5×106; 11. 4≠x ; 12.1.66;13.720; 14. 5.5; 15.50; 16. 12π; 17. 6,16/3. 三、解答题(共89分) 18.原式=3-6+1-4(8分)=-6(9分)19.原式=2234x x x -+-(4分)=43-x (6分) 当12+=x 时,原式=123-(9分) 20. (1)报名总人数是=400(人).3分(2)因为选排球的人数是100人,所以100400100⨯%=25% 6分 (3)补全图形 9分21. 证明:∵ABCD 为平行四边形,∴∠B =∠D ,AB =CD . 4分 在△ABF 和△CDE 中,AB=CD ∠B=∠D BF=DE 7分 ∴△ABF ≌△CDE (SAS ) 9分22. 解:(1)画出树形图或列表 5分(2)按题意,组成的两位数共9个.这其中是3的倍数的为:24、33、42. 7分 所以符合条件的概率为:P =31. 9分 23. 解:(1)∠AOC =60° 3分(2)CP 与⊙O 相切,∠PCO=90° 5分 Cos60°=PO47分 PO=8 9分 24.解:(1)30-x . 3分(2)由题意得⎩⎨⎧≤-+≤-+16203060501900303080)()(x x x x 5分解这个不等式组得18≤x ≤20. 7分由于x 只能取整数,∴x 的取值是18,19,20. 8分 故有三种组建方案:方案一,组建中型图书角18个,小型图书角12个; 方案二,组建中型图书角19个,小型图书角11个;方案三,组建中型图书角20个,小型图书角10个. 9分25. 解:(1)3=a 3分(2)抛物线的对称轴为直线2=x 对称轴与x 轴的交点为H A(1,0) B(3,0) 4分设P (2,y )作PD ⊥BC ,垂足为D ,作PE ⊥y 轴,垂足为E ,则PD =PE =2 ∴当P 在x 轴上方时 ∵33tan ==∠OB OC CBO ∴∠CBO=30° 5分 GH=33∴∠PGD =60° ∴PG =y -33=33460sin = PD PH =335 6分 当P 在x 轴下方时PH =3 7分∴P 的坐标为(2,335)或(2,-3) 8分(3)作MN ⊥x 轴,垂足为N 由平移可知,A ′B ′=AB =2 ∵△MA ′B ′的面积为63 ∴MN =63 9分 当63=y 时,633334332=+-x x 10分 ∴264±=x ∴m =264264--+=6 11分 当63-=y 时,633334332-=+-x x 12分 ∴224±=x ∴m =224224--+=2 13分 HGyXEDPCBAO∴m 的值为6或2 26. (1)4. 3分(2)则由折叠知,△MBQ 与△MB ′Q 关于直线MN 对称∴MQ ⊥BB ′. 4分 在△RNM 和△ABB ′中,∠A=∠MRN=90° 5分 ∠ABB ′+∠BMQ=∠RNM+∠BMN=90° ∴∠ABB ′=∠RNM, 6分 又 RN=AB=1 7分 ∴△RNM ≌△ABB ′ 8分 (3)由(2)可知 △MQB ∽△B ′AB ∵MBBB BQ AB MQ AB ''== 9分 ∵AB ′=x 则BB ′=21x + BQ=2121x + ,代入上式得:MB ′=BM=)1(212+x 10分 CN=BR=BM-MR=)1(212+x -x =2)1(21-x 11分∵MB ′∥NC ′ ∴ 四边形MNC ′B ′是梯形∴S=1)]1(21)1(21[2122⨯++-x x =)1(212+-x x 12分由S=)1(212+-x x =83)21(212+-x ,得当21=x 时,即B 落在AD 的中点处时,梯形面积最小,其最小值为83. 13分。
福建省泉州市永春县八年级下期末数学考试卷(解析版)(初二)期末考试.doc

福建省泉州市永春县八年级下期末数学考试卷(解析版)(初二)期末考试姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题评卷人得分(每空xx 分,共xx分)【题文】若分式的值等于0,则x的值是()A.x=1 B.x=2 C.x≠1 D.x≠2【答案】A【解析】试题分析:分式值为零的条件是分子等于零且分母不等于零.解:∵分式的值等于0,∴x﹣1=0,x2+2≠0.解得:x=1.故选:A.【题文】一组数据:2、2、3、3、3、4、4中位数是()A.2 B.3 C.3.5 D.4【答案】B【解析】试题分析:找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数.解:先对这组数据按从小到大的顺序重新排序:2、2、3、3、3、4、4.位于最中间的数是3,所以这组数的中位数是3.故选B【题文】在平面直角坐标系中,点(3,﹣4)所在的象限是()A.第一象限 B.第二象限 C.第三象限 D.第四象限【答案】D【解析】试题分析:应先判断出点的横纵坐标的符号,进而判断点所在的象限.解:∵点的横坐标3>0,纵坐标﹣4<0,∴点P(3,﹣4)在第四象限.故选D.【题文】函数y=3x+1的图象一定经过点()A.(3,5) B.(﹣2,3) C.(2,7) D.(4,10)【解析】试题分析:将各点坐标代入一次函数表达式,验证是解本题的关键.解:A、把x=3代入y=3x+1,解得y=10,所以图象不经过点(3,5),B、把x=﹣2代入y=3x+1,解得y=﹣5,所以图象不经过点(﹣2,3),C、把x=2代入y=3x+1,解得y=7,所以图象经过点(2,7),D、把x=4代入y=3x+1,解得y=13,所以图象不经过点(4,10).故选C.【题文】甲、乙两辆汽车同时分别从A、B两城驶向C城.已知A、C两城的距离为450千米,B、C两城的距离为400千米,甲车比乙车的速度快10千米/小时,结果两辆车同时到达C城.若设甲车的速度为x千米/小时,则可列方程为()A. B. C. D.【答案】D【解析】试题分析:根据甲车的速度为x千米/小时,得出乙车的速度为每小时(x﹣10)千米;再根据路程÷速度=时间和两辆车同时到达C城,列出方程即可.解:设甲车的速度为x千米/小时,则乙车的速度为(x﹣10)千米/小时,根据题意得:=,故选D.【题文】已知菱形ABCD的对角线AC,BD的长分别为6和8,则该菱形面积是()A.14 B.24 C.30 D.48【答案】B【解析】试题分析:根据菱形的面积等于对角线乘积的一半即可解决问题.解:∵四边形ABCD是菱形,AC=6,BD=8,∴菱形ABCD的面积=•AC•BD=×6×8=24.故答案为B.【题文】如图,P是双曲线上一点,且图中的阴影部分的面积为3,则此反比例函数的解析式为()A.y= B.y=﹣ C.y= D.y=﹣【答案】B【解析】试题分析:此题可从反比例函数系数k的几何意义入手,阴影部分的面积为点P向两条坐标轴作垂线,与坐标轴围成的矩形面积的一半即S=.解:由题意得:点P是反比例函数图象上一点,S==3.又由于反比例函数图象位于二、四象限,k<0,则k=﹣6,故反比例函数的解析式为y=﹣.【题文】20160=.【答案】1【解析】试题分析:直接利用零指数幂的性质化简求出答案.解:20160=1.故答案为:1.【题文】计算:=.【答案】2【解析】试题分析:根据同分母分式相加减,分母不变,只把l【解析】试题分析:绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.解:0.0002用科学记数法表示为:2×10﹣4,故答案为:2×10﹣4.【题文】某小组8位同学的体育测试成绩分别是66,67,78,78,79,79,79,80,这8位同学体育成绩的众数是.【答案】79【解析】试题分析:众数即出现次数最多的数.解:数据79出现了3次,因此众数为79;故答案为:79【题文】平行四边形ABCD中,∠A=80°,则∠C=°.【答案】80【解析】试题分析:利用平行四边形的对角相等,进而求出即可.解:∵四边形ABCD是平行四边形,∴∠A=∠C=80°.故答案为:80.【题文】把直线y=5x向上平移2个单位,得到的直线是.【答案】y=5x+2【解析】试题分析:直接根据“上加下减,左加右减”的原则进行解答.解:把直线y=5x向上平移2个单位,得到的直线是y=5x+2.故答案为:y=5x+2.【题文】对甲、乙两个小麦品种各100株的株高进行测量,求得甲=0.88,乙=0.88,S甲2=1.03,S乙2=0.96,则株高较整齐的小麦品种是.(填“甲”或“乙”)【答案】乙【解析】试题分析:根据方差的意义可作出判断.方差是用来衡量一组数据波动大小的量,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.解:因为乙的方差最小,所以株高较整齐的小麦品种是乙;故答案为:乙【题文】如图,在矩形ABCD中,AD=5,AB=3,在BC边上取一点E,使BE=4,连结AE,沿AE剪下△ABE,将它平移至△DCF的位置,拼成四边形AEFD.(1)CF=;(2)四边形AEFD是什么特殊四边形,你认为最准确的是:.【答案】(1)4;(2)菱形【解析】试题分析:(1)根据平移的性质可直接得到答案;(2)首先根据矩形的性质可得∠B=90°,AD∥BC,再利用勾股定理计算AE,进而可得AE=AD,然后证明四边形AEFD是平行四边形,进而可得四边形AEFD是菱形.解:(1)根据平移可得BE=CF=4,故答案为:4;(2)∵四边形ABCD是矩形,∴∠B=90°,AD∥BC,∵AN=3,BE=4,∴AE==5,∵AD=5,∴AD=AE,根据平移可得AE∥DF,∵AD∥BC,∴AD∥EF,∴四边形AEFD是平行四边形,∵AD=AE,∴四边形AEFD是菱形,故答案为:菱形.【题文】如图,在矩形ABCD中,AB=6,BC=8,点E是BC边上一点,将△ABE沿AE折叠,使点B落在点B′处.(1)矩形ABCD的面积=;(2)当△CEB′为直角三角形时,BE=.【答案】(1)48;(2)3或6.【解析】试题分析:(1)直接利用矩形的面积求出答案;(2)当△CEB′为直角三角形时,有两种情况:①当点B′落在矩形内部时,如答图1所示.连结AC,先利用勾股定理计算出AC=10,根据折叠的性质得∠AB′E=∠B=90°,而当△CEB′为直角三角形时,只能得到∠EB′C=90°,所以点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,则EB=EB′,AB=AB′=6,可计算出CB′=4,设BE=x,则EB′=x,CE=8﹣x,然后在Rt△CEB′中运用勾股定理可计算出x.②当点B′落在AD边上时,如答图2所示.此时四边形ABEB′为正方形.解:(1)∵在矩形ABCD中,AB=6,BC=8,∴矩形ABCD的面积=6×8=48;故答案为:48;(2)当△CEB′为直角三角形时,有两种情况:①当点B′落在矩形内部时,如答图1所示.连结AC,在Rt△ABC中,AB=6,BC=8,∴AC==10,∵∠B沿AE折叠,使点B落在点B′处,∴∠AB′E=∠B=90°,当△CEB′为直角三角形时,只能得到∠EB′C=90°,∴点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,如图,∴EB=EB′,AB=AB′=6,∴CB′=10﹣6=4,设BE=x,则EB′=x,CE=8﹣x,在Rt△CEB′中,∵EB′2+CB′2=CE2,∴x2+42=(8﹣x)2,解得x=3,∴BE=3;②当点B′落在AD边上时,如答图2所示.此时ABEB′为正方形,∴BE=AB=6.综上所述,BE的长为3或6.故答案为:3或6.【题文】①计算:.②解方程:.【答案】①原式=2;②经检验x=3是分式方程的解.【解析】试题分析:①原式利用同分母分式的加法法则计算即可得到结果;②分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.解:①原式===2;②方程两边同乘以(2x+1)(x+2),得10x+5=7x+14,解得:x=3,经检验x=3是分式方程的解.【题文】如图,在矩形ABCD中,E、F分别在AB、CD上,且DE=BF.求证:四边形DEBF是平行四边形.【答案】见解析【解析】试题分析:根据矩形的性质得出∠A=∠C=90°AD=BC,求出Rt△ADE≌Rt△CBF,根据全等得出AE=CF,根据矩形的性质得出AB=CD,AB∥CD,求出BE=DF,BE∥DF,根据平行四边形的判定推出即可.证明:∵四边形ABCD是矩形,∴∠A=∠C=90°AD=BC,在Rt△AD E和Rt△CBF中∴Rt△ADE≌Rt△CBF(HL),∴AE=CF,∵矩形ABCD中AB=CD,AB∥CD,∴BE=DF,BE∥DF,∴四边形DEBF是平行四边形.【题文】学校准备推荐一位选手参加知识竞赛,对甲、乙两位选手进行四项测试,他们各自的成绩(百分制)如表:选手表达能力阅读理解综合素质汉字听写甲85788573乙73808283学校将表达能力、阅读理解、综合素质和汉字听写分别以20%、10%、30%、40%记入个人最后成绩,并根据成绩择优推荐,请你通过计算说明谁将被推荐参加比赛?【答案】乙将会被推荐参加比赛.【解析】试题分析:首先根据加权平均数的含义和求法,分别求出甲、乙的平均成绩各是多少;然后比较大小,判断出谁的平均成绩最高,即可判断出谁将被公司录取.解:甲的最后成绩=85×20%+78×10%+85×30%+73×40%(2分)=79.5,乙的最后成绩=73×20%+80×10%+82×30%+83×40%(4分)=80.4,∵80.4>79.5,∴乙将会被推荐参加比赛.【题文】如图,在菱形ABCD中,BD=AB,求这个菱形的各个内角的度数.【答案】120°【解析】试题分析:由菱形的性质和已知条件易证△ABD是等边三角形,所以∠A的度数可求出,进而可求出菱形其他内角的度数.解:∵四边形ABCD是菱形,∴AB=AD,∠A=∠C,∠A+∠ADC=180°,∵BD=AB,∴AB=AD=BD,∴△ABD是等边三角形,∴∠A=60°,∴∠C=60°,∴∠ABC=∠ADC=120°.【题文】如图是一辆汽车离出发地的距离S(千米)和行驶时间t(小时)之间的函数图象.(1)汽车在DE段行驶了小时;(2)汽车在BC段停留了小时;(3)汽车出发1小时时,离出发地多少千米?【答案】(1)1.5;(2)0.5;(3)行驶1小时时,离出发地千米.【解析】试题分析:(1)由DE段图象对应时间t的值可知;(2)由BC段图象对应时间t的值可知;(3)待定系数求得AB段解析式,令t=1求得对应s的值.解:(1)汽车在DE段行驶时间为:4.5﹣3=1.5(小时),故答案为:1.5;(2)汽车在BC段停留时间为:2﹣1.5=0.5(小时),故答案为:0.5;(3)由图象可设AB段图象的函数表达式为y=kx,当x=1.5时,y=80;解得:k=,即y=x,(0≤x≤1.5),当x=1时,y=,答:行驶1小时时,离出发地千米.【题文】如图,直线y=﹣x+b与反比例函数的图象相交于点A(a,3),且与x轴相交于点B.(1)求a、b的值;(2)若点P在x轴上,且△AOP的面积是△AOB的面积的,求点P的坐标.【答案】(1)a=﹣1,b=2;(2)P的坐标为(1,0 )或(﹣1,0 ).【解析】试题分析:(1)直接利用待定系数法把A(a,3)代入反比例函数中即可求出a的值,然后把A的坐标代入y=﹣x+b即可求得b的值;(2)根据直线解析式求得B的坐标,然后根据题意即可求得P的坐标.解:(1)∵直线y=﹣x+b与反比例函数的图象相交于点A(a,3),∴3=﹣,∴a=﹣1.∴A(﹣1,3).把A的坐标代入y=﹣x+b得,3=1+b,∴b=2;(2)直线y=﹣x+2与x轴相交于点B.∴B(2,0),∵点P在x轴上,△AOP的面积是△AOB的面积的,∴OB=2PO,∴P的坐标为(1,0 )或(﹣1,0 ).【题文】某商店准备购进一批电冰箱和空调,每台电冰箱的进价比每台空调的进价多400元,商店用8000元购进电冰箱的数量与用6400元购进空调的数量相等.(1)求每台电冰箱与空调的进价分别是多少?(2)已知电冰箱的销售价为每台2100元,空调的销售价为每台1750元.若商店准备购进这两种家电共100台,其中购进电冰箱x台(33≤x≤40),那么该商店要获得最大利润应如何进货?【答案】(1)每台电冰箱的进价2000元,每台空调的进价1600元.(2)此时应购进电冰箱33台,则购进空调67台.【解析】试题分析:(1)设每台电冰箱的进价m元,每台空调的进价(m﹣400)元,根据:“用8000元购进电冰箱的数量与用6400元购进空调的数量相等”列分式方程求解可得;(2)设购进电冰箱x台,则购进空调(100﹣x)台,根据:总利润=冰箱每台利润×冰箱数量+空调每台利润×空调数量,列出函数解析式,结合x的范围和一次函数的性质可知最值情况.解:(1)设每台电冰箱的进价m元,每台空调的进价(m﹣400)元依题意得,,解得:m=2000,经检验,m=2000是原分式方程的解,∴m=2000;∴每台电冰箱的进价2000元,每台空调的进价1600元.(2)设购进电冰箱x台,则购进空调(100﹣x)台,根据题意得,总利润W=100x+150(100﹣x)=﹣50x+15000,∵﹣50<0,∴W随x的增大而减小,∵33≤x≤40,∴当x=33时,W有最大值,即此时应购进电冰箱33台,则购进空调67台.【题文】如图,在矩形OABC中,点A、C的坐标分别为(10,0),(0,2),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=﹣x+m交线段OA于点E.(1)矩形OABC的周长是;(2)连结OD,当OD=DE时,求m的值;(3)若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1,试探究四边形O1A1B1C1与矩形OABC重叠部分的面积是否会随着E点位置的变化而变化,若不变,求出该重叠部分的面积;若改变,请说明理由.【答案】(1)24;(2)m=4;(3)矩形O1A1B1C1与矩形OABC重叠部分的面积不会随着点E位置的变化而变化,且面积始终为5.【解析】试题分析:(1)根据点A、C的坐标可得出线段OA、OC的长,再根据矩形的周长公式即可得出结论;(2)根据直线DE的解析式可得出点D、E的坐标,再根据等腰三角形的性质可得出OE=2CD,从而得出关于m的一元一次方程,解方程即可得出结论;(3)设O1A1与CB相交于点M,OA与C1B1相交于点N,过点D作DH⊥OA于点H,由此得出矩形O1A1B1C1与矩形OABC的重叠部分的面积即为四边形DNEM的面积.根据对称的性质可得出四边形DNEM为平行四边形,再根据平行线的性质可找出∠MED=∠MDE,从而得出四边形DNEM为菱形,设该菱形的边长为a,通过在RT△DHN中利用勾股定理求出a的值,再根据菱形的面积公式求出S菱形DNEM为定值即可得出结论.解:(1)∵在矩形OABC中,点A、C的坐标分别为(10,0),(0,2),∴AB=OC=2,BC=OA=10,∴C矩形OABC=(OC+OA)×2=24.故答案为:24.(2)令y=﹣x+m中y=0,则﹣x+m=0,解得:x=2m,即点E(2m,0);令y=﹣x+m中y=2,则﹣x+m=2,解得:x=2m﹣4,即点D(2m﹣4,2).∵OD=DE,四边形OABC为矩形,∴OE=2CD,即2m=2×(2m﹣4),解得:m=4.(3)设O1A1与CB相交于点M,OA与C1B1相交于点N,过点D作DH⊥OA于点H,如图所示.矩形O1A1B1C1与矩形OABC的重叠部分的面积即为四边形DNEM的面积.由题意知:DM∥NE,DN∥ME,∴四边形DNEM为平行四边形.根据轴对称知,∠MED=∠NED,∵DM∥NE,∴∠MDE=∠NED,∴∠MED=∠MDE,∴MD=ME,∴平行四边形DNEM为菱形.∵OC=2,∴DH=2,∵直线DE的解析式为y=﹣x+m,∴HE=2DH=4.设菱形DNEM 的边长为a,∴HN=HE﹣NE=OE﹣OH﹣NE=4﹣a,在RT△DHN中,(4﹣a)2+22=a2,解得:a=,∴S菱形DNEM=NE•DH=5,∴矩形O1A1B1C1与矩形OABC重叠部分的面积不会随着点E位置的变化而变化,且面积始终为5.【题文】如图1,函数y=﹣x+4的图象与坐标轴交于A、B两点,点M(2,m)是直线AB上一点,点N与点M关于y轴对称.(1)填空:m=;(2)点P在平面上,若以A、M、N、P为顶点的四边形是平行四边形,直接写出点P的坐标;(3)如图2,反比例函数的图象经过N、E(x1,y1)、F(x2,y2)三点.且x1>x2,点E、F关于原点对称,若点E到直线MN的距离是点F到直线MN的距离的3倍,求E、F两点的坐标.【答案】(1)2.(2)点P的坐标为(0,0)、(8,0)或(﹣4,4).(3)点E(4,﹣1),点F(﹣4,1).【解析】试题分析:(1)由点M的横坐标利用一次函数图象上点的坐标特征可得出关于m的一元一次方程,解方程即可得出结论;(2)连接AN,分别以△AMN的三条边为对角线找平行四边形,由直线AB的解析式可找出点A的坐标,再由M、N关于y轴对称即可得出点N的坐标,根据平行四边形对角线互相平分的性质,结合点A、M、N的坐标即可得出点P的坐标;(3)根据点N的坐标利用反比例函数图象上点的坐标特征即可求出反比例函数的解析式,由点E、F关于原点对称,可得出x1=﹣x2,y1=﹣y2,再根据M、N的坐标求出直线MN的关系式,分点F在直线MN的上方或下方两种情况,结合点E到直线MN的距离是点F到直线MN的距离的3倍,即可得出y1、y2的关系,由此即可得出点E、F的坐标.解:(1)∵点M(2,m)是直线AB:y=﹣x+4上一点,∴m=﹣2+4,解得:m=2.故答案为:2.(2)连接AN,以A、M、N、P为顶点的平行四边形分三种情况,如图1所示.∵直线y=﹣x+4的图象与坐标轴交于A、B两点,∴A(4,0),B(0,4),∵点N与点M关于y轴对称,点M(2,2),∴N(﹣2,2).以A、M、N、P为顶点的平行四边形分三种情况:①当线段AN为对角线时,∵A(4,0)、M(2,2)、N(﹣2,2),∴点P的坐标为(4﹣2﹣2,0+2﹣2),即(0,0);②当线段AM为对角线时,∵A(4,0)、M(2,2)、N(﹣2,2),∴点P的坐标为(4+2﹣(﹣2),0+2﹣2),即(8,0);③当线段MN为对角线时,∵A(4,0)、M(2,2)、N(﹣2,2),∴点P的坐标为(2﹣2﹣4,2+2﹣0),即(﹣4,4).综上可知:若以A、M、N、P为顶点的四边形是平行四边形,点P的坐标为(0,0)、(8,0)或(﹣4,4).(3)∵反比例函数的图象经过N(﹣2,2)、E(x1,y1)、F(x2,y2)三点,∴k=﹣2×2=﹣4,∴反比例函数解析式为.∵点E、F关于原点对称,∴x1=﹣x2,y1=﹣y2,∵x1>x2,∴点E在第四象限,点F在第二象限.直线MN的关系式为y=2,点E到直线MN的距离是点F到直线MN的距离的3倍.①当点F在直线MN的上方时,点E到直线MN的距离是:2﹣y1,点F到直线MN的距离是:y2﹣2,∴3(y2﹣2)=2﹣y1,y1=﹣y2,∴y1=﹣4,y2=4,∴点E(1,﹣4),点F(﹣1,4);②当点F在直线MN的下方时,点E到直线MN的距离是:2﹣y1,点F到直线MN的距离是:2﹣y2,∴3(2﹣y2)=2﹣y1,y1=﹣y2,∴y1=﹣1,y2=1,∴点E(4,﹣1),点F(﹣4,1).。
永春县侨中片区20102011学年度八年级数学上册期末试题
永春县侨中片区2010—2011年度秋季八年级期末检测数 学 试 题题号 一 二 三 四 五 六 附加题 总分 得分一、精心挑选一个正确答案(每小题2分,共12分)1. 9的平方根是 ( ) A . 3; B .±3; C . 9; D .±9. 2.计算23)(a 的结果是 ( ) A. 6a ; B. 5a ; C. 3a ; D. 2a . 3.把多项式652--x x 分解因式,下列结果正确的是 ( ) A .)2)(3(+-x x ; B .)3)(2(--x x ; C .)3)(2(+-x x ; D .)1)(6(+-x x .4.若)(a x +与)(b x +乘积的结果不含x 的一次项,则下面说法正确的是( ) A .0=a ; B .0=b ; C .0=+b a ; D .0=-b a .5.平行四边形ABCD 中,CE ⊥AB 于点E ,∠D=52°, 则∠BCE 的大小是 ( ) A .52° ; B .48° ; C .42° ; D .38° .6.如图,边长为)5(+m 的正方形纸片剪出一个边长为m 的正方形之后,剩余部分又剪 拼成一个矩形(不重叠无缝隙),若拼成的矩形一边长为5,则另一边长是( ) A .52+m ; B .102+m ; C .5+m ; D .10+m .二、请你耐心细算(每空格2分,共26分)1.8的立方根是 .5+mm5?BCDE A2.分解因式:=+x x 32_____________ .3.计算: 323x x ⋅= ; =⨯543)31(______;223)5(x x x ÷-= .4.矩形相邻两条边的长分别为3cm 和2cm ,则它的面积为 cm 2.5.请你写出一个无理数,使它与3的积是有理数 . 6.在□ABCD 中, AB=4,AD=5,则□ABCD 的周长等于 . 7.如图,△ABC 沿BC 方向平移得到△DEF ,CE=2,CF=4,则平移的距离是 . 8.如图,已知△ABC ≌△ADC , ∠BAC =65°,∠ACB =20°,那么∠D = °. 9.下列三种图形:等边三角形、等腰梯形、菱形,既是轴对称图形又是中心对称 图形的是 .10. 已知△ABC 是腰长为1的等腰直角三角形,以△ABC 的斜边AC 为直角边,画第二个 等腰直角三角形ACD ,再以△ACD 的斜边AD 为直角边,画第三个等腰直角三角形ADE ,…, 依此类推,第7个等腰直角三角形的腰长是 .11.观察下列等式19×21=202-1,28×32=302-22,37×43=402-32,…,已知m ,n为实数,仿照上述的表示方法可得:mn = .三、请你细心算(第1题10分,第2题15分,第3题5分,共30分)1.因式分解: 42-ax xy xy 962++2.计算:2332)()(b a a -⋅-)4)(13(++a a)3()36123(3223ab ab b a b a -÷-+3. 先化简,再求值:第8题第7题A DECBF第10题)1)(2()1(3--++x x x x ,其中2=x .四、(每小题6分,共18分)1.如图,正方形网格中的每个小正方形的边长都是1,△ABC 的顶点都在格点上. (1)画出△ABC 向下平移4个单位长度后的△A 1B 1C 1; (2)画出△ABC 绕点A 沿逆时针方向旋转90º后的△AB 2C 2;(3)若点C 1向.左.平移..4个单位长度得到点C 3,点C 3向上平移....x 个单位长度后落在△AB 2C 2的内部..,请直接写出x 的取值范围.2. 已知菱形ABCD 的边长为2cm ,∠ABC =60°,对角线AC 、BD 相交于点O ,求这个菱形的两条对角线AC 与BD 的长.3.如图,在梯形ABCD 中,AD ∥BC ,AD =AB , BC =BD ,∠A =120°,求梯形 其他各内角的度数.B CDOA五、(7分) 如图,一张直角三角形纸片ABC ,已知∠C=90°,AC=8,BC=6.将该纸片折叠, 若折叠后点A 与点B 重合,折痕DE 与边AC 交于点D ,与边AB 交于点E . (1)求△ABC 的面积; (2)求AB 的长; (3)求折痕DE 的长.六.(7分)在△ABC 中,∠ACB =90°,将△ABC 绕点A 顺时针旋转得到△ADE .(1)如图1,∠AED= °;(2)连结CE 交直线AB 于点F ,直线CE 交BD 于点H. ①如图2所示,试说明∠DBA=∠ECA ;②设∠ABC=α,旋转的角度∠CAE =β(0°<β<360°),当α、β满足 什么关系时,△BCF 是等腰三角形.图1DBECAF H图2DBE CA附加题(每小题5分,共10分)友情提示:请同学们做完上面考题后,再认真检查一遍.估计一下你的得分情况.如果你全卷得分低于60分(及格线),则本题的得分将计入全卷总分.但计入后全卷总分最多不超过60分;如果你全卷得分已经达到或超过60分.则本题的得分不计入总分. 1. 因式分解:x x 32.2. 在□ABCD 中,若∠A =120°,求∠B 的度数.。
福建省永县八年级语文下学期期末考试试题(扫描版) 语文版
福建省永春县2012-2013学年八年级下学期期末考试语文试题(扫描版)语文版永春县2013年春季八年级期末考试语文试卷参考答案及评分标准一、积累与运用(35分)二、阅读(55分)(三)(24分)13.(6分)不见母亲,再次离家;发现外衣,抛到河里;母亲回家,道明真相。
14. (5分)示例一:“火炉熄了,屋里很冷。
”渲染了凄冷的气氛,烘托了“我”对母亲抛弃我们的失望和不满,为下文寻找母亲、发现外衣,纽扣脱落等情节作铺垫。
示例二:“炉火生起了,屋里渐渐暖和起来。
”渲染了一种温馨的气氛,烘托了“我”因误解母亲的不安和愧疚,为下文母亲道明真相作铺垫。
三、作文(60分)基本等级50 分内容25分一等(25–22分) 二等(21–18分) 三等(17–15分) 四等(14–0分) 切题,中心突出,内容充实,有真情实感切题,中心明确,内容具体,感情较真实基本切题,中心基本明确,内容尚完整偏离题意,中心不明确或立意不当,内容空泛、凌乱表达22分一等(22–20分) 二等(19–16分) 三等(15–13分) 四等(12–0分) 文体规范,结构完整,语言通顺,字迹清楚文体较规范,结构较完整,语言较通顺,字迹较清楚基本符合文体要求,结构基本完整,语言基本通顺,字迹不够清楚文体不规范,结构混乱,语病多,字迹模糊标题3分拟题正确(3分)未拟题(0分)发展等级10分一等(10–8分)二等(7–4分)三等(3–1分)立意新颖构思精巧语言生动、流畅立意较新颖构思较精巧语言较生动立意正确思路顺畅用语准确附:①错别字每字扣0.5分,重现不计,扣满3分为止。
不满600字的,每50字扣1分。
②发展等级采用分点评分法,如果“立意”、“构思”、“文采”三项中一项突出的,就可得10分。
永春县春期末(八年级)数学答案
永春县2016年春季八年级期末考数学科参考答案一.选择题(单项选择,每小题3分,共21分)1.A ;2.B ;3.C ;4.C ;5.D ;6.B ;7.B.二.填空题(每小题4分,共40分)8.1 ; 9. 2;10.23-≠x ;11.2×10-4; 12. 79; 13.80; 14. 25+=x y ; 15. 乙; 16.(1) 4 (2)菱形; 17. (1)48 (2) 3,6三、解答题(共89分)18.①原式=yx y x 242++ (5分)=2 8分 ②方程两边同乘以)2)(12(++x x ,2分 得10x +5=7x +14 5分解得x =3. 7分 检验: 8分19.∵四边形ABCD 是矩形,∴AB=CD ,AB ∥CD 4分∵AE=CF . ∴EB=FD ,EB ∥FD 6分∴四边形DEBF 是平行四边形. 8分20.甲的最后成绩=85×20%+78×10%+85×30%+73×40%(2分)=79.5 3分 乙的最后成绩=73×20%+80×10%+82×30%+83×40%(4分)=80.4 6分∴乙将会被推荐参加比赛 8分21.在菱形ABCD 中, AB=AD 2分∵BD=AB ∴△ABD 是等边三角形∴∠A=60° 4分 ∴∠C=60° 6分∴∠ABC=∠ADC=120° 8分22.(1)1.5 2分 (2) 0.5 4分(3)由图象可设AB 段图象的函数表达式为kx y = 5分当x =1.5时,y =80;解得k =3160 6分 即y =3160x ,(0≤x ≤1.5) 当x =1时,y =3160 7分 答:行驶1小时时,离出发地3160千米. 8分23.(1)∵直线b x y +-=与反比例函数xy 3-=的图象相交于点A (a ,3) ∴a =-1. 2分 ∴A (﹣1,3). ∴=b 2 4分(2)直线2+-=x y 与x 轴相交于点B .∴B (2,0), 5分∵点P 在x 轴上,△AOP 的面积是△AOB 的面积的21, ∴OB=2PO , 6分 ∴P 的坐标为(1,0 )或(-1,0 ). 8分24(1)设每台电冰箱的进价m 元,每台空调的进价(m -400)元 依题意得,40064008000-=m m ,2分 解得m =2000, 3分经检验,m =2000是原分式方程的解, ∴m =2000; 4分 ∴每台电冰箱的进价2000元,每台空调的进价1600元.(2)设购进电冰箱x 台,则购进空调(100﹣x )台,根据题意得,总利润W=100x +150(100﹣x )=-50x +15000 6分∵-50<0 ∴W 随x 的增大而减小, 7分∵33≤x ≤40 ∴当x =33时,W 有最大值,即此时应购进电冰箱33台,则购进空调67台. 8分25.(1)24 3分(2)∵OC=2 OA=10∴D(2m -4,2),E(2m ,0) 5分∵OD=DE ∴OE=2CD 6分2m =2(2m -4) ∴m =4 7分(3)设O 1A 1与CB 相交于点M ,OA 与C 1B 1相交于点N ,则矩形O 1A 1B 1C 1与矩形OABC 的重叠部分的面积即为四边形DNEM 的面积.由题意知,DM ∥NE ,DN ∥ME , ∴四边形DNEM 为平行四边形 8分 根据轴对称知,∠MED=∠NED∵DM ∥NE ∴∠MDE=∠NED∴∠MED=∠MDE ∴MD=ME ∴平行四边形DNEM 为菱形 9分 过点D 作DH ⊥OA ,垂足为H , ∴DH=2设菱形DNEM 的边长为a ,∴HN=HE-NE=OE-OH-NE=4-a , 10分在RT △DHN 中,2222)4(a a =+- 解得25=a 11分 ∴菱形DNEM 的面积=NE ·DH=5∴矩形O 1A 1B 1C 1与矩形OABC 重叠部分的面积不会随着点E 位置的变化而变化, 面积始终为5. 12分26.(1)m =2 3分(2) P(0,0), P(8,0),P(-4,4) 6分(3)反比例函数xk y =的图象经过N 、E (1x ,1y )、F (2x ,2y )三点 ∵点N 与点M 关于y 轴对称, ∴N (﹣2,2), ∴反比例函数xy 4-= 7分 点E 、F 关于原点对称, ∴1x =-2x ,1y =-2y ∵1x >2x ∴点E 在第四象限,点F 在第二象限. 直线MN 的表达式为2=y点E 到直线MN 的距离是点F 到直线MN 的距离的3倍①当点F 在直线MN 的上方点E 到直线MN 的距离是:2-1y 点F 到直线MN 的距离是: 2y -2 8分 3(2y -2)=2-1y 9分 ∴1y =-4 2y =4∴E(1,-4) F(-1,4) 10分②当点F 在直线MN 的下方点E 到直线MN 的距离是:2-1y 点F 到直线MN 的距离是: 2-2y 11分 3(2-2y )=2-1y 12分 ∴1y =-1 2y =1∴E(4,-1) F(-4,1) 13分。
精品解析:福建永春县第一中学八年级上学期期末考试英语试题
永春一中八年级期末考试英语科试卷I. 听力第一节听句子听五个单句,从所给图片中选出与所听到的句子情景相同或相近的图片.1.A. B. C.2. A. B. C.3. A. B. C.4. A. B. C.5. A. B. C.第二节对话理解听下面七段对话,从题中所给的A、B、C三个选项中选出最佳选项。
每段对话读两遍。
听第一段对话,完成第6小题。
6. What does the man enjoy?A. Riding a bike.B. Climbing mountains.C. Playing football.听第二段对话,完成第7小题。
7. What does Dona think of the dress?A. Ugly.B. Cheap.C. Dear.听第三段对话,完成第8小题。
8. Who is the man in the meeting room now?A. Jane’s math teacher.B. Jane’s headmaster.C. Jane’s uncle.听第四段对话,完成第9小题。
9. How many hours may George need to finish the work?A. One hours.B. Two hours.C. Three hours.听第五段对话,完成第10、11小题。
10. What was Lily doing from 8:00 a.m. to 10:00 a.m. last Saturday?A. She was watering flowers.B. She was planting flowers.C. She was planting trees.11. Kate was _______ at that time.A. calling her friendsB. chatting with her friendsC. watching TV plays听第六段对话,完成第12、13小题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
永春县2011年秋季八年级期末检测
数 学 试 题
一、选择题(每小题3分,共21分)
1. 27的立方根是 ( ) A .3; B .-3; C .±3 ; D .±9.
2. 计算2)(ab 的结果是 ( ) A. 22b a ; B. b a 2 ; C. 2
ab ; D. ab . 3.在△ABC 中,已知AB=3,AC=4,BC=5,则该三角形为( ).
A .锐角三角形
B .直角三角形
C .钝角三角形
D .等腰直角三角形.
4. 把多项式652
+-x x 分解因式,下列结果正确的是 ( ) A .)6)(1(+-x x ; B .)1)(6(+-x x ; C .)3)(2(++x x ; D .)3)(2(--x x .
5. 已知□ABCD 的周长为32,AB=4,则BC 的长为 ( )
A.4 ;
B.12 ;
C.24 ;
D.28.
6.下面的图形中,既是轴对称图形又是中心对称图形的是( )
7. 如图,方格图中小正方形的边长为1.将方格图中阴影
第7题
部分图形剪下来,再把剪下的阴影部分重新剪拼成一个
正方形(不重叠无缝隙),那么所拼成的这个正方形的边长等于( ). A
.2; C
二、填空题(每小题4分,共40分) 8. 9的平方根是 . 9. 计算:2
62x x ÷= . 10. 分解因式:a a +2= . 11. 在□ABCD 中,若∠A=60°,则∠C= °. 12. 比较大小:
(填入“>”或“<”号).
13.已知:△ABC ≌△A ′B ′C ′,∠A=50°,∠B=70°,则∠C ′= °. 14. 若6a b +=,4ab =,则2()a b -= .
15. 边长为13cm 的菱形,一条对角线长是10cm ,则另一条对角线的长是 cm . 16. 如下图,△ADC 是等边三角形,以点A 为中心,把△ABD 顺时针旋转60°得到△ACE.
连结BE ,则△ABE 是什么特殊三角形 .
17. 在△ABC 纸片中,已知AB=AC ,按图中所示方法可折成一个四边形,其中,点A 与点B 重合,点C 与点D 重合.则原△ABC 中的∠B= °.
第16题
E
B
C
D
A
第17题
B
A
B
D
C
C
(草 稿)
三、解答题(共89分) 18.(12分)计算:
)124(22+-x x x
a a a a 2)246(23÷+-
19.(12分)因式分解:
92-a
8822+-m m
20.(8分)先化简,再求值:2)2()2)(2(++-+x x x ,其中2
1=x .
21.(8分)如图,在8×8的正方形网格中,每个小正方形的边长均为1. (1)在网格中画出△ABC 向下平移3个单位得到的△A ′B ′C ′; (2)在网格中画出△ABC 绕点B 顺时针方向旋转90°
得到的△A ″B ″C ″.(不写作法,保留作图痕迹)
22. (8分 ) 已知:菱形ABCD 的两条对角线AC 与BD 相交于点O ,且AC=6,BD=8,
求菱形的周长和面积.
23.(8分)如图,Rt △ABC 中,∠ACB=90°,AC=3,AB=5,将△ABC 沿AB 边所在直线
向右平移3个单位,记平移后的对应三角形为△DEF , (1)求DB 的长;
(2)求此时梯形CAEF 的面积.
O
D
E F C B A
24.(9分)如图,在△ABC 中,∠ACB=90°,∠A=30°,BC=2.将△ABC 绕点C 按顺
时针方向旋转n 度后得到△EDC ,此时点D 在AB 边上,斜边DE 交AC 边于点F. (1)求DC 的长和旋转的角度n ; (2)求图中阴影部分的面积.
25.(12分)如图,长为2,宽为a 的矩形纸片(21<<a ),剪去一个边长等于矩形
宽度的正方形(称为第一次操作);
(1)第一次操作后剩下的矩形长为a ,宽为 ;
(2)再把第一次操作后剩下的矩形剪去一个边长等于此时矩形宽度的正方形(称 为第二次操作);如此反复操作下去. ①求第二次操作后剩下的矩形的面积;
②若在第3次操作后,剩下的图形恰好是正方形,求a 的值.
26.(12分)如图,矩形ABCD 中,AB=8,AD=10. (1)求矩形ABCD 的周长;
(2)E 是CD 上的点,将△ADE 沿折痕AE 折叠,使点D 落在BC 边上点F 处.
2
a
a
第一次操作
第二次操作
①求DE 的长;
② 点P 是线段CB 延长线上的点,连接PA ,若△PAF 是等腰三角形,求PB 的长. (3)M 是AD 上的动点,在DC 上存在点N,使△MDN 沿折痕MN 折叠,点D 落在BC 边
上点T 处, 求线段CT 长度的最大值与最小值之和..
E
F P
D
C
B
A
A
B
C
D
备用图
四、附加题(共10分)
友情提示:请同学们做完上面考题后,再认真检查一遍,估计一下你的得分情况,如果你全卷得分低于90分(及格线),则本题的得分将计入全卷总分,但计入后全卷总分最多不超过90分;如果你全卷总分已经达到或超过90分,则本题的得分不计入全卷总分。
1.(5分)化简:=100 . 2.(5分)因式分解:x x 32
-=_________.
草 稿。
