高中数学解题思维提升专题08数列大题部分训练手册
2019年高考数学二轮复习解题思维提升专题08数列大题部分训练手册

专题08 数列大题部分【训练目标】1、 理解并会运用数列的函数特性;2、 掌握等差数列,等比数列的通项公式,求和公式及性质;3、 掌握根据递推公式求通项公式的方法;4、 掌握常用的求和方法;5、 掌握数列中简单的放缩法证明不等式。
【温馨小提示】高考中一般有一道小题,一道大题,小题侧重于考等差数列与等比数列的性质,熟练的灵活的使用数列的性质会大大减少计算量;大题则侧重于考查根据递推公式求通项公式,求和的方法。
总之,此类题目难度中等,属于必拿分题。
【名校试题荟萃】1、(宁夏长庆高级中学2019届高三上学期第四次月考数学(理)试卷)设数列{}n a 的前n 项和,且123,1,a a a +成等差数列. (1)求数列{}n a 的通项公式;(2)记数列1{}na 的前n 项和n T ,求使得成立的n 的最小值.【答案】(1)2nn a = (2)10(2)由(1)可得112nn a ⎛⎫= ⎪⎝⎭,所以,由,即21000n>,因为,所以10n ≥,于是使得成立的n 的最小值为10.2、(宁夏长庆高级中学2019届高三上学期第四次月考数学(理)试卷)设等差数列{}n a 的公差为d ,点(,)n n a b 在函数()2x f x =的图象上(*n N ∈)。
(1)若12a =-,点87(,4)a b 在函数()f x 的图象上,求数列{}n a 的前n 项和n S ; (2)若11a =,函数()f x 的图象在点22(,)a b 处的切线在x 轴上的截距为12ln 2-,求数列{}n na b 的前n 项和n T .【答案】(1) (2)(2)由函数()f x 的图象在点22(,)a b 处的切线方程为所以切线在x 轴上的截距为21ln 2a -,从而,故22a =从而n a n =,2n n b =,2n nn a nb =所以故。
3、(辽宁省辽河油田第二高级中学2019届高三上学期期中考试数学(文)试题)设n S 为数列{}n a 的前项和,已知10a ≠,,n *∈N .(1)求1a ,2a ;(2)求数列{}n a 的通项公式; (3)求数列{}n na 的前n 项和. 【答案】(1)1,2 (2)12-=n n a (3)(3)由(2)知12-=n n n na ,记其前n 项和为n T ,于是①②①-②得从而.4、(湖南省浏阳一中、株洲二中等湘东六校2019届高三12月联考数学(理)试题)已知数列}{n a 的前n 项 和n S 满足,且11=a 。
专题08规律题方法总结与例题专训(原卷版)

专题08 规律题方法总结与例题专训【知识点睛】常见规律题类型❖周期性循环特点:常以3个或4个数据为一周期,以此循环往复;总数比较大,常和年份结合考察处理方法步骤:1.找出第一周期的几个数,确定周期数2.算出题目中的总数和待求数3.用总数÷周期数=m……n(表示这列数中有m个整周期,最后余n个)4.最后余几,待求数就和每周期的第几个一样;❖周期性递变循环特点:常以2个或3个一周期,后边的每组,周期数不变,但是数据的大小会以相同的关系递增或递减;处理方法:同周期性循环基本一致,最后一步需要加入递变的关系❖递变增减型特点:分以此递增和以此递减,通常是数据之间的直接变化,偶尔借助图形;常和年份结合考察处理方法:熟记单独数据规律,直接应用于考察问题;❖算式类比性特点:常给出几个算式或等式,先算简单的,再从简单的类比到复杂题目的计算处理办法:1.正确计算出前面简单算式的答案2.找出数字间的规律3.将简单数字间的关系推导到字母n的关系中❖常见数字间固定规律识记:1.裂项相消法:将一项拆分成多项,前后保持相等,然后利用某些项相消的原则简化运算;2.错位相减法:适用于两个式子间有相同项的题目,两式相减直接抵消掉中间项,剩余首项、尾项再计算;3.倒序求和发:如:计算1+2+3+......+50,可以设S=1+2+3+......+50,则亦有S=50+49+48+ (1)∴2S=51×50,∴S=51×25=…裂项法公式:kn n k n n k +-=+11)(【类题训练】1.填在下面各正方形中的四个数之间都有一定的规律,按此规律得出a ,b 的值分别为( )A .16,257B .16,91C .10,101D .10,1612.观察下列一组数:,,,,,…,它们是按一定规律排列的,那么这组数的第2022个数是( ) A .B .C .D .3.一只小球落在数轴上的某点P 0,第一次从P 0向左跳1个单位到P 1,第二次从P 1向右跳2个单位到P 2,第三次从P 2向左跳3个单位到P 3,第四次从P 3向右跳4个单位到P 4……若按以上规律跳了100次时,它落在数轴上的点P 100所表示的数恰好是2021,则这只小球的初始位置点P 0所表示的数是( ) A .1971B .1970C .﹣1971D .﹣19704.有一列数a 1,a 2,a 3,…,a n ,从第二个数开始,每一个数都等于1与它前面那个数的倒数的差,若a 1=2,则a 2022为( ) A .B .2C .﹣1D .20225.如图所示,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3,先让圆周上数字0所对应的点与数轴上的数﹣2所对应的点重合,再让圆沿着数轴按顺时针方向滚动,那么数轴上的数﹣2022将与圆周上的哪个数字重合( )A .0B .1C .2D .36.观察图中正方形四个顶点所标的数字规律,可知数2022应标在( )A.第506个正方形的右上角B.第506个正方形的左下角C.第505个正方形的右上角D.第505个正方形的左下角7.等边三角形(三条边都相等的三角形是等边三角形)纸板ABC在数轴上的位置如图所示,点A、B 对应的数分别为2和1,若△ABC绕着顶点逆时针方向在数轴上连续翻转,翻转第1次后,点C所对应的数为0,则翻转2023次后,点C所对应的数是()A.﹣2021B.﹣2022C.﹣2023D.﹣20248.下列图形都是由圆和几个黑色围棋子按一定规律组成,图①中有4个黑色棋子,图②中有7个黑色棋子,图③中有10个黑色棋子,…,依次规律,图中黑色棋子的个数是()A.6067B.6066C.6065D.60649.算筹是古代用来进行计算的工具,它是将几寸长的小竹棍摆在平面上进行运算,算筹的摆放形式有纵横两种形武(如图).当表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间:个位、百位、万位数用纵式表示;十位、千位、十万位数用横式表示;“0”用空位来代替,以此类推例如3306用算筹表示就是,则2022用算筹可表示为()A.B.C.D.10.根据图中数字的排列规律,在第⑦个图中,a﹣b﹣c的值是()A.﹣190B.﹣66C.62D.6411.已知整数m1,m2,m3,m4,…满足下列条件:m1=0,m2=﹣|1+m1|,m3=﹣|2+m2|,m4=﹣|3+m3|,…,以此类推,m2020=.12.在2020个“□”中依次填入一列数字m1,m2,m3…,m2020,使得其中任意四个相邻的“□”中所填的数字之和都等于15.已知m3=2,m6=7,则m1+m2020的值为.27…13.有一数值转换器,原理如图所示,若开始输入x的值是1,可发现第一次输出的结果是4,第二次输出的结果是2,……,请你探索第2021次输出的结果是.14.如图,数字都是按一定规律排列的,其中x的值是.15.观察图,找出规律.,则的值为.16.观察以下等式:第1个等式:×(2﹣)=1+;第2个等式:×(2﹣)=1+;第3个等式:×(2﹣)=1+;第4个等式:×(2﹣)=1+;第2021个等式:.17.请你观察:,,;…+=+=1﹣=;++=++=1﹣=;…以上方法称为“裂项相消求和法”.请类比完成:(1)+++=;(2)++++…+=;(3)计算:的值.18.先阅读下列内容,然后解答问题.因为.所以.请解答:(1)应用上面的方法计算:….(2)类比应用上面的方法计算:….19.观察以下图案和算式,解答问题:(1)1+3+5+7+9=;(2)1+3+5+7+9+…+19=;(3)请猜想1+3+5+7+……+(2n﹣1)=;(4)求和号是数学中常用的符号,用表示,例如,其中n=2是下标,5是上标,3n+1是代数式,表示n取2到5的连续整数,然后分别代入代数式求和,即:=3×2+1+3×3+1+3×4+1+3×5+1=46请求出的值,要求写出计算过程,可利用第(2)(3)题结论.20.从2开始,连续的偶数相加,它们的和的情况如表:加数m的个数和S12=1×222+4=6=2×332+4+6=12=3×442+4+6+8=20=4×552+4+6+8+10=30=5×6(1)按这个规律,当m=6时,和为;(2)从2开始,m个连续偶数相加,它们的和S与m之间的关系,用公式表示出来为:=.(3)应用上述公式计算:①2+4+6+ (200)②202+204+206+ (300)21.观察算式:1×3+1=4=22;2×4+1=9=32;3×5+1=16=42;4×6+1=25=52;……(1)请根据你发现的规律填空:7×9+1=()2;(2)用含n的等式表示上面的规律:;(3)用找到的规律解决下面的问题:计算:22.(1)①观察一列数1,2,3,4,5,…,发现从第二项开始,每一项与前一项之差是一个常数,这个常数是;根据此规律,如果a n(n为正整数)表示这个数列的第n项,那么a18=,a n =;②如果欲求1+2+3+4+…+n的值,可令S=1+2+3+4+…+n❶,将①式右边顺序倒置,得S =n+…+4+3+2+1❷,由❷式+❶式,得2S=;∴S=;由结论求1+2+3+4+…+55=;(2)①观察一列数2,4,8,16,32,…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是;根据此规律,如果a n(n为正整数)表示这个数列的第n项,那么a18=,a n=;②为了求1+3+32+33+…+32018的值,可令M=1+3+32+33+…+32018❶,则3M=3+32+33+…+32019❷,由❷式﹣❶式,得3M﹣M=32019﹣1,∴M=,即1+3+32+33+...+32018=.仿照以上推理,计算1+5+52+53+ (551)。
专题08 数列-2022年高考真题和模拟题数学分类汇编(解析版)

专题08 数列1.【2022年全国乙卷】已知等比数列{a n }的前3项和为168,a 2−a 5=42,则a 6=( ) A .14 B .12 C .6 D .3【答案】D 【解析】 【分析】设等比数列{a n }的公比为q,q ≠0,易得q ≠1,根据题意求出首项与公比,再根据等比数列的通项即可得解. 【详解】解:设等比数列{a n }的公比为q,q ≠0, 若q =1,则a 2−a 5=0,与题意矛盾, 所以q ≠1,则{a 1+a 2+a 3=a 1(1−q 3)1−q =168a 2−a 5=a 1q −a 1q 4=42,解得{a 1=96q =12 , 所以a 6=a 1q 5=3. 故选:D .2.【2022年全国乙卷】嫦娥二号卫星在完成探月任务后,继续进行深空探测,成为我国第一颗环绕太阳飞行的人造行星,为研究嫦娥二号绕日周期与地球绕日周期的比值,用到数列{b n }:b 1=1+1α1,b 2=1+1α1+1α2,b 3=1+1α1+1α2+1α3,…,依此类推,其中αk ∈N ∗(k =1,2,⋯).则( ) A .b 1<b 5 B .b 3<b 8C .b 6<b 2D .b 4<b 7【答案】D 【解析】 【分析】根据αk ∈N ∗(k =1,2,…),再利用数列{b n }与αk 的关系判断{b n }中各项的大小,即可求解. 【详解】解:因为αk ∈N ∗(k =1,2,⋯),所以α1<α1+1α2,1α1>1α1+1α2,得到b 1>b 2,同理α1+1α2>α1+1α2+1α3,可得b 2<b 3,b 1>b 3又因为1α2>1α2+1α3+1α4, α1+1α2+1α3<α1+1α2+1α3+1α4,故b 2<b 4,b 3>b 4;以此类推,可得b 1>b 3>b 5>b 7>⋯,b 7>b 8,故A 错误; b 1>b 7>b 8,故B 错误;1α2>1α2+1α3+⋯1α6,得b 2<b 6,故C 错误;α1+1α2+1α3+1α4>α1+1α2+⋯1α6+1α7,得b 4<b 7,故D 正确.故选:D.3.【2022年新高考2卷】中国的古建筑不仅是挡风遮雨的住处,更是美学和哲学的体现.如图是某古建筑物的剖面图,DD 1,CC 1,BB 1,AA 1是举, OD 1,DC 1,CB 1,BA 1是相等的步,相邻桁的举步之比分别为DD 1OD 1=0.5,CC 1DC 1=k 1,BB 1CB 1=k 2,AA1BA 1=k 3,若k 1,k 2,k 3是公差为0.1的等差数列,且直线OA 的斜率为0.725,则k 3=( )A .0.75B .0.8C .0.85D .0.9【答案】D 【解析】 【分析】设OD 1=DC 1=CB 1=BA 1=1,则可得关于k 3的方程,求出其解后可得正确的选项. 【详解】设OD 1=DC 1=CB 1=BA 1=1,则CC 1=k 1,BB 1=k 2,AA 1=k 3,依题意,有k3−0.2=k1,k3−0.1=k2,且DD1+CC1+BB1+AA1OD1+DC1+CB1+BA1=0.725,所以0.5+3k3−0.34=0.725,故k3=0.9,故选:D4.【2022年北京】设{a n}是公差不为0的无穷等差数列,则“{a n}为递增数列”是“存在正整数N0,当n>N0时,a n>0”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【答案】C【解析】【分析】设等差数列{a n}的公差为d,则d≠0,利用等差数列的通项公式结合充分条件、必要条件的定义判断可得出结论.【详解】设等差数列{a n}的公差为d,则d≠0,记[x]为不超过x的最大整数.若{a n}为单调递增数列,则d>0,若a1≥0,则当n≥2时,a n>a1≥0;若a1<0,则a n=a1+(n−1)d,由a n=a1+(n−1)d>0可得n>1−a1d ,取N0=[1−a1d]+1,则当n>N0时,a n>0,所以,“{a n}是递增数列”⇒“存在正整数N0,当n>N0时,a n>0”;若存在正整数N0,当n>N0时,a n>0,取k∈N∗且k>N0,a k>0,假设d<0,令a n=a k+(n−k)d<0可得n>k−a kd ,且k−a kd>k,当n>[k−a kd]+1时,a n<0,与题设矛盾,假设不成立,则d>0,即数列{a n}是递增数列.所以,“{a n}是递增数列”⇐“存在正整数N0,当n>N0时,a n>0”.所以,“{a n}是递增数列”是“存在正整数N0,当n>N0时,a n>0”的充分必要条件.故选:C.5.【2022年浙江】已知数列{a n}满足a1=1,a n+1=a n−13a n2(n∈N∗),则()A.2<100a100<52B.52<100a100<3C.3<100a100<72D.72<100a100<4【答案】B【解析】【分析】先通过递推关系式确定{a n}除去a1,其他项都在(0,1)范围内,再利用递推公式变形得到1 a n+1−1a n=13−a n>13,累加可求出1a n>13(n+2),得出100a100<3,再利用1a n+1−1a n=13−a n<1 3−3n+2=13(1+1n+1),累加可求出1a n−1<13(n−1)+13(12+13+⋯+1n),再次放缩可得出100a100>52.【详解】∵a1=1,易得a2=23∈(0,1),依次类推可得a n∈(0,1)由题意,a n+1=a n(1−13a n),即1a n+1=3a n(3−a n)=1a n+13−a n,∴1a n+1−1a n=13−a n>13,即1a2−1a1>13,1a3−1a2>13,1a4−1a3>13,…,1a n−1a n−1>13,(n≥2),累加可得1a n −1>13(n−1),即1a n>13(n+2),(n≥2),∴a n<3n+2,(n≥2),即a100<134,100a100<10034<3,又1a n+1−1a n=13−a n<13−3n+2=13(1+1n+1),(n≥2),∴1a2−1a1=13(1+12),1a3−1a2<13(1+13),1a4−1a3<13(1+14),…,1a n−1a n−1<13(1+1n),(n≥3),累加可得1a n −1<13(n−1)+13(12+13+⋯+1n),(n≥3),∴1a100−1<33+13(12+13+⋯+199)<33+13(12×4+16×94)<39,即1a100<40,∴a100>140,即100a100>52;综上:52<100a100<3.故选:B.【点睛】关键点点睛:解决本题的关键是利用递推关系进行合理变形放缩.6.【2022年全国乙卷】记S n为等差数列{a n}的前n项和.若2S3=3S2+6,则公差d=_______.【答案】2【解析】【分析】转化条件为2(a1+2d)=2a1+d+6,即可得解.【详解】由2S3=3S2+6可得2(a1+a2+a3)=3(a1+a2)+6,化简得2a3=a1+a2+6,即2(a1+2d)=2a1+d+6,解得d=2.故答案为:2.7.【2022年北京】己知数列{a n}各项均为正数,其前n项和S n满足a n⋅S n=9(n=1,2,⋯).给出下列四个结论:①{a n}的第2项小于3;②{a n}为等比数列;③{a n}为递减数列;④{a n}中存在小于1100的项.其中所有正确结论的序号是__________.【答案】①③④【解析】【分析】推导出a n=9an −9a n−1,求出a1、a2的值,可判断①;利用反证法可判断②④;利用数列单调性的定义可判断③.【详解】由题意可知,∀n∈N∗,a n>0,当n=1时,a12=9,可得a1=3;当n≥2时,由S n=9an 可得S n−1=9an−1,两式作差可得a n=9an−9a n−1,所以,9a n−1=9a n−a n,则9a2−a2=3,整理可得a22+3a2−9=0,因为a2>0,解得a2=3√5−32<3,①对;假设数列{a n}为等比数列,设其公比为q,则a22=a1a3,即(9S2)2=81S1S3,所以,S22=S1S3,可得a12(1+q)2=a12(1+q+q2),解得q=0,不合乎题意,故数列{a n}不是等比数列,②错;当n ≥2时,a n =9a n−9an−1=9(a n−1−a n )a n a n−1>0,可得a n <a n−1,所以,数列{a n }为递减数列,③对;假设对任意的n ∈N ∗,a n ≥1100,则S 100000≥100000×1100=1000, 所以,a 100000=9S100000≤91000<1100,与假设矛盾,假设不成立,④对.故答案为:①③④. 【点睛】关键点点睛:本题在推断②④的正误时,利用正面推理较为复杂时,可采用反证法来进行推导.8.【2022年全国甲卷】记S n 为数列{a n }的前n 项和.已知2S n n+n =2a n +1.(1)证明:{a n }是等差数列;(2)若a 4,a 7,a 9成等比数列,求S n 的最小值. 【答案】(1)证明见解析; (2)−78. 【解析】 【分析】(1)依题意可得2S n +n 2=2na n +n ,根据a n ={S 1,n =1S n −S n−1,n ≥2 ,作差即可得到a n −a n−1=1,从而得证;(2)由(1)及等比中项的性质求出a 1,即可得到{a n }的通项公式与前n 项和,再根据二次函数的性质计算可得. (1) 解:因为2S n n+n =2a n +1,即2S n +n 2=2na n +n ①,当n ≥2时,2S n−1+(n −1)2=2(n −1)a n−1+(n −1)②,①−②得,2S n +n 2−2S n−1−(n −1)2=2na n +n −2(n −1)a n−1−(n −1), 即2a n +2n −1=2na n −2(n −1)a n−1+1,即2(n −1)a n −2(n −1)a n−1=2(n −1),所以a n −a n−1=1,n ≥2且n ∈N*, 所以{a n }是以1为公差的等差数列. (2)解:由(1)可得a 4=a 1+3,a 7=a 1+6,a 9=a 1+8,又a 4,a 7,a 9成等比数列,所以a 72=a 4⋅a 9,即(a 1+6)2=(a 1+3)⋅(a 1+8),解得a 1=−12, 所以a n =n −13,所以S n =−12n +n(n−1)2=12n 2−252n =12(n −252)2−6258,所以,当n =12或n =13时(S n )min =−78.9.【2022年新高考1卷】记S n 为数列{a n }的前n 项和,已知a 1=1,{S na n}是公差为13的等差数列.(1)求{a n }的通项公式; (2)证明:1a 1+1a 2+⋯+1a n<2.【答案】(1)a n =n (n+1)2(2)见解析 【解析】 【分析】(1)利用等差数列的通项公式求得S na n=1+13(n −1)=n+23,得到S n =(n+2)a n3,利用和与项的关系得到当n ≥2时,a n =S n −S n−1=(n+2)a n3−(n+1)a n−13,进而得:a nan−1=n+1n−1,利用累乘法求得a n =n (n+1)2,检验对于n =1也成立,得到{a n }的通项公式a n =n (n+1)2;(2)由(1)的结论,利用裂项求和法得到1a 1+1a 2+⋯+1a n=2(1−1n+1),进而证得.(1)∵a 1=1,∴S 1=a 1=1,∴S1a 1=1,又∵{S na n}是公差为13的等差数列,∴S na n=1+13(n −1)=n+23,∴S n =(n+2)a n3,∴当n ≥2时,S n−1=(n+1)a n−13,∴a n =S n −S n−1=(n+2)a n3−(n+1)a n−13,整理得:(n −1)a n =(n +1)a n−1, 即a nan−1=n+1n−1,∴a n =a 1×a2a 1×a3a 2×…×an−1a n−2×ana n−1=1×32×43×…×nn−2×n+1n−1=n(n+1)2,显然对于n=1也成立,∴{a n}的通项公式a n=n(n+1)2;(2)1 a n =2n(n+1)=2(1n−1n+1),∴1a1+1a2+⋯+1a n=2[(1−12)+(12−13)+⋯(1n−1n+1)]=2(1−1n+1)<210.【2022年新高考2卷】已知{a n}为等差数列,{b n}是公比为2的等比数列,且a2−b2= a3−b3=b4−a4.(1)证明:a1=b1;(2)求集合{k|b k=a m+a1,1≤m≤500}中元素个数.【答案】(1)证明见解析;(2)9.【解析】【分析】(1)设数列{a n}的公差为d,根据题意列出方程组即可证出;(2)根据题意化简可得m=2k−2,即可解出.(1)设数列{a n}的公差为d,所以,{a1+d−2b1=a1+2d−4b1a1+d−2b1=8b1−(a1+3d),即可解得,b1=a1=d2,所以原命题得证.(2)由(1)知,b1=a1=d2,所以b k=a m+a1⇔b1×2k−1=a1+(m−1)d+a1,即2k−1=2m,亦即m=2k−2∈[1,500],解得2≤k≤10,所以满足等式的解k=2,3,4,⋯,10,故集合{k |b k=a m+a1,1≤m≤500}中的元素个数为10−2+1=9.11.【2022年北京】已知Q:a1,a2,⋯,a k为有穷整数数列.给定正整数m,若对任意的n∈{1, 2,⋯,m},在Q中存在a i,a i+1,a i+2,⋯,a i+j(j≥0),使得a i+a i+1+a i+2+⋯+a i+j=n,则称Q为m−连续可表数列.(1)判断Q:2,1,4是否为5−连续可表数列?是否为6−连续可表数列?说明理由;(2)若Q:a1,a2,⋯,a k为8−连续可表数列,求证:k的最小值为4;(3)若Q:a1,a2,⋯,a k为20−连续可表数列,且a1+a2+⋯+a k<20,求证:k≥7.【答案】(1)是5−连续可表数列;不是6−连续可表数列.(2)证明见解析.(3)证明见解析.【解析】【分析】(1)直接利用定义验证即可;(2)先考虑k≤3不符合,再列举一个k=4合题即可;(3)k≤5时,根据和的个数易得显然不行,再讨论k=6时,由a1+a2+⋯+a6<20可知里面必然有负数,再确定负数只能是−1,然后分类讨论验证不行即可.(1)a2=1,a1=2,a1+a2=3,a3=4,a2+a3=5,所以Q是5−连续可表数列;易知,不存在i,j使得a i+a i+1+⋯+a i+j=6,所以Q不是6−连续可表数列.(2)若k≤3,设为Q:a,b,c,则至多a+b,b+c,a+b+c,a,b,c,6个数字,没有8个,矛盾;当k=4时,数列Q:1,4,1,2,满足a1=1,a4=2,a3+a4=3,a2=4,a1+a2=5,a1+a2+ a3=6,a2+a3+a4=7,a1+a2+a3+a4=8,∴k min=4.(3)Q:a1,a2,⋯,a k,若i=j最多有k种,若i≠j,最多有C k2种,所以最多有k+C k2=k(k+1)种,2=15个数,矛盾,若k≤5,则a1,a2,…,a k至多可表5(5+1)2=21个数,从而若k<7,则k=6,a,b,c,d,e,f至多可表6(6+1)2而a+b+c+d+e+f<20,所以其中有负的,从而a,b,c,d,e,f可表1~20及那个负数(恰21个),这表明a~f中仅一个负的,没有0,且这个负的在a~f中绝对值最小,同时a~f中没有两数相同,设那个负数为−m(m≥1),则所有数之和≥m+1+m+2+⋯+m+5−m=4m+15,4m+15≤19⇒m=1,∴{a,b,c,d,e,f}={−1,2,3,4,5,6},再考虑排序,排序中不能有和相同,否则不足20个,∵1=−1+2(仅一种方式),∴−1与2相邻,若−1不在两端,则"x , −1 , 2 , __,__,__"形式,若x=6,则5=6+(−1)(有2种结果相同,方式矛盾),∴x≠6,同理x≠5,4,3,故−1在一端,不妨为"−1 ,2, A, B, C, D"形式,若A=3,则5=2+3(有2种结果相同,矛盾),A=4同理不行,A=5,则6=−1+2+5(有2种结果相同,矛盾),从而A=6,由于7=−1+2+6,由表法唯一知3,4不相邻,、故只能−1,2,6,3,5,4,①或−1,2,6,4,5,3,②这2种情形,对①:9=6+3=5+4,矛盾,对②:8=2+6=5+3,也矛盾,综上k≠6∴k≥7.【点睛】关键点睛,先理解题意,是否为m−可表数列核心就是是否存在连续的几项(可以是一项)之和能表示从1到m中间的任意一个值.本题第二问k≤3时,通过和值可能个数否定k≤3;第三问先通过和值的可能个数否定k≤5,再验证k=6时,数列中的几项如果符合必然是{−1,2,3,4,5,6}的一个排序,可验证这组数不合题.12.【2022年浙江】已知等差数列{a n}的首项a1=−1,公差d>1.记{a n}的前n项和为S n(n ∈N∗).(1)若S4−2a2a3+6=0,求S n;(2)若对于每个n∈N∗,存在实数c n,使a n+c n,a n+1+4c n,a n+2+15c n成等比数列,求d的取值范围.(n∈N∗)【答案】(1)S n=3n2−5n2(2)1<d≤2【解析】【分析】(1)利用等差数列通项公式及前n项和公式化简条件,求出d,再求S n;(2)由等比数列定义列方程,结合一元二次方程有解的条件求d的范围.(1)因为S4−2a2a3+6=0,a1=−1,所以−4+6d−2(−1+d)(−1+2d)+6=0,所以d 2−3d =0,又d >1, 所以d =3, 所以a n =3n −4, 所以S n =(a 1+a n )n2=3n 2−5n2,(2)因为a n +c n ,a n+1+4c n ,a n+2+15c n 成等比数列, 所以(a n+1+4c n )2=(a n +c n )(a n+2+15c n ),(nd −1+4c n )2=(−1+nd −d +c n )(−1+nd +d +15c n ),c n 2+(14d −8nd +8)c n +d 2=0,由已知方程c n 2+(14d −8nd +8)c n +d 2=0的判别式大于等于0,所以Δ=(14d −8nd +8)2−4d 2≥0,所以(16d −8nd +8)(12d −8nd +8)≥0对于任意的n ∈N ∗恒成立, 所以[(n −2)d −1][(2n −3)d −2]≥0对于任意的n ∈N ∗恒成立, 当n =1时,[(n −2)d −1][(2n −3)d −2]=(d +1)(d +2)≥0, 当n =2时,由(2d −2d −1)(4d −3d −2)≥0,可得d ≤2 当n ≥3时,[(n −2)d −1][(2n −3)d −2]>(n −3)(2n −5)≥0, 又d >1 所以1<d ≤21.(2022·河南·通许县第一高级中学模拟预测(文))在等差数列{}n a 中,35a =,1511109a a +=,则15a a ⋅=( )A .92B .9C .10D .12【答案】B 【解析】 【分析】将已知等式变形,由等差数列下标和计算即可得到结果. 【详解】 由1511109a a +=得:153********a a a a a a a +==,315995aa a ∴⋅==.故选:B.2.(2022·福建省德化第一中学模拟预测)设等差数列{}n a 的前n 项和为n S ,若728S =,则237a a a ++的值为( )A .8B .10C .12D .14【答案】C 【解析】 【分析】根据等差数列的求和公式,求得44a =,结合等差数列的性质,化简得到27433a a a a =++,即可求解. 【详解】因为728S =,由等差数列的性质和求和公式得17747()7282a a S a +===,即44a =, 则112374393(3)312a d a a a a a d =+=+==++. 故选:C.3.(2022·北京·北大附中三模)已知数列{}n a 满足2123n a a a a n =,其中1,2,3,n =,则数列{}n a ( ) A .有最大项,有最小项 B .有最大项,无最小项 C .无最大项,有最小项 D .无最大项,无最小项【答案】A 【解析】 【分析】求得数列{}n a 的通项公式,再分析数列的单调性即可 【详解】依题意,因为2123n a a a a n =,其中1,2,3,n =,当1n =时,2111a ==,当2n ≥时,21231(1)n a a a a n -=-,2123n a a a a n =,两式相除有22211,2(1)1n n a n n n ⎛⎫=+≥ ⎪--⎝⎭=,易得n a 随着n 的增大而减小,故24n a a ≤=,且11n a a >=,故最小项为11a =,最大项为24a = 故选:A4.(2022·辽宁实验中学模拟预测)已知数列{}()*N n a n ∈是首项为1的正项等差数列,公差不为0,若1a 、数列{}2n a 的第2项、数列{}2n a 的第5项恰好构成等比数列,则数列{}n a 的通项公式为( ) A .21n a n =- B .21n a n =+ C .1n a n =- D .1n a n =+【答案】A 【解析】 【分析】根据题意设()11n a n d =+-,所以()2121n d a n =+-,()2211n d a n =+-,所以1,13d +,124d +构成等比数列,即()()2131124d d +=⨯+,求出d 即可求解. 【详解】设等差数列{}n a 的公差为()0d d >,所以()11n a n d =+-,所以()2121n d a n =+-, ()2211n d a n =+-,又1a 、数列{}2n a 的第2项、数列{}2n a 的第5项恰好构成等比数列,即1,13d +,124d +构成等比数列,所以()()2131124d d +=⨯+, 解得2d =,0d =(舍去),所以21n a n =-. 故选:A.5.(2022·四川·绵阳中学实验学校模拟预测(文))已知数列{}n a 的前n 项和为n S ,且11a =,0n a ≠,11n n n a a S λ+=-,若存在实数λ使{}n a 是等差数列,则{}n a 的公差为( )A .1B .2C .2λD .λ【答案】B 【解析】 【分析】利用1(2)n n n S S a n --=≥得{}n a 的递推关系,从而求得λ与公差d 的关系,再由21a a d -=求得d .【详解】 设公差为d ,因为11n n n a a S λ+=-,所以2n ≥时,111n n n a a S λ--=-, 两式相减得:111()()n n n n n n a a a S S a λλ+---=-=, 因为0n a ≠,所以112n n a a d λ+--==,由1211a a S λ=-121da =-得221a d =-.从而21211a a d d -=--=,2d =, 故选:B .6.(2022·湖南·邵阳市第二中学模拟预测)已知正项等比数列{}n a 满足3212a a a =+,若存在m a 、n a ,使得2116m n a a a ⋅=,则14m n+的最小值为( ) A .83B .16C .114 D .32【答案】D 【解析】 【分析】设等比数列{}n a 的公比为q ,则0q >,根据已知条件求出q 的值,由已知条件可得出6m n +=,将代数式14m n +与()16m n +相乘,利用基本不等式可求得14m n+的最小值. 【详解】设等比数列{}n a 的公比为q ,则0q >,由3212a a a =+可得220q q --=,解得2q,因为2116m n a a a ⋅=,则2112112216m n a a --⋅⋅=,24m n ∴+-=,可得6m n +=,由已知m 、N n *∈,所以,()1411414566m n m n m n m n n m ⎛⎫⎛⎫+=++=++ ⎪ ⎪⎝⎭⎝⎭13562⎛≥+= ⎝, 当且仅当24n m ==时,等号成立, 因此,14m n +的最小值为32. 故选:D.7.(2022·浙江·三模)设数列{}n a 满足()21192,24n n n a a a n N a *+=-+∈=,记数列221n a ⎧⎫⎨⎬-⎩⎭的前n 项的和为n S ,则( ) A .10127a < B .存在k *∈N ,使1k k a a += C .1012S < D .数列{}n a 不具有单调性【答案】C 【解析】 【分析】 根据题意求得54n a ≥,进而得到132n a +-与32n a -同号,结合作差法比较法,可判定B 、D 错误;由()()11214n n n n a a a a +-=--+,得到114n n a a +-≥,利用叠加法,可判定A 错误;化简得到1111133222n n n a a a +=----,利用裂项法求和,可判定C 正确. 【详解】由于()211551,244n n a a a +=-+≥=,则54n a ≥,又由21333122422n n n n n a a a a a +⎛⎫⎛⎫-=-+=-- ⎪⎪⎝⎭⎝⎭,则132n a +-与32n a -同号. 又由12a =,则32n a >,可得221933042n n nn n a a a a a +⎛⎫-=-+=-> ⎪⎝⎭, 所以数列{}n a 单调递增,故B 、D 错误; 又因为()()11214n n n n a a a a +-=--+, 由数列{}n a 单调递增,且12a =,所以20,10n n a a ->->,所以114n n a a +-≥, 累加得1011100254a a -≥=,所以10127a ≥,故A 错误; 由21924n nn a a a +=-+可得1111133222n n n a a a +=----, 因为12n a a >=,所以101110211112333222S a a a =-<=---,故C 正确.故选:C .8.(2022·吉林·东北师大附中模拟预测(理))数列{}n a 为等差数列,前n 项的和为n S ,若10110a <,101110120a a +>,则当0n S <时,n 的最大值为( )A .1011B .1012C .2021D .2022【答案】C 【解析】 【分析】分析数列{}n a 的单调性,计算2021S 、2022S ,即可得出结论. 【详解】因为10110a <,101110120a a +>,则10120a >,故数列{}n a 为递增数列, 因为()12021202110112021202102a a S a +==<,()()120222022101110122022101102a a S a a +==+>,且当1012n ≥时,10120n a a ≥>,所以,当2022n ≥时,20220n S S ≥>, 所以,满足当0n S <时,n 的最大值为2021. 故选:C.9.(2022·辽宁·渤海大学附属高级中学模拟预测)已知等差数列{}n a 的前n 项和为n S ,且满足()552sin 2350a a +--=,()201820182sin 2370a a +--=,则下列结论正确的是( ) A .20222022S =,且52018a a > B .20222022S =-,且52018a a < C .20224044S =-,且52018a a > D .20224044S =,且52018a a <【答案】C 【解析】 【分析】根据题意构造函数()2sin 3f x x x =-,确定函数的奇偶性及单调性,进而根据()()520182,2f a f a ++的关系即可确定答案.【详解】设函数()2sin 3f x x x =-,则()f x 为奇函数,且()2cos 30f x x '=-<,所以()f x 在R 上递减,由已知可得()()552sin 2321a a +-+=-,()()201820182sin 2321a a +-+=,有()521f a +=-,()201821f a +=,所以()()5201822f a f a +<+,且()()5201822f a f a +=-+,所以520185201822a a a a +>+⇒>,且()5201822a a +=-+,所以520184a a +=-,120222022520182022()1011()40442a a S a a +==+=-.故选:C.10.(2022·全国·模拟预测)已知数列{}n a 满足对任意的*n ∈N ,总存在*m ∈N ,使得n m S a =,则n a 可能等于( ) A .2022n B .2022n C .22022n D .2022n【答案】B 【解析】 【分析】A 选项,利用等比数列求和公式列出方程,令n =2时,得到120222023m -=,m 不存在,A 错误;B 选项,利用等差数列求和公式进行求解得到方程()101112022n n m +=,取()12n n m +=即可,C 选项,利用平方和公式得到()()21216n n n m ++=,当n =2时,25m =,m 不存在;D 选项,当n =2时,1112m+=,m 不存在. 【详解】对于选项A :当2022nn a =时,则{}n a 是等比数列,因为n m S a =所以()20222022120222021n m -=,当n =2时,120222023m -=,m 不存在,A 错误;对于选项B :当2022n a n =时,{}n a 是等差数列,因为n m S a =,则()()120221*********n n n S n n m +=⨯=+=,取()12n n m +=即可,B 正确; 对于选项C :当22022n a n =时,n m S a =,则()()()2222121202212202220226n n n n S n m ++=⨯++⋅⋅⋅+=⨯=,当n =2时,25m =,m 不存在,C 错误; 对于选项D :当2022n a n =时,n m S a =,则11120222022123n m ⎛⎫+++⋅⋅⋅+= ⎪⎝⎭,当n =2时,1112m+=,m 不存在,D 错误. 故选:B .11.(2022·江苏·南京外国语学校模拟预测)已知数列{}n a 各项都不为0,121,3a a ==且满足141n n n a a S +=-,(1)求{}n a 的通项公式; (2)若114n n n a b a -=-,{}n b 的前n 项和为n T ,求n T 取得最小值时的n 的值. 【答案】(1)21n a n =-; (2)7n =. 【解析】 【分析】(1)由141n n n a a S +=-得2n ≥时,1141n n n a a S --=-, ①-②得114n n a a +--=,分奇偶项即可求出n a (2)由114n n n a b a -=-得22215n n b n -=-,当7n ≤时,0n b ≤,当7n >时,0n b > 当7n =时,n T 取得最小值 (1)141n n n a a S +=-①当2n ≥时,1141n n n a a S --=-② ①-②114n n n n n a a a a a +-⇒-=0n a ≠114n n a a +-∴-={}n a ∴的奇数项和偶数项各自成等差数列且121,3a a ==()()21141432211,21(n n a n n n a n n -∴=+-=-=--∴=-为奇数),()234141221,21n n a n n n a n =+-=-=⋅-∴=-(n 为偶数),21n a n ∴=-(2)22131215215n n b n n -==+--,当7n ≤时,0n b ≤, 当7n >时,0n b >∴当7n =时,n T 取得最小值12.(2022·福建·厦门双十中学模拟预测)等差数列{}n a 的前n 项和为n S ,已知19a =,2a 为整数,且5n S S ≤. (1)求{}n a 的通项公式; (2)设11n n n b a a +=,求数列{}n b 的前n 项和n T . 【答案】(1)112n a n =- (2)()992n nT n =-【解析】 【分析】(1)根据题意得公差d 为整数,且50a ≥,60a ≤,分析求出d 即可;(2)111292112n b n n ⎛⎫=- ⎪--⎝⎭,再利用裂项相消法求和即可.(1)由19a =,2a 为整数知,等差数列{}n a 的公差d 为整数. 又5n S S ≤,故50a ≥,60a ≤. 于是940d +≥,950d +≤,解得9945d -≤≤-, 因此2d =-,故数列{}n a 的通项公式为112n a n =-. (2)()()111111292292112n b n n n n ⎛⎫==- ⎪----⎝⎭,于是1211111112795792112n n T b b b n n ⎡⎤⎛⎫⎛⎫⎛⎫=++⋅⋅⋅+=-+-+⋅⋅⋅+- ⎪ ⎪ ⎪⎢⎥--⎝⎭⎝⎭⎝⎭⎣⎦()1112929992n n n ⎛⎫=-= ⎪--⎝⎭. 13.(2022·宁夏·银川一中模拟预测(理))已知数列{}n a 是等差数列,{}n b 是等比数列,且22b =,34b =,11a b =,851a b +=.(1)求数列{}n a 、{}n b 的通项公式; (2)设11n n n a c b ++=,数列{}n c 的前n 项和为n S ,若不等式12n n nS λ-<+对任意的*n ∈恒成立,求实数λ的取值范围.【答案】(1)21n a n =-,12n n b -=;(2)(),2-∞. 【解析】 【分析】(1)利用等差数列()11n a a n d +-=,等比数列11n n b b q -=代入计算;(2)利用错位相减法可得1242n n n S -+=-,令2142nn c -=-,由{}n c 为递增数列,结合恒成立思想可得答案. (1)解:因为数列{}n b 是等比数列,则可得2123124b b q b b q ==⎧⎨==⎩,解得112b q =⎧⎨=⎩, 所以12n n b -=.因为数列{}n a 是等差数列,且111a b ==,8117116a a d +=++=,则公差2d =, 所以()12121n a n n =+-=-.故21n a n =-,12n n b -=;(2)解:由(1)得:1112n n n n a nc b -++==, 数列{}n c 的前n 项和为121231222n n nS -=+++⋅⋅⋅+①所以22111231222222n n n n n S --=+++⋅⋅⋅++②由①-②得:121111112121222222222n n n n n n n n n S -+⎛⎫=+++⋅⋅⋅+-=--=- ⎪⎝⎭,所以1242n n n S -+=-.不等式12n n n S λ-<+恒成立,化为不等式2142n λ-<-恒成立,令2142n n c -=-且{}n c 为递增数列,即转化为()min n c λ<当1n =时,()12min 1422n c -=-=,所以2λ<. 综上可得:实数λ的取值范围是(),2-∞.14.(2022·湖北·襄阳四中模拟预测)已知等差数列{}n a 满足11a =,且前四项和为28,数列{}n b 的前n 项和n S 满足()233n n S b R λλ=-∈.(1)求数列{}n a 的通项公式,并判断{}n b 是否为等比数列;(2)对于集合A ,B ,定义集合{}A B x x A x B -=∈∉且.若1λ=,设数列{}n a 和{}n b 中的所有项分别构成集合A ,B ,将集合A B -的所有元素按从小到大依次排列构成一个新数列{}n c ,求数列{}n c 的前30项和30T .【答案】(1)43n a n =-,判断答案见解析 (2)1926 【解析】 【分析】(1)根据等数列的前n 项和公式和通项公式可求出{}n a 的通项公式,根据等比数列的定义可判断{}n b 是否为等比数列;(2)结合等差数列的前n 项和,等差数列与等比数列的通项公式可求出结果. (1)∵{}n a 是等差数列,11a =,且前四项和为28, ∵43441282S d ⨯=⨯+⨯=,解得4d =∵()14143n a n n =+-=-.∵233n nn S b λ=-,∵当2n ≥时,11233n n S b λ--=-,两式相减得()12332n n n b b b n -=-≥, 即()132n n b b n -=≥,又11233b b λ=-∵13b λ=∵当0λ=时,数列{}n b 的通项公式为0n b =.不是等比数列当0λ≠时,数列{}n b 是首项为,公比为3的等比数列,∵3nn b λ=.(2)由(1)知3nn b =,则4581,243b b ==因为304303127a =⨯-=, 所以4305b a b <<,所以,30T 中要去掉{}n b 的项最多4项,即3,9,27,81, 其中9,81是{}n a 和{}n b 的公共项,所以数列{}n c 的前30项和30T 由{}n a 的前32项和,去掉9,81, ()()()330122321+1259+81=-90=19262a a a T ⨯=++⋅⋅⋅+-所以数列{}n c 的前30项和30T 为1926.15.(2022·浙江省江山中学模拟预测)在数列{}n a 中,121,2a a ==,且对任意的n *∈N ,都有2132n n n a a a ++=-. (1)求数列{}n a 的通项公式;(2)若{}1234A x x x x x x x =<<<<或,定义集合A 的长度为4321x x x x -+-.已知数列{}n b 的通项公式为()()()()12111n n na xb n a x a x a x *=∈+++N ,若关于x 不等式1220221b bb +++>的解集A ,求集合A 的长度. 【答案】(1)12n na(2)101121(1)34-【解析】 【分析】(1)构造等比数列结合累加法即可求通项;(2)根据不等式特点,巧用作差转换成高次不等式求解. (1)21211()322n n n n n n n a a a a a a a +++++==-⇒--,211a a -=,所以112n n n a a -+-=,12112132112()()()11221212n n n n n n a a a a a a a a -----=+-+-+⋅⋅⋅+-=+++⋅⋅⋅+=+=-,即12n na ;(2) 因为()()()()12111n n na xb n a x a x a x *=∈+++N ,1220221b bb +++>即就是2021202124211(1)(21)(1)(21)(41)(1)(21)(2+1)x x x x x x x x x x x x x +++⋅⋅⋅+>++++++++⋅⋅⋅, 2021202124211(1)(21)(1)(21)(41)(1)(21)(2+1)11x x x x x x x x x x x x x x ++⋅⋅⋅+>-=+++++++⋅⋅⋅++,2021202142121(1)(21)(41)(1)(21)(2+1)1(1)(21)(1)(21)x x x x x x x x x x x x x x +⋅⋅⋅+>-=+++++⋅⋅⋅+++++,⋅⋅⋅,202110(1)(21)(41)(2+1)x x x x >+++⋅⋅⋅,即2021(1)(21)(41)(2+1)0x x x x +++⋅⋅⋅<,根据数轴标根法可知不等式的解集为1|12A x x ⎧=-<<-⎨⎩或1148x -<<-或⋅⋅⋅或202020211122x ⎫-<<-⎬⎭,集合A 的长度为10112021101111[1()]1112124(1)12823414-++⋅⋅⋅+==--. 【点睛】数列求通项分方法有构造等比或等差数列法,累加法,累乘法等.。
2024年高考数学二轮复习解题思维提升专题08数列大题部分训练手册

专题08 数列大题部分【训练目标】1、 理解并会运用数列的函数特性;2、 驾驭等差数列,等比数列的通项公式,求和公式及性质;3、 驾驭依据递推公式求通项公式的方法;4、 驾驭常用的求和方法;5、 驾驭数列中简洁的放缩法证明不等式。
【温馨小提示】高考中一般有一道小题,一道大题,小题侧重于考等差数列与等比数列的性质,娴熟的敏捷的运用数列的性质会大大削减计算量;大题则侧重于考查依据递推公式求通项公式,求和的方法。
总之,此类题目难度中等,属于必拿分题。
【名校试题荟萃】1、(宁夏长庆高级中学2025届高三上学期第四次月考数学(理)试卷)设数列{}n a 的前n 项和,且123,1,a a a +成等差数列.(1)求数列{}n a 的通项公式;(2)记数列1{}na 的前n 项和n T ,求使得成立的n 的最小值.【答案】(1)2nn a = (2)10(2)由(1)可得112nn a ⎛⎫= ⎪⎝⎭,所以,由,即21000n>,因为,所以10n ≥,于是使得成立的n 的最小值为10.2、(宁夏长庆高级中学2025届高三上学期第四次月考数学(理)试卷)设等差数列{}n a 的公差为d ,点(,)n n a b 在函数()2x f x =的图象上(*n N ∈)。
(1)若12a =-,点87(,4)a b 在函数()f x 的图象上,求数列{}n a 的前n 项和n S ; (2)若11a =,函数()f x 的图象在点22(,)a b 处的切线在x 轴上的截距为12ln 2-,求数列{}n na b 的前n 项和n T .【答案】(1)(2)(2)由函数()f x 的图象在点22(,)a b 处的切线方程为所以切线在x 轴上的截距为21ln 2a -,从而,故22a =从而n a n =,2n n b =,2n n n a n b =所以故。
3、(辽宁省辽河油田其次高级中学2025届高三上学期期中考试数学(文)试题)设n S 为数列{}n a 的前项和,已知10a ≠,,n *∈N .(1)求1a ,2a ;(2)求数列{}n a 的通项公式; (3)求数列{}n na 的前n 项和. 【答案】(1)1,2 (2)12-=n n a (3)(3)由(2)知12-=n n n na ,记其前n 项和为n T ,于是① ②①-②得从而.4、(湖南省浏阳一中、株洲二中等湘东六校2025届高三12月联考数学(理)试题)已知数列}{n a 的前n 项 和n S 满意,且11=a 。
专题08 数列小题综合(学生卷)- 十年(2015-2024)高考真题数学分项汇编(全国通用)
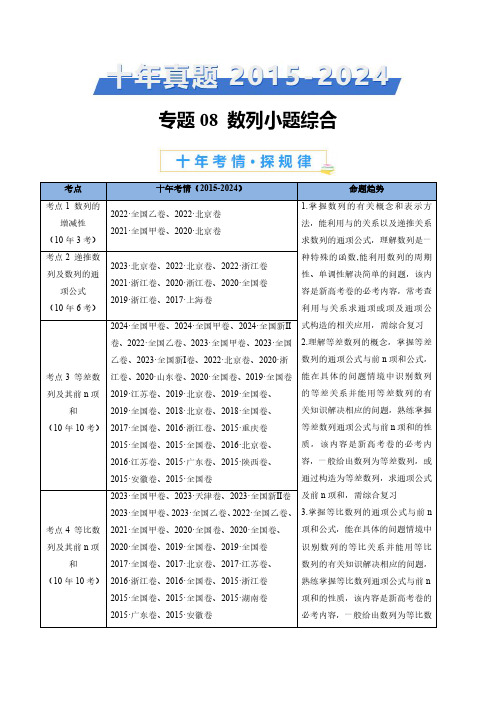
专题08数列小题综合考点十年考情(2015-2024)命题趋势考点1数列的增减性(10年3考)2022·全国乙卷、2022·北京卷2021·全国甲卷、2020·北京卷1.掌握数列的有关概念和表示方法,能利用与的关系以及递推关系求数列的通项公式,理解数列是一种特殊的函数,能利用数列的周期性、单调性解决简单的问题,该内容是新高考卷的必考内容,常考查利用与关系求通项或项及通项公式构造的相关应用,需综合复习2.理解等差数列的概念,掌握等差数列的通项公式与前n项和公式,能在具体的问题情境中识别数列的等差关系并能用等差数列的有关知识解决相应的问题,熟练掌握等差数列通项公式与前n项和的性质,该内容是新高考卷的必考内容,一般给出数列为等差数列,或通过构造为等差数列,求通项公式及前n项和,需综合复习3.掌握等比数列的通项公式与前n项和公式,能在具体的问题情境中识别数列的等比关系并能用等比数列的有关知识解决相应的问题,熟练掌握等比数列通项公式与前n项和的性质,该内容是新高考卷的必考内容,一般给出数列为等比数考点2递推数列及数列的通项公式(10年6考)2023·北京卷、2022·北京卷、2022·浙江卷2021·浙江卷、2020·浙江卷、2020·全国卷2019·浙江卷、2017·上海卷考点3等差数列及其前n项和(10年10考)2024·全国甲卷、2024·全国甲卷、2024·全国新Ⅱ卷、2022·全国乙卷、2023·全国甲卷、2023·全国乙卷、2023·全国新Ⅰ卷、2022·北京卷、2020·浙江卷、2020·山东卷、2020·全国卷、2019·全国卷2019·江苏卷、2019·北京卷、2019·全国卷、2019·全国卷、2018·北京卷、2018·全国卷、2017·全国卷、2016·浙江卷、2015·重庆卷2015·全国卷、2015·全国卷、2016·北京卷、2016·江苏卷、2015·广东卷、2015·陕西卷、2015·安徽卷、2015·全国卷考点4等比数列及其前n项和(10年10考)2023·全国甲卷、2023·天津卷、2023·全国新Ⅱ卷2023·全国甲卷、2023·全国乙卷、2022·全国乙卷、2021·全国甲卷、2020·全国卷、2020·全国卷、2020·全国卷、2019·全国卷、2019·全国卷2017·全国卷、2017·北京卷、2017·江苏卷、2016·浙江卷、2016·全国卷、2015·浙江卷2015·全国卷、2015·全国卷、2015·湖南卷2015·广东卷、2015·安徽卷列,或通过构造为等比数列,求通项公式及前n 项和。
08 数列的概念+等差数列(原卷版)-高二数学寒假进阶学习方案(人教A版2019选择性必修第二册)

08数列的概念+等差数列一、典例精析拓思维(名师点拨)核心问题1数列例1.(2022·全国·高三专题练习)设数列{}n a 中,1112,1n n a a a -=+=(2n ≥且*n N ∈),则2022a =()A.1-B.12C.2D.52练习1-1.(2022·全国·高三专题练习)数列{}n a 满足112a =,111n n a a +=-,则2021a 等于()A.1-B.12C.2D.3练习1-2.(2022·全国·高三专题练习(理))已知“整数对”按如下规律排列:()()()()()1,11,22,11,32,2,,,,,()()()3,11,42,3,,()3,2,,()4,1,…,则第68个“整数对”为()A.()1,12B.()3,10C.()2,11D.()3,9核心问题2数列单调性例1.(2020·陕西·渭南市杜桥中学高二期中(理))设数列2328n a n n =-,则数列的最小项是()A.第4项B.第5项C.第6项D.第7项例2.(2021·全国·高二期末)已知数列{}n a 的通项公式是342n n a n =+,那么这个数列是()A.摆动数列B.递减数列C.递增数列D.常数列练习2-1.(2021·全国·高二课时练习)已知数列{}n a 是递增数列,且其通项公式为2n a n n λ=+,则实数λ的取值范围是()A.7,2⎛⎫-+∞ ⎪⎝⎭B.[)0,+∞C.[)2,-+∞D.()3,-+∞例4.(2021·广西南宁·高二期末(文))已知数列{}n a 满足9(21),10n n a n n N +⎛⎫=+∈ ⎪⎝⎭,设{}n a 中的最大项为0n a ,则0n =()A.10B.9C.11D.14核心问题3等差通项1.(2021·全国·高二专题练习)已知等差数列{}n a ,满足23418a a a ++=,23466=a a a 求数列{}n a 的通项公式.2.(2019·安徽·天长市关塘中学高一期末)已知等差数列{}n a 的前n 项和为n S ,且1320a S +=,550S =.(1)求数列{}n a 的通项公式;(2)请确定3998是否是数列{}n a 中的项?核心问题4等差下标和性质例1.(2020·四川·宁南中学高二开学考试(理))已知等差数列{}n a 中,815a =,则17915a a a a +++=()A.15B.30C.45D.60练习1-1.(2021·四川·射洪中学高三阶段练习(理))已知数列{}n a 是等差数列,满足120214a a +=,则1011a =()A.4B.2C.0D.2-练习1-2.(2018·山西·怀仁市第一中学校高二阶段练习(理))在等差数列{}n a 中,1815360a a a ++=,则9102a a -的值为()A.6B.8C.12D.13核心问题5等差求和公式例1.(2021·陕西·西安市第八十九中学高二阶段练习(文))已知数列{}n a 的前n 项和为n S ,满足1n a ≥,且()241,n n S a n N *=+∈.(1)求123,,a a a 的值;(2)猜想数列{}n a 的通项公式,并计算数列{}n a 前100项和100S .例2.(2022·全国·模拟预测)已知n S 为数列{}n a 的前n 项和,且28n S n n =-+.(1)求证:数列{}n a 是等差数列;(2)记n n b a =,试求数列{}n b 的前n 项和n T .例3.(2021·北京·高二期末)在等差数列{}n a 中,48108,12a a a +==.(1)求数列{}n a 的首项1a 和公差d ;(2)设数列{}n a 的前n 项和为n S ,求n S 的最小值.核心问题6等差数列和的性质例1.(2021·河南·高二阶段练习)记等差数列{}n a 的前n 项和为n S ,已知55S =,1521S =,则10S =()A.9B.10C.12D.13练习1-1.(2021·江苏·高二专题练习)等差数列{}n a 中,n S 表示其前n 项和,若10100S =,20110S =,则30S =()A.-80B.120C.30D.111练习1-2.(2022·重庆市育才中学模拟预测)已知等差数列{}n a 前n 项和为n S ,且4813S S =,则816S S 等于()A.18B.19C.13D.310例2.(2021·福建省平和第一中学高二阶段练习)记等差数列{}n a 与{}n b 的前n 项和分别为n S 与n T ,若123n n S n T n +=+,则55a b =()A.2110B.4241C.1021D.4142练习2-1.(2021·山西师范大学实验中学高二阶段练习)若等差数列{}n a 与等差数列{}n b 的前n 项和分别为n S 和n T ,且2531+=-n n S n T n ,则88a b =()A.2123B.1311C.3544D.3747例3.(2020·甘肃省会宁县第一中学高二阶段练习(理))设等差数列{}n a 、{}n b 的前n 项和分别是n S 、n T .若237n n S n T n =+,则63a b 的值为()A.511B.38C.1D.2二、厚积薄发勤演练(题型归类练)一、单选题1.(黑龙江省牡丹江地区四校2021-2022学年高二上学期12月联合考试数学试题)在等差数列{}n a 中,若233a a +=,564a a +=,则公差d =()A.1B.2C.13D.162.(2021·湖北·武汉中学高二阶段练习)在等差数列{}n a 中,已知12a =,2313a a +=,则456a a a ++等于()A.40B.42C.43D.453.(2021·河南·高三阶段练习(文))等差数列{}n a 满足344a a +=,788a a +=,则1112a a +=()A.10B.12C.14D.164.(2022·江苏·高二)已知在数列{}n a 中,*11(n n a a n N -=+∈且2)n ≥,设n S 为{}n a 的前n 项和,若972S =,则9a =()A.8B.12C.16D.365.(2021·山西·芮城中学高二阶段练习)设n S 是等差数列{}n a 的前n 项和,若80,a <且98,a a >则使0n S >成立的正整数n 的最小值为()A.15B.16C.17D.186.(2021·河北·武安市第三中学高二阶段练习)等差数列{}n a 的前n 项和为n S ,若18240,a S S <=,则满足0n S >的最小的正整数n 的值为()A.31B.32C.33D.347.(2021·河南·永城高中高二期中(理))我国古代的数学专著《九章算术》里有一段叙述:今有良马与驽马发长安至齐,齐去长安一千一百二十五里,良马初日行一百零三里,日增十三里;驽马初日行九十七里,日减半里;良马先至齐,复还迎驽马,二马相逢.问:二马相逢时驽马所走的路程为()A.855里B.1062里C.1188里D.1395里8.(2021·新疆昌吉·模拟预测(文))已知数列{}n a 满足()()111N n n n a na n *+-+=∈,且前n 项和为n S ,若N n *∀∈,6n S S ≥,则6S 的取值范围为()A.73,2⎡⎤⎢⎥⎣⎦B.90,2⎡⎤⎢⎥⎣⎦C.92,2⎡⎤⎢⎥⎣⎦D.[]0,3二、填空题9.(2021·山西·芮城中学高二阶段练习)已知等差数列{}n a 的前n 项和为n S ,且20202019120202019S S -=,则数列{}n a 的公差为_______.10.(2021·福建省平和第一中学高二阶段练习)已知数列{}n a 的首项12a =,122n n n a a a +=+,1n =,2,3,…,则2012a =________.11.(2021·陕西·咸阳市实验中学高二阶段练习)记等差数列{}n a 的前n 项和为n S ,若311a a =,且公差0d <,则当n S 取最大值时,n =_______.12.(2021·陕西·泾阳县教育局教学研究室高二期中(理))我国古代,9是数字之极,代表尊贵之意,所以中国古代皇家建筑中包含许多与9相关的设计.例如,北京天坛圆丘的底面由扇环形的石板铺成(如图),最高一层的中心是一块天心石,围绕它的第圈有9块石板,从第二圈开始,每一圈比前一圈多9块共有9圈,则第六圈的石板块数是________.三、解答题13.(2022·江苏·高二)已知n S 是等差数列{}n a 的前n 项和,且412S =,840S =.(1)求数列{}n a 的通项公式;(2)设n n S b n=,n T 为数列{}n b 的前n 项和,求n T .14.(2021·山西·高二阶段练习)在等差数列{}n a 中,2186a =-,901000a a +=.(1)求{}n a 的通项公式;(2)求数列{}n a 的前n 项和n T .。
高考数学《数列》大题训练50题含答案解析整理版

高考数学《数列》大题训练50题1 .数列{}的前n 项和为,且满足,.n a n S 11a =2(1)n n S n a =+(1)求{}的通项公式; (2)求和T n =.n a 1211123(1)na a n a ++++L 2 .已知数列,a 1=1,点在直线上.}{n a *))(2,(1N n a a P n n ∈+0121=+-y x (1)求数列的通项公式;}{n a (2)函数,求函数最小值.)2*,(1111)(321≥∈++++++++=n N n a n a n a n a n n f n且 )(n f 3 .已知函数(a ,b 为常数)的图象经过点P (1,)和Q (4,8)x ab x f =)(81(1) 求函数的解析式;)(x f (2) 记a n =log 2,n 是正整数,是数列{a n }的前n 项和,求的最小值。
)(n f n S n S 4 .已知y =f (x )为一次函数,且f (2)、f (5)、f (4)成等比数列,f (8)=15.求=f (1)+f (2)+…+f (n )的表达式.n S 5 .设数列的前项和为,且,其中是不等于和0的实常数.{}n a n n S 1n n S c ca =+-c 1-(1)求证: 为等比数列;{}n a (2)设数列的公比,数列满足,试写出 的{}n a ()q f c ={}n b ()()111,,23n n b b f b n N n -==∈≥1n b ⎧⎫⎨⎬⎩⎭通项公式,并求的结果.12231n n b b b b b b -+++L 6 .在平面直角坐标系中,已知A n (n,a n )、B n (n,b n )、C n (n -1,0)(n ∈N *),满足向量与向量共线,且1+n n A A n n C B 点B n (n,b n ) (n ∈N *)都在斜率为6的同一条直线上.(1)试用a 1,b 1与n 来表示a n ;(2)设a 1=a ,b 1=-a ,且12<a ≤15,求数列{a n }中的最小项.7 .已知数列的前三项与数列的前三项对应相同,且…对任意的{}n a {}n b 212322a a a +++12n n a -+8n =∈n N*都成立,数列是等差数列.1{}n n b b +-(1)求数列与的通项公式;{}n a {}n b (2)问是否存在N *,使得?请说明理由.k ∈(0,1)k k b a -∈8 .已知数列),3,2(1335,}{11 =-+==-n a a a a nn n n 且中(I )试求a 2,a 3的值;(II )若存在实数为等差数列,试求λ的值.}3{,nn a λλ+使得9 .已知数列的前项和为,若,{}n a n n S ()1,211++=⋅=+n n S a n a n n(1)求数列的通项公式;{}n a (2)令,①当为何正整数值时,:②若对一切正整数,总有,求的n nn S T 2=n 1+>n n T T n m T n ≤m 取值范围。
高中数学--数列大题专项训练(含详解)

高中数学--数列大题专项训练(含详解)一、解答题(本大题共16小题,共192.0分)1.已知{}n a 是等比数列,满足12a =,且2a ,32a +,4a 成等差数列,数列{}n b 满足*1231112()23n b b b b n n N n+++⋅⋅⋅+=∈(1)求{}n a 和{}n b 的通项公式;(2)设(1)()n n n n c a b =--,求数列{}n c 的前2n 项和2.n S 2.已知数列{}n a 的前n 项和为n S ,且233.n n S a +=(1)求数列{}n a 的通项公式;(2)若32log n n n b a a +=⋅,求数列{}n b 的前n 项和.n T 3.在数列{}n a 中,111,(1n n n a a a c c a +==⋅+为常数,*)n N ∈,且1a ,2a ,5a 成公比不为1的等比数列.(1)求证:数列1{}na 是等差数列;(2)求c 的值;(3)设1n n n b a a +=,求数列{}n b 的前n 项和.n S4.在ABC 中,已知三内角A ,B ,C 成等差数列,且11sin().214A π+=()Ⅰ求tan A 及角B 的值;()Ⅱ设角A ,B ,C 所对的边分别为a ,b ,c ,且5a =,求b ,c 的值.5.在数列{}n a 中,11a =,11(1)(1)2nn n a a n n +=+++⋅(1)设n n a b n=,求数列{}n b 的通项公式(2)求数列{}n a 的前n 项和nS 6.已知数列的各项均为正数,前项和为,且()Ⅰ求证数列是等差数列;()Ⅱ设求7.已知数列{}n a 的前n 项和为n S ,且22n n a a S S =+对一切正整数n 都成立.(1)求1a ,2a 的值;(2)设10a >,数列110lg n a a ⎧⎫⎨⎬⎩⎭的前n 项和为n T ,当n 为何值时,n T 最大?并求出n T 的最大值.8.已知等差数列{}n a 的前四项和为10,且2a ,3a ,7a 成等比数列.(1)求通项公式na (2)设2n a nb =,求数列n b 的前n 项和.n S 9.已知在数列{}n a 中,13a =,1(1)1n n n a na ++-=,*.n N ∈(1)证明数列{}n a 是等差数列,并求n a 的通项公式;(2)设数列11{}n n a a +的前n 项和为n T ,证明:1.(126n T <分)10.已知函数2(1)4f x x +=-,在等差数列{}n a 中,1(1)a f x =-,232a =-,3().a f x =(1)求x 的值;(2)求数列{}n a 的通项公式.n a 11.已知数列{}n a 是公比大于1的等比数列,1a ,3a 是函数2()109f x x x =-+的两个零点.(1)求数列{}n a 的通项公式;(2)若数列{}n b 满足3log n n b a n =+,求数列{}n b 的前n 项和n S 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题08 数列大题部分【训练目标】1、 理解并会运用数列的函数特性;2、 掌握等差数列,等比数列的通项公式,求和公式及性质;3、 掌握根据递推公式求通项公式的方法;4、 掌握常用的求和方法;5、 掌握数列中简单的放缩法证明不等式。
【温馨小提示】高考中一般有一道小题,一道大题,小题侧重于考等差数列与等比数列的性质,熟练的灵活的使用数列的性质会大大减少计算量;大题则侧重于考查根据递推公式求通项公式,求和的方法。
总之,此类题目难度中等,属于必拿分题。
【名校试题荟萃】1、(宁夏长庆高级中学2019届高三上学期第四次月考数学(理)试卷)设数列{}n a 的前n 项和,且123,1,a a a +成等差数列. (1)求数列{}n a 的通项公式;(2)记数列1{}na 的前n 项和n T ,求使得成立的n 的最小值.【答案】(1)2nn a = (2)10(2)由(1)可得112nn a ⎛⎫= ⎪⎝⎭,所以,由,即21000n>,因为,所以10n ≥,于是使得成立的n 的最小值为10.2、(宁夏长庆高级中学2019届高三上学期第四次月考数学(理)试卷)设等差数列{}n a 的公差为d ,点(,)n n a b 在函数()2x f x =的图象上(*n N ∈)。
(1)若12a =-,点87(,4)a b 在函数()f x 的图象上,求数列{}n a 的前n 项和n S ; (2)若11a =,函数()f x 的图象在点22(,)a b 处的切线在x 轴上的截距为12ln 2-,求数列{}n na b的前n 项和n T .【答案】(1) (2)(2)由函数()f x 的图象在点22(,)a b 处的切线方程为所以切线在x 轴上的截距为21ln 2a -,从而,故22a =从而n a n =,2n n b =,2n nn a nb =所以故。
3、(辽宁省辽河油田第二高级中学2019届高三上学期期中考试数学(文)试题)设n S 为数列{}n a 的前项和,已知10a ≠,,n *∈N .(1)求1a ,2a ;(2)求数列{}n a 的通项公式; (3)求数列{}n na 的前n 项和.【答案】(1)1,2 (2)12-=n n a (3)(3)由(2)知12-=n n n na ,记其前n 项和为n T ,于是① ②①-②得从而.4、(湖南省浏阳一中、株洲二中等湘东六校2019届高三12月联考数学(理)试题)已知数列}{n a 的前n 项 和n S 满足,且11=a 。
(1)求数列的通项公式n a ; (2)记,n T 为}{n b 的前n 项和,求使nT n 2≥成立的n 的最小值. 【答案】(1)12-=n a n (2)5(2)由(1)知,∴,由nT n 2≥有242+≥n n ,有6)2(2≥-n ,所以5≥n , ∴n 的最小值为5.5、(黑龙江省哈尔滨市第六中学2019届高三12月月考数学(理)试题)已知数列{}n a 满足12a =,且, *n N ∈.(1)设2nn na b =,证明:数列{}n b 为等差数列,并求数列{}n b 的通项公式; (2)求数列{}n a 的前n 项和n S . 【答案】 (1)(2)【解析】(1)把2n n n a b =代入到,得,同除12n +,得11n n b b +=+,∴{}n b 为等差数列,首项1112a b ==,公差为1,∴.(2)由,再利用错位相减法计算得: .。
6、(安徽省肥东县高级中学2019届高三11月调研考试数学(理)试题)已知数列{}n a 满足:11a =,.(1)设nn a b n=,求数列{}n b 的通项公式; (2)求数列{}n a 的前n 项和n S . 【答案】(1)(2)(2)由(Ⅰ)可知,设数列12n n -⎧⎫⎨⎬⎩⎭的前n 项和n T则①②。
7、(广东省中山一中、仲元中学等七校2019届高三第二次联考(11月)数学(理)试题)已知数列{}n a 为公差不为0的等差数列,满足15a =,且2930,,a a a 成等比数列. (1)求{}n a 的通项公式; (2) 若数列{}n b 满足(n *∈N ),且13b =,求数列1n b ⎧⎫⎨⎬⎩⎭的前n 项和n T .【答案】 (1)23n a n =+ (2)对13b =上式也成立,所以,即,所以.8、(江西省玉山县一中2019届高三上学期期中考试数学(理)试卷)数列{n a }中,81=a ,24=a ,且满足,)(*N n ∈(1)设,求n S ;(2)设,)(*N n ∈,,)(*N n ∈,是否存在最大的正整数m ,使得对任意*N n ∈均有32mT n >成立?若存在求出m 的值;若不存在,请说明理由。
【答案】(1)(2)7从而故数列T n 是单调递增数列,又因是数列中的最小项,要使恒成立,故只需成立即可,由此解得m <8,由于m ∈Z *, 故适合条件的m 的最大值为7.9、(辽宁省沈阳市东北育才学校2019届高三上学期第三次模拟数学(文)试题)已知数列{}n a 满足N *.(1)求数列{}n a 的通项公式; (2)设以2为公比的等比数列{}n b 满足N *),求数列的前n 项和n S . 【答案】(1)243n a n =-(2)【解析】(1)由题知数列{}3n a +是以2为首项,2为公差的等差数列,.10、(江西省南康中学2019届高三上学期第四次月考数学(理)试题)已知数列{}n a 的前n 项和为n S ,且12-=n n a S .(1)求数列{}n a 的通项公式;(2)记,求数列{}n b 的前n 项和n T .【答案】 (1)12n -(2)2121n n -+【解析】 (1)当时,,得当时,有,所以即,满足时,, 所以是公比为2,首项为1的等比数列,故通项公式为.11、已知数列{a n }各项均不相同,a 1=1,定义,其中n ,k ∈N*.(1)若n b n =)1(,求5a ; (2)若b n +1(k )=2b n (k )对2,1=k 均成立,数列{a n }的前n 项和为S n . (i )求数列{a n }的通项公式;(ii )若k ,t ∈N *,且S 1,S k -S 1,S t -S k 成等比数列,求k 和t 的值. 【答案】 (1)95-=a(2)(i )12-=n n a ;(ii )k =2,t =3【解析】 (1)因为,所以,所以95-=a .(2)(i )因为b n +1(k )=2b n (k ),得,令k =1,,……………①k =2,,……………② 由①得,……………③②+③得,……………④①+④得n n a a 21=+,又011≠=a ,所以数列{}n a 是以1为首项,2为公比的等比数列,所以12-=n n a .12、(江苏省盐城市2019届高三上学期期中考试)已知正项数列}{n a 的首项11a =,前n 项和n S 满足.(1)求数列}{n a 的通项公式;(2)若数列}{n b 是公比为4的等比数列,且也是等比数列,若数列+n n a b λ⎧⎫⎨⎬⎩⎭单调递增,求实数λ的取值范围;(3)若数列}{n b 、}{n c 都是等比数列,且满足n n n a b c -=,试证明:数列}{n c 中只存在三项. 【答案】(1)n a n = (2)23λ>-(3)见解析【解析】 (1),故当2≥n 时,两式作差得:,由}{n a 为正项数列知,,即}{n a 为等差数列,故n a n = 。
(2)由题意,,化简得 311-=b ,所以,所以,由题意知恒成立,即3>13n λ-恒成立,所以133λ-<,解得23λ>-;13、(浙江省诸暨中学2019届高三期中考试题)已知数列}{n a ,满足11=a ,232=a ,,(1)证明:为等比数列并求}{n a 的通项公式;(2)n S 为数列}{n a 的前n 项和,是否存在*∈N t r ,,)(t r <使得t r S S S ,,1成等差数列,若存在求出t r ,,不存在,请说明理由。
【答案】(1) (2)不存在(2),11=∴S ,,.等式的左边是一个偶数,右边是一个奇数,所以不存在这样的t r ,,使得t r S S S ,,1成等差数列.14、(浙江省诸暨中学2019届高三期中考试题)设数列{}n a 满足:(1).求数列{}n a 的通项公式;(2).设,求数列{}n b 的前n 项和n S . 【答案】(1)n n a 31=∴ (2)见解析(2)①当n为奇数时,.②当n为偶数时,.15、(河北省衡水中学2019届高三上学期三调考试数学(文)试卷)已知数列中,,.(1)求的通项公式;(2)数列满足,数列的前项和为,若不等式对一切恒成立,求的取值范围.【答案】(1)见解析(2).所以数列是以3为公比,以为首项的等比数列,从而;(2),.,两式相减得,∴.∴,若为偶数,则,∴,若为奇数,则,∴,∴,∴.16、(湖南省长沙市雅礼中学2019届高三上学期月考(一)数学(理)试题)已知是等比数列,满足,且成等差数列.(1)求数列的通项公式;(2)设,数列的前项和为,求正整数的值,使得对任意均有.【答案】(1)(2)5.①-②得:,所以,则.由得:当时,; 当时,…;所以对任意,且均有故k=5.。
