大物复习题汇总
大学物理试题库及答案详解【考试必备】
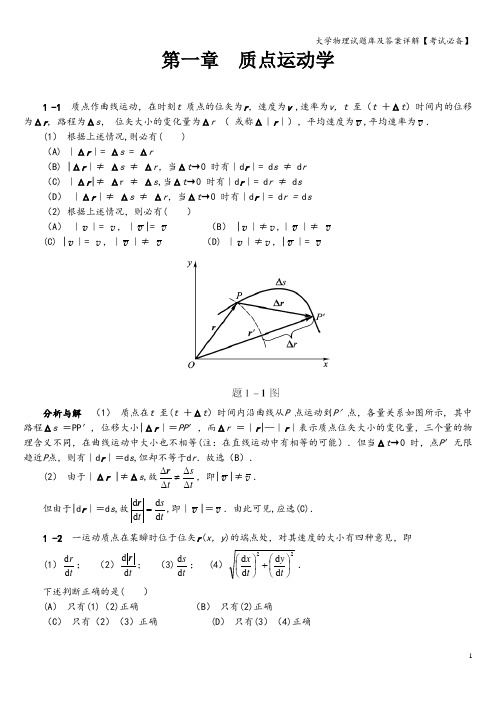
第一章 质点运动学1 -1 质点作曲线运动,在时刻t 质点的位矢为r ,速度为v ,速率为v ,t 至(t +Δt )时间内的位移为Δr , 路程为Δs , 位矢大小的变化量为Δr ( 或称Δ|r |),平均速度为v ,平均速率为v .(1) 根据上述情况,则必有( ) (A) |Δr |= Δs = Δr(B) |Δr |≠ Δs ≠ Δr ,当Δt →0 时有|d r |= d s ≠ d r (C) |Δr |≠ Δr ≠ Δs ,当Δt →0 时有|d r |= d r ≠ d s (D ) |Δr |≠ Δs ≠ Δr ,当Δt →0 时有|d r |= d r = d s (2) 根据上述情况,则必有( )(A ) |v |= v ,|v |= v (B ) |v |≠v ,|v |≠ v (C) |v |= v ,|v |≠ v (D) |v |≠v ,|v |= v分析与解 (1) 质点在t 至(t +Δt )时间内沿曲线从P 点运动到P′点,各量关系如图所示, 其中路程Δs =PP′, 位移大小|Δr |=PP ′,而Δr =|r |—|r |表示质点位矢大小的变化量,三个量的物理含义不同,在曲线运动中大小也不相等(注:在直线运动中有相等的可能).但当Δt →0 时,点P ′无限趋近P 点,则有|d r |=d s ,但却不等于d r .故选(B ).(2) 由于|Δr |≠Δs ,故ts t ΔΔΔΔ≠r ,即|v |≠v . 但由于|d r |=d s ,故tst d d d d =r ,即|v |=v .由此可见,应选(C). 1 -2 一运动质点在某瞬时位于位矢r (x ,y )的端点处,对其速度的大小有四种意见,即(1)t r d d ; (2)t d d r ; (3)t s d d ; (4)22d d d d ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛t y t x .下述判断正确的是( )(A ) 只有(1)(2)正确 (B ) 只有(2)正确(C ) 只有(2)(3)正确 (D ) 只有(3)(4)正确分析与解trd d 表示质点到坐标原点的距离随时间的变化率,在极坐标系中叫径向速率.通常用符号v r 表示,这是速度矢量在位矢方向上的一个分量;td d r 表示速度矢量;在自然坐标系中速度大小可用公式t sd d =v 计算,在直角坐标系中则可由公式22d d d d ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛=t y t x v 求解.故选(D ).1 -3 质点作曲线运动,r 表示位置矢量, v 表示速度,a 表示加速度,s 表示路程, a t表示切向加速度.对下列表达式,即(1)d v /d t =a ;(2)d r /d t =v ;(3)d s /d t =v ;(4)d v /d t |=a t. 下述判断正确的是( )(A ) 只有(1)、(4)是对的 (B ) 只有(2)、(4)是对的(C ) 只有(2)是对的 (D ) 只有(3)是对的分析与解 td d v表示切向加速度a t,它表示速度大小随时间的变化率,是加速度矢量沿速度方向的一个分量,起改变速度大小的作用;t r d d 在极坐标系中表示径向速率v r (如题1 -2 所述);t sd d 在自然坐标系中表示质点的速率v ;而td d v表示加速度的大小而不是切向加速度a t.因此只有(3) 式表达是正确的.故选(D). 1 —4 一个质点在做圆周运动时,则有( ) (A ) 切向加速度一定改变,法向加速度也改变 (B) 切向加速度可能不变,法向加速度一定改变 (C) 切向加速度可能不变,法向加速度不变 (D) 切向加速度一定改变,法向加速度不变分析与解 加速度的切向分量a t起改变速度大小的作用,而法向分量a n 起改变速度方向的作用.质点作圆周运动时,由于速度方向不断改变,相应法向加速度的方向也在不断改变,因而法向加速度是一定改变的.至于a t是否改变,则要视质点的速率情况而定.质点作匀速率圆周运动时, a t恒为零;质点作匀变速率圆周运动时, a t为一不为零的恒量,当a t改变时,质点则作一般的变速率圆周运动.由此可见,应选(B ).*1 -5 如图所示,湖中有一小船,有人用绳绕过岸上一定高度处的定滑轮拉湖中的船向岸边运动.设该人以匀速率v 0 收绳,绳不伸长且湖水静止,小船的速率为v ,则小船作( )(A) 匀加速运动,θcos 0v v =(B) 匀减速运动,θcos 0v v = (C) 变加速运动,θcos 0v v =(D ) 变减速运动,θcos 0v v = (E) 匀速直线运动,0v v =分析与解 本题关键是先求得小船速度表达式,进而判断运动性质.为此建立如图所示坐标系,设定滑轮距水面高度为h ,t 时刻定滑轮距小船的绳长为l ,则小船的运动方程为22h l x -=,其中绳长l 随时间t而变化.小船速度22d d d d h l t llt x -==v ,式中t l d d 表示绳长l 随时间的变化率,其大小即为v 0,代入整理后为θlh l cos /0220v v v =-=,方向沿x 轴负向.由速度表达式,可判断小船作变加速运动.故选(C ). 讨论 有人会将绳子速率v 0按x 、y 两个方向分解,则小船速度θcos 0v v =,这样做对吗?1 -6 已知质点沿x 轴作直线运动,其运动方程为32262t t x -+=,式中x 的单位为m ,t 的单位为 s .求: (1) 质点在运动开始后4.0 s 内的位移的大小; (2) 质点在该时间内所通过的路程;(3) t =4 s 时质点的速度和加速度.分析 位移和路程是两个完全不同的概念.只有当质点作直线运动且运动方向不改变时,位移的大小才会与路程相等.质点在t 时间内的位移Δx 的大小可直接由运动方程得到:0Δx x x t -=,而在求路程时,就必须注意到质点在运动过程中可能改变运动方向,此时,位移的大小和路程就不同了.为此,需根据0d d =tx来确定其运动方向改变的时刻t p ,求出0~t p 和t p ~t 内的位移大小Δx 1 、Δx 2 ,则t 时间内的路程21x x s ∆+∆=,如图所示,至于t =4.0 s 时质点速度和加速度可用t x d d 和22d d tx两式计算.解 (1) 质点在4.0 s 内位移的大小m 32Δ04-=-=x x x(2) 由 0d d =tx得知质点的换向时刻为s 2=p t (t =0不合题意)则m 0.8Δ021=-=x x x m 40Δ242-=-=x x x所以,质点在4。
大物一复习资料

2 r1
Acos(ω
t
φ 1
2π λ
r1
)
2 2 1 (r1 r2 )
18
13. 如图a所示,一光学平板玻璃 A与待测工件 B 之间 形成空气 劈 尖,用波长 =500nm (1nm=10-9m)的单 色光垂直照射,看到的反射光的干涉条纹如图b所示, 有些条纹弯曲部分的顶点恰好于其右边条纹的直线 部分的切线相切,则工件的上表面缺陷是
(重力加速度g取10m·s-2).
(A)2J
(B)1J (C)3J (D)4J (E)20J
F
20cm
[ C]
M
7
解:
A Mgh 1 Kx 2 2
Kx Mg
x h 20(cm)
X=10cm, h=10cm A = 3J
8
6.一力学系统由两个质点组成,它们之间只 有引力作用,若两质点所受外力的矢量和为零, 则此系统
(A) 2 i +2 j
(B)-2 i +2j
(C) -2i-2j vB
y (D)2i-2j
A
x
[b ]
2
2. 质量为m=0.5kg的质点,在XOY坐标 平面内运动,其运动方程为x=5t,y=0.5t2 (SI),从t=2s到t=4s这段时间内,外力对 质点作的功为
(A) 1.5J (C) 4.5J
(A)是自然光。
(B)是完全偏振光且光矢量的振动方向垂直于 入射面。
(C)是完全偏振光且光矢量的振动方向平行于
入射面。
i0
(D)是部分偏振光。
1
2
[B ]
29
解:
i0
1
i
2
n1 sini0 n2 sin
大学物理期末复习题及答案

j i r )()(t y t x +=大学物理期末复习题力学局部一、填空题:,则质点的速度为,加速度为。
2.一质点作直线运动,其运动方程为221)s m 1()s m 2(m 2t t x --⋅-⋅+=,则从0=t 到s 4=t 时间间隔内质点的位移大小质点的路程。
3.设质点沿x 轴作直线运动,加速度t a )s m 2(3-⋅=,在0=t 时刻,质点的位置坐标0=x 且00=v ,则在时刻t ,质点的速度,和位置。
4.一物体在外力作用下由静止沿直线开场运动。
第一阶段中速度从零增至v,第二阶段中速度从v 增至2v ,在这两个阶段中外力做功之比为。
5.一质点作斜上抛运动〔忽略空气阻力〕。
质点在运动过程中,切向加速度是,法向加速度是 ,合加速度是。
〔填变化的或不变的〕6.质量m =40 kg 的箱子放在卡车的车厢底板上,箱子与底板之间的静摩擦系数为s =,滑动摩擦系数为k =,试分别写出在以下情况下,作用在箱子上的摩擦力的大小和方向.(1)卡车以a = 2 m/s 2的加速度行驶,f =_________,方向_________.(2)卡车以a = -5 m/s 2的加速度急刹车,f =________,方向________.7.有一单摆,在小球摆动过程中,小球的动量;小球与地球组成的系统机械能;小球对细绳悬点的角动量〔不计空气阻力〕.〔填守恒或不守恒〕二、单项选择题:1.以下说法中哪一个是正确的〔〕〔A 〕加速度恒定不变时,质点运动方向也不变 〔B 〕平均速率等于平均速度的大小 〔C 〕当物体的速度为零时,其加速度必为零 〔D 〕质点作曲线运动时,质点速度大小的变化产生切向加速度,速度方向的变化产生法向加速度。
2.质点沿Ox 轴运动方程是m 5)s m 4()s m 1(122+⋅-⋅=--t t x ,则前s 3内它的〔〕 〔A 〕位移和路程都是m 3 〔B 〕位移和路程都是-m 3 〔C 〕位移为-m 3,路程为m 3〔D 〕位移为-m 3,路程为m 53. 以下哪一种说法是正确的〔〕〔A 〕运动物体加速度越大,速度越快〔B 〕作直线运动的物体,加速度越来越小,速度也越来越小〔C 〕切向加速度为正值时,质点运动加快〔D 〕法向加速度越大,质点运动的法向速度变化越快4.一质点在平面上运动,质点的位置矢量的表示式为j i r 22bt at +=〔其中a 、b 为常量〕,则该质点作〔〕〔A 〕匀速直线运动 〔B 〕变速直线运动〔C 〕抛物线运动〔D 〕一般曲线运动5. 用细绳系一小球,使之在竖直平面内作圆周运动,当小球运动到最高点时,它〔 〕 〔A 〕将受到重力,绳的拉力和向心力的作用〔B 〕将受到重力,绳的拉力和离心力的作用〔C 〕绳子的拉力可能为零〔D 〕小球可能处于受力平衡状态6.功的概念有以下几种说法〔1〕保守力作功时,系统内相应的势能增加〔2〕质点运动经一闭合路径,保守力对质点作的功为零〔3〕作用力和反作用力大小相等,方向相反,所以两者作功的代数和必为零以上论述中,哪些是正确的〔〕〔A 〕〔1〕〔2〕〔B 〕〔2〕〔3〕〔C 〕只有〔2〕〔D 〕只有〔3〕7.质量为m 的宇宙飞船返回地球时,将发动机关闭,可以认为它仅在地球引力场中运动,当它从与地球中心距离为1R 下降到距离地球中心2R 时,它的动能的增量为〔〕〔A 〕2E R mm G ⋅〔B 〕2121E R R R R m Gm -〔C 〕2121E R R R m Gm -〔D 〕222121E R R R R m Gm --8.以下说法中哪个或哪些是正确的〔〕〔1〕作用在定轴转动刚体上的力越大,刚体转动的角加速度应越大。
大物复习题汇总

L B dl B 2 r u0 I
r a,
I
I a2
r2, B
0 I 2 a2
r
a
r
b,
I
I , B
u0 I 2 r
b r c,
I
I
(c
I 2
b2
)
(r2
b2)
(c2
I b2)
(c2
r2 ),
B
u0I (c2 2 r(c2
r2) b2)
r b,I 0,B 0
EX8 电磁感应定律,动生电动势
解: 球内外 E 的分布都具有球对称性, 所以在球内外做同心球面为高斯面 由高斯定理:
E • dS EdS cos
S
S
E cos0 dS E dS E4r2
S
S
q i
r R包围整个电荷 q
0
r R时q' 4r 3 3
当 r>R 时
E cos0 dS E dS E4r2
dm dt
N 0n r2
dI dt
8-9 长为 l 的一金属棒 ab,水平放置在均匀磁场 B 中,如图所示。
金属棒可绕 O 点在水平面内以角速度旋转,O 点离 a 端的距离为 l/k
(设 k >2)。试求 a、b 两端的电势差,并指出那端电势高。
解:
以 O 点为坐标原点。距离原点 x 位置取微元 dx,
q 4 0
3l
q 4 0l
q 6 0l
单位正电荷从 O 点移到 D 点,电场力做功为:
WOD
q(U O
UD)
1[0
(
q 6
0l
)]
q 6
0l
大物期末复习题答案

大物期末复习题答案一、选择题1. 根据牛顿第二定律,物体的加速度与作用力成正比,与物体的质量成反比。
以下哪个选项正确描述了这一定律?A. F = maB. F = ma^2C. F = 1/maD. F = m/a答案:A2. 一个物体从静止开始自由下落,其下落的距离与时间的关系可以用以下哪个公式表示?A. s = gtB. s = 1/2gtC. s = 1/2gt^2D. s = gt^2答案:C3. 根据能量守恒定律,一个物体的动能和势能之和在没有外力作用的情况下保持不变。
以下哪个选项正确地描述了动能的表达式?A. KE = 1/2mv^2B. KE = mv^2C. KE = 1/2mvD. KE = mv答案:A二、填空题1. 一个弹簧的劲度系数为 \( k \) ,当它受到 \( F \) 的拉力时,弹簧伸长的长度 \( x \) 与力 \( F \) 之间的关系是 \( x =\frac{F}{k} \) 。
2. 根据动量守恒定律,如果一个系统没有外力作用,那么系统的总动量保持不变。
动量的表达式是 \( p = mv \) ,其中 \( m \) 是质量,\( v \) 是速度。
3. 根据万有引力定律,两个物体之间的引力 \( F \) 与它们的质量\( m_1 \) 和 \( m_2 \) 成正比,与它们之间的距离 \( r \) 的平方成反比。
其表达式为 \( F = G \frac{m_1 m_2}{r^2} \) ,其中\( G \) 是引力常数。
三、简答题1. 简述牛顿第三定律的内容及其在日常生活中的应用。
答案:牛顿第三定律指出,对于每一个作用力,都有一个大小相等、方向相反的反作用力。
在日常生活中,例如当我们推墙时,墙也会对我们施加一个相等大小但方向相反的力。
2. 解释什么是临界速度,并给出一个物理现象的例子。
答案:临界速度是指物体在某种条件下维持平衡状态所需的最小速度。
大学物理复习题和答案

大学物理复习题和答案# 大学物理复习题和答案一、选择题1. 根据牛顿第二定律,物体的加速度与作用力成正比,与物体的质量成反比。
如果一个物体的质量是另一个物体的两倍,而作用力是另一个物体的一半,那么两个物体的加速度是相等的。
这种说法正确吗?- A. 正确- B. 错误2. 电磁波的传播速度在真空中是恒定的,其值是多少?- A. 299792458 m/s- B. 3×10^8 m/s- C. 1.6×10^-19 m/s- D. 9.11×10^-31 kg二、填空题1. 根据能量守恒定律,一个物体的总能量等于其_________能和_________能之和。
2. 欧姆定律表达式为V = I × R,其中 V 代表电压,I 代表电流,R 代表_________。
三、简答题1. 简述牛顿第三定律的内容,并给出一个日常生活中的例子。
2. 描述麦克斯韦方程组的四个基本方程,并简述它们各自的含义。
四、计算题1. 一个质量为 5 kg 的物体在水平面上受到一个 20 N 的恒定力作用。
如果摩擦力忽略不计,求物体的加速度。
2. 一个电子在电场中受到3×10^-16 N 的电场力作用。
如果电子的初始速度为零,求电子在电场中加速 1 米所需的时间。
五、论述题1. 论述相对论中时间膨胀和长度收缩的概念,并解释它们在高速运动中的物理意义。
2. 讨论量子力学中的不确定性原理,并举例说明它在现代科技中的应用。
参考答案一、选择题1. 答案:A. 正确2. 答案:B. 3×10^8 m/s二、填空题1. 答案:动;势2. 答案:电阻三、简答题1. 牛顿第三定律的内容是:对于任何两个相互作用的物体,它们之间的作用力和反作用力总是大小相等、方向相反。
例如,当你推墙时,墙也会以相等的力推你。
2. 麦克斯韦方程组包括:高斯定律、高斯磁定律、法拉第电磁感应定律和安培定律。
它们分别描述了电荷产生电场、电流和变化的磁场产生磁场、变化的磁场产生电场以及电流和变化的电场产生磁场。
大物期末复习题

大物期末复习题1. 一均匀带电球面,电荷面密度为σ,球面内电场强度处处为零,球面上面元d S 带有σ d S 的电荷,该电荷在球面内各点产生的电场强度(A) 处处为零(B) 不一定都为零.(C) 处处不为零.(D)无法判定. 2. 下列几个说法中哪一个是正确的?(A) 电场中某点场强的方向,就是将点电荷放在该点所受电场力的方向.(B) 在以点电荷为中心的球面上,由该点电荷所产生的场强处处同.(C) 场强可由q F E /=定出,其中q 为试验电荷,q 可正、可负,F为试验电荷所受的电场力. (D) 以上说法都不正确. 3.如图所示,在坐标(a ,0)处放置一点电荷+q ,在坐标(-a ,0)处放置另一点电荷-q .P 点是y 轴上的一点,坐标为(0,y ).当y >>a 时,该点场强的大小为: (A)204y qεπ. (B)202y qεπ.(C) 302y qa επ. (D) 304y qaεπ.[ ]4.设有一“无限大”均匀带正电荷的平面.取x 轴垂直带电平面,坐标原点在带电平面上,则其周围空间各点的电场强度E随距离平面的位置坐标x 变化的关系曲线为(规定场强方向沿x 轴正向为正、反之为负):[]x5.有一边长为a 的正方形平面,在其中垂线上距中心O 点a /2处,有一电荷为q 的正点电荷,如图所示,则通过该平面的电场强度通量为(A) 03εq . (B) 04επq(C) 03επq . (D) 06εq6. 已知一高斯面所包围的体积内电荷代数和∑q =0,则可肯定:(A) 高斯面上各点场强均为零.(B) 穿过高斯面上每一面元的电场强度通量均为零.(C) 穿过整个高斯面的电场强度通量为零. (D) 以上说法都不对.7.半径为R 的“无限长”均匀带电圆柱面的静电场中各点的电场强度的大小E 与距轴线的距离r 的关系曲线为:[]8. 半径为R 的均匀带电球面,若其电荷面密度为σ,则在距离球面R 处的电场强度大小为:(A)εσ.(B) 02εσ.(C) 04εσ. (D) 08εσ.9. 如图所示,两个同心的均匀带电球面,内球面半径为R 1、带有电荷1Q , 外球面半径为R 2、带有电荷Q 2,则在内球面里面、距离球心为r 处的P 点的场强大小E 为:qE O r(A) E ∝1/r(A)20214r Q Q επ+. (B) 2202210144R Q R Q εεπ+π (C) 2014rQ επ. (D) 0.10. 如图所示,两个“无限长”的共轴圆柱面,半径分别为R 1和R 2,其上均匀带电,沿轴线方向单位长度上所带电荷分别为λ1和λ2,则在两圆柱面之间、距离轴线为r 的P 点处的场强大小E 为:(A) r012ελπ.(B) r 0212ελλπ+. (C) ()rR -π2022ελ. (D) ()1012R r -πελ.[]11.半径为R 的均匀带电球面,总电荷为Q .设无穷远处电势为零,则该带电体所产生的电场的电势U ,随离球心的距离r 变化的分布曲线为[]12.在点电荷+q 的电场中,若取图中P 点处为电势零点,则M点的电势为(A)a q 04επ. (B) a q08επ.(C) a q 04επ-. (D) aq08επ- 13. 如图,在点电荷q 的电场中,选取以q 为中心、R 为半径的球面上一点P 则与点电荷q 距离为r 的P'点的电势为 (A) rq04επ (B) ??? ??-πR r q 1140ε(C) ()R r q-π04ε (D) ??? ??-πr R q 1140ε(A) (B)(C) 2(D)2 (E)14. 如图所示,边长为l 的正方形,在其四个顶点上各放有等量的点电荷.若正方形中心O 处的场强值和电势值都等于零,则:(A) 顶点a 、b 、c、d 处都是正电荷.(B) 顶点a 、b 处是正电荷,c 、d 处是负电荷. (C) 顶点a 、c 处是正电荷,b 、d 处是负电荷. (D) 顶点a 、b 、c 、d 处都是负电荷.[] 15.如图所示,边长为 0.3 m 的正三角形abc ,在顶点a 处有一电荷为10-8 C 的正点电荷,顶点b 处有一电荷为-10-8 C 的负点电荷,则顶点c 处的电场强度的大小E 和电势U 为: (41επ=9×10-9 N m /C 2) (A) E =0,U =0. (B) E =1000 V/m ,U =0. (C) E =1000 V/m ,U =600 V .(D) E =2000 V/m ,U =600 V . 16. 如图所示,半径为R 的均匀带电球面,总电荷为Q ,设无穷远处的电势为零,则球内距离球心为r 的P 点处的电场强度的大小和电势为:(A) E =0,r QU 04επ=. (B) E =0,RQU 04επ=. (C) 204r QE επ=,r Q U 04επ= .(D)204r Q E επ=,RQU 04επ=.17. 有N 个电荷均为q 的点电荷,以两种方式分布在相同半径的圆周上:一种是无规则地分布,另一种是均匀分布.比较这两种情况下在过圆心O 并垂直于圆平面的z 轴上任一点P (如图所示)的场强与电势,则有(A) 场强相等,电势相等. (B) 场强不等,电势不等.ba(C) 场强分量E z 相等,电势相等. (D) 场强分量E z 相等,电势不等.18. 如图所示,两个同心球壳.内球壳半径为R 1,均匀带有电荷Q ;外球壳半径为R 2,壳的厚度忽略,原先不带电,但与地相连接.设地为电势零点,则在内球壳里面,距离球心为r 处的P 点的场强大小及电势分别为:(A) E =0,U =104R Qεπ. (B) E =0,U =-π210114R R Qε. (C) E =204r Q επ,U =r Q04επ. (D) E =204r Q επ, U =104R Qεπ.19. 如图所示,两个同心的均匀带电球面,内球面半径为R 1、带电荷Q 1,外球面半径为R 2、带有电荷Q 2.设无穷远处为电势零点,则在内球面之内、距离球心为r 处的P 点的电势U 为: (A) r Q Q 0214επ+. (B) 20210144R Q R Q εεπ+π.(C) 0. (D) 1014R Q επ.20.点电荷-q 位于圆心O 处,A 、B 、C 、D 为同一圆周上的四点,如图所示.现将一试验电荷从A 点分别移动到B 、C 、D 各点,则 (A) 从A 到B ,电场力作功最大.(B) 从A 到C ,电场力作功最大.(C) 从A 到D ,电场力作功最大. (D) 从A 到各点,电场力作功相等. 21. 在已知静电场分布的条件下,任意两点P 1和P 2之间的电势差决定于(A) P 1和P 2两点的位置. (B) P 1和P 2两点处的电场强度的大小和方向.(C) 试验电荷所带电荷的正负.(D) 试验电荷的电荷大小. 22.半径为r 的均匀带电球面1,带有电荷q ,其外有一同心的半径为R 的均匀带电球面2,带有电荷Q ,则此两球面之间的电势差U 1-U 2A为: (A)-πR r q 1140ε . (B) ??? ??-πr R Q 1140ε .(C) ??? ??-πR Q r q 041ε . (D)rq04επ . 23. 面积为S 的空气平行板电容器,极板上分别带电量±q ,若不考虑边缘效应,则两极板间的相互作用力为(A)S q 02ε. (B) Sq 022ε.(C) 2022S q ε. (D) 202S q ε.24.充了电的平行板电容器两极板(看作很大的平板)间的静电作用力F与两极板间的电压U 的关系是:(A) F ∝U .(B) F ∝1/U .(C) F ∝1/U 2.(D) F ∝U 2.25. 如图所示,在真空中半径分别为R 和2R 的两个同心球面,其上分别均匀地带有电荷+q 和-3q .今将一电荷为+Q的带电粒子从内球面处由静止释放,则该粒子到达外球面时的动能为:(A)R Qq 04επ. (B) R Qq02επ.(C) R Qq 08επ. (D) RQq083επ.26. 密立根油滴实验,是利用作用在油滴上的电场力和重力平衡而测量电荷的,其电场由两块带电平行板产生.实验中,半径为r 、带有两个电子电荷的油滴保持静止时,其所在电场的两块极板的电势差为U 12.当电势差增加到4U 12时,半径为2r 的油滴保持静止,则该油滴所带的电荷为: (A) 2e (B) 4e(C) 8e (D) 16e 27.一个静止的氢离子(H +)在电场中被加速而获得的速率为一静止的氧离子(O +2)在同一电场中且通过相同的路径被加速所获速率的: (A) 2倍. (B) 22倍.(C) 4倍. (D) 42倍.28. 真空中有两个点电荷M 、N ,相互间作用力为F,当另一点电荷Q 移近这两个点电荷时,M 、N 两点电荷之间的作用力 (A) 大小不变,方向改变. (B) 大小改变,方向不变. (C) 大小和方向都不变. (D) 大小和方向都改.29. 有一带正电荷的大导体,欲测其附近P 点处的场强,将一电荷量为q 0 (q 0 >0 )的点电荷放在P 点,如图所示,测得它所受的电场力为F .若电荷量q 0不是足够小,则(A) F / q 0比P 点处场强的数值大. (B) F / q 0比P 点处场强的数值小. (C) F / q 0与P 点处场强的数值相等. (D) F / q 0与P 点处场强的数值哪个大无法确定. 30.有一接地的金属球,用一弹簧吊起,金属球原来不带电.若在它的下方放置一电荷为q 的点电荷,如图所示,则(A) 只有当q > 0时,金属球才下移. (B) 只有当q < 0时,金属球才下移. (C) 无论q 是正是负金属球都下移.(D) 无论q 是正是负金属球都不动.31. 半径分别为R 和r 的两个金属球,相距很远.用一根细长导线将两球连接在一起并使它们带电.在忽略导线的影响下,两球表面的电荷面密度之比σR / σr 为(A) R / r . (B) R 2 / r 2. (C) r 2 / R 2. (D) r / R .q 0P32. 如图所示,一厚度为d 的“无限大”均匀带电导体板,电荷面密度为σ ,则板的两侧离板面距离均为h 的两点a 、b 之间的电势差为:(A) 0. (B) 02εσ.(C) 0εσh .(D) 02εσh.33. 一空心导体球壳,其内、外半径分别为R 1和R 2,带电荷q ,如图所示.当球壳中心处再放一电荷为q 则导体球壳的电势(设无穷远处为电势零点)为 (A)104R qεπ . (B)204R qεπ .(C) 102R q επ . (D) 20R qε2π .34. 如图所示,一带负电荷的金属球,外面同心地罩一不带电的金属球壳,则在球壳中一点P 处的场强大小与电势(设无穷远处为电势零点)分别为: (A) E = 0,U > 0. (B) E = 0,U < 0. (C) E = 0,U = 0. (D) E > 0,U < 0. 35. 同心导体球与导体球壳周围电场的电场线分布如图所示,由电场线分布情况可知球壳上所带总电荷(A) q > 0. (B) q = 0.(C) q < 0. (D) 无法确定.36.一长直导线横截面半径为a ,导线外同轴地套一半径为b 的薄圆筒,两者互相绝缘,并且外筒接地,如图所示.设导线单位长度的电荷为+λ,并设地的电势为零,则两导体之间的P 点( OP = r )的场强大小和电势分别为:q(A) 204r E ελπ=,a bU ln20ελπ=. (B) 204rE ελπ=,r bU ln 20ελπ=.(C) r E 02ελπ=,r aU ln 20ελπ=.(D) r E 02ελπ=,rbU ln 20ελπ=.[] 37. 关于高斯定理,下列说法中哪一个是正确的?(A) 高斯面内不包围自由电荷,则面上各点电位移矢量D为零. (B) 高斯面上处处D为零,则面内必不存在自由电荷.(C) 高斯面的D通量仅与面内自由电荷有关.(D) 以上说法都不正确. 38. 一导体球外充满相对介电常量为εr 的均匀电介质,若测得导体表面附近场强为E ,则导体球面上的自由电荷面密度σ为 (A) ε 0 E .(B) ε 0 ε r E .(C) ε r E .(D) (ε 0 ε r - ε 0)E . 39. 在一点电荷q 产生的静电场中,一块电介质如图放置,以点电荷所在处为球心作一球形闭合面S ,则对此球形闭合面:(A) 高斯定理成立,且可用它求出闭合面上各点的场强. (B) 高斯定理成立,但不能用它求出闭合面上各点的场强.(C) 由于电介质不对称分布,高斯定理不成立.(D) 即使电介质对称分布,高斯定理也不成立. 40. 设有一个带正电的导体球壳.当球壳内充满电介质、球壳外是真空时,球壳外一点的场强大小和电势用E 1,U 1表示;而球壳内、外均为真空时,壳外一点的场强大小和电势用E2,U2表示,则两种情况下壳外同一点处的场强大小和电势大小的关系为(A) E1 = E2,U1 = U2.(B) E1 = E2,U1 > U2.(C) E1 > E2,U1 > U2.(D) E1 < E2,U1 < U2.41.一个平行板电容器,充电后与电源断开,当用绝缘手柄将电容器两极板间距离拉大,则两极板间的电势差U12、电场强度的大小E、电场能量W将发生如下变化:(A)U12减小,E减小,W减小.(B) U12增大,E增大,W增大.(C) U12增大,E不变,W增大.(D) U12减小,E不变,W不变.42. C1和C2两空气电容器并联以后接电源充电.在电源保持联接的情况下,在C1中插入一电介质板,如图所示, 则(A) C1极板上电荷增加,C2极板上电荷减少.(B) C1极板上电荷减少,C2极板上电荷增加.(C) C1极板上电荷增加,C2极板上电荷不变.(D) C1极板上电荷减少,C2极板上电荷不变.43.如果某带电体其电荷分布的体密度增大为原来的2倍,则其电场的能量变为原来的(A) 2倍.(B) 1/2倍.(C) 4倍.(D) 1/4倍.44.通有电流I 的无限长直导线有如图三种形状,则P ,Q ,O 各点磁感强度的大小B P ,B Q ,B O 间的关系为: (A) B P > B Q > B O . (B) B Q >B P >B O (C )B Q > B O > B P . (D) B O > B Q > Bp45. 一个电流元l Id 位于直角坐标系原点,电流沿z 轴方向,点P (x ,y ,z )的磁感强度沿x 轴的分量是:(A) 0.(B) 2/32220)/(d )4/(z y x l Iy ++π-μ.(C) 2/32220)/(d )4/(z y x l Ix ++π-μ.(D) )/(d )4/(2220z y x l Iy ++π-μ. 46. 电流I 由长直导线1沿垂直bc 边方向经a 点流入由电阻均匀的导线构成的正三角形线框,再由b 点沿垂直ac 边方向流出,经长直导线2返回电源(如图).若载流直导线1、2和三角形框中的电流在框中心O 点产生的磁感强度分别用1B 、2B 和3B 表示,则O 点的磁感强度大小(A) B = 0,因为B 1 = B 2 = B 3 = 0.(B) B = 0,因为虽然B 1≠ 0、B 2≠ 0,但021=+B B,B 3 = 0.(C) B ≠ 0,因为虽然B 3= 0,但021≠+B B.(D) B ≠ 0,因为虽然021=+B B,但B 3≠ 0. 47. 图中,六根无限长导线互相绝缘,通过电流均为I ,区域Ⅰ、Ⅱ、Ⅲ、Ⅳ均为相等的正方形,哪一个区域指向纸内的磁通量最大?(A) Ⅰ区域.(B) Ⅱ区域.(C) Ⅲ区域.(D) Ⅳ区域.(E) 最大不止一个. 48. 无限长直圆柱体,半径为R ,沿轴向均匀流有电流.设圆柱体内( rⅠⅡⅢⅣ< R )的磁感强度为B i ,圆柱体外( r > R )的磁感强度为B e ,则有 (A) B i 、B e 均与r 成正比. (B) B i 、B e 均与r 成反比. (C) B i 与r 成反比,B e 与r 成正比. (D) B i 与r 成正比,B e 与r 成反比.49.磁场由沿空心长圆筒形导体的均匀分布的电流产生,圆筒半径为R ,x 坐标轴垂直圆筒轴线,原点在中心轴线上.图(A)~(E)哪一条曲线表示B -x 的关系?50. 如图,一个电荷为+q 、质量为m 的质点,以速度v沿x 轴射入磁感强度为B 的均匀磁场中,磁场方向垂直纸面向里,其范围从x = 0延伸到无限远,如果质点在x = 0和y = 0处进入磁场,则它将以速度v-从磁场中某一点出来,这点坐标是x = 0 和(A) qB m y v +=. (B) qBm y v 2+=. (C) qB m y v 2-= (D) qBm y v -=. 51. 一电子以速度v垂直地进入磁感强度为B的均匀磁场中,此电子在磁场中运动轨道所围的面积内的磁通量将 (A) 正比于B ,反比于v 2. (B) 反比于B ,正比于v 2.(C) 正比于B ,反比于v . (D) 反比于B ,反比于v .52. α 粒子与质子以同一速率垂直于磁场方向入射到均匀磁场中,它们各自作圆周运动的半径比R α / R p 和周期比T α / T p 分别为:Bx OR(D) Bx O R(C) BxOR (E)(A) 1和2 ; (B) 1和1 ; (C) 2和2 ; (D) 2和1 .53.如图,长载流导线ab 和cd 相互垂直,它们相距l ,ab 固定不动,cd 能绕中点O 转动,并能靠近或离开ab .当电流方向如图所示时,导线cd 将(A) 顺时针转动同时离开ab . (B) 顺时针转动同时靠近ab . (C) 逆时针转动同时离开ab . (D) 逆时针转动同时靠近ab . 54. 两个同心圆线圈,大圆半径为R ,通有电流I 1;小圆半径为r ,通有电流I 2,方向如图.若r << R (大线圈在小线圈处产生的磁场近似为均匀磁场),当它们处在同一平面内时小线圈所受磁力矩的大小为 (A) R r I I 22210πμ. (B)R r I I 22210μ.(C) rR I I 22210πμ. (D) 0.55. 三条无限长直导线等距地并排安放,导线Ⅰ、Ⅱ、Ⅲ分别载有1 A ,2 A ,3 A 同方向的电流.由于磁相互作用的结果,导线Ⅰ,Ⅱ,Ⅲ单位长度上分别受力F 1、F 2和F 3,如图所示.则F 1与F 2的比值是:(A) 7/16. (B) 5/8.(C) 7/8. (D) 5/4.[] 56. 把通电的直导线放在蹄形磁铁磁极的上方,如图所示.导线可以自由活动,且不计重力.当导线内通以如图所示的电流时,导线将 (A) 不动.O r R I 1 I 2F 1F 2F 31 A2 A3 AⅠⅡⅢI(B) 顺时针方向转动(从上往下看). (C) 逆时针方向转动(从上往下看),然后下降. (D) 顺时针方向转动(从上往下看),然后下降. (E) 逆时针方向转动(从上往下看),然后上升. 57. 四条皆垂直于纸面的载流细长直导线,每条中的电流皆为I .这四条导线被纸面截得的断面,如图所示,它们组成了边长为2a 的正方形的四个角顶,每条导线中的电流流向亦如图所示.则在图中正方形中心点O 的磁感强度的大小为 (A) I a B π=02μ. (B) I aB 2π=2μ. (C) B = 0. (D) I aB π=μ.58. 如图两个半径为R 的相同的金属环在a 、b 两点接触(ab 连线为环直径),并相互垂直放置.电流I 沿ab 连线方向由a 端流入,b端流出,则环中心O 点的磁感强度的大小为(A) 0.(B)R I40μ.(C) R I 420μ. (D) R I0μ.(E)RI820μ. 59.一无限长直导体薄板宽为l ,板面与z 轴垂直,板的长度方向沿y 轴,板的两侧与一个伏特计相接,如图.整个系统放在磁感强度为B 的均匀磁场中,B的方向沿z 轴正方向.如果伏特计与导体平板均以速度v向y 则伏特计指示的电压值为(A) 0. (B)21v Bl . (C) v Bl . (D) 2v Bl . 60. 将形状完全相同的铜环和木环静止放置,并使通过两环面的磁通量随时间的变化率相等,则不计自感时(A) 铜环中有感应电动势,木环中无感应电动势.IaI Ib a(B) 铜环中感应电动势大,木环中感应电动势小.(C) 铜环中感应电动势小,木环中感应电动势大.(D)两环中感应电动势相等.61. 一个圆形线环,它的一半放在一分布在方形区域的匀强磁场B中,另一半位于磁场之外,如图所示.磁场B的方向垂直指向纸内.欲使圆线环中产生逆时针方向的感应电流,应使(A) 线环向右平移. (B) 线环向上平移. (C) 线环向左平移. (D) 磁场强度减弱. 62. 在如图所示的装置中,把静止的条形磁铁从螺线管中按图示情况抽出时(A) 螺线管线圈中感生电流方向如A 点处箭头所示.(B) 螺线管右端感应呈S 极.(C) 线框EFGH 从图下方粗箭头方向看去将逆时针旋转.(D) 线框EFGH 从图下方粗箭头方向看去将顺时针旋转.[]63.如图所示,一矩形线圈,以匀速自无场区平移进入均匀磁场区,又平移穿出.在(A)、(B)、(C)、(D)各I --t 曲线中哪一种符合线圈中的电流随时间的变化关系(取逆时针指向为电流正方向,且不计线圈的自感)?[] 64. 如图所示,M 、N 为水平面内两根平行金属导轨,ab 与cd 为垂直于导轨并可在其上自由滑动的两根直裸导线.外磁场垂直水平面向上.当外力使ab 向右平移时,cd (A) 不动. (B) 转动. (C) 向左移动. (D) 向右移动.[]磁极磁极 0 t I0 t I0 t I 0t I(A) (B)(C) (D)c ab d N M B65. 一根长度为L 的铜棒,在均匀磁场 B中以匀角速度ω绕通过其一端O 的定轴旋转着,B的方向垂直铜棒转动的平面,如图所示.设t =0时,铜棒与Ob 成θ 角(b 为铜棒转动的平面上的一个固定点),则在任一时刻t 这根铜棒两端之间的感应电动势是:(A) )cos(2θωω+t B L .(B) t B L ωωcos 212.(C) )cos(22θωω+t B L .(D) B L 2ω.(E) B L 221ω.66. 自感为 0.25 H 的线圈中,当电流在(1/16) s 内由2 A 均匀减小到零时,线圈中自感电动势的大小为:(A) 7.8 ×10-3 V . (B) 3.1 ×10-2 V .(C) 8.0 V . (D) 12.0 V . 67. 两个通有电流的平面圆线圈相距不远,如果要使其互感系数近似为零,则应调整线圈的取向使(A) 两线圈平面都平行于两圆心连线. (B) 两线圈平面都垂直于两圆心连线. (C) 一个线圈平面平行于两圆心连线,另一个线圈平面垂直于两圆心连线.(D) 两线圈中电流方向相反. 68. 在一个塑料圆筒上紧密地绕有两个完全相同的线圈aa ′和bb ′,当线圈aa ′和bb ′如图(1)绕制时其互感系数为M 1,如图(2)绕制时其互感系数为M 2,M 1与M 2的关系是(A) M 1 = M 2 ≠0. (B) M 1 = M 2 = 0.(C) M 1 ≠M 2,M 2 = 0.(D) M 1 ≠M 2,M 2 ≠0.B(2)69. 如图所示,两个线圈P 和Q 并联地接到一电动势恒定的电源上.线圈P 的自感和电阻分别是线圈Q 的两倍,线圈P 和Q 之间的互感可忽略不计.当达到稳定状态后,线圈P 的磁场能量与Q 的磁场能量的比值是 (A) 4. (B) 2. (C) 1. (D)21.选择题答案:填空题答案:70.静电场中某点的电场强度,其大小和方向与(单位正试验电荷在该点所受的静电力相同).71.由一根绝缘细线围成的边长为l 的正方形线框,使它均匀带电,其电荷线密度为λ,则在正方形中心处的电场强度的大小E =_______0______.72.两根相互平行的“无限长”均匀带正电直线1、2,相距为d ,其电荷线密度分别为λ1和λ2如图所示,则场强等于零的点与直线1的距离a 为+σ +2σ.73.“无限大”均匀带电平面,σ和+2 σ,如图所示,则A 、B 、C 三个区域的电场强度分别为:E A =,E B =,E C=设方向向右为正).74.R 的均匀带电球面带有电荷Q (Q >0).今在球面上挖去非常小块的面积△S (连同电荷),如图所示,假设不影响其他处原来的挖去△S 后球心处电场强度的大小E =,其方向为_(由球心指向△S )__.电荷线密度为λ,其单位长度上总共发出的电场线条数(即电场强度通量).76.静电场中某点的电势,其数值等于_单位正试验电荷在该点的电势能___或_把单位正电荷由该点沿任意路_径移到零势点时电场力所作的功__.77.图中曲线表示一种轴对称性静电场的场强大小E 的分布,r 表示离对称轴的距离,这是由_半径为R 的无限长均匀带电圆柱面___产生的电场.78.真空中,有一均匀带电细圆环,电荷线密度为λ,其圆心处的电场强度E 0= 0 ,电势U 0=.(选无穷远处电势为零)79.+Q r 1吹胀到r 2,则半径为R (r 1<R <r 2=的球面上任一点的场强大小E变为_0_;电势U 由80.,两同心带电球面,内球面半径为r 1=5 cm ,带电荷q 1=3×10-8C ;外球面半径为r 2=20 cm ,带电荷q 2=-6×10-8C间另一电势为零的球面半径r = 10 cm ___.81.半径为0.1 m 的孤立导体球其电势为300 V ,则离导体球中心30 cm 处的电势U = 100V (以无穷远为电势零点).82.在点电荷q 的电场中,把一个-1.0×10-9 C 的电荷,从无限远处(设无限远处电势为零)移到离该点电荷距离 0.1 m 处,克服电场力作功1.8×10-5 J ,则该点电荷q =7102-?-.(真空介电常量ε0=8.85×10-12 C 2·N -1·m -2 ) 83.如图所示.试验电荷q ,在点电荷+Q 产生的电场中,沿半径为R 的整个圆弧的3/4圆弧轨道由a 点移到d 点的过程中电场力作功为S____0____________;从d 点移到无穷远处的过程中,电场力作功为.84.图示BCD 是以O 点为圆心,以R 为半径的半圆弧,在A 点有一电荷为+q 的点电荷,O 点有一电荷为-q 的点电荷.线段R BA =B 点沿半圆弧轨道BCD 移到D 点,则电功为.85.(带电荷e =1.6×10-19 C)沿四分之一的圆弧轨道从A 点移到B 点(如图),电场力作功8.0×10-15 J .则当质子沿四分之三的圆弧轨道从B 点回到A 点时,电场力作功A =-8.0×10-15 J .设A 点电势为零,则B 点电势U =-5×104V . 86.一电子和一质子相距2×10-10 m (两者静止),将此两粒子分开到无穷远距离(两者仍静止)所需要的最小能量是_7.2_eV . (041επ=9×109 N ·m 2/C 2 , 质子电荷e =1.60×10-19C, 1 eV=1.60×10-19J )87.在点电荷q 的静电场中,若选取与点电荷距离为r0的一点为电势零点,则点电荷距离为r 处的电势U 88.如图所示, 在场强为E的均匀电场中,A 、B 两点间距离为d .AB连线方向与E方向一致.从A 点经任意路径到B 点的场强线积分??ABl Ed =Ed . 89.静电场中有一质子(带电荷e =1.6×10-19 ) 沿图示路径从a 点经c 点移动到b 点时,电场力作功8×10-15 J .则当质子从b 点沿另一路径回到a 点过程中,电场力作功A =-8×10-15 J ;若设a 点电势为零,则b 点电势U b =5×104V90.真空中,一边长为a 的正方形平板上均匀分布着电荷q ;在其中垂线上距离平板d 处放一点电荷q 0如图所示.在d 与a 满足____d >>a___条件下,q 0所受的电场力可写成q 0q / (4πε0d 2 ).91.一电矩为p 的电偶极子在场强为E 的均匀电场中,p与E 间的夹角为α,则它所受的电场力F=0,力矩的大小M =__pEsin α__.92.一空气平行板电容器,两极板间距为d ,充电后板间电压为U .然后将电源断开,在两板间平行地插入一厚度为d /3的金属板,则板间电压变成U ' .93.在一个不带电的导体球壳内,先放进一电荷为+q 的点电荷,点电荷不与球壳内壁接触.然后使该球壳与地接触一下,再将点电荷+q 取走.此时,球壳的电荷为_-q __,电场分布的范围是_球壳外的整个空间.Aa 0。
大学物理复习题及解答

大学物理(一)复习题及解答一、选择题1.某质点的运动方程为)(6532SI t t x +-=,则该质点作( )。
A 、匀加速直线运动,加速度沿x 轴正方向;B 、匀加速直线运动,加速度沿x 轴负方向;C 、变加速直线运动,加速度沿x 轴正方向;D 、变加速直线运动,加速度沿x 轴负方向。
2.下列表述中正确的是( )。
A 、质点沿x 轴运动,若加速度0<a ,则质点必作减速运动;B 、在曲线运动中,质点的加速度必定不为零;C 、若质点的加速度为恒矢量,则其运动轨道必为直线;D 、当质点作抛体运动时,其法向加速度n a 、切向加速度t a 是不断变化的;因此, 22t n a a a +=也是不断变化的。
3.下列表述中正确的是:A 、质点作圆周运动时,加速度方向总是指向圆心;B 、质点作抛体运动时,由于加速度恒定,所以加速度的切向分量和法向分量也是恒定的;C 、质点作曲线运动时,加速度方向总是指向曲线凹的一侧;D 、质点作曲线运动时,速度的法向分量总是零,加速度的法向分量也应是零。
4.某物体的运动规律为t kv dtdv 2-=,式中的k 为大于零的常数;当t =0时,初速为0v ,则速度v 与时间t 的函数关系是( )。
A 、0221v kt v +=;B 、0221v kt v +-=;C 、02121v kt v +=;D 、02121v kt v -=。
5.质点在xoy 平面内作曲线运动,则质点速率的正确表达式为( )。
A 、dt dr v =;B 、dt r d v =;C 、dtds v =;D 、22)()(dt dy dt dx v += ;E 、dt r d v =。
6.质点作曲线运动,r表示位置矢量,s 表示路程,t a 表示切向加速度,下列表达式中,(1)a dt dv =;(2)v dt dr =;(3)v dtds =;(4)t a dt v d = |; A 、只有(1)、(4)是对的; B 、只有(2)、(4)是对的;C 、只有(2)是对的;D 、只有(3)是对的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【7-11】一条无限长直导线在一处弯折成半径为 R 的圆弧,
如图所示,若已知导线中电流强度为 I,试利用毕奥-萨伐
I
尔定律求:(1)当圆弧为半圆周时,圆心 O 处的磁感应强度 B;
(2)当圆弧为 1/4 圆周时,圆心 O 处的磁感应强度。
解:(1) B B左 B中 B右 因左右两边的半无限长的延迟线经
S
S
4R3 30
E R3 3r 20
当 r < R 时,同理有
S
E
E
• dS EdS
S
qr 4 0R3
cos
0
E
E dS E4 r2 q
S
qr 4 0R3
rˆ, (r
R)
r3 R3
q 4r 3 3
Ex3 静电场环路定理,电势能,电势
6-17 如图所示,A 点有电荷+q,B 点有电荷-q,AB=2l,OCD 是以 B 为中心、 l 为半径的半圆。
强 dE1
dE1i
且 dE1
dx 40 x2
,
La dx
L
EP1 Q dE1 i a
40 x2
i 40a(a L)
即
P1
点场强大小为
L 4 0 a(a
L)
,方向沿
AP1
方向。
6.5 一根玻璃棒被弯成半径为 R 的半圆形,其上电荷均匀分布,总电荷为 q,求半圆中心 O 点
的场强。
解:如图,以半圆圆心为原点、对称轴为 x 轴建立坐标系,在棒上取电荷元 dq。
q 4 0
3l
q 4 0l
q 6 0l
单位正电荷从 O 点移到 D 点,电场力做功为:
WOD
q(U O
UD)
1[0
(
q 6
0l
)]
q 6
0l
(2)单位正电荷从 D 点移到无穷远处,电场力做功为:
WD
q(U D
U)
1[(
q 6
0l
)
0]
q 6
0l
6-19. 在半径分别为 R1 和 R2 的两个同心球面上,分别均匀带电,电荷量各为 Q1 和 Q2,且 R1<R2。求下列区域内的电势分布:(1)r<R1;(2)R1<r<R2;(3) r>R2。 解:半径为 R 的均匀带电球面在空间产生的电势为:
dq dS q Rd q d
R
dq 与其对称电荷元 dq 在 O 点产生的场强沿 y 轴的分量抵消,
合场强沿 x 轴正向。关于 x 轴对称分布的任一对电荷元皆如此。
EO EOxi i qdEx
dE
dq 4 0 R 2
q 4 2 0R2
d
dEx
dE
cos
4
q 2 0 R2
cosd
故
E0
解: 球内外 E 的分布都具有球对称性, 所以在球内外做同心球面为高斯面 由高斯定理:
E • dS EdS cos
S
S
E cos0 dS E dS E4r2
S
S
q i
r R包围整个电荷 q
0
r R时q' 4r 3 3
当 r>R 时
E cos0 dS E dS E4r2
we
1 E2 2
Q2 32 2 r4
则球形电容器的电场能量为We
RB 1 E2dV 2 RA
RB Q2 4 r2dr Q2 ( 1 1 )
RA 32 2 r4
8 RA RB
又因为即 We
Q2 2C
EX6 直线电流和圆电流的磁场 磁场的高斯定理
过圆心,因而在圆心产生的磁感应强度为
0,
B
0
B中 =
0I 4R
(2)类似前面,得到向下和向左流向的电流通过圆心,因而在圆心产生
⑴r<R1 处:
E dS
q 0 E0
0 0
⑵R1< r<R2 处:
E dS 上 下 侧 侧E dS 2 rh E
qi h
0
0
E
2 0r
在图示情况,方向沿径向向外
⑶ r>R2 处:
E dS
qi 0 E 0
0 0
6-14、一半径为 R 的均匀带电球体,其电荷体密度 为一常数,求此带电球体内外的场强分布。
上电荷的面密度为 。试计算将电介质从电容器中取出过程中外力所作的功。
解: 外力做功等于电容器电场能的增加:
W
We2
We1
q2 2
(1 C0
1) C
将C
0 r S d
, C0
0S d
,q
S ,V
Sd 代入求得
W 2V ( r 1) 2 0 r
6.29 若球形电容器两同心金属球面半径分别为 RA 和 RB(RA<RB),带电荷分别为+Q 和-Q,
(1) 将单位正电荷从 O 点沿 OCD 移到 D 点,电场力做功多少? (2) 将单位负电荷从 D 点沿 AB 延长线移到无穷远处,电场力做功多少?
解:(1)选择无穷远处为电势零点
O 点电势:UO
qA 4 0RA
qB 4 0RB
q 4 0l
q 4 0l
0
D
点电势:U D
qA 4 0RA '
qB 4 0RB '
i
2 2
q 4 2 0R2
cosd
2
q 2 0 R2
i
或
E0
2i
2 0
4
q 2 0 R2
cosd
q 2 2 0R2
i
EX2 静电场的高斯定理
6-13.两无限长同轴圆柱面,半径分别为 R1 和 R2( R1< R2),带有等值异号电荷,单位长度的电 荷量为 和-,求距离轴线 r 远处的场强,当⑴ r<R1 处,⑵ R1< r<R2 处,⑶ r>R2 处 解:作同轴半径为 r 高为 h 的封闭高斯面
r R r R
U1
Q 4 0R
U2
Q 4 0r
根据球面电势的叠加原理
(1)r
R1时
U Q1 Q2 4 0R1 4 0R2
因此
(2)R1
r
R2时
U Q1 Q2 4 0r 4 0R2
(3)r R2时
U Q1 Q2 4 0r
EX5 电容器,电场能量
6.29 平板电容器两板间的空间(体积为 V)被相对介电常数为 r 的均匀电介质填满。极板
两球面间充满介电常量为 的均匀电介质,设其电容量为 C,试证明次电容器电场的能量
为 We
Q2 2C
。
证明:在球形电容器两极板间作半径为 r 的同心高斯球面 S
由高斯定理
D dS D 4 r2 Q
(RA r RB )
得D Q 4 r 2
则E D Q 4 r2
则半径为
r
处的能量密度为
EX1 电场强度与场强叠加原理
6.4 如图所示,长为 L 的均匀带电细棒 AB。设电荷的线密度为 。求:(1)AB 棒延长线上 P1 点的场强(P1 点到 B 点的距离为 a)。 解:(1)如图,取 P1 点为原点、P1A 向为 x 轴正向建立坐标系。
在 AB 上距 P1 为 x 处取电荷元 dq=dx,其在 P1 产生的元场
