家庭每月收入与消费支出统计表
家庭日常开销记录表

家庭日常开销记录表1. 引言1.1 概述家庭日常开销记录表是一种用于记录和管理家庭支出的工具,它可以帮助家庭成员更好地了解和分析自己的花费情况。
在现代社会中,随着物价的上涨和生活成本的增加,合理控制家庭开销变得尤为重要。
因此,一个系统化且可操作的记录表将有助于我们管理经济,并更好地进行预算规划。
1.2 文章结构本文将以"家庭日常开销记录表"为主题,探讨其在经济管理中的重要性及应用方法。
首先,我们将介绍为何需要一张记录表来管理家庭开支,并指出其对健康理财的重要意义。
接下来,我们将详细讲解如何设计和制作一张有效的开销记录表,并提供使用方式和注意事项。
然后,我们将聚焦于实践应用部分,介绍如何有效地收集、分类和总结家庭开销数据,并提供建议来制定预算并调整消费习惯。
最后,我们将总结家庭日常开销记录表所带来的好处,并展望未来可能的发展方向和改进之处。
1.3 目的本文旨在向读者阐明家庭日常开销记录表的重要性,并指导读者如何有效地应用该工具来管理家庭支出。
通过掌握正确的经济管理方法,我们可以更好地规划和分配资源,实现家庭经济的可持续发展。
无论是为了降低生活压力、提升生活质量,还是为了实现理想中的未来,建立一个规范且高效的家庭日常开销记录系统都是不可或缺的。
请问还有其他问题我可以帮助您吗?2. 家庭日常开销记录表的重要性2.1 经济管理的必要性经济管理是家庭生活中至关重要的一部分。
通过有效地管理经济资源,家庭可以提高财务状况并实现理想的生活目标。
家庭日常开销记录表作为一个工具,在经济管理中起到了至关重要的作用。
它能够帮助家庭成员掌握每笔开销的细节和情况,从而更好地进行预算编制、支出管理和理财规划。
2.2 开支统计与分析的意义家庭日常开销记录表有助于统计和分析家庭的支出情况,让家庭成员更清楚地知道资金流向。
通过对各项开销进行分类和总结,可以发现不必要的花费,并找到节省和合理利用资金的方法。
此外,开支统计与分析还可以帮助制定合理的消费预算并检查是否超支,使家庭能够更好地控制开支并保持可持续的财务健康。
2.1回归分析概述

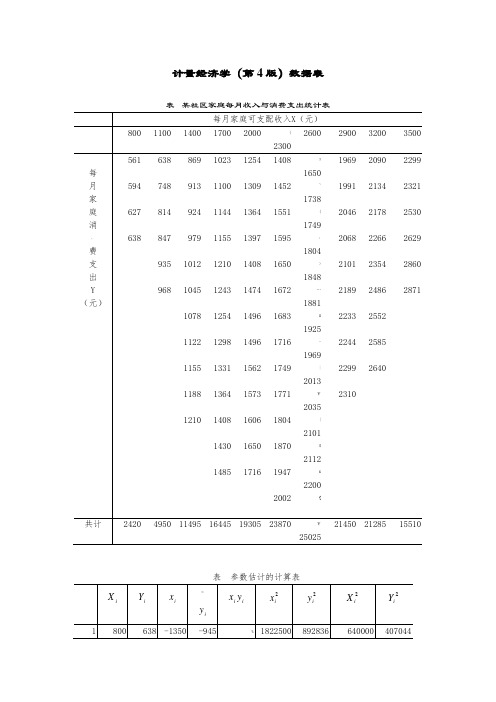
表 2.1.1 某社区家庭每月收入与消费支出统计表 每月家庭可支配收入X(元) 800 每 月 家 庭 消 费 支 出 Y (元) 561 594 627 638 1100 638 748 814 847 935 968 1400 869 913 924 979 1012 1045 1078 1122 1155 1188 1210 1700 1023 1100 1144 1155 1210 1243 1254 1298 1331 1364 1408 1430 1485 2000 1254 1309 1364 1397 1408 1474 1496 1496 1562 1573 1606 1650 1716 2300 2600 2900 1969 1991 2046 2068 2101 2189 2233 2244 2299 2310 3200 2090 2134 2178 2266 2354 2486 2552 2585 2640 3500 2299 2321 2530 2629 2860 2871 1408 1650 1452 1738 1551 1749 1595 1804 1650 1848 1672 1881 1683 1925 1716 1969 1749 2013 1771 2035 1804 2101 1870 2112 1947 2200 2002 4950 11495 16445 19305 23870 25025
2、回归分析的基本概念 、 回归分析(regression analysis) 回归分析(regression analysis)是研究一个 变量关于另一个(些)变量的具体依赖关系 的计算方法和理论。 其目的 其目的在于通过后者的已知或设定值,去估 计和(或)预测前者的(总体)均值。 被解释变量 被解释变量(Explained Variable)或应变 应变 量(Dependent Variable)。 解释变量 解释变量(Explanatory Variable)或自变 自变 量(Independent Variable)。
一元线性回归模型(计量经济学)

总体回归函数说明被解释变量Y的平均状 态(总体条件期望)随解释变量X变化的 规律。至于具体的函数形式,则由所考 察的总体的特征和经济理论来决定。
在例2.1中,将居民消费支出看成是其可 支配收入的线性函数时,该总体回归函
数为: E (Y |X i)01 X i
它是一个线性函数。其中,0,1是未知
第二章 经典单方程计量经济学模型: 一元线性回归模型
§2.1 回归分析概述 §2.2 一元线性回归模型的基本假设 §2.3 一元线性回归模型的参数估计 §2.4 一元线性回归模型的统计检验 §2.5 一元线性回归模型的预测 §2.6 一元线性回归建模实例
§2.1 回归分析概述
一、变量间的关系及回归分析的基本概念 二、总体回归函数 三、随机扰动项 四、样本回归函数
1430 1650 1870 2112
1485 1716 1947 2200
2002
2420 4950 11495 16445 19305 23870 25025 21450 21285 15510
一个抽样
由于调查的完备性,给定收入水平X的消费 支出Y的分布是确定的。即以X的给定值为条 件的Y的分布是已知的,如 P(Y=561 | X = 800) =1/4。 进而,给定某收入Xi,可得消费支出Y的条 件均值,如 E(Y | X = 800) =605。 这样,可依次求出所有不同可支配收入水平 下相应家庭消费支出的条件概率和条件均值 ,见表2.1.2.
相关分析主要研究随机变量间的相关形式 及相关程度。变量间的相关程度可通过计 算相关系数来考察。
具有相关关系的变量有时存在因果关系,
这时,我们可以通过回归分析来研究它们
之间的具体依存关系。
课堂思考题
计量经济学(李子奈第4版)大数据表(全)
计量经济学(第4版)数据表表某社区家庭每月收入与消费支出统计表表中国各地区居民家庭人均全年可支配收入与人均全年消费性支出(元)资料来源:《中国统计年鉴》(2014)。
第2章练习12中国某年各地区税收Y和国内生产总值GDP的统计资料单位:亿元{表 2013年中国各地区城镇居民人均收入与人均消费性支出(元)表 2010年中国制造业各行业的总产出及要素投入资料来源:根据《中国统计年鉴》(2011年)整理。
表 2013年中国居民人均收入与人均生活消费支出数据(元)资料来源:《中国统计年鉴》(2014)。
表 2012年中国农村居民对蛋类食物的消费及相关食物的价格指数蛋类$消费量Q (千克)各类食品的消费价格指数(上年=100)居民消费价格指数P0(上年=100)人均消费支出X(元)蛋类P肉禽类P1水产类P2粮食P01油脂P02蔬菜P03北京(天津`河北;山西(内蒙古…辽宁'吉林…黑龙江^上海| 江苏"浙江安徽*福建:江西【山东'河南?湖北·湖南-广东、广西:海南【重庆|四川)贵州@云南|西藏|陕西*甘肃?青海@ 宁夏(新疆资料来源:《中国统计年鉴》(2013)。
第3章练习17中国某年按行业分的全部制造业国有企业及规模以上制造业非国有企业的工业总产值Y,资表中国粮食生产与相关投入资料表中国2001年各地区农村居民家庭人均纯收入与消费支出(单位:元)注:从事农业经营的纯收入由从事第一产业的经营总收入与从事第一产业的经营支出之差计算,其他来源的纯收入由总纯收入减去从事农业经营的纯收入后得到。
资料来源:《中国农村住户调查年鉴(2002)》、《中国统计年鉴(2002)》。
;AR · AZCA ~COCT !DE FL GAIA &ID IL IN $ KSKY 《LAMA {MD ME MIMN ;MO MS MT / NCND 】NENH ,NJ NM资源来源:根据Introduction to Econometrics (2 edition) 整理。
计量分位数回归 eviews

分位数回归(Quantile Regression)最早由科恩克 和巴塞特 (Koenker 和Bassett, 1978)于1978年提出 ,它 提供了回归变量 X 和因变量Y 的分位数之间线性关系的
估计方法。绝大多数的回归模型都关注因变量的条件均
值,但是人们对于因变量条件分布的其他方面的模拟方 法也越来越有兴趣,尤其是能够更加全面地描述因变量 的条件分布的分位数回归。
利用分位数回归解决经济学问题的文献越来越多, 尤其是在劳动经济学中取得了广泛应用。如在教育回报和 劳动市场歧视等方面都出现了很好的研究成果。在经济学 中的应用研究还包括诸如财富分配不均问题、失业持续时
间问题、食品支出的恩格尔曲线问题、酒精需求问题和日
间用电需求问题等。在金融学领域也涌现出大量使用分位 数回归的应用研究成果,主要应用领域包括风险价值 (Value at Risk, VaR)研究和刻画共同基金投资类型的指 数模型。
(4.7.4)
即F() = ,也就是说F(Y)的第 个分位数是上述优化问题的解。 F(y) 可以由如下的经验分布函数替代:
1 FN ( y ) N
I(y
i 1Байду номын сангаас
N
i
y)
(4.7.5)
其中 y1,y2,…,yn 为Y 的 N 个样本观测值;I(z) 是指示函数,z 是条件关系式,当 z 为真时,I(z) = 1;当 z 为假时,I(z) = 0。式 (4.7.3)中条件关系式 z 为 yi y,当 yi y 时,I(yi y) = 1,否 则取值为0。
为线性函数。其中,0,1是未知参数,称为 回归系数(regression coefficients)。
1、样本回归函数
一季度居民收入和消费支出情况

一季度居民收入和消费支出情况来源:国家统计局发布时间:2017-04-17 10:00一、居民收入情况一季度,全国居民人均可支配收入7184元,比上年同期名义增长8.5%,扣除价格因素,实际增长7.0%。
其中,城镇居民人均可支配收入9986元,增长7. 9%,扣除价格因素,实际增长6.3%;农村居民人均可支配收入3880元,增长8. 4%,扣除价格因素,实际增长7.2%。
一季度,全国居民人均可支配收入中位数6067元,增长6.7%(以下如无特别说明,均为同比名义增长),中位数是平均数的84.4%。
其中,城镇居民人均可支配收入中位数8700元,增长6.7%,是平均数的87.1%;农村居民人均可支配收入中位数3060元,增长7.1%,是平均数的78.9%。
图1 一季度居民人均可支配收入平均数与中位数按收入来源分,一季度,全国居民人均工资性收入4084元,增长8.7%,占可支配收入的比重为56.9%;人均经营净收入1280元,增长6.1%,占可支配收入的比重为17.8%;人均财产净收入583元,增长6.9%,占可支配收入的比重为8.1%;人均转移净收入1237元,增长11.4%,占可支配收入的比重为17.2%。
二、居民消费支出情况一季度,全国居民人均消费支出4796元,比上年同期名义增长7.7%,扣除价格因素,实际增长6.2%。
其中,城镇居民人均消费支出6387元,增长7.0%,扣除价格因素,实际增长5.4%;农村居民人均消费支出2921元,增长8.0%,扣除价格因素,实际增长6.8%。
一季度,全国居民人均食品烟酒消费支出1535元,增长4.6%,占人均消费支出的比重为32.0%;人均衣着消费支出403元,降低0.5%,占人均消费支出的比重为8.4%;人均居住消费支出978元,增长8.9%,占人均消费支出的比重为20.4%;人均生活用品及服务消费支出277元,增长3.7%,占人均消费支出的比重为5.8%;人均交通通信消费支出645元,增长12.3%,占人均消费支出的比重为13.4%;人均教育文化娱乐消费支出480元,增长13.5%,占人均消费支出的比重为10.0%;人均医疗保健消费支出352元,增长15.8%,占人均消费支出的比重为7.3%;人均其他用品和服务消费支出127元,增长10.7%,占人均消费支出的比重为2.6%。
每月开销表格

每月开销表格及分析报告在日常生活和工作中,合理的财务管理对于每个人来说都至关重要。
为了更好地掌握自己的财务状况,制定一个每月开销表格并进行分析是非常必要的。
以下是一个详细的每月开销表格及其分析报告。
一、每月开销表格类别开销金额(元)备注住房3000包括房租、水电费等交通800包括公共交通、打车等费用餐饮2000包括日常饮食、外卖等费用通讯200包括手机费、网络费等娱乐500包括电影、旅游、聚会等费用学习800包括购买书籍、参加培训等费用二、分析报告1.开销概览从上表可以看出,每月总开销为8000元。
其中,住房开销最大,占到了总开销的37.5%,其次是餐饮和交通,分别占比25%和10%。
这些开销占据了每月开销的大部分,是日常生活中必不可少的支出。
2.开销分析(1)住房开销:住房是人们生活中最大的开销之一。
在本表中,住房开销占到了总开销的近四成。
为了降低住房开销,可以考虑合租或者寻找性价比更高的住房。
(2)餐饮开销:餐饮开销也是每月的重要支出。
在保持饮食质量的同时,可以尝试自己做饭,减少外卖和外出就餐的频率,从而降低餐饮开销。
(3)交通开销:交通开销虽然占比不高,但也是一笔不可忽视的支出。
在规划出行时,可以尝试使用公共交通,减少打车的次数,以降低交通开销。
(4)娱乐和学习开销:娱乐和学习是提升生活质量和个人技能的重要方面。
在保持适当娱乐的同时,可以根据个人需求和兴趣选择性地投入学习开销。
(5)其他开销:其他开销包括了一些不可预见的支出,如购物、礼品等。
这部分开销可以通过制定预算和合理消费观念来降低。
3.建议为了更好地管理财务,建议制定一个每月预算计划,并严格按照预算进行支出。
同时,可以通过调整消费观念和习惯,降低不必要的开销。
例如,可以尝试减少外出就餐和购物的频率,增加自己做饭和健身的时间。
此外,还可以考虑将部分储蓄用于投资理财,以增加收入来源。
第二章 一元线性回归模型(本科生计量经济学)

即:正规方程组揭示的是残差的性质。
26
普通最小二乘估计有关 的其他性质(课后习题)
Y Y
^
e Y e y
i ^ i
^
i
0 0
27
i
2、由普通最小二乘估计系数的性质可证
得普通最小二乘估计与参数的关系如下:
1 1 k i u i
^
0 0 wi ui
( 1) ( 2)
( 1)
0 Y 1 X
^
^
Y
1 n
Y , X X
i 1 i 1 n i 1
n
n
i
18
参数的普通最小二乘估计量
ˆ ˆ X )0 (Yi 0 1 i ˆ ˆ X )X 0 ( Y i 0 1 i i
^
33
三、一元线性回归模型参数的最大似 然法(Maximum Likehood,ML)估计
• 基本原理:似然原理
• 一元线性回归模型ML使用的条件:已知随机扰动 项的分布。
34
Y1 , Y2 ,...,Yn
1 f (Yi ) e 2
1 2
1 2
2
Yi ~ N (0 1 X i , 2 )
w 1
i
22
普通最小二乘估计的例
年份
1991 1992 1993 1994
ED(X)
708 793 958 1278
FI(Y)
3149 3483 4349 5218
ed(x)
-551 -466 -301 19
fi(y)
-2351 -2017 -1151 -282
