基于最小错误率的贝叶斯决策
基于最小错误率的贝叶斯分类器设计
基于最小错误率的贝叶斯分类器设计实验原理:在已知P(w i),P(X|w i) ,i=1,…,c 及给出待识别的X的情况下,根据贝叶斯公式计算出后验概率:将X归类于后验概率最小的那一类。
实验数据:假定某个局部区域细胞识别中正常(w1)和非正常(w2)两类先验概率分别为正常状态:P(w1)=0.9;异常状态:P(w2)=0.1。
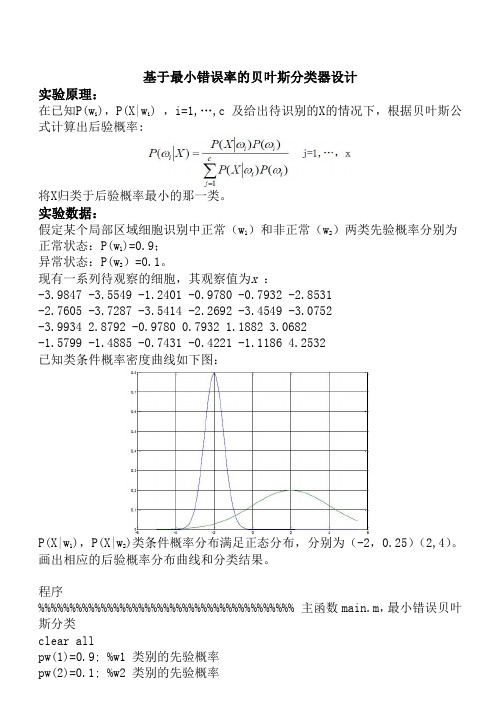
现有一系列待观察的细胞,其观察值为x :-3.9847 -3.5549 -1.2401 -0.9780 -0.7932 -2.8531-2.7605 -3.7287 -3.5414 -2.2692 -3.4549 -3.0752-3.9934 2.8792 -0.9780 0.7932 1.1882 3.0682-1.5799 -1.4885 -0.7431 -0.4221 -1.1186 4.2532已知类条件概率密度曲线如下图:P(X|w1),P(X|w2)类条件概率分布满足正态分布,分别为(-2,0.25)(2,4)。
画出相应的后验概率分布曲线和分类结果。
程序%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 主函数main.m,最小错误贝叶斯分类clear allpw(1)=0.9; %w1 类别的先验概率pw(2)=0.1; %w2 类别的先验概率x=[-3.9847,-3.5549,-1.2401,-0.9780,-0.7932,-2.8531,-2.7605,-3.7287, -3.5414,-2.2692,-3.4549,-3.0752,-3.9934,2.8792,-0.9780,0.7932,1.1882,3.0682,-1.5799,-1.4885,-0.7431 ,-0.4221,-1.1186,4.2532];%%观察值xy=zeros(2,length(x));y(1,:)=normpdf(x,-2,0.5); %w1类别在观察值x条件下得出的概率y(2,:)=normpdf(x,2,2); %w2类别在观察值x条件下得出的概率for n=1:length(x)!echo ==============================================!echo 第n个细胞nfor i=1:2pwx(n,i)=p(pw,y,n,i);%贝叶斯后验概率enddisp('判断为正常类的后验概率为:');p1=pwx(n,1)disp('判断为异常类的条后验概率为:');p2=pwx(n,2)if pwx(n,1)>pwx(n,2)disp(' 根据观察值x判断为正常类!');elsedisp(' 根据观察值x判断为异常类!');endend %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 类条件概率密度图和后验概率密度图xplot=-6:0.1:6;yplot=zeros(2,length(xplot));yplot(1,:)=normpdf(xplot,-2,0.5);yplot(2,:)=normpdf(xplot,2,2);for n=1:length(xplot)for i=1:2pwx2(n,i)=p(pw,yplot,n,i);endend %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%子图1,最小错误率的后验概率分布subplot(2,1,1),plot(xplot,pwx2(:,1),'b');hold onplot(xplot,pwx2(:,2),'r'); hold onfor n=1:length(x)plot(x(n),pwx(n,1),'b*');hold onplot(x(n),pwx(n,2),'r*');hold onendgrid onaxis([-6,6,0,1]);xlabel('x'), ylabel('后验概率p(w|x)'),title('最小错误率的后验概率密度')legend('正常状态后验概率密度','异常状态后验概率密度') %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%子图2,最小错误率的分类结果subplot(2,1,2),for n=1:length(x)if pwx(n,1)>pwx(n,2)plot(x(n),pwx(n,1),'b*');hold onelseplot(x(n),pwx(n,2),'r*');hold onendendgrid onaxis([-6,6,0,1]);xlabel('x'), ylabel('选取较大的后验概率值p'),title('最小错误率的分类结果')子程序%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 调用子程序p.m,计算贝叶斯后验概率function pcount=p(pw,y,n,i)%%%%%%%%%%%计算在类别条件下观察值的概率值,pw为类别先验概率,y为在某类别下的观察值的概率矩阵,n为第n个细胞,i为所分类别pcount=pw(i)*y(i,n)/(pw(1)*y(1,n)+pw(2)*y(2,n));。
模式识别练习题

模式识别练习(1)主题:1.“基于最小错误率的贝叶斯决策”模式识别练习2.“基于最小风险的贝叶斯决策”模式识别练习3.基于“主成分分析”的贝叶斯决策模式识别练习已知训练样本集由“”、“”组成:={(0,0),(0,1),(1,0)};={(4,4),(4,5),(5,4),(5,5)},而测试样本集为C={(2,2),(2.2,2.2),(3,3)}。
(1)利用“基于最小错误率的贝叶斯决策”判别测试集为C中的样本的归类;(2)利用“基于最小风险的贝叶斯决策”判别测试集为C中的样本的归类;(3)在进行“主成分分析”的基础上,采用90%的主成分完成前面的(1)、(2),比较结果的异同。
模式识别练习(2)主题:很多情况下,希望样本维数(特征数)越少越好,降维是解决问题的一个有效的方法。
主成分分析希望得到较少的特征数,而Fisher准则方法则将维数直接降到1维。
一、已知训练样本集由“”、“”组成:={(0,0),(0,1),(1,0)};={(4,4),(4,5),(5,4),(5,5)},而测试样本集为C={(i,i)|i=0:0.005:5}。
分别利用基于最小错误率的贝叶斯决策、基于最小风险的贝叶斯决策、仅使用第一主成分、使用Fisher准则等四种方法(自编函数文件或用书上的函数文件)计算出测试集C中线段(0,0)-(5,5)的临界点;要求:将计算结果自动写入数据文件中二、已知训练样本集为教材上的10类手写数字集。
分别利用基于最小错误率的贝叶斯决策、基于最小风险的贝叶斯决策、仅使用第一主成分、使用Fisher准则等四种方法,统计出各大类的错误率和计算机cpu的计算时间,采用的测试集C依旧是10类手写数字集(虽然分类已知,但用不同的方法实际判别时可能有误判情况!)要求:使用书上的函数文件,并将计算结果自动写入数据文件中模式识别练习(3)一、已知训练样本集由“”、“”组成:={(0,0),(0,1),(1,0)};={(4,4),(4,5),(5,4),(5,5)},而测试样本集为C={(i,i)|i=0:0.01:5}。
基于最小错误率贝叶斯分类器的设计

最小错误贝叶斯决策方法
对于两类情况:
( w1 , w2 ), x [ x1 , x 2 , x3 , , x d ]T
P( w j | x) x wi 如果 P( wi | x) max j 1, 2 对于多类情况:
( w1 , w2 ,, wc ), x [ x1 , x 2 , x3 ,, xd ]T
P( B j / A)
P( A / B j ) P( B j ) P( A / B i ) P( Bi )
i 1 n
, i 1,2,...n
称为Bayes公式。从公式可以看出基于贝叶斯决策的决策结果取决于实际
已给出训练样本的类条件概率和先验概率。贝叶斯概率是通过先验知识和统 计现有数据,使用概率的方法对某一事件未来可能发生的概率进行估计的。
最小错误贝叶斯分类的Matlab实现
D=[373.3 222.85 401.3 363.34 104.8 499.85 172.78 341.59 291.02 237.63 3087.05 3059.54 3259.94 3477.95 3389.83 3305.75 3084.49 3076.62 3095.68 3077.78 2429.47 2002.33 2150.98 2462.86 2421.83 3196.251.96]; % D belongs to w4 %以上为学习样本数据的输入 X1=mean(A')';X2=mean(B')';X3=mean(C')';X4=mean(D')'; %求样本均值 S1=cov(A');S2=cov(B');S3=cov(C');S4=cov(D'); %求样本协方差矩阵 S1_=inv(S1);S2_=inv(S2);S3_=inv(S3);S4_=inv(S4); % 求协方差矩阵的逆矩 阵 S11=det(S1);S22=det(S2);S33=det(S3);S44=det(S4); % 求协方差矩阵的行列 式 Pw1=N1/N;Pw2=N2/N;Pw3=N3/N;Pw4=N4/N; %先验概率
基于最小错误率的贝叶斯决策

基于最⼩错误率的贝叶斯决策理论上的东西,就不写了,也写不出什么有价值的东西,资料太多了。
后⽂很多关于原理的讲述都给出了其他⽂章的引⽤。
分享⼀个⽐较简单易懂的。
数据集:328 个同学的⾝⾼、体重、性别数据(78 个⼥⽣、250 个男⽣)124 个同学的数据(40 ⼥、84 男)90 个同学的数据(16 ⼥,74 男)问题描述:以dataset1为训练数据库,假设⾝⾼与体重满⾜⾼斯分布,进⾏⾼斯分布的参数估计,并进⾏基于最⼩错误率的贝叶斯分类,分别考虑男⼥的先验概率,0.5-0.5;0.6-0.4;0.7-0.3,0.8-0.2,并以dataset2和dataset3为测试数据库分析分类性能,并探讨先验概率对分类性能的影响需要解决的问题:通过⽂章开头提供的资料可以看出,其实判别的函数就是下图,就是给定⼀个待测向量X,它是类别Wi的概率。
等号右边,P(Wi)就是先验概率,⽽p(X|Wi)则需要根据⾼斯概率密度函数(什么是⾼斯分布?)进⾏估计:然⽽,上⾯常见的⾼斯概率密度函数只是针对⼀维的参数X,对于⼤多数情况,输⼊参数会是多维的,多元⾼斯概率密度函数怎么求解呢?可以参考这篇⽂章:。
于是,我们得到针对⼆元变量的概率密度函数求解为:重点说明下,上⾯的参数,是多元变量间的相关性参数,设定值应该⼩于1。
⼆元变量相关系数求法:解决问题(python,numpy库⽀持):#-*-encoding:utf-8-*-import numpyimport mathdef importdata(filename = 'dataset1.txt') :'''导⼊训练集'''f = open(filename,'r')dataset = []arr = []for item in f :vars = item.split()dataset.append([float(vars[0]), float(vars[1]), vars[2].upper()])return datasetdef getParameters(dataset) :'''从训练集分别获取不同类别下的期望、⽅差、标准差、类别的先验概率以及变量间相关系数'''class1 = []class2 = []class_sum = []for item in dataset :class_sum.append([item[0],item[1]])if item[-1] == 'F' :class1.append([item[0],item[1]])if item[-1] == 'M' :class2.append([item[0],item[1]])class1 = numpy.array(class1)class2 = numpy.array(class2)class_total = numpy.array(class_sum)mean1 = numpy.mean(class1,axis=0)variance1 = numpy.var(class1,axis=0)stand_deviation1 = numpy.std(class1,axis=0)mean2 = numpy.mean(class2,axis=0)variance2 = numpy.var(class2,axis=0)stand_deviation2 = numpy.std(class2,axis=0)class_total = (len(class1) + len(class2)) * 1.0mean = numpy.mean(class_sum, axis=0)stand_deviation = numpy.std(class_sum, axis=0)new_arr = [ ((item[0] - mean[0]) * (item[1] - mean[1]) / stand_deviation[0] / stand_deviation[1]) for item in dataset]coefficient = numpy.mean(new_arr)return (mean1,mean2),(variance1,variance2),(stand_deviation1, stand_deviation2),(len(class1)/class_total,len(class2)/class_total),coefficient def GaussianFunc(mean, variance, stand_deviation, coefficient) :'''根据指定参数(期望、⽅差、标准差、多元向量间的相关性)⽣成⾼斯函数多元变量的⾼斯函数'''def func(X) :X = [X[0] - mean[0], X[1] - mean[1]]B = [[variance[0], coefficient * stand_deviation[0] * stand_deviation[1]],[coefficient * stand_deviation[0] * stand_deviation[1], variance[1]]] inv_B = numpy.linalg.inv(B)A = inv_BB_val = (1.0 - coefficient**2) * variance[0] * variance[1]tmp1 = 2*math.pi * (B_val ** 0.5)X = numpy.array([X])tmp2 = (-0.5) * numpy.dot(numpy.dot(X, A), X.T)res = 1.0 / tmp1 * (math.e ** tmp2)return resreturn funcdef f(X, funcs, class_ps, index) :'''贝叶斯概率计算函数'''tmp1 = funcs[index](X) * class_ps[index]tmp2 = funcs[0](X) * class_ps[0] + funcs[1](X) * class_ps[1]return tmp1 / tmp2def classify(X,funcs,class_ps,labels) :'''基于最⼩错误率的贝叶斯判别分类。
正态分布下最小错误率的变量喷施贝叶斯决策

正态分布下最小错误率的变量喷施贝叶斯决策陈晓倩;唐晶磊;苗荣慧【摘要】传统农田除草采用田间统一定量均匀喷洒,导致了除草剂浪费和环境污染问题. 智能变量喷施能够保护环境和提高作物产量,是促进农业可持续发展战略的重要途径. 为此,对经典的杂草监测参数进行改进并提出了正态分布下最小错误率的贝叶斯决策以实现精确变量喷施. 首先对农田图像进行灰度化、二值化及去噪等预处理;然后依据作物行中心线对农田图像进行网格单元的划分,并在网格单元格内提取改进的杂草监测参数;最后将贝叶斯决策分为两个阶段:线下阶段利用改进的杂草监测参数数据库计算正态分布参数,线上阶段根据改进的杂草监测参数实现正态分布下最小错误率的贝叶斯决策,从而为变量喷施提供决策依据. 实验结果表明:正态分布下最小错误率的贝叶斯决策正确率可达9 2%,与BP 算法和SVM 算法相比决策正确率相对较高.%Traditional farmland spraying is united quantitative and evenly, and this cause the waste of herbicide and envi-ronment pollution.Intelligent variables spraying, which not only can protect environment but also increase crop output, is the crucial way to promote sustainable agriculture development.In this paper, first modified the classic weed infestation rate( WIR) and then an accurate variables spraying based on the minimum error Bayes decision under normal distribution is presented.Firstly, farmland images are pre-processing using graying, binary and de-noising.Secondly, grid unit of farmland images are divided according to the centerline of crop rows and then compute the modified weed infestation rate ( MWIR) in the grid unit.Finally, bayesian decision is divided into two stages.Normal distribution parameters are com-putedbase on database of MWIR in the offline stage, and Bayes online decision based on minimum error according to MWIR under normal distribution, which provide basis for decision making of intelligent variables spraying.The experi-mental results showed that the accuracy of this algorithm is as high as 92%, which exceeded BP algorithm and SVM algo-rithm.【期刊名称】《农机化研究》【年(卷),期】2016(038)007【总页数】6页(P114-119)【关键词】变量喷施;杂草监测参数;正态分布;最小错误率;贝叶斯决策【作者】陈晓倩;唐晶磊;苗荣慧【作者单位】西北农林科技大学信息工程学院,陕西杨凌 712100;西北农林科技大学信息工程学院,陕西杨凌 712100;西北农林科技大学信息工程学院,陕西杨凌712100【正文语种】中文【中图分类】S491;TP391.4我国是一个发展中的农业大国,农业发展关乎国家经济和社会的发展。
基于最小错误率与最小风险的贝叶斯分类比较与研究

的 充 要 条 件 是 a軆·b軋=b軋·c軆 =c軆·a軆 . 通过对闭折线性质定理的探讨,既使学生认识到闭折线性质定理
的内容简明,应用广泛,又培养了学生探究意识,为学生开辟了广阔的 思维空间,提供了创新机遇。 科
● 【参考文献】
[1]孟祥亚.浅谈培养学生应用向量的意识 [J].中学数学研究,2002,5. [2] 刘 八 芝 .向 量 在 中 学 数 学 教 学 中 的 应 用 .镇 江 高 专 学 报 [J].2003,02. [3]史建军, 张 无 忌.平 面 向 量 的 数 量 积 在 中 学 数 学 解 题 中 的 妙 用 [J].数 学 教 学 研 究 ,2007,9.
abc
此 题 是 用 柯 西 不 等 式 的 向 量 表 示 式|p軋·q軋|≤|p軋||q軋|等 号 成 立 的 条 件 证明的,另外我们对具有向量特征的代数总是问题,若注意观察,发现 其特征,通过构造向量来解题,往往有独到之处。
例 4 已知 a,b,c 为正数, 求函数 y= 姨x2+a2 + 姨(c-x)2+b2 的极小 值.
器。
2.4 关于 P(Hj|X)与 P(X|Hj)的区别
首先,要明确,从我们前面的理论大家可以发 现 P(Hj|X)是 后 演 概
率,是结论;P(X|Hj)是类条件概率密度函数,是已知的前提。 类概率条
件密度函数是前人总结的统计的概率分布, 我们是直接拿来使用的,
用它来补充先演概率的信息不足。
大学课程光电探测与目标识别作业及答案

第一次作业题一:什么是Johnson 判则?答:Johnson 依据实验,将视觉辨别分为四类:探测、取向、识别和确认,并把人眼对目标的观察感知同对“等效条带图案”的视觉联系起来,使人们可以不必顾及目标的具体类别和形态,直接以其“临界尺寸”中所包含的可分辨条带数来评定视觉感知水平。
Johnson 判则给出了在50%概率等级上,所需的可分辨等效条带周数。
通过这一方法探测能力大致与传感器的阈值条带图像分辨能力相关联,其实验结果已成为今天所用的目标辨别方法学的基础。
在工业应用中,Johnson 判则通常采用如下标准。
工业上采用的Johnson 判则题二:观察2km 外宽2m 、高1.5m 的坦克,如果人眼的空间分辨能力是20线对/度,用一个望远镜观察该坦克,要求对目标的识别概率达到50%,试求望远镜的视放大率。
解:坦克最小尺寸对人眼的张角为1.5/2000=0.00075rad 0.04297α≈≈︒要使识别概率达到50%,需在最小尺寸上观测到4个线对,对应的张角为4/200.2t α==︒则望远镜的视放大率应为tan 0.2 4.65tan 0.04297β︒Γ==≈︒题三:如果某人的瞳孔间距为60mm ,体视锐度为10”,试求(1)他的体视半径;(2)在50m 距离上,他的体视误差。
解:体视半径为2max min560mm 6.010/1237.610 4.84810D b α--⨯=∆===''⨯ 在50m 距离上的体视误差为()522250mmin 24.8481050/1050m /60mm= 2.02m 6.010D D b α--⨯⨯''∆=∆⋅=⨯=⨯第二次作业题一:一个年龄50岁的人,近点距离为-0.4m ,远点距离为无限远,试求他的眼睛的屈光调节范围。
解:远点对应的视度为1/0f SD =∞=近点对应的视度为1/0.4 2.5n SD =-=- 他眼睛的屈光调节范围是-2.5。
第2章贝叶斯决策理论

损 失状态(正常类)(异常类)
决策
ω1
ω2
α1(正常)0
6
α(2 异常)1
0
这意味着: 把异常类血细胞判别为正常类细胞所冒风险太大,所以 宁肯将之判别为异常类血细胞。
2.2.3 基于最小风险的贝叶斯决策应用实例
例:细胞识别
w1类
w2类
x
假设在某个局部地区细胞识别中, 率分别为
则 x wi
w1类 w3 类
w2 类
x
2.2 基于最小风险的贝叶斯决策
2.2.1 为什么要引入基于风险的决策
基于最小错误率的贝叶斯决策
错误率
如果 P w1 | x P w2 | x 则 x w1 如果 P w2 | x P w1 | x 则 x w2
误判为:x w2 误判为:x w1
正常(1)和异常(
2)两类的先验概
正常状态: 异常状态:
P P
((21))
=0.9; =0.1.
现有一待识别的细胞,其观察值为x ,从类条件概率密度分布曲线上
查得
P(x | 1 )=0.2, P(x | 2)=0.4.
且因误判而带来的风险如下页表所表示,试对该细胞x进行分类。
解: (1)利用贝叶斯公式,分别计算出 1及 2的后验概率。
wi
PD | wi Pwi
n
PD | wi Pwi
i 1
2.1.1 预备知识(续)
贝叶斯公式:
Pwi | D
PD | wi Pwi PD
(1763年提出)
贝叶斯公式由于其权威性、一致性和典雅性而被列入最优美的数 学公式之一 ;
由贝叶斯公式衍生出贝叶斯决策、贝叶斯估计、贝叶斯学习等 诸多理论体系,进而形成一个贝叶斯学派;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P(e
|
x)
P(2 P(1
| |
x) x)
1 1
P(1 P(2
| |
x) x)
1
max i
P(i
|
x)
x (, t) x (t, )
13
贝叶斯决策的错误率
条件错误率: P(e | x) (平均)错误率是条件错误率的数学期望。 (平均)错误率:
Bayes公 式 : 假 设 已 知 先 验 概 率 P ( ω i ) 和 观测值x的类条件概率密度函数p(x|ωi), i=1,2。
P(i
| x)
P(i , x)
p(x)
P(i ) p(x | i )
2
P( j ) p(x | j )
j 1
7
导弹目标及诱饵的检测、识别问题
23
No Pain, No Gain!
24
习题
1. 试简述先验概率,类条件概率密度函 数和后验概率等概念间的关系:
2. 试写出利用先验概率和分布密度函数 计算后验概率的公式
3. 用Matlab计算两类识别问题:根据血 液中白细胞的浓度来判断病人是否患 血液病。
25
Thank You!
26
应用:SAR图像处理
8
决策规则简化
P(i
| x)
P(i , x)
p(x)
P(i ) p(x | i )
P( j ) p(x | j )
j
9
决策规则简化
比较大小不需要计算p(x):
argmax P(i | x)
i
argmax p(x | i )P(i )
i
p(x)
argmax p(x | i )P(i )
4
导弹目标及诱饵的检测、识别问题
目标、诱饵识别问题:诱饵(ω1)和导弹(ω2) 根据已有知识和经验,两类的先验概率为:
诱饵(ω1): P(ω1)=0.9 导弹(ω2): P(ω2)=0.1 某一目标样本的红外特征观察值为x,从类条
件概率密度分布曲线得到: p(x|ω1)=0.2, p(x|ω2)=0.4 如何对该目标样本进行分类?
i
10
基于最小错误率Bayes决策图解
P (ωi|x) X=t
P (ω1|x)
P (ω2|x)
x
后验概率曲线
11
基于最小错误率Bayes决策图解
P (ωi|x) X=t
P (ω1|x)
P (ω2|x)
x
后验概率曲线
12
贝叶斯决策的错误率分析
条件错误率P(e|x)的计算: 以两类问题为例,当获得特征观测值x后,根据x 所在的区域,有两种决策可能:判定 x∈ω1 ,或 者x∈ω2。
p(x|ω1)P(ω1) X=t
p(x|ω2)P(ω2)
p2 P2e p1P1e
x
错误率分析曲线
16
贝叶斯决策的错误率分析
设t为两类的分界面,则在特征向量x是一 维时,t为x轴上的一点。形成两个决策区
域:R1~(-∞,t)和R2~(t,+∞)
ห้องสมุดไป่ตู้
P(e) E(P(e | x)) P(e | x) p(x)dx
• 问题的转换:
–基于样本估计P(Ci)和p(x|Ci)
–基于样本确定判别函数
21
应用:遥感图像地表分类
22
相关文献
●基于朴素贝叶斯分类的图像消噪,陈弋兰,安 庆师范学院学报(自然科学版)2008年8月 ●一种基于朴素贝叶斯分类的特征选择方法,余 芳等,中山大学学报(自然科学版)2004年9月
●基于朴素贝叶斯分类模型的车型识别方法,孙 青等,五邑大学学报(自然科学版)2008年8月
17
贝叶斯决策的错误率分析
P(e)
Pe
xPxdx
t
P
2
xPxdx
t
P(1
x) Px dx
利用条件概率的性质:
P(A | B)P(B) P(B | A)P(A)
t
P2
xPxdx
t
P(1
x)Pxdx
t
px
p(x|ω1)P(ω1) X=t
p(x|ω2)P(ω2)
p2 P2e p1P1e
x
错误率分析曲线
20
基于最小错误率的Bayes决策
• 基于最小错误率的Bayes决策是一致最优 决策。
• 基于最小错误率的Bayes决策的三个前提:
–类别数确定
–各类的先验概率P(Ci)已知 –各类的条件概率密度函数p(x|Ci)已知
5
贝叶斯公式
事件Ai的先验概率
在事件Ai发生的条件下 事件B发生的概率
P( Ai | B )
P( Ai ) P( B| Ai ) , k 1,..., n k P(Ak )P(B | Ak )
事件B发生的概率 在事件B发生的条件下,
事件Ai发生的概率
6
后验概率P (ωi| x)的计算
美国加州洛杉矶的卫星雷达图像 27
应用:SAR图像处理
28
相关论文
●基于朴素贝叶斯分类的图像消噪,陈弋兰,安 庆师范学院学报(自然科学版)2008年8月 ●一种基于朴素贝叶斯分类的特征选择方法,余 芳等,中山大学学报(自然科学版)2004年9月
目标、诱饵识别问题:诱饵(ω1)和导弹(ω2) 根据已有知识和经验,两类的先验概率为:
诱饵(ω1): P(ω1)=0.9 导弹(ω2): P(ω2)=0.1 某一目标样本的红外特征观察值为x,从类条
件概率密度分布曲线得到: p(x|ω1)=0.2, p(x|ω2)=0.4 如何对该目标样本进行分类?
2
P2
dx
t
px
1 P1
dx
18
贝叶斯决策的错误率分析
P(e)
t
P(2 ) p(x 2 )dx P(1) t p(x 1)dx
P(2 )P2 (e) P(1)P1(e)
19
基于最小错误率Bayes决策图解
p(x|ωi)P(ωi)
模式识别
Pattern Recognition
教材
《模式识别》 (第二版)
边肇祺等编 清华大学出版社
1
基于最小错误率的贝叶斯决策
余华
2
内容回顾
模式识别:使计算机模仿人的感知能力,从感知 数据中提取信息(判别物体和行为)的过程。
姚明
ROCKETS 11 YAO
3
敌方在发射导弹的同时发射多枚诱饵弹
P(e) E(P(e | x)) P(e | x) p(x)dx 14
贝叶斯决策的错误率
基于最小错误率的Bayes决策使得每个观测 值下的条件错误率最小,因而保证了(平均) 错误率最小。
Bayes决策是一致最优决策。
15
基于最小错误率Bayes决策图解
p(x|ωi)P(ωi)
