2018北京各区初中数学二模分类汇编27号题及答案
北京市2018年中考数学二模试题汇编(20份)

代几综合题2018昌平二模28.在平面直角坐标系xOy 中,对于任意三点A 、B 、C 我们给出如下定义:“横长”a :三点中横坐标的最大值与最小值的差,“纵长”b :三点中纵坐标的最大值与最小值的差,若三点的横长与纵长相等,我们称这三点为正方点.例如:点A (2-,0) ,点 B (1,1) ,点 C (1-, 2-),则A 、B 、C 三点的 “横长”a =|1(2)--|=3,A 、B 、C 三点的“纵长”b =|1(2)--|=3. 因为a =b ,所以A 、B 、C 三点为正方点.(1)在点R (3,5) ,S (3,2-) ,T (4-,3-)中,与点A 、B 为正方点的是 ; (2)点P (0,t )为y 轴上一动点,若A ,B ,P 三点为正方点,t 的值为 ; (3)已知点D (1,0).①平面直角坐标系中的点E 满足以下条件:点A ,D ,E 三点为正方点,在图中画出所有符合条件的点E 组成的图形; ②若直线l :12y x m =+上存在点N ,使得A ,D ,N 三点为正方点,直接写出m 的取值范围.y xxy yx2018朝阳二模28. 对于平面直角坐标系xOy 中的点P 和直线m ,给出如下定义:若存在一点P ,使得点P 到直线m 的距离等于,则称P 为直线m 的平行点. (1)当直线m 的表达式为y =x 时, ①在点P 1(1,1),P 2(0,2),P 3(22-,22)中,直线m 的平行点是 ; ②⊙O 的半径为10,点Q 在⊙O 上,若点Q 为直线m 的平行点,求点Q 的坐标. (2)点A 的坐标为(n ,0),⊙A 半径等于1,若⊙A 上存在直线x y 3=的平行点,直接写出n 的取值范围.2018东城二模28. 研究发现,抛物线214y x =上的点到点F (0,1)的距离与到直线l :1y =-的距离相等.如图1所示,若点P 是抛物线214y x =上任意一点,PH ⊥l 于点H ,则PH PF =.基于上述发现,对于平面直角坐标系x O y 中的点M ,记点M 到点P 的距离与点P 到点F 的距离之和的最小值为d ,称d 为点M 关于抛物线214y x =的关联距离;当24d ≤≤时,称点M 为抛物线214y x =的关联点.(1)在点1(20)M ,,2(12)M ,,3(45)M ,,4(04)M -,中,抛物线214y x =的关联点是______ ;(2)如图2,在矩形ABCD 中,点(1)A t ,,点(13)C t +, ①若t =4,点M 在矩形ABCD 上,求点M 关于抛物线214y x =的关联距离d 的取值范围;②若矩形ABCD 上的所有点都是抛物线214y x =的关联点,则t 的取值范围是__________.2018房山二模28. 已知点P,Q为平面直角坐标系xOy中不重合的两点,以点P为圆心且经过点Q作⊙P,则称点Q为⊙P的“关联点”,⊙P为点Q的“关联圆”.(1)已知⊙O的半径为1,在点E(1,1),F(-12,32),M(0,-1)中,⊙O的“关联点”为;(2)若点P(2,0),点Q(3,n),⊙Q为点P的“关联圆”,且⊙Q的半径为 5 ,求n的值;(3)已知点D(0,2),点H(m,2),⊙D是点H的“关联圆”,直线443y x=-+与x轴,y轴分别交于点A,B. 若线段AB上存在⊙D的“关联点”,求m的取值范围.2018丰台二模28.在平面直角坐标系xOy 中,将任意两点()11,y x P 与()22y x Q ,之间的“直距”定义为:2121y y x x D PQ -+-=.例如:点M (1,2-),点N (3,5-),则132(5)5MN D =-+---=. 已知点A (1,0)、点B (-1,4).(1)则_______=AO D ,_______=BO D ;(2)如果直线AB 上存在点C ,使得CO D 为2,请你求出点C 的坐标; (3)如果⊙B 的半径为3,点E 为⊙B 上一点,请你直接写出EO D 的取值范围.2018海淀二模28.对某一个函数给出如下定义:若存在实数k ,对于函数图象上横坐标之差为1的任意两点1(,)a b ,2(1,)a b +,21b b k -≥都成立,则称这个函数是限减函数,在所有满足条件的k 中,其最大值称为这个函数的限减系数.例如,函数2y x =-+,当x 取值a 和1a +时,函数值分别为12b a =-+,21b a =-+,故211b b k -=-≥,因此函数2y x =-+是限减函数,它的限减系数为1-.(1)写出函数21y x =-的限减系数; (2)0m >,已知1y x=(1,0x m x -≤≤≠)是限减函数,且限减系数4k =,求m 的取值范围.(3)已知函数2y x =-的图象上一点P ,过点P 作直线l 垂直于y 轴,将函数2y x =-的图象在点P 右侧的部分关于直线l 翻折,其余部分保持不变,得到一个新函数的图象,如果这个新函数是限减函数,且限减系数1k ≥-,直接写出P 点横坐标n 的取值范围.2018平谷二模28.对于平面直角坐标系xOy 中的点P 和⊙M ,给出如下定义:若⊙M 上存在两个点A ,B ,使AB =2PM ,则称点P 为⊙M 的“美好点”. (1)当⊙M 半径为2,点M 和点O 重合时,○1点()120P -, ,()211P ,,()322P ,中,⊙O 的“美好点”是 ; ○2点P 为直线y=x+b 上一动点,点P 为⊙O 的“美好点”,求b 的取值范围; (2)点M 为直线y=x 上一动点,以2为半径作⊙M ,点P 为直线y =4上一动点,点P 为⊙M 的“美好点”,求点M 的横坐标m 的取值范围.2018石景山二模28.在平面直角坐标系xOy 中,对于任意点P ,给出如下定义:若⊙P 的半径为1,则称⊙P 为点P 的“伴随圆”. (1)已知,点()1,0P ,①点1,2A ⎛⎝⎭在点P 的“伴随圆” (填“上”或“内”或“外”); ②点()1,0B -在点P 的“伴随圆” (填“上”或“内”或“外”);(2)若点P 在x 轴上,且点P 的“伴随圆”与直线x y 33=相切,求点P 的坐标; (3)已知直线2+=x y 与x 、y 轴分别交于点A ,B ,直线2-=x y 与x 、y 轴分别交于点C ,D ,点P 在四边形ABCD 的边上并沿DA CD BC AB →→→的方向移动,直接写出点P 的“伴随圆”经过的平面区域的面积.2018西城二模28. 对于平面直角坐标系xOy 中的点(,)Q x y (x ≠0),将它的纵坐标y 与横坐标x 的比yx称为点Q 的“理想值”,记作Q L .如(1,2)Q -的“理想值”221Q L ==--. (1)①若点(1,)Q a 在直线4y x =-上,则点Q 的“理想值”Q L 等于_________;②如图,C ,⊙C 的半径为1. 若点Q 在⊙C 上,则点Q 的“理想值”Q L 的取值范围是 .(2)点D 在直线+3y =上,⊙D 的半径为1,点Q 在⊙D 上运动时都有0≤L Q ,求点D 的横坐标D x 的取值范围;(3)(2,)M m (m >0),Q 是以r 为半径的⊙M 上任意一点,当0≤L Q ≤件的最大圆,并直接写出相应的半径r 的值.(要求画图位置准确,但不必尺规作图)2018怀柔二模28. A 为⊙C 上一点,过点A 作弦AB ,取弦AB 上一点P ,若满足131<≤ABAP ,则称P 为点A 关于⊙C 的黄金点.已知⊙C 的半径为3,点A 的坐标为(1,0). (1)当点C 的坐标为(4,0)时,①在点D (3,0),E (4,1),F (7,0)中,点A 关于⊙C 的黄金点是 ; ②直线3333-=x y 上存在点A 关于⊙C 的黄金点P ,求点P 的横坐标的取值范围; (2)若y 轴上存在..点A 关于⊙C 的黄金点,直接写出点C 横坐标的取值范围.2018门头沟二模28.在平面直角坐标系xOy中的某圆上,有弦MN,取MN的中点P,我们规定:点P到某点(直”表示.线)的距离叫做“弦中距”,用符号“d中以(3,0)W-为圆心,半径为2的圆上.(1)已知弦MN长度为2.①如图1:当MN∥x轴时,直接写出到原点O的d的长度;中的取值范围.②如果MN在圆上运动时,在图2中画出示意图,并直接写出到点O的d中(2)已知点(5,0)y x=-,求到直线2=-的dy xM-,点N为⊙W上的一动点,有直线2中备用图2018顺义二模28.已知边长为2a 的正方形ABCD ,对角线AC 、BD 交于点Q ,对于平面内的点P 与正方形ABCD ,给出如下定义:如果a ≤PQ,则称点P 为正方形ABCD 的“关联点”.在平面直角坐标系xOy 中,若A (-1,1),B (-1,-1),C (1,-1),D (1,1) .(1)在11(,0)2-P,21(2P,3P 中,正方形ABCD 的“关联点”有 ; (2)已知点E 的横坐标是m ,若点E在直线=y 上,并且E 是正方形ABCD 的“关联点”,求m 的取值范围;(3)若将正方形ABCD 沿x 轴平移,设该正方形对角线交点Q 的横坐标是n ,直线1=+y 与x 轴、y 轴分别相交于M 、N 两点.如果线段MN 上的每一个点都是正方形ABCD 的“关联点”,求n 的取值范围.代数综合题2018昌平二模26.在平面直角坐标系xOy 中,抛物线223(0)y ax ax a a =--≠,与x 轴交于A 、B 两点(点A 在点B 的左侧). (1)求点A 和点B 的坐标;(2)若点P (m ,n )是抛物线上的一点,过点P 作x 轴的垂线,垂足为点D .①在0a >的条件下,当22m -≤≤时,n 的取值范围是45n -≤≤,求抛物线的表达式; ②若D 点坐标(4,0),当PD AD >时,求a 的取值范围.2018朝阳二模26.已知二次函数)0(222≠--=a ax ax y .(1)该二次函数图象的对称轴是直线 ;(2)若该二次函数的图象开口向上,当-1≤x ≤5时,函数图象的最高点为M ,最低点为N ,点M 的纵坐标为211,求点M 和点N 的坐标;(3)对于该二次函数图象上的两点A (x 1,y 1),B (x 2,y 2),设t ≤ x 1 ≤ t +1,当x 2≥3时,均有y 1 ≥ y 2,请结合图象,直接写出t 的取值范围.2018东城二模26.在平面直角坐标系xOy 中,抛物线()230y ax bx a =+-≠经过点()1,0A -和点()45B ,. (1)求该抛物线的表达式;(2)求直线AB 关于x 轴的对称直线的表达式;(3)点P 是x 轴上的动点,过点P 作垂直于x 轴的直线l ,直线l 与该抛物线交于点M ,与直线AB 交于点N .当PM PN <时,求点P 的横坐标P x 的取值范围.2018房山二模26. 在平面直角坐标系xOy 中,二次函数2y ax bx c =++(0a ≠)的图象经过A (0,4),B (2,0),C (-2,0)三点.(1)求二次函数的表达式;(2)在x 轴上有一点D (-4,0),将二次函数的图象沿射线DA 方向平移,使图象再次经过点B .①求平移后图象顶点E 的坐标;②直接写出此二次函数的图象在A ,B 两点之间(含A ,B 两点)的曲线部分在平移过程中所扫过的面积.2018丰台二模26.在平面直角坐标系xOy 中,二次函数22y x hx h =-+的图象的顶点为点D . (1)当1h =-时,求点D 的坐标; (2)当1x ≤≤≤1-≤1时,求函数的最小值m .(用含h 的代数式表示m )2018海淀二模26.在平面直角坐标系xOy 中,已知点(3,1)A -,(1,1)B -,(,)C m n ,其中1n >,以点,,A B C 为顶点的平行四边形有三个,记第四个顶点分别为123,,D D D ,如图所示.(1)若1,3m n =-=,则点123,,D D D 的坐标分别是( ),( ),( ); (2)是否存在点C ,使得点123,,,,A B D D D 在同一条抛物线上?若存在,求出点C 的坐标;若不存在,说明理由.2018平谷二模26.在平面直角坐标系中,点D 是抛物线223y ax ax a =--()0a >的顶点,抛物线与x轴交于点A ,B (点A 在点B 的左侧). (1)求点A ,B 的坐标;(2)若M 为对称轴与x 轴交点,且DM =2AM ,求抛物线表达式; (3)当30°<∠ADM <45°时,求a 的取值范围.2018石景山二26.在平面直角坐标系xOy 中,抛物线()240y ax x c a =++≠经过点()34,A -和()02,B .(1)求抛物线的表达式和顶点坐标;(2)将抛物线在A 、B 之间的部分记为图象M (含A 、B 两点).将图象M 沿直线3x =翻折,得到图象N .若过点()94,C 的直线y kx b =+与图象M 、图象N 都相交,且只有两个交点,求b 的取值范围.2018西城二模26. 抛物线M :241y ax ax a =-+- (a ≠0)与x 轴交于A ,B 两点(点A 在点B 左侧),抛物线的顶点为D .(1)抛物线M 的对称轴是直线____________; (2)当AB =2时,求抛物线M 的函数表达式;(3)在(2)的条件下,直线l :y kx b =+(k ≠0)经过抛物线的顶点D ,直线y n =与抛物线M 有两个公共点,它们的横坐标分别记为1x ,2x ,直线y n =与直线l 的交点的横坐标记为3x (30x >),若当2-≤n ≤1-时,总有13320x x x x ->->,请结合函数的图象,直接写出k 的取值范围.2018怀柔二模26.在平面直角坐标系xOy 中,二次函数C 1:()332--+=x m mx y (m >0)的图象与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C . (1)求点A 和点C 的坐标; (2)当AB =4时,①求二次函数C 1的表达式;②在抛物线的对称轴上是否存在点D ,使△DAC 的周长最小,若存在,求出点D 的坐标,若不存在,请说明理由;(3)将(2)中抛物线C 1向上平移n 个单位,得到抛物线C 2,若当0≤x ≤25时,抛物线C 2与x 轴只有一个公共点,结合函数图象,求出n 的取值范围.2018门头沟二模26.在平面直角坐标系xOy 中,有一抛物线其表达式为222y x mx m =-+. (1)当该抛物线过原点时,求m 的值;(2)坐标系内有一矩形OABC ,其中(4,0)A 、(4,2)B . ①直接写出C 点坐标;②如果抛物线222y x mx m =-+与该矩形有2个交点,求m 的取值范围.x2018顺义二模26.在平面直角坐标系中,二次函数221y x ax a =+++的图象经过点 M (2,-3). (1)求二次函数的表达式;(2)若一次函数(0)y kx b k =+≠的图象与二次函数221y x ax a =+++的图象经过x 轴上同一点,探究实数k ,b 满足的关系式;(3)将二次函数221y x ax a =+++的图象向右平移2个单位,若点P (x 0,m )和Q (2,n )在平移后的图象上,且m >n ,结合图象求x 0的取值范围.反比例综合题2018昌平二模22.如图,在平面直角坐标系xOy 中,一次函数+(0)y ax b a =≠与反比例函数ky k x=≠(0)的图象交于点A (4,1)和B (1-,n ). (1)求n 的值和直线+y ax b =的表达式;(2)根据这两个函数的图象,直接写出不等式0kax b x+-<的解集.x2018朝阳二模21. 如图,在平面直角坐标系xOy 中,直线61+=x k y 与函数)0(2>=x xk y 的图象的两个交点分别为A (1,5),B . (1)求21,k k 的值;(2)过点P (n ,0)作x 轴的垂线,与直线61+=x k y 和函数)0(2>=x xk y 的图象的交点分别为点M ,N ,当点M 在点N 下方时,写出n 的取值范围.2018东城二模22. 已知函数1y x =的图象与函数()0y kx k =≠的图象交于点(),P m n .(1)若2m n =,求k 的值和点P 的坐标;(2)当m n ≤时,结合函数图象,直接写出实数k 的取值范围.2018房山二模22. 如图,在平面直角坐标系xOy 中,直线y kx m =+与双曲线2y x=-相交于 点A (m ,2).(1)求直线y kx m =+的表达式; (2)直线y kx m =+与双曲线2y x=-的另一个交点为B ,点P 为x 轴上一点,若AB BP =,直接写出P 点坐标 .2018丰台二模22.在平面直角坐标系xOy 中,直线l :21(0)y mx m m =-+≠. (1)判断直线l 是否经过点M (2,1),并说明理由; (2)直线l 与反比例函数ky x=的图象的交点分别为点M ,N ,当OM =ON 时,直接写出点N 的坐标.2018海淀二模22.已知直线l 过点(2,2)P ,且与函数(0)ky x x=>的图象相交于,A B 两点,与x 轴、y 轴分别交于点,C D ,如图所示,四边形,ONAE OFBM 均为矩形,且矩形OFBM 的面积为3. (1)求k 的值;(2)当点B 的横坐标为3时,求直线l 的解析式及线段BC 的长; (3)如图是小芳同学对线段,AD BC 的长度关系的思考示意图.记点B 的横坐标为s ,已知当23s <<时,线段BC 的长随s 的增大而减小,请你参考小芳的示意图判断:当3s ≥时,线段BC 的长随s 的增大而 . (填“增大”、“减小”或“不变”)2018平谷二模21.如图,在平面直角坐标系xOy 中,函数()0ky k x=≠的图象与直线y =x -2交于点A (a ,1). (1)求a ,k 的值;(2)已知点P (m ,0)(1≤m < 4),过点P 作平行于y 轴的直线,交直线y =x -2于点M (x 1,y 1),交函数()0ky k x=≠的图象于点N (x 1,y 2),结合函数的图象,直接写出12y y -的取值范围.2018石景山二模22.在平面直角坐标系xOy 中,直线1:2l y x b =-+与x 轴,y 轴分别交于点1(,0)2A ,B ,与反比例函数图象的一个交点为(),3M a . (1)求反比例函数的表达式;(2)设直线2:2l y x m =-+与x 轴,y 轴分别交于点C ,D ,且3OCD OAB S S ∆∆=,直接写出m 的值 .2018西城二模23. 如图,在平面直角坐标系xOy 中,函数my x=(0x <)的图象经过点(4,)A n -,AB ⊥x 轴于点B ,点C 与点A 关于原点O 对称, CD ⊥x 轴于点D ,△ABD 的面积为8.(1)求m ,n 的值;(2)若直线y kx b =+(k ≠0)经过点C ,且与x 轴,y 轴的交点分别为点E ,F ,当2CF CE =时,求点F 的坐标.2018怀柔二模23.在平面直角坐标系xOy 中,直线y =kx +b (k ≠0)与双曲线)0(≠=m xmy 相交于A ,B 两点,A 点坐标为(-3,2),B 点坐标为(n ,-3). (1)求一次函数和反比例函数表达式;(2)如果点P 是x 轴上一点,且△ABP 的面积是5,直接写出点P 的坐标.2018门头沟二模20. 如图,在平面直角坐标系xOy 中,一次函数y x =与反比例函数ky x=(k ≠0)的图象相交于点(2,2)M . (1)求k 的值;(2)点(0,)P a 是y 轴上一点,过点P 且平行于x 轴的直线分别与一次函数y x =、反比例函数ky x=的图象相交于点1(,)A x b 、2(,)B x b ,当12x x <时,画出示意图并直接写出a 的取值范围.2018顺义二模20.如图,在平面直角坐标系xOy 中,函数ky x=(x >0)的图象与直线21y x =+交于点A (1,m ).(1)求k 、m 的值;(2)已知点P (n ,0)(n ≥1),过点P 作平行于y 轴的直线,交直线21y x =+于点B ,交函数ky x=(x >0)的图象于点C .横、纵坐标都是整数的点叫做整点. ①当3n =时,求线段AB 上的整点个数; ②若ky x=(x >0)的图象在点A 、C 之间的部分与线段AB 、BC 所围成的区域内(包括边界)恰有5个整点,直接写出n 的取值范围.函数操作题2018昌平二模25.有这样一个问题:探究函数3126y x x =-的图象与性质.小彤根据学习函数的经验,对函数3126y x x =-的图象与性质进行了探究.下面是小彤探究的过程,请补充完整:(1)求m 的值为 ;(2)如图,在平面直角坐标系xOy 中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出了图象的一部分,请根据剩余的点补全此函数的图象;(3)方程31226x x -=-实数根的个数为 ; (4)观察图象,写出该函数的一条性质 ; (5)在第(2)问的平面直角坐标系中画出直线12y x =,根据图象写出方程311262x x x -=的一个正数根约为 (精确到0.1).2018朝阳二模25. 在数学活动课上,老师提出了一个问题:把一副三角尺如图1摆放,直角三角尺的两条直角边分别垂直或平行,60°角的顶点在另一个三角尺的斜边上移动,在这个运动过程中,有哪些变量,能研究它们之间的关系吗?小林选择了其中一对变量,根据学习函数的经验,对它们之间的关系进行了探究.下面是小林的探究过程,请补充完整:(1)画出几何图形,明确条件和探究对象;如图2,在Rt △ABC 中,∠C =90°,AC =BC =6cm ,D 是线段AB 上一动点,射线DE ⊥BC 于点E ,∠EDF = °,射线DF 与射线AC 交于点F .设B ,E 两点间的距离为x cm ,E ,F 两点间的距离为y cm .图1 图2(说明:补全表格时相关数据保留一位小数)(3)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(4)结合画出的函数图象,解决问题:当△DEF为等边三角形时,BE的长度约为 cm.2018东城二模25. 小强的妈妈想在自家的院子里用竹篱笆围一个面积为4平方米的矩形小花园,妈妈问九年级的小强至少需要几米长的竹篱笆(不考虑接缝).小强根据他学习函数的经验做了如下的探究. 下面是小强的探究过程,请补充完整:建立函数模型:设矩形小花园的一边长为x米,篱笆长为y米.则y关于x的函数表达式为 ;列表(相关数据保留一位小数):根据函数的表达式,得到了x与y的几组值,如下表:描点、画函数图象:如图,在平面直角坐标系xOy 中,描出了以上表中各对对应值为坐标的点, 根据描出的点画出该函数的图象; 观察分析、得出结论:根据以上信息可得,当x = 时,y 有最小值. 由此,小强确定篱笆长至少为 米.2018房山二模25. 有这样一个问题:探究函数3126y x x =-的图象与性质. 小东根据学习函数的经验,对函数3126y x x =-的图象与性质进行了探究.下面是小东的探究过程,请补充完整: (1)函数3126y x x =-的自变量x 的取值范围是 ; (2) 下表是y 与x 的几组对应值则m的值为;(3) 如下图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;(4)观察图象,写出该函数的两条性质.2018丰台二模25.数学活动课上,老师提出问题:如图,有一张长4dm,宽3dm的长方形纸板,在纸板的四个角裁去四个相同的小正方形,然后把四边折起来,做成一个无盖的盒子,问小正方形的边长为多少时,盒子的体积最大.下面是探究过程,请补充完整:Array(1)设小正方形的边长为x dm,体积为y dm3,根据长方体的体积公式得到y和x的关系式:;(2)确定自变量x的取值范围是;(3)列出y与x的几组对应值.(说明:表格中相关数值保留一位小数)(4)在下面的平面直角坐标系xOy中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(5)结合画出的函数图象,解决问题:当小正方形的边长约为 dm时,盒子的体积最大,最大值约为 dm3.2018海淀二模25.小明对某市出租汽车的计费问题进行研究,他搜集了一些资料,部分信息如下:备注:出租车计价段里程精确到500米;出租汽车收费结算以元为单位,元以下四舍五入。
2018北京13区初三二模数学分类汇编--第27题

(2018海淀二模)27.在平面直角坐标系xOy 中,抛物线224y mx m m x -++=与y 轴交于点A (0,3),与x 轴交于点B ,C (点B 在点C 左侧).(1)求该抛物线的表达式及点B ,C 的坐标;(2)抛物线的对称轴与x 轴交于点D ,若直线y kx b =+经过点D 和点E (1,2)--,求直线DE 的表达式;(3)在(2)的条件下,已知点P (t ,0),过点P 作垂直于x 轴的直线交抛物线于点M ,交直线DE 于点N ,若点M 和点N 中至少有一个点在x 轴下方,直接写出t 的取值范围.(2018东城二模)27.在平面直角坐标系中,抛物线2+3y ax bx =+()0≠a 与x 轴交于点A (-3,0)、B (1,0)两点, D 是抛物线顶点,E 是对称轴与x 轴的交点. (1)求抛物线的解析式;(2)若点F 和点D 关于x 轴对称, 点P 是x 轴上的一个动点,过点P 作PQ ∥OF 交抛物线于点Q ,是否存在以点O ,F ,P ,Q 为顶点的平行四边形?若存在,求出点P 坐标;若不存在,请说明理由.(2018西城二模)27. 已知一次函数1y k x b =+(k ≠0)的图象经过(2,0),(4,1)两点,二次函数 2224y x a x =-+(其中a >2). (1)求一次函数的表达式及二次函数图象的顶点坐标(用含a 的代数式表示);(2)利用函数图象解决下列问题:①若25=a ,求当10y >且2y ≤0时,自变量x 的取值范围;xy()–5–4–3–2–112345–5–4–3–2–112345o②如果满足10y >且2y ≤0时的自变量x的取值范围内恰有一个整数,直接写出a 的取值范围.(2018朝阳二模)27. 已知:关于x 的一元二次方程22(1)20(0)a x a x a a --+-=>. (1)求证:方程有两个不相等的实数根;(2)设方程的两个实数根分别为1x ,2x (其中1x >2x ).若y 是关于a 的函数,且21y ax x =+,求这个函数的表达式;(3)在(2)的条件下,结合函数的图象回答:若使231y a ≤-+,则自变量a 的取值范围为 .(2018丰台二模)27.在平面直角坐标系xOy 中,抛物线21y ax bx =++经过(13)A ,,(21)B ,两点.(1)求抛物线及直线AB 的解析式;(2)点C 在抛物线上,且点C 的横坐标为3.将抛物线在 点A ,C 之间的部分(包含点A ,C )记为图象G ,如 果图象G 沿y 轴向上平移t (0t >)个单位后与直线 AB 只有一个公共点,求t 的取值范围.75676544123123321213xOy(2018顺义二模)27.已知关于x 的方程()2230x m x m +-+-=.(1)求证:方程()2230x m x m +-+-=总有两个实数根; (2)求证:抛物线()223y x m x m =+-+-总过x 轴上的一个定点;(3)在平面直角坐标系xOy 中,若(2)中的“定点”记作A ,抛物线()223y x m x m =+-+-与x 轴的另一个交点为B , 与y 轴交于点C ,且△OBC 的面积小于或等于8,求m 的 取值范围.(2018平谷二模) 27.如图,在平面直角坐标系中,点 A (5,0),B (3,2),点C 在线段OA 上,BC =BA ,点Q 是线段BC 上一个动点,点P 的坐标是(0,3),直线PQ 的解析式为y=kx+b (k ≠0),且与x 轴交于点D .(1)求点C 的坐标及b 的值;(2)求k 的取值范围;(3)当k 为取值范围内的最大整数时,过点B作BE ∥x 轴,交PQ 于点E ,若抛物线y=ax 2﹣5ax (a ≠0)的顶点在四边形ABED 的内部,求a 的取值范围.(2018门头沟二模)xyOyx D P BA O C QxyO27.在平面直角坐标系xOy 中,抛物线214y x bx c =-++经过点A (4,0)和B (0,2).(1)求该抛物线的表达式;(2)在(1)的条件下,如果该抛物线的顶点为C ,点B 关于抛物线对称轴对称的点为D ,求直线CD 的表达式;(3)在(2)的条件下,记该抛物线在点A ,B 之间的部分(含点A ,B )为图象G ,如果图象G 向上平移m (m >0)个单位后与直线CD 只有一个公共点,请结合函数的图象,直接写出m 的取值范围.(2018房山二模)27.已知关于x 的一元二次方程()23130kx k x +++= (k ≠0).(1)求证:无论k 取何值,方程总有两个实数根; (2)点()()120,0A x B x ,、在抛物线()2313y kx k x =+++上,其中12x x <0<,且12x x 、和k 均为整数,求A ,B 两点的坐标及k 的值;(3) 设(2)中所求抛物线与y 轴交于点C ,问该抛物线上是否存在点E ,使得ABEABCS S=,若存在,求出E 点坐标,若不存在,说明理由.(2018昌平二模)yx11O27.已知抛物线2y ax bx c =++经过原点O 及点A (-4,0)和点B (-6,3). (1)求抛物线的解析式以及顶点坐标;(2)如图1,将直线2y x =沿y 轴向下平移后与(1)中所求抛物线只有一个交点C ,平移后的直线与y 轴交于点D ,求直线CD 的解析式;(3)如图2,将(1)中所求抛物线向上平移4个单位得到新抛物线,请直接写出新抛物线上到直线CD 距离最短的点的坐标及该最短距离.yx图1BACD Oyx图2CD O(2018通州二模)27.已知关于x 的方程mx 2-(3m -1)x +2m -2=0(1)求证:无论m 取任何实数时,方程恒有实数根.(2)若关于x 的二次函数y = mx 2-(3m -1)x +2m -2的图象与x 轴两交点间的距离为2时,求二次函数的表达式.。
2018年北京市西城区中考二模数学试卷附答案

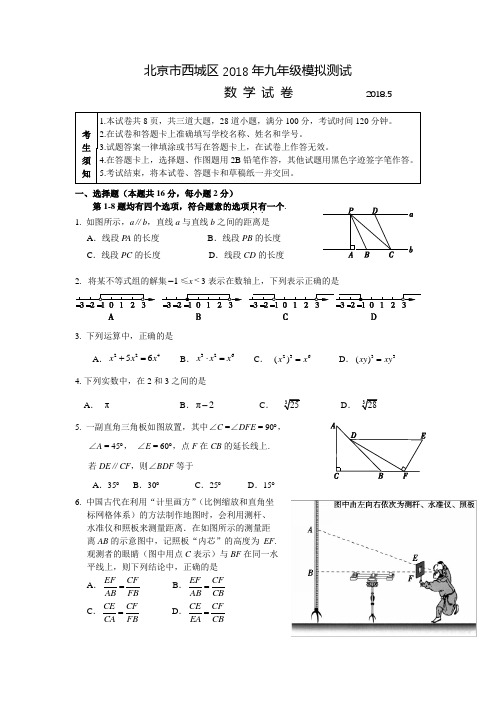
北京市西城区2018年九年级模拟测试2分)第1-8题均有四个选项,符合题意的选项只有一个.1. 如图所示,a ∥b ,直线a 与直线b 之间的距离是A .线段PA 的长度 B .线段PB 的长度C .线段PC 的长度D .线段CD 的长度2. 将某不等式组的解集1-≤x <3表示在数轴上,下列表示正确的是3. 下列运算中,正确的是A .22456x x x +=B .326x x x ⋅=C . 236()x x =D .33()xy xy =4.下列实数中,在2和3之间的是A . πB .π2-C .325D .3285. 一副直角三角板如图放置,其中∠C =∠DFE = 90︒,∠A = 45︒, ∠E = 60︒,点F 在CB 的延长线上.若DE ∥CF ,则∠BDF 等于A .35︒ B .30︒ C .25︒D .15︒6. 中国古代在利用“计里画方”(比例缩放和直角坐标网格体系)的方法制作地图时,会利用测杆、 水准仪和照板来测量距离.在如图所示的测量距离AB 的示意图中,记照板“内芯”的高度为 EF . 观测者的眼睛(图中用点C 表示)与BF 在同一水平线上,则下列结论中,正确的是A .B .EF CFAB FB =EF CFAB CB =C .D .CE CFCA FB=CE CFEA CB=7. 在一次男子马拉松长跑比赛中,随机抽取了10名选手,记录他们的成绩(所用的时间)如下:A .这组样本数据的平均数超过130B .这组样本数据的中位数是147C .在这次比赛中,估计成绩为130 min 的选手的成绩会比平均成绩差D .在这次比赛中,估计成绩为142 min 的选手,会比一半以上的选手成绩要好 8.如图1所示,甲、乙两车沿直路同向行驶,车速分别为20 m/s 和v (m/s),起初甲车在乙 车前a (m)处,两车同时出发,当乙车追上甲车时,两车都停止行驶.设x (s)后两车相距y(m),y 与x 的函数关系如图2所示.有以下结论:①图1中a 的值为500;②乙车的速度为35 m/s ;③图1中线段EF 应表示为;5005x +④图2中函数图象与x 轴交点的横坐标为100.其中所有的正确结论是A .①④B .②③C .①②④D .①③④二、填空题(本题共16分,每小题2分)9.有意义,那么x 的取值范围是 .10.不透明袋子中装有5个红色球和3个蓝色球,这些球除了颜色外没有其他差别.从袋子中随机摸出一个球,摸出蓝色球的概率为 .11. 如图,等边三角形ABC 内接于⊙O ,若⊙O 的半径为2,则图中阴影部分的面积等于 .12.某校“百变魔方”社团为组织同学们参加学校科技节的“最强大脑”大赛,准备购买A ,B 两款魔方.社长发现若购买2个A 款魔方和6个B 款魔方共需170元,购买3个A 款魔方和购买8个B 款魔方所需费用相同. 求每款魔方的单价.设A 款魔方的单价为x 元,B 款魔方的单价为y 元,依题意可列方程组为.13. 如图,在矩形ABCD 中,顺次连接矩形四边的中点得到四边形EFGH .若AB=8,AD=6,则四边形EFGH 的周长等于 .A 款B 款14.在平面直角坐标系xOy 中,将抛物线平移后得到抛物线.请你写出一种平移23(2)1y x =+-232y x =+方法. 答:.15. 如图,AB 为⊙O 的直径,AC 与⊙O 相切于点A ,弦BD ∥OC .若,则∠DOC=.36C ∠=︒︒16. 我们知道:四边形具有不稳定性.如图,在平面直角坐标系xOy 中,矩形ABCD 的边AB 在x 轴上,(3,0)A -,(4,0)B ,边AD 长为5. 现固定边AB ,“推”矩形使点D 落在y 轴的正半轴上(落点记为D '),相应地,点C 的对应点C '的坐标为.三、解答题(本题共68分,第17~21题每小题5分,第22、23题每小题6分,第24题5分,第25、26题每小题6分,第27、28题每小题7分)17.计算:.06cos6027(π2)32︒+---18.解方程:.1322x x x+=--19. 如图,在四边形ABCD 中,E 为AB 的中点,DE ⊥AB 于点E ,,,BC= AD ,求∠C 的度数.66A ∠=︒90ABC ∠=︒20.先化简,再求值:,其中.2569122x x x x -+⎛⎫-÷⎪++⎝⎭5x =-21.如图,在Rt △ABC 中,,CD ⊥AB 于点D ,90ACB ∠=︒BE ⊥AB 于点B ,BE=CD ,连接CE ,DE .(1)求证:四边形CDBE 为矩形;(2)若AC =2,,求DE 的长.1tan 2ACD ∠=22.阅读下列材料:材料一:早在2011年9月25日,北京故宫博物院就开始尝试网络预售门票,2011年全年网络售票仅占1.68%.2012年至2014年,全年网络售票占比都在2%左右.2015年全年网络售票占17.33%,2016年全年网络售票占比增长至41.14%.2017年8月实现网络售票占比77%.2017年10月2日,首次实现全部网上售票.与此同时,网络购票也采用了“人性化”的服务方式,为没有线上支付能力的观众提供代客下单服务.实现全网络售票措施后,在北京故宫博物院的精细化管理下,观众可以更自主地安排自己的行程计划,获得更美好的文化空间和参观体验.材料二:以下是某同学根据网上搜集的数据制作的2013-2017年度中国国家博物馆参观人数及年增长率统计表.年度20132014201520162017参观人数(人次)7 450 0007 630 0007 290 0007 550 0008 060 000年增长率(%)38.72.4-4.53.66.8他还注意到了如下的一则新闻:2018年3月8日,中国国家博物馆官方微博发文,宣布取消纸质门票,观众持身份证预约即可参观. 国博正在建设智慧国家博物馆,同时馆方工作人员担心的是:“虽然有故宫免(纸质)票的经验在前,但对于国博来说这项工作仍有新的挑战.参观故宫需要观众网上付费购买门票,他遵守预约的程度是不一样的.但(国博)免费就有可能约了不来,挤占资源,所以难度其实不一样.” 尽管如此,国博仍将积极采取技术和服务升级,希望带给观众一个更完美的体验方式.根据以上信息解决下列问题:(1)补全以下两个统计图;(2)请你预估2018年中国国家博物馆的参观人数,并说明你的预估理由.23. 如图,在平面直角坐标系xOy 中,函数()的图象经过点,AB ⊥x 轴于点B ,点C my x=0x <(4,)A n -与点A 关于原点O 对称, CD ⊥x 轴于点D ,△ABD 的面积为8.(1)求m ,n 的值;(2)若直线(k ≠0)经过点C ,且与x 轴,y 轴的交点分别为点E ,F ,当时,y kx b =+2CF CE =求点F 的坐标.24.如图,AB 是⊙O 的直径,C 是圆上一点,弦CD ⊥AB 于点E ,且DC=AD .过点A 作⊙O 的切线,过点C 作DA 的平行线,两直线交于点F ,FC 的延长线交AB 的延长线于点G .(1)求证:FG 与⊙O 相切;(2)连接EF ,求的值.tan EFC25.阅读下面材料:已知:如图,在正方形ABCD 中,边.1AB a 按照以下操作步骤,可以从该正方形开始,构造一系列的正方形,它们之间的边满足一定的关系,并且一个比一个小.请解决以下问题:(1)完成表格中的填空:① ;② ; ③ ;④ ;(2)根据以上第三步、第四步的作法画出第三个正方形CHIJ (不要求尺规作图).26. 抛物线M : (a ≠0)与x 轴交于A ,B 两点(点A 在点B 左侧),抛物线的顶点为D .241y ax ax a =-+-(1)抛物线M 的对称轴是直线____________;(2)当AB =2时,求抛物线M 的函数表达式;(3)在(2)的条件下,直线l :(k ≠0)经过抛物线的顶点D ,直线与抛物线M 有两个y kx b =+y n =公共点,它们的横坐标分别记为,,直线与直线l 的交点的横坐标记为3x (30x >),1x 2x y n =若当2-≤n ≤1-时,总有,请结合函数的图象,直接写出k 的取值范围.13320x x x x ->->27. 如图1,在等边三角形ABC中,CD为中线,点Q在线段CD上运动,将线段QA绕点Q顺时针旋转,使得点A的对应点E落在射线BC上,连接BQ,设∠DAQ=α(0°<α<60°且α≠30°).(1)当0°<α<30°时,①在图1中依题意画出图形,并求∠BQE(用含α的式子表示);②探究线段CE,AC,CQ之间的数量关系,并加以证明;(2)当30°<α<60°时,直接写出线段CE,AC,CQ之间的数量关系.图1 备用图28. 对于平面直角坐标系xOy 中的点(x ≠0),将它的纵坐标y 与横坐标x 的比称为点Q 的“理想(,)Q x y yx值”,记作.如的“理想值”.Q L (1,2)Q -221Q L ==--(1)①若点在直线上,则点Q 的“理想值”等于_________;(1,)Q a 4y x =-Q L ②如图,,⊙C 的半径为1. 若点Q 在⊙C 上,则点Q 的“理想值”的取值范围是.3,1)C Q L (2)点D 在直线上,⊙D 的半径为1,点Q 在⊙D 上运动时都有3+3y =0≤L Q ,求点D 的横坐标的取值范围;3D x (3)(m >0),Q 是以r 为半径的⊙M 上任意一点,当0≤L Q ≤(2,)M m 22圆,并直接写出相应的半径r 的值.(要求画图位置准确,但不必尺规作图)北京市西城区2018年九年级模拟测试数学试卷答案及评分标准2018.5一、选择题(本题共16分,每小题2分)题号12345678答案ABCCDBCA二、填空题(本题共16分,每小题2分)9. x ≤2. 10. 38. 11. 4π3.12. 26170,38.x y x y +=⎧⎨=⎩13. 20.14.答案不唯一,例如,将抛物线23(2)1y x =+-先向右平移2个单位长度,再向上平移3个单位长度得到抛物线.232y x =+15. 54. 16. (7,4).三、解答题(本题共68分,第17~21题每小题5分,第22、23题每小题6分,第24题5分,第25、26题每小题6分,第27、28题每小题7分)17.解: 06cos6027(π2)32︒--- ……………………………………………………… 4分16331(23)2=⨯-+-333123=-+-+. ……………………………………………………………………………5分223=-18.解方程:1322x x x+=--.解:去分母,得13(2)x x -=-.……………………………………………………… 1分去括号,得136x x -=-. ……………………………………………………… 2分移项,得 361x x -=-.合并同类项,得 25x =.………………………………………………………… 3分系数化为1,得52x =.…………………………………………………………… 4分经检验,原方程的解为52x =.……………………………………………………5分19. 解:如图1,连接BD .∵ E 为AB 的中点,DE ⊥AB 于点E ,∴ AD= BD , …………………………………………… 1分∴ 1A ∠=∠.∵ 66A ∠=︒,∴ 166∠=︒.………………………………………………2分∵ 90ABC ∠=︒,∴ 2124ABC ∠=∠-∠=︒. …………………………… 3分∵ AD=BC ,∴ BD=BC .…………………………………………………………………………4分∴ 3C ∠=∠.∴. …………………………………………………… 5分1802==782C ︒-∠∠︒20.解: 2569122x x x x -+⎛⎫-÷⎪++⎝⎭2322(3)x x x x -+=⨯+- ………………………………………………………………… 3分13x =-.……………………………………………………………………………… 4分当5x =-时,原式18=-.……………………………………………………………5分21. (1)证明:如图2.∵ CD ⊥AB 于点D ,BE ⊥AB 于点B ,∴ .90CDA DBE ∠=∠=︒∴ CD ∥BE .………………………………… 1分又∵ BE=CD ,图1∴ 四边形CDBE 为平行四边形.……………2分又∵,90DBE ∠=︒∴ 四边形CDBE 为矩形. ……………………………………………… 3分(2)解:∵ 四边形CDBE 为矩形,∴ DE=BC .………………………………………………………………… 4分∵ 在Rt △ABC 中,90ACB ∠=︒,CD ⊥AB ,可得 1ACD ∠=∠.∵ 1tan 2ACD ∠=,∴ 1tan 1tan 2ACD ∠=∠=.∵ 在Rt △ABC 中,90ACB ∠=︒,AC =2,1tan 12∠=,∴ 4tan 1ACBC ==∠.∴ DE=BC=4.…………………………………………………………… 5分22.解:(1)补全统计图如图3.………………………………………………………………… 4分(2)答案不唯一,预估理由合理,支撑预估数据即可. ……………………… 6分23. 解:(1)如图4.∵ 点A 的坐标为(4,)A n -,点C 与点A 关于原点O 对称,图3∴ 点C 的坐标为(4,)C n -.∵ AB ⊥x 轴于点B ,CD ⊥x 轴于点D ,∴ B ,D 两点的坐标分别为(4,0)B -,(4,0)D .∵ △ABD 的面积为8,11()8422ABD S AB BD n n =⨯=⨯-⨯=- ,∴ 48n -=.解得 2n =-. …………………………………………………………… 2分∵ 函数my x=(0x <)的图象经过点(4,)A n -,∴ 48m n =-=.…………………………………………………………… 3分(2)由(1)得点C 的坐标为(4,2)C .① 如图4,当0k <时,设直线y kx b =+与x 轴,y 轴的交点分别为点1E ,1F .由 CD ⊥x 轴于点D 可得CD ∥1OF .∴ △1E CD ∽△1E 1F O .∴1111E CDC OF E F =.∵ 112CF CE =,∴113DC OF =.∴ 136OF DC ==.图4∴ 点1F 的坐标为1(0,6)F .②如图5,当0k >时,设直线y kx b =+与x 轴,y 轴的交点分别为点2E ,2F .同理可得CD ∥2OF ,2222E CDC OF E F =.∵ 222CF CE =,∴ 2E 为线段2CF 的中点,222E C E F =.∴ .22OF DC ==∴ 点2F 的坐标为2(0,2)F -.…………6分综上所述,点F 的坐标为1(0,6)F ,2(0,2)F -.24. (1)证明:如图6,连接OC ,AC .∵ AB 是⊙O 的直径,弦CD ⊥AB 于点E ,∴ CE=DE ,AD=AC .∵ DC=AD ,∴ DC=AD= AC .∴ △ACD 为等边三角形.∴ ∠D =∠DCA=∠DAC =60︒.∴ 11302DCA ∠=∠=︒.∵ FG ∥DA ,∴ .180DCF D ∠+∠=︒图6图5∴ 180120DCF D ∠=︒-∠=︒.∴ 190OCF DCF ∠=∠-∠=︒.∴ FG ⊥OC .∴ FG 与⊙O 相切.……………………………………………………… 3分(2)解:如图6,作EH ⊥FG 于点H .设CE= a ,则DE= a ,AD=2a .∵ AF 与⊙O 相切,∴ AF ⊥AG .又∵ DC ⊥AG ,可得AF ∥DC .又∵ FG ∥DA ,∴ 四边形AFCD 为平行四边形.∵ DC =AD ,AD=2a ,∴ 四边形AFCD 为菱形.∴ AF=FC=AD=2 a ,∠AFC=∠D = 60︒.由(1)得∠DCG= 60︒,,.3sin 60EH CE =⋅︒=1cos602CH CE a=⋅︒=∴.52FH CH CF a=+=∵ 在Rt △EFH 中,∠EHF= 90︒,∴ . …………………………………… 5分332tan 5aEH EFC FH a ∠===25.解:(1)①斜边和一条直角边分别相等的两个直角三角形全等.………………… 1分②.………………… 2分121)a -③.…………………3分21(21)a -④.……………… 4分11(21)n a -(2)所画正方形CHIJ 见图7.……………………………6分26.解:如图8.(1)2x =.…………………………… 1分(2)∵ 抛物线的对称轴为直线2x =,抛物线M 与x 轴的241y ax ax a =-+-交点为点A ,B (点A 在点B 左侧),AB =2,∴ A ,B 两点的坐标分别为(1,0)A ,(3,0)B .……………………………… 2分∵ 点A 在抛物线M 上,∴ 将(1,0)A 的坐标代入抛物线的函数表达式,得410a a a -+-=.解得 12a =-. ………………………………………………………………… 3分∴ 抛物线M 的函数表达式为. ………………………… 4分213222y x x =-+-(3). …………………… 6分54k >图727. 解:(1)当0°<α<30°时,①画出的图形如图9所示.…………… 1分∵ △ABC 为等边三角形,∴ ∠ABC=60°.∵ CD 为等边三角形的中线,Q 为线段CD 上的点,由等边三角形的对称性得QA=QB .∵ ∠DAQ =α,∴ ∠ABQ =∠DAQ=α,∠QBE =60°-α.∵ 线段QE 为线段QA 绕点Q 顺时针旋转所得,∴ QE = QA .∴ QB=QE .可得 1802BQE QBE ∠=︒-∠.……… 2分1802(60)602αα=︒-︒-=︒+②3CE AC CQ +=.……………………………………………………… 3分 证法一:如图10,延长CA 到点F ,使得AF=CE ,连接QF ,作QH ⊥AC 于点H . ∵ ∠BQE =60°+2α,点E 在BC 上,∴ ∠QEC =∠BQE+∠QBE =(60°+2α)+( 60°-α)=120°+α.图9图8∵ 点F 在CA 的延长线上,∠DAQ =α,∴ ∠QAF =∠BAF +∠DAQ=120°+α.∴ ∠QAF=∠QEC . 又∵ AF =CE ,QA=QE ,∴ △QAF ≌△QEC .∴ QF=QC .∵ QH ⊥AC 于点H ,∴ FH=CH ,CF=2CH .∵ 在等边三角形ABC 中,CD 为中线,点Q 在CD 上,∴ ∠ACQ==30°,12ACB∠即△QCF 为底角为30°的等腰三角形.∴.3cos cos30CH CQ HCQ CQ =⋅∠=⋅︒=∴ .CE AC AF AC CF +=+=23CH CQ ==即3CE AC CQ +=. ………………………………………… 6分思路二:如图11,延长CB 到点G ,使得BG=CE ,连接QG ,可得△QBG ≌△QEC ,△QCG 为底角为30°的等腰三角形,与证法一同理可得.CE AC BG BC CG +=+=3CQ =图10(2)如图12,当30°<α<60°时,3AC CE CQ -=.………………………… 7分28.解:(1)①3-. ………………………………………………………………………… 1分② 0≤3.……………………………………………………………… 2分Q L (2)设直线与x 轴,y 轴的交点分别为点A ,点B ,可得,3+3y =(33,0)A .(0,3)B ∴ ,,.33OA =3OB =30OAB ∠=︒由0≤3,作直线.Q L 3y x =①如图13,当⊙D 与x 轴相切时,相应的圆心满1D 足题意,其横坐标取到最大值.作轴11D E x ⊥于点,1E 可得∥OB ,.11D E 111D E AE BO AO =∵ ⊙D 的半径为1,∴ .111D E =∴ .13AE 1123OE OA AE =-=图12图13∴ .123D x =②如图14,当⊙D 与直线相切时,3y x =相应的圆心满足题意,其横坐标取到2D 最小值.作轴于点,则⊥OA .22D E x ⊥2E 22D E 设直线与直线的3y x =3+3y x =交点为F .可得,OF ⊥AB .60AOF ∠=︒则.39cos 332AF OA OAF =⋅∠==∵ ⊙D 的半径为1,∴ .21D F =∴ .2272AD AF D F =-=∴ ,22cos AE AD OAF =⋅∠73732==.2253OE OA AE =-=∴ 253D x =由①②可得,≤≤.D x 53D x 23………………………………………… 5分图14(3)画图见图15..…………………………………………… 7分2图15。
2018年北京市西城区初三数学二模试题及答案
北京市西城区2018年九年级模拟测试数 学 试 卷 2018.5一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有..一个. 1. 如图所示,a ∥b ,直线a 与直线b 之间的距离是 A .线段P A 的长度 B .线段PB 的长度 C .线段PC 的长度 D .线段CD 的长度2. 将某不等式组的解集≤x 3表示在数轴上,下列表示正确的是3. 下列运算中,正确的是A .B .C .D .4.下列实数中,在2和3之间的是A .B .C .D .5. 一副直角三角板如图放置,其中∠C =∠DFE = 90︒, ∠A = 45︒, ∠E = 60︒,点F 在CB 的延长线上. 若DE ∥CF ,则∠BDF 等于A .35︒B .30︒C .25︒D .15︒ 6. 中国古代在利用“计里画方”(比例缩放和直角坐 标网格体系)的方法制作地图时,会利用测杆、水准仪和照板来测量距离.在如图所示的测量距 离AB 的示意图中,记照板“内芯”的高度为 EF . 观测者的眼睛(图中用点C 表示)与BF 在同一水 平线上,则下列结论中,正确的是A .EF CF AB FB = B .EF CFAB CB=C .CE CFCA FB = D .CE CF EA CB=1-<22456x x x +=326x x x ⋅=236()x x =33()xy xy =π π2-7. 在一次男子马拉松长跑比赛中,随机抽取了10名选手,记录他们的成绩(所用的时间)如下:A .这组样本数据的平均数超过130B .这组样本数据的中位数是147C .在这次比赛中,估计成绩为130 min 的选手的成绩会比平均成绩差D .在这次比赛中,估计成绩为142 min 的选手,会比一半以上的选手成绩要好8.如图1所示,甲、乙两车沿直路同向行驶,车速分别为20 m/s 和v (m/s),起初甲车在乙 车前a (m)处,两车同时出发,当乙车追上甲 车时,两车都停止行驶.设x (s)后两车相距y (m),y 与x 的函数关系如图2所示.有以下 结论:①图1中a 的值为500; ②乙车的速度为35 m/s ; ③图1中线段EF 应表示为5005x +;④图2中函数图象与x 轴交点的横坐标为100. 其中所有的正确结论是A .①④B .②③C .①②④D .①③④ 二、填空题(本题共16分,每小题2分)9. 有意义,那么x 的取值范围是 .10.不透明袋子中装有5个红色球和3个蓝色球,这些球除了颜色外没有其他差别.从袋子中随机摸出一个球,摸出蓝色球的概率为 .11. 如图,等边三角形ABC 内接于⊙O ,若⊙O 的半径为2,则图中阴影部分的面积等于 .12.某校“百变魔方”社团为组织同学们参加学校科技节的 “最强大脑”大赛,准备购买A ,B 两款魔方.社长发现 若购买2个A 款魔方和6个B 款魔方共需170元,购买 3个A 款魔方和购买8个B 款魔方所需费用相同. 求每 款魔方的单价.设A款魔方的单价为x 元,B款魔方的单价为y 元,依题意可列方程组为 .13. 如图,在矩形ABCD 中,顺次连接矩形四边的中点得到四边形EFGH . 若AB=8,AD=6,则四边形EFGH 的周长等于 .14.在平面直角坐标系xOy 中,将抛物线23(2)1y x =+-平移后得到抛物线232y x =+.请你写出一种平移方法. 答: .15. 如图,AB 为⊙O 的直径,AC 与⊙O 相切于点A ,弦BD ∥OC .若36C ∠=︒,则∠DOC= ︒.16. 我们知道:四边形具有不稳定性.如图,在平面直角坐标系xOy 中,矩形ABCD 的边AB 在x 轴上,,,边AD 长为5. 现固定边AB ,“推”矩形使点D 落在y 轴的正半轴上(落点记为),相应地,点C 的对应点的坐标为 .三、解答题(本题共68分,第17~21题每小题5分,第22、23题每小题6分,第24题5分,第25、26题每小题6分,第27、28题每小题7分) 17.计算:06cos60(π2)2︒-.18.解方程:1322x x x+=--.19. 如图,在四边形ABCD 中,E 为AB 的中点,DE ⊥AB 于点E ,66A ∠=︒,90ABC ∠=︒,BC= AD ,求∠C 的度数.20.先化简,再求值:2569122x x x x -+⎛⎫-÷⎪++⎝⎭,其中5x =-.21.如图,在Rt △ABC 中,90ACB ∠=︒,CD ⊥AB 于点D ,BE ⊥AB 于点B ,BE=CD ,连接CE ,DE . (1)求证:四边形CDBE 为矩形; (2)若AC =2,1tan 2ACD ∠=,求DE 的长.(3,0)A -(4,0)B D 'C'22.阅读下列材料:材料一:早在2011年9月25日,北京故宫博物院就开始尝试网络预售门票,2011年全年网络售票仅占1.68%.2012年至2014年,全年网络售票占比都在2%左右.2015年全年网络售票占17.33%,2016年全年网络售票占比增长至41.14%.2017年8月实现网络售票占比77%.2017年10月2日,首次实现全部网上售票.与此同时,网络购票也采用了“人性化”的服务方式,为没有线上支付能力的观众提供代客下单服务.实现全网络售票措施后,在北京故宫博物院的精细化管理下,观众可以更自主地安排自己的行程计划,获得更美好的文化空间和参观体验.材料二:以下是某同学根据网上搜集的数据制作的2013-2017年度中国国家博物馆参观人数及年增长率统计表.他还注意到了如下的一则新闻:2018年3月8日,中国国家博物馆官方微博发文,宣布取消纸质门票,观众持身份证预约即可参观. 国博正在建设智慧国家博物馆,同时馆方工作人员担心的是:“虽然有故宫免(纸质)票的经验在前,但对于国博来说这项工作仍有新的挑战.参观故宫需要观众网上付费购买门票,他遵守预约的程度是不一样的.但(国博)免费就有可能约了不来,挤占资源,所以难度其实不一样.”尽管如此,国博仍将积极采取技术和服务升级,希望带给观众一个更完美的体验方式.根据以上信息解决下列问题:(1)补全以下两个统计图;(2)请你预估2018年中国国家博物馆的参观人数,并说明你的预估理由.23.如图,在平面直角坐标系xOy中,函数myx=(0x<)的图象经过点(4,)A n-,AB⊥x轴于点B,点C与点A关于原点O对称,CD⊥x轴于点D,△ABD的面积为8.(1)求m,n的值;(2)若直线y kx b=+(k≠0)经过点C,且与x轴,y轴的交点分别为点E,F,当2CF CE=时,求点F的坐标.24.如图,AB是⊙O的直径,C是圆上一点,弦CD⊥AB于点E,且DC=AD.过点A作⊙O的切线,过点C作DA的平行线,两直线交于点F,FC的延长线交AB的延长线于点G.(1)求证:FG与⊙O相切;(2)连接EF,求tan EFC∠的值.25.阅读下面材料:已知:如图,在正方形ABCD 中,边1AB a .按照以下操作步骤,可以从该正方形开始,构造一系列的正方形,它们之间的边满足一定的关系,并且一个比一个小.请解决以下问题:(1)完成表格中的填空:① ;② ; ③ ;④ ;(2)根据以上第三步、第四步的作法画出第三个正方形CHIJ (不要求尺规作图).26. 抛物线M :241y ax ax a =-+- (a ≠0)与x 轴交于A ,B 两点(点A 在点B 左侧),抛物线的顶点为D .(1)抛物线M 的对称轴是直线____________; (2)当AB =2时,求抛物线M 的函数表达式;(3)在(2)的条件下,直线l :y kx b =+(k ≠0)经过抛物线的顶点D ,直线y n =与抛物线M 有两个公共点,它们的横坐标分别记为1x ,2x ,直线y n =与直线l 的交点的横坐标记为(),若当≤n ≤时,总有13320x x x x ->->,请结合函数的图象,直接写出k 的取值范围.27. 如图1,在等边三角形ABC 中,CD 为中线,点Q 在线段CD 上运动,将线段QA 绕点Q 顺时针旋转,使得点A 的对应点E 落在射线BC 上,连接BQ ,设∠DAQ =α (0°<α<60°且α≠30°). (1)当0°<α<30°时,①在图1中依题意画出图形,并求∠BQE (用含α的式子表示); ②探究线段CE ,AC ,CQ 之间的数量关系,并加以证明; (2)当30°<α<60°时,直接写出线段CE ,AC ,CQ 之间的数量关系.3x 30x >2-1-28. 对于平面直角坐标系xOy 中的点(,)Q x y (x ≠0),将它的纵坐标y 与横坐标x 的比yx称为点Q 的“理想值”,记作Q L .如(1,2)Q -的“理想值”221Q L ==--. (1)①若点(1,)Q a 在直线4y x =-上,则点Q 的“理想值”Q L 等于_________;②如图,C ,⊙C 的半径为1. 若点Q 在⊙C 上,则点Q 的“理想值”QL 的取值范围是 .(2)点D 在直线+3y =上,⊙D 的半径为1,点Q 在⊙D 上运动时都有0≤L Q D 的横坐标D x 的取值范围;(3)(2,)M m (m >0),Q 是以r 为半径的⊙M 上任意一点,当0≤L Q ≤满足条件的最大圆,并直接写出相应的半径r 的值.(要求画图位置准确,但不必尺规作图)北京市西城区2018年九年级模拟测试数学试卷答案及评分标准 2018.5二、 填空题(本题共16分,每小题2分) 9. x ≤2. 10.. 11. .12.13. 20. 14.答案不唯一,例如,将抛物线先向右平移2个单位长度,再向上平移3个单位长度得到抛物线232y x =+. 15. 54. 16. .三、解答题(本题共68分,第17~21题每小题5分,第22、23题每小题6分,第24题5分,第25、26题每小题6分,第27、28题每小题7分) 17.解:161(22=⨯-- ……………………………………………………… 4分313=-+-2=-. ……………………………………………………………………………5分18.解方程:. 解:去分母,得.……………………………………………………… 1分去括号,得.……………………………………………………… 2分 移项,得.合并同类项,得 .………………………………………………………… 3分系数化为1,得.…………………………………………………………… 4分 经检验,原方程的解为.……………………………………………………5分19. 解:如图1,连接BD .∵ E 为AB 的中点,DE ⊥AB 于点E ,∴ AD= BD , ……………… ………… 1分∴ . ∵ ,∴ .………………………… ……2分 ∵ ,384π326170,38.x y x y +=⎧⎨=⎩23(2)1y x =+-(7,4)06cos60(π2)2︒-1322x x x+=--13(2)x x -=-136x x -=-361x x -=-25x =52x =52x =1A ∠=∠66A ∠=︒166∠=︒90ABC ∠=︒∴ . …………………………… 3分 ∵ AD=BC ,∴ BD=BC .…………………………………………………………………………4分 ∴ .∴1802==782C ︒-∠∠︒. …………………………………………………… 5分20.解: ………………………………………………………………… 3分 .……………………………………………………………………………… 4分 当时,原式.……………………………………………………………5分21. (1)证明:如图2.∵ CD ⊥AB 于点D ,BE ⊥AB 于点B , ∴ 90CDA DBE ∠=∠=︒.∴ CD ∥BE .………………………………… 1分 又∵ BE=CD ,∴ 四边形CDBE 为平行四边形.……………2分 又∵90DBE ∠=︒,∴ 四边形CDBE 为矩形. ……………………………………………… 3分(2)解:∵ 四边形CDBE 为矩形,∴ DE=BC .………………………………………………………………… 4分 ∵ 在Rt △ABC 中,,CD ⊥AB , 可得 .∵ , ∴ . ∵ 在Rt △ABC 中,,AC =2,, ∴ . ∴ DE=BC=4.…………………………………………………………… 5分22.解:(1)补全统计图如图3.2124ABC ∠=∠-∠=︒3C ∠=∠2569122x x x x -+⎛⎫-÷⎪++⎝⎭2322(3)x x x x -+=⨯+-13x =-5x =-18=-90ACB ∠=︒1ACD ∠=∠1tan 2ACD ∠=1tan 1tan 2ACD ∠=∠=90ACB ∠=︒1tan 12∠=4tan 1ACBC ==∠图2………………………………………………………………… 4分(2)答案不唯一,预估理由合理,支撑预估数据即可. ……………………… 6分23. 解:(1)如图4.∵ 点A 的坐标为,点C 与点A 关于原点O 对称,∴ 点C 的坐标为.∵ AB ⊥x 轴于点B ,CD ⊥x 轴于点D ,∴ B ,D 两点的坐标分别为,.∵ △ABD 的面积为8,, ∴ .解得 . …………………………………………………………… 2分 ∵ 函数()的图象经过点, ∴ . …………… 3分(2)由(1)得点C 的坐标为. ① 如图4,当时,设直线与x 轴,y 轴的交点分别为点,.由 CD ⊥x 轴于点D 可得CD ∥.∴ △CD ∽△O .∴ . ∵ ,∴.∴ . ∴ 点的坐标为.②如图5,当时,设直线与x 轴,y 轴的交点分别为(4,)A n -(4,)C n -(4,0)B -(4,0)D 11()8422ABD S AB BD n n =⨯=⨯-⨯=- 48n -=2n =-m y x=0x <(4,)A n -48m n =-=(4,2)C 0k <y kx b =+1E 1F 1OF 1E 1E 1F 1111E C DC OF E F =112CF CE =113DC OF =136OF DC ==1F 1(0,6)F 0k >y kx b =+图4点,.同理可得CD ∥,. ∵ ,∴ 为线段的中点,.∴ 22OF DC ==.∴ 点的坐标为.…………6分综上所述,点F 的坐标为,.24. (1)证明:如图6,连接OC ,AC .∵ AB 是⊙O 的直径,弦CD ⊥AB 于点E ,∴ CE=DE ,AD=AC .∵ DC=AD ,∴ DC=AD= AC .∴ △ACD 为等边三角形.∴ ∠D =∠DCA=∠DAC =60︒.∴ . ∵ FG ∥DA ,∴ 180DCF D ∠+∠=︒. ∴ .∴ .∴ FG ⊥OC .∴ FG 与⊙O 相切.……………………………………………………… 3分(2)解:如图6,作EH ⊥FG 于点H .设CE= a ,则DE= a ,AD=2a .∵ AF 与⊙O 相切,∴ AF ⊥AG .又∵ DC ⊥AG ,可得AF ∥DC .又∵ FG ∥DA ,∴ 四边形AFCD 为平行四边形.∵ DC =AD ,AD=2a ,∴ 四边形AFCD 为菱形.∴ AF=FC=AD=2 a ,∠AFC=∠D = 60︒.由(1)得∠DCG= 60︒,sin60EH CE =⋅︒=,1cos602CH CE a =⋅︒=. ∴52FH CH CF a =+=. ∵ 在Rt △EFH 中,∠EHF= 90︒,∴2tan 52EH EFC FH a ∠===. …………………………………… 5分2E 2F 2OF 2222E C DC OF E F =222CF CE =2E 2CF 222E C E F =2F 2(0,2)F -1(0,6)F 2(0,2)F -11302DCA ∠=∠=︒180120DCF D ∠=︒-∠=︒190OCF DCF ∠=∠-∠=︒图6图525.解:(1)①斜边和一条直角边分别相等的两个直角三角形全等 .………………… 1分②11)a .………………… 2分③211)a .…………………3分④111)n a -.……………… 4分(2)所画正方形CHIJ 见图7.……………………………6分26.解:如图8.(1).…………………………… 1分 (2)∵ 抛物线241y ax ax a =-+-的对称轴为直线,抛物线M 与x 轴的 交点为点A ,B (点A 在点B 左侧),AB =2,∴ A ,B 两点的坐标分别为,.……………………………… 2分∵ 点A 在抛物线M 上,∴ 将的坐标代入抛物线的函数表达式,得.解得 . ………………………………………………………………… 3分 ∴ 抛物线M 的函数表达式为213222y x x =-+-. ………………………… 4分 (3)54k >. …………………… 6分27. 解:(1)当0°<α<30°时,①画出的图形如图9所示.…………… 1分∵ △ABC 为等边三角形,∴ ∠ABC=60°.∵ CD 为等边三角形的中线,Q 为线段CD上的点,由等边三角形的对称性得QA=QB .∵ ∠DAQ =α,∴ ∠ABQ =∠DAQ=α,∠QBE =60°-α.2x =2x =(1,0)A (3,0)B (1,0)A 410a a a -+-=12a =-∵ 线段QE 为线段QA 绕点Q 顺时针旋转所得,∴ QE = QA .∴ QB=QE .可得 1802(60)602αα=︒-︒-=︒+.……… 2分②.……………………………………………………… 3分证法一:如图10,延长CA 到点F ,使得AF=CE ,连接QF ,作QH ⊥AC于点H .∵ ∠BQE =60°+2α,点E 在BC 上,∴ ∠QEC =∠BQE+∠QBE =(60°+2α)+( 60°-α)=120°+α.∵ 点F 在CA 的延长线上,∠DAQ =α,∴ ∠QAF =∠BAF +∠DAQ=120°+α.∴ ∠QAF=∠QEC .又∵ AF =CE ,QA=QE ,∴ △QAF ≌△QEC .∴ QF=QC .∵ QH ⊥AC 于点H ,∴ FH=CH ,CF=2CH .∵ 在等边三角形ABC 中,CD 为中线,点Q 在CD 上,∴ ∠ACQ=12ACB ∠=30°,即△QCF 为底角为30°的等腰三角形. ∴cos cos30CH CQ HCQ CQ =⋅∠=⋅︒=.∴ CE AC AF AC CF +=+=2CH =.即. ………………………………………… 6分思路二:如图11,延长CB 到点G ,使得BG=CE ,连接QG ,可得△QBG ≌△QEC ,△QCG 为底角为30°的等腰三角形,与证法一同理可得CE AC BG BC CG +=+=.1802BQE QBE ∠=︒-∠CE AC +=CE AC +=图10(2)如图12,当30°<α<60°时,.………………………… 7分28.解:(1)①. ………………………………………………………………………… 1分② 0≤Q L ……………………………………………………………… 2分(2)设直线+3y =与x 轴,y 轴的交点分别为点A ,点B ,可得A ,(0,3)B .∴OA =,3OB =,30OAB ∠=︒.由0≤Q L ,作直线y .①如图13,当⊙D 与x 轴相切时,相应的圆心1D 满足题意,其横坐标取到最大值.作11D E x ⊥轴于点1E ,可得11D E ∥OB ,111D E AE BO AO =. ∵ ⊙D 的半径为1,∴ 111D E=.∴ 1AE11OE OA AE =-=∴ 1D x =②如图14,当⊙D 与直线y 相切时,相应的圆心2D 满足题意,其横坐标取到最小值.AC CE -=3-图11 图12作22D E x ⊥轴于点2E ,则22D E ⊥OA .设直线y =与直线+3y =的 交点为F .可得60AOF ∠=︒,OF ⊥AB .则9cos 2AF OA OAF =⋅∠==. ∵ ⊙D 的半径为1,∴ 21D F =.∴ 2272AD AF D F =-=.∴ 22cos AE AD OAF =⋅∠72==,22OE OA AE =-=.∴2D x =.由①②可得,D x的取值范围是≤D x≤.………………………………………… 5分(3)画图见图15.7分。
北京市海淀区2018年中考数学二模试题标准答案

海淀区九年级第二学期期末练习数学参考答案及评分标准2018.5一、选择题(本题共16分,每小题2分)二、填空题(本题共16分,每小题2分)9.23(1)a + 10.6π 11.412.1213.10010018.752.74x x-= 14.4 15.①直径所对的圆周角为直角②线段垂直平分线上的点与这条线段两个端点的距离相等 16.532m ≤≤三、解答题(本题共68分,第17~22题,每小题5分;第23~26小题,每小题6分;第27~28小题,每小题7分)17.解:原式=414+- 3.18.解:去分母,得63(2)2(2)x x x -+<-. 去括号,得63642x x x --<-. 移项,合并得510x <. 系数化为1,得2x <.不等式的解集在数轴上表示如下:19.证明:∵3AD =,4AE =,5ED =,∴222AD AE ED +=.∴90A ∠=︒. ∴DA AB ⊥. ∵90C ∠=︒. ∴DC BC ⊥.∵BD 平分ABC ∠, ∴DC AD =. ∵3AD =, ∴3CD =.20.(1)证明:依题意,得22[(3)]413(3)m m m ∆=-+-⨯⨯=-.∵2(3)0m -≥, ∴方程总有实数根.(2)解:∵原方程有两个实数根3,m , ∴取4m =,可使原方程的两个根中只有..一个根小于4. 注:只要4m ≥均满足题意. 21.(1)解:∵AB ∥CD , ∴∠ABE =∠EDC . ∵∠BEA =∠DEF , ∴△ABE ∽△FDE . ∴AB BEDF DE=. ∵E 是BD 的中点, ∴BE =DE . ∴AB =DF .∵F 是CD 的中点, ∴CF =FD . ∴CD =2AB .∵∠ABE =∠EDC ,∠AGB =∠CGD , ∴△ABG ∽△CDG . ∴12BG AB GD CD ==. (2)证明:∵AB ∥CF ,AB =CF , ∴四边形ABCF 是平行四边形. ∵CE =BE ,BE =DE , ∴CE =ED . ∵CF =FD , ∴EF 垂直平分CD . ∴∠CF A =90°.∴四边形ABCF 是矩形.EGF ABCD22.解:(1)设点B 的坐标为(x ,y ),由题意得:BF y =,BM x =. ∵矩形OMBF 的面积为3, ∴3xy =. ∵B 在双曲线ky x=上, ∴3k =. (2)∵点B 的横坐标为3,点B 在双曲线上, ∴点B 的坐标为(3,1). 设直线l 的解析式为y ax b =+. ∵直线l 过点(2,2)P ,B (3,1), ∴22,3 1.a b a b +=⎧⎨+=⎩解得1,4.a b =-⎧⎨=⎩∴直线l 的解析式为4y x =-+. ∵直线l 与x 轴交于点C (4,0),∴BC =.(3)增大23.解:(1)60;(2)连接OD ,∵CD AB ⊥,AB 是O 的直径, ∴CM MD =. ∵M 是OA 的中点, ∴AM MO =.又∵AMC DMO ∠=∠, ∴AMC OMD ≅△△. ∴ACM ODM ∠=∠. ∴CA ∥OD . ∵DE CA ⊥, ∴90E ∠=︒.∴18090ODE E ∠=︒-∠=︒. ∴DE OD ⊥.B∴DE 与⊙O 相切. (3)连接CF ,CN , ∵OA CD ⊥于M , ∴M 是CD 中点. ∴NC ND =. ∵45CDF ∠=︒, ∴45NCD NDC ∠=∠=︒. ∴90CND ∠=︒. ∴90CNF ∠=︒.由(1)可知60AOD ∠=︒. ∴1302ACD AOD ∠=∠=︒. 在Rt △CDE 中,90E ∠=︒,30ECD ∠=︒,3DE =, ∴6sin 30DECD ==︒. 在Rt △CND 中,90CND ∠=︒,45CDN ∠=︒,6CD =,∴sin 45CN CD =⋅︒=由(1)知2120CAD OAD ∠=∠=︒, ∴18060CFD CAD ∠=︒-∠=︒.在Rt △CNF 中,90CNF ∠=︒,60CFN ∠=︒,CN =∴tan 60CNFN ==︒24.(1)补充表格:(2)答案不唯一,可参考的答案如下:B甲选手:和乙选手的平均成绩相同,中位数高于乙,打出9环及以上的次数更多,打出7环的次数较少,说明甲选手相比之下发挥更加稳定;乙选手:与甲选手平均成绩相同,打出10环次数和7环次数都比甲多,说明乙射击时起伏更大,但也更容易打出10环的成绩.(2)如图所示:(3)①231w w w <<; ②如上图所示.26.解:(1)1D (-3,3),2D (1,3),3D (-3,-1) (2)不存在.理由如下:假设满足条件的C 点存在,即A ,B ,1D ,2D ,3D 在同一条抛物线上,则线段AB 的垂直平分线2x =-即为这条抛物线的对称轴,而1D ,2D 在直线y n =上,则1D 2D 的中点C 也在抛物线对称轴上,故2m =-,即点C 的坐标为(-2,n ). 由题意得:1D (-4,n ),2D (0,n ),3D (-2,2n -).注意到3D 在抛物线的对称轴上,故3D 为抛物线的顶点. 设抛物线的表达式是()222y a x n =++-.当1x =-时,1y =,代入得1a n =-. 所以()()2122y n x n =-++-.令0x =,得()41232y n n n n =-+-=-=,解得1n =,与1n >矛盾. 所以不存在满足条件的C 点.27.(1)DE DF =;(2)解:连接DE ,DF , ∵△ABC 是等边三角形, ∴60C ∠=︒. ∵DBC α∠=, ∴120BDC α∠=︒-.∵点C 与点F 关于BD 对称,∴120BDF BDC α∠=∠=︒-,DF DC =. ∴1202FDC α∠=︒+. 由(1)知DE DF =.∴F ,E ,C 在以D 为圆心,DC 为半径的圆上. ∴1602FEC FDC ∠=∠=︒+α. (3)BG GF FA =+.理由如下: 连接BF ,延长AF ,BD 交于点H , ∵△ABC 是等边三角形,∴60ABC BAC ∠=∠=︒,AB BC CA ==.GFED CBA∵点C 与点F 关于BD 对称, ∴BF BC =,FBD CBD ∠=∠. ∴BF BA =. ∴BAF BFA ∠=∠. 设CBD α∠=, 则602ABF α∠=︒-. ∴60BAF α∠=︒+. ∴FAD α∠=. ∴FAD DBC ∠=∠. 由(2)知60FEC α∠=︒+. ∴60BGE FEC DBC ∠=∠-∠=︒. ∴120FGB ∠=︒,60FGD ∠=︒.四边形AFGB 中,360120AFE FAB ABG FGB ∠=︒-∠-∠-∠=︒. ∴60HFG ∠=︒. ∴△FGH 是等边三角形. ∴FH FG =,60H ∠=︒. ∵CD CE =, ∴DA EB =.在△AHD 与△BGE 中,,,.AHD BGE HAD GBE AD BE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△△AHD BGE ≅. ∴BG AH =.∵AH HF FA GF FA =+=+, ∴BG GF FA =+.28.解:(1)函数21y x =-的限减系数是2;(2)若1m >,则10m ->,(1m -,11m -)和(m ,1m)是函数图象上两点,HGFEDCBA11101(1)m m m m -=-<--,与函数的限减系数4k =不符,∴1m ≤. 若102m <<,(1t -,11t -)和(t ,1t)是函数图象上横坐标之差为1的任意两点,则0t m <≤,1111(1)t t t t -=---,∵(1)0t t -->,且2211111(1)()()24244t t t m --=--+≤--+<,∴1141t t ->-,与函数的限减系数4k =不符. ∴12m ≥. 若112m ≤≤,(1t -,11t -)和(t ,1t)是函数图象上横坐标之差为1的任意两点,则0t m <≤,1111(1)t t t t -=---,∵(1)0t t -->,且2111(1)()244t t t --=--+≤,∴11141(1)t t t t -=≥---,当12t =时,等号成立,故函数的限减系数4k =. ∴m 的取值范围是112m ≤≤. (3)11-n ≤≤.。
2018北京各区初中数学二模分类汇编27号题和答案

2018北京各区初中数学二模分类汇编27号题及答案门头沟 27. 如图,在正方形ABCD 中,连接BD ,点E 为CB 边的延长线上一点,点F 是线段AE 的中点,过点F 作AE 的垂线交BD 于点M ,连接ME 、MC . (1)根据题意补全图形,猜想MEC ∠与MCE ∠的数量关系并证明; (2)连接FB ,判断FB 、FM 之间的数量关系并证明.西城27. 如图1,在等边三角形ABC 中,CD 为中线,点Q 在线段CD 上运动,将线段QA 绕点Q 顺时针旋转,使得点A 的对应点E 落在射线BC 上,连接BQ ,设∠DAQ =α (0°<α<60°且α≠30°). (1)当0°<α<30°时,①在图1中依题意画出图形,并求∠BQE (用含α的式子表示); ②探究线段CE ,AC ,CQ 之间的数量关系,并加以证明;(2)当30°<α<60°时,直接写出线段CE ,AC ,CQ 之间的数量关系.平谷27.正方形ABCD 的对角线AC ,BD 交于点O ,作∠CBD 的角平分线BE ,分别交CD ,OC 于点E ,F .(1)依据题意,补全图形(用尺规作图,保留作图痕迹);(2)求证:CE=CF ; (3)求证:DE =2OF .顺义27.在等边ABC △外侧作直线AM ,点C 关于AM 的对称点为D ,连接BD 交AM于点E ,连接CE ,CD ,AD .(1)依题意补全图1,并求BEC ∠的度数; (2)如图2 ,当30MAC ∠=︒时,判断线段BE 与DE 之间的数量关系,并加以证明; (3)若0120MAC ︒<∠<︒,当线段2DE BE =时,直接写出MAC ∠的度数.图1MCBA东城27. 如图所示,点P 位于等边ABC △的内部,且∠ACP =∠图2MEDCBACBP .(1) ∠BPC 的度数为________°;(2) 延长BP 至点D ,使得PD =PC ,连接AD ,CD .①依题意,补全图形; ②证明:AD +CD =BD ;(3) 在(2)的条件下,若BD 的长为2,求四边形ABCD 的面积.房山27. 已知AC =DC ,AC ⊥DC ,直线MN 经过点A ,作DB ⊥MN ,垂足为B ,连接CB . (1)直接写出∠D 与∠MAC 之间的数量关系;(2)① 如图1,猜想AB ,BD 与BC 之间的数量关系,并说明理由;② 如图2,直接写出AB ,BD 与BC 之间的数量关系;(3)在MN 绕点A 旋转的过程中,当∠BCD =30°,BC 的值.昌平27.如图,在△ABC 中,AB =AC >BC ,BD 是AC 边上的高,点C 关于直线BD 的对称点为点E ,连接BE .图1图2(1) ①依题意补全图形;②若∠BAC =α,求∠DBE 的大小(用含α的式子表示); (2) 若DE =2AE ,点F 是BE 中点,连接AF ,BD =4,求AF 的长.(备用图)海淀27.如图,在等边ABC △中, ,D E 分别是边,AC BC 上的点,且C D C E= ,30DBC ∠<︒ ,点C 与点F 关于BD 对称,连接,AF FE ,FE 交BD 于G .(1)连接,DE DF ,则,D ED F之间的数量关系是 ;(2)若DBC α∠=,求FEC ∠的大小; (用α的式子表示) (2)用等式表示线段,BG GF 和FA 之间的数量关系,并证明.石景山27.在△ABC 中,∠ABC =90°,AB =BC =4,点M 是线段BC 的中点,点N 在射线MB 上,连接AN ,平移△ABN ,使点N 移动到点M ,得到△DEM (点D 与点A 对应,点E 与点B 对应),DM 交AC 于点P .(1)若点N 是线段MB 的中点,如图1.① 依题意补全图1;② 求DP 的长;(2)若点N 在线段MB 的延长线上,射线DM 与射线AB 交于点Q ,若MQ =DP ,求D CB A DCB AGFEDCBA怀柔27.在△ABC 中,AB=BC =AC ,点M 为直线BC 上一个动点(不与B ,C 重合),连结AM ,将线段AM 绕点M 顺时针旋转60°,得到线段MN ,连结NC .(1)如果点M 在线段BC 上运动. ①依题意补全图1;②点M 在线段BC 上运动的过程中,∠MCN 的度数是否确定?如果确定,求出∠MCN 的度数;如果不确定,说明理由;(2)如果点M 在线段CB 的延长线上运动,依题意补全图2,在这个过程中,∠MCN 的度数是否确定?如果确定,直接写出∠MCN 的度数;如果不确定,说明理由.朝阳27.如图,在△ABC 中,AB=AC ,∠BAC =90°,M 是BC 的中点,延长AM 到点D ,AE = AD ,∠EAD =90°,CE 交AB 于点F ,CD =DF . (1)∠CAD = 度; (2)求∠CDF 的度数;(3)用等式表示线段CD 和CE 之间的数量关系,并证明.BA AB丰台27.如图,正方形ABCD 中,点E 是BC 边上的一个动点,连接AE ,将线段AE 绕点A 逆时针旋转90°,得到AF ,连接EF ,交对角线BD 于点G ,连接AG . (1)根据题意补全图形;(2)判定AG 与EF 的位置关系并证明;(3)当AB = 3,BE = 2时,求线段BG 的长.答案门头沟 27.(本小题满分7分)(1)补全图形正确 ……………………………………………1分 MEC ∠=MCE ∠ ………………………………………2分 证明:连接AM∵点F 是AE 的中点,FM AE ⊥A B CE D∴MA ME =∵点A 、点C 是关于正方形ABCD 对角线BD 所在直线的对称点 ∴MA MC =………………………………………3分 ∴ME MC =∴MEC ∠=MCE ∠………………………………………4分 (2)数量关系:FB FM = ……………………5分 ∵点M 在正方形对角线上,可得MAD MCD △≌△∴MAD ∠=MCD ∠ ∵MEC ∠=MCE ∠∴90MEC MAD DCM MCE ∠+∠=∠+∠=︒ ∵AD CE ∥∴180DAE CEA ∠+∠=︒ ∴90MAE MEA ∠+∠=︒ ∴90AME ∠=︒∴EMA △是等腰直角三角形……………………6分 ∴12FM AE = ∵12FB AE =∴FB FM = ……………………7分西城27. 解:(1)当0°<α<30°时,①画出的图形如图9所示.…………… 1分∵ △ABC 为等边三角形,∴ ∠ABC=60°.∵ CD 为等边三角形的中线,Q 为线段CD 上的点,由等边三角形的对称性得QA=QB . ∵ ∠DAQ =α,∴ ∠ABQ =∠DAQ=α,∠QBE =60°-α.∵ 线段QE 为线段QA 绕点Q 顺时针旋转所得, ∴ QE = QA .∴ QB=QE .可得 1802BQE QBE ∠=︒-∠1802(60)602αα=︒-︒-=︒+.……… 2分②CE AC +=.……………………………………………………… 3分图9证法一:如图10,延长CA 到点F ,使得AF=CE ,连接QF ,作QH ⊥AC 于点H . ∵ ∠BQE =60°+2α,点E 在BC 上,∴ ∠QEC =∠BQE+∠QBE =(60°+2α)+( 60°-α)=120°+α.∵ 点F 在CA 的延长线上,∠DAQ =α, ∴ ∠QAF =∠BAF +∠DAQ=120°+α. ∴ ∠QAF=∠QEC . 又∵ AF =CE ,QA=QE , ∴ △QAF ≌△QEC . ∴ QF=QC .∵ QH ⊥AC 于点H , ∴ FH=CH ,CF=2CH .∵ 在等边三角形ABC 中,CD 为中线, 点Q 在CD 上,∴ ∠ACQ=12ACB∠=30°,即△QCF 为底角为30°的等腰三角形.∴cos cos30CH CQ HCQ CQ =⋅∠=⋅︒=.∴ CE AC AF AC CF +=+=2CH ==.即CE AC +=. ………………………………………… 6分思路二:如图11,延长CB 到点G ,使得BG=CE ,连接QG ,可得△QBG ≌△QEC ,△QCG 为底角为30°的等腰三角形,与证法一同理可得CE AC BG BC CG +=+=.(2)如图12,当30°<α<60°时,AC CE -=.………………………… 7分平谷27.(1)如图 (1)图10图11 图12y yxx E DMCBA(2)证明:∵BE 平分∠CBD ,∴∠CBE =∠DBE . ························ 2 ∵正方形ABCD 的对角线AC ,BD 交于点O ,∴∠BOC =∠BCD =90°.∵∠CBE +∠CEB =90°, ∠DBE +∠BFO =90°,∴∠CEB =∠BFO . ························ 3 ∵∠EFC =∠BFO , ∴∠EFC =∠CEB .∴CF=CE . ··························· 4 (3)证明:取BE 的中点M ,连接OM . ···················· 5 ∵O 为AC 的中点,∴OM ∥DE , DE =2OM . ...................... 6 ∴∠OMF =∠CEF .∵∠OFM =∠EFC =∠CEF , ∴∠OMF =∠OFM .∴OF=OM . ∴DE =2OF . (7)顺义27.解:(1)补全图形如右图: …………………………………………………… 1分依题意显然可以得出AD =AC ,∠=∠=DAE CAE x ,∠=∠DEM CEM . ∵等边ABC △,∴AB =AC ,60∠=︒BAC .∴AB =AD .∴∠=∠=ABD ADB y .在△ABD 中,2260180++︒=︒x y , ∴60+=︒x y .∴60∠=∠=+=︒DEM CEM x y .∴60∠=︒BEC .………………………………………………………… 4分(2)判断:2=BE DE .证明:∵30MAC ∠=︒,结合(1)中证明过程,显然可以得出30∠=︒ABD , 又∵等边ABC △, ∴60∠=︒ABC . ∴30∠=︒DBC . 又∵60∠=︒BEC , ∴90∠=︒ECB . ∴2=BE CE .∵=CE DE , ∴2=BE DE .(3)90∠=︒MAC .………………………………………………………… 7分 4东城 27. 解:(1)120°. ---------------------------------------------------2分(2)①∵如图1所示.②在等边ABC △中,60ACB ∠=︒, ∴60.ACP BCP ∠+∠=︒ ∵=ACP CBP ∠∠,∴60.CBP BCP ∠+∠=︒∴()180120.BPC CBP BCP ∠=︒-∠+∠=︒ ∴18060.CPD BPC ∠=︒-∠=︒ ∵=PD PC ,∴CDP △为等边三角形.∵60ACD ACP ACP BCP ∠+∠=∠+∠=︒, ∴.ACD BCP ∠=∠ 在ACD △和BCP △中,AC BC ACD BCP CD CP =⎧⎪∠=∠⎨⎪=⎩,,, ∴()SAS ACD BCP △≌△. ∴.AD BP = ∴.AD CD BP PD BD +=+=-----------------------------------------------------------------4分(3)如图2,作BM AD ⊥于点M ,BN DC ⊥延长线于点N .∵=60ADB ADC PDC ∠∠-∠=︒, ∴=60.ADB CDB ∠∠=︒ ∴=60.ADB CDB ∠∠=︒∴=2BM BN BD == 又由(2)得,=2AD CD BD +=,ABD BCD ABCD S S S ∴△△四边形=+1122AD BMCD BN =+()2AD CD =+22==----------------------------------------------------------7分房山27. 解:(1)相等或互补;………………………………………………2分 (注:每个1分)(2)① 猜想:BD +AB =2BC …………………………………………………………3分如图1,在射线AM 上截取AE =BD ,连接CE .又∵∠D =∠EAC ,CD =AC ∴△BCD ≌△ECA ∴BC =EC ,∠BCD =∠ECA ∵AC ⊥CD ∴∠ACD =90° 即∠ACB +∠BCD =90° ∴∠ACB +∠ECA =90° 即∠ECB =90° ∴BE =2BC ∵AE +AB =BE =2BC∴BD +AB =2BC ……………………………………………………………4分 ② AB -BD =2BC ……………………………………………………………5分 (3)BC =3+1 或3-1 ……………………………………………………………7分 昌平27.如图,在△ABC 中,AB =AC >BC ,BD 是AC 边上的高,点C 关于直线BD 的对称点为点E ,连接BE . (1)①补全图形;②若∠BAC =α,求∠DBE 的大小(用含α的式子表示); (2)若DE =2AE ,点F 是BE 中点,连接AF ,BD =4,求AF 的长. (1)解:①如图. ……………………… 1分 ②∵ AB =AC ,∠BAC =α,M图1DBAE∴ ∠ABC =∠ACB =90°-12α.∵点C 关于直线BD 的对称点为点E ,BD 是AC 边上的高.∴ BD ⊥CE ,CD =DE . ∴ BE =BC .∴ ∠BEC =∠ACB =90°-12α. …………………… 2分 ∴∠DBE =12α.……………… 3分(2)解:作FG ⊥AC 于G , ∵BD ⊥CE ,∴FG ∥BD∵点F 是BE 中点,∴EG =DG .∴1FG=BD 2…………4分 ∵DE =2AE ,∴AE =EG =DG .……………… 5分 设AE =EG =DG=x ,则CD =DE=2x ,AC =5x ,∴AB=AC =5x .∴BD =4x . ∵BD =4,∴x =1.……………… 6分 ∴AG =2.∵1FG=BD 2=2, ∴AF= 7分海淀 27.(1)DE DF =;(2)解:连接DE ,DF , ∵△ABC 是等边三角形, ∴60C ∠=︒. ∵DBC α∠=, ∴120BDC α∠=︒-. ∵点C 与点F 关于BD 对称,∴120BDF BDC α∠=∠=︒-,DF DC =. ∴1202FDC α∠=︒+. 由(1)知DE DF =.∴F ,E ,C 在以D 为圆心,DC 为半径的圆上.EABCDFG GFED CBA∴1602FEC FDC ∠=∠=︒+α.(3)BG GF FA =+.理由如下: 连接BF ,延长AF ,BD 交于点H , ∵△ABC 是等边三角形,∴60ABC BAC ∠=∠=︒,AB BC CA ==. ∵点C 与点F 关于BD 对称, ∴BF BC =,FBD CBD ∠=∠. ∴BF BA =. ∴BAF BFA ∠=∠. 设CBD α∠=, 则602ABF α∠=︒-. ∴60BAF α∠=︒+. ∴FAD α∠=.∴FAD DBC ∠=∠. 由(2)知60FEC α∠=︒+. ∴60BGE FEC DBC ∠=∠-∠=︒.∴120FGB ∠=︒,60FGD ∠=︒.四边形AFGB 中,360120AFE FAB ABG FGB ∠=︒-∠-∠-∠=︒. ∴60HFG ∠=︒.∴△FGH 是等边三角形. ∴FH FG =,60H ∠=︒. ∵CD CE =, ∴DA EB =.在△AHD 与△BGE 中,,,.AHD BGE HAD GBE AD BE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△△AHD BGE ≅.HGFEDCBA∴BG AH=.∵AH HF FA GF FA=+=+,∴BG GF FA=+.石景山27.解:(1)①如图1,补全图形. ………………… 1分②连接AD,如图2.在Rt△ABN中,∵∠B=90°,AB=4,BN=1,∴17=AN.∵线段AN平移得到线段DM,∴DM=AN=17,AD=NM=1,AD∥MC,∴△ADP∽△CMP.∴21==MCADMPDP.∴317=DP.………………… 3分(2)连接NQ,如图3.由平移知:AN∥DM,且AN=DM.∵MQ DP=,∴PQ DM=.∴AN∥PQ,且AN=PQ.∴四边形ANQP是平行四边形.∴NQ∥AP.∴45BQN BAC∠=∠=︒.又∵90NBQ ABC∠=∠=︒,∴BN BQ=.∵AN∥MQ,∴AB NBBQ BM=.又∵M是BC的中点,且4AB BC==∴42NBNB=.∴NB=舍负).∴ME BN==∴2CE= (7)(2)法二,连接AD,如图4.图1图2A B 设CE 长为x ,∵线段AB 移动到得到线段DE , ∴4+==x BE AD ,AD ∥BM . ∴△ADP ∽△CMP . ∴24xMC AD MP DP +==. ∵MQ =DP , ∴x xMP DP DP QD MQ 21042++=+=. ∵△QBM ∽△QAD , ∴xAD BM QD MQ +==42. 解得222-=x .∴222-=CE . ………………… 7分27. (1)①补全图形,如图:…………………………………………….………………….…………………………………1分②点M 在线段BC 上运动的过程中,∠MCN 的度数确定,为120°理由如下:在AB 上取点P ,使得BP=BM ,连结PM ……………………………………………………2分∵BP =BM ,∠B =60º,∴△BPM 是等边三角形. ∴∠BPM =∠BMP =60º. ∴∠APM =120º.∴∠PAM +∠AMP =60º.∴∠PAM +∠AMP +∠BMP =120º.即∠PAM +∠AMB =120º. ∵AB=BC , ∴AP=MC .∵∠AMN =60º, ∴∠AMB +∠NMC =120º. ∴∠PAM =∠NMC .又∵AM=MN ,∴△APM ≌△NMC .∴∠MCN =∠APM =120º………………5分 (2) 补全图形,如图……………………………………………………………….………………………6分B∠MCN =60º……………………………………………………………….……………………7分 朝阳27. 解:(1)45 ……………………………………………………………………………………1分(2)解:如图,连接DB.∵90 AB AC BAC =∠=,°,M 是BC 的中点, ∴∠BAD=∠CAD=45°.∴△BAD ≌△CAD . ………………………………2分 ∴∠DBA =∠DCA ,BD = CD . ∵CD =DF ,∴B D =DF . ………………………………………3分 ∴∠DBA =∠DFB =∠DCA . ∵∠DFB +∠DFA =180°, ∴∠DCA +∠DFA =180°. ∴∠BAC +∠CDF=180°.∠CDF =90°. …………………………………………………………………………4分 (3)CE =)1CD . ………………………………………………………………………5分证明:∵90 EAD ∠=°,∴∠EAF =∠DAF =45°. ∵AD =AE ,∴△EAF ≌△DAF . ……………………………………………………………………6分 ∴DF =EF .由②可知,CF . ∴CE =)1C D . ………………………………………………………………7分丰台27.解:(1)图形补全后如图…………………1分(2)结论:AG ⊥EF . …………………2分证明:连接FD ,过F 点FM ∥BC ,交BD 的延长线于点M .∵四边形ABCD 是正方形,∴AB=DA=DC=BC ,∠DAB =∠ABE =∠ADC =90°, ∠ADB =∠5=45°.∵线段AE 绕点A 逆时针旋转90°,得到AF , ∴AE=AF ,∠FAE =90°.∴∠1=∠2.∴△FDA ≌△EBA . …………………3分∴∠FDA =∠EBA =90°,FD=BE .∵∠ADC =90°, ∴∠FDA +∠ADC =180°。
北京市东城区2018届中考数学二模试题含答案

北京市东城区 2018届中考数学二模试题学校______________班级______________姓名_____________考号____________一、选择题(本题共16分,每小题2分)下面各题均有四个选项,其中只有一个..是符合题意的1. 长江经济带覆盖上海、江苏、浙江、安徽、江西、湖北、湖南、重庆、四川、云南、贵州等11省市,面积约2 050 000平方公里,约占全国面积的21% .将2 050 000用科学记数法表示应为 A. 205万 B. 420510⨯ C. 62.0510⨯ D. 72.0510⨯ 2. 在平面直角坐标系xOy 中,函数31y x =+的图象经过A. 第一、二、三象限B. 第一、二、四象限C. 第一、三、四象限D. 第二、三、四象限3. 在圆锥、圆柱、球、正方体这四个几何体中,主视图不可能...是多边形的是 A. 圆锥 B. 圆柱 C. 球 D. 正方体4. 七年级1班甲、乙两个小组的14名同学身高(单位:厘米)如下:甲组 158 159 160 160 160 161 169 乙组158159160161161163165以下叙述错误..的是 A. 甲组同学身高的众数是160 B. 乙组同学身高的中位数是161 C. 甲组同学身高的平均数是161 D. 两组相比,乙组同学身高的方差大 5. 在平面直角坐标系xOy 中,若点()3,4P 在O 内,则O 的半径r 的取值范围是A. 0r <<3B. r >4C. 0r <<5D. r >56. 如果23510a a +-=,那么代数式()()()5323+232a a a a +--的值是A. 6B. 2C. - 2D. - 67. 在以下三个图形中,根据尺规作图的痕迹,能判断射线AD 平分∠BAC 的是A. 图2B. 图1与图2C. 图1与图3D. 图2与图38. 有一圆形苗圃如图1所示,中间有两条交叉过道AB ,CD ,它们为苗圃O e 的直径,且AB ⊥CD . 入口K 位于»AD 中点,园丁在苗圃圆周或两条交叉过道上匀速行进.设该园丁行进的时间为x ,与入口K 的距离为y ,表示y 与x 的函数关系的图象大致如图2所示,则该园丁行进的路线可能是图2A. A →O →DB. C→A→O→ BC. D →O →CD. O→D→B→C 二、填空题(本题共16分,每小题2分) 9.若分式22xx +的值为正,则实数x 的取值范围是__________________. 10.在平面直角坐标系xOy 中,点P 到x 轴的距离为1,到y 轴的距离为2.写出一个..符合条件的点P 的坐标________________.11. 如图,在△ABC 中,AB =AC ,BC =8. O e 是△ABC 的外接圆,其半径为5. 若点A 在优弧BC 上,则tan ABC ∠的值为_____________.第11题图 第15题图 12. 抛物线221y mx mx =++(m 为非零实数)的顶点坐标为_____________.13.自2008年9月南水北调中线京石段应急供水工程通水以来,截至2018年5月8日5 时52分,北京市累计接收河北四库来水和丹江口水库来水达50亿立方米. 已知丹江口水库来水量比河北四库来水量的2倍多1.82亿立方米,求河北四库来水量. 设河北四库来水量为x 亿立方米,依题意,可列一元一次方程为_________ .14. 每年农历五月初五为端午节,中国民间历来有端午节吃粽子、赛龙舟的习俗.某班同学为了更好地了解某社区居民对鲜肉粽、豆沙粽、小枣粽、蛋黄粽的喜爱情况,对该社区居民进行了随机抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).分析图中信息,本次抽样调查中喜爱小枣粽的人数为 ;若该社区有10 000人,估计爱吃鲜肉粽的人数约为 .15. 如图,在平面直角坐标系xOy 中,点A ,P 分别在x 轴、 y 轴上,30APO ∠=︒ .先将线段PA 沿y 轴翻折得到线段PB ,再将线段PA 绕点P 顺时针旋转30°得到 线段PC ,连接BC . 若点A 的坐标为()1,0- ,则线段BC 的长为 . 16. 阅读下列材料:数学课上老师布置一道作图题:小东的作法如下:老师说:“小东的作法是正确的.”请回答:小东的作图依据是 .三、解答题(本题共68分,第17-24题,每小题5分,第25题6分,第26-27,每小题7分,第28题8分)17.计算:()332sin 60+2+12--︒-18. 解不等式()()41223x x --->,并把它的解集表示在数轴上.19. 如图,在Rt ABC △中,90C ∠=︒,AB 的垂直平分线交AC 于点D ,交AB 于点E .(1)求证:ADE ABC △≌△;(2)当8AC =,6BC =时,求DE 的长.20. 已知关于x 的一元二次方程2610kx x -+=有两个不相等的实数根.(1)求实数k 的取值范围;(2)写出满足条件的k 的最大整数值,并求此时方程的根.21.如图,在菱形ABCD 中,BAD α∠=,点E 在对角线BD 上. 将线段CE 绕点C 顺时针旋转α,得到CF ,连接DF . (1)求证:BE =DF ;(2)连接AC , 若EB =EC ,求证:AC CF ⊥.22. 已知函数1y x=的图象与函数()0y kx k =≠的图象交于点(),P m n . (1)若2m n =,求k 的值和点P 的坐标;(2)当m n ≤时,结合函数图象,直接写出实数k 的取值范围. 23. 如图,AB 为O 的直径,直线BM AB ⊥于点B .点C 在O 上,分别连接BC ,AC ,且AC的延长线交BM 于点D .CF 为O 的切线交BM 于点F .(1)求证:CF DF =;(2)连接OF . 若10AB =,6BC =,求线段OF 的长.24.十八大报告首次提出建设生态文明,建设美丽中国. 十九大报告再次明确,到2035年美丽中国目标基本实现.森林是人类生存发展的重要生态保障,提高森林的数量和质量对生态文明建设非常关键 .截止到2013年,我国已经进行了八次森林资源清查,其中全国和北京的森林面积和森林覆盖率情况如下:表1 全国森林面积和森林覆盖率表2 北京森林面积和森林覆盖率(以上数据来源于中国林业网)请根据以上信息解答下列问题:(1) 从第________次清查开始,北京的森林覆盖率超过全国的森林覆盖率;(2) 补全以下北京森林覆盖率折线统计图,并在图中标明相应数据;(3) 第八次清查的全国森林面积20768.73(万公顷)记为a,全国森林覆盖率21.63%记为b,到2018年第九次森林资源清查时,如果全国森林覆盖率达到27.15%,那么全国森林面积可以达到________万公顷(用含a和b的式子表示).25. 小强的妈妈想在自家的院子里用竹篱笆围一个面积为4平方米的矩形小花园,妈妈问九年级的小强至少需要几米长的竹篱笆(不考虑接缝).小强根据他学习函数的经验做了如下的探究. 下面是小强的探究过程,请补充完整: 建立函数模型:设矩形小花园的一边长为x 米,篱笆长为y 米.则y 关于x 的函数表达式为 ; 列表(相关数据保留一位小数):根据函数的表达式,得到了x 与y 的几组值,如下表:描点、画函数图象:如图,在平面直角坐标系xOy 中,描出了以上表中各对对应值为坐标的点,根据描出的点画出该函数的图象; 观察分析、得出结论:根据以上信息可得,当x = 时,y 有最小值. 由此,小强确定篱笆长至少为 米.26.在平面直角坐标系xOy 中,抛物线()230y ax bx a =+-≠经过点()1,0A -和点()45B ,. (1)求该抛物线的表达式;(2)求直线AB 关于x 轴的对称直线的表达式;(3)点P 是x 轴上的动点,过点P 作垂直于x 轴的直线l ,直线l 与该抛物线交于点M ,与直线AB交于点N .当PM PN <时,求点P 的横坐标P x 的取值范围.27. 如图所示,点P 位于等边ABC △的内部,且∠ACP =∠CBP . (1) ∠BPC 的度数为________°;(2) 延长BP 至点D ,使得PD =PC ,连接AD ,CD .①依题意,补全图形; ②证明:AD +CD =BD ;(3) 在(2)的条件下,若BD 的长为2,求四边形ABCD 的面积.28. 研究发现,抛物线214y x =上的点到点F (0,1)的距离与到直线l :1y =-的距离相等.如图1所示,若点P 是抛物线214y x =上任意一点,PH ⊥l 于点H ,则PH PF =.基于上述发现,对于平面直角坐标系x O y 中的点M ,记点M 到点P 的距离与点P 到点F 的距离之和的最小值为d ,称d 为点M 关于抛物线214y x =的关联距离;当24d ≤≤时,称点M 为抛物线214y x =的关联点.(1)在点1(20)M ,,2(12)M ,,3(45)M ,,4(04)M -,中,抛物线214y x =的关联点是______ ; (2)如图2,在矩形ABCD 中,点(1)A t ,,点(13)A t +,C ( t .①若t =4,点M 在矩形ABCD 上,求点M 关于抛物线214y x =的关联距离d 的取值范围; ②若矩形ABCD 上的所有点都是抛物线214y x =的关联点,则t 的取值范围是__________. 东城区2017-2018学年度第二学期初三年级统一测试(二)数学试题卷参考答案及评分标准 2018.5一、选择题(本题共16分,每小题2分)二、填空题(本题共16分,每小题 2分)9. x >0 10. ()()()()21212121--,,,-,,,,-(写出一个即可) 11. 2 12. ()1,1m -- 13. ()2 1.8250x x ++= 14. 120 ;3 000 15. 22 16. 三边分别相等的两个三角形全等;全等三角形的对应角相等;两点确定一条直线;内错角相等两直线平行.三、解答题(本题共68分,17-24题,每题5分,第25题6分,26-27题,每小题7分,第28题8分)3=3-232⨯17.解:原式--------------------------------------------------------------------4分-------------------------------------------------------------------------------------------------- 5分 18. 解:移项,得()1213x -<, 去分母,得 23x -<, 移项,得x <5.∴不等式组的解集为x <5.--------------------------------------------------------------------3分--------------------------------5分 19. 证明:(1) ∵DE 垂直平分AB ,∴ 90AED ∠=︒. ∴AED C ∠=∠. ∵A A ∠=∠, ∴ADE ABC △∽△.--------------------------------------------------------------------2分(2) ABC Rt △中,8AC =,6BC =, ∴10AB =.∵DE 平分AB , ∴5AE =.∵ADE ABC △∽△,∴DE AEBC AC =. ∴568DE = .∴154DE = . ---------------------------------------------------------------------5分20. 解:(1) 依题意,得()20,640k k ≠⎧⎪⎨∆=--⎪⎩>,解得k k ≠<9且0.----------------------------------------------------------------------2分(2) ∵k 是小于9的最大整数,∴=8k .此时的方程为28610x x -+=. 解得11=2x ,21=4x . ---------------------------------------------------------------------5分21 . (1) 证明:∵四边形ABCD 是菱形,∴=BC DC ,BAD BCD α==∠∠. ∵ECF α=∠,∴ BCD ECF ∠=∠. ∴=BCE DCF ∠∠.∵线段CF 由线段CE 绕点C 顺时针旋转得到, ∴=CE CF .在BEC △和DFC △中,BC DC BCE DCF CE CF =⎧⎪∠=∠⎨⎪=⎩,,, ∴BEC △≌()SAS DFC △.∴=.BE DF ----------------------------------------------------------------------2分 (2) 解:∵四边形ABCD 是菱形, ∴ACB ACD ∠=∠,AC BD ⊥. ∴+90ACB EBC ∠=︒∠. ∵=EB EC ,∴=EBC BCE ∠∠.由(1)可知,∵=EBC DCF ∠∠,∴+90DCF ACD EBC ACB ∠=∠+∠=︒∠.∴90ACF =︒∠.∴AC CF ⊥. ---------------------------------------------------------------------5分22. 解:(1)12k =,222P ,,或22P ⎛- ⎝⎭,;---------------------------3分 (2) 1k ≥.---------------------------------------------------------------------5分23. (1)证明:∵AB 是O 的直径,∴90ACB ∠=︒.∴90DCB ∠=︒.∴90CDB FBC ∠+∠=︒.∵ AB 是O 的直径,MB AB ⊥, ∴MB 是O 的切线. ∵CF 是O 的切线,∴FC FB =.∴=FCB FBC ∠∠.∵90FCB DCF ∠+∠=︒ ,∴=CDB DCF ∠∠.∴=CF DF . ---------------------------------------------------------------------3分(2)由(1)可知,ABC △是直角三角形,在Rt ABC △中,=10AB ,=6BC ,根据勾股定理求得=8AC .在Rt ABC △和Rt ADB △中,A A ACB ABD ∠=∠⎧⎨∠=∠⎩,, ∴Rt ABC △∽Rt ADB △. ∴AB AC AD AB=.∴10810AD = . ∴252AD =. 由(1)知,∵=CF DF ,=CF BF ,∴=DF BF .∵=AO BO ,∴ OF 是ADB △的中位线. ∴125.24OF AD ==---------------------------------------------------------------------5分 24. 解:(1)四; ---------------------------------------------------------------------1分(2)如图: ---------------------------------------------------------------------3分(3)5432000a b.------------------------------------------------------5分 25. 解:42y x x ⎛⎫=+ ⎪⎝⎭;----------------------------------------------1分 810,; --------------------------------------------------------3分如图; ----------------------------------------------------------4分28,. -----------------------------------------------------------5分26. 解:(1)把点(10)-,和(45),分别代入23(0)y ax bx a =+-≠, 得 0--35164-3a b a b =⎧⎨=+⎩,,解得12a b ==-,. ∴抛物线的表达式为223y x x =--. -------------------------------------------------------------2分(2)设点()45B ,关于x 轴的对称点为B ',则点B '的坐标为()45,-.∴直线AB 关于x 轴的对称直线为直线AB '.设直线AB '的表达式为y mx n =+,把点(10)-,和(45)-,分别代入y mx n =+,得054m n m n =-+⎧⎨-=+⎩,,解得11m n =-=-,.∴直线AB '的表达式为1y x =--.即直线AB 关于x 轴的对称直线的表达式为1y x =--.--------------------------------------4分(3)如图,直线AB '与抛物线223y x x =--交于点C .设直线l 与直线AB '的交点为N ',则 'PN PN =.∵PM PN <,∴'PM PN <.∴点M 在线段'NN 上(不含端点).∴点M 在抛物线223y x x =--夹在点C 与点B 之间的部分上.联立223y x x =--与1y x =--, 可求得点C 的横坐标为2.又点B 的横坐标为4,∴点P 的横坐标P x 的取值范围为24P x <<. --------------------------------------------------7分27. 解:(1)120°.---------------------------------------------------2分(2)①∵如图1所示.②在等边ABC △中,60ACB ∠=︒,∴60.ACP BCP ∠+∠=︒∵=ACP CBP ∠∠,∴60.CBP BCP ∠+∠=︒∴()180120.BPC CBP BCP ∠=︒-∠+∠=︒∴18060.CPD BPC ∠=︒-∠=︒∵=PD PC ,∴CDP △为等边三角形.∵60ACD ACP ACP BCP ∠+∠=∠+∠=︒,∴.ACD BCP ∠=∠在ACD △和BCP △中,AC BC ACD BCP CD CP =⎧⎪∠=∠⎨⎪=⎩,,,∴()SAS ACD BCP △≌△.∴.AD BP =∴.AD CD BP PD BD +=+=-----------------------------------------------------------------4分(3)如图2,作BM AD ⊥于点M ,BN DC ⊥延长线于点N .∵=60ADB ADC PDC ∠∠-∠=︒,∴=60.ADB CDB ∠∠=︒∴=60.ADB CDB ∠∠=︒ ∴3= 3.BM BN == 又由(2)得,=2AD CD BD +=,ABD BCD ABCD S S S ∴△△四边形=+1122AD BM CD BN =+)32AD CD =+ 32= 3.=----------------------------------------------------------7分28. (1) 12M M ,; -----------------------------------------------------------------2分(2)①当4t =时,()41A ,,()51B ,,()53C ,,()43D ,, 此时矩形ABCD 上的所有点都在抛物线214y x =的下方, ∴.d MF =∴.AF d CF ≤≤∵=4=29AFCF ,∴d 4≤ ---------------------------------------------------------------------------------- 5分t≤② 1. ------------------------------------------------------------------------8分。
2018北京市海淀区中考二模数学试卷(含答案)

海淀区九年级第二学期期末练习数 学2018.5学校 姓名 成绩考生须知1.本试卷共8页,共三道大题,28道小题,满分100分。
考试时间120分钟。
2.在试卷和答题卡上准确填写学校名称、班级和准考证号。
3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效。
4.在答题卡上,选择题、作图题用2B 铅笔作答,其他试题用黑色字迹签字笔作答。
5.考试结束,将本试卷、答题卡和草稿纸一并交回。
一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有一个.1.若代数式有意义,则实数的取值范围是31x -x A . B. 1x >1x ≥ C.D.1x ≠0x ≠2.如图,圆的弦,,,中最短的是O GH EF CD AB A . B. GH EF C.D. CD AB3.2018年4月18日,被誉为“中国天眼”的FAST 望远镜首次发现的毫秒脉冲星得到国际认证.新发现的脉冲星自转周期为0.00519秒,是至今发现的射电流量最弱的高能毫秒脉冲星之一.将0.00519用科学记数法表示应为A. -25.1910⨯ B. -35.1910⨯ C. -551910⨯ D. -651910⨯4.下列图形能折叠成三棱柱的是ABE DCD 5.如图,直线经过点,,°,°,则等于DE A DE BC ∥=45B ∠1=65∠2∠A .° 60B .° 65C .° 70D .°756.西周时期,丞相周公旦设置过一种通过测定日影长度来确定时间的仪器,称为圭表.如图是一个根据北京的地理位置设计的圭表,其中,立柱高为.已知,冬至时北京的正午日AC a 光入射角约为°,则立柱根部与圭表的冬至线的距离(即的长)约为ABC ∠26.5BC A .B .sin 26.5a ︒tan 26.5a︒C .D .cos 26.5a ︒cos 26.5a ︒7.实数在数轴上的对应点的位置如图所示,若,,,a b c a b >则下列结论中一定成立的是A. B . 0b c +>2a c +<-C.D. 1ba<0abc ≥8.“单词的记忆效率”是指复习一定量的单词,一周后能正确默写出的单词个数与复习的单词个数的比值.右图描述了某次单词复习中四位同学的单词记忆,,,M N S T 效率与复习的单词个数的情况,则这四位同学在这次单词复习中正确默写出的y x 单词个数最多的是A .B .M N c ba 光光光光光光光光光光光光光光光光光光光光光光光光光光EDCB A21C .D .S T二、填空题(本题共16分,每小题2分)9. 分解因式:.2363a a ++=10.如图,是⊙的直径,是⊙上一点,,,则AB O C O 6OA =30B ∠=︒图中阴影部分的面积为 .11.如果,那么代数式的值是.3m n =n m mm n n m⎛⎫-⋅ ⎪-⎝⎭12.如图,四边形与四边形是以为位似中心的位似图形,满足,,,ABCD 1111A B C D O 11=OA A A E F ,1E 分别是,,的中点,则1F AD BC ,11A D 11B C 11=E F EF.13.2017年全球超级计算机500强名单公布,中国超级计算机“神威·太湖之光”和“天河二号”携手夺得前两名.已知“神威·太湖之光”的浮点运算速度是“天河二号”的2.74倍.这两种超级计算机分别进行100亿亿次浮点运算,“神威·太湖之光”的运算时间比“天河二号”少18.75秒,求这两种超级计算机的浮点运算速度.设“天河二号”的浮点运算速度为亿亿次/秒,依题意,可列方程为.x 14.袋子中有20个除颜色外完全相同的小球. 在看不到球的条件下,随机地从袋子中摸出一个球,记录颜色后放回,将球摇匀. 重复上述过程150次后,共摸到红球30次,由此可以估计口袋中的红球个数是__________..BA请回答:在上面的作图过程中,①是直角三角形的依据是 ;②是等腰三角形的依据是 ABC △ABC △.16.在平面直角坐标系中,点绕坐标原点顺时针旋转后,恰好落在右图中阴影区域(包xOy (2,)A m -O 90︒括边界)内,则的取值范围是.m 三、解答题(本题共68分,第17~22题,每小题5分;第23~26小题,每小题6分;第27~28小题,每小题7分)解答应写出文字说明、演算步骤或证明过程.17.214sin 452)(2--︒+--18.解不等式,并把解集在数轴上表示出来.2223x xx +--<19.如图,四边形中,°,平分,,为上一点, ,ABCD 90C ∠=BD ABC ∠3AD =E AB 4AE =,求的长.5ED =CD E DCBA20.关于的一元二次方程.x 2(3)30x m x m -++=(1)求证:方程总有实数根;(2)请给出一个的值,使方程的两个根中只有一个根小于.m 421.如图,在四边形中,, 交于,是的中点,连接并延长,交于ABCD AB CD BD AC G E BD AE CD 点,恰好是的中点.F F CD GBC(1)求的值;BGGD(2)若,求证:四边形是矩形.CE EB =ABCF 22.已知直线过点,且与函数的图象l (2,2)P (0)ky x x =>相交于两点,与轴、轴分别交于点,如图,A B x y ,C D 所示,四边形均为矩形,且矩形,ONAE OFBM 的面积为.OFBM 3(1)求的值;k (2)当点的横坐标为时,求直线的解析式及线段的长;B 3l BC (3)如图是小芳同学对线段的长度关系的思考示意图.,AD BC 记点的横坐标为,已知当时,线段的长随的增大而减小,请你参考小芳的示意图判断:B s 23s <<BC s 当时,线段的长随的增大而 . (填“增大”、“减小”或“不变”)3s ≥BC s23.如图,是的直径,是的中点,弦于点,过点作交的延长线AB O M OA CD AB ⊥M D DE CA ⊥CA 于点.E (1)连接,则= ;AD OAD ∠︒(2)求证:与相切;DE O (3)点在上,,交于点.若,求的长.F BC45CDF ∠=︒DF AB N 3DE =FN24.如图是甲、乙两名射击运动员的10次射击测试成绩的折线统计图.(1)根据折线图把下列表格补充完整;运动员平均数中位数众数甲8.59乙8.5(2)根据上述图表运用所学统计知识对甲、乙两名运动员的射击水平进行评价并说明理由.25.小明对某市出租汽车的计费问题进行研究,他搜集了一些资料,部分信息如下:收费项目收费标准3公里以内收费13元基本单价 2.3元/公里…………备注:出租车计价段里程精确到500米;出租汽车收费结算以元为单位,元以下四舍五入。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018北京各区初中数学二模分类汇编27号题及答案2018北京各区初中数学二模分类汇编27号题及答案门头沟 27. 如图,在正方形ABCD 中,连接BD ,点E 为CB 边的延长线上一点,点F 是线段AE 的中点,过点F 作AE 的垂线交BD 于点M ,连接ME 、MC .(1)根据题意补全图形,猜想MEC ∠与MCE ∠的数量关系并证明;(2)连接FB ,判断FB 、FM 之间的数量关系并证明.西城27. 如图1,在等边三角形ABC 中,CD为中线,点Q 在线段CD 上运动,将线段QA 绕点Q 顺时针旋转,使得点A 的对应点E 落在射线BC 上,连接BQ ,设∠DAQ =α (0°<α<60°且α≠30°). (1)当0°<α<30°时,①在图1中依题意画出图形,并求∠BQE (用含α的式子表示);F A平谷27.正方形ABCD的对角线AC,BD交于点O,作∠CBD的角平分线BE,分别交CD,OC于点E,F.O (1)依据题意,补全图形(用尺规作图,保留作图痕迹);(2)求证:CE=CF;(3)求证:DE=2OF.顺义27.在等边ABC△外侧作直线AM,点C关于AM 的对称点为D,连接BD交AM于点E,连接CE,CD,AD.(1)依题意补全图1,并求BEC的度数;(2)如图2 ,当30MAC ∠=︒时,判断线段BE 与DE之间的数量关系,并加以证明;(3)若0120MAC ︒<∠<︒,当线段2DE BE =时,直接写出MAC ∠的度数.图1MCBA东城27.如图所示,点P 位于等边ABC △的内部,且∠ACP =∠CBP . (1) ∠BPC 的度数为________°;(2) 延长BP 至点D ,使得PD =PC ,连接AD ,CD .图2MEDCBA①依题意,补全图形; ②证明:AD +CD =BD ;(3) 在(2)的条件下,若BD 的长为2,求四边形ABCD 的面积.房山27. 已知AC =DC ,AC ⊥DC ,直线MN 经过点A ,作DB ⊥MN ,垂足为B ,连接CB . (1)直接写出∠D 与∠MAC 之间的数量关系;(2)① 如图1,猜想AB ,BD 与BC 之间的数量关系,并说明理由;② 如图2,直接写出AB ,BD 与BC之间的数量关系;(3)在MN 绕点A 旋转的过程中,当∠BCD =30°,BD = 2 时,直接写出BC 的值.C ADBN昌平27.如图,在△ABC 中,AB =AC >BC ,BD 是AC 边上的高,点C 关于直线BD 的对称点为点E ,连接BE .(1) ①依题意补全图形;②若∠BAC =α,求∠DBE 的大小(用含α的式子表示);(2) 若DE =2AE ,点F 是BE 中点,连接AF ,BD =4,求AF 的长.D CBADCBA(备用图)海淀27.如图,在等边ABC △中, ,D E 分别是边,AC BC 上的点,且CD CE = ,30DBC ∠<︒ ,点C 与点F 关于BD 对称,连接,AF FE ,FE 交BD 于G .(1)连接,DE DF ,则,DE DF 之间的数量关系是 ; (2)若DBC α∠=,求FEC ∠的大小;(用α的式子表示)(2)用等式表示线段,BG GF 和FA 之间的数量关系,GF EDCBA并证明.石景山27.在△ABC 中,∠ABC =90°,AB =BC =4,点M 是线段BC 的中点,点N 在射线MB 上,连接AN ,平移△ABN ,使点N 移动到点M ,得到△DEM (点D 与点A 对应,点E 与点B 对应),DM 交AC 于点P .(1)若点N 是线段MB 的中点,如图1.① 依题意补全图1;② 求DP 的长; (2)若点N 在线段MB 的延长线上,射线DM 与射线AB 交于点Q ,若MQ =DP ,求CE 的长.怀柔27.在△ABC 中,AB=BC =AC ,点M 为直线BC 上一个动点(不与B ,C 重合),连结AM ,将线段AM 绕点M 顺时针旋转60°,得到线段MN ,连结NC .图1N MA B C N M A B C 备用图BA A B第27第27(1)BC①依题意补全图1;②点M在线段BC上运动的过程中,∠MCN的度数是否确定?如果确定,求出∠MCN的度数;如果不确定,说明理由;(2)如果点M在线段CB的延长线上运动,依题意补全图2,在这个过程中,∠MCN的度数是否确定?如果确定,直接写出∠MCN的度数;如果不确定,说明理由.朝阳27.如图,在△ABC中,AB=AC,∠BAC=90°,M是BC的中点,延长AM到点D,AE= AD,∠EAD=90°,CE交AB于点F,CD=DF.(1)∠CAD= 度;(2)求∠CDF的度数;(3)用等式表示线段CD和CE之间的数量关系,并证明.丰台27.如图,正方形ABCD 中,点E 是BC 边上的一个动点,连接AE ,将线段AE绕点A 逆时针旋转90°,得到AF ,连接EF ,交对角线BD 于点G ,连接AG . (1)根据题意补全图形;(2)判定AG 与EF 的位置关系并证明;(3)当AB = 3,BE = 2时,求线段BG 的长.A B CE D答案门头沟 27.(本小题满分7分)(1)补全图形正确 ……………………………………………1分MEC∠=MCE ∠ ………………………………………2分 证明:连接AM∵点F 是AE 的中点,FM AE ⊥ ∴MA ME =∵点A 、点C 是关于正方形ABCD 对角线BD 所在直线的对称点∴MA MC =………………………………………3分 ∴ME MC = ∴MEC∠=MCE ∠………………………………………4分(2)数量关系:FB FM = ……………………5分∵点M 在正方形对角线上,可得MFCA DMAD MCD△≌△∴MAD ∠=MCD ∠ ∵MEC ∠=MCE ∠∴90MEC MAD DCM MCE ∠+∠=∠+∠=︒ ∵AD CE ∥ ∴180DAE CEA ∠+∠=︒ ∴90MAE MEA ∠+∠=︒ ∴90AME ∠=︒ ∴EMA△是等腰直角三角形……………………6分∴12FM AE = ∵12FB AE = ∴FB FM= ……………………7分西城27. 解:(1)当0°<α<30°时,①画出的图形如图9所示.…………… 1分∵ △ABC 为等边三角形,∴ ∠ABC=60°.∵ CD 为等边三角形的中线,MFCADQ 为线段CD 上的点, 由等边三角形的对称性得QA=QB .∵ ∠DAQ =α,∴ ∠ABQ =∠DAQ=α,∠QBE =60°-α.∵ 线段QE 为线段QA 绕点Q顺时针旋转所得,∴ QE = QA .∴ QB=QE .可得1802BQE QBE ∠=︒-∠1802(60)602αα=︒-︒-=︒+.……… 2分②3CE AC CQ+=.……………………………………………………… 3分证法一:如图10,延长CA 到点F ,使得AF=CE ,连接QF ,作QH ⊥AC 于点H .∵ ∠BQE =60°+2α,点E 在BC 上,∴ ∠QEC =∠BQE+图∠QBE =(60°+2α)+( 60°-α)=120°+α.∵点F在CA的延长线上,∠DAQ=α,∴∠QAF=∠BAF+∠DAQ=120°+α.∴∠QAF=∠QEC.又∵AF =CE,QA=QE,∴△QAF≌△QEC.∴QF=QC.∵QH⊥AC于点H,∴FH=CH,CF=2CH.∵在等边三角形ABC 中,CD为中线,点Q在CD上,∴∠ACQ=12ACB=30°,即△QCF为底角为30°的等腰三角形.图∴3cos cos30CH CQ HCQ CQ =⋅∠=⋅︒=. ∴CE AC AF AC CF +=+=23CH CQ==. 即3CE AC CQ+=. ………………………………………… 6分思路二:如图11,延长CB 到点G ,使得BG=CE ,连接QG ,可得△QBG ≌△QEC ,△QCG 为底角为30°的等腰三角形,与证法一同理可得CE AC BG BC CG +=+=3CQ=.(2)如图12,当30°<α<60°时,图113AC CE CQ-=.………………………… 7分平谷27.(1)如图 (1)FE DO(2)证明:∵BE 平分∠CBD ,∴∠CBE =∠DBE . ······ 2 ∵正方形ABCD 的对角线AC ,BD 交于点O ,∴∠BOC =∠BCD =90°.∵∠CBE +∠CEB =90°, ∠DBE +∠BFO =90°,∴∠CEB =∠BFO . ······ 3 ∵∠EFC =∠BFO , ∴∠EFC =∠CEB . ∴CF=CE . ········· 4 (3)证明:取BE 的中点M ,连接OM . ·· 5 ∵O 为AC 的中点,∴OM ∥DE , DE =2OM . ···· 6 ∴∠OMF =∠CEF .∵∠OFM =∠EFC =∠CEF ,∴∠OMF =∠OFM .∴OF=OM . ∴DE =2OF . (7)M FOy yxx E DMCBA顺义27.解:(1)补全图形如右图: …………………………………………………… 1分依题意显然可以得出AD =AC ,∠=∠=DAE CAE x ,∠=∠DEM CEM .∵等边ABC △, ∴AB =AC ,60∠=︒BAC . ∴AB =AD . ∴∠=∠=ABD ADB y . 在△ABD 中,2260180++︒=︒x y ,∴60+=︒x y .∴60∠=∠=+=︒DEM CEM x y . ∴60∠=︒BEC .………………………………………………………… 4分 (2)判断:2=BE DE .证明:∵30MAC ∠=︒,结合(1)中证明过程,显然可以得出30∠=︒ABD , 又∵等边ABC △, ∴60∠=︒ABC . ∴30∠=︒DBC . 又∵60∠=︒BEC ,∴90ECB.∠=︒∴2=BE CE.∵=CE DE,∴2=BE DE.(3)MAC.…………………………………………90∠=︒……………… 7分4东城27.解:(1)120°.---------------------------------------------------2分(2)①∵如图1所示.②在等边ABC△中,∠=︒,60ACB∴60.∠+∠=︒ACP BCP∵=∠∠,ACP CBP∴60.∠+∠=︒CBP BCP∴()180120.∠=︒-∠+∠=︒BPC CBP BCP∴18060.∠=︒-∠=︒CPD BPC∵=PD PC,∴CDP△为等边三角形.∵60ACD ACP ACP BCP ∠+∠=∠+∠=︒, ∴.ACD BCP ∠=∠ 在ACD △和BCP △中,AC BC ACD BCP CD CP =⎧⎪∠=∠⎨⎪=⎩,,,∴()SAS ACD BCP △≌△. ∴.AD BP = ∴.AD CD BP PD BD +=+=-----------------------------------------------------------------4分(3)如图2,作BM AD ⊥于点M ,BN DC ⊥延长线于点N .∵=60ADB ADC PDC ∠∠-∠=︒, ∴=60.ADB CDB ∠∠=︒ ∴=60.ADB CDB ∠∠=︒ ∴3= 3.2BM BN BD ==又由(2)得,=2AD CD BD +=,ABD BCD ABCD S S S ∴△△四边形=+1122AD BM CD BN =+)3AD CD =+322=⨯ 3.=----------------------------------------------------------7分 房山27. 解:(1)相等或互补; (2)分(注:每个1分)(2)① 猜想:BD +AB =2BC …………………………………………………………3分如图1,在射线AM 上截取AE =BD ,连接CE .又∵∠D =∠EAC ,CD =AC ∴△BCD ≌△ECA∴BC =EC ,∠BCD =∠ECA ∵AC ⊥CD ∴∠ACD =90°即∠ACB +∠BCD =90°∴∠ACB +∠ECA =90° 即∠ECB =90° ∴BE =2BC ∵AE +AB =BE =2BC∴NM图1E ADBBD +AB =2BC ……………………………………………………………4分② A B -BD =2BC ……………………………………………………………5分 (3)BC =3+1 或3-1 ……………………………………………………………7分昌平27.如图,在△ABC 中,AB =AC >BC ,BD 是AC 边上的高,点C 关于直线BD 的对称点为点E ,连接BE . (1)①补全图形;②若∠BAC =α,求∠DBE 的大小(用含α的式子表示);(2)若DE =2AE ,点F 是BE 中点,连接AF ,BD =4,求AF 的长.(1)解:①如图. ……………………… 1分 ②∵ AB =AC ,∠BAC =α,∴∠ABC =∠ACB =90°-12α.∵点C 关于直线BD 的对称点为点E ,BD 是AC 边上的高.D C BA E∴ BD ⊥CE ,CD =DE . ∴ BE =BC .∴∠BEC =∠ACB =90°-12α. …………………… 2分∴∠DBE =12α.……………… 3分(2)解:作FG ⊥AC 于G , ∵BD ⊥CE ,∴FG ∥BD∵点F 是BE 中点,∴EG =DG .∴1FG=BD 2…………4分∵DE =2AE ,∴AE =EG =DG .……………… 5分设AE =EG =DG=x ,则CD =DE=2x ,AC =5x ,∴AB=AC =5x .∴BD =4x . ∵BD =4,∴x =1.……………… 6分∴AG =2.∵1FG=BD 2=2,∴AF=22………………7分海淀 27.(1)DE DF =;(2)解:连接DE ,DF , ∵△ABC 是等边三角形, ∴60C ∠=︒.EABCDFG GFEDCBA∵DBC α∠=, ∴120BDC α∠=︒-.∵点C 与点F 关于BD 对称,∴120BDF BDC α∠=∠=︒-,DF DC =. ∴1202FDC α∠=︒+. 由(1)知DE DF =.∴F ,E ,C 在以D 为圆心,DC 为半径的圆上.∴1602FEC FDC ∠=∠=︒+α.(3)BG GF FA =+.理由如下: 连接BF ,延长AF ,BD 交于点H , ∵△ABC 是等边三角形,∴60ABC BAC ∠=∠=︒,AB BC CA ==. ∵点C 与点F 关于BD 对称, ∴BF BC =,FBD CBD ∠=∠. ∴BF BA =. ∴BAF BFA ∠=∠. 设CBD α∠=, 则602ABF α∠=︒-. ∴60BAF α∠=︒+. ∴FAD α∠=.∴FAD DBC ∠=∠. 由(2)知60FEC α∠=︒+. ∴60BGE FEC DBC ∠=∠-∠=︒. ∴120FGB ∠=︒,60FGD ∠=︒.四边形AFGB 中,360120AFE FAB ABG FGB ∠=︒-∠-∠-∠=︒. ∴60HFG ∠=︒.∴△FGH 是等边三角形. ∴FH FG =,60H ∠=︒. ∵CD CE =,HGFEDCBA∴DA EB =.在△AHD 与△BGE 中,,,.AHD BGE HAD GBE AD BE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△△AHD BGE ≅. ∴BG AH =.∵AH HF FA GF FA =+=+, ∴BG GF FA =+.石景山27.解:(1)①如图1,补全图形. ………………… 1分② 连接AD ,如图2.在Rt △ABN 中,∵∠B =90°,AB =4,BN =1, ∴17=AN .∵线段AN 平移得到线段DM , ∴DM =AN =17,AD =NM =1,AD ∥MC ,∴△ADP ∽△CMP .∴21==MC AD MP DP . ∴317=DP .………………… 3分(2)连接NQ ,如图3.由平移知:AN ∥DM ,且AN =DM .图图∵MQ DP =, ∴PQ DM =.∴AN ∥PQ ,且AN =PQ . ∴四边形ANQP 是平行四边形. ∴NQ ∥AP . ∴45BQN BAC ∠=∠=︒. 又∵90NBQ ABC ∠=∠=︒ ∴BN BQ =. ∵AN ∥MQ ,∴AB NBBQ BM=. 又∵M 是BC 的中点,且4AB BC ==,∴42NBNB =. ∴22NB =舍负). ∴22ME BN ==∴222CE =.………………… 7分(2)法二,连接AD ,如图4. 设CE 长为x ,∵线段AB 移动到得到线段DE , ∴4+==x BE AD ,AD ∥BM . ∴△ADP ∽△CMP .∴24x MC AD MP DP +==.P NQDEMAC BPN QDEMAC B图NABP ∵MQ =DP ,∴xxMP DP DP QD MQ 21042++=+=. ∵△QBM ∽△QAD ,∴xAD BM QD MQ +==42. 解得222-=x .∴222-=CE .………………… 7分27. (1)①补全图形,如图:…………………………………………….………………….…………………………………1分 ②点M 在线段BC 上运动的过程中,∠MCN 的度数确定,为120°理由如下:在AB 上取点P ,使得BP=BM ,连结PM ……………………………………………………2分∵BP =BM ,∠B =60º,NAB∴△BPM 是等边三角形. ∴∠BPM =∠BMP =60º. ∴∠APM =120º. ∴∠PAM +∠AMP =60º.∴∠PAM +∠AMP +∠BMP =120º. 即∠PAM +∠AMB =120º. ∵AB=BC , ∴AP=MC .∵∠AMN =60º, ∴∠AMB +∠NMC =120º.∴∠PAM =∠NMC . 又∵AM=MN , ∴△APM ≌△NMC .∴∠MCN =∠APM =120º………………5分 (2)补全图形,如图……………………………………………………………….………………………6分 ∠MCN =60º……………………………………………………………….……………………7分 朝阳27.解:(1)CABM45 ……………………………………………………………………………………1分(2)解:如图,连接DB.∵90,°,M是BC的中=∠=AB AC BAC点,∴∠BAD=∠CAD=45°.∴△BAD≌△CAD. ………………………………2分∴∠DBA=∠DCA,BD = CD.∵CD=DF,∴B D=DF. ………………………………………3分∴∠DBA=∠DFB=∠DCA.∵∠DFB+∠DFA=180°,∴∠DCA+∠DFA=180°.∴∠BAC+∠CDF=180°.∠CDF =90°.…………………………………………………………………………4分(3)CE=)21CD. ………………………………………………………………………5分证明:∵90∠=°,EAD∴∠EAF=∠DAF=45°.∵AD=AE,∴△EAF≌△DAF. ……………………………………………………………………6分∴DF=EF.由②可知,CF2CD.∴CE=)21C D. ………………………………………………………………7分丰台27.解:(1)图形补全后如图…………………1分D CG(2)结论:AG⊥EF.…………………2分证明:连接FD,过F点FM∥BC,交BD的延长线于点M.∵四边形ABCD是正方形,∴AB=DA=DC=BC,∠DAB=∠ABE=∠ADC=90°,54321H M G F B D C E ∠ADB =∠5=45°.∵线段AE 绕点A 逆时针旋转90°,得到AF ,∴AE=AF ,∠FAE =90°. ∴∠1=∠2. ∴△FDA ≌△EBA .…………………3分 ∴∠FDA =∠EBA =90°,FD=BE .∵∠ADC =90°, ∴∠FDA +∠ADC =180°。
