第3章凸轮资料
合集下载
第三章 凸轮机构及其设计

O
等速运动规律 a
o
v
1
2
a
正弦加速度运动规律
五、从动件运动规律(Law of Motion of Follower ) 设计应考虑的问题 (1)应满足机器工作的要求; (2)对于高速凸轮机构,应使凸轮机构具有良好 的运动和动力性能;
(3)设计从动件运动规律时,应考虑到凸轮轮廓
§3-1凸轮机构的应用及分类
3)按从动件的运动形式分: 摆动从动件 (Oscillating Follower)
§3-1凸轮机构的应用及分类
4)按凸轮高副的锁合方式分:力锁合 (Force Closure)
§3-1凸轮机构的应用及分类
4)按凸轮高副的锁合方式分:形锁合(Profile Closure)。
0
/2
0
/2
a
等加速等减速运动规律从动件位移曲线绘制方法一
S
0 1
4
9 4
1
o
1
2
δ1
3
4
5
6Hale Waihona Puke t δ等加速等减速运动规律从动件位移曲线绘制方法二
S
6 5 4 3 2
1
o
1
2
δ1
3
4
5
6
t δ
三、从动件常用运动规律
4'
s
5'
6'
(二)三角函数类基本运动规律 1.余弦加速度运动规律(推程)
的工艺性要好。 从动件动量 mvmax 在选择从动件的运动规律时,除要考虑刚性冲击与柔性 amax 从动件惯性力 ma 冲击外,还应该考虑各种运动规律的速度幅值 vmax 、加速 max 度幅值 amax 及其影响加以分析和比较。 对于重载凸轮机构,应选择 值较小的运动规律; max
第3章 凸轮机构

机械原理—凸轮机构
等宽凸轮机构
凸轮廓线上任意两条 平行切线间的距离都等于 框架内侧的宽度。 框架内侧的宽度。
缺点:从动件的运动规律的选择受到一定的限制, 从动件的运动规律的选择受到一定的限制,
180º 当180º范围内的凸轮廓线根据从动件运动规律确定 后,其余180º内的凸轮廓线必须符合等宽原则 其余180º 180
r = a +l
投影得凸轮廓线B点坐标: 投影得凸轮廓线 点坐标: 点坐标
x = a sin δ − l sin( δ + ϕ + ϕ 0 ) y = a cos δ − l cos( δ + ϕ + ϕ 0 )
r02 = a 2 + l 2 − 2 al cos ϕ 0
a 2 + l 2 − r02 ϕ 0 = arccos 2 al
机械原理—凸轮机构
第3章 凸轮机构
凸轮机构的组成与类型 从动件运动规律设计 凸轮轮廓的设计 凸轮机构基本尺寸的确定 凸轮机构的计算机辅助设计
机械原理—凸轮机构
3.1 凸轮机构的组成与类型 3.1.1 凸轮机构的组成
1 ─凸轮 ─从动件 2 ─从动件 3 ─机架 ─机架
}
高副机构
机械原理—凸轮机构
结束
机械原理—凸轮机构
3.4 凸轮机构基本尺寸的确定
3.4.1 移动滚子从动件盘形凸轮
机械原理—凸轮机构
(1) 压力角与许用值
F' = F cosα F → '' F = F sin α
F < fF → 锁 自 −1 1 即 α > tg : ⇒αmax ≤ [α] f
' ''
凸轮传动
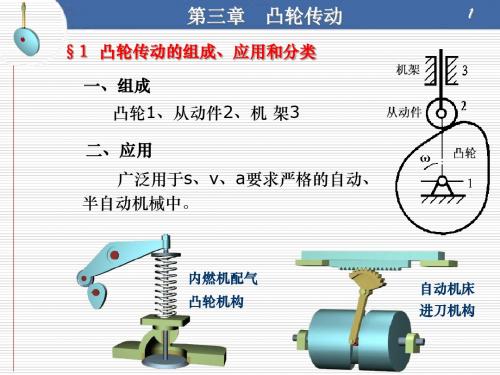
第三章 凸轮传动
6
一般凸轮机构的命名原则:
布置形式+运动形式+推杆形状+凸轮形状
对心直动尖顶推 杆盘形凸轮机构
偏置直动滚子推 杆盘形凸轮机构
摆动平底推杆 盘形凸轮机构
第三章 凸轮传动
§2 从动件的常用运动规律及其选择 设计凸轮传动:
工作要求
从动件运动规律
7 凸轮轮廓曲线
从动件运动:上升——停——下降——停
1、内凹曲线
ρ0——理论轮廓曲线
曲率半径
ρ——实际轮廓曲线
ρ0
曲率半径
ρ
ρ= ρ0+rT
无论rT为多大,都能作出
第三章 凸轮传动
2、外凸曲线 ρ= ρ0-rT
29 ρ0
ρ ρ0
rT<ρ0时,可作出。
rT=ρ0时,尖点,易 磨损——失真。
ρ0
rT>ρ0时,ρ<0,轮廓线交叉,加
工时交叉部分被切掉——失真。
4
s v
c0 c11 c212 (1 c1 2c21)
a 2c212
10 1 2
δt/2
v2
边界条件
0
a2
1 0, s 0, v 0, c0 0, c1 0
1
t
/
2, s
h/
2, c2
2h
t2
0
345
δt
h/2
h
6 δ1 δ1 δ1
1.一次多对项于式多(项n=式1)运:动等规速律运,动其规多律项式中待定系数的数 2.二目要次应求多与来项边确式界定(条。n=件但2)的当:数边等目界加相条速等件与,增等其多减数时速目,运多会动少使规应设律根计据计工算作复 3.五杂次,多加项工式精运度动也规难律以(达n=到5),故通常不宜采用太高次数
第三章 凸轮机构

图3-9 等加速、等减速 运动规律线图
3.2.2.3 简谐运动规律(余弦加速度运动规律)
图3-10 简谐运动线图 当一质点在圆周上作匀速运动时,该点在这个圆的直径上
的投影所构成的运动,称为简谐运动。从动件的位移按简 谐运动变化的运动规律,称为简谐运动规律。 如图3-10所 示,设从动件升程h为直径,其从动件的位移方程为 h (3-4) s (1 cos ) 2 由图3-10可知,当θ=π时,φ=φ0,故θ=πφ/φ0代入上式可导 出从动件推程时简谐运动方程为
单,是凸轮最基本的形式。盘形凸轮分为两种:利用外轮 廓推动从动件运动的称为盘形外轮廓凸轮,如图3-1、图3-2 所示;利用曲线沟槽推动从动件运动的称为盘形槽凸轮, 如图3-4所示。 盘形凸轮作等速回转时,从动件在垂直于凸轮轴线的平面 内运动(往复移动或摆动),因此,盘形凸轮机构属于平面凸 轮机构。由于从动件的行程或摆动太大会引起凸轮径向尺 寸变化过大,不利于机构正常工作。因此,盘形凸轮机构 一般用于从动件行程或摆动较小的场合。
凸轮轮廓,便可得到从动件所需的运动规律。 缺点:凸轮与从动件属高副接触,压强大,易磨损。适用 于传力不大的控制机构和调节机构中。
3.1.2 凸轮机构的类型
3.1.2.1 按凸轮的形状分类
按凸轮的形状可分为盘形凸轮、移动凸轮和柱体凸轮3类。
(1) 盘形凸轮。是一个具有变化半径的圆盘形构件,结构简
图3-10 简谐运动线图
3.余弦加速度运动规律
5 特点: 4 加速度变化连续平缓. 3 始、末点有软性冲击. 2 6
S
7
8 H
d0
1 0
1 V
2
3
4
5
6
7
第3章 凸轮机构

e ω
r0
A O
凸轮曲线组成: 凸轮曲线组成: 基圆--- ---以凸轮轮廓曲 1、基圆---以凸轮轮廓曲 线最小矢径ro为半径所作之圆 线最小矢径ro为半径所作之圆 ro 称为基圆,ro称为基圆半径 称为基圆半径。 称为基圆,ro称为基圆半径。 B 偏置距离e--凸轮回转中心O 偏置距离e--凸轮回转中心 凸轮回转中心O 点到从动件导路之间的距离e 点到从动件导路之间的距离e
D
O
SD
C
Sc
ω
制作: 制作:电子科大机电学院 郭连忠
二、 如图示凸轮机构中,试用图解法在图中标出:
(6)、 (6)、从动件的最大行程 Hmax
C D
O
F
ω
r0
Hmax
制作: 制作:电子科大机电学院 郭连忠
先将导路旋转到B 先将导路旋转到B点。
导路与基圆的交点为B 导路与基圆的交点为B1 圆弧AB 才是尖底A 圆弧AB1才是尖底A实际转过 的圆弧段。 的圆弧段。 ∠AOB1才是凸轮在推程中 实际转过的角度。 实际转过的角度。 故推程角是: 故推程角是: OA与 之间的夹角。 OA与OB1之间的夹角。 制作: 制作:电子科大机电学院 郭连忠
-ω
凸轮转角线: 凸轮转角线: --导路与基圆的交点 --导路与基圆的交点 与回转中心O B1与回转中心O的连线 5、远休止角: 远休止角: BC段为一段圆弧, BC段为一段圆弧,故凸轮 段为一段圆弧 BC段停止不动 段停止不动。 在BC段停止不动。 BC段对应的中心角Φs称 BC段对应的中心角Φs称 段对应的中心角Φs 为远休止角。 为远休止角。 故远休止角是: 故远休止角是: 之间的夹角。 OB1与OC1之间的夹角。
故凸轮的转角是: 故凸轮的转角是:导路与基圆的交点 OA之间的夹角 之间的夹角。 线OA之间的夹角。
凸轮机构运动规律.完美版PPT

当凸轮连续转动时,从动件将重复上述运动过程。
移动凸轮 其凸轮是具有曲线轮廓、作往复直线移动的构件,它可看成是转动轴线位于无穷远处的盘形凸轮。
凸轮机构由凸轮1、从动件2、机架3三个基本构件及锁合装置组成。 用图解法绘制凸轮轮廓曲线的方法;
当凸轮连续转动时,从动件将重复上述运动过程。
从动件的常用运动规律
形锁合凸轮机构 依靠凸轮和从动件几何形状来保证 锁合。
按从动件相对机架的运动方式分为:
移动从动件凸轮机构 摆动从动件凸轮机构 按其从动件导路是否通过凸轮
分为对心移动从动件 偏置移动从动件凸轮机构
40Cr 40-45HRC 20Cr 56-62HRC
从动件的常用运动规律
1.凸轮轮廓曲线与从动件运动规律的关系
第三章凸轮机构运动规律
第三章 凸轮机构
主要内容:
1.凸轮机构的结构、特点、类型及应用; 2.从动件的常用运动规律及其选择; 3.用图解法绘制凸轮轮廓曲线的方法; 4. 凸轮机构的设计。
凸轮机构的应用与分类
1. 组成
凸轮机构由凸轮1、从动件2、 机架3三个基本构件及锁合装 置组成。是一种高副机构。其 中凸轮是一个具有曲线轮廓或 凹槽的构件,通常作连续等速 转动,从动件则在凸轮轮廓的 控制下按预定的运动规律作往 复移动或摆动。
凸轮机构的应用与分类
3. 应用
平面连杆机构虽然应用广泛,但它只能近似地实 现给定的运动规律,且设计比较复杂。当从动件须 精确地按预定运动规律尤其是复杂运动规律工作时, 则常采用凸轮机构。
凸轮机构的应用与分类
4. 类型 按从动件末端形状分:
平底从动件凸轮机构 其从动件端部为一平底。若 不计摩擦,凸轮对从动件的作用力始终垂直于平底, 传力性能良好,且凸轮与平底接触面间易形成润滑 油膜,摩擦磨损小、效率高,故可用于高速,缺点 是不能用于凸轮轮廓有内凹的情况。
机械原理 第3章 凸轮机构
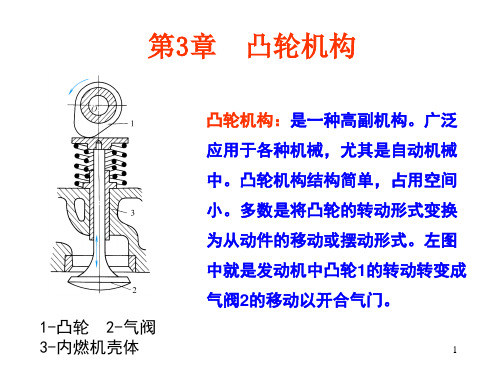
2
26
§3.3 凸轮轮廓曲线的设计 一、凸轮轮廓曲线设计是根据凸轮参数如 基圆半径、推程和推程运动角、回程及回程 运动角、远、近休止角、偏距等参数,用反 转法设计凸轮轮廓曲线。
27
二、1-对心反转图解法设计凸轮廓线,见下图:
28
29
2-偏心反转 图解法设计凸轮轮廓
主要介绍已知从动件运动规律线图设计凸轮轮廓。 一、直动从动件盘形凸轮轮廓的绘制 分别介绍以下两种类型。 1、偏置尖顶直动从动件盘形凸轮 已知从动件位移线图如图3-8 (b)所示,基圆半径 r0,凸轮行程h,推程运动角Φ=1800,休止角 Φs=300,回程角Φ'=900,按图示画出凸轮轮廓线。 作图步骤按反转法如下: 1)将Φ、Φ'各平为4等份,如图(b)中1-1';...8-8'。 并以偏距e和r0画圆,如图(a)所示。基圆与导 路的交点B0(C0)即为从动件的起始点。 2)以OC0为起点,在基圆上平分Φ=180和Φ'=90 分别得C1、C2、C3、和C6、C7、C8各点,并过 C0、C1 . . . 各点向偏距圆作切线,这些切线就是 反转法导路在此点的位置。 3)在各对应的切线上,取C1B1=11' ;C2B2=22' ....得从动件尖顶位置B1、B2、B3... 4)将B0、B1、B2…连接成光滑的曲线就是凸轮 轮廓线(注意:B4、B5是圆弧,B9、B0之间是基 圆) 最后画出图纸进行加工。 30 当e=0时,各切线变成通过O点的射线。
10
一、从动件的运动规律的描述与术语
从动杆位移线图的作图方法及基本名词术语
首先应确认,从动件的运 动规律是由主动件凸轮的轮 廓形状决定的。在图 3-5 中, 回转中心 O 到半径最小点 A 的 K' 圆叫基圆。图 3-5 中凸轮的轮 ϕk 廓规律是,弧 AB 间的半径逐 渐变大,对应的圆心角为 ϕ; 弧 BC 间半径保持不变,对应 K ϕk 的圆心角为 ϕ s ;弧 CD 间半径 逐步变小到基圆半径,对应 的圆心角为 ϕ ' ;弧 DA 间半径 保持基圆半径不变,对应的 圆心角为ϕs'。现凸轮以ω速度 顺时针转动,以 φ=ωt 为横坐 标,从动杆的移动 S为纵坐标, 则从动杆的移动曲线展开图 图3-12:凸轮轮廓与从动件位移线图 如(b)所示。其中: h--升程;ϕ--推程运动角;ϕs--远休止角; ϕ‘--回程运动角;ϕ's--近休止角。这 些角度总和为360˚。从图中可知,当凸轮从A点转过ϕk角到K点时,从动杆升高 到K’点;当凸轮从A点转过ϕ角度,从动杆升高了h到B点。其他各点作图方法 11 一样,然后将各点连成光滑的曲线,就是从杆的位移线图(b).
《机械设计原理》第3章凸轮机构

5’ 3’
1’
12’
13’ 14’
1 3 5 7 8 9 11 13 15
设计:潘存云
设计步骤小结:
①选比例尺μl作基圆rmin。 ②反向等分各运动角。原则是:陡密缓疏。
③确定反转后,从动件尖顶在各等份点的位置。
④将各尖顶点连接成一条光滑曲线。
中南大学专用
作者: 潘存云教授
2.偏置直动尖顶从动件盘形凸轮
回 凸 轮
作者:潘存云教授
优点:只需要设计适当的轮廓曲线,从动件便可获得
任意的运动规律,且结构简单、紧凑、设计方便。
缺点:线接触,容易磨损。
中南大学专用
作者: 潘存云教授
应用实例:
3
线 2 A 设计:潘存云 1
中南大学专用
绕线机构
作者: 潘存云教授
卷带轮
12 1 放 放音 音键 键
设计:潘存云
5
1.等速运动(一次多项式)运动规律 s2
在推程起始点:δ1=0, s2=0
在推程终止点:δ1=δt ,s2=h 代推入程得运: 动方C0=程0:, C1=h/δt
δt
v2
s2 =hδ1/δt
v2 a2
= =
hω1 0
/δt
同理得回程运动方程:
a2 刚性冲击 +∞
s2=h(1-δ1/δh ) v2=-hω1 /δh a =0 2 中南大学专用
5)摆动尖顶从动件盘形凸轮机构
中南大学专用
作者: 潘存云教授
一、凸轮廓线设计方法的基本原理
反转原理:
给整个凸轮机构施以-ω1时,不影响各构件之间
的相对运动,此时,凸轮将静止,而从动件尖顶复合
运动的轨迹即凸轮的轮廓曲线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重写加速段推程运动方程为:
s2 =2hδ2 1 /δ2t
v2 =4hω1δ1 /δ2t
a =4hω /δ 湖北工学院专用
2
22 1t
s2
设计:潘存云
1 23 4 5
δt
v2 2hω/δt
h/2
h/2
6 δ1
δ1
a2 4hω2/δ2t
δ1
柔性冲击
作者: 潘存云教授
同理可得回程等加速段的运动方程为:
s2 =h-2hδ21/δ2h v2 =-4hω1δ1/δ2h a2 =-4hω21/δ2h
凸轮转过推程运动角δt-从动件上升h 凸轮转过回程运动角δh-从动件下降h
湖北工学院专用
作者: 潘存云教授
s2 = C0+ C1δ1+ C2δ21+…+Cnδn1 v2 = C1ω+ 2C2ω1δ+…+nCnω1δn-11
a2 = 2 C2ω21+ 6C3ω21δ1…+n(n-1)Cnω21δn-21
湖北工学院专用
作者: 潘存云教授
推程减速上升段边界条件:
中间点:δ1=δt/2,s2=h/2 终止点:δ1=δt ,s2=h,v2=0
求得:C0=-h, C1=4h/δt , C2=-2h/δ2t
减速段推程运动方程为:
s2 v2
==h-4-2hhω(1δ(tδ–t-δδ11))2//δδ22tt
a2 =-4hω21 /δ2t
优点:可精确实现任意运动规律,简单紧凑。 实例 缺点:高副,线接触,易磨损,传力不大。
应用:内燃机 、牙膏生产等自动线、补 鞋机、配钥匙机等。
分类:1)按凸轮形状分:盘形、 移动、 圆柱凸轮 ( 端面 ) 。
2)按推杆形状分:尖顶、 滚子、 特点: 平底从动件。 尖顶--构造简单、易磨损、用于仪表机构; 滚子――磨损小,应用广; 平底――受力好、润滑好,用于高速传动。
湖北工学院专用
作者: 潘存云教授
3).按推杆运动分:直动(对心、偏置)、 摆动
4).按保持接触方式分: 力封闭(重力、弹簧等)
几何形状封闭(凹槽、等宽、等径、主回凸轮)
刀架
o 2
1
内燃机气门机构
湖北工学院专用
机床进给机构
作者: 潘存云教授
凹 槽 凸 轮
等
宽
凸
ቤተ መጻሕፍቲ ባይዱ
W
轮
等
径
r1
凸
主
轮
r2
r1+r2 =const
第3章 凸轮机构
§3-1 凸轮机构的应用和类型 §3-2 从动件的常用运动规律 §3-3 凸轮机构的压力角 §3-4 图解法设计凸轮的轮廓 §3-5 解析法设计凸轮的轮廓
湖北工学院专用
作者: 潘存云教授
§3-1 凸轮机构的应用和类型
结构:三个构件、盘(柱)状曲线轮廓、从动件呈杆状。
作用:将连续回转 => 从动件直线移动或摆动。
回 凸 轮
作者:潘存云教授
优点:只需要设计适当的轮廓曲线,从动件便可获得
任意的运动规律,且结构简单、紧凑、设计方便。
缺点:线接触,容易磨损。
湖北工学院专用
作者: 潘存云教授
应用实例:
3
线 2 A 设计:潘存云 1
湖北工学院专用
绕线机构
作者: 潘存云教授
卷带轮
12 1 放 放音 音键 键
设计:潘存云
s2
h a2
δ1 δt
湖北工学院专用
作者: 潘存云教授
二、三角函数运动规律 1.余弦加速度(简谐)运动规律
5 4
6
s2
推程: s2=h[1-cos(πδ1/δt)]/2
v2 =πhω1sin(πδ1/δt)δ1/2δt a2 =π2hω21 cos(πδ1/δt)/2δ2t
3
2 1
h
设计:潘存云
δ1
1 2 34 5 6
δt v2 Vmax=1.57hω/2δ0
回程等减速段运动方程为:
s2 =2h(δh-δ1)2/δ2h v2 =-4hω1(δh-δ1)/δ2h a2 =4hω21/δ2h
湖北工学院专用
作者: 潘存云教授
3.五次多项式运动规律
位移方程:
s2=10h(δ1/δt)3-15h (δ1/δt)4+6h (δ1/δt)5
无冲击,适用于高速凸轮。
v2
1.等速运动(一次多项式)运动规律 s2
在推程起始点:δ1=0, s2=0
在推程终止点:δ1=δt ,s2=h 代推入程得运: 动方C0=程0:, C1=h/δt
δt
v2
s2 =hδ1/δt
v2 a2
= =
hω1 0
/δt
同理得回程运动方程:
a2 刚性冲击 +∞
s2=h(1-δ1/δh ) v2=-hω1 /δh a =0 2 湖北工学院专用
B’
一、推杆的常用运动规律 名词术语:
基圆、基圆半径、 推程、 推程运动角、远休止角、
h
A D δ’s rmin
o δt δs
δt
δh
ω1
δs 设计:潘存云 B
回程、回 程 运 动 角 、
近休止角、 行程。一个循环
C
t δh δ’s δ1
湖北工学院专用
作者: 潘存云教授
运动规律:推杆在推程或回程时,其位移S2、速度V2、
和加速度a2 随时间t 的变化规律。
S2=S2(t)
V2=V2(t)
a2=a2(t)
形式:多项式、三角函数。
D
B’
A δ’s rmin
s2
h
o
位移曲线
t δt δs δh δ’s δ1
δ 设计:t 潘存云
δh
ω1
δs
B
湖北工学院专用
C
作者: 潘存云教授
一、多项式运动规律
一般表达式:s2=C0+ C1δ1+ C2δ21+…+Cnδn1 (1)
求一阶导数得速度方程:
v2 = ds2/dt = C1ω1+ 2C2ω1δ1+…+nCnω1δn-11
求二阶导数得加速度方程:
a2 =dv2/dt =2 C2ω21+ 6C3ω21δ1…+n(n-1)Cnω21δn-21 其中:δ1-凸轮转角,dδ1/dt=ω1-凸轮角速度,
Ci-待定系数。
边界条件:
5
3
3
摩擦轮
4 4
录音机卷带机构
皮皮带带轮轮
湖北工学院专用
作者: 潘存云教授
2
设计:潘存云
3
湖北工学院专用
1 送料机构
作者: 潘存云教授
§3-2 推杆的运动规律
凸轮机构设计的基本任务: 1)根据工作要求选定凸轮机构的形式;
2)推杆运动规律; 3)合理确定结构尺寸;
4)设计轮廓曲线。
s2
而根据工作要求选定推杆运动规律,是设计凸轮轮廓曲线的前提。
h
δ1
δ1
δ1
-∞
作者: 潘存云教授
2. 等加等减速(二次多项式)运动规律 位移曲线为一抛物线。加、减速各占一半。
推程加速上升段边界条件:
起始点:δ1=0, s2=0, v2=0 中间点:δ1=δt /2,s2=h/2
求得:C0=0, C1=0,C2=2h/δ2t
加速段推程运动方程为:
s2 =2hδ21 /δ2t v2 =4hω1δ1 /δ2t a2 =4hω21 /δ2t
