Turbo码LDPC码的译码方法
Turbo码详解

第十三章 Turbo 码Shannon 理论证明,随机码是好码,但是它的译码却太复杂。
因此,多少年来随机编码理论一直是作为分析与证明编码定理的主要方法,而如何在构造码上发挥作用却并未引起人们的足够重视。
直到1993年,Turbo 码的发现,才较好地解决了这一问题,为Shannon 随机码理论的应用研究奠定了基础。
Turbo 码,又称并行级连卷积码(PCCC),是由C. Berrou 等在ICC ’93会议上提出的。
它巧妙地将卷积码和随机交织器结合在一起,实现了随机编码的思想,同时,采用软输出迭代译码来逼近最大似然译码。
本章首先介绍Turbo 码的提出与构成原理;介绍迭代反馈译码算法(包括AWGN 信道与Rayleigh 衰落信道下的译码);然后针对Turbo 码编译码特性,对几个问题进行了说明;最后介绍Turbo 码在3GPP 中的具体应用。
§13.1 Turbo 码的提出Turbo 码,又称并行级连卷积码(PCCC),是由C.Berrou 等在ICC ’93会议上提出的。
它巧妙地将卷积码和随机交织器结合在一起,实现了随机编码的思想,同时,采用软输出迭代译码来逼近最大似然译码。
模拟结果表明,如果采用大小为65535的随机交织器,并且进行18次迭代,则在E N b /0≥0.7dB 时,码率为1/2的Turbo 码在AWGN 信道上的误比特率(BER )≤-105,达到了近Shannon 限的性能(1/2码率的Shannon 限是0dB )。
因此,这一超乎寻常的优异性能,立即引起信息与编码理论界的轰动。
图13-1中给出了Turbo 码及其它编码方案的性能比较,从中可以看出Turbo 编码方案的优越性。
由于Turbo 码的上述优异性能并不是从理论研究的角度给出的,而仅是计算机仿真的结果。
因此,Turbo 码的理论基础还不完善。
后来经过不少人的重复性研究与理论分析,发现Turbo 码的性能确实是非常优异的。
Turbo码基础

前言
Shannon在其“通信的数学理论”一 文中提出并证明了著名的有噪信道编 码定理,它在证明信息速率达到信道 容量可实现无差错传输时引用了3个 基本条件:
前言
采用随机性编译码。 编码长度L趋于无穷,即分组的 码组长度无限。 译码过程采用最佳的最大似然译 码。
前言
dk R x R p Rk \ d k Bk exp 2
s k p k p k
由上两式可得
k m ', m P(dk ) P(Rk \ dk )
MAP算法
1 p p 定义 m ', m exp Lc Rk xk 2
\ m)
MAP算法
归一化之后,
MAP算法
P(dk ) P( Rk \ dk )
P(dk )是 dk 的先验概率, 式中, P( Rk \ dk ) 由信道转移概率决定。
MAP算法
k 1 m0'
m0’
i m0', m
m
k m
m0’’
k 1 m0''
ln
d k 1
( m ', m ) dk 0
MAP算法
上式中的求和是对所有由 uk 1 (或 uk )引起的 的状态转 mk 1 mk 0 移进行的。 其中,
N 1 k 1 1 N k 1
p(m ', m, R ) p(m ', R )p( m, Rk \ m ') p( R k 1 (m ') k (m ', m) k (m)
Turbo码的各种译码算法及比较

Turbo 码的各种译码算法及比较Turbo 码有一重要特点是其译码较为复杂,比常规的卷积码要复杂的多,这种复杂不仅在于其译码要采用迭代的过程,而且采用的算法本身也比较复杂。
这些算法的关键是不但要能够对每比特进行译码,而且还要伴随着译码给出每比特译出的可靠性信息,有了这些信息,迭代才能进行下去。
用于Turbo 码译码的具体算法有:MAP(Maximum A Posterori)、Max-Log-MAP 、Log-MAP 和SOV A(Soft Output Viterbi Algorithm)算法。
MAP 算法是1974年被用于卷积码的译码,但用作Turbo 码的译码还是要做一些修改;Max-Log-MAP 与Log-MAP 是根据MAP 算法在运算量上做了重大改进,虽然性能有些下降,但使得Turbo 码的译码复杂度大大的降低了,更加适合于实际系统的运用;Viterbi 算法并不适合Turbo 码的译码,原因就是没有每比特译出的可靠性信息输出,修改后的具有软信息输出的SOV A 算法,就正好适合了Turbo 码的译码。
这些算法在复杂度上和性能上具有一定的差异,系统地了解这些算法的原理是对Turbo 码研究的基础,同时对这些算法的复杂度和性能的比较研究也将有助于Turbo 的应用研究。
MAP 算法MAP 算法最初是用来估计无记忆噪声下的马尔可夫过程的,它是一种最优的算法。
Bahl 等人于1974年把它用于线性分组码和卷积码的译码中,在用于卷积码的译码时,对于给定接收序列Y ,它不像Viterbi 算法那样以栅格路径上的比特组错误最少为目的,而是以译码出来的符号i x 的错误最少为目的。
即,(){}arg max ii i x x P x Y = (1.1)不过在大多情况下,它和Viterbi 算法的作用是一致的。
由于在卷积码的译码中,MAP 算法要考虑栅格图中的所有可能路径,这样运算量就非常大,实际系统中很少用到。
Turbo码译码算法

网Vi格ter图bi译编码码过举程例
(2,1,2)码L=5的网格图
4.SOVA译码算法
译码器输入序列y=(11 10 01 11 00 10 11)
网Vi格ter图bi译编码码过举程例
(2,1,2)码L=5的网格图
4.SOVA译码算法
SOVA译码算法思想
SOVA译码过程与Viterbi译码过程相似,区别在于将先验信 息结合在 SOVA 度量中,利用修正的度量来寻找最大似然序列, 提供对估计信息比特更可靠的判决度量。
信息熵。
译码迭代终止条件
2.SOVA译码算法
2.SOVA译码算法
软输出Viterbi算法
SOVA算法的全称是: 软输出Viterbi算法(Soft Output Viterbi Algorithm)。它是Viterbi算法的改进类型,Viterbi算法是一种最大似 然译码算法。
4.SOVA译码算法
延时
交织
Turbo码译码器的基本结构图
Le21
软输 入 软输 出 译码 器
DEC 2Байду номын сангаас
+
L(un)
解 交
织
判 ^uk 决
Turbo译码器有以下的特点: (1)串行级联。 (2)迭代译码。 (3)在迭代译码过程中交换的是外信息。
1.Turbo码的迭代译码原理
1.指定迭代次数。 2.在信息序列中加入CRC校验字。 3.检测成员编码器输出之间的交叉
网Vi格ter图bi译编码码过举程例
(2,1,2)码L=5的网格图
4.SOVA译码算法
译码器输入序列y=(11 10 01 11 00 10 11)
网Vi格ter图bi译编码码过举程例
Turbo译码算法综述
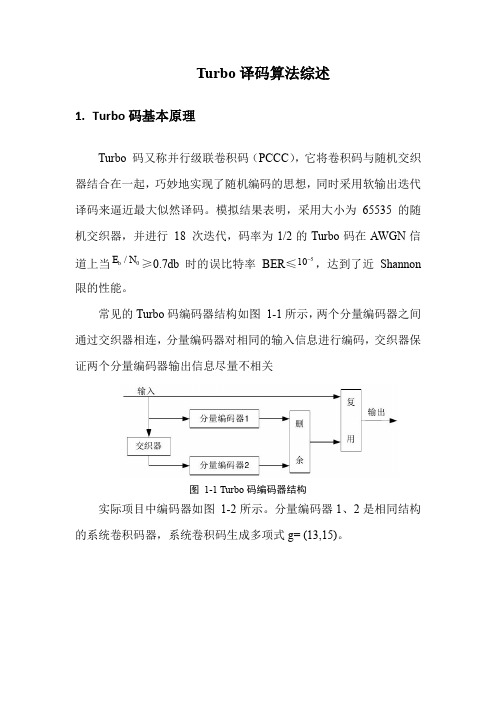
图 1-1 Turbo 码编码器结构
实际项目中编码器如图 1-2 所示。分量编码器 1、2 是相同结构 的系统卷积码器,系统卷积码生成多项式 g= (13,15)。
)
|
(|
r(q) n
|
4
/
42) | 2 /
42
n
(a6
)
|
(|
r(q) n
|
4
/
42) | 2 /
42
4) 自己的想法(以 64-QAM 为例说明)
I、Q 两路信号分别解调自己的比特,即 a1 、a3 、a5 软信息由 I 路 信号计算出来,a2 、a4 、a6 的软信息由 Q 路信号计算出来。以 I 路为 例计算相应比特的软信息。星座图如图 2.3 所示,其中 D 1/ 42 。
号代表的比特数。设 n 时刻收到的星座符号为Qn ,包括 I、Q 两路信
号设为 rn(i) 、 rn(q) ,则
r(i) n
s(i) n
n(i) n
r(q) n
s(q) n
n(q) n
其中
s(i) K
、
s(q) K
表示发射信号的
I、Q
两路信号, nn(i)
、 n(q) n
为相互独
立的服从零均值的正态分布的随机序列,其方差 2
图 2-4 BPSK 调制下的 Turbo 码迭代译码原理
2.2 分量译码算法介绍
分量译码算法采用的 SISO 译码算法,主要包括两类,一类是 MAP 算法以及基于 MAP 算法的修正算法;另一类则是基于 Viterbi 算法的 Viterbi 算法(SOVA)以及它的一些修正算法,总的来说, MAP 类算法比 SOVA 算法新能要好,但这是以复杂度来保证的。
Turbo译码算法综述

(2-7)
2) 对于编码后的比特采用 M-QAM 方式调制, 信道为高斯信道或 者衰落信道。其中 M 表示调制点数,且 M 2m ,m 表示每个 QAM 符 号代表的比特数。设 n 时刻收到的星座符号为 Qn ,包括 I、Q 两路信 号设为 rn(i ) 、 rn( q ) ,则
0010 0010
1110 1110
1100 1100
0100 0100
0110 0110
II
1111 1111
1101 1101
0101 0101
0111 0111
图 2-2 16-QAM 星座映射
将星座图中符号的平均能量归一化为 1,则星座图中的最小单位 (如图 2-2 所示) ,对于 16-QAM 和 64-QAM 分别为 1/ 10 和 1/ 42 。 则 M-QAM 解调的软信息(似然比)可以有下面几种形式: 1) 第一种形式
Turbo 译码算法综述
1. Turbo 码基本原理
Turbo 码又称并行级联卷积码(PCCC) ,它将卷积码与随机交织 器结合在一起,巧妙地实现了随机编码的思想,同时采用软输出迭代 译码来逼近最大似然译码。模拟结果表明,采用大小为 65535 的随 机交织器,并进行 18 次迭代,码率为 1/2 的 Turbo 码在 AWGN 信 道上当 Eb / N0 ≥0.7db 时的误比特率 BER≤ 10 ,达到了近 Shannon
(2-2)
上式中 Eb 表示每个传输比特的能量, 2 为噪声方差,它和信噪
比的关系为 2 R10
2
Eb / N0
10
,R 为编码码率,a 为信道的衰落,对于无
PCCC码(Turbo码)编码和译码算法

目录一、概述 (1)二、PCCC码的编码算法 (3)三、PCCC码的译码算法 (13)一、概述虽然软判决译码、级联码和编码调制技术都对信道码的设计和发展产生了重大影响,但是其增益与Shannon 理论极限始终都存在2~3dB 的差距。
因此,在Turbo 码提出以前,信道截止速率R0一直被认为是差错控制码性能的实际极限,shannon 极限仅仅是理论上的极限,是不可能达到的。
根据shannon 有噪信道编码定理,在信道传输速率R 不超过信道容量C 的前提下,只有在码组长度无限的码集合中随机地选择编码码字并且在接收端采用最大似然译码算法时,才能使误码率接近为零。
但是最大似然译码的复杂性随编码长度的增加而加大,当编码长度趋于无穷大时,最大似然译码是不可能实现的。
所以人们认为随机性编译码仅仅是为证明定理存在性而引入的一种数学方法和手段,在实际的编码构造中是不可能实现的。
在1993 年于瑞士日内瓦召开的国际通信会议(1CC,93)上,两位任教于法国不列颠通信大学的教授C.Berrou、A.Glavieux 和他们的缅甸籍博士生P.thitimajshima 首次提出了一种新型信道编码方案——Turbo 码,由于它很好地应用了shannon 信道编码定理中的随机性编、译码条件,从而获得了几乎接近shannon 理论极限的译码性能。
仿真结果表明,在采用长度为65536 的随机交织器并译码迭代18 次情况下,在信噪比E b/N0≥0.7dB 并采用BPSK 调制时,码率为1/2 的Turbo 码在AWGN 信道下的误比特率≤10-5,达到了与Shannon 极限仅相差0.7dB 的优异性能(1/2 码率的Shannon 极限是0dB)。
Turbo 码又称并行级联卷积码(PCCC,Parallel Concatenated Convolutional Code),它巧妙地将卷积码和随机交织器结合在一起,在实现随机编码思想的同时,通过交织器实现了由短码构造长码的方法,并采用软输出迭代译码来逼近最大似然译码。
Turbo码LDPC码的译码方法

20
2013年7月29日
LDPC码的提出
北 京 邮 电 大 学 信 息 理 论 与 技 术 教 研 中 心
• 后来人们进一步发现,在同样足够长的 码长条件下,其性能甚至还优于Turbo码, 从而重新引起人们广泛关注与进一步的 研究。
21
2013年7月29日
LDPC码研究的方向
北 京 邮 电 大 学 信 息 理 论 与 技 术 教 研 中 心
15
2013年7月29日
各类算法小结
北 京 邮 电 大 学 信 息 理 论 与 技 术 教 研 中 心
• 就硬件实现而言, log-MAP的计算复杂 度比MAP低,但译码精度一样;而对于 logMAP、 Max-log-MAP、双向SOVA和 单向SOVA,它们的计算复杂度依次降低, 但译码精度也相应的依次降低。
27
2013年7月29日
LDPC码与Turbo码之间的对比
北 京 邮 电 大 学 信 息 理 论 与 技 术 教 研 中 心
从性能上看,Turbo码更适合于中、短长度 码长,比如在3G中,Turbo码就是首选,而 对于更长的码长时,LDPC码的性能将超过 Turbo码。
28
2013年7月29日
这里主要比较常用的MAP、logMAP、 Max- logMAP以及SOVA算法之间的关系。 • logMAP算法: 它与MAP算法等效,只是将 、 、 转 移至对数域中去计算,并且将乘法运算映 射为加法运算,加法运算映射为E运算, 其目的是为了便于硬件实现。
7
2013年7月29日
各类算法之间的关系
显然对于分子,SOVA算法可以从众多满 足 u k 为1的序列概率中找到最大的序列概率; 但对于分母,SOVA算法则不一定能从众多 uk 满足 为1的序列概率中找到最大的序列概 率; 而是从延时窗中更新得到的那条件随 路径所对应的后验概率。所以SOVA输出似 然比的绝对值比Max-log-MAP算法大,既 存在似然比高估问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
将Gallager提出的规则的LDPC码,即其校 验矩阵的列重与行重为固定值,进一步拓 广至不规则的二元LDPC码,亦即校验矩 阵的每列、每行重量不相等,其性能亦得 到很大的提高。其中Chung提出将最大列 重增至2000,1/2码率,当码长为107比特 时,在AWGN信道下,仿真表明,二元非 规则的LDPC码的性能与Shannon限仅相差 0.01的dB。它远远超出Turbo码的性能。
Max{ k 1 ( s ') k ( s ', s) k ( s)} L(uk YN ) ln
s ', s uk 1
one of{ k 1 ( s ') k ( s ', s) k ( s)}
12
2013年7月29日
各类算法之间的关系
北 京 邮 电 大 学 信 息 理 论 与 技 术 教 研 中 心
• 对于软判决
Lk (uk )out Lk (uk YN ) L信息输出,经过交织或者 反交织传递给下一个译码器,并作为下一个译 码器的先验信息的输入。
6 2013年7月29日
各类算法之间的关系
北 京 邮 电 大 学 信 息 理 论 与 技 术 教 研 中 心
27
2013年7月29日
LDPC码与Turbo码之间的对比
北 京 邮 电 大 学 信 息 理 论 与 技 术 教 研 中 心
从性能上看,Turbo码更适合于中、短长度 码长,比如在3G中,Turbo码就是首选,而 对于更长的码长时,LDPC码的性能将超过 Turbo码。
28
2013年7月29日
15
2013年7月29日
各类算法小结
北 京 邮 电 大 学 信 息 理 论 与 技 术 教 研 中 心
• 就硬件实现而言, log-MAP的计算复杂 度比MAP低,但译码精度一样;而对于 logMAP、 Max-log-MAP、双向SOVA和 单向SOVA,它们的计算复杂度依次降低, 但译码精度也相应的依次降低。
这里主要比较常用的MAP、logMAP、 Max- logMAP以及SOVA算法之间的关系。 • logMAP算法: 它与MAP算法等效,只是将 、 、 转 移至对数域中去计算,并且将乘法运算映 射为加法运算,加法运算映射为E运算, 其目的是为了便于硬件实现。
7
2013年7月29日
各类算法之间的关系
2
2013年7月29日
Turbo 码的译码算法
北 京 邮 电 大 学 信 息 理 论 与 技 术 教 研 中 心
• Turbo码通用译码器的结构为:
L(U )in
L(U YN )
最大似然译码器 (MAP、logMAP、MaxlogMAP、SOVA)
YN
L(U )out
3
2013年7月29日
Turbo 码的译码算法
13
2013年7月29日
各类算法之间的关系
北 京 邮 电 大 学 信 息 理 论 与 技 术 教 研 中 心
对于双向SOVA算法,对前向和后向SOVA 算法输出的似然比取最小值,有助于缓解 这一问题,但是如果满足 u k 为-1的最大似 然序列出现在k时刻为中心的前后延时窗以 外,则双向SOVA算法仍存在似然比高估的 问题。
北 京 邮 电 大 学 信 息 理 论 与 技 术 教 研 中 心
北邮信息理论 与技术教研中心
Turbo 码 的译码算法
Turbo 码的译码算法
北 京 邮 电 大 学 信 息 理 论 与 技 术 教 研 中 心
• Turbo码的译码算法是BCJR算法,其实质是按码 元的最大后验概率的MAP算法,是一类采用双向 递推的后验概率算法; • MAP算法完全等效于最小误码率算法,且当信源 等概率分布时,亦与最大似然算法等效; • 决定递推式最大似然算法的核心是满足马尔科夫 性,这是后验概率的似然比值仅决定于前向递推 概率 、后向递推概率 以及分支转移概率 。
ln
s ', s uk 1
k 1
s ', s uk 1
其中 : s ', s分别表示k -1和k时刻寄存器RSC的状态
5 2013年7月29日
Turbo 码的译码算法
北 京 邮 电 大 学 信 息 理 论 与 技 术 教 研 中 心
• 对于硬判决
ˆ uk sign[ L(uk YN )]
20
2013年7月29日
LDPC码的提出
北 京 邮 电 大 学 信 息 理 论 与 技 术 教 研 中 心
• 后来人们进一步发现,在同样足够长的 码长条件下,其性能甚至还优于Turbo码, 从而重新引起人们广泛关注与进一步的 研究。
21
2013年7月29日
LDPC码研究的方向
北 京 邮 电 大 学 信 息 理 论 与 技 术 教 研 中 心
显然对于分子,SOVA算法可以从众多满 足 u k 为1的序列概率中找到最大的序列概率; 但对于分母,SOVA算法则不一定能从众多 uk 满足 为1的序列概率中找到最大的序列概 率; 而是从延时窗中更新得到的那条件随 路径所对应的后验概率。所以SOVA输出似 然比的绝对值比Max-log-MAP算法大,既 存在似然比高估问题。
18
2013年7月29日
LDPC码的提出
北 京 邮 电 大 学 信 息 理 论 与 技 术 教 研 中 心
监督矩阵中每列包含很小的固定数目 j>=3的1; 每行亦包含一个很小固定数目k>j的1; Gallager证明,这种码字的典型最小距离 随着码长的增加而线性增加,而且在 BSC信道下其译码差错的典型概率将随 码长指数下降。
10
2013年7月29日
各类算法之间的关系
北 京 邮 电 大 学 信 息 理 论 与 技 术 教 研 中 心
• SOVA算法 SOVA算法可以看作是Max-log-MAP算法 的进一步简化: Max-log-MAP输出的后验概率似然比为:
Max{ k 1 ( s ') k ( s ', s) k ( s)} L(uk YN ) ln
• 其中,最核心的后验概率似然比为:
P (uk 1 YN ) L(uk YN ) ln P (uk 1 YN ) P (uk 1, YN ) ln P (uk 1, YN )
k 1
( s ') k ( s ', s ) k ( s ) ( s ') k ( s ', s ) k ( s )
• 目前对LDPC码进一步研究主要集中在以下 两个方向上: 将GF(2)的二元域上的LDPC码进一步拓 广至多元域,比如GF(22)、 GF(23)等, 并进一步精心构造多元域上的校验矩阵, 可以使LDPC码性能得到进一步提高。
22
2013年7月29日
LDPC码研究的方向
北 京 邮 电 大 学 信 息 理 论 与 技 术 教 研 中 心
14
2013年7月29日
各类算法小结
北 京 邮 电 大 学 信 息 理 论 与 技 术 教 研 中 心
• logMAP算法完全等效于MAP,只是更便于 硬件实现;Max-log-MAP算法是logMAP算 法的简化;双向SOVA算法又是Max-logMAP算法的简化;单向SOVA算法则又是双 向SOVA算法的进一步简化;
24
2013年7月29日
LDPC码与Turbo码之间的对比
北 京 邮 电 大 学 信 息 理 论 与 技 术 教 研 中 心
两者的编译码方法是类似的,都可以采 用Tanner图、二分图乃至更抽象的因子 图概念来统一描述,而译码算法则可统 一到因子图上和、积算法加以概括;
25
2013年7月29日
LDPC码与Turbo码之间的对比
aEb ln(e e ) min( a, b) ln(1 e aEb min(a, b)
当 a b 0时
a
b
a b
)
其中min运算与加法运算一样均满足交换率 和结 合率,并用它取代logMAP 算法中的E运算,其计 算复杂度降低了,但译码精度亦会相应降低。
23 2013年7月29日
LDPC码与Turbo码之间的对比
北 京 邮 电 大 学 信 息 理 论 与 技 术 教 研 中 心
• LDPC码与Turbo码之间的相似之处有: 两者均符合Shannon信道编码定理证明中 引用的三个重要的假设条件:码长足够 长、随机编码方法和采用最佳的译码 MAP算法。因此都具有逼近的Shannon限 的优异性能;
16
2013年7月29日
北 京 邮 电 大 学 信 息 理 论 与 技 术 教 研 中 心
北邮信息理论 与技术教研中心
LDPC 码
LDPC码的提出
北 京 邮 电 大 学 信 息 理 论 与 技 术 教 研 中 心
• 早在1962年,著名信息论专家Gallager在 他的博士论文中首先提出低密度分组校 验码(Low Density Parity-Check Code) 即LDPC码的概念,它是基于监督矩阵定 义的一种码,具有以下性质:
26
2013年7月29日
LDPC码与Turbo码之间的对比
北 京 邮 电 大 学 信 息 理 论 与 技 术 教 研 中 心
对于Turbo码实现的主要难点在接收端的 译码,计算复杂度以及交织器的设计与 时延。因此Turbo码的译码时延要远大于 LDPC码的译码时延; 在接收端译码的具体实现时,通常Turbo 码的译码是采用串行处理,而LDPC码则 可以采用并行处理,因此它更适合于硬 件实现;
北 京 邮 电 大 学 信 息 理 论 与 技 术 教 研 中 心
引入映射f : y ln( x);
