材料力学计算题库完整讲解学习
材料力学习题解答[第三章]
![材料力学习题解答[第三章]](https://img.taocdn.com/s3/m/ffe185e2551810a6f52486fd.png)
解:A-A截面上内力为:
截面的几何性:
欲使柱截面内不出现拉应力,则有:
=0(a)
分别代入(a)式得:
解之得:
此时: MPa
3-25传动轴上装有甲、乙两个皮带轮,它们的直径均为 ,重量均为 ,其受力情况如图示。若轴的直径为 。试分析该轴的危险截面和危险点,计算危险点的应力大小,并用图形标明该点所受应力的方向。
解:(1)约束反力:
(2)各杆轴力
题3-3图
(3)各杆的正应力
3-4钢杆 直径为20mm,用来拉住刚性梁 。已知F=10kN,求钢杆横截面上的正应力。
解:
题3-4图
3-5图示结构中,1、2两杆的横截面直径分别为10mm和20mm,试求两杆内的应力。设结构的横梁为刚体。
解:取BC段分析, 题3-5图
取AB段分析:
根据力矩平衡:
内力图如图所示。截面的几何特性计算:
危险点面在A面的D1和D2点,则合成弯矩为:
3-28圆截面短柱,承受一与轴线平行但不与轴线重合的压载荷F作用,圆截面半径为r,现要求整个截面只承受压应力,试确定F作用的范围。
解:压力引起的压应力:
而
解之得Zc=题3-21图所以:来自最大压应力在槽底上各点:
(3)如果在左侧也开槽,则为轴心受压:
3-22图示短柱受载荷 和 作用,试求固定端角点A、B、C及D的正应力,并确定其中性轴的位置。
题3-22图
解:在ABCD平面上的内力:
横截面的几何特性:
应力计算:
中性轴方程为:
3-23图3-64所示为一简易悬臂式吊车架。横梁AB由两根10号槽钢组成。电葫芦可在梁上来回移动。设电动葫芦连同起吊重物的重量共重 。材料的 。试求在下列两种情况下,横梁的最大正应力值:(1)、只考虑由重量W所引起的弯矩影响;(2)、考虑弯矩和轴力的共同影响。
工程力学---材料力学(第七章- 梁弯曲时位移计算与刚度设计)经典例题及详解

得: D 0
Pl 2 得: C 16
AC段梁的转角方程和挠曲线方程分别为:
P 2 2 (4 x l ) 16 EI Px y (4 x 2 3 l 2 ) 48 EI
y
P
B
A
x
l 2
C
l 2
x
最大转角和最大挠度分别为:
max A B
ymax y
q 7qa 8k 384 EI
3
q/2
B C
q/2
A B C
顺时针
q/2
例16:图示梁B处为弹性支座,弹簧刚 度
EI k 求C端挠度fC。 2a 3
q
A
EI k
B
C
2a
a
解:(1)梁不变形,仅弹簧变形引起的C点挠度为 4 3 qa 3qa B处反力=qa fC 1 2 k EI
q
B
x
l
由边界条件: x 0时,y 0
x l时,y 0
得:
ql 3 C , D0 24
梁的转角方程和挠曲线方程分别为:
y
q 2 3 3 (6lx 4 x l ) 24 EI
q
x
A qx y (2lx 2 x 3 l 3 ) 24 EI
ql 3 24 EI
A a a
q
B C
a
qa 12 EI
顺时针
3 3
P=qa
A B
P=qa
m=qɑ²/2
qa qa C B 6 EI 4 EI
4
顺时针
B
q
C
qa 5qa fC B a 8EI 24 EI
材料力学辅导

T2 WP2
T2 D23 [1 (
d
)4 ]
100103 223 [1 (18 /
16 22)4
]
86.7Mpa
16
D2
11
故 max=86.7MPa
功率为150kW,转速为15.4转/秒的电动机转子轴,许用剪应力
[]=30M Pa, 试校核其强度。
m
m
解:(1)求扭矩及扭矩图
A T
B
C
解: 1) 画扭矩图。
2) 计算各段剪应力: AB段:
MA f18 MB
MC
f24 f22
max 1
T1 WP1
T1 D13 [1 (
d
)4 ]
16
D1
150103 16 243 [1 (18 / 24)4 ] 80.8MPa
A
1000 B 1000 C
T/kN·m 150 100
o x
max 2
x y
主
0
1
单元体
若 max 0, min 0,则:
1 max 2 0 3 min
3
若 max 0, min 0,则: 1 max 2 min 3 0
x y
若 max 0, min 0,则: 1 0 2 max 3 min
主 单元体
0
3
1
注:需代入轴力的正负号计算应力!
变形计算:
l
Nl EA
3
作图示杆件的轴力图,并求1-1、2-2、3-3截面的应力。
1 f 30
2 f 20
60kN
40kN
3 f 35
30kN
50kN
1
2
3
《材料力学》第2章 轴向拉(压)变形 习题解讲解

第二章轴向拉(压变形[习题2-1]试求图示各杆1-1和2-2横截面上的轴力,并作轴力图。
(a)解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(b)解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(c)解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(d)解:(1)求指定截面上的轴力(2)作轴力图中间段的轴力方程为:轴力图如图所示。
[习题2-2]试求图示等直杆横截面1-1、2-2和平3-3上的轴力,并作轴力图。
若横截面面积,试求各横截面上的应力。
解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(3)计算各截面上的应力[习题2-3] 试求图示阶梯状直杆横截面1-1、2-2和平3-3上的轴力,并作轴力图。
若横截面面积,,,并求各横截面上的应力。
解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(3)计算各截面上的应力[习题2-4] 图示一混合屋架结构的计算简图。
屋架的上弦用钢筋混凝土制成。
下面的拉杆和中间竖向撑杆用角钢构成,其截面均为两个的等边角钢。
已知屋面承受集度为的竖直均布荷载。
试求拉杆AE和EC横截面上的应力。
解:(1)求支座反力由结构的对称性可知:(2)求AE和EG杆的轴力①用假想的垂直截面把C铰和EG杆同时切断,取左部分为研究对象,其受力图如图所示。
由平衡条件可知:②以C节点为研究对象,其受力图如图所示。
由平平衡条件可得:(3)求拉杆AE和EG横截面上的应力查型钢表得单个等边角钢的面积为:[习题2-5] 石砌桥墩的墩身高,其横截面面尺寸如图所示。
荷载,材料的密度,试求墩身底部横截面上的压应力。
解:墩身底面的轴力为:墩身底面积:因为墩为轴向压缩构件,所以其底面上的正应力均匀分布。
[习题2-6]图示拉杆承受轴向拉力,杆的横截面面积。
如以表示斜截面与横截面的夹角,试求当时各斜截面上的正应力和切应力,并用图表示其方向。
解:斜截面上的正应力与切应力的公式为:式中,,把的数值代入以上二式得:轴向拉/压杆斜截面上的应力计算题目编号10000 100 0 100 100.0 0.0 习题2-6100 30 100 75.0 43.310000100 45 100 50.0 50.010000100 60 100 25.0 43.310000100 90 100 0.0 0.010000[习题2-7]一根等直杆受力如图所示。
材料力学习题解答

解: (3) 梁可简化, 为图示简朴支梁。
B
(m / 2)a 6EI
ma 12EI
(逆时针)
wC 0
mm
m
2
B
C
m
m
2a a a a a 2a
4.如图所示各梁旳抗弯刚度为EI,试用叠加法计算梁 B截面旳转角以及C点旳挠度。
解: (4) 梁可简化,为图示简朴支梁。 B
q
2qqaa22
C
B
qa3 24EI
φ w3 w2
q EI a
A a/4
θ w1
w1
a 4
qa3 a qa4 24EI 4 96EI
w2
q 8EI
a 4
4
qa 4 2048EI
φ w3
w3
a 4
a 3EI
1 2
q
a 4
2
a 4
qa 4 384EI
w2
w
w1
w2
w3
15qa 4 2048EI
7.试用叠加法计算图示各梁C点旳挠度。
解: (1) 梁可简化, 为图示悬臂梁。
A
B
F (2a)2 2EI
Fa 2 2EI
B
3Fa 2 2EI
(逆时针)
wC
wA
F (2a)3 3EI
( Fa3 3EI
Fa 2 2EI
a)
F
F
B C
Fa
a
a
F
a
BF
C
F
11Fa3 wC 6EI (向下)
4.如图所示各梁旳抗弯刚度为EI,试用叠加法计算梁 B截面旳转角以及C点旳挠度。
A
先考虑载荷作用下梁旳变形。
工程力学--材料力学(第五、六章)经典例题及讲解
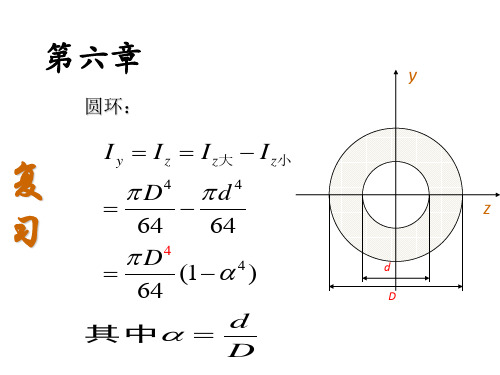
P
A
0.5 m
C D
0.4 m 1m
B
20
40
解:C点的应力 σ C = E ε = 200 × 10 3 × 6 × 10 − 4
= 120M Pa
C截面的弯矩
M C = σ C W z = 640 N ⋅ m
由 M C = 0.5 R A = 0.5 × 0.4 P = 0.2 P = 640 N ⋅ m 得 P = 3.2kN
度减小一半时,从正应力强度条件考虑, 该梁的承载能力将是原来的多少倍? 解: 由公式
σ max
M max M max = = 2 Wz bh 6
可以看出:该梁的承载能力将是原来的2 可以看出:该梁的承载能力将是原来的2倍。
例4:主梁AB,跨度为l,采用加副梁CD AB,跨度为l 采用加副梁CD
的方法提高承载能力, 的方法提高承载能力,若主梁和副梁材料 相同,截面尺寸相同, 相同,截面尺寸相同,则副梁的最佳长度 a为多少? 为多少?
2 2
2
bh b( d − b ) Wz = = 6 6
2 2 2
∂ Wz d 2 b 2 = − =0 ∂b 6 2
d 由此得 b = 3
d
2 2
h
h = d −b =
h = 2 ≈3:2 b
2 d 3
b
例12:跨长l =2m的铸铁梁受力如图示,已知材料许用拉、 12:跨长l =2m的铸铁梁受力如图示 已知材料许用拉、 的铸铁梁受力如图示,
10 kN / m
200 2m 4m 100
10 kN / m
200
2m
Fs( kN ) 25 Fs(
45 kN
4m
100
(完整版)材料力学试题及答案
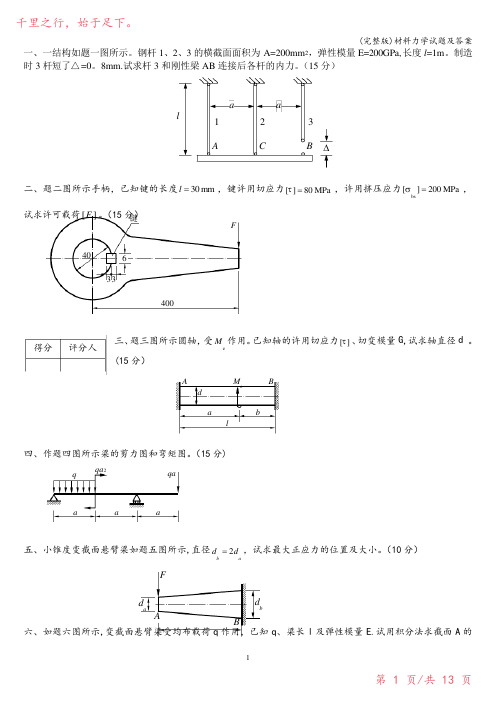
一、一结构如题一图所示。
钢杆1、2、3的横截面面积为A=200mm 2,弹性模量E=200GPa,长度l =1m 。
制造时3杆短了△=0。
8mm.试求杆3和刚性梁AB 连接后各杆的内力。
(15分)aalABC123∆二、题二图所示手柄,已知键的长度30 mm l =,键许用切应力[]80 MPa τ=,许用挤压应力bs[]200 MPa σ=,试求许可载荷][F 。
(15分)三、题三图所示圆轴,受eM 作用。
已知轴的许用切应力[]τ、切变模量G ,试求轴直径d 。
(15分)四、作题四图所示梁的剪力图和弯矩图。
(15分)五、小锥度变截面悬臂梁如题五图所示,直径2bad d =,试求最大正应力的位置及大小。
(10分)六、如题六图所示,变截面悬臂梁受均布载荷q 作用,已知q 、梁长l 及弹性模量E .试用积分法求截面A 的得分评分人F键40633400Aal bM eBd a a aqqaqa 2dbBda AF挠度w A 和截面C 的转角θC .(15分)七、如图所示工字形截面梁AB ,截面的惯性矩672.5610zI -=⨯m 4,求固定端截面翼缘和腹板交界处点a 的主应力和主方向。
(15分)一、(15分)(1)静力分析(如图(a))1N F2N F3N F图(a)∑=+=231,0N N N yF F F F(a)∑==31,0N N CF F M(b)(2)几何分析(如图(b))1l∆2l∆3l∆∆图(b)wql /3x lhb 0b (x )b (x )BAC 50kN AB0.75m303030140150zya∆=∆+∆+∆3212l l l(3)物理条件EA l F l N 11=∆,EA l F l N 22=∆,EAl F l N 33=∆ (4)补充方程∆=++EAlF EA l F EA l F N N N 3212 (c) (5)联立(a)、(b)、(c)式解得:kN FkN FF N N N 67.10,33.5231===二、(15分)以手柄和半个键为隔离体,S0, 204000OM F F ∑=⨯-⨯=取半个键为隔离体,bsS20F F F ==由剪切:S []s FA ττ=≤,720 N F = 由挤压:bs bs bs bs[][], 900N FF Aσσ=≤≤取[]720N F =.三、(15分)eABM M M +=0ABϕ=, A B M a M b ⋅=⋅得 e B a M M a b =+, e A b MM a b=+当a b >时 e316π ()[]M ad a b τ≥+;当b a >时 e316π ()[]M bd a b τ≥+。
材料力学典型例题与详解(经典题目)
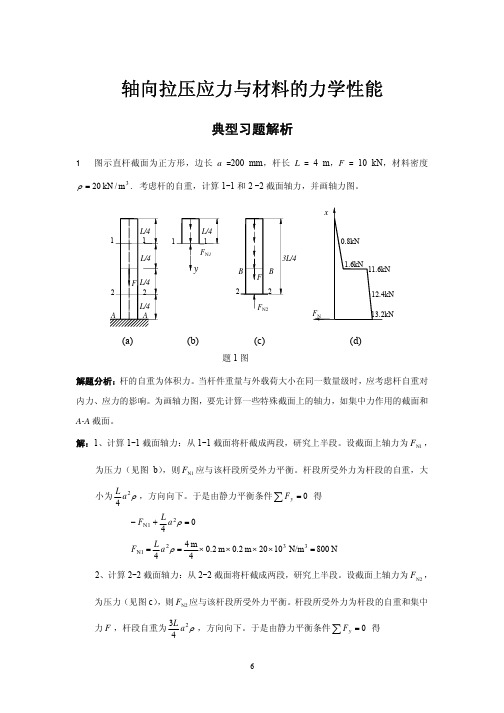
所以石柱体积为
V3
=
G ρ
=
[σ ]A(l) − ρ
F
= 1×106 Pa ×1.45 m 2 −1000 ×103 N = 18 m3 25 ×103 N/m3
三种情况下所需石料的体积比值为 24∶19.7∶18,或 1.33∶1.09∶1。 讨论:计算结果表明,采用等强度石柱时最节省材料,这是因为这种设计使得各截面的正应 力均达到许用应力,使材料得到充分利用。 3 滑轮结构如图,AB 杆为钢材,截面为圆形,直径 d = 20 mm ,许用应力 [σ ] = 160 MPa ,BC 杆为木材,截面为方形,边长 a = 60 mm ,许用应力 [σ c ] = 12 MPa 。试计算此结构的许用载
= 1.14 m 2
A
2=
F+ρ [σ ] −
A1 l1 ρ l2
=
1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m 1×106 N/m 2 − 25×103 N/m3 × 5 m
= 1.31 m 2
A
3=
F
+ ρA1l1 + ρA2l2 [σ ] − ρ l3
= 1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m + 25×103 N/m3 ×1.31 m 2 × 5 m = 1.49m 2 1×106 N/m 2 − 25 ×103 N/m3 × 5 m
解:1、计算 1-1 截面轴力:从 1-1 截面将杆截成两段,研究上半段。设截面上轴力为 FN1 ,
为压力(见图 b),则 FN1 应与该杆段所受外力平衡。杆段所受外力为杆段的自重,大
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
材料力学计算题库完整第一章绪论【例1-1】钻床如图1-6a所示,在载荷P作用下,试确定截面m-m上的内力。
【解】(1)沿m-m 截面假想地将钻床分成两部分。
取m-m 截面以上部分进行研究(图1-6b),并以截面的形心O为原点。
选取坐标系如图所示。
(2)为保持上部的平衡,m-m 截面上必然有通过点O的内力N和绕点O的力偶矩M。
(3)由平衡条件∴【例1-2】图1-9a所示为一矩形截面薄板受均布力p作用,已知边长=400mm,受力后沿x方向均匀伸长Δ=0.05mm。
试求板中a点沿x方向的正应变。
【解】由于矩形截面薄板沿x方向均匀受力,可认为板内各点沿x方向具有正应力与正应变,且处处相同,所以平均应变即a点沿x方向的正应变。
x方向【例1-3】图1-9b所示为一嵌于四连杆机构内的薄方板,b=250mm。
若在p 力作用下CD杆下移Δb=0.025,试求薄板中a点的剪应变。
【解】由于薄方板变形受四连杆机构的制约,可认为板中各点均产生剪应变,且处处相同。
第二章拉伸、压缩与剪切【例题2.1】 一等直杆所受外力如图2. 1 (a)所示,试求各段截面上的轴力,并作杆的轴力图。
解:在AB 段范围内任一横截面处将杆截开,取左段为脱离体(如图2. 1 (b)所示),假定轴力N1F 为拉力(以后轴力都按拉力假设),由平衡方程0xF=∑,N1300F -=得 N130kN F =结果为正值,故N1F 为拉力。
同理,可求得BC 段内任一横截面上的轴力(如图2. 1 (c)所示)为N2304070(kN)F =+=在求CD 段内的轴力时,将杆截开后取右段为脱离体(如图2. 1 (d)所示),因为右段杆上包含的外力较少。
由平衡方程0xF=∑,N330200F --+=得 N3302010(kN)F =-+=-结果为负值,说明N3F 为压力。
同理,可得DE 段内任一横截面上的轴力N4F 为N420kN F =F N4(a)EC BA 30kNF30kN(b)(c)20kN20kN (e)(d)(a)N1F N2F N3(a)EDCBA 20kNF 30kN40kN (b)(c)30kN20kN(d)(b) F N2F N3(a)30kNED C 20kN80kN40kN F(b)(c)30kN 20kN(d)30kN(c)精品资料F N2F N4(f)70kN30kN30kNF30kN40kN (b)(c)20kN (e)(d)(d)F N2F N3F (f)ED C BA 70kN30kN30kNF 30kN40kN(b)(c)(e)(d)(f)(a)30kN ED CBA20kN80kN40kN 30kNF30kN(b)(c)20kN(e)(d)30kN(f)图2. 1 例题2.1图【例题2.2】 一正方形截面的阶梯形砖柱,其受力情况、各段长度及横截面尺寸如图2.8(a)所示。
已知40kN P =。
试求荷载引起的最大工作应力。
解:首先作柱的轴力图,如图2.8(b)所示。
由于此柱为变截面杆,应分别求出每段柱的横截面上的正应力,从而确定全柱的最大工作应力。
Ι、ΙΙ两段柱横截面上的正应力,分别由已求得的轴力和已知的横截面尺寸算得3N1114010N 0.69(MPa)(240mm)(240mm)σ-⨯===-⨯F A (压应力)3N22212010N 0.88(MPa)(370mm)(370mm)F A σ-⨯===-⨯(压应力)由上述结果可见,砖柱的最大工作应力在柱的下段,其值为0.88MPa ,是压应力。
【例题2.3】 一钻杆简图如图2.9(a)所示,上端固定,下端自由,长为l ,截面面积为A ,材料容重为γ。
试分析该杆由自重引起的横截面上的应力沿杆长的分布规律。
解:应用截面法,在距下端距离为x 处将杆截开,取下段为脱离体(如图2.8(b)所示),设下段杆的重量为()G x ,则有()G x xA γ= (a)设横截面上的轴力为N ()F x ,则由平衡条件0=∑xF,N ()()0-=F x G x (b)将(a)式值代入(b)式,得N ()F x A x γ=⋅⋅ (c)即N ()F x 为x 的线性函数。
当0x =时,N (0)0F =当x l =时,N N,max ()F l F A l γ==⋅⋅(a) (b) (a) (b) (c)图2.8 例题2.2图 图2.9 例题2.3图 式中N,max F 为轴力的最大值,即在上端截面轴力最大,轴力图如图2.9(c)所示。
那么横截面上的应力为N ()()F x x x Aσγ==⋅ (d) 即应力沿杆长是x 的线性函数。
当0x =时,(0)0σ= 当x l =时,max ()l l σσγ==⋅式中max σ为应力的最大值,它发生在上端截面,其分布类似于轴力图。
【例题2.4】 气动吊钩的汽缸如图2.10(a)所示,内径180mm D =,壁厚8mm δ=,气压2MPa p =,活塞杆直径10mm d =,试求汽缸横截面B —B 及纵向截面C —C 上的 应力。
解:汽缸内的压缩气体将使汽缸体沿纵横方向胀开,在汽缸的纵、横截面上产生拉应力。
(1) 求横截面B —B 上的应力。
取B —B 截面右侧部分为研究对象(如图2.10(c)所示),由平衡条件0xF=∑,22N ()04D d p F π--=当D d >>时,得B —B 截面上的轴力为2N 4F D p π≈B —B 截面的面积为2()()A D D D δδδδδ=π⋅+⋅=π⋅+≈π那么横截面B —B 上的应力为2N 1802411.25(MPa)448x D p F Dp A D σδδπ⨯=≈===π⨯x σ称为薄壁圆筒的轴向应力。
图2.10 例题2.4图(2) 求纵截面C —C 上的应力。
取长为l 的半圆筒为研究对象(如图2.10(d)所示),由平衡条件0y F =∑,N10d sin 202D p l F θθπ⎛⎫⋅⋅⋅-= ⎪⎝⎭⎰ 得C —C 截面上的内力为N12F plD =C —C 截面的面积为12A l δ=当20D δ≥时,可认为应力沿壁厚近似均匀分布,那么纵向截面C —C 上的应力为N112180222.5(MPa)2228σδδ⨯=====⨯y F plD pD A l y σ称为薄壁圆筒的周向应力。
计算结果表明:周向应力是轴向应力的两倍。
【例题2.7】 螺纹内径15mm d =的螺栓,紧固时所承受的预紧力为22kN F =。
若已知螺栓的许用应力[]150σ=MPa ,试校核螺栓的强度是否足够。
解:(1) 确定螺栓所受轴力。
应用截面法,很容易求得螺栓所受的轴力即为预紧力,有N 22kN F F ==(2) 计算螺栓横截面上的正应力。
根据拉伸与压缩杆件横截面上正应力计算公式(2-1),螺栓在预紧力作用下,横截面上的正应力为3N 2242210124.63.14154σ⨯⨯====π⨯F F d A (MPa)(3) 应用强度条件进行校核。
已知许用应力为[]150(MPa)σ=螺栓横截面上的实际应力为124.6σ=MPa <[]150σ=(MPa)所以,螺栓的强度是足够的。
【例题2.8】 一钢筋混凝土组合屋架,如图2.25(a)所示,受均布荷载q 作用,屋架的上弦杆AC 和BC 由钢筋混凝土制成,下弦杆AB 为Q235钢制成的圆截面钢拉杆。
已知:10kN/m q =,8.8m l =, 1.6m h =,钢的许用应力[]170σ=MPa ,试设计钢拉杆AB 的 直径。
解:(1) 求支反力A F 和B F ,因屋架及荷载左右对称,所以11108.844(kN)22A B F F ql ===⨯⨯=图2.25 例题2.8图(2) 用截面法求拉杆内力N AB F ,取左半个屋架为脱离体,受力如图2.25(b)所示。
由0C M =∑,N 4.4 1.6024AAB l lF q F ⨯-⨯⨯-⨯= 得22N 144 4.4108.8184.4/1.660.5(kN)8 1.6ABA F F ql ⨯-⨯⨯⎛⎫=⨯-== ⎪⎝⎭(3) 设计Q235钢拉杆的直径。
由强度条件N N 24[]σ=πAB ABF F A d ≤ 得21.29(mm)d【例题2.9】 防水闸门用一排支杆支撑着,如图2.26(a)所示,AB 为其中一根支撑杆。
各杆为100mm d =的圆木,其许用应力[]10σ=MPa 。
试求支杆间的最大距离。
解:这是一个实际问题,在设计计算过程中首先需要进行适当地简化,画出简化后的计算简图,然后根据强度条件进行计算。
(1) 计算简图。
防水闸门在水压作用下可以稍有转动,下端可近似地视为铰链约束。
AB 杆上端支撑在闸门上,下端支撑在地面上,两端均允许有转动,故亦可简化为铰链约束。
于是AB 杆的计算简图如图2.26(b)所示。
图2.26 例题2.9图(2) 计算AB 杆的内力。
水压力通过防水闸门传递到AB 杆上,如图2.26(a)中阴影部分所示,每根支撑杆所承受的总水压力为2P 12F h b γ=其中γ为水的容重,其值为103kN/m ;h 为水深,其值为3m ;b 为两支撑杆中心线之间的距离。
于是有323P 11010345102F b b =⨯⨯⨯⨯=⨯根据如图2.26(c)所示的受力图,由平衡条件0CM=∑,P N 10AB F F CD -⨯+⨯=其中223sin 3 2.4(m)34CD α=⨯==+得33P N 451018.75102.4 2.4ABF b F b ⨯===⨯ (3) 根据AB 杆的强度条件确定间距b 的值。
由强度条件3N 2418.7510[]σσπ⨯⨯==⨯AB F b A d ≤得26233[]1010 3.140.1 4.19(m)418.7510418.7510σ⨯π⨯⨯⨯⨯==⨯⨯⨯⨯d b ≤【例题2.10】 三角架ABC 由AC 和BC 两根杆组成,如图2.34(a)所示。
杆AC 由两根No.14a 的槽钢组成,许用应力[]160σ=MPa ;杆BC 为一根No.22a 的工字钢,许用应力为[]100σ=MPa 。
求荷载F 的许可值[]F 。
(a) (b)图2.34 例题2.10图解:(1) 求两杆内力与力F 的关系。
取节点C 为研究对象,其受力如图2.34(b)所示。
节点C 的平衡方程为0xF=∑,N N cos cos 066BC AC F F ππ⨯-⨯= 0yF=∑,N N sinsin 066BC AC F F F ππ⨯+⨯-= 解得N N BC AC F F F ==(a)(2) 计算各杆的许可轴力。
由型钢表查得杆AC 和BC 的横截面面积分别为44218.5110237.0210m AC A --=⨯⨯=⨯,424210m BC A -=⨯。
