第二章参考答案
第二章市场营销环境(参考答案)

第二章市场营销环境(参考答案)一、单选:1.C 2.D 3.B 4.B 5.A 6.C 7.B二、多选:1.ABCDE 2.ABC 3.ABCD 4.ABE 5.ABCDE三、基本概念1.市场营销环境:是指影响企业市场营销活动及其目标实现的各种因素和动向。
2.市场机会:是指对企业市场营销管理富有吸引力的领域。
3.市场威胁:营销环境中出现的不利于企业生存和发展的因素。
4.微观环境:是指对企业营销活动发生直接影响的组织和力量。
5.宏观环境:又称间接营销环境,包括人口,经济,政治,法律,社会文化,自然,科技六大要素。
四、问答1.什么是市场营销环境?企业如何分析和评价市场营销环境的变化对企业营销的影响?企业应采取什么对策?答:(1)市场营销环境是指在企业的营销活动之外,能够影响营销部门建立并保持与目标顾客良好关系的能力的各种因素和力量。
(2) 企业如何分析和评价市场营销环境的变化对企业营销的影响?在企业实际面临的客观环境中,单纯的威胁环境和机会环境是少有的。
一般情况下,营销环境带来的对企业的威胁和机会是并存的,威胁中有机会,机会中也有挑战。
企业还可以运用“威胁—机会矩阵”综合分析,更清楚地认识企业在环境中的位置。
第1象限为理想环境。
机会水平高,威胁水平低,企业有非常好的发展前景。
企业须抓住机遇,开拓经营,创造营销佳绩,万万不可错失良机。
第2象限为冒险环境。
冒险环境是机会和威胁同在,利益与风险并存,在有很高利益的同时,存在很大的风险。
面对这样的环境,企业必须加强调查研究,进行全面分析,发挥专家优势,审慎决策,以降低风险,争取利益。
第3象限为成熟环境。
成熟环境是机会和威胁水平都比较低,是一种比较平稳的环境。
面对这样的环境,企业一方面要按常规经营,规范管理,以维持正常运转,取得平均利润;另企业要积蓄力量,为进入理想环境或冒险环境作准备。
第4象限为困难环境。
困难环境是风险大于机会,企业处境十分困难。
企业面对困难环境,必须想方设法扭转局面。
参考答案(第2章)

9 × 0.0049
= 9.3 × 10−3 m ⋅ s −1
3、 1、 根据均质形核的公式,得到:
r* =
2σ SLTm 2σ SLTm 2σ SLTmVm 2σ T V × N = = = SL m Fe * A * * Δ H ΔH v ΔT ΔH m × Δ T m × ΔT * ΔH m × ΔT Vm
= 1μ m 的液泡,需要的附加压力为
2σ 2 × 860 × 10−3 p= = = 1.72MPa r 10−6
对于半径 r
= 0.1μ m 的液泡,需要的附加压力为
2σ 2 × 860 × 10−3 p= = = 17.2MPa r 10−7
2、 根据 Stokes 公式,得到:
2r 2 (γ l − γ MnO ) 2r 2 ( ρl − ρ MnO ) g v= = 9η 9η = 2 × ( 0.1 × 10−3 ) × (7500 − 5400) × 9.8
其中 ΔH m 是摩尔原子的结晶潜热,Tm 是凝固点温度, R 是普适气体常数,η 是表面 配位数,ν 是晶体内部配位数,对于不同类型的晶体以及表面的晶面取向不同, 最大为 0.5。 当 α 1). Al
η ν
不同,
≤ 2 ,得到粗糙界面,当 α > 2 ,得到光滑界面。
Al 是 fcc 结构,
η Tm = 933K , ΔH b = 290.93 × 103 J/mol , = 0.5 , 从气态凝结时, ν
2
3
ρ MnO = 5400kg / m3 。若 MnO 为球形,半径为 0.1mm ,求它在钢液中的上浮速度?
3、 金属元素 Fe 的结晶潜热 ΔH m = 15.17 kJ / mol ,熔点 Tm = 1811K ,固/液界面张力
第二章 烷烃习题参考答案

第二章 烷烃习题参考答案1、用系统命名法命名下列化合物。
(1)(2)CH 3CHCHCH 2CHCH 3CH 2CH 3CH 3CH 3(CH 3CH 2)2CHCH(CH 2CH 3)CH 2CHCH 2CH 3CH(CH 3)2(3)(4)CH 3CH(CH 2CH 3)CH 2C(CH 3)2CH(CH 2CH 3)CH 3(5)(6)解:(1) 2,5-二甲基-3-乙基己烷;(2) 2-甲基-3,5,6-三乙基辛烷; (3) 3,4,4,6-四甲基辛烷; (4) 2,2,4-三甲基戊烷; (5)3,3,6,7-四甲基癸烷;(6)4-甲基-3,3-二乙基-5-异丙基辛烷 2、写出下列化合物的构造式和键线式。
并用系统命名法命名之。
(1) 仅含有伯氢,没有仲氢和叔氢的C 5H 12: (2) 仅含有一个叔氢的C 5H 12: (3) 仅含有伯氢和仲氢的C 5H 12: 解:(1)(2)(3)CH 3CH 2CH 2CH 2CH 3CH 3 C CH 3CH 3CH 3CH 3CH 2CHCH3CH32,2-二甲基丙烷2-甲基丁烷戊烷3、写出下列化合物的构造式。
(1)2,2,3,3-四甲基戊烷;(2)由一个丁基和一个异丙基组成的烷烃 (3)含有一个侧链甲基和分子质量86的烷烃:(4)相对分子质量为100,同时含有伯、叔、季碳原子的烷烃。
(5)3-ethyl-2-methylpentane; (6) 2,2,5-trimethyl-4-propylheptane; (7) 2,2,4,4-tetramethylhexane; (8) 4-tert-butyl-5-methylnonane(1)(2)CH 3CH 2CH 2CH 2CHCH 3CH 3CH 3CH 2 C C CH 3CH 3CH 3CH 3CH 3解:(3)所以该烷烃为C 6H 14,含一个支链甲基的异构体为:由M 得= 86(CnH 2n n)+n=6CH 3CH 2CH 2CHCH 3CH 3CH 3CH 2CHCH 2CH 3CH 3(4)按题意,该烷烃为:由M 得= 100(CnH 2n n)+n =7CH 3CHC(CH 3)3CH 3(6)(5)CH 3CHCHCHCH 3CH 3CH 2CH 3(CH 3)3CCH 2CHCHCH 2CH 3CH 2CH 2CH 3CH 3(CH 3)3CCH 2C(CH 3)2CH 2CH 3(7)(8)CH 2CH 2CH 2CHCHCH 2CH 2CH 2CH 3CH 3C(CH 3)34、试指出下列各组化合物是否相同?为什么?(2)C C C C C CCCCCCC(1)Cl C H ClH Cl C Cl H H解:(1)相同,二氯甲烷是四面体构型,四个原子在四面体的四个顶点,只有一种构型,这两个式子为一种构型的两种不同的投影式。
第二章作业 参考答案
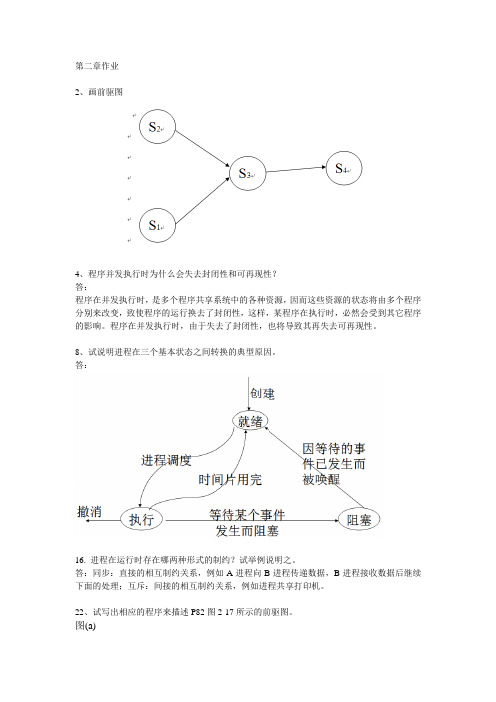
第二章作业2、画前驱图4、程序并发执行时为什么会失去封闭性和可再现性?答:程序在并发执行时,是多个程序共享系统中的各种资源,因而这些资源的状态将由多个程序分别来改变,致使程序的运行换去了封闭性,这样,某程序在执行时,必然会受到其它程序的影响。
程序在并发执行时,由于失去了封闭性,也将导致其再失去可再现性。
8、试说明进程在三个基本状态之间转换的典型原因。
答:16. 进程在运行时存在哪两种形式的制约?试举例说明之。
答:同步:直接的相互制约关系,例如A进程向B进程传递数据,B进程接收数据后继续下面的处理;互斥:间接的相互制约关系,例如进程共享打印机。
22、试写出相应的程序来描述P82图2-17所示的前驱图。
图(a)int a1=0,a2=0,a3=0,a4=0,a5=0,a6=0;a7=0;a8=0;parbeginbegin S1;V(a1);V(a2);end;begin P(a1);S2;V(a3);V(a4);end;begin P(a2);S3;V(a5);end;begin P(a3);S4;V(a6);end;begin P(a4);S5;V(a7);end;begin P(a5);S6;V(a8);end;begin P(a6);P(a7);P(a8);S7;end;parend图(b)int a1=0,a2=0,a3=0,a4=0,a5=0,a6=0;a7=0;a8=0;a9=0;a10=0;parbeginbegin S1;V(a1);V(a2);end;begin P(a1);S2;V(a3);V(a4);end;begin P(a2);S3;V(a5);V(a6);end;begin P(a3);S4;V(a7);end;begin P(a4);S5;V(a8);end;begin P(a5);S6;V(a9);end;begin P(a6);S7;V(a10);end;begin P(a7);P(a8);P(a9);P(a10);S8;end;parend28、在测量控制系统中的数据采集任务,把所采集的数据送一单缓冲区;计算任务从该单缓冲中取出数据进行计算。
第2章作业参考答案

2. 一批晶体管中有个 9 个合格品和 3 个不合格品,从中任取一个安装在电子设备上。若取 出不合格品不再放回,求取得合格品前已取出的不合格品个数的分布律和分布函数。 解:
X0 1 2
3
p 3/4 9/44 9/220 1/220
⎧ 0,
x<0
F (x) = ⎪⎪⎪⎨321/ 4/ ,22,
0≤ x <1 1≤ x < 2
求: (1) 系数 A,B; (2) X 落在区间(-1,1)的概率; (3) X 的概率密度。 解:
x∈R
7. 从一批子弹中任意抽出 5 发试射,若没有一发子弹落在靶心 2 厘米以外,则接受该批子 弹。设弹着点与靶心的距离 X(厘米)的概率密度为
f
(
x)
=
⎪⎧ ⎨
Axe−
x2
,
⎪⎩ 0,
0< x<3 其他
X
~
B
⎛ ⎜⎝
4,
1 5
⎞ ⎟⎠
, 故分布律为
P( X = k) = C4k (0.2)k (0.8)4−k , k = 0,1, 2, 3, 4
( ) (2)P X = k
=
C5k
*
C 4− 20
k
C245
k = 0,1,2,3,4
5. 临床观察表明,某药物产生副作用的概率为 0.002。现在 900 个患者服用该药物,求至 少有3例患者出现副作用的概率.
试求:(1)系数 批子弹被接受的概率。 解:
⎧ 0,
x<0
∫ ∫ (2) F(x) =
x −∞
f
(t)dt
=
⎪⎪ ⎨ ⎪
x2 0 1 − e−9
材料化学第二章习题参考答案与解析

第二章参考答案1.原子间的结合键共有几种?各自特点如何?2.为什么可将金属单质的结构问题归结为等径圆球的密堆积问题?答:金属晶体中金属原子之间形成的金属键即无饱和性又无方向性, 其离域电子为所有原子共有,自由流动,因此整个金属单质可看成是同种元素金属正离子周期性排列而成,这些正离子的最外层电子结构都是全充满或半充满状态,电子分布基本上是球形对称,由于同种元素的原子半径都相等,因此可看成是等径圆球。
又因金属键无饱和性和方向性, 为使体系能量最低,金属原子在组成晶体时总是趋向形成密堆积结构,其特点是堆积密度大,配位数高,因此金属单质的结构问题归结为等径圆球的密堆积问题.3.计算体心立方结构和六方密堆结构的堆积系数。
(1) 体心立方 a :晶格单位长度 R :原子半径a 34R = 34R a =,n=2, ∴68.0)3/4()3/4(2)3/4(23333===R R a R bccππζ (2)六方密堆 n=64. 试确定简单立方、体心立方和面心立方结构中原子半径和点阵参数之间的关系。
解:简单立方、体心立方和面心立方结构均属立方晶系,点阵参数或晶格参数关系为90,=====γβαc b a ,因此只求出a 值即可。
对于(1)fcc(面心立方)有a R 24=, 24R a =, 90,=====γβαc b a(2) bcc 体心立方有:a 34R = 34R a =; 90,=====γβαc b a(3) 简单立方有:R a 2=, 90,=====γβαc b a74.0)3(3812)3/4(6)2321(6)3/4(633hcp =⋅=⋅R R R R a a c R ππξ=R a a c 238==5. 金属铷为A2型结构,Rb 的原子半径为0.2468 nm ,密度为1.53g·cm-3,试求:晶格参数a 和Rb 的相对原子质量。
解:AabcN nM=ρ 其中, ρ为密度, c b a 、、为晶格常数, 晶胞体积abc V =,N A 为阿伏加德罗常数6.022×1023 mol -1,M 为原子量或分子量,n 为晶胞中分子个数,对于金属则上述公式中的M 为金属原子的原子量,n 为晶胞中原子的个数。
第二章 习题参考答案(修正)

第二章 需求、供给与均衡价格(题目及习题解答)一、判断题1.需求曲线描述了:其它条件不变,市场需求量与价格之间的关系。
解答:√。
知识点:课本第14页倒数第3行。
2.以纵轴代表价格,横轴代表数量,如果两条需求曲线通过同一点,则在那一点处,较陡的那条的弹性更大。
解答:×。
知识点:(考察弹性的几何意义)课本21页公式2.6和22页6-15行。
应该是“较陡的那条的弹性更小”。
理由:图中,直线AC 、BD 分别为需求曲线1和需求曲线2,AC 比BD 陡峭。
AC 之上的E 点弹性等于|AE|/|CE|,而BD 之上的E 点弹性等于|BE|/|DE|。
不难判定,|BE|>|AE|,而|DE|<|CE|,所以|AE|/|CE|<|BE|/|DE|,即“在那一点处,较陡的那条的弹性更小”。
3.如果需求是一条倾斜的直线,则价格水平越高,需求的价格弹性(绝对值)越大。
解答:√。
知识点:两种解法。
第一种是利用弹性的几何意义,课本22页6-7行。
如左下图所示:D 点价格大于B 点,D 点弹性=|AD|/|CD|>B 点弹性=|AB| /|BC|;第二种利用21页公式2.6。
因为B 点和D 点都在同一条直线上,所以dQ/dP 都相同,而P2<P 1,Q 2>Q1。
2121E E B D P P dQ dQ dP Q dP Q =⋅<=⋅ 4.如供给是一条直线,则供给的价格弹性为常数。
解答:×。
26页2.10b 。
“供给的价格弹性不确定”。
设供给函数为P=a+b ·Q s ,则dQ s /dP=-1/b 2,5.需求曲线越陡峭,则供给的变化对价格的影响越大。
P=a 1+b 1·Q s ,需求曲线P=a 2-b 2·Q d 。
令Q *=Q s =Q d ,得P *=(a 1b 2+b 1a 2)/(b 1+b 2)。
需求曲线a 1变化而b 1不变(平行移动)。
第二章 参考答案

第二章参考答案【思考题】一、资金时间价值同一般的利息率是什么关系?答:一般的利息率充分考虑了风险因素和通货膨胀因素,而表示资金时间价值的利息率则是指在无通货膨胀、无风险情况下的社会平均资金利润率。
二、对资金时间价值产生的原因通常有哪些解释?其真正的来源是什么?答:对资金时间价值产生的原因通常的解释有:其一,货币时间价值是人们认知心理的反映,认为现在单位资金价值要高于未来单位资金的价值;其二,资金时间价值是资源稀缺性的体现。
其三,资金时间价值是对机会成本的补偿。
因资金持有者的“放弃”而得到好处的人就应该做出相应的补偿,资金的时间价值就可以看出是对放弃流动偏好或者当前消费所产生的机会成本的补偿。
资金时间价值真正的来源是工人劳动者创造的剩余价值,资本使用者支付给资本所有者以利息,实质上是工人创造的剩余价值的再分配。
三、对单一项目进行取舍与否的决策,计算其风险价值的基本步骤有哪些?答:基本步骤如下:1.计算预期收益;2.计算收益标准差;3.计算收益标准差率;4.计算应得风险收益率;5.计算预测投资收益率和预测风险收益率;6.比较预测风险收益率和应得风险收益率,进行方案取舍。
四、后付年金和先付年金终值和现值之间有怎样的关联?答:n期后付年金和n期先付年金,两者付款期数相同,但先付年金终值比后付年金终值多一个计息期;n期后付年金和n期先付年金,两者付款期数相同,但先付年金现值比后付年金现值少一个贴现期。
【练习题】一、名词解释:资金时间价值资金风险价值年金风险性投资决策答:资金时间价值——资金的时间价值是指资金在周转过程中随着时间的推移而形成的增值。
资金风险价值——资金风险价值是指由于冒险投资而获得的超过资金时间价值的额外收益。
年金——年金是指在一定期限内等额定期的系列收付款项。
风险性投资决策——是指各个因素的未来情况不能完全确定,但未来情况发生的可能性即概率为已知的投资决策。
二、选择题(1-5为单项选择,6-9为多项选择)1.年金的收付款方式有多种,其中每期期末收付款的年金是( A )A.普通年金B.预付年金C.延期年金D.永续年金2.下面有关资金时间价值的表述,正确的是( A )A.资金时间价值的实质是资金周转使用后的增值额B.资金时间价值是推迟消费所获得的报酬C.资金时间价值只能用绝对数来表示D.资金时间价值的量无法进行计量3.下列可用于衡量投资风险程度的指标是( C )A.概率B.预期收益C.标准离差率D.风险价值系数4.用于比较预期收益不同的投资项目风险程度的指标是( A )A.标准离差率B.标准离差C.预期收益的概率D.预期收益5.在下列各项年金中,无法计算出确切终值的是( D )A.后付年金B.先付年金C.递延年金D.永续年金6.年金是指一定期间内每期相等金额的收付款项,通常采取年金形式的有( A C)A.保险金B.普通股股息C.租金 D.税金E.利润7.关于投资风险价值,下列表述正确的有( A C D E )A.投资风险价值有风险收益额和风险收益率两种表示方法B.风险收益额是投资者进行投资所获得的投资收益总额C.风险收益率是风险收益额与投资额的比率D.在实际工作中,投资风险价值通常以风险收益率进行计量E.一般来说,风险越大,获得的风险价值应该越高8.风险价值系数的确定方法包括( B C D )A.根据市场平均利润率确定B.由企业领导或有关专家确定C.根据以往同类项目的有关数据确定D.由国家有关部门组织专家确定E.根据投资人要求的最低报酬率确定9.下列关于年金的表述正确的有(C D E )A.年金是指一定时期发生的系列收付款项B.年金是指一定时期等额的系列收付款项C.普通年金是指一定时期每期期末等额的系列收付款项D.先付年金是指一定时期每期期初等额的系列收付款项E.递延年金是指最初若干期没有收付款项,随后若干期等额的系列收付款项【技能训练】一、向银行存入本金1000元,年利率为6%,则5年后的终值为多少?(分别用单利和复利计算)答:用单利计算有:F=P ×(1+i×n)=1000×(1+6%×5)=1300(元)用复利计算有:F=P ×(1+i) n =P ×(F/P ,6%,5)=1000×1.338=1338 (元)二、某人在5年后需要使用一笔20 000元资金,银行利率为8%,则现在应该一次存入本金多少钱?(分别用单利和复利计算)答:用单利计算有:11P F i n =⨯+⨯=20000×118%5+⨯=14286(元) 用复利计算有:1(1)nP F i =⨯+= F ×(P / F ,8%,5) =20000×0.681=13620 (元) 三、存入银行10 000元,年利率为10%,按季复利计息,存款期限2年,试计算: 1.两年后的本利和; 2.计算其实际利率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2章 参考答案2写出下列十进制数的原码、反码、补码和移码表示(用8位二进制数)。
如果是小数,则用定点小数表示;若为整数,则用定点整数表示。
其中MSB 是最高位(符号位),LSB 是最低位。
(1)-1 (2) -38/64解:(1)-1=(-0000001)2原码: 10000001反码: 11111110 吧 补码: 11111111移码: 01111111(2)-38/64=-0.59375=(-0.1001100)2或-38/64=-(32+4+2)*2-6=-(100110)*2-6=(-0.1001100)2原码: 1.1001100 反码: 1.0110011 补码: 1.0110100 移码: 0.0110100注:-1如果看成小数,那么只有补码和移码能表示得到,定点小数-1的补码为:1.0000000此例类似于8位定点整数的最小值-128补码为100000003 有一字长为32位的浮点数,符号位1位;阶码8位,用移码表示;尾数23位,用补码表示;基数为2.请写出:(1)最大数的二进制表示,(2)最小数的二进制表示,(3)规格化数所能表示的数的范围。
解:(题目没有指定格式的情况下,用一般表示法做)(1)最大数的二进制表示:0 11111111 11111111111111111111111(2)最小数的二进制表示:1 11111111 00000000000000000000000(1) )(231221*27--- (2) )(1*2127--(3)规格化最大正数:0 11111111 11111111111111111111111)(231221*27---规格化最小正数:0 00000000 10000000000000000000000122*27-- 规格化最大负数:1 00000000 01111111111111111111111 )(231222*27---+- 规格化最小负数:1 11111111 00000000000000000000000 )(1*2127--规格化数的表示的数的范围为: )]21*2,2*2[]22*2,1*2[231212*********---------+--()()( 4. 将下列十进制数表示成IEEE754标准的32位浮点规格化数。
-27/64解:X =(-27/64)10=(-11011.×2 _6)2 =(-0.011011)2 =-(1.1011×2 -2) S=1 E=-2+127=125=01111101 M=1011IEEE754标准的32位浮点规格化数为:1 01111101 101100000000000000000005. 已知X 和Y , 用变形补码计算X+Y , 同时指出运算结果是否溢出。
(1) x=11011 y=00011解: [X]补=0011011, [Y]补=0000011[X+Y]补=[X]补+ [Y]补[X]补 0011011+ [Y]补 0000011------------------------[X+Y]补 0011110符号位为00,结果无溢出X+Y =111106. 已知X 和Y , 用变形补码计算X-Y , 同时指出运算结果是否溢出。
(1) x=11011 y=-11111解:[X]补=0011011, [Y]补=1100001,[-Y]补=0011111[X+Y]补=[X]补+ [-Y]补[X]补0011011+ [-Y]补0011111------------------------[X-Y]补0111010符号位为01,结果溢出X-Y=110107. 用原码阵列乘法器计算X×Y。
(1)X=11011 Y= -11111解:[x]补=0 11011 [y]补=100001符号位单独运算:0⊕1=1尾数部分算前求补器输出为|x|=11011, |y|=111111 1 0 1 1×) 1 1 1 1 1----------------------------------1 1 0 1 11 1 0 1 11 1 0 1 11 1 0 1 11 1 0 1 1-----------------------------------------1 1 0 1 0 0 0 1 0 1乘积符号位1,算后求补器输出为0010111011,最后补码乘积值为:(算后求补器输出不带符号位,详见课本36页图2.7;该图中符号位输入到算后求补器是为了作为控制信号,详见课本35页图2.6中的控制性号线E)【x×y】补= 100101110118.用原码阵列除法器计算X÷Y。
(1)X=11000 Y= -11111解:X和Y先都乘以一个比例因子2-101X=0.11000 ,Y= -0.11111[∣x∣]补=0.11000,[∣y∣]补=0.11111,[-∣y∣]补=1.00001符号位单独运算:0⊕1=11)余数左移的解法(恢复余数法):被除数 X 00.11000+[-|y|]补11.00001----------------------余数为负 11.11001 →q0=0余数为负,商上0+[|y|]补 00.11111 恢复余数----------------------00.11000左移 01.10000+[-|y|]补11.00001----------------------余数为正 00.10001 →q1=1余数为正,商上1左移 01.00010+[-|y|]补 11.00001----------------------余数为正 00.00011 →q2=1 余数为正,商上1左移 00.00110+[-|y|]补 11.00001----------------------余数为负 11.00111 →q3=0余数为负,商上0+[|y|]补 00.11111 恢复余数----------------------00.00110左移 00.01100+[-|y|]补11.00001----------------------余数为负 11.01101 →q4=0余数为负,商上0+[|y|]补 00.11111 恢复余数----------------------00.01100左移 00.11000+[-|y|]补11.00001----------------------余数为负 11.11001 →q5=0余数为负,商上0+[|y|]补 00.11111----------------------余数 00.11000故[x÷y]原=1.11000 即x÷y= -0.11000,余数=0.11000*2-101*2101=0.110002)余数左移的解法(加减交替法):被除数 X 00.11000+[-|y|]补11.00001----------------------余数为负 11.11001 →q0=0余数为负,商上0左移 11.10010+[|y|]补 00.11111----------------------余数为正 00.10001 →q1=1 余数为正,商上1左移 11.00010+[-|y|]补 11.00001----------------------余数为正 00.00011 →q2=1 余数为正,商上1左移 00.00110+[-|y|]补 11.00001----------------------余数为负 11.00111 →q3=0余数为负,商上0左移 10.01110+[|y|]补 00.11111----------------------余数为负 11.01101 →q4=0余数为负,商上0左移 10.11010+[|y|]补 00.11111----------------------余数为负 11.11001 →q5=0余数为负,商上0+[|y|]补 00.11111----------------------余数 00.11000故[x÷y]原=1.11000 即x÷y= -0.11000,余数=0.11000*2-101*2101 =0.11000 3)除数右移的解法(加减交替法):被除数 X 0.1100000000+[-∣y∣]补 1.00001-------------------------余数为负 1.1100100000 →q0=0余数为负,商上0+[|y|]补 0.011111-------------------------余数为正 0.010******* →q1=1余数为正,商上1+[-|y|]补 1.1100001------------------------余数为正 0.0000011000 →q2=1余数为正,商上1+[-|y|]补 1.11100001------------------------余数为负 1.1110011100 →q3=0余数为负,商上0+[|y|]补 0.000011111------------------------余数为负 1.1111011010 →q4=0余数为负,商上0+[|y|]补 0.0000011111------------------------余数为负 1.1111111001 →q5=0余数为负,商上0+[|y|]补 0.0000011111-------------------------余数 0.0000011000故[x÷y]原=1.11000 即x÷y= -0.11000,余数= 0.0000011*2101=0.11000 9 设阶码5位(包含2位符号位), 尾数9位(包含2位符号位), 都为补码表示,采用0舍1入,计算X+Y,X-Y:X=2-101×(-0.1001011) Y=2-011×0.0101011解:[x]=11011,11.0110101浮=11101,00.0101011[y]浮[-y]=11101,11.1010101浮① 0操作数检查两数都非0②对阶[ΔE]补=[Ex]补+[-Ey]补=11011+00011=11110可见ΔE=-2将Mx 右移2位,[x]浮=11101,11.11 01101(01)③尾数相加相加相减11.1101101(01) 11.1101101(01) + 00.0101011 + 11.1010101------------------------ ------------------------00.0011000(01) 11.1000010(01)④结果规格化[x+y]浮=11101,00.0011000(01)左规[x+y]浮=11011,00.1100001[x-y]浮=11101, 11.1000010(01)左规[x-y]浮=11100, 11.0000100(1)⑤舍入处理(用0舍1入)得[x+y]浮不需舍入处理[x-y]浮=11100, 11.0000101⑥判溢出X+Y和X-Y的阶符都是11,都没溢出最终的结果为:x+y=2-101×(0.1100001)x-y=2-100×(-0.1111011)。
