《结构动力学》课程作业解析
结构力学课后答案第10章结构动力学

解:
若 为静力荷载,弹簧中反力为 。
已知图示体系为静定结构,具有一个自由度。设为B点处顺时针方向转角 为坐标。建立动力方程:
则弹簧支座的最大动反力为 。
10-21设图a所示排架在横梁处受图b所示水平脉冲荷载作用,试求各柱所受的最大动剪力。已知EI=6×106Nm2,t1=,FP0=8×104N。
(a)
则同样有: 。
10-9图示结构AD和DF杆具有无限刚性和均布质量 ,A处转动弹簧铰的刚度系数为kθ,C、E处弹簧的刚度系数为k,B处阻尼器的阻尼系数为c,试建立体系自由振动时的运动方程。
*
解:
取DF隔离体, :
取AE隔离体:
将R代入,整理得:
/
10-10试建立图示各体系的运动方程。
(a)
解:(1)以支座B处转角作为坐标,绘出梁的位移和受力图如下所示。图中惯性力为三角形分布,方向与运动方向相反。
图 图
(1)求结构运动方程
如所示弯矩图,图乘后,
其中 ,稳态解:
所示结构的运动方程为 ,C点最大动位移幅值为
(2)求B点的动位移反应
,
!
B点的动位移幅值为
(3)绘制最大动力弯矩图
图 图
最大动力弯矩图
10-20试求图示集中质量体系在均布简谐荷载作用下弹簧支座的最大动反力。设杆件为无限刚性,弹簧的刚度系数为k。
(2)画出 和 图(在B点处作用一附加约束)
…
(3)列出刚度法方程
, ,
代入 、 的值,整理得:
(b)
解:
图 图
】
试用柔度法解题
此体系自由度为1 。设质量集中处的竖向位移y为坐标。
y是由动力荷载 和惯性力矩 共同引起的。
《结构动力学》课程作业解析

研究生课程考核试卷(适用于课程论文、提交报告)科目:结构动力学大作业教师:姓名:学号:专业:岩土工程类别:专硕上课时间:2015年9 月至2015 年11 月考生成绩:卷面成绩平时成绩课程综合成绩阅卷评语:阅卷教师(签名)重庆大学研究生院制土木工程学院2015级硕士研究生考试试题1 题目及要求1、按规范要求设计一个3跨3层钢筋混凝土平面框架结构(部分要求如附件名单所示;未作规定部分自定)。
根据所设计的结构参数,求该结构的一致质量矩阵、一致刚度矩阵;2、至少采用两种方法求该框架结构的频率和振型;3、输入地震波(地震波要求如附件名单所示),采用时程分析法,利用有限元软件或自编程序求出该框架结构各层的线性位移时程反应。
2 框架设计2.1 初选截面尺寸取所设计框架为3层3跨,跨度均为4.5m ,层高均为3.9m 。
由于基础顶面离室内地面为1m ,故框架平面图中底层层高取 4.9m 。
梁、柱混凝土均采用C30,214.3/c f N mm =,423.010/E N mm =⨯,容重为325/kN m 。
估计梁、柱截面尺寸如下: (1)梁:梁高b h 一般取跨度的11218,取梁高b h =500mm ; 取梁宽300b b mm =;所以梁的截面尺寸为:300500mm mm ⨯ (2)柱:框架柱的截面尺寸根据柱的轴压比限值,按下列公式计算: ①柱组合的轴压力设计值...E N F g n β=其中:β:考虑地震作用组合后柱轴压力增大系数; F :按简支状态计算柱的负荷面积;E g :折算在单位建筑面积上的重力荷载代表值,可近似取为21214/KN m ;n :验算截面以上的楼层层数。
②c N cNA u f ≥其中:N u :框架柱轴压比限值;8度(0.2g ),查抗震规范轴压比限值0.75N u =;c f :混凝土轴心抗压强度设计值,混凝土采用30C ,214.3/c f N mm =。
经计算取柱截面尺寸为:300300mm mm ⨯ 该榀框架立面图如图2.1所示。
结构动力学课后习题答案

结构动力学课后习题答案结构动力学是研究结构在动态载荷作用下的响应和行为的学科。
它涉及到结构的振动、冲击响应、疲劳分析等方面。
课后习题是帮助学生巩固课堂知识、深化理解的重要手段。
以下内容是结构动力学课后习题的一些可能答案,供参考:习题1:单自由度系统自由振动分析解答:对于一个单自由度系统,其自由振动的频率可以通过以下公式计算:\[ f = \frac{1}{2\pi}\sqrt{\frac{k}{m}} \]其中,\( k \) 是系统的刚度,\( m \) 是系统的总质量。
系统自由振动的振幅随着时间的衰减可以通过阻尼比 \( \zeta \) 来描述,其衰减系数 \( \delta \) 可以通过以下公式计算:\[ \delta = \sqrt{1-\zeta^2} \]习题2:单自由度系统受迫振动分析解答:当单自由度系统受到周期性外力作用时,其受迫振动的振幅可以通过以下公式计算:\[ A = \frac{F_0}{\sqrt{(k-m\omega^2)^2+(m\zeta\omega)^2}} \] 其中,\( F_0 \) 是外力的幅值,\( \omega \) 是外力的角频率。
习题3:多自由度系统模态分析解答:对于多自由度系统,可以通过求解特征值问题来得到系统的模态。
特征值问题通常表示为:\[ [K]{\phi} = \lambda[M]{\phi} \]其中,\( [K] \) 是系统的刚度矩阵,\( [M] \) 是系统的质量矩阵,\( \lambda \) 是特征值,\( {\phi} \) 是对应的特征向量,即模态形状。
习题4:结构的冲击响应分析解答:对于结构的冲击响应分析,通常需要考虑冲击载荷的持续时间和冲击能量。
结构的冲击响应可以通过冲击响应谱(IRF)来分析,它描述了结构在不同频率下的响应。
冲击响应分析的结果可以用来评估结构的耐冲击性能。
习题5:疲劳分析解答:结构的疲劳分析需要考虑结构在重复载荷作用下的寿命。
结构动力学习题解答

然后积分求初始速度
̇̇ d t = θ̇0 = θ 0
0+ 0+ 0+
∫
0
∫ hδ ( t ) d t = h ∫ δ ( t ) d t = h
0 0 0+
;
再积分求初位移
̇̇ d t == h )d t = 0 ; θ0 = θ 0
0+
∫
0
∫
0
̇̇ 、 θ̇ 和 θ 的瞬态响应 这样方程(6)的解就是系统对于初始条件 θ 0 0 0
1.6 求图 1-35 所示系统的固有频率。图中磙子半径为 R,质量为 M,作纯滚动。弹簧刚度 为K 。 解:磙子作平面运动, 其动能 T=T 平动 +T 转动 。
K R M 图 1-35 x
T平动 = T转动
1 ̇2; Mx 2 2 2 ̇ ⎞ 1 ⎛ MR 2 ⎞ ⎛ x ̇⎞ 1 ⎛x = I⎜ ⎟ = ⎜ ⎟⎜ ⎟ ; 2 ⎝R⎠ 2 ⎝ 2 ⎠⎝ R ⎠
U= r 2 1 1 1 1⎛ K A ϕ A 2 + K B ϕ B 2 = K Aϕ A 2 + K B ϕ B 2 = ⎜ K A + K B A 2 2 2 2 2⎜ rB ⎝
(
)
⎞ 2 ⎟ϕ ; ⎟ A ⎠
系统的机械能为
T +U = r 2 1 1⎛ ̇ A2 + ⎜ K A + K B A (m A + m B )rA 2ϕ 4 2⎜ rB 2 ⎝
d (T + U ) = 0 ,进一步得到系 dt
统的运动微分方程; (3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。 1.2 叙述用衰减法求单自由度系统阻尼比的方法和步骤。 用衰减法求单自由度系统阻尼比的方法有两个:衰减曲线法和共振法。 方法一:衰减曲线法。 求解步骤: (1)利用试验测得单自由度系统的衰减振动曲线,并测得周期和相邻波峰和波谷 的幅值 Ai 、 Ai +1 。 (2)由对数衰减率定义 δ = ln(
结构动力学-习题解答
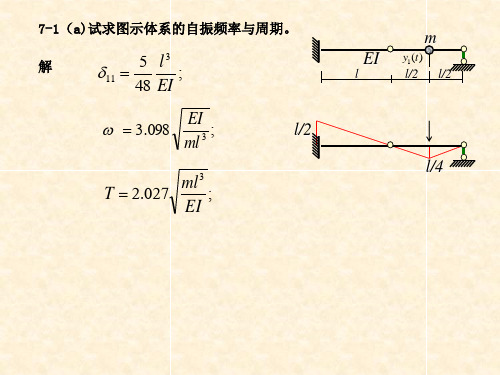
7-1(a)试求图示体系的自振频率与周期。
解
11
5 48
l3 EI
;
3.098
EI ml 3
;
l/2
T 2.027
ml 3 ;
7-6 某结构在自振10个周期后,振幅降为原来初始位移的10% (初位移为零),试求其阻尼比。
解: 1 ln10 0.0366 2 10
8-1试求图示梁的自振频率和振型。 m
y1(t)
解
EI 2m
a
a
y2
(t
)
a
12
21
1 4
a3 EI
a
I 2 m 0
11m1 1/ 2
m212
0
m1 21
22m2 1/ 2
1 1.153
a/2
2 0.181
令
1
11m1
2
1 1/ 2
0
1/ 4 1/3 2 4 / 3 5 / 24 0
x11 / x21 3.277; x12 / x22 0.61
;
9l / 64 (a)
5l / 32
11.817
EI ml 3 ;
l/2
T 0.531
ml3 ;
(b)
EI
7-1(c)试求图示体系的自振频率与周期。
m 刚性杆
解 由右面竖杆的平衡可求出铰处约束力。
EI
由水平杆的平衡:
[美]R.克里夫《结构动力学》补充详解及习题解
![[美]R.克里夫《结构动力学》补充详解及习题解](https://img.taocdn.com/s3/m/198055225627a5e9856a561252d380eb629423b8.png)
前言结构动力学是比较难学的一门课程,但是你一旦学会并且融会贯通,你就会为成为结构院士、大师和总工垫定坚实的基础。
结构动力学学习的难点主要有以下两个方面。
1 概念难理解,主要表现在两个方面,一是表达清楚难,如果你对概念理解的很透彻,那么你写的书对概念的表述也会言简意赅,切中要害(克里夫的书就是这个特点),有的书会对一个概念用了很多文字进行解释,但是还是没有说清楚,也有的书受水平限制,本身表述就不清楚。
二是理解难,有点只可意会不可言传的味道,老师讲的头头是道,自己听得云山雾绕。
2 公式推导过程难,一是力学知识点密集,推导过程需要力学概念清析,并且需要每一步的力学公式熟悉;二是需要一定的数学基础,而且有的是在本科阶段并没有学习的数学知识。
克里夫《结构动力学》被称为经典的结构动力学教材,但是也很难看懂。
之所以被称为经典,主要就是对力学的概念表达的语言准确,概念清楚。
为什么难懂呢?是因为公式的推导过程比较简单,省略过多。
本来公式的推导过程既需要力学概念清楚也需要数学公式熟悉,但是一般人不是力学概念不清楚,就是数学公式不熟悉,更有两者都不熟悉者。
所以在学习过程中感觉很难,本学习详解是在该书概念清楚的基础上,对力学公式推导过程进行详细推导,并且有的加以解释,帮助你在学习过程中加深理解和记忆。
达到融会贯通,为你成为结构院士、大师和总工垫定坚实的基础。
以下黑体字是注释,其它为原书文字。
[美] R∙克里夫《结构动力学》辅导学习详解第1章结构动力学概述… …第Ⅰ篇单自由度体系第2章基本动力体系的组成… …§2-5 无阻尼自由振动分析如上一节所述,有阻尼的弹簧-质量体系的运动方程可表示为mv̈(t)+cv̇(t)+kν(t)=p(t)(2-19)其中ν(t)是相对于静力平衡位置的动力反应;p(t)是作用于体系的等效荷载,它可以是直接作用的或是支撑运动的结构。
为了获得方程(2-19)的解,首先考虑方程右边等于零的齐次方程,即mv̈(t)+cv̇(t)+kν(t)=0(2-20)mv(t)+kν(t)=0(2-20a)此处公式应该为mv(t)+kν(t)=0,因为该节是无阻尼自由振,而且(2-20)的解,式(2-21)也是公式mv(t)+kν(t)=0的解在作用力等于零时产生的运动称为自由振动,现在要研究的即为体系的自由振动反应。
结构动力学大作业1.

结构动力学课程论文结构动力学课程论文一、题目1、试设计一个3层框架,根据实际结构参数,求出该结构的一致质量矩阵、一致刚度矩阵;2、至少采用两种方法求3层框架的频率和振型;3、采用时程分析法,输入地震波,求出所设计的3层框架各层的非线性位移时程反应,要求画出所设计的框架图、输入的地震波的波形图、所求得的各楼层位移时程反应图。
二、问题解答1、问题1解答1.1、框架设计框架立面图如下图一所示,梁截面均为400⨯700mm2,柱子的截面均为600⨯600mm2,跨度为7.2m,层高为3.6m,混凝土采用C30。
图一框架立面图设梁、柱均不产生轴向变形,且只考虑在框架的平面内变形,那么有3个平结构动力学课程论文移自由度和12个转角自由度,一共有15个自由度,自由度以及梁柱单元编号如下图二所示:V1V2V3图二单元编号及自由度方向先计算各个单元的一致质量矩阵和一致刚度矩阵,然后把相关的单元叠加组合计算得到整个结构的一致质量矩阵和一致刚度矩阵。
1.2、结构的一致质量矩阵梁:=0.4⨯0.7⨯2500=700kg/m, L=7.2m;梁、柱都为均布质量,故:⎧f⎪f⎪⎨⎪f⎪⎩fI1I2I3I4⎫⎪⎪L⎬=420⎪⎪⎭5622L⎡156⎢5415613L⎢⎢22L13L4L⎢⎣-13L-22L-3L-13L⎤-22L⎥⎥-3L⎥⎥4L⎦221⎫⎧v⎪v⎪⎪ 2⎪⎨⎬3⎪⎪v⎪ 4⎪⎩v⎭结构动力学课程论文结构动力学课程论文柱:=0.6⨯0.6⨯2500=900kg/m,L=3.6m 单元刚度矩阵如下:结构动力学课程论文结构动力学课程论文(m)(n)(p)ˆijˆijˆij由mij=m+m+m+....可计算一致质量矩阵中的各元素:(1)(2)(3)(10)(11)(12)(13)ˆ11ˆ11ˆ11ˆ11ˆ11ˆ11ˆ11m11=m+m+m+m+m+m+m=3⨯5040+ 4⨯1203.43=19933.72(10)(11)(12)(13)ˆ12ˆ12ˆ12ˆ12m12=m+m+m+m=4⨯416.57=1666.28结构动力学课程论文m13=0(10)m14=m15=m16=m17=m14=610.97(10)m18=m19=m1,10=m1,11=m18=-361.03 m1,12=m1,13=m1,14=m1,15=0(4)(5)(6)(10)(11)(12)(13)(14)(15)(16)(17)ˆ22ˆ22ˆ22ˆ22ˆ22ˆ22ˆ22ˆ22ˆ22ˆ22ˆ22m22=m+m+m+m+m+m+m+m+m+m+m=3⨯5040+8⨯1203.43=24747.44(14)(15)(16)(17)ˆ23ˆ23ˆ23ˆ23m23=m+m+m+m=4⨯416.57=1666.28(10)m24=m25=m26=m27=m24=361.03(14)(10)ˆ28ˆ28m28=m+m=610.97-610.97=0 同理 m29=m2,10=m2,11=0(14)m2,12=m2,13=m2,14=m2,15=m2.03 ,12=-361(7)(8)(9)(14)(15)(16)(17)(18)(19)(20)(21)ˆ33ˆ33ˆ33ˆ33ˆ33ˆ33ˆ33ˆ33ˆ33ˆ33ˆ33m33=m+m+m+m+m+m+m+m+m+m+m=3⨯5040+8⨯1203.43=24747.44(14)m34=m35=m36=m37=0 m38=m39=m3,10=m3,11=m38=361.03 (14)ˆ3ˆ(18)m3,12=m3,13=m3,14=m3,15=m.97-610.97=0 ,12+m3,12=610(1)(10)(1)ˆ44ˆ44ˆ45m44=m+m=2488.32+399.91=2888.23 m45=m=-1866.24m46=m47=0(10)ˆ48m48=m=-299.93m49=m4,10=m4,11=m4,12=m4,13=m4,14=m4,15=0(2)(1)(2)(11)ˆ56ˆ55ˆ55ˆ55=-1866.24m55=m+m+m=2488.32+2488.32+399.91=5376.55m56=mm57=m58=0(11)ˆ59m59=m=-299.93 m5,10=m5,11=m5,12=m5,13=m5,14=m5,15=0(2)(3)(12)ˆ66ˆ66ˆ66m66=m+m+m=2488.32+2488.32+399.91=5376.55(3)ˆ67m67=m=-1866.24 m68=m69=0(12)ˆ6m6,10=m.93 m6,11=m6,12=m6,13=m6,14=m6,15=0 ,10=-299(3)(13)ˆ77ˆ77m77=m+m=2488.32+399.91=2888.23m78=m79=m7,10=0(13)ˆ7m7,11=m.93 m7,12=m7,13=m7,14=m7,15=0 ,11=-299结构动力学课程论文(4)(10)(14)ˆ88ˆ88ˆ88m88=m+m+m=2488.32+399.91+399.91=3288.14(4)ˆ89m89=m=-1866.24 m8,10=m8,11=0(14)ˆ8m8,12=m.93 m8,13=m8,14=m8,15=0 ,12=-299(4)(5)(11)(15)ˆ99ˆ99ˆ99ˆ99m99=m+m+m+m=2488.32+2488.32+399.91+399.91=5776.46(5)ˆ9m9,10=m.24 ,10=-1866(15)ˆ9.93 m9,14=m9,15=0 m9,11=m9,12=0 m9,13=m,13=-299(5)(6)(12)(16)ˆ10ˆ10ˆ10ˆ10m10,10=m.32+2488.32+399.91+399.91=5776.46 ,10+m,10 +m,10+m,10=2488(6)(16)ˆ10ˆ m10,11=m=-1866.24m=m.93 m10,15=0m=m=010,1210,13,1110,1410,14=-299(6)(13)(17)ˆ11ˆ11ˆ11m11,11=m.32+399.91+399.91=3288.14,11+m,11+m,11=2488m11,12=m11,13=m11,14=0(17)ˆ11m11,15=m.93,15=-299(7)(14)(18)ˆ12ˆ12ˆ12m12,12=m.32+399.91+399.91=3288.14 ,12+m,12+m,12=2488 (7)ˆ12m12,13=m.24 m12,14=m12,15=0 ,13=-1866(7)(8)(15)(19)ˆ13ˆ13ˆ13ˆ13m13,13=m.32+2488.32+399.91+399.91=5776.46 ,13+m,13 +m,13+m,13=2488(8)ˆ13m13,14=m.24 m13,15=0 ,14=-1866(8)(9)(16)(20)ˆ14ˆˆˆm14,14=m+m+m+m.32+2488.32+399.91+399.91=5776.46 ,1414,1 414,1414,14=2488(9)ˆ14m14,15=m.24 ,15=-1866(9)(17)(21)ˆ15ˆ15ˆ15m15,15=m.32+399.91+399.91=3288.14 ,15+m,15+m,15=2488则得:一致质量矩阵(该矩阵为对称矩阵,故下三角省略)单位(kg)结构动力学课程论文0⎡19933.721666.28⎢24747.441666.28⎢⎢24747.44⎢⎢⎢⎢⎢⎢⎢M=⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣610.97361.0302888.23610.97361.030-1866.245376.55610.97361.0300-1866.245376.55610.97361.03000-1866.242888.23-361.030361.03-299.930003288.14-361.030361.030-299.9300-1866.245776.46-361.030361.0300-299.9300-1866.245776.46-361.030361.03000-299.9300-1866.243288.140-361.0300000-299.930003288.14⎤-361.03-361.03-361.03⎥⎥⎥000⎥000⎥⎥000⎥000⎥⎥000⎥000⎥⎥-299.9300⎥⎥0-299.930⎥00-299.93⎥⎥-1866.2400⎥5776.46-1866.240⎥5776.46-1866.24⎥⎥3288.14⎦⎥0001.3、结构的一致刚度矩阵各梁、柱均为等截面,故单元刚度矩阵为:-63L3L⎤⎧v1⎫⎧fs1⎫⎡6⎪f⎪⎪v⎪⎢6-3L-3L⎥⎪s2⎪2EI⎢-6⎪2⎪⎥=⎨⎬⎨⎬ 223⎢⎥f3L-3L2LLL⎪s3⎪⎪v3⎪⎢22⎥⎪⎪f3L-3LL2L⎣⎦⎪⎩v4⎪⎭⎩s4⎭框架梁:C30混凝土E=3⨯107KN/m2,0.40⨯0.73EI=3⨯10⨯=3.43⨯105kN·m2,L=7.2m 127结构动力学课程论文7框架柱:0.60⨯0.603EI=3⨯10⨯=3.24⨯105KN·m2 L=3.6m12结构动力学课程论文结构动力学课程论文结构动力学课程论文ˆ(m)+kˆ(n)+kˆ(p)+....可计算一致刚度矩阵中的各元素:由kij=kijijijˆ(10)+kˆ(11)+kˆ(12)+kˆ(13)=4⨯0.833⨯105=3.332⨯105 k11=k11111111ˆ(10)+kˆ(11)+kˆ(12)+kˆ(13)=4⨯(-0.833k12=k)⨯105=-3.332⨯105 k13=0 12121212 (10)k14=k15=k16=k17=k18=k19=k1,10=k1,11=k14=1.50⨯105k1,12=k1,13=k1,14=k1,15=0ˆ(10)+kˆ(11)+kˆ(12)+kˆ(13)+kˆ(14)+kˆ(15)+kˆ(16)+kˆ(17)=8⨯0.833⨯105=6.664⨯105 k22=k2222222222222222ˆ(14)+kˆ(15)+kˆ(16)+kˆ(17)=4⨯(-0.833k23=k)⨯105=-3.332⨯1052323232310k24=k25=k26=k27=k24=-0.861⨯105ˆ(10)+kˆ(14)=0.861⨯105-0.861⨯105=0 同理 k28=k2828k29=k2,10=k2,11=0结构动力学课程论文ˆ(14)=1.50⨯105 k2,12=k2,13=k2,14=k2,15=k2,12ˆ(14)+kˆ(15)+kˆ(16)+kˆ(17)+kˆ(18)+kˆ(19)+kˆ(20)+kˆ(21)=8⨯0.833⨯105=6.664⨯105 k33=k3333333333333333k34=k35=k36=k37=0(14)k38=k39=k3,10=k3,11=k38=-1.50⨯105ˆ(14)+kˆ(18)=1.50⨯105-1.50⨯105=0 k3,12=k3,13=k3,14=k3,15=k3,123,12ˆ(1)=0.953⨯105 ˆ(1)+kˆ(10)=1.906⨯105+3.60⨯105=5.506⨯105 k=kk44=k44444545 k46=k47=0ˆ(10)=1.80⨯105k48=k48k49=k4,10=k4,11=k4,12=k4,13=k4,14=k4,15=0ˆ(1)+kˆ(2)+kˆ(11)=1.906⨯105+1.906⨯105+3.60⨯105=7.412⨯105k55=k555555ˆ(2)=0.953⨯105 k56=k56k57=k58=0 ˆ(11)=1.80⨯105 k59=k59k5,10=k5,11=k5,12=k5,13=k5,14=k5,15=0ˆ(2)+kˆ(3)+kˆ(12)=1.906⨯105+1.906⨯105+3.60⨯105=7.412⨯105k66=k666666ˆ(3)=0.953⨯105 k67=k67ˆ(12)=1.80⨯105 k=k=k=k=k=0 k68=k69=0 k6,10=k6,116,126,136,146,156,10ˆ(3)+kˆ(13)=1.906⨯105+3.60⨯105=5.506⨯105k77=k7777k78=k79=k7,10=0ˆ(13)=1.80⨯105 k=k=k=k=0 k7,11=k7,127,137,147,157,11ˆ(4)+kˆ(10)+kˆ(14)=1.906⨯105+3.60⨯105+3.60⨯105=9.106⨯105k88=k888888ˆ(4)=0.953⨯105 k89=k89ˆ(14)=1.80⨯105 k=k=k=0 k8,10=k8,11=0 k8,12=k8,138,148,158,12ˆ(4)+kˆ(5)+kˆ(11)+kˆ(15)=1.906⨯105+1.906⨯105+3.60⨯105+3.60⨯105k99=k999999 99=11.012⨯105 14结构动力学课程论文ˆ(5)=0.953⨯105 k9,10=k9,10k9,14=k9,15=0k9,11=k9,12=0ˆ(15)=1.80⨯105 k9,13=k9,13ˆ(5)+kˆ(6)+kˆ(12)+kˆ(16)=1.906⨯105+1.906⨯105+3.60⨯105+3.60⨯105k10,10=k10,1010,1010,1010,10=11.012⨯1055ˆ(6)=0.953⨯105 kˆ(16)k10,11=k10,12=k10,13=0 k10,14=k10,14=1.80⨯10 k10,15=0 10,11ˆ(6)+kˆ(13)+kˆ(17)=1.906⨯105+3.60⨯105+3.60⨯105=9.106⨯105k11,11=k11,1111,1111,11ˆ(17)=1.80⨯105 k11,12=k11,13=k11,14=0 k11,15=k11,15 ˆ(4)+kˆ(7)+kˆ(18)=1.906⨯105+3.60⨯105+3.60⨯105=9.106⨯105k12,12=k12,1212,1212,12ˆ(7)=0.953⨯105 kk12,13=k12,14=k12,15=0 12,13ˆ(7)+kˆ(8)+kˆ(15)+kˆ(19)=1.906⨯105+1.906⨯105+3.60⨯105+3.60⨯105k13,13=k13,1 313,1313,1313,13=11.012⨯105ˆ(8)=0.953⨯105 kk13,14=k13,15=0 13,14ˆ(8)+kˆ(9)+kˆ(16)+kˆ(20)=1.906⨯105+1.906⨯105+3.60⨯105+3.60⨯105k14,14=k14,1 414,1414,1414,14=11.012⨯105ˆ(9)=0.3125⨯105k14,15=k14,15ˆ(9)+kˆ(17)+kˆ(21)=1.906⨯105+3.60⨯105+3.60⨯105=9.106⨯105k15,15=k15,1515,1515,15得到一致刚度矩阵(该矩阵为对称矩阵,故下三角省略)单位(kN/m)⎡3.332⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢K=105⨯⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣-3.3326.6640-3.3326.6641.50-1.5005.5061.50-1.5000.9537.4121.50-1.50000.9537.4121.50-1.500000.9535.5061.500-1.501.800009.1061.500-1.5001.80000.95311.0121.500-1.50001.80000.95311.0121.500-1.500001.80000.9539.10601.50000001.800009.10601.500000001.80000.95311.01201.5000000001.80000.95311.01201.50000000001.80000.9539.106⎤⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦结构动力学课程论文 2 问题2 解答2.1采用振型分解反应谱法,求解框架的频率和振型ˆ}={0}的特征值得到频率ω和振型φ:由[K]-ω2[M]{v在Matlab中导入质量矩阵[M]和刚度矩阵[K],输[v,ω2]=eig(K,M);ω=sqrt(ω2)可得框架的频率为: []ωT={ω1ω2ω3........ω14ω15}={32.861, 109.022, 199.133, 234.897, 299.589, 307.809 , 378.000, 388.414, 454.501, 480.646, 583.896 , 637.664, 747.045, 828.365, 1056.507 }框架的振型为[φ]=[{φ1}{φ2}{φ3}......{φ14}{φ15}]=φ1 φ2 φ3 φ4 φ5 φ6 φ7 φ8φ9 φ10 φ11 φ12 φ13 φ14 φ15结构动力学课程论文2.2 用Stodola法计算三层框架的频率和振型此结构的柔度矩阵是f=K-1=D=fm=⎡52612⎢34661⎢⎢13564⎢⎢-2919⎢-2009⎢⎢-2009⎢-2919⎢10-5⨯⎢-4627⎢-3739⎢⎢-3739⎢⎢-4627⎢-4436⎢⎢-3429⎢-3429⎢⎢⎣-4436453153846316844-648-547-547-648-3237-2622-2622-3237-5313-4034-4034-5313179831712511915-95-55.4-55.4-95-395-408-408-395-2546-1883-1883-2546 1933.61502.4600.3585.14-403.97.9103-69.43-330.8-46.98-141.3-151.2-164.3-169.8-202-2022088.51495.3606.51-631828.14-463.5-16.66-39.22-52.13-197.9-226.6-226.6-114.2-168.9-189.520471488.4605.89-7.983-467.4891.72-635.4-193.6-45.69-344.3-30.81-189.2-169.2-112.1-227.41933.61502.4600.3-69.437.9103-403.9585.14-151.2-141.3-46.98-330.8-202-149.4-169.8-164.3-959-507-53.6-141139.935.2281.15567.3-144114.5114.5109.7-71.595.5537.1-466.3-466.3-74.97214.41-174.8143.1345.392-214.1713.23-171.7134.55129.58-99.996.75140.084-885-466-7545.39143.1-175214.4134.6-172713.2-21440.0896.75-99.9129.6-959.1-507.2-53.6281.15235.225139.93-141.1109.67114.46-143.6567.357.99237.09595.548-71.52-959.1-507.2-53.6281.15235.225139.93-141.1109.67114.46-143.6567.357.99237.09595.548-71.52-768.9-687.5-306.5-28.0246.216-14.4511.743129.09-99.9796.6839.588-186.8664.53-159.7122.14-768.9-687.5-306.511.743-14.4546.216-28.0239.58896.68-99.97129.09122.14-159.7664.53-186.8-898.5⎤-828.5⎥⎥-387.3⎥⎥-1.176⎥7.242⎥⎥-15.89⎥45.168⎥⎥58.04⎥37.49⎥⎥95.943⎥⎥-71.48⎥113.72⎥⎥107.89⎥-127.1⎥⎥525⎥⎦结构动力学课程论文V1(1)=DV1(0)迭代过程列表如下根据D V1(0)⎡52612⎢34661⎢⎢13564⎢⎢-2919⎢-2009⎢⎢-2009⎢-2919⎢10-5⨯⎢-4627⎢-3739⎢⎢-3739⎢⎢-4627⎢-4436⎢⎢-3429⎢-3429⎢⎢-4436⎣453153846316844-648-547-547-648-3237-2622-2622-3237-5313-4034-4034-5313179831712511915-95-55.4-55.4-95-395-408-408-395-2546-1883-1883-2546 1933.61502.4600.3585.14-403.97.9103-69.43-330.8-46.98-141.3-151.2-164.3-169.8-202-2022088.51495.3606.51-631828.14-463.5-16.66-39.22-52.13-197.9-226.6-226.6-114.2-168.9-189.520471488.4605.89-7.983-467.4891.72-635.4-193.6-45.69-344.3-30.81-189.2-169.2-112.1-227.41933.61502.4600.3-69.437.9103-403.9585.14-151.2-141.3-46.98-330.8-202-149.4-169.8-164.3-959-507-53.6-141139.935.2281.15567.3-144114.5114.5109.7-71.595.5537.1-466.3-466.3-74.97214.4-174.8143.145.39-214.1713.2-171.7134.5129.5-99.996.7540.08-885-466-7545.39143.1-175214.4134.6-172713.2-21440.0896.75-99.9129.6-959.1-507.2-53.6281.1535.22139.93-141.1109.67114.46-143.6567.357.9937.0195.54-71.52-959.1-507.2-53.6281.1535.22139.93-141.1109.67114.46-143.6567.357.9937.0995.54-71.52-768.9-768.9-687.5-306.5-28.0246.21-14.4511.74129.1-99.9796.6839.58-186.8664.5-159.7122.14-687.5-306.511.743-14.4546.216-28.0239.58896.68-99.97129.09122.14-159.7664.53-186.8-898.5⎤-828.5-387.3⎥-1.1767.242-15.89⎥45.1658.04⎥37.4995.94⎥-71.48113.7107.8⎥-127.1525⎦⎥⎡1⎤⎢1⎥⎢⎥⎢1⎥⎢⎥⎢1⎥⎢1⎥⎢⎥⎢1⎥⎢1⎥⎢⎥⎢1⎥⎢1⎥⎢⎥⎢1⎥⎢⎥⎢1⎥⎢1⎥⎢⎥⎢1⎥⎢1⎥⎢⎥⎢⎣1⎥⎦V1(1) V1(1) V1(2) V1(2) V1(3) V1(3) V1(4) V1(4 ) V1(5)⎡116889⎤⎢91257.8⎥⎢⎥⎢43091⎥⎢⎥-3558.1⎢⎥⎢-2480.4⎥⎢⎥⎢-2412.9⎥⎢-3571.2⎥⎢⎥-8221.3⎢⎥⎢-6697.9⎥⎢⎥⎢-6710.8⎥⎢⎥-8217.2⎢⎥⎢-12347⎥⎢⎥-9334.2⎢⎥⎢-9331.7⎥⎢⎥⎢⎣-12348⎥⎦10.7810.369-0.03-0.02-0.02-0.03-0.07-0.06-0.06-0.07-0.11-0.08-0.08-0.11949641928321926271926086917330082-3452-2444-2446-3451-7208-5858-5857-7208-9276-7082-7082-9276712580.7504311920.3285-3477-0.037-2465-0.026-2465-0.026-3477-0.037-7335-0.077-5965-0.063-5965-0.063-7335-0.077-9574-0.101-7305-0.077-7305-0.077-9574-0.101693690.7473301840.3252-3454-0.037-2446-0.026-2448-0.026-3454-0.037-7221-0.078-5868-0.063-5868-0.063-7221-0.078-0.1-9304-7103-0.077-7103-0.077-0.1-9304691890.747300910.325-3452-0.04-2444-0.03-2446-0.03-3451-0.04-7209-0.08-5859-0.06-5858-0.06-7209-0.08-9278-0.1-7084-0.08-7084-0.08-9278-0.1则得到第一振型形式为φ1=(-0.1585 -0.1184 -0.0515 0.005910.00418 0.00419 0.00591 0.01234 0.01003 0.01002 0.01234 0.01588 0.01212 0.01212 0.01588)再用公式ω12=(V1)TmV1(0)(V)mV(1)T1(1)1(1),将数据代入得ω1=32.75。
高等结构动力学大作业

高等结构动力学大作业1. 简介高等结构动力学是结构工程学中的一门重要课程,主要研究结构在外力作用下的动力响应。
本次大作业将探讨高等结构动力学的相关内容,包括结构振动、模态分析和地震反应等。
2. 结构振动结构振动是结构动力学的基础知识,是研究结构在外力作用下的运动规律的重要手段。
结构振动可以分为自由振动和受迫振动两种。
2.1 自由振动自由振动是指结构在没有外力作用下的振动。
结构的自由振动可以通过求解结构的固有振型和固有频率来得到。
固有振型是指结构在自由振动时的形态,固有频率是指结构在自由振动时的振动频率。
2.2 受迫振动受迫振动是指结构在外力作用下的振动。
外力可以是周期性的,也可以是非周期性的。
受迫振动可以通过求解结构的响应函数和激励函数来得到。
3. 模态分析模态分析是研究结构振动特性的重要方法,通过模态分析可以得到结构的模态参数,包括模态振型和模态频率。
模态振型是指结构在特定模态下的振动形态,模态频率是指结构在特定模态下的振动频率。
3.1 模态分析的方法常用的模态分析方法包括有限元法、模态超级位置法和模态伸缩法等。
有限元法是一种基于数值计算的方法,通过离散化结构并求解特征值问题来得到结构的模态参数。
模态超级位置法是一种基于振动测量的方法,通过测量结构的振动响应来得到结构的模态参数。
模态伸缩法是一种基于模态参数估计的方法,通过估计结构的模态参数来得到结构的模态参数。
3.2 模态分析的应用模态分析在结构工程中有广泛的应用,包括结构设计、结构优化和结构监测等。
通过模态分析可以评估结构的动力性能,指导结构的设计和优化,以及监测结构的健康状况。
4. 地震反应地震反应是指结构在地震作用下的振动响应。
地震是一种破坏性的外力,对结构的安全性和稳定性具有重要影响。
地震反应分为静力反应和动力反应两种。
4.1 静力反应静力反应是指结构在地震作用下的静态响应。
静力反应可以通过结构的刚度矩阵和地震力谱来计算得到。
静力反应的计算可以采用静力分析和动力分析两种方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
研究生课程考核试卷(适用于课程论文、提交报告)科目:结构动力学大作业教师:姓名:学号:专业:岩土工程类别:专硕上课时间:2015年9 月至2015 年11 月考生成绩:卷面成绩平时成绩课程综合成绩阅卷评语:阅卷教师(签名)重庆大学研究生院制土木工程学院2015级硕士研究生考试试题1 题目及要求1、按规范要求设计一个3跨3层钢筋混凝土平面框架结构(部分要求如附件名单所示;未作规定部分自定)。
根据所设计的结构参数,求该结构的一致质量矩阵、一致刚度矩阵;2、至少采用两种方法求该框架结构的频率和振型;3、输入地震波(地震波要求如附件名单所示),采用时程分析法,利用有限元软件或自编程序求出该框架结构各层的线性位移时程反应。
2 框架设计2.1 初选截面尺寸取所设计框架为3层3跨,跨度均为4.5m ,层高均为3.9m 。
由于基础顶面离室内地面为1m ,故框架平面图中底层层高取 4.9m 。
梁、柱混凝土均采用C30,214.3/c f N mm =,423.010/E N mm =⨯,容重为325/kN m 。
估计梁、柱截面尺寸如下: (1)梁:梁高b h 一般取跨度的11218,取梁高b h =500mm ; 取梁宽300b b mm =;所以梁的截面尺寸为:300500mm mm ⨯ (2)柱:框架柱的截面尺寸根据柱的轴压比限值,按下列公式计算: ①柱组合的轴压力设计值...E N F g n β=其中:β:考虑地震作用组合后柱轴压力增大系数; F :按简支状态计算柱的负荷面积;E g :折算在单位建筑面积上的重力荷载代表值,可近似取为21214/KN m ;n :验算截面以上的楼层层数。
②c N cNA u f ≥其中:N u :框架柱轴压比限值;8度(0.2g ),查抗震规范轴压比限值0.75N u =;c f :混凝土轴心抗压强度设计值,混凝土采用30C ,214.3/c f N mm =。
经计算取柱截面尺寸为:300300mm mm ⨯ 该榀框架立面图如图2.1所示。
图2.1 框架立面图2.2 框架几何刚度特征(1)梁:截面惯性矩:3394300500 3.125101212b bh I mm ⨯===⨯; 刚度:491323.010 3.125109.37510b EI N mm =⨯⨯⨯=⨯⋅ 293750KN m =⋅ 梁的单位长度质量(按照计算重力荷载代表值的方法计算): 一二层(考虑楼板恒载及楼面活载作用):分布质量:b (0.30.52500 4.50.12500 4.5200)2400/m kg m =⨯⨯+⨯⨯+⨯= 顶层(仅考虑楼板恒载不考虑屋面活载作用):分布质量:b (0.30.52500 4.50.122500)1725/m kg m =⨯⨯+⨯⨯=; (2)柱:截面惯性矩:3384300300 6.75101212c bh I mm ⨯===⨯; 刚度:481323.010 6.7510 2.02510c E I N mm =⨯⨯⨯=⨯⋅ 220250KN m =⋅ 分布质量:c 0.30.32500/225/m bh kg m kg m γ==⨯⨯=根据以上计算结果,将其列入表中,如下表2.1所示:2.3 动力自由度框架单元编号及动力自由度编号见图2.2所示:图2.2框架单元编号及自由度编号框架结构可以理想化为在节点处相互连接的单元(梁和柱)的集合。
设梁、柱的轴向变形均忽略不计,只考虑节点的转角和横向位移,则该框架有3个平动自由度和12个转角自由度,共15个自由度。
3一致质量矩阵、一致刚度矩阵3.1 一致质量矩阵在节点位移作用下框架梁和柱上所引起的变形形状采用Hermite 多项式。
因此均布质量梁的一致质量矩阵为:2222156542213541561322221343420132234L L L L mL L LL L L L LL -⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥---⎣⎦式(3.1)下面开始计算质量影响系数,依次对每一个自由度施加单位加速度,利用式(3.1)的系数确定质量影响系数:1图3.1.1()()1121415161718191101111225 3.9156431564317254.524591.2420420225 3.9544544451.3420420225 3.92222 3.9179.3420420225 3.91313 3.9105.9420420c b c c c m h m m L m h m m h m m m m h m h m m m m h ⨯=⨯⨯+=⨯⨯+⨯⨯=⨯=⨯⨯=⨯⨯=⨯====⨯=⨯⨯=⨯====⨯-=⨯-⨯=-2图3.1.2221232425262728292102112122225 3.915683156832400 4.535007.4420420225 3.9544544451.3420420225 3.91313 3.9105.942042022220420420c b c c c c m h m m L m h m m m h m m m m h m h m hm m m m h h m ⨯=⨯⨯+=⨯⨯+⨯⨯=⨯==⨯⨯=⨯⨯=⨯====⨯=⨯⨯=====⨯-+⨯==,,,()132142152225 3.91313 3.9105.9420420c m h m m m h ⨯===⨯-=⨯-⨯=-,,,()()3图3.1.3123323225 3.9225 4.91564156431564156442042042042032400 4.535341.7225 3.9544544451.3420420c c b c m h m h m m L m h m ⨯⨯=⨯⨯+⨯⨯+=⨯⨯+⨯⨯+⨯⨯=⨯=⨯⨯=⨯⨯=839310,311,3225 3.91313 3.9105.9420420c m h m m m m h ⨯====⨯=⨯⨯= ()1212,313,314,315,312225 3.9222222 3.9420420420225 4.922 4.9103.7420c c m h m h m m m m h h ⨯====⨯-+⨯=⨯-⨯⨯+⨯⨯=()4图3.1.422224422542284142225 3.91725 4.5444 3.94 4.51624.24204204204201725 4.5(3)(3) 4.51122.8420420225 3.9(3)(3) 3.995.3420420225 3.92222 3.9179.3420420c b b c c m h m L m h L m L m L m h m h m h m h m ⨯⨯=⨯+⨯=⨯⨯+⨯⨯=⨯=⨯-=⨯-⨯=-⨯=⨯-=⨯-⨯=-⨯=⨯=⨯⨯=4225 3.91313 3.9105.9420420c m h h ⨯=⨯=⨯⨯=由于框架为对称结构,对自由度4V 施加单位加速度引起的质量影响系数与对自由度7V 施加单位加速度引起的质量影响系数相同,可得结果如下:22227722672211,717225 3.91725 4.5444 3.94 4.51624.24204204204201725 4.5(3)(3) 4.51122.8420420225 3.9(3)(3) 3.995.3420420225 3.92222 3.9179.3420420c b b c c m h m L m h L m L m L m h m h m h m h ⨯⨯=⨯+⨯=⨯⨯+⨯⨯=⨯=⨯-=⨯-⨯=-⨯=⨯-=⨯-⨯=-⨯=⨯=⨯⨯=27225 3.91313 3.9105.9420420c m h m h ⨯=⨯=⨯⨯=5图3.1.52222552245652295225 3.91725 4.54244 3.924 4.53121.24204204204201725 4.5(3)(3) 4.51122.8420420225 3.9(3)(3) 3.993.5420420c b b c m h m L m h L m L m m L m h m h ⨯⨯=⨯+⨯⨯=⨯⨯+⨯⨯⨯=⨯==⨯-=⨯-⨯=-⨯=⨯-=⨯-⨯=-1525225 3.92222 3.9179.3420420225 3.91313 3.9105.9420420c c m h m h m h m h ⨯=⨯=⨯⨯=⨯=⨯=⨯⨯=由于框架为对称结构,对自由度5V 施加单位加速度引起的质量影响系数与对自由度6V 施加单位加速度引起的质量影响系数相同,可得结果如下:2222662256762210,6225 3.91725 4.54244 3.924 4.53121.24204204204201725 4.5(3)(3) 4.51122.8420420225 3.9(3)(3) 3.993.5420420c b b c m h m L m h L m L m m L m h m h ⨯⨯=⨯+⨯⨯=⨯⨯+⨯⨯⨯=⨯==⨯-=⨯-⨯=-⨯=⨯-=⨯-⨯=- 1626225 3.92222 3.9179.3420420225 3.91313 3.9105.9420420c c m h m h m h m h ⨯=⨯=⨯⨯=⨯=⨯=⨯⨯=8图3.1.6()()2222882298224812,818225 3.92400 4.54244 3.924 4.52337.14204204204202490 4.5(3)(3) 4.51562.1420420225 4.5(3)(3) 4.595.3420420225 3.91313420420c b b c c m h m L m h L m L m L m h m m h m h m h ⨯⨯=⨯⨯+⨯=⨯⨯⨯+⨯⨯=⨯=⨯-=⨯-⨯=-⨯==⨯-=⨯-⨯=-⨯=⨯-=⨯-2838 3.9105.922220420420225 3.91313 3.9105.9420420c c c m h m h m h h m h m h ⨯=-=⨯-+⨯=⨯=⨯=⨯⨯=()由于框架为对称结构,对自由度8V 施加单位加速度引起的质量影响系数与对自由度11V 施加单位加速度引起的质量影响系数相同,可得结果如下:()222211,112210,11227,1115,111,11225 3.92400 4.54244 3.924 4.52337.142042042042024904.5(3)(3) 4.51562.1420420225 4.5(3)(3) 4.595.342042022513420c b b c c m h m L m h L m L m L m h m m h m h m h ⨯⨯=⨯⨯+⨯=⨯⨯⨯+⨯⨯=⨯=⨯-=⨯-⨯=-⨯==⨯-=⨯-⨯=-=⨯-=()2,113,11 3.913 3.9105.942022220420420225 3.91313 3.9105.9420420c c c m h m h m h h m h m h ⨯⨯-⨯=-=⨯-+⨯=⨯=⨯=⨯⨯=() (7)对自由度9V 施加单位加速度,并约束其他自由度,如图3.1.7所示。
