三年级奥数第十讲 简单的行程问题
三年级下册数学试题-奥数:行程问题—追及(练习含答案)全国通用
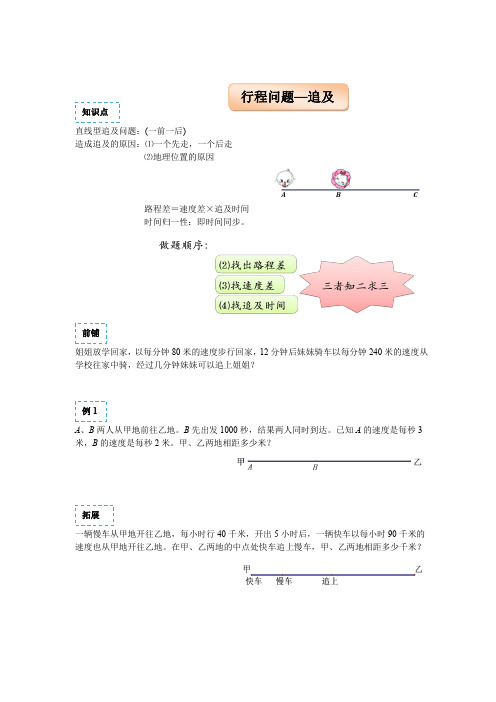
直线型追及问题:(一前一后)造成追及的原因:⑴一个先走,一个后走⑵地理位置的原因路程差=速度差×追及时间时间归一性:即时间同步。
姐姐放学回家,以每分钟80米的速度步行回家,12分钟后妹妹骑车以每分钟240米的速度从学校往家中骑,经过几分钟妹妹可以追上姐姐?A、B两人从甲地前往乙地。
B先出发1000秒,结果两人同时到达。
已知A的速度是每秒3米,B的速度是每秒2米。
甲、乙两地相距多少米?一辆慢车从甲地开往乙地,每小时行40千米,开出5小时后,一辆快车以每小时90千米的速度也从甲地开往乙地。
在甲、乙两地的中点处快车追上慢车,甲、乙两地相距多少千米?拓展例1前铺知识点行程问题—追及甲、乙二人练习跑步,若甲让乙先跑10米,则甲跑5秒钟可追上乙;若甲让乙先跑2秒钟,则甲跑4秒钟就能追上乙。
问:甲、乙二人的速度各是多少?兄弟两人骑自行车同时从学校出发回家。
哥哥每小时行15千米,弟弟每小时行10千米。
出发半个小时后哥哥因事返回学校,到学校后又耽搁了1小时,然后动身去追弟弟。
当哥哥追上弟弟时,距学校多少千米?两人在环形跑道中同时同地同向而行1.两个人每追及一次,路程差增加一个周长;反之,两个人路程差每增加一周,必定追及一次。
2.两个人每追及一次,每次所需要的时间均相等,即每次增加t。
幸福村小学有一条200米长的环形跑道,冬冬和晶晶同时从起跑线起跑,冬冬每秒钟跑6米,晶晶每秒钟跑4米,问冬冬第2次追上晶晶时两人各跑了多少圈?在周长为400米的圆形跑道的一条直径的两端,甲、乙两人分别以每秒6米和每秒4米的速例5例4知识点例3例2度骑自行车同时同向出发(顺时针)沿圆周行驶,经过多长时间,甲第二次追上乙?测试题1.甲、乙两地相距240千米,一列慢车从甲地出发,每小时行60千米.同时一列快车从乙地出发,每小时行90千米。
两车同向行驶,快车在慢车后面,经过多少小时快车可以追上慢车?A.6 B.8 C.10 D.122.小红和小蓝练习跑步,若小红让小蓝先跑20米,则小红跑5秒钟就可追上小蓝;若小红让小蓝先跑4秒钟,则小红跑6秒钟就能追上小蓝、小红、小蓝二人的速度各是多少?A.10,6 B.6,10 C.6,8 D.8,63.王芳和李华放学后,一起步行去体校参加排球训练,王芳每分钟走110米,李华每分钟走70米,出发5分钟后,王芳返回学校取运动服,在学校又耽误了2分钟,然后追赶李华。
小学奥数行程问题教案

小学奥数行程问题教案一、教学目标1. 让学生理解行程问题的基本概念,如行程、速度、时间等。
2. 培养学生解决行程问题的基本思路和方法。
3. 提高学生逻辑思维能力和解决问题的能力。
二、教学内容1. 行程问题的基本概念介绍。
2. 行程问题的解决步骤和方法讲解。
3. 典型行程问题案例分析。
三、教学重点与难点1. 教学重点:行程问题的基本概念,行程问题的解决步骤和方法。
2. 教学难点:行程问题的灵活应用和解决。
四、教学方法1. 采用讲解法,讲解行程问题的基本概念和解决方法。
2. 采用案例分析法,分析典型行程问题。
3. 采用互动教学法,引导学生积极参与,提高解决问题的能力。
五、教学准备1. 教学课件或黑板。
2. 典型行程问题案例。
3. 练习题。
教案内容:一、教学目标让学生理解行程问题的基本概念,如行程、速度、时间等。
培养学生解决行程问题的基本思路和方法。
提高学生逻辑思维能力和解决问题的能力。
二、教学内容1. 行程问题的基本概念介绍。
行程:物体在一段时间内所经过的路线长度。
速度:物体单位时间内所经过的路线长度。
时间:物体完成一段行程所需的时间。
2. 行程问题的解决步骤和方法讲解。
步骤一:明确行程问题中的已知量和未知量。
步骤二:根据已知量和未知量之间的关系,列出方程。
步骤三:解方程,求解未知量。
步骤四:检验解是否符合实际情况。
3. 典型行程问题案例分析。
案例一:一个人以60千米/小时的速度行驶,行驶了3小时,求他行驶的距离。
案例二:两辆火车相向而行,第一辆火车以40千米/小时的速度行驶,第二辆火车以50千米/小时的速度行驶,两火车相遇需要多长时间?三、教学重点与难点1. 教学重点:行程问题的基本概念,行程问题的解决步骤和方法。
2. 教学难点:行程问题的灵活应用和解决。
四、教学方法1. 采用讲解法,讲解行程问题的基本概念和解决方法。
2. 采用案例分析法,分析典型行程问题。
3. 采用互动教学法,引导学生积极参与,提高解决问题的能力。
奥数行程问题(含答案)

行程问题讨论有关物体运动的速度、时间、路程三者关系的应用题叫做行程应用题。
行程问题的主要数量关系是:路程=速度×时间如果用字母s表示路程,t表示时间,v表示速度,那么,上面的数量关系可用字母公式样表示为:s=vt。
行程问题内容丰富多彩、千变万化。
主要有一个物体的运动和两个或几物体的运动两大类。
两个或几个物体的运动又可以分为相遇问题、追及问题两类。
这一讲我们学习一个物体运动的问题的一些简单的相遇问题。
例题与方法例1.小明上学时坐车,回家时步行,在路上一共用了90分。
如果他往返都坐车,全部行程需30分。
如果他往返都步行,需多少分?(90-30÷2)×2=150例2.甲、乙两城相距280千米,一辆汽车原定用8小时从甲城开到乙城。
汽车行驶了一半路程,在中途停留30分。
如果汽车要按原定时间到达乙城,那么,在行驶后半段路程时,应比原来的时速加快多少?280÷2÷﹙8÷2-0.5﹚-280÷8=5例3.一列火车于下午1时30分从甲站开出,每小时行60千米。
1小时后,另一列火车以同样的速度从乙站开出,当天下午6时两车相遇。
甲、乙两站相距多少千米?6-1.5=4.5﹙60+60﹚×﹙4.5-1﹚+60=480例4.苏步青教授是我国著名的数学家。
一次出国访问,他在电车上碰到了一位外国数学家,这位外国数学家出了一道题目让苏步青做,题目是:甲、乙两人同时从两地出发,相向而行,距离是100千米。
甲每小时行6千米,乙每小时行4千米。
甲带着一只狗,狗每小时行10千米。
这只狗同甲一道出发,碰到乙的时候,它就掉头朝甲这边走,碰到甲时又往乙那边走,直到两人相遇。
这只狗一共走了多少千米?苏步青略加思索,就把正确答案告诉了这位外国数学家。
小朋友们,你能解答这道题吗?100÷(6+4)×10=100例5.甲、乙两辆汽车同时从东、西两地相向开出,甲车每小时行56千米,乙车每小时行48千米,两辆汽车在距中点32千米处相遇。
小升初奥数之基本行程问题老师用版本

戴氏教育中高考名校冲刺教育中心【我生命中最最最重要的朋友们,请你们认真听老师讲并且跟着老师的思维走。
学业的成功重在于考点的不断过滤,相信我赠予你们的是你们学业成功的过滤器。
谢谢使用!!!】小升初奥数之基本行程问题我们把研究路程、速度、时间以及这三者之间关系的一类问题,总称为行程问题.在三年级的学习中,我们已经接触过一些简单的行程应用题,行程问题主要涉及时间(t)、速度(v)和路程(s)这三个基本量,它们之间的关系如下:(1)速度×时间=路程可简记为:s=vt(2)路程÷速度=时间可简记为:t=s÷v(3)路程÷时间=速度可简记为:v=s÷t显然,知道其中的两个量就可以求出第三个量.关于平均速度的计算,需要知道整个过程的总路程与总时间,平均速度=总路程÷总时间【例1】摩托车驾驶员以每小时30千米的速度行驶了90千米到达某地,返回时每小时行驶45千米,求摩托车驾驶员往返全程的平均速度.分析:要求往返全程的平均速度是多少,必须知道摩托车“往”与“返”的总路程和“往”与“返”的总时间.摩托车“往”行了90千米,“返”也行了90千米,所以摩托车的总路程是:90×2=180(千米),摩托车“往”的速度是每小时30千米,所用时间是:90÷30=3(小时),摩托车“返”的速度是每小时45千米,所用时间是:90÷45=2(小时),往返共用时间是:3+2=5(小时),由此可求出往返的平均速度,列式为:90×2÷(90÷30+90÷45)=180÷5=36(千米/小时)练习1:胡老师骑自行车过一座桥,上桥速度为每小时12千米,下桥速度为每小时24千米,而且上桥与下桥所经过的路程相等,中间也没有停顿,问这个人骑车过这座桥的平均速度是多少?分析:题目中没有告诉我们总的路程,给计算带来不便,仔细想一想,只要上下桥路程相等,总路程是不影响平均速度的,我们自己设一个路程好了,不妨设为48千米,来回两段路,所以每段路程为:48÷2=24(千米),总时间是:24÷12+24÷24=3(小时),所以平均速度是:48÷3=16(千米/小时)【例2】有一座桥,过桥需要先上坡,再走一段平路,最后下坡,并且上坡、平路及下坡的路程相等.某人骑电动车过桥时,上坡、走平路和下坡的速度分别为11米/秒、22米/秒和33米/秒,求他过桥的平均速度.分析:假设上坡、平路及下坡的路程均为66米,(引导学生思考设为66的原因),那么总时间=66÷11+66÷22+66÷33=6+3+2=11(秒),过桥的平均速度=66×3÷11=18(米/秒).练习2:甲、乙两地相距6720米,某人从甲地步行去乙地,前一半时间平均每分钟行80米,后一半时间平均每分钟行60米.问他走后一半路程用了多少分钟?分析:(方法1)由于前一半时间与后一半时间的平均速度是已知的,因此可以计算出这人步行的时间.而如果了解清楚各段的路程、时间与速度,题目结果也就自然地被计算出来了.应指出,如果前一半时间平均速度为每分钟80米,后一半时间平均速度为每分钟60米,则这个人从甲走到乙的平均速度就为每分钟走(80+60)÷2=70米.这是因为一分钟80米,一分钟60米,两分钟一共140米,平均每分钟70米.而每分钟走80米的时间与每分钟走60米的时间相同,所以平均速度始终是每分钟70米.这样,就可以计算出这个人走完全程所需要的时间是6720÷70=96分钟.由于前一半时间的速度大于后一半时间的速度,所以前一半的时间所走路程大于6720÷2=3360米.则前一个3360米用了3360÷80=42分钟;后一半路程所需时间为96-42=54分钟.(方法2)设走一半路程时间是x分钟,则80x+60x=6720,解方程得:x=48分钟,因为80×48=3840(米),大于一半路程3360米,所以走前一半路程速度都是80米,时间是3360÷80=42(分钟),后一半路程时间是48+(48-42)=54(分钟).行程问题的两大方面:追及问题和相遇问题二、追及问题有两个人同时在行走,一个走得快,一个走得慢,当走得慢的在前,走得快的过了一些时间就能追上他.这就产生了“追及问题”.实质上,要算走得快的人在某一段时间内,比走得慢的人多走的距离,也就是要计算两人走的距离之差.如果设甲走得快,乙走得慢,在相同时间内,甲走的距离-乙走的距离= 甲的速度×时间-乙的速度×时间=(甲的速度-乙的速度)×时间.通常,“追及问题”要考虑速度差.【例3】龟、兔进行1000米的赛跑.小兔斜眼瞅瞅乌龟,心想:“我小兔每分钟能跑100米,而你乌龟每分钟只能跑10米,哪是我的对手.”比赛开始后,当小兔跑到全程的一半时,发现把乌龟甩得老远,便毫不介意地躺在旁边睡着了.当乌龟跑到距终点还有40米时,小兔醒了,拔腿就跑.请同学们解答两个问题:(1)它们谁胜利了?为什么?(2)胜者到终点时,另一个距终点还有几米?分析:(1)乌龟胜利了.因为兔子醒来时,乌龟离终点只有40米,乌龟需要40÷10=4(分钟)就能到达终点,而兔子离终点还有500米,需要500÷100=5(分钟)才能到达,所以乌龟胜利了.(2)乌龟跑到终点还要(40÷10)=4(分钟),而小兔跑到终点还要1000÷2÷100=5(分钟),慢1分钟.当胜利者乌龟跑到终点时,小兔离终点还有:100×1=100(米).练习3:小轿车的速度比面包车速度每小时快6千米,小轿车和面包车同时从学校开出,沿着同一路线行驶,小轿车比面包车早10分钟到达城门,当面包车到达城门时,小轿车已离城门9千米,问学校到城门的距离是多少千米?解:先计算,从学校开出,到面包车到达城门用了多少时间.此时,小轿车比面包车多走了9千米,而小轿车与面包车的速度差是6千米/小时,因此所用时间=9÷6=1.5(小时).小轿车比面包车早10分钟到达城门,面包车到达时,小轿车离城门9千米,说明小轿车的速度是面包车速度是54-6=48(千米/小时).城门离学校的距离是48×1.5=72(千米).答:学校到城门的距离是72千米.【例4】解放军某部开往边境,原计划需要行军18天,实际平均每天比原计划多行12千米,结果提前3天到达,这次共行军多少千米?分析:“提前3天到达”可知实际需要18-3=15天的时间,而“实际平均每天比原计划多行12千米”,则15天内总共比原来15天多行的路程为:12×15=180千米,这180千米正好填补了原来3天的行程,因此原来每天行程为180÷3=60千米,问题就能很容易求解.原来的速度为:(18-3)×12÷3=60(千米/天),因此总行程为:60×18=1080(千米)练习4:小张从家到公园,原打算每分种走50米.为了提早10分钟到,他把速度加快,每分钟走75米.问家到公园多远?解一:可以作为“追及问题”处理.假设另有一人,比小张早10分钟出发.考虑小张以75米/分钟速度去追赶,追上所需时间是50 ×10÷(75- 50)=20(分钟)〃因此,小张走的距离是75×20=1500(米).答:从家到公园的距离是1500米.【例5】一辆自行车在前面以固定的速度行进,有一辆汽车要去追赶.如果速度是30千米/小时,要1小时才能追上;如果速度是 35千米/小时,要 40分钟才能追上.问自行车的速度是多少?解一:自行车1小时走了30×1-已超前距离,自行车40分钟走了自行车多走20分钟,走了因此,自行车的速度是答:自行车速度是20千米/小时.解二:因为追上所需时间=追上距离÷速度差1小时与40分钟是3∶2.所以两者的速度差之比是2∶3.请看下面示意图:马上可看出前一速度差是15.自行车速度是35- 15=20(千米/小时).解二的想法与第二讲中年龄问题思路完全类同.这一解法的好处是,想清楚后,非常便于心算.练习5:上午8点8分,小明骑自行车从家里出发,8分钟后,爸爸骑摩托车去追他,在离家4千米的地方追上了他.然后爸爸发现忘带了东西又立即回家拿,拿到后又立刻回头去追小明,再追上小明的时候,离家恰好是8千米,这时是几点几分?解:画一张简单的示意图:图上可以看出,从爸爸第一次追上到第二次追上,小明走了8-4=4(千米).而爸爸骑的距离是4+8=12(千米).这就知道,爸爸骑摩托车的速度是小明骑自行车速度的12÷4=3(倍).按照这个倍数计算,小明骑8千米,爸爸可以骑行8×3=24(千米).但事实上,爸爸少用了8分钟,骑行了4+12=16(千米).少骑行24-16=8(千米).摩托车的速度是1千米/分,爸爸骑行16千米需要16分钟.8+8+16=32.答:这时是8点32分.下面讲“相遇问题”.小王从甲地到乙地,小张从乙地到甲地,两人在途中相遇,实质上是小王和小张一起走了甲、乙之间这段距离.如果两人同时出发,那么甲走的距离+乙走的距离=甲的速度×时间+乙的速度×时间=(甲的速度+乙的速度)×时间.“相遇问题”,常常要考虑两人的速度和.【例6】小张从甲地到乙地步行需要36分钟,小王骑自行车从乙地到甲地需要12分钟.他们同时出发,几分钟后两人相遇?解:走同样长的距离,小张花费的时间是小王花费时间的 36÷12=3(倍),因此自行车的速度是步行速度的3倍,也可以说,在同一时间内,小王骑车走的距离是小张步行走的距离的3倍.如果把甲地乙地之间的距离分成相等的4段,小王走了3段,小张走了1段,小张花费的时间是36÷(3+1)=9(分钟).【例7】小张从甲地到乙地,每小时步行5千米,小王从乙地到甲地,每小时步行4千米.两人同时出发,然后在离甲、乙两地的中点1千米的地方相遇,求甲、乙两地间的距离.解:画一张示意图离中点1千米的地方是A点,从图上可以看出,小张走了两地距离的一半多1千米,小王走了两地距离的一半少1千米.从出发到相遇,小张比小王多走了2千米小张比小王每小时多走(5-4)千米,从出发到相遇所用的时间是2÷(5-4)=2(小时).因此,甲、乙两地的距离是(5+4)×2=18(千米).本题表面的现象是“相遇”,实质上却要考虑“小张比小王多走多少?”岂不是有“追及”的特点吗?对小学的应用题,不要简单地说这是什么问题.重要的是抓住题目的本质,究竟考虑速度差,还是考虑速度和,要针对题目中的条件好好想一想.千万不要“两人面对面”就是“相遇”,“两人一前一后”就是“追及”.练习7、课后练习题1、一列火车通过530米的桥需40秒钟,以同样的速度穿过380米的山洞需30秒钟。
小学三年级数学行程问题应用题

【导语】⾏程问题是⼩学奥数中的⼀⼤基本问题。
⾏程问题有相遇问题、追及问题等近⼗种,是问题类型较多的题型之⼀。
⾏程问题包含多⼈⾏程、⼆次相遇、多次相遇、⽕车过桥、流⽔⾏船、环形跑道、钟⾯⾏程、⾛⾛停停、接送问题等。
以下是整理的《⼩学三年级数学⾏程问题应⽤题》相关资料,希望帮助到您。
【篇⼀】⼩学三年级数学⾏程问题应⽤题 1、甲⼄两列⽕车同时从相距700千⽶的'两地相向⽽⾏,甲列车每⼩时⾏85千⽶,⼄列车每⼩时⾏90千⽶,⼏⼩时两列⽕车相遇? 2、甲⼄两车从两地同时出发相向⽽⾏,甲车每⼩时⾏40千⽶,⼄车每⼩时⾏60千⽶,经过3⼩时相遇。
两地相距多少千⽶? 3、甲⼄两艘轮船从相距654千⽶的两地相对开出,8⼩时两船还相距22千⽶。
已知⼄船每⼩时⾏42千⽶,甲船每⼩时⾏多少千⽶? 4、甲⼄两艘轮船同时从相距126千⽶的两个码头相对开出,3⼩时相遇,甲船每⼩时航⾏22千⽶,⼄船每⼩时航⾏多少千⽶? 5、甲、⼄两车同时从相距480千⽶的两地相对⽽⾏,甲车每⼩时⾏45千⽶,途中因汽车故障甲车停了1⼩时,5⼩时后两车相遇。
⼄车每⼩时⾏多少千⽶? 6、甲、⼄两地相距280千⽶,⼀辆汽车和⼀辆拖拉机同时分别从两地相对开出,经过4⼩时两车相遇。
已知汽车的速度是拖拉机速度的4倍,相遇时,汽车⽐拖拉机多⾏多少千⽶? 7、甲、⼄两车同时从相距960千⽶的A、B两地相向开出,8⼩时后相遇。
已知甲车每⼩时⽐⼄车快4千⽶,求甲车的速度是多少?相遇时⼄车⾏驶了多少千⽶? 8、某零件加⼯⼚要加⼯零件1200个。
第⼀车间每天能加⼯190个,⽐⼆车间每天少加⼯20个。
现在两个车间共同加⼯这批零件,要加⼯多少天?完成时每个车间各加⼯了多少个? 9、⾃⾏车商店要装配2380辆⾃⾏车,甲组每天装配120辆,⼄组每天装配140辆。
两个组共同装配7天后,由⼄组单独装配。
⼄组还要多少天才能完成任务? 10、甲⼄两列⽕车同时从A、B两地相对开出,甲车每⼩时⾏90千⽶,⼄车每⼩时⾏84千⽶,相遇时甲车⽐⼄车多⾏了78千⽶,A、B两地相距多少千⽶?【篇⼆】⼩学三年级数学⾏程问题应⽤题 1、⽺跑5步的时间马跑3步,马跑4步的距离⽺跑7步,现在⽺已跑出30⽶,马开始追它。
完整)三年级奥数行程问题

完整)三年级奥数行程问题教师讲义:日期:_________ 星期:_________ 时段:_________ 学生签字:_________课题:熟练掌握解题技巧研究目标:掌握解题技巧,提高解题能力研究重点:解题方法和技巧研究方法:启发式教学行程问题:无研究内容与过程:例题1:两车同时从相距860千米的两地出发,汽车每小时行45千米,摩托车每小时行70千米。
6小时后两车相距多少千米?例题2:一列火车长120米,以每秒20米的速度穿过长200米的隧道,从车头进入隧道到车尾离开隧道共需多少秒?例题3:甲、乙两个车队同时从相隔330千米的两地相向而行,甲队每小时行60千米,乙队每小时行50千米,一个人骑摩托车以每小时行80千米的速度在两个车队间不断地往返联络,两车队相遇时,摩托车行驶了多少千米?改写后的教师讲义:日期:_________ 星期:_________ 时段:_________ 学生签字:_________课题:熟练掌握解题技巧研究目标:本课程旨在帮助学生掌握解题技巧,提高解题能力。
研究重点:本课程的重点是解题方法和技巧。
研究方法:本课程采用启发式教学方法,帮助学生更好地理解和掌握解题技巧。
行程问题:本课程无行程问题。
研究内容与过程:例题1:两车同时从相距860千米的两地出发,汽车每小时行45千米,摩托车每小时行70千米。
6小时后两车相距多少千米?例题2:一列火车长120米,以每秒20米的速度穿过长200米的隧道,从车头进入隧道到车尾离开隧道共需多少秒?例题3:甲、乙两个车队同时从相隔330千米的两地相向而行,甲队每小时行60千米,乙队每小时行50千米,一个人骑摩托车以每小时行80千米的速度在两个车队间不断地往返联络,两车队相遇时,摩托车行驶了多少千米?1、甲乙相向而行,第一次相遇在C处,求A、C之间的距离。
甲每分钟行50米,乙每分钟行70米。
根据速度公式,两人相向而行的速度之和为120米/分钟。
小学奥数---行程问题

行程问题教学目标:1、理解行程的基本概念,会解一些简单的行程题.2、掌握单个变量的平均速度问题及其三种基本解题方法:“特殊值法”、“设而不求法”、“设单位1法”3、利用对比分析法解终(中)点问题知识点讲解:一、路程s、速度v、时间t三者的基本关系我们经常在解决行程问题的过程中用到s、v、t三个字母,并用它们来分别代表路程、速度和时间。
速度×时间=路程可简记为:s vt=路程÷速度=时间可简记为:t s v=÷路程÷时间=速度可简记为:v s t=÷二、平均速度平均速度的基本关系式为:平均速度=总路程÷总时间;总时间=总路程÷平均速度;总路程=平均速度⨯总时间。
题型一、简单行程公式解题1、韩雪的家距离学校480米,原计划7点40从家出发8点可到校,现在还是按原时间离开家,不过每分钟比原来多走16米,那么韩雪几点就可到校?2、小白从家骑车去学校,每小时15千米,用时2小时,回来以每小时10千米的速度行驶,需要多少时间?【考点】行程问题【难度】2星【题型】解答3、甲、乙两地相距100千米。
下午3点,一辆马车从甲地出发前往乙地,每小时走10千米;晚上9点,一辆汽车从甲地出发驶向乙地,为了使汽车不比马车晚到达乙地,汽车每小时最少要行驶多少千米?.4、两辆汽车都从北京出发到某地,货车每小时行60千米,15小时可到达。
客车每小时行50千米,如果客车想与货车同时到达某地,它要比货车提前开出几小时?5、一天,梨和桃约好在天安门见面,梨每小时走200千米,桃每小时走150千米,他们同时出发2小时后还相距500千米,则梨和桃之间的距离是多少千米?6、两列火车从相距480千米的两城相向而行,甲列车每小时行40千米,乙列车每小时行42千米,5小时后,甲、乙两车还相距多少千米?7、甲、乙两辆汽车分别从 A、B 两地出发相向而行,甲车先行三小时后乙车从B 地出发,乙车出发5 小时后两车还相距15千米.甲车每小时行 48千米,乙车每小时行 50千米.求 A、 B 两地间相距多少千米?8、小燕上学时骑车,回家时步行,路上共用50分。
小学奥数 行程问题之接送问题 完整版例题讲解 后面带详细解析

接送问题知识精讲一、校车问题——行走过程描述队伍多,校车少,校车来回接送,队伍不断步行和坐车,最终同时到达目的地,即到达目的地的最短时间,不要求证明。
二、常见接送问题类型根据校车速度(来回不同)、班级速度(不同班不同速)、班数是否变化分类为四种常见题型:(1)车速不变-班速不变-班数2个(最常见)(2)车速不变-班速不变-班数多个(3)车速不变-班速变-班数2个(4)车速变-班速不变-班数2个三、标准解法:画图+列3个式子1、总时间=一个队伍坐车的时间+这个队伍步行的时间;2、班车走的总路程;3、一个队伍步行的时间=班车同时出发后回来接它的时间。
模块一、汽车接送问题——接一个人【例1】某校和某工厂之间有一条公路,该校下午2时派车去该厂接某劳模来做报告,往返需用1小时.这位劳模在下午1时便离厂步行向学校走来,途中遇到接他的汽车,便立刻上车驶向学校,在下午2时40分到达.问:汽车速度是劳模步行速度的几倍?【巩固1】张工程师每天早上8点准时被司机从家接到厂里。
一天,张工程师早上7点就出了门,开始步行去厂里,在路上遇到了接他的汽车,于是,他就上车行完了剩下的路程,到厂时提前20分钟。
这天,张工程师还是早上7点出门,但15分钟后他发现有东西没有带,于是回家去取,再出门后在路上遇到了接他的汽车,那么这次他比平常要提前分钟到厂。
模块二、汽车接送问题——接两个人或多人【例1】A、B两个连队同时分别从两个营地出发前往一个目的地进行演习,A连有卡车可以装载正好一个连的人员,为了让两个连队的士兵同时尽快到达目的地,A连士兵坐车出发一定时间后下车让卡车回去接B连的士兵,两营的士兵恰好同时到达目的地,已知营地与目的地之间的距离为32千米,士兵行军速度为8千米/小时,卡车行驶速度为40千米每小时,求两营士兵到达目的地一共要多少时间?【巩固1】甲班与乙班学生同时从学校出发去公园,两班的步行速度相等都是4千米/小时,学校有一辆汽车,它的速度是每小时48千米,这辆汽车恰好能坐一个班的学生.为了使两班学生在最短时间内到达公园,设两地相距150千米,那么各个班的步行距离是多少?【例2】甲、乙、丙三个班的学生一起去郊外活动,他们租了一辆大巴,但大巴只够一个班的学生坐,于是他们计划先让甲班的学生步行,乙丙两班的学生步行,甲班学生搭乘大巴一段路后,下车步行,然后大巴车回头去接乙班学生,并追赶上步行的甲班学生,再回头载上丙班学生后一直驶到终点,此时甲、乙两班也恰好赶到终点,已知学生步行的速度为5千米/小时,大巴车的行驶速度为55千米/小时,出发地到终点之间的距离为8千米,求这些学生到达终点一共所花的时间.【例3】海淀区劳动技术学校有100名学生到离学校33千米的郊区参加采摘活动,学校只有一辆限乘25人的中型面包车.为了让全体学生尽快地到达目的地.决定采取步行与乘车相结合的办法.已知学生步行的速度是每小时5千米,汽车行驶的速度是每小时55千米.请你设计一个方案,使全体学生都能到达目的地的最短时间是多少小时?1份【例4】甲、乙两班学生到离校39千米的博物馆参观,但只有一辆汽车,一次只能乘坐一个班的学生.为了尽快到达博物馆,两个班商定,由甲班先坐车,乙班先步行,同时出发,甲班学生在途中某地下车后步行去博物馆,汽车则从某地立即返回去接在途中步行的乙班学生.如果甲、乙两班学生步行速度相同,汽车速度是他们步行速度的10倍,那么汽车应在距博物馆多少千米处返回接乙班学生,才能使两班同时到达博物馆?A B C D【例5】甲、乙两班学生到离校24千米的飞机场参观,但只有一辆汽车,一次只能乘坐一个班的学生.为了尽快到达飞机场,两个班商定,由甲班先坐车,乙班先步行,同时出发,甲班学生在途中某地下车后步行去飞机场,汽车则从某地立即返回接在途中步行的乙班学生.如果甲、乙两班学生步行速度相同,汽车速度是他们步行速度的7倍,那么汽车应在距飞机场多少千米处返回接乙班学生,才能使两班同时到达飞机场?【例6】A、B两地相距22.4千米.有一支游行队伍从A出发,向B匀速前进;当游行队伍队尾离开A 时,甲、乙两人分别从A、B两地同时出发.乙向A步行;甲骑车先追向队头,追上队头后又立即骑向队尾,到达队尾后再立即追向队头,追上队头后又立即骑向队尾……当甲第5次追上队头时恰与乙相遇在距B地5.6千米处;当甲第7次追上队头时,甲恰好第一次到达B地,那么此时乙距A地还有__________千米.【例7】甲班与乙班学生同时从学校出发去公园,甲班步行的速度是每小时4千米,乙班步行的速度是每小时3千米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三年级数学提升班
学生姓名:
第十讲:简单的行程问题
所谓大师,就是这样的人:他们用自己的眼睛去看别人见过的东西,在别人司空见惯的东西上能够发现出美来。
——奥古斯特·罗丹知识纵横
行程问题包括相遇问题、追及问题、火车过桥等,这类问题思维灵活性大,辐射面广,但依据都只有一个,必须掌握速度、时间和路程之间的数量关系,这三个量间的关系可以用下列等式表示出来:
路程=时间×速度
速度=路程÷时间
时间=路程÷速度
例题求解
【例1】甲、乙二人同地同方向出发,甲每小时走7千米,乙每小时走5千米,乙先走2小时后,甲才开始走,甲追上乙需要几小时?
【例2】一辆公共汽车和一辆小轿车同时从相距200千米的两地相向而行,公共汽车每小时行20千米,小轿车每小时行30千米,问几小时后两车相遇?
【例3】小伟和小明从学校到电影院看电影,小伟以每分钟60米的速度向影院走去,5分钟后,小明以每分钟80米的速度向影院走去,结果两人同时到达影
院学校到电影院的路程是多少米?
【例4】小聪和小刚从学校到相距2400米的电影院去看电影,小聪每分钟行60米,他出发8分钟后,小刚才出发,结果两人同时到达电影院,小刚每分钟行多少米?
【例5】一辆汽车从甲地开往乙地,每小时行40千米,开出5小时候,一列火车以每小时行90千米的速度也从甲地开往乙地,在甲、乙两地的中点处火车追上汽车,甲、乙两地相距多少千米?
【例6】一列火车长150米,每秒行60米,问全车通过450米长的大桥,需要行多少时间?
学力训练
1.一架飞机每分钟行18千米,一天从机场起飞,航行半小时到达A地执行救灾任务,机场与A地之间的路程是多少千米?
2.早晨8时一辆汽车从甲地开往乙地,每小时行80千米,下午1时到达乙地,甲、乙两地的路程是多少?
3.一天小红到学校参加合唱,每分钟行50米,行了2分钟后发现歌谱未带,转身回家去拿,前后一共用了20分钟才到学校,小红家到学校的路程是多少米?
4.良马每天行120千米,劣马每天行75千米,劣马先行12天,良马几天可以追上劣马?
5.小智和小慧从学校到森林公园春游,小智步行,每小时走5千米,他出发后4小时,小慧骑自行车,每小时行15千米,小慧追上小智时,正好到达森林公园,学校离森林公园有多少千米?
6.汽车上坡每小时行6千米,从原路返回下坡每小时行12千米,上、下坡平均每小时行多少千米?
家长签字:。
