三角形折叠问题中的角度运算
折叠问题中的角度运算

专题7:折叠问题中的角度运算1如图,将矩形ABCD沿AE折叠,若∠BAD′=30°,则∠AED′=2如图将六边形ABCDEF沿着直线GH折叠,使点A、B落在六边形CDEFGH的内部,则∠1+∠2=3如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=4已知△ABC是一张三角形的纸片.(1)如图①,沿DE折叠,使点A落在边AC上点A′的位置,∠DA′E与∠1的之间存在怎样的数量关系?为什么?(2)如图②所示,沿DE折叠,使点A落在四边形BCED的内部点A′的位置,∠A、∠1与∠2之间存在怎样的数量关系?为什么?(3)如图③,沿DE折叠,使点A落在四边形BCED的外部点A′的位置,∠A、∠1与∠2之间存在怎样的数量关系?为什么?5 65已知,如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的内部时,则∠A与∠1+∠2之间有一种数量关系:2∠A=∠1+∠2始终保持不变,为什么?.6如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,(1)设∠AED的度数为x,∠ADE的度数为y,那么∠1、∠2的度数分别是多少?(用含有x或y的代数式表示)(2)∠A与∠1+∠2之间有一种数量关系始终保持不变,请找出这个规律,并说明理由.折一折,想一想,如图所示,在△ABC中,将纸片一角折叠,使点C落在△ABC内一点C′上,若∠1=40°,∠2=30°(1)求∠C的度数;(2)试通过第(1)问,直接写出∠1、∠2、∠C三者之间的关系.如图(1),△ABC是一个三角形的纸片,点D、E分别是△ABC边上的两点;研究(1):若沿直线DE折叠,则∠BDA′与∠A的关系是∠BDA′=2∠A;研究(2):若折成图2的形状,猜想∠BDA′,∠CEA′和∠A关系,并说明理由;研究(3):若折成图3的形状,猜想∠BDA′,∠CEA′和∠A的关系,并说明理由.图1、图2、7如图①,把△ABC纸片沿DE折叠,使点A落在四边形BCED内部点A′的位置,通过计算我们知道:2∠A=∠1+∠2.请你继续探索:(1)如果把△ABC纸片沿DE折叠,使点A落在四边形BCED的外部点A′的位置,如图②,此时∠A与∠1、∠2之间存在什么样的关系?为什么?请说明理由.(2)如果把四边形ABCD沿EF折叠,使点A、D落在四边形BCFE的内部A′、D′的位置,如图③,你能求出∠A、∠D、∠1与∠2之间的关系吗?(直接写出关系式即可)8三角形纸片ABC中,∠A=55°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内(如图),则∠1+∠2的度数为度.9如图,已知四边形ABCD,∠C=72°,∠D=81°.沿EF折叠四边形,使点A、B分别落在四边形内部的点A′、B′处,求∠1+∠2的大小.10、如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=22°,则∠BDC等于()11、将五边形纸片ABCDE按如图方式折叠,折痕为AF,点E、D分别落在E′、D′,已知∠AFC=76°,则∠CFD′等于12如图,在平面内,把矩形ABCD沿EF对折,若∠1=50°,则∠AEF等于13如图,把△ABC沿线段DE折叠,使点A落在点F处,BC∥DE;若∠B=50°,则∠BDF的度数为1 1如图,把一张长方形纸片ABCD,沿EF折叠后,ED′与BC的交点为G,点D,C分别落在D′,C′的位置上.若∠EFG=55°,则∠1等于14将一条两边沿互相平行的纸带按如图折叠.设∠1=x°,则∠α的度数为()15将长方形ABCD沿折痕EF折叠,使CD落在GH的位置,若∠FGH=55°,则∠HEF=()16如图,一个宽度相等的纸条按如图所示方法折叠一下,则∠1=()17如图,D、E分别为△ABC的边AB、AC上的点,DE∥BC,将△ABC沿线段DE折叠,使点A落在BC上的点F处,若∠B=55°,则∠BDF的度数为()18如图所示,将一张长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置上,ED′的延长线与BC的交点为G.若∠EFG=80°,则∠BFC′的度数为()19如图a是长方形纸带,∠DEF=24°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数()20如图,三角形纸片ABC,AB=10cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E 处,折痕为BD,则△AED的周长为()21如图,将长方形ABCD沿对角线BD折叠,使点C恰好落在如图C′的位置,若∠DBC=15°,则∠ABC′=()22一张长方形纸条折成如图的形状,如果∠1=130°,∠2=()23如图:将一张长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,ED′的延长线与BC交于点G.若∠EFG=55°,则∠1=()24如图,已知长方形ABCD,我们按如下步骤操作可以得到一个特定角:(1)以点A所在直线为折痕,折叠纸片,使点B落在AD上,折痕与BC交于E;(2)将纸片展平后,再一次折叠纸片,以E所在直线为折痕,使点A落在BC上,折痕EF交AD于F,则∠AEF的度数25如图,将纸片△ABC沿着DE折叠压平,且∠1+∠2=72°,则∠A=()26如图,把△ABC纸片沿DE折叠,当点A落在四边形BCED的外部时,则∠A与∠1和∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是()27如图,三角形纸片ABC,AB=10cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E 处,折痕为BD,则△AED的周长为()28一个宽度相等纸条,按如图所示的方式折叠一下,已知∠3=120°,则∠1的度数为()29如图,把一张长方形纸条折叠后,若∠AOB′=70°,则∠OGC的度数为()30如图,∠A=60°,∠B=70°,将纸片的一角折叠,使点C落在△ABC内,若∠2=80°,则∠1的度数为()31如图(1)是长方形纸带,∠DEF=α,将纸带沿EF折叠成图(2),再沿BF折叠成图(3),则图(3)中的∠CFE 的度数是()32如图,生活中,将一个宽度相等的纸条按右图所示折叠一下,如果∠1=140°,那么∠2的度数为()33如图,四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B =()34如图,一张长方形纸条沿AB折叠,如果∠1=124°,那么∠2的度数是()35如图,把长方形ABCD沿EF对折后使两部分重合,若∠AEF=110°,则∠1=()36如图,一张三角形纸片△ABC,沿DE折叠使得顶点C落在边AB上,若DE∥AB,∠A=45°,则∠ADC的度数是()37如图所示,把一个三角形纸片ABC顶角向内折叠3次之后,3个顶点不重合,那么图中∠1+∠2+∠3+∠4+∠5+∠6的度数和是()38如图,将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处,则∠1+∠2的度数为()39如图,正方形纸片ABCD的边长为8,将其沿EF折叠,则图中①②③④四个三角形的周长之和为()40如图,将五边形ABCDE沿AE对折到如图的位置,其中∠AEC=72°,则∠CED′=()41如图,在△ABC中,∠A=35°,在平面内沿直线DE将△ABC折叠后,量得∠BDA′=110°,那么∠CEA′的度数为()42如图,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB=65°,则∠AED′等于()43如图,已知△ABC中,∠BAC=140°,现将△ABC进行折叠,使顶点B、C均与顶点A重合,求∠DAE的度数.。
初一数学第二学期名校优选小专题06 三角形折叠中的角度问题

初一数学第二学期名校优选小专题06 三角形折叠中的角度问题 【例题讲解】【原题再现】有这样一道题:如图1,将ABC ∆纸片沿DE 折叠,使点A 落在四边形BCDE 内点A '的位置.试探索A ∠与12∠+∠之间的数量关系,并说明理由.(1)小明提出一种正确的解题思路:连接AA ',则么1∠、2∠分别为AEA '∆、ADA '∆的外角,…… 请你按照小明的思路解决上述问题.(2)【变式探究】如图2,若将原题中“点A 落在四边形BCDE 内点A '的位置”变为“点A 落在四边形BCDE 外点A '的位置”,试猜想此时A ∠与1∠、2∠之间的数量关系,并说明理由.(3)【结论运用】将四边形纸片(90ABCD C ∠=︒,AB 与CD 不平行)沿EF 折叠成图3的形状,若1110∠=︒,240∠=︒,直接写出ABC ∠的度数.解:(1)图1中,结论:2∠BAC =∠1+∠2, 理由是:连接AA ′. ∵沿DE 折叠A 和A ′重合,∴∠DAE =∠DA ′E ,∠EA ′A =∠EAA ′,∠DA ′A =∠DAA ′, ∵∠1=∠EA ′A +∠EAA ′,∠2=∠DA ′A +∠DAA ′, ∴∠1+∠2=∠EA ′A +∠EAA ′+∠DA ′A +∠DAA ′=2∠BAC ; (2)如图2,结论:2∠A =∠1-∠2. 理由:设EA ′交AC 于J .∵∠1=∠EJA +∠A ,∠EJA =∠A ′+∠2, ∴∠1=∠A ′+∠A +∠2=2∠A +∠2, ∴2∠A =∠1-∠2; (2)如图,根据折叠知:∠AEF =∠A EF ',∠EFD =∠'EFD ,AEA'=∠AEF=180°-110°=70°,∵∠1=110°,∴∠2∴∠AEF=35°,∵∠2=40°,∴2∠EFD=180°+∠2=220°,∴∠EFD=110°,∴∠A+∠D=360°-(∠AEF+∠EFD)= 215°,∴∠B=360°-(∠A+∠D)-∠C = 55°.【综合演练】1.如图,在△ABC中,点D是BC上的点,将△ABD沿着AD翻折得到△AED,若∠B=∠BAE=50°,则∠CDE的度数是()A.25°B.30°C.35°D.40°2.如图,△ABC中∠A=40°,E是AC边上的点,先将△ABE沿着BE翻折,翻折后△ABE的AB边交AC 于点D,又将△BCD沿着BD翻折,点C恰好落在BE上的点G处,此时∠BDC=82°,则原三角形的∠B 的度数为()A.57°B.60°C.63°D.70°3.将△ABC纸片沿DE按如图的方式折叠.若∠C=50°,∠1=85°,则∠2的度数等于()A.10°B.15°C.20°D.25°4.如图,将三角形纸片ABC沿DE折叠,当点A落在四边形BCDE的外部时,测量得∠1=70°,∠2=152°,则∠A 为( )A .40°B .42°C .30°D .52°第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题(共0分)5.如图,三角形纸片ABC 中,70A ∠=︒,75B ∠=︒.将三角形纸片的一角折叠,使点C 落在ABC 内,那么12∠+∠=_____________︒.6.在△ABC 中,点E 、F 分别为边AB 、AC 上的点,把△ABC 沿EF 翻折,翻折后的图形如图所示.若1+2110∠∠=︒,则A ∠的度数为___________.7.如图,把一张长方形纸片ABCD 沿EF 折叠,∠1=55°,则∠2=________°.8.将△ABC 纸片沿DE 按如图的方式折叠.若∠C =50°,∠1=85°,则∠2等于______.三、解答题(共0分)9.如图,将ABC纸片沿DE折叠,使点A落在四边形BCDE内点'A的位置,∠+∠之间的数量关系,并说明理由.(1)探索A∠与12(2)如果点A落在四边形BCDE外点''A的位置,A∠与1∠之间的数量关系有何变化,请说明理由.∠、210.在我们苏科版义务教育教科书数学七下第42页曾经研究过双内角平分线的夹角和内外角平分线夹角问题.聪聪在研究完上面的问题后,对这类问题进行了深入的研究,他的研究过程如下:(1)【问题再现】如图1,在△ABC中,∠ABC、∠ACB的角平分线交于点P,若∠A=50°.则∠P=_______;(2)【问题推广】如图2,在△ABC中,∠BAC的角平分线与△ABC的外角∠CBM的角平分线交于点P,过点B作BH⊥AP 于点H,若∠ACB=80°,求∠PBH的度数.(3)如图3,在△ABC中,∠ABC、∠ACB的角平分线交于点P,将△ABC沿DE折叠使得点A与点P重合,若∠1+∠2=100°,则∠BPC=_______;(4)【拓展提升】在四边形BCDE中,EB∥CD,点F在直线ED上运动(点F不与E,D两点重合),连接BF,CF,∠EBF、∠DCF 的角平分线交于点Q ,若∠EBF =α,∠DCF =β,直接写出∠Q 和α,β之间的数量关系. 11.如图,将一张三角形纸片ABC 的一角折叠,使得点A 落在四边形BCDE 的外部A '的位置且A '与点C 在直线AB 的异侧,折痕为DE ,已知90C ∠=︒,30A ∠=︒.(1)求12∠-∠的度数;(2)若保持A DE '的一边与BC 平行,求ADE ∠的度数.12.将ABC 纸片的一角CAB ∠折叠,使点A 落在点P 的位置,折痕为DE . (1)如图1,点A 落在ABC 内的点P 的位置.①若//PE AC ,那么PD 与AB 有怎样的位置关系,请说明理由; ②如图2,1∠、2∠与A ∠之间有怎样的数量关系?并说明理由;③连接CP 、BP ,已知CP 、BP 恰好分别平分ACB ∠、ABC ∠(如图3),1∠、2∠与CPB ∠之间有怎样的数量关系,并说明理由;(2)如图4,点A 落在ABC 外的点P 的位置.连接CP 、BP ,如果CP 、BP 恰好分别平分ABC 的两个外角MCB ∠,NBC ∠,那么1∠、2∠与CPB ∠之间的数量关系是______.(请直接写出结果)13.问题1:现有一张△ABC 纸片,点D 、E 分别是△ABC 边上两点,若沿直线DE 折叠. (1)探究1:如果折成图①的形状,使A 点落在CE 上,则∠1与∠A 的数量关系是 ; (2)探究2:如果折成图②的形状,猜想∠1+∠2和∠A 的数量关系是 ; (3)探究3:如果折成图③的形状,猜想∠1、∠2和∠A 的数量关系,并说明理由.(4)问题2:将问题1推广,如图④,将四边形ABCD 纸片沿EF 折叠,使点A 、B 落在四边形EFCD 的内部时,∠1+∠2与∠A 、∠B 之间的数量关系是 .14.在△ABC 中,∠BAC =90°,点D 是BC 上一点,将△ABD 沿AD 翻折后得到△AED ,边AE 交射线BC 于点F .(友情提醒:翻折前后的两个三角形的对应边相等,对应角相等.)(1)如图①,当AE ⊥BC 时,求证:DE ∥AC . (2)若10C B ∠-∠=︒,∠BAD =x° . ①如图②,当DE ⊥BC 时,求x 的值;②是否存在这样的x 的值,使得△DEF 中有两个角相等.若存在,并求x 的值;若不存在,请说明理由. 15.在△ABC 中,∠BAC =90°,点D 是BC 上一点,将△ABD 沿AD 翻折后得到△AED ,边AE 交BC 于点F .(1)如图①,当AE ⊥BC 时,写出图中所有与∠B 相等的角: ;所有与∠C 相等的角: .(2)若∠C -∠B =50°,∠BAD =x °(0<x ≤45) . ① 求∠B 的度数;②是否存在这样的x 的值,使得△DEF 中有两个角相等.若存在,并求x 的值;若不存在,请说明理由. 16.如图1,将△ABC 纸片沿DE 折叠,使点C 落在四边形ABDE 内点C ’的位置, (1)①若00120,250∠=∠=,则C ∠= ; ②若042C ∠=,则12∠+∠= ;③探索C ∠ 、1∠与2∠之间的数量关系,并说明理由; (2)直接按照所得结论,填空:①如图中,将△ABC 纸片再沿FG 、MN 折叠,使点A 、B 分别落在△ABC 内点A ’、B ’的位置,则123456∠+∠+∠+∠+∠+∠= ;②如图中,将四边形ABCD 按照上面方式折叠,则128∠+∠++∠= ; ③若将n 边形123n A A A A 也按照上面方式折叠,则122n ∠+∠++∠= ;(3)如图,将△ABC 纸片沿DE 折叠,使点C 落在△ABC 边AC 上方点'C 的位置, 探索C ∠、1∠与2∠之间的数量关系,并说明理由.17.直线MN 与直线PQ 垂直相交于O ,点A 在射线OP 上运动,点B 在射线OM 上运动,连接AB, (1)如图,已知AC 、BC 分别是∠BAP 和∠ABM 角的平分线,①点A 、B 在运动的过程中,∠ACB 的大小是否发生变化?若发生变化,请说明理由;若不发生变化,试求出∠ACB 的大小.②如图,将△ABC 沿直线AB 折叠,若点C 落在直线PQ 上,记作点C′,则∠ABO = °;如图,将△ABC 沿直线AB 折叠,若点C 落在直线MN 上,记作点C′′,则∠ABO = °.(2)如图,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及其延长线交于E、F,在△AEF中,如果有一个角是另一个角的32倍,求∠ABO的度数.答案与解析【例题讲解】【原题再现】有这样一道题:如图1,将ABC ∆纸片沿DE 折叠,使点A 落在四边形BCDE 内点A '的位置.试探索A ∠与12∠+∠之间的数量关系,并说明理由.(1)小明提出一种正确的解题思路:连接AA ',则么1∠、2∠分别为AEA '∆、ADA '∆的外角,…… 请你按照小明的思路解决上述问题.(2)【变式探究】如图2,若将原题中“点A 落在四边形BCDE 内点A '的位置”变为“点A 落在四边形BCDE 外点A '的位置”,试猜想此时A ∠与1∠、2∠之间的数量关系,并说明理由.(3)【结论运用】将四边形纸片(90ABCD C ∠=︒,AB 与CD 不平行)沿EF 折叠成图3的形状,若1110∠=︒,240∠=︒,直接写出ABC ∠的度数.解:(1)图1中,结论:2∠BAC =∠1+∠2, 理由是:连接AA ′. ∵沿DE 折叠A 和A ′重合,∴∠DAE =∠DA ′E ,∠EA ′A =∠EAA ′,∠DA ′A =∠DAA ′, ∵∠1=∠EA ′A +∠EAA ′,∠2=∠DA ′A +∠DAA ′, ∴∠1+∠2=∠EA ′A +∠EAA ′+∠DA ′A +∠DAA ′=2∠BAC ; (2)如图2,结论:2∠A =∠1-∠2. 理由:设EA ′交AC 于J .∵∠1=∠EJA +∠A ,∠EJA =∠A ′+∠2, ∴∠1=∠A ′+∠A +∠2=2∠A +∠2, ∴2∠A =∠1-∠2; (2)如图,根据折叠知:∠AEF =∠A EF ',∠EFD =∠'EFD ,AEA'=∠AEF=180°-110°=70°,∵∠1=110°,∴∠2∴∠AEF=35°,∵∠2=40°,∴2∠EFD=180°+∠2=220°,∴∠EFD=110°,∴∠A+∠D=360°-(∠AEF+∠EFD)= 215°,∴∠B=360°-(∠A+∠D)-∠C = 55°.【综合演练】1.如图,在△ABC中,点D是BC上的点,将△ABD沿着AD翻折得到△AED,若∠B=∠BAE=50°,则∠CDE的度数是()A.25°B.30°C.35°D.40°【答案】B【分析】根据翻折的性质得到∠BAD=∠EAD=25°,∠E=∠B=50°,根据三角形内角和定理推出∠ADE=∠ADB=105°,进一步计算即可解答.【解析】解:∵∠B=∠BAE=50°,将△ABD沿着AD翻折得到△AED,∴∠BAD=∠EAD=25°,∠E=∠B=50°,∴∠ADE=∠ADB=180°-50°-25°=105°,∴∠ADC=180°-∠ADB=75°,∴∠CDE=105°-75°=30°,故选:B.【点评】此题考查翻折的性质,三角形内角和定理,关键是掌握翻折的性质.2.如图,△ABC中∠A=40°,E是AC边上的点,先将△ABE沿着BE翻折,翻折后△ABE的AB边交AC 于点D,又将△BCD沿着BD翻折,点C恰好落在BE上的点G处,此时∠BDC=82°,则原三角形的∠B 的度数为()A .57°B .60°C .63°D .70°【答案】C【分析】根据折叠的性质可知:∠BDG =∠BDC =82°,∠ABE =∠A 'BE =∠A 'BG=∠A 'BC ,根据三角形外角性质可得:∠DBA =∠BDC ﹣∠A =82°﹣40°=42°,进一步可求出∠ABE =∠A 'BE =21°,∠ABC =3×21°=63°,即原三角形的∠B =63°.【解析】解:由折叠性质可得,∠BDG =∠BDC =82°,∠ABE =∠A 'BE =∠A 'BG=∠A 'BC , ∵∠BDC 是△BDA 的外角,∴∠DBA =∠BDC ﹣∠A =82°﹣40°=42°, ∴∠ABE =∠A 'BE =21°,∴∠ABC =3×21°=63°,即原三角形的∠B =63°, 故选:C .【点评】此题主要考查的是图形的折叠及三角形外角性质,能够根据折叠的性质发现∠BDG =∠BDC =82°,∠ABE =∠A 'BE =∠A 'BG=∠A 'BC 是解答此题的关键.3.将△ABC 纸片沿DE 按如图的方式折叠.若∠C =50°,∠1=85°,则∠2的度数等于( )A .10°B .15°C .20°D .25°【答案】B【分析】由四边形的内角和及三角形内角和即可求得. 【解析】∵180A B C ∠+∠+∠=︒,且∠C =50゜ ∴180130A B C ∠+∠=︒-∠=︒同理,在△CDE 中,180130CDE CED C ∠+∠=︒-∠=︒ 由折叠性质得:A A ∠'=∠,B B '∠=∠ ∴130A B ''∠+∠=︒在四边形A B ED ''中,360A B A DE DEB ''''∠+∠+∠+∠=︒ ∴12360A B CDE CED ''∠+∠+∠+∠+∠+∠=︒ ∴130851302360︒+︒+︒+∠=︒ ∴∠2=15゜ 故选:B .【点评】本题考查了折叠的性质,多边形的内角和定理等知识,掌握多边形内角和定理及折叠的性质是关键.4.如图,将三角形纸片ABC 沿DE 折叠,当点A 落在四边形BCDE 的外部时,测量得∠1=70°,∠2=152°,则∠A 为( )A .40°B .42°C .30°D .52°【答案】B【分析】利用四边形的内角和定理求出B C ∠+∠,再利用三角形的内角和定理可得结果. 【解析】解:∵1=70∠︒,2=152∠︒,∴3601236070152138B C ∠+∠=︒-∠-∠=︒-︒-︒=︒, ∴180()18013842A B C ∠=︒-∠+∠=︒-︒=︒, 故选:B .【点评】此题考查了多边形内角与外角、三角形内角和定理,熟练掌握相关知识是解题的关键.第II 卷(非选择题)请点击修改第II 卷的文字说明5.如图,三角形纸片ABC 中,70A ∠=︒,75B ∠=︒.将三角形纸片的一角折叠,使点C 落在ABC 内,那么12∠+∠=_____________︒.【答案】70【分析】延长AF、BE交于点D,根据∠A=70°,∠B=75°,可得∠D=35°,由将纸片的一角折叠,使点C落在△ABC内,可得∠DFC+∠DEC=290°,即可得答案.【解析】解:延长AF、BE交于点D,∵∠A=70°,∠B=75°,∴∠D=180°﹣∠A﹣∠B=35°,∴∠DFE+∠DEF=180°﹣∠D=145°,∵将纸片的一角折叠,使点C落在△ABC内,∴∠CFE=∠DFE,∠CEF=∠DEF,∴∠DFC+∠DEC=2(∠DFE+∠DEF)=290°,∴∠1+∠2=(180°﹣∠DFC)+(180°﹣∠DEC)=360°﹣(∠DFC+∠DEC)=360°﹣290°=70°,故答案为:70.【点评】本题考查三角形中的折叠问题,解题的根据是掌握折叠的性质,灵活应用三角形内角和定理.6.在△ABC中,点E、F分别为边AB、AC上的点,把△ABC沿EF翻折,翻折后的图形如图所示.若∠的度数为___________.1+2110∠∠=︒,则A【答案】55︒【分析】如图,延长B′E交C′F的延长线于点A′,连接AA′.证明∠1+∠2=2∠EAF,可得结论.【解析】解:如图,延长B′E交C′F的延长线于点A′,连接AA′.∵∠1=∠EAA′+∠EA′A,∠2=∠F AA′+∠F A′A,∴∠1+∠2=∠EAF+∠EA′F,∵∠EAF=∠EA′F,∴∠1+∠2=2∠EAF=110°,∴∠A=55°.故答案为:55°.【点评】本题考查三角形内角和定理,翻折变换等知识,解题的关键是证明∠1+∠2=2∠EAF.7.如图,把一张长方形纸片ABCD沿EF折叠,∠1=55°,则∠2=________°.【答案】70【分析】根据长方形的对边平行知AD∥BC,得∠DEF=∠1=55°,再根据折叠的性质知∠GEF=∠DEF =55°,继而由∠AEG=180°−∠DEF−∠GEF可得答案.【解析】解:由题意知AD∥BC,∠1=55°,∴∠DEF=∠1=55°,根据折叠的性质知∠GEF=∠DEF=55°,则∠AEG=180°−∠DEF−∠GEF=180°-55°-55°=70°,∴∠2=70°,故答案为:70.【点评】本题考查了平行线的性质和折叠的性质,解题的关键是掌握两直线平行内错角相等的性质、折叠的性质.8.将△ABC纸片沿DE按如图的方式折叠.若∠C=50°,∠1=85°,则∠2等于______.【答案】15︒【分析】利用三角形的内角和定理以及折叠的性质,求出130CDE CED ∠+∠=︒,''130A B ∠+∠=︒,利用四边形内角和为360︒,即可求出∠2.【解析】解:在ABC ∆中,180130A B C ∠+∠=︒-∠=︒, 在CDE ∆中,180130CDE CED C ∠+∠=-∠=︒, 由折叠性质可知:''130A B A B ∠+∠=∠+∠=︒ , 四边形''DEB A 的内角和为360︒,''''360A B ADE B ED ∴∠+∠+∠+∠=︒,1A DE CDE ∠=∠+∠','2B ED CED ∠=∠+∠,''12()360CDE CED A B ∴∠+∠+∠+∠+∠+∠=︒,130CDE CED ∠+∠=︒,''130A B ∠+∠=︒,且∠1=85°, 215∴∠=︒,故答案为:15︒.【点评】本题主要是考查了三角形和四边形的内角和定理,熟练利用三角形内角和定理,求出两角之和,最后利用四边形的内角和求得某角的度数,这是解决该题的关键.9.如图,将ABC 纸片沿DE 折叠,使点A 落在四边形BCDE 内点'A 的位置,(1)探索A ∠与12∠+∠之间的数量关系,并说明理由.(2)如果点A 落在四边形BCDE 外点''A 的位置,A ∠与1∠、2∠之间的数量关系有何变化,请说明理由. 【答案】(1)2∠A =∠1+∠2,理由见解析 (2)∠A =12(∠2-∠1),理由见解析【分析】(1)根据折叠性质得出∠AED=∠A′ED,∠ADE=∠A′DE,根据三角形内角和定理得出∠AED+∠ADE=180°-∠A,代入∠1+∠2=180°+180°-2(∠AED+∠ADE)求出即可;(2)先根据翻折的性质表示出∠1、∠2,再根据四边形的内角和定理列式整理即可得解.(1)2∠A=∠1+∠2,理由是:∵沿DE折叠A和A′重合,∴∠AED=∠A′ED,∠ADE=∠A′DE,∵∠AED+∠ADE=180°-∠A,∠1+∠2=180°+180°-2(∠AED+∠ADE),∴∠1+∠2=360°-2(180°-∠A)=2∠A.(2)∵沿DE折叠A和A'′重合,∴∠AED=∠A′'ED,∠ADE=∠A′'DE,又∵∠1=∠A'ED-∠BED=∠AED-(180°-∠AED)=2∠AED-180°,∠2=180°-2∠ADE,∠AED+∠ADE=180°-∠A,∴12∠1+90°+90°-12∠2=180°-∠A,即∠A=12(∠2-∠1).【点评】本题考查了折叠的性质,三角形外角性质,三角形内角和定理及四边形内角和的应用,主要考查学生运用定理进行推理和计算的能力.10.在我们苏科版义务教育教科书数学七下第42页曾经研究过双内角平分线的夹角和内外角平分线夹角问题.聪聪在研究完上面的问题后,对这类问题进行了深入的研究,他的研究过程如下:(1)【问题再现】如图1,在△ABC中,∠ABC、∠ACB的角平分线交于点P,若∠A=50°.则∠P=_______;(2)【问题推广】如图2,在△ABC中,∠BAC的角平分线与△ABC的外角∠CBM的角平分线交于点P,过点B作BH⊥AP 于点H,若∠ACB=80°,求∠PBH的度数.(3)如图3,在△ABC中,∠ABC、∠ACB的角平分线交于点P,将△ABC沿DE折叠使得点A与点P重合,若∠1+∠2=100°,则∠BPC=_______;(4)【拓展提升】在四边形BCDE中,EB∥CD,点F在直线ED上运动(点F不与E,D两点重合),连接BF,CF,∠EBF、∠DCF的角平分线交于点Q,若∠EBF=α,∠DCF=β,直接写出∠Q和α,β之间的数量关系.当F 在D 、E 之间时,如图4-2所示:同理可得112222FBQ EBF QCF DCF αβ∠=∠===,∠∠,180180FBC FCB DCF EBF αβ∠+∠=︒-∠-=︒--∠,∴1801802Q QBC QCB QBF FBC FCB QCF αβ+=︒--=︒----=∠∠∠∠∠∠∠;当点F 在D 点右侧时,如图4-3所示:同理可得1801802Q QBC QCB QBF FBC DCB QCD αβ-=︒--=︒----=∠∠∠∠∠∠∠; 综上所述,F 在E 左侧2Q βα-∠=;F 在ED 中间2Q αβ+∠=;F 在D 右侧2Q αβ-∠=.【点评】本题主要考查了三角形内角和定理,角平分线的定义,三角形外角的性质,平行线的性质,垂线的定义,熟知相关知识是解题的关键.11.如图,将一张三角形纸片ABC 的一角折叠,使得点A 落在四边形BCDE 的外部A '的位置且A '与点C 在直线AB 的异侧,折痕为DE ,已知90C ∠=︒,30A ∠=︒.(1)求12∠-∠的度数;(2)若保持A DE '的一边与BC 平行,求ADE ∠的度数. 【答案】(1)60°;(2)45°或30°【分析】(1)先求出∠B 的度数,在根据四边形内角和求出∠1+∠BFD 的度数,由∠BFD =∠A ′FE 和∠A ′的度数可求出答案.(2)分EA '∥BC 和DA '∥BC 两种情况讨论.当DA '∥BC 时,先求出∠A ′DA =90°,再根据折叠可得出∠ADE =45°;当EA '∥BC 时,根据平行线的性质求出∠2=∠ABC =60°,由(1)得出∠1=120°,再根据折叠可求出∠ADE 的度数.【解析】解:(1)由折叠可知,30A A '∠=∠=︒在A EF '△中,2180A A FE ''∠+∠+∠=︒2180150A AFE A FE ''∴∠=︒-∠-∠=︒-∠在ABC 中,18060B C A ∠=︒-∠-∠=︒在四边形BCDF 中,1360C B BFD ∠+∠+∠+∠=︒1360210C B BFD BFD ∴∠=︒-∠-∠-∠=︒-∠因为BFD A FE '∠=∠1221015060∴∠-∠=︒-︒=︒(2)①当//DA BC '时,90ADA ACB '∠=∠=︒ADE 沿DE 折叠A DE '1452ADE A DE ADA ''∴∠=∠=∠=︒②当//EA BC '时,260ABC ∠=∠=︒由(1)知,1260∠-∠=︒,1260120∴∠=∠+︒=︒,ADE 沿DE 折叠A DE '()11801302ADE A DE ADA ''∴∠=∠=∠=︒-∠=︒综上,∠ADE 的度数为:45°或30°.【点评】本题考查了翻折变换的性质,三角形的一个外角等于与它不相邻的两个内角的和,三角形的内角和等于180°,平行线的性质,属于综合题,但难度不大.熟记性质准确识图是解题的关键.12.将ABC 纸片的一角CAB ∠折叠,使点A 落在点P 的位置,折痕为DE .(1)如图1,点A 落在ABC 内的点P 的位置.①若//PE AC ,那么PD 与AB 有怎样的位置关系,请说明理由;②如图2,1∠、2∠与A ∠之间有怎样的数量关系?并说明理由;③连接CP 、BP ,已知CP 、BP 恰好分别平分ACB ∠、ABC ∠(如图3),1∠、2∠与CPB ∠之间有怎样的数量关系,并说明理由;(2)如图4,点A 落在ABC 外的点P 的位置.连接CP 、BP ,如果CP 、BP 恰好分别平分ABC 的两个外角MCB ∠,NBC ∠,那么1∠、2∠与CPB ∠之间的数量关系是______.(请直接写出结果)【答案】(1)①//PD AB ,理由见解析;②122A ∠+∠=∠,理由见解析;③123604CPB ∠+∠+︒=∠,理由见解析;(2)124360CPB ∠+∠+∠=︒,理由见解析【分析】(1)①若//PE AC ,则可推出ADE DEP ∠=∠,然后根据翻折的性质可推出PDE DEA ∠=∠,从而得出结论即可;②根据翻折的性质推出()123602ADE AED ∠+∠=︒-∠+∠,然后结合三角形的内角和推出180A ADE AED ︒-∠=∠+∠,从而代入替换得出结论即可;③根据CP 、BP 恰好分别平分ACB ∠、ABC ∠,可推出()12PCB PBC ACB ABC ∠+∠=∠+∠,然后结合②的结论进行变形整理即可; (2)根据题意可推出()12ACB ABC CPB ∠+∠=∠,然后结合三角形的内角和以及(1)中②的结论,综合整理求解即可.【解析】(1)//PD AB ,理由如下:∵//PE AC ,∴ADE DEP ∠=∠,由翻折的性质可得:ADE PDE ∠=∠,AED PED ∠=∠,∴PDE DEA ∠=∠,∴//PD AB ;②122A ∠+∠=∠,理由如下:由翻折的性质可得:ADE PDE ∠=∠,AED PED ∠=∠,∴11802ADE ∠=︒-∠,21802AED ∠=︒-∠,∴()123602ADE AED ∠+∠=︒-∠+∠,在ADE 中,180A ADE AED ︒-∠=∠+∠,∴()1236021802A A ∠+∠=︒-︒-∠=∠,在ABC 中,由②可知,∠ACB ∠+∠在PBC 中,180CPB ︒-∠12∠+∠+2)1∠+∠CP 、BP 恰好分别平分ABC 的两个外角)ACB ,PBC ∠∴在PBC 中,180PBC ∠=(11801802ABC ︒-∠︒-∠整理得:(12ACB ∠在ABC 中,∠由②可知,∠ACB ∠+∠1118022⎡︒-⎢⎣13.问题1:现有一张△ABC 纸片,点D 、E 分别是△ABC 边上两点,若沿直线DE 折叠.(1)探究1:如果折成图①的形状,使A 点落在CE 上,则∠1与∠A 的数量关系是 ;(2)探究2:如果折成图②的形状,猜想∠1+∠2和∠A 的数量关系是 ;(3)探究3:如果折成图③的形状,猜想∠1、∠2和∠A 的数量关系,并说明理由.(4)问题2:将问题1推广,如图④,将四边形ABCD 纸片沿EF 折叠,使点A 、B 落在四边形EFCD 的内部时,∠1+∠2与∠A 、∠B 之间的数量关系是 . 【答案】(1)12A ∠=∠;(2)122A ∠+∠=∠;(3)见解析;(4)1222360A B ∠+∠=∠+∠-︒【分析】(1)根据三角形外角性质可得;(2)在四边形A EAD '中,内角和为360°,∠BDA=∠CEA=180°,利用这两个条件,进行角度转化可得关系式;(3)如下图,根据(1)可得∠1=2∠DAA ',∠2=2∠EAA ',从而推导出关系式;(4)根据平角的定义以及四边形的内角和定理,与(2)类似思路探讨,可得关系式.【解析】(1)∵△'EDA 是△EDA 折叠得到∴∠A=∠A '∵∠1是△'ADA 的外角∴∠1=∠A+∠A '∴12A ∠=∠;(2)∵在四边形A EAD '中,内角和为360°∴∠A+A '+∠A DA '+∠A EA '=360°同理,∠A=∠A '∴2∠A+∠A DA '+∠A EA '=360°∵∠BDA=∠CEA=180∴∠1+∠A DA '+∠A EA '+∠2=360°∴122A ∠+∠=∠ ;(3)数量关系:212A ∠-∠=∠理由:如下图,连接AA '由(1)可知:∠1=2∠DAA ',∠2=2∠EAA '∴212()2EAA DAA DAE ∠-∠=∠-=∠'∠';(4)由折叠性质知:∠2=180°-2∠AEF ,∠1=180°-2∠BFE相加得:123602(360)22360A B A B ∠+∠=︒-︒-∠-∠=∠+∠-︒.【点评】本题考查角度之间的关系,(4)问的解题思路是相同的,主要运用三角形的内角和定理和四边形的内角和定理进行角度转换.14.在△ABC 中,∠BAC =90°,点D 是BC 上一点,将△ABD 沿AD 翻折后得到△AED ,边AE 交射线BC 于点F .(友情提醒:翻折前后的两个三角形的对应边相等,对应角相等.)(1)如图①,当AE ⊥BC 时,求证:DE ∥AC .(2)若10C B ∠-∠=︒,∠BAD =x°. ①如图②,当DE ⊥BC 时,求x 的值; ②是否存在这样的x 的值,使得△DEF 中有两个角相等.若存在,并求x 的值;若不存在,请说明理由.【答案】(1)见解析;(2)①5x =,②存在,15x =或30.【分析】(1)根据折叠的性质得到∠B=∠E ,根据平行线的判定定理证明;(2)①根据三角形内角和定理分别求出∠C=60°,∠B=30°,根据折叠的性质计算即可;②分∠EDF=∠DFE 、∠DFE=∠E 、∠EDF=∠E 三种情况,列方程解答即可.【解析】(1)∵AE ⊥BC∴∠EAC+∠C=90°∵∠BAC=90°∴∠B+∠C=90°∴∠B=∠EAC∵将△ABD 沿AD 翻折后得到△AED∴∠B=∠E∴∠EAC=∠E∴DE ∥AC(2)①∵∠B+∠C=90°,10C B ∠-∠=︒∴∠B=40°,∠C=50°∵DE ⊥BC∴∠EDF=90°∵将△ABD 沿AD 翻折后得到△AED∴∠B=∠E=40°,∠BAD=∠EAD=x °∴∠DFE=50°∵∠DFE=B BAF ∠+∠∴24050x +=∴5x =②由题意可得,∠ADC=40x +, ∠ABD=140x - ,∠EDF=140(40)1002x x x --+=-∠DFE=402x +(ⅰ)若∠EDF=∠DFE ,可得100-2402x x =+,解得15x =(ⅱ)若∠EDF=∠E ,可得100-240x =解得30x =(ⅲ)若∠DFE =∠E ,可得40240x +=解得0x =(舍去)综上可得15x =或30.【点评】本题考查了三角形折叠中的角度问题,熟知折叠的性质,平行的判定定理是解题的关键.15.在△ABC 中,∠BAC =90°,点D 是BC 上一点,将△ABD 沿AD 翻折后得到△AED ,边AE 交BC 于点F .(1)如图①,当AE ⊥BC 时,写出图中所有与∠B 相等的角: ;所有与∠C 相等的角: .(2)若∠C -∠B =50°,∠BAD =x °(0<x ≤45) .① 求∠B 的度数;②是否存在这样的x 的值,使得△DEF 中有两个角相等.若存在,并求x 的值;若不存在,请说明理由. 【答案】(1)∠E 、∠CAF ;∠CDE 、∠BAF ; (2)①20°;②30【分析】(1)由翻折的性质和平行线的性质即可得与∠B 相等的角;由等角代换即可得与∠C 相等的角; (2)①由三角形内角和定理可得90B C ∠+∠=︒,再由50C B ∠∠︒-=根据角的和差计算即可得∠C 的度数,进而得∠B 的度数.②根据翻折的性质和三角形外角及三角形内角和定理,用含x 的代数式表示出∠FDE 、∠DFE 的度数,分三种情况讨论求出符合题意的x 值即可.【解析】(1)由翻折的性质可得:∠E =∠B ,∵∠BAC =90°,AE ⊥BC ,∴∠DFE =90°,∴180°-∠BAC =180°-∠DFE =90°,即:∠B +∠C =∠E +∠FDE =90°,∴∠C =∠FDE ,∴AC ∥DE ,∴∠CAF =∠E ,∴∠CAF =∠E =∠B故与∠B 相等的角有∠CAF 和∠E ;∵∠BAC =90°,AE ⊥BC ,∴∠BAF +∠CAF =90°, ∠CFA =180°-(∠CAF +∠C )=90°∴∠BAF +∠CAF =∠CAF +∠C =90°∴∠BAF =∠C又AC ∥DE ,∴∠C =∠CDE ,∴故与∠C 相等的角有∠CDE 、∠BAF ;(2)①∵90BAC ∠=︒∴90B C ∠+∠=︒又∵50C B ∠∠︒-=,∴∠C =70°,∠B =20°;②∵∠BAD =x °, ∠B =20°则160ADB x ∠︒︒=-,20ADF x ∠︒︒=+,由翻折可知:∵160ADE ADB x ∠∠︒︒==-, 20E B ∠∠︒==,∴1402FDE x ∠︒︒=-, 202DFE x ∠︒︒=+,当∠FDE =∠DFE 时,1402202x x ︒︒︒︒-=+, 解得:30x ︒︒=;当∠FDE =∠E 时,140220x ︒︒︒-=,解得:60x ︒︒=(因为0<x ≤45,故舍去);当∠DFE =∠E 时,20220x ︒︒︒+=,解得:0x ︒=(因为0<x ≤45,故舍去);综上所述,存在这样的x 的值,使得△DEF 中有两个角相等.且30x =.【点评】本题考查图形的翻折、三角形内角和定理、平行线的判定及其性质、三角形外角的性质、等角代换,解题的关键是熟知图形翻折的性质及综合运用所学知识.16.如图1,将△ABC 纸片沿DE 折叠,使点C 落在四边形ABDE 内点C ’的位置,(1)①若00120,250∠=∠=,则C ∠= ;②若042C ∠=,则12∠+∠= ;③探索C ∠ 、1∠与2∠之间的数量关系,并说明理由;(2)直接按照所得结论,填空:①如图中,将△ABC 纸片再沿FG 、MN 折叠,使点A 、B 分别落在△ABC 内点A ’、B ’的位置,则123456∠+∠+∠+∠+∠+∠= ;②如图中,将四边形ABCD 按照上面方式折叠,则128∠+∠++∠= ; ③若将n 边形123n A A A A 也按照上面方式折叠,则122n ∠+∠++∠= ;(3)如图,将△ABC 纸片沿DE 折叠,使点C 落在△ABC 边AC 上方点'C 的位置, 探索C ∠、1∠与2∠之间的数量关系,并说明理由.【答案】(1)①35︒;②84︒;③212C=+∠∠∠;(2)①360︒;②720︒;③3602(n )︒-;(3)221C=∠∠-∠【分析】(1)①由邻补角的定义可知∠CEC′=160°,∠CDC′=130°,根据折叠的性质可求出∠CED=80°,∠CDE=65°,然后根据三角形内角和定理求解即可;②由三角形内角和可求出∠CED+∠CDE=138°,再由折叠的性质可知∠CEC′+∠CDC′=276°,然后根据邻补角的定义可求出12∠+∠=84°;③由邻补角定义可知1+'=180CEC ∠∠︒,从而2+'=180CDC ∠∠︒,所以,∠1+ ∠CEC′+ ∠2+ ∠CDC′=360 °,结合+'+'+'=360C CEC C CDC ∠∠∠∠︒,可求出2=1+2C ∠∠∠;(2)① 由(1)得12∠∠+=2∠C ,34∠+∠=2∠B ,56∠+∠=2∠A ,从而123456∠+∠+∠+∠+∠+∠=2(∠A+∠B +∠C),结合三角形内角和求解即可;②由①可知,128∠+∠++∠= 2(∠A+∠B +∠C+∠D),结合四边形内角和求解即可;③由①可知,()()122218023602n n n ∠+∠++∠=⨯︒⨯-=︒⨯- ;(3)由外角的性质可知∠2=∠3+∠C ,∠3=∠1+∠C ,整理可得2=21C ∠∠-∠.【解析】解:(1)①∵00120,250∠=∠=,∴∠CEC′=160°,∠CDC′=130°,∵ ∠CED=80°,∠CDE=65°,∴∠C= 180°-80°-65°=35°;②∵042C ∠=,∴ ∠CED+∠CDE=180°-42°=138°,∴∠CEC′+∠CDC′=276°,∴12∠+∠=360°-276°=84°;③2=1+2C ∠∠∠,因为1+'=180CEC ∠∠︒,2+'=180CDC ∠∠︒,所以1+'+2+'=360CEC CDC ∠∠∠∠︒,因为在四边形'CEC D 中,+'+'+'=360C CEC C CDC ∠∠∠∠︒,所以1+2=+'C C ∠∠∠∠,因为='C C ∠∠,所以2=1+2C ∠∠∠.(2)① 由①得12∠∠+=2∠C ,34∠+∠=2∠B ,56∠+∠=2∠A ,∴123456∠+∠+∠+∠+∠+∠=2(∠A+∠B +∠C)=360°; ②∵12∠∠+=2∠C ,34∠+∠=2∠B ,56∠+∠=2∠A ,78∠+∠=2∠D ,∴128∠+∠++∠= 2(∠A+∠B +∠C+∠D)=2×360°=720°; ③∵n 边形内角和是()1802n ︒⨯-,∴()()122218023602n n n ∠+∠++∠=⨯︒⨯-=︒⨯- ;(3)2=21C ∠∠-∠.∵∠2=∠3+∠C ,∠3=∠1+∠'C =∠1+∠C ,∴∠2=∠1+∠C +∠C=∠1+2∠C ,∴2=21C ∠∠-∠.【点评】本题考查了折叠性质,三角形内角和定理,多边形的内角和定理,三角形外角的性质及图形类的规律与探究.熟练掌握折叠的性质和三角形内角和定理是解(1)的关键,利用(1)中规律是解(2)的关键,熟练掌握三角形外角的性质是解(3)的关键.17.直线MN 与直线PQ 垂直相交于O ,点A 在射线OP 上运动,点B 在射线OM 上运动,连接AB,(1)如图,已知AC 、BC 分别是∠BAP 和∠ABM 角的平分线,①点A 、B 在运动的过程中,∠ACB 的大小是否发生变化?若发生变化,请说明理由;若不发生变化,试求出∠ACB 的大小.②如图,将△ABC 沿直线AB 折叠,若点C 落在直线PQ 上,记作点C′,则∠ABO = °;如图,将△ABC 沿直线AB 折叠,若点C 落在直线MN 上,记作点C′′,则∠ABO = °.(2)如图,延长BA 至G ,已知∠BAO 、∠OAG 的角平分线与∠BOQ 的角平分线及其延长线交于E 、F ,在△AEF 中,如果有一个角是另一个角的32倍,求∠ABO 的度数.【答案】(1)①∠ACB 的大小不变,∠ACB=45°;②30°,60°;(2)∠ABO 为60°或72°.【分析】(1)①由直线MN 与直线PQ 垂直相交于O ,得到∠AOB=90°,根据三角形的外角的性质得到∠PAB+∠ABM=270°,根据角平分线的定义得到∠BAC=12∠PAB ,∠ABC=12∠ABM ,于是得到结论; ②由于将△ABC 沿直线AB 折叠,若点C 落在直线PQ 上,得到∠CAB=∠BAQ ,由角平分线的定义得到∠PAC=∠CAB ,根据三角形的内角和即可得到结论;根据将△ABC 沿直线AB 折叠,若点C 落在直线MN 上,得到∠ABC=∠ABN ,由于BC 平分∠ABM ,得到∠ABC=∠MBC ,于是得到结论;(2)由∠BAO 与∠BOQ 的角平分线相交于E 可知∠EAO=12∠BAO ,∠EOQ=12∠BOQ ,进而得出∠E 的度数,由AE 、AF 分别是∠BAO 和∠OAG 的角平分线可知∠EAF=90°,在△AEF 中,由一个角是另一。
图形的折叠问题的习题带答案

折叠问题中的角度运算1、三角形纸片ABC中,∠A=55°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内(如图),则∠1+∠2的度数为_____度。
分析:利用三角形的内角和和四边形的内角和即可求得.解:∠A+∠B+∠C=180°,∠C=180°-∠A-∠B=180°-55°-75°=50°①,∠C+∠CED+∠CDE=180°,∠CED+∠CDE=180°-∠C=180°-50°=130°②,∠B+∠A+∠CED+∠CDE+∠1+∠2=360°③,把①②分别代入③得75°+55°+130°+∠1+∠2=360°,得∠1+∠2=100°2、如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处。
若∠A=22°,则∠BDC等于______。
分析:△ABC中,∠ACB=90°,∠A=22°,∴∠B=90°-∠A=68°。
由折叠的性质可得:∠CED=∠B=68°,∠BDC=∠EDC,∴∠ADE=∠CED﹣∠A=46°。
3、如图,在平面内,把矩形ABCD沿EF对折,若∠1=50°,则∠AEF等于______。
分析:根据折叠前后角相等可知.解:∵∠1=50°,∴∠AEF=180°-∠BFE=180°-(180°-50°)÷2=115°.点评:本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.4、如图,把一张长方形纸条ABCD沿EF折叠,若∠1=56°,则∠EGF应为______.分析:本题根据平行线的性质和翻折的性质,求解即可.解答:解:因为折叠,且∠1=56°,所以∠C′FB=180°-2×56°=68°,∵D′E//C′F,∴∠EGF=∠C′FB=68°.5、如图,D、E分别为△ABC的边AB、AC上的点,DE∥BC,将△ABC沿线段DE折叠,使点A落在BC上的点F处,若∠B=55°,则∠BDF的度数为______。
考点38 图形折叠中的直角、等腰三角形问题及落点固定问题(

专题38 图形折叠中的直角三角形问题【精典讲解】1、如图例3-1,在Rt △ABC 中,∠ACB =90°,∠B =30°,BC =3,点D 是BC 边上一动点(不与点B 、C 重合),过点D 作DE ⊥BC 交AB 边于点E ,将∠B 沿直线DE 翻折,点B 落在射线BC 上的点F 处,当△AEF 为直角三角形时,BD 的长为ACBF EDAC BFED图例3-1 图例3-2图例3-3【解析】从题目所给的“当△AEF 为直角三角形时”条件出发,以直角顶点所在位置进行分类讨论. 通过观察及分析可知∠BED =∠DEF =60°,所以∠AEF =180-120°=60°. 即点E 不可能为直角顶点.分两种情况考虑: ①当∠EAF =90°时,如图例3-2所示. ∵∠B =30°,BC =3∴3303=33AC tan BC =︒⨯=,2=23AB AC = ∵∠EAF =90°∴∠AFC =60°,∠CAF =30°在Rt △ACF 中,有:3cos =32AF AC CAF =÷∠÷,24BF AF == 由折叠性质可得:∠B =∠DFE =30°,122BD DF BF === ②当∠AFE =90°时,如图例3-3所示.由折叠性质得:∠B =∠DFE =30°,122BD DF BF === ∴∠AFC =60°,∠F AC =30°∴3tan 313CF FAC AC =∠⨯=⨯= 所以,BF =2,112BD DF BF === 综上所述,BD 的长为2或1.【点睛】本题难度适中,要求学生具备分类讨论思想及数形结合解决问题的能力,另外还需要熟练运用勾股定理及相似三角形知识. 通过此题,可总结出:①遇到直角三角形存在性问题时,分类讨论的出发点在于直角顶点的位置;②解决直角三角形存在性问题的方法是数形结合,先作出符合题意的图形,再用勾股定理或相似三角形、三角函数性质解题.2、如图例4-1,矩形ABCD 中,AB =3,BC =4,点E 是BC 边上一点,连接AE ,把∠B 沿AE 折叠,使点B 落在点B ′处.当△CEB ′为直角三角形时,BE 的长为 .ABCDEB'ABC DEB'图例4-1 图例4-2 图例4-3【解析】此题以“当△CEB ′为直角三角形时”为突破口,分析可能是直角顶点的点,得出存在两种情况,即点B ′及点E 分别为直角顶点.分两种情况考虑:①当∠CEB ′=90°时,如图例4-2所示.由折叠性质得:AB =AB ′,四边形ABE B ′是矩形. 所以四边形ABE B ′是正方形. 此时,BE =AB =3.②当∠CB ′E =90°时,如图例4-3所示.由折叠性质知,∠AB ′C =90°,所以∠AB ′C+∠CB ′E =180°. ∴点A 、B ′、C 共线在Rt △ABC 中,由勾股定理得AC =5 由折叠得:AB = AB ′=3 所以B ′C =2设BE =x ,则B ′E =x ,EC =4-x在Rt △ABC 中,由勾股定理得:EC 2=B ′E 2+B ′C 2 即:(4-x )2=x 2+22 解得:x =1.5.综上所述,BE 的值为3或1.5.【点睛】本题解题关键在准确对问题进行分类讨论且作出相应图形,要求学生掌握三点共线的理由,折叠的性质及勾股定理的应用.3、如图例5-1,在Rt ABC ∆中,90A ∠=︒,AB AC =,21BC =+,点M ,N 分别是边BC ,AB 上的动点,沿MN 所在的直线折叠B ∠,使点B 的对应点'B 始终落在边AC 上.若'MB C ∆为直角三角形,则BM 的长为 .A (B')BCMN ABCM NB'图例5-1图例5-2图例5-3【解析】通过观察及分析可知,C 点不可能为直角顶点,分两种情况讨论. ①当∠CM B ′=90°时,如图例5-2所示.由折叠知:∠BMN =∠B ′MB =45°,又因为∠B =45°,所以∠BNM =90°,∠MNB ′=90° 即∠BNM +∠MN B ′=180°,所以B 、N 、B ′三点共线,此时B ′与点A 重合.所以,12122BM BC +==①当∠CB ′M =90°时,如图例5-3所示.由折叠知∠B =∠B ′=45°,因为∠C =45°,可得∠B ′MC =45°,所以△B ′MC 是等腰直角三角形设BM = B ′M =x ,B ′C =x ,则MC =2x因为BC =2+1所以x +2x =2+1 解得:x =1,即BM =1.综上所述,BM 的值为212+或1. 【点睛】根据题意判断出C 点不可能为直角顶点,分两种情况讨论,利用等腰直角三角形的三边关系求解. 4、 如图例6-1,在∠MAN =90°,点C 在边AM 上,AC =4,点B 为边AN 上一动点,连接BC ,△A’BC 与△ABC 关于BC 所在直线对称. D 、E 分别为AC 、BC 的中点,连接DE 并延长交A’B 所在直线于点F ,连接A’E . 当△A’EF 为直角三角形时,AB 的长为 .M N AA'FEDC B图例6-1图例6-2图例6-3【解析】分两种情况讨论.①当∠A’FE=90°时,如图例6-2所示. ∵D、E分别为AC、BC的中点∴DE是三角形ABC的中位线即DE∥BA∴∠A’BA=90°∴四边形AB A’C为矩形由折叠得AC=A’C∴四边形AB A’C为正方形即AB=AC=4.②当∠A’EF=90°时,如图例6-3所示. ∵∠A’EF=∠CDE=90°∴A’E∥CD∴∠DCE=∠CEA’由折叠知:∠DCE=∠A’CE∴∠CEA’=∠A’CE∴A’C=A’E=4又∵E是BC中点即A’E是Rt△A’BC的中线∴BC=2A’E=8在Rt△A’BC中,由勾股定理得,A’B=43由折叠性质得:AB=A’B=43.综上所述,AB的长为4或43.【点睛】利用中位线性质(三角形的中位线平行于第三边)及正方形判定,用勾股定理求解.【针对训练】1、矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为( )A.3 B.32C.2或3 D.3或32【解析】【分析】当△CEB′为直角三角形时,有两种情况:①当点B′落在矩形内部时,如图1所示.连结AC,先利用勾股定理计算出AC=5,根据折叠的性质得∠AB′E=∠B=90°,而当△CEB′为直角三角形时,只能得到∠EB′C=90°,所以点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,则EB=EB′,AB=AB′=3,可计算出CB′=2,设BE=x,则EB′=x,CE=4-x,然后在Rt△CEB′中运用勾股定理可计算出x.②当点B′落在AD边上时,如图2所示.此时ABEB′为正方形.【详解】当△CEB′为直角三角形时,有两种情况:①当点B′落在矩形内部时,如图1所示.连结AC,在Rt△ABC中,AB=3,BC=4,∴AC=2243=5,∵∠B沿AE折叠,使点B落在点B′处,∴∠AB′E=∠B=90°,当△CEB′为直角三角形时,只能得到∠EB′C=90°,∴点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,∴EB=EB′,AB=AB′=3,∴CB′=5-3=2,设BE=x,则EB′=x,CE=4-x,在Rt△CEB′中,∵EB′2+CB′2=CE2,∴x2+22=(4-x)2,解得x=32,∴BE=32;②当点B′落在AD边上时,如图2所示.此时ABEB′为正方形,∴BE=AB=3.综上所述,BE的长为32或3.故选D.【点睛】本题考查了折叠问题:折叠前后两图形全等,即对应线段相等;对应角相等.也考查了矩形的性质以及勾股定理.注意本题有两种情况,需要分类讨论,避免漏解.2、如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE、DE分别交AB于点O、F,且OP=OF,则ADDF的值为A.1113B.1315C.1517D.1719【解析】【分析】根据折叠的性质可得出DC =DE 、CP =EP ,由∠EOF =∠BOP 、∠B =∠E 、OP =OF 可得出△OEF ≌△OBP (AAS ),根据全等三角形的性质可得出OE =OB 、EF =BP ,设EF =x ,则BP =x 、DF =4﹣x 、BF =PC =3﹣x ,进而可得出AF =1+x .在Rt △DAF 中,利用勾股定理可求出x 的值,即可得出答案. 【详解】根据折叠,可知:△DCP ≌△DEP ,∴DC =DE =4,CP =EP .在△OEF 和△OBP 中,∵90EOF BOPB E OP OF ∠∠∠∠=⎧⎪==︒⎨⎪=⎩,∴△OEF ≌△OBP (AAS ),∴OE =OB ,EF =BP .设EF =x ,则BP =x ,DF =DE ﹣EF =4﹣x .又∵BF =OB +OF =OE +OP =PE =PC ,PC =BC ﹣BP =3﹣x ,∴AF =AB ﹣BF =1+x .在Rt △DAF 中,AF 2+AD 2=DF 2,即(1+x )2+32=(4﹣x )2,解得:x =0.6,∴DF =4﹣x =3.4,∴1517AD DF =. 故选C .【点睛】本题考查了全等三角形的判定与性质、勾股定理以及解直角三角形,利用勾股定理结合AF =1+x ,求出AF 的长度是解题的关键.3、如图,已知正方形ABCD 的边长为3,E 是BC 上一点,3,Q 是CD 上一动点,将△CEQ 沿直线EQ 折叠后,点C 落在点P 处,连接PA .点Q 从点C 出发,沿线段CD 向点D 运动,当PA 的长度最小时,CQ 的长为( )A .333-B .33-C .32D .3【解析】试题解析:如图所示:在Rt △ABE 中,AE=.∵BC=3,BE=,∴EC=3-.由翻折的性质可知:PE=CE=3-.∵AP+PE≥AE , ∴AP≥AE -PE .∴当点A 、P 、E 一条直线上时,AP 有最小值.∴AP=AE-PE=2-(3-)=3-3.故选A .考点:翻折变换(折叠问题).4、如图,矩形ABCD 中,3AB =,4BC =,点E 是BC 边上一点,连接AE ,把矩形沿AE 折叠,使点B 落在点B '处.当CEB '∆为直角三角形时,BE 的长为____________.【解析】 【分析】当△CEB′为直角三角形时,有两种情况: ①当点B′落在矩形内部时,如答图1所示.连结AC ,先利用勾股定理计算出AC=10,根据折叠的性质得∠AB′E=∠B=90°,而当△CEB′为直角三角形时,只能得到∠E B′C=90°,所以点A 、B′、C 共线,即∠B 沿AE 折叠,使点B 落在对角线AC 上的点B′处,则EB=EB′,AB=AB′=6,可计算出CB′=4,设BE=x ,则EB′=x ,CE=8-x ,然后在Rt △CEB′中运用勾股定理可计算出x .②当点B′落在AD 边上时,如答图2所示.此时四边形ABEB′为正方形. 【详解】由题意知,需分两种情况讨论:①当90CB E ︒'∠=时,如图1,由折叠得,90AB E B ︒'∠=∠=,AB AB '=, ∴180AB C ︒'∠=,∴,,A B C '三点共线.在矩形ABCD 中,3AB =,4BC =, ∴5AC =. ∵AB AB 3'==, ∴2B C AC AB ''=-=.设BE x =,则4CE BC BE x =-=-,B E x '=,在Rt B CE '∆中,222B E B C CE ''+=,即2222(4)x x +=-,解得32x =. ②当90B EC ︒'∠=时,如图2,由折叠可知ABE AB E '∆∆≌, ∴BE B E '=,90B AB E ︒'∠=∠=, ∴四边形ABEB '是正方形, ∴3BE AB ==.综上所述,当CEB '∆为直角三角形时,BE 的长为32或3.故答案是:32或3. 【点睛】考查了折叠问题:折叠前后两图形全等,即对应线段相等;对应角相等.也考查了矩形的性质以及勾股定理.注意本题有两种情况,需要分类讨论,避免漏解.5、如图,在矩形ABCD 中,AB =6,AD =23,E 是AB 边上一点,AE =2,F 是直线CD 上一动点,将△AEF 沿直线EF 折叠,点A 的对应点为点A ′,当点E ,A ′,C 三点在一条直线上时,DF 的长为_____.【解析】【分析】利用勾股定理求出CE,再证明CF=CE即可解决问题.(注意有两种情形)【详解】解:如图,由翻折可知,∠FEA=∠FEA′,∵CD∥AB,∴∠CFE=∠AEF,∴∠CFE=∠CEF,∴CE=CF,在Rt△BCE中,EC==,∴CF=CE=,∵AB=CD=6,∴DF=CD﹣CF=6﹣,当点F在DC的延长线上时,易知EF⊥EF′,CF=CF′=,∴DF=CD+CF′=故答案为6﹣或.【点睛】本题考查翻折变换、矩形的性质、勾股定理等知识,本题的突破点是证明△CFE的等腰三角形,属于中考常考题型.6、如图,在菱形ABCD中,∠DAB=45°,AB=4,点P为线段AB上一动点,过点P作PE⊥AB交直线AD 于点E,将∠A沿PE折叠,点A落在F处,连接DF,CF,当△CDF为直角三角形时,线段AP的长为__________.【解析】【分析】分两种情形讨论:①如图1,当DF⊥AB时,△CDF是直角三角形;②如图2,当CF⊥AB时,△DCF是直角三角形,分别求出即可.【详解】分两种情况讨论:①如图1,当DF⊥AB时,△CDF是直角三角形.∵在菱形ABCD中,AB=4,∴CD=AD=AB=4.在Rt△ADF中,∵AD=4,∠DAB=45,DF=AF=22,∴AP12=AF2=.②如图2,当CF⊥AB时,△DCF是直角三角形.在Rt△CBF中,∵∠CFB=90°,∠CBF=∠A=45°,BC=4,∴BF=CF2,∴AF2,∴AP12=AF=22+综上所述:线段AP2或22+.222+【点睛】本题考查了菱形的性质,等腰直角三角形的性质,折叠的性质,熟练掌握折叠的性质是解题的关键,正确画出图象,注意分类讨论的思想,属于中考常考题型.专题39 图形折叠中的等腰三角形问题【精典讲解】1、如图例7-1,正方形ABCD 的边长是16,点E 在边AB 上,AE =3,点F 是边BC 上不与点B 、C 重合的一个动点,把△EBF 沿EF 折叠,点B 落在B ′处,若△CDB ′恰为等腰三角形,则DB ′的长为 .A BCDB'F E图例7-1【解析】根据△CDB ′为等腰三角形,以CD 为腰或底分三种情况讨论,①DB ′=DC ;②CB ′=CD ;③CB ′=DB ′. 对于①DB ′=DC ,作图方法以E 为圆心BE 长为半径作弧,以D 为圆心CD 长为半径作弧,两弧交点即为B ′. 对于②CB ′=CD ,作图方法以E 为圆心BE 长为半径作弧,以C 为圆心CD 长为半径作弧,两弧交点即为B ′. 对于③CB ′=DB ′,作图方法以E 为圆心BE 长为半径作弧,弧与CD 垂直平分线的交点为B ′.A BCDB'FEA BC DB'(F )EA BCDB'F EMN图例7-2 图例7-3 图例7-4详解:①DB ′=DC , 如图例7-2所示. 易知:DB ′=DC =16.②CB ′=CD ,如图例7-3所示.由折叠性质可知:BF = B ′F =CD =16,此时F 点与C 点重合,不符题意.③CB′=DB′,如图例7-4所示.由题意得,DN=CN=8,因为AE=3,所以EM=5. B′E=BE=13.在Rt△EB′M中,由勾股定理得,B′M=12.所以B′N=4.在Rt△DB′N中,由勾股定理得,B′D=54.综上所述,B′D的长为16或54.【点睛】以CD为腰或底分三种情况讨论,排除其中一种,利用勾股定理求解.【针对训练】1、如图,在矩形ABCD中,AB=2,BC=4,P为边AD上一动点,连接BP,把△ABP沿BP折叠,使A 落在A′处,当△A′DC为等腰三角形时,AP的长为()A.2 B 23C.223D.243【解析】【分析】根据△A′DC为等腰三角形,分三种情况进行讨论:①A'D=A'C,②A'D=DC,③CA'=CD,分别求得AP的长,并判断是否符合题意.【详解】①如图,当A′D=A′C时,过A′作EF⊥AD,交DC于E,交AB于F,则EF垂直平分CD,EF垂直平分AB∴A'A=A'B由折叠得,AB=A'B,∠ABP=∠A'BP ∴△ABA'是等边三角形∴∠ABP=30°∴AP=223333 AB==;②如图,当A'D=DC时,A'D=2由折叠得,A'B=AB=2∴A'B+A'D=2+2=4连接BD,则Rt△ABD中,BD=22222425AB AD+=+=∴A'B+A'D<BD(不合题意)故这种情况不存在;③如图,当CD=CA'时,CA'=2由折叠得,A'B=AB=2 ∴A'B+A'C=2+2=4∴点A'落在BC 上的中点处此时,∠ABP=12∠ABA'=45° ∴AP=AB=2.综上所述,当△A′DC 为等腰三角形时,AP 的长为2 33或2. 故选C. 【点睛】本题以折叠问题为背景,主要考查了等腰三角形的性质,解决问题的关键是画出图形进行分类讨论,分类时注意不能重复,不能遗漏.2、如图,菱形ABCD 的边,8AB =,60B ∠=,P 是AB 上一点,3BP =,Q 是CD 边上一动点,将梯形APQD 沿直线PQ 折叠,A 的对应点'A .当'CA 的长度最小时,'C Q 的长为( )A .5B .7C .8D .132【解析】 【分析】作CH AB ⊥于H ,如图,根据菱形的性质可判断ABC ∆为等边三角形,则3432CH AB ==4AH BH ==,再利用7CP =勾股定理计算出,再根据折叠的性质得点'A 在以点P 为圆心,PA 为半径的弧上,利用点与圆的位置关系得到当点'A 在PC 上时,'CA 的值最小,然后证明CQ CP =即可. 【详解】解:作CH AB ⊥于H ,如图,菱形ABCD 的边8AB =,60B ∠=,ABC ∆∴为等边三角形,CH AB ∴==,4AH BH ==, 3PB =,1HP ∴=,在Rt CHP ∆中,7CP ==, 梯形APQD 沿直线PQ 折叠,A 的对应点'A ,∴点'A 在以点P 为圆心,PA 为半径的弧上, ∴当点'A 在PC 上时,'CA 的值最小,APQ CPQ ∴∠=∠,而//CD AB ,APQ CQP ∴∠=∠,CQP CPQ ∴∠=∠, 7CQ CP ∴==.故选:B.【点睛】考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.也考查了折叠的性质.解决本题的关键是确定A′在PC上时CA′的长度最小.3、如图,在矩形ABCD中,AB=,BC=3,将△ABC沿对角线AC折叠,点B恰好落在点P处,CP与AD交于点F,连接BP交AC于点G,交AD于点E,下列结论不正确的是()A.B.△PBC是等边三角形C.AC=2AP D.S△BGC=3S△AGP【解析】【分析】如图,首先运用勾股定理求出AC的长度,进而求出∠ACB=30°,此为解决该题的关键性结论;运用翻折变换的性质证明△BCP为等边三角形;运用射影定理求出线段CG、AG之间的数量关系,进而证明选项A、B、C成立,选项A不成立.【详解】如图,∵四边形ABCD为矩形,∴∠ABC=90°;由勾股定理得:AC2=AB2+BC2,而AB=,BC=3,∴AC=2,AB=AC,∴∠ACB=30°;由翻折变换的性质得:BP⊥AC,∠ACB=∠ACP=30°,BC=PC,AB=AP,BG=PG,∴GC=BG=PG,∠BCP=60°,AC=2AP,∴△BCP为等边三角形,故选项B、C成立,选项A不成立;由射影定理得:BG2=CG•AG,∴AG=BG,CG=3AG,∴S△BCG=3S△ABG;由题意得:S△ABG=S△AGP,∴S△BGC=3S△AGP,故选项D正确;故选:A.【点睛】考查了翻折变换的性质、矩形的性质、射影定理、三角形的面积公式等几何知识点及其应用问题;解题的关键是灵活运用矩形的性质、射影定理等几何知识点来分析、判断、推理或解答;对综合的分析问题解决问题的能力提出了较高的要求.4、如图,将一张正方形纸片ABCD对折,使CD与AB重合,得到折痕MN后展开,E为CN上一点,将△CDE 沿DE所在的直线折叠,使得点C落在折痕MN上的点F处,连接AF,BF,BD.则下列结论中:①△ADF是等边三角形;②tan∠EBF=2-;③S△ADF=S正方形ABCD;④BF2=DF·EF.其中正确的是()A.①②③B.①②④C.①③④D.②③④【解析】【分析】由正方形的性质得出AB=CD=AD,∠C=∠BAD=∠ADC=90°,∠ABD=∠ADB=45°,由折叠的性质得出MN垂直平分AD,FD=CD,BN=CN,∠FDE=∠CDE,∠DFE=∠C=90°,∠DEF=∠DEC,由线段垂直平分线的性质得出FD=FA,得出△ADF是等边三角形,①正确;设AB=AD=BC=4a,则MN=4a,BN=AM=2a,由等边三角形的性质得出∠DAF=∠AFD=∠ADF=60°,FA=AD=4a,FM=AM=2a,得出FN=MN-FM=(4-2)a,由三角函数的定义即可得出②正确;求出△ADF的面积=AD•FM=4a2,正方形ABCD的面积=16a2,得出③错误;求出∠BFE=∠DFB,∠BEF=∠DBF,证出△BEF∽△DBF,得出对应边成比例,得出④正确;即可得出结论.【详解】∵四边形ABCD是正方形,∴AB=CD=AD,∠C=∠BAD=∠ADC=90°,∠ABD=∠ADB=45°,由折叠的性质得:MN垂直平分AD,FD=CD,BN=CN,∠FDE=∠CDE,∠DFE=∠C=90°,∠DEF=∠DEC,∴FD=FA,∴AD=FD=FA,即△ADF是等边三角形,①正确;设AB=AD=BC=4a,则MN=4a,BN=AM=2a,∵△ADF是等边三角形,∴∠DAF=∠AFD=∠ADF=60°,FA=AD=4a,FM=AM=2a,∴FN=MN-FM=(4-2)a,∴tan∠EBF==2-,②正确;∵△ADF的面积=AD•FM=×4a×2a=4a2,正方形ABCD的面积=(4a)2=16a2,∴,③错误;∵AF=AB,∠BAF=90°-60°=30°,∴∠AFB=∠ABF=75°,∴∠DBF=75°-45°=30°,∠BFE=360°-90°-60°-75°=135°=∠DFB,∵∠BEF=180°-75°-75°=30°=∠DBF,∴△BEF∽△DBF,∴,∴BF 2=DF•EF ,④正确; 故选B . 【点睛】本题是相似形综合题目,考查了正方形的性质、折叠的性质、线段垂直平分线的性质、等边三角形的判定与性质、相似三角形的判定与性质、三角函数等知识;本题综合性强,有一定难度,证明三角形是等边三角形和证明三角形相似是解决问题的关键.5、已知ABC 中, AC BC =, Rt C ∠=∠.如图,将ABC 进行折叠,使点A 落在线段BC 上(包括点B 和点C ),设点A 的落点为D ,折痕为EF ,当DEF 是等腰三角形时,点D 可能的位置共有( ).A .2种B .3种C .4种D .5种 【解析】(1)当点D 与C 重合时,∵AC=BC ,AE=DE (即CE ),AF=DF (即CF ),∴此时△AFC (即△AFD )是等腰直角三角形,点E 是斜边AC 的中点, ∴EF=DE ,∴△EDF 为等腰三角形.(2)当点D 与B 点重合时,点C 与E 重合, ∵AC=BC ,AF=DF (即BF ),∴此时EF=12AB=DF (即BF ), ∴△DEF 是等腰三角形;(3)当点D 移动到使DE=DF 的位置时,△DEF 是等腰三角形. 综上所述,当△DEF 为等腰三角形时,点D 的位置存在3中可能. 故选B.6、如图,正方形ABCD 的边长是16,点E 在边AB 上,3AE =,点F 是边BC 上不与点B 、C 重合的一个动点,把EBF ∆沿EF 折叠,点B 落在'B 处,若'CDB ∆恰为等腰三角形,则'DB 的长为______.【解析】 【分析】根据翻折的性质,可得B’E 的长,根据勾股定理可得CE 的长,然后再根据等腰三角形的判定进行分情况讨论 【详解】需分三种情况讨论:(1)若'DB DC =,则'16DB =(易知此时点F 在BC 上且不与点C 、B 重合);(2)若'CB CD =,因为'EB EB =,'CB CB =,所以点E 、C 在'BB 的垂直平分线上,则EC 垂直平分'BB ,由折叠可知点F 与点C 重合,不符合题意,则这种情况不成立;(3)如图,若''CB DB =,作'B G AB ⊥与AB 交于点G ,交CD 于点H .因为AB CD ∥,所以'B H CD ⊥.因为''CB DB =,所以182DH CD ==,所以8AG DH ==,则5GE AG AE =-=,因为'13B E BE ==.在'Rt B EG ∆中,由勾股定理求得'12B G =,所以''4B H GH B G =-=.在'Rt B DH ∆中,由勾股定理求得'45DB =DB 或45.综上,'16【点睛】本题考查折叠性质和勾股定理,本题关键在于能够对等腰三角形的情况进行分类讨论7、在菱形ABCD中,∠B=60°,BC=2cm,M为AB的中点,N为BC上一动点(不与点B重合),将△BMN 沿直线MN折叠,使点B落在点E处,连接DE,CE,当△CDE为等腰三角形时,线段BN的长为_____.【解析】【分析】分两种情况:①如图1,当DE=DC时,连接DM,作DG⊥BC于G,由菱形的性质得出AB=CD=BC=2,AD∥BC,AB∥CD,得出∠DCG=∠B=60°,∠A=120°,DE=AD=2,求出33BG=BC+CG=3,由折叠的性质得:EN=BN,EM=BM=AM,∠MEN=∠B=60°,证明△ADM≌△EDM,得出∠A=∠DEM=120°,证出D、E、N三点共线,设BN=EN=x,则GN=3-x,DN=x+2,在Rt△DGN中,由勾股定理得出方程,解方程即可;②如图2,当CE=CD上,CE=CD=AD,此时点E与A重合,N与点C重合,CE=CD=DE=DA,△CDE是等边三角形,BN=BC=2(含CE=DE这种情况).【详解】解:分两种情况,①如图1,当DE=DC时,连接DM,作DG⊥BC于G,∵四边形ABCD是菱形,∴AB=CD=BC=2,AD∥BC,AB∥CD,∴∠DCG=∠B=60°,∠A=120°,∴DE=AD=2,∵DG⊥BC,∴∠CDG=90°-60°=30°,∴CG=12CD=1,∴DG=3CG=3,BG=BC+CG=3,∵M为AB的中点,∴AM=BM=1,由折叠的性质得:EN=BN,EM=BM=AM,∠MEN=∠B=60°,在△ADM和△EDM中,AD=ED,AM=EM ,DM=DM,∴△ADM≌△EDM(SSS),∴∠A=∠DEM=120°,∴∠MEN+∠DEM=180°,∴D、E、N三点共线,设BN=EN=x,则GN=3-x,DN=x+2,在Rt△DGN中,由勾股定理得:(3-x)²+(3)² =(x+2)²,解得:x=45,,即BN=45;②当CE=CD时,CE=CD=AD,此时点E与A重合,N与点C重合,如图2所示:CE=CD=DE=DA ,△CDE 是等边三角形,BN=BC=2(符合题干要求); 综上所述,当△CDE 为等腰三角形时,线段BN 的长为45或2; 故答案为45或2. 【点睛】本题考查了折叠变换的性质、菱形的性质、全等三角形的判定与性质、三点共线、勾股定理、直角三角形的性质、等腰三角形的性质等知识,熟练掌握并灵活运用是解题的关键.专题40 图形折叠中的落点固定问题【精典讲解】1、如图例8-1,矩形ABCD 中,AD =5,AB =7,点E 为DC 上一个动点,把△ADE 沿AE 折叠,当点D 的对应点D ′落在∠ABC 的角平分线上时,DE 的长为 .图例8-1DCB AD'D'DCB A D'E M N图例8-2图例8-3【解析】如图例8-2.发现有两个不同的D’点,对不同的位置分别求解.如图例8-3所示.因为BD′是∠ABC的平分线所以∠D′BN=45°,D′N=NB由折叠知AD′=AD=5.设D′N=NB=x,则AN=7-x在Rt△AD′N中,由勾股定理得,AD′2=D′N2+AN252=x2+(7-x)2,解得x=3或4.①当x=3时,D′M=2,AN=4. 设DE=y,则D′E=y,EM=4-y 在Rt△ED′M中,由勾股定理得,ED′2=D′M2+EM2即y2=22+(4-y)2,解得y=5 2 .②当x=4时,D′M=1,AN=3. 设DE=y,则D′E=y,EM=3-y 在Rt△ED′M中,由勾股定理得,ED′2=D′M2+EM2y2=12+(3-y)2,解得y=5 3 .综上所述,DE的长为52或53.【点睛】D′落在∠ABC的角平分线上,作出∠ABC的角平分线,再以A为圆心以AD长半径画弧,弧与∠ABC 的角平分线的交点即为D’点. 根据折叠中,折痕是对应点连线的垂直平分线作出折痕.2、如图例9-1,已知AD∥BC,AB⊥BC,AB=3,点E为射线BC上一个动点,连接AE,将△ABE沿AE 折叠,点B落在点B’处,过点B’作AD的垂线,分别交AD、BC于点M、N,当点B’为线段MN的三等分点时,BE的长为.图例9-1【解析】取线段AB 的三等分点P 、G ,过点P 、G 作PQ ∥AD ,GH ∥AD以点A 为圆心,以AB 长为半径画弧,该弧与PQ 、GH 的交点即为B ’. 如图例9-2.BA B'B'C D P G Q HBA B'C DG H E NMBA B'C D PQE NM图例9-2图例9-3 图例9-4①取弧BB ’与GH 的交点,如图例9-3所示因为BG = B ’N =1,B ’M =AG =2,由折叠得AB =AB ’=3.在Rt △AGB ’中,由勾股定理得:B ’G 5,所以AM 5. 因为∠MAB ’=∠EB ’N 所以cos ∠MAB ’=cos ∠EB ’N即:'''AM B NAB B E=设BE = B ’E =x 513x= 解得:x 355BE 355②取弧BB ’与PQ 的交点,如图例9-4所示因为BP= B’N=2,B’M=AP=1,由折叠得AB=AB’=3.在Rt△APB’中,由勾股定理得:B’P=22,所以AM=22.因为∠MAB’=∠EB’N所以cos∠MAB’=cos∠EB’N即:''' AM B N AB B E=设BE= B’E=x,则222 3x=解得:x=322,即BE=322.综上所述,BE的长为355或322.【点睛】根据题意画出图形后,利用一线三直角的线段比例相等求解.【针对训练】1、如图,将边长为6的正方形纸片ABCD对折,使AB与DC重合,折痕为EF,展平后,再将点B折到边CD上,使边AB经过点E,折痕为GH,点B的对应点为M,点A的对应点为N(1)若CM=x,则CH=(用含x的代数式表示);(2)求折痕GH的长.【解析】(1)∵CM=x,BC=6,∴设HC=y,则BH=HM=6﹣y,故y2+x2=(6﹣y)2,整理得:y=﹣x2+3,∵∠HMC+∠MHC=90°,∴∠EMD=∠MHC,∴△EDM∽△MCH,∴=,∴=,解得:HC=﹣x2+2x,故答案为:﹣x2+3或﹣x2+2x;(2)方法一:∵四边形ABCD为正方形,∴∠B=∠C=∠D=90°,设CM=x,由题意可得:ED=3,DM=6﹣x,∠EMH=∠B=90°,故∠HMC+∠EMD=90°,∵∠HMC+∠MHC=90°,∴∠EMD=∠MHC,∴△EDM∽△MCH,∴=,即=,解得:x1=2,x2=6,当x=2时,∴CM=2,∴DM=4,∴在Rt△DEM中,由勾股定理得:EM=5,∴NE=MN﹣EM=6﹣5=1,∵∠NEG=∠DEM,∠N=∠D,∴△NEG∽△DEM,∴=,∴=,解得:NG=,由翻折变换的性质,得AG=NG=,过点G作GP⊥BC,垂足为P,则BP=AG=,GP=AB=6,当x=2时,CH=﹣x2+3=,∴PH=BC﹣HC﹣BP=6﹣﹣=2,在Rt△GPH中,GH===2.当x=6时,则CM=6,点H和点C重合,点G和点A重合,点M在点D处,点N在点A处.MN同样经过点E,折痕GH的长就是AC的长.所以,GH长为6.方法二:有上面方法得出CM=2,连接BM,可得BM⊥GH,则可得∠PGH=∠HBM,在△GPH和△BCM中,∴△GPH≌△BCM(SAS),∴GH=BM,∴GH=BM==2.2、已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(11,0),点B(0,6),点P为BC边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,得点B′和折痕OP.设BP=t.(1)如图①,当∠BOP=30°时,求点P的坐标;(2)如图②,经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ,若AQ=m,求m(用含有t的式子表示);(3)在(2)的条件下,当点C′恰好落在边OA上时,求点P的坐标(直接写出结果).【解析】(1)根据题意,∠OBP=90°,OB=6,在Rt△OBP中,由∠BOP=30°,BP=t,得OP=2t.∵OP2=OB2+BP2,即(2t)2=62+t2,解得:t1=2,t2=﹣2(舍去).∴点P的坐标为(2,6);(2)∵△OB′P、△QC′P分别是由△OBP、△QCP折叠得到的,∴△OB′P≌△OBP,△QC′P≌△QCP,∴∠OPB′=∠OPB,∠QPC′=∠QPC,∵∠OPB′+∠OPB+∠QPC′+∠QPC=180°,∴∠OPB+∠QPC=90°,∵∠BOP+∠OPB=90°,∴∠BOP=∠CPQ,又∵∠OBP=∠C=90°,∴△OBP∽△PCQ,∴=,由题意设BP=t,AQ=m,BC=11,AC=6,则PC=11﹣t,CQ=6﹣m.∴=,∴m=t2﹣t+6(0<t<11);(3)过点P作PE⊥OA于E,如图3,∴∠PEA=∠QAC′=90°,∴∠PC′E+∠EPC′=90°,∵∠PC′E+∠QC′A=90°,∴∠EPC′=∠QC′A,∴△PC′E∽△C′QA,∴=,在△PC′E和△OC′B′中,,∴△PC′E≌△OC′B′(AAS),∴PC'=OC'=PC,∴BP=AC',∵AC′=PB=t,PE=OB=6,AQ=m,EC′=11﹣2t,∴=,∵m=t2﹣t+6,∴3t2﹣22t+36=0,解得:t1=,t2=故点P的坐标为(,6)或(,6).3、如图,在菱形纸片ABCD中,AB=15,tan∠ABC=,将菱形纸片沿折痕FG翻折,使点B落在AD边上的点E处,若CE⊥AD,则cos∠EFG的值为.【解析】如图,过点A作AH⊥BC于点H,连接BE,过点P作PE⊥AB,∵AB=15,tan∠ABC=,∴AH=9,BH=12,∴CH=3,∵四边形ABCD是菱形,∴AB=BC=15,AD∥BC,∵AH⊥BC,∴AH⊥AD,且AH⊥BC,CE⊥AD,∴四边形AHCE是矩形∴EC=9,AE=CH=3,∴BE===3,∵将菱形纸片沿折痕FG翻折,使点B落在AD边上的点E处,∴BF=EF,BE⊥FG,BO=EO=∵AD∥BC,∴∠ABC=∠P AE,∴tan∠ABC=tan∠P AE=,且AE=3,∴AP=,PE=,∵EF2=PE2+PF2,∴EF2=+(15﹣EF+)2,∴EF=,∴FO===∴cos∠EFG==,故答案为:4、如图,在菱形ABCD中,AB=5,tan D=,点E在BC上运动(不与B,C重合),将四边形AECD沿直线AE翻折后,点C落在C′处,点D′落在D处,C′D′与AB交于点F,当C′D'⊥AB时,CE长为.【解析】如图,作AH⊥CD于H,交BC的延长线于G,连接AC′.由题意:AD=AD′,∠D=∠D′,∠AFD′=∠AHD=90°,∴△AFD′≌△AHD(AAS),∴∠F AD′=∠HAD,∵∠EAD′=∠EAD,∴∠EAB=∠EAG,∴=(角平分线的性质定理,可以用面积法证明)∵AB∥CD,AH⊥CD,∴AH⊥AB,∴∠BAG=90°,∵∠B=∠D,∴tan B=tan D==,∴=,∴AG=,∴BG===,∴BE:EG=AB:AG=4:3,∴EG=BG=,在Rt△ADH中,∵tan D==,AD=5,∴AH=3,CH=4,∴CH=1,∵CG∥AD,∴=,∴CG=,∴EC=EG﹣CG=﹣=.故答案为.5、如图,已知E为长方形纸片ABCD的边CD上一点,将纸片沿AE对折,点D的对应点D′恰好在线段BE上.若AD=3,DE=1,则AB=5.【解析】∵折叠,∴△ADE≌△AD'E,∴AD=AD'=3,DE=D'E=1,∠DEA=∠D'EA,∵四边形ABCD是矩形,∴AB∥CD,∴∠DEA=∠EAB,∴∠EAB=∠AEB,∴AB=BE,∴D'B=BE﹣D'E=AB﹣1,在Rt△ABD'中,AB2=D'A2+D'B2,∴AB2=9+(AB﹣1)2,∴AB=5故答案为:56、如图,矩形ABCD中,AB=8,BC=10,点N为边BC的中点,点M为AB边上任意一点,连接MN,把△BMN沿MN折叠,使点B落在点E处,若点E恰在矩形ABCD的对称轴上,则BM的长为5或.【解析】①当E在矩形的对称轴直线PN上时,如图1此时∠MEN=∠B=90°,∠ENB=90°,∴四边形BMEN是矩形.又∵ME=MB,∴四边形BMEN是正方形.∴BM=BN=5.②当E在矩形的对称轴直线FG上时,如图2,过N点作NH⊥FG于H点,则NH=4.根据折叠的对称性可知EN=BN=5,∴在Rt△ENH中,利用勾股定理求得EH=3.∴FE=5﹣3=2.设BM=x,则EM=x,FM=4﹣x,在Rt△FEM中,ME2=FE2+FM2,即x2=4+(4﹣x)2,解得x=,即BM=.故答案为5或.7、如图,在矩形ABCD中,AB=6,点E 在边AD上且AE =4,点F是边BC上的一个动点,将四边形ABFE沿EF翻折,A、B的对应点A1、B1与点C在同一直线上,A1B 1与边AD交于点G,如果DG=3,那么BF的长为.【解析】∵△CDG∽△A'EG,A'E=4∴A'G=2∴B'G=4由勾股定理可知CG'=则CB'=由△CDG∽△CFB'设BF=x∴解得x=故答案为第41 页共41 页。
【微专题】2023学年八年级数学上册常考点微专题提分精练(人教版) 三角形折叠求角(解析版)

三角形折叠求角类型一 三角形折叠1.如图 在折纸活动中 小明制作了一张三角形纸片(即ABC ∆) 点D 、E 分别在边AB 、AC 上 将ABC ∆沿着DE 折叠压平后点A 与'A 重合 若75A ∠=︒ 则12∠+∠= ( )A .150︒B .210︒C .105︒D .75︒【答案】A【解析】【分析】 连接A A ' 根据折叠的性质可得∠EA D '=∠EAD=75° 然后根据三角形外角的性质和等量代换即可得出结论.【详解】解:连接A A '由折叠的性质可得∠EA D'=∠EAD=75°∠∠1和∠2分别为∠EA A'和∠DA A'的外角∠∠1=∠EA A'+∠EAA'∠2=∠DA A'+∠DAA'∠∠1+∠2=∠EA A'+∠EAA'+∠DA A'+∠DAA'=(∠EA A'+∠DA A')+(∠EAA'+∠DAA')=∠EA D'+∠EAD=150°故选A.【点睛】此题考查的是三角形中的折叠问题掌握折叠的性质和三角形外角的性质是解决此题的关键.2.如图把△ABC纸片沿DE折叠当A落在四边形BCDE内时则∠A与∠1+∠2之间有始终不变的关系是()A.∠A=∠1+∠2B.2∠A=∠1+∠2C.3A=∠1+∠2D.3∠A=2(∠1+∠2)【答案】B【解析】【分析】本题问的是关于角的问题当然与折叠中的角是有关系的∠1与∠AED的2倍和∠2与∠ADE的2倍都组成平角结合△AED的内角和为180°可求出答案.【详解】∠∠ABC纸片沿DE折叠∠∠1+2∠AED=180°,∠2+2∠ADE=180°∠∠AED=12(180°−∠1),∠ADE=12(180°−∠2)∠∠AED+∠ADE=12(180°−∠1)+12(180°−∠2)=180°−12(∠1+∠2)在△ADE中,∠A=180°−(∠AED+∠ADE)=180°−[180°−12(∠1+∠2)]= 12(∠1+∠2)则2∠A=∠1+∠2 故选择B项.【点睛】本题考查折叠和三角形内角和的性质 解题的关键是掌握折叠的性质.3.已知:如图所示 将△ABC 的∠C 沿DE 折叠 点C 落在点C '处 设,C α∠= ∠AEC ′=β ∠BDC '=γ 则下列关系式成立的是( )A .2α=β+γB .α=β+γC .α+β+γ=180°D .α+β=2γ【答案】A【解析】【分析】 通过平角关系用∠CEC ′、∠CDC ′表示出β、γ 通过三角形的内角和用∠CEC ′、∠CDC ′表示出∠C 、∠C ′ 计算可得结论.【详解】解:由折叠的性质知:∠C =∠C ′=α.∠∠AEC ′+∠CEC ′=180° ∠BDC ′+∠CDC ′=180°∠β=180°-∠CEC ′ γ=180°-∠CDC ′.∠β+γ=360°-∠CEC ′-∠CDC ′.∠∠C +∠CEC ′+CDC ′+∠C ′=360°∠2α=360°-∠CEC ′-∠CDC ′.∠β+γ=2α.故选:A .【点睛】本题考查了三角形的内角和 掌握折叠的性质 用含∠CEC ′、∠CDC ′表示出α、β、γ是解决本题的关键. 4.如图,将∠ABC 沿着DE 翻折,使B 点与B'点重合,若∠1+∠2=80°,则∠B 的度数为( )A .20°B .30°C .40°D .50°【答案】C【解析】【分析】 由折叠的性质可知','BED B ED BDE B DE ∠=∠∠=∠,再利用平角的定义可求出BED BDE ∠+∠的度数 进而利用三角形内角和可求∠B 的度数.【详解】由折叠的性质可知','BED B ED BDE B DE ∠=∠∠=∠∠1'180,2'180BED B ED BDE B DE ∠+∠+∠=︒∠+∠+∠=︒ ∠11(36012)(36080)14022BED BDE ∠+∠=︒-∠-∠=⨯︒-︒=︒ ∠180()18014040B BED BDE ∠=︒-∠+∠=︒-︒=︒故选C【点睛】本题主要考查折叠的性质及三角形内角和定理 掌握折叠的性质及三角形内角和定理是解题的关键. 5.如图 三角形纸片ABC 中 ∠A =65° ∠B =75° 将∠C 沿DE 对折 使点C 落在∠ABC 外的点C′处 若∠1=20° 则∠2的度数为( )A .80°B .90°C .100°D .110°【答案】C【解析】【分析】 先根据平角的定义和翻折变换的性质求出∠DEC 再根据三角形内角和定理求出∠CDE 即可得出答案.解:∠A=65° ∠B=75° ∠1=20°∠∠C=∠C′ =180°-∠A -∠B=40°由翻折变换的性质可得:∠DEC=∠DE C′∠DEC+∠DEB=∠DEC+∠DE C′-∠1=180°∠∠DEC=100°∠∠CDE=∠ED C′=180°-∠C -∠DEC=40°∠∠2=180°-∠CDE -∠ED C′=100°.故选C.【点睛】本题主要考查了翻折变换的性质与三角形内角和定理 解题关键是准确识图 理清题目中角的关系. 6.如图 将三角形纸片ABC 沿DE 折叠 当点A 落在四边形BCED 的外部时 测量得∠1=70° ∠2=132° 则∠A 为( )A .40°B .22°C .30°D .52°【答案】B【解析】【分析】 利用四边形的内角和定理求出B C ∠+∠ 再利用三角形的内角和定理可得结果.【详解】∠1=70∠︒ 2=132∠︒∠3601236070132158B C ∠+∠=︒-∠-∠=︒-︒-︒=︒∠180()18015822A B C ∠=︒-∠+∠=︒-︒=︒故选:B .本题主要考查了多边形的内角和定理及三角形的内角和定理 关键是运用多边形的内角和定理求出B C ∠+∠的度数.7.如图所示 把ABC 沿直线DE 翻折后得到A DE ' 如果36A EC '∠=︒ 那么AED =∠___度.【答案】72【解析】【分析】根据折叠的性质:折叠前后图形的形状和大小不变 只是位置改变 对应边和对应角相等 可以得到AED A ED '∠=∠ 再根据平角的定义即可求解.【详解】 ABC 沿直线DE 翻折后得到A DE '∴AED A ED '∠=∠180AED A ED A EC ''∠+∠+∠=︒ 36A EC '∠=︒∴18036722AED ︒-︒∠==︒. 故答案为:72.【点睛】本题考查了折叠的性质 三角形折叠中的角度问题 它属于轴对称 熟练掌握折叠的性质是解题的关键. 8.如图 把ABC 纸片沿DE 折叠 使点B 落在图中的B '处 设'B ∠EC ∠= 1 'B ∠DA ∠=2.若B ∠=25︒ 则∠2∠-1=______︒【答案】50【解析】【分析】由折叠性质求得'25B ∠=︒ 由三角形的外角性质 用1∠表示 2∠ 进而求得21∠-∠.【详解】解:25B ∠=︒'25B B ∠∠∴==︒31'125B ∠∠∠∠=+=+︒2312525B ∠∠∠∠=+=+︒+︒2150∠∠∴-=︒故答案为50.【点睛】本题主要考查三角形外角的性质 折叠的性质 关键是根据三角形的外角的性质表示出1∠与2∠的关系式.类型二多边形折叠9.如图将四边形纸片ABCD沿EF折叠点A落在A1处若∠1+∠2=90°则∠A的度数是()A.45°B.40°C.35°D.30°【答案】A【解析】【分析】根据翻折变换的性质和平角的定义求出∠3+∠4 再利用三角形的内角和定理列式计算即可得解.【详解】解:∠四边形纸片ABCD沿EF折叠点A落在A1处∠∠3+∠4=12(180°-∠1)+12(180°-∠2)=180°-12(∠1+∠2)∠∠1+∠2=90°∠∠3+∠4=180°-12×90°=180°-45°=135°在∠AEF中∠A=180°-(∠3+∠4)=180°-135°=45°.故选:A.【点睛】本题考查了三角形的内角和定理翻折变换的性质平角的定义熟记各性质并整体思想的利用是解题的关键.10.如图所示在四边形纸片ABCD中∠A=80° ∠B=70° 将纸片沿着MN折叠使C D分别落在直线AB 上的C'D处则∠AMD'+∠BNC'等于()A .50°B .60°C .70°D .80°【答案】B【解析】【分析】 首先根据四边形内角和定理可得∠D+∠C=210° 再利用折叠性质可得∠'MD B =∠D ∠'NC A =∠C 即∠'MD B +∠'NC A =210° 从而得出∠'MD A +∠'NC B =150° 最后进一步利用三角形内角和定理求解即可.【详解】∠∠A=80° ∠B=70°∠∠D+∠C=360°−∠A −∠B=210°由折叠性质可得:∠'MD B =∠D ∠'NC A =∠C∠∠'MD B +∠'NC A =210°∠∠'MD A +∠'NC B =360°−(∠'MD B +∠'NC A )=150°∠∠'AMD +∠'BNC =360°−(∠'MD A +∠'NC B )−(∠A +∠B )=60°故选:B .【点睛】本题主要考查了三角形与四边形内角和定理以及折叠的性质 熟练掌握相关概念是解题关键.11.如图所示 将三角形纸片ABC 沿DE 折叠 使点B 落在点B ′处 若EB ′恰好与BC 平行 且∠B =80° 则∠CDE =_____°.【答案】130【解析】【分析】先求出∠B=∠B′=80° ∠BDE=∠B′DE根据平行线的性质得到∠B′DC=80° 进而得到∠BD B′=100° ∠BDE=50° 即可求出∠CDE=130°.【详解】解:由折叠的定义得∠B=∠B′=80° ∠BDE=∠B′DE∠EB′∠BC∠∠B′=∠B′DC=80°∠∠BD B′=180°-∠B′DC=100°∠∠BDE=∠B′DE=50°∠∠CDE=180°-∠BDE=130°.故答案为:130【点睛】本题考查了折叠的定义平行线的性质邻补角的定义等知识熟知相关知识并根据图形灵活应用是解题关键.12.如图△ABC中将边BC沿虚线翻折若∠1+∠2=102°,则∠A的度数是______.【答案】51°【解析】【分析】延长折叠后的直线交于A’ 根据折叠的性质及内角和即可求解.【详解】如图延长折叠后的直线交于A’由于折叠∠∠1+2∠3=180° ∠2+2∠4=180°∠∠1+∠2=102° ∠1+2∠3+∠2+2∠4=360°∠2∠3+2∠4=258°∠∠3+∠4=129°∠∠A=∠A’=180°-(∠3+∠4)=51°【点睛】此题主要考查折叠的性质 解题的关键是根据折叠作出辅助线进行求解.13.将一张纸如图所示折叠后压平 点F 在线段BC 上 EF 、GF 为两条折痕 若∠1=57° ∠2=20° ∠3的度数_____度【答案】23【解析】【分析】根据折叠的性质可知 1EFB '∠=∠ 3GFC '∠=∠ 然后对123180EFB GFC '∠+∠+∠+∠+∠'=︒计算求解即可.【详解】解:由折叠的性质可知 157EFB '∠=∠=︒ 3GFC '∠=∠∠123180EFB GFC '∠+∠+∠+∠+∠'=︒ ∠1805757203232︒-︒-︒-︒∠==︒ 故答案为:23°.【点睛】本题考查了折叠的性质 角的计算.解题的关键在于找出角度的数量关系.14.利用折纸可以作出角平分线 如图1则OC 为AOB ∠的平分线 如图2、图3 折叠长方形纸片 OC OD 均是折痕 折叠后 点A 落在点'A 点B 落在点'B 连接'OA .①如图2 若点'B 恰好落在'OA 上 且32AOC ∠=︒ 则BOD ∠=__________;②如图3 当点'B 在'COA ∠的内部时 连接'OB 若44AOC ∠=︒ 61BOD ∠=︒ 求''A OB ∠的度数为__________.【答案】 58︒ 30【解析】【分析】①由题意知AOC A OC '∠=∠ BOD B OD '∠=∠ 根据180AOC A OC BOD B OD ''∠+∠+∠+∠=︒ 计算求解即可;② 由题意知AOC A OC '∠=∠ BOD B OD '∠=∠ 根据180AOC A OC A OD BOD ''∠+∠+∠+∠=︒ 求出A OD '∠的值 进而根据A OB B OD A OD ''''∠=∠-∠计算求解即可.【详解】解:①由题意知AOC A OC '∠=∠ BOD B OD '∠=∠∠180AOC A OC BOD B OD ''∠+∠+∠+∠=︒ 32AOC ∠=︒∠58BOD ∠=︒故答案为:58°.②由题意知AOC A OC '∠=∠ BOD B OD '∠=∠∠180AOC A OC A OD BOD ''∠+∠+∠+∠=︒ 44AOC ∠=︒ 61BOD ∠=︒∠1802446131A OD '∠=︒-⨯︒-︒=︒∠30A OB B OD A OD ''''∠=∠-∠=︒故答案为:30°.【点睛】本题考查了角平分线.解题的关键在于找出角度的数量关系.类型三 多次折叠15.如图所示 把一个三角形纸片ABC 顶角向内折叠3次之后 3个顶点不重合 那么图中∠1+∠2+∠3+∠4+∠5+∠6的度数和是()A.180°B.270°C.360°D.无法确定【答案】C【解析】【详解】由题意知∠1+∠2+∠3+∠4+∠5+∠6=∠B+∠B'+∠C+∠C'+∠A+∠A'∠∠B=∠B' ∠C=∠C' ∠A=∠A'∠∠1+∠2+∠3+∠4+∠5+∠6=2(∠B+∠C+∠A)=360° 故选C.16.如图将∠ABC沿DE、HG、EF翻折三个顶点均落在点O处若∠1=131° 则∠2的度数为()A.49°B.50°C.51°D.52°【答案】A【解析】【分析】先根据折叠性质得:∠HOG=∠B∠DOE=∠A∠EOF=∠C根据三角形内角和为180°和周角360°求出结论.【详解】由折叠得:∠HOG=∠B∠DOE=∠A∠EOF=∠C∠∠A+∠B+∠C=180°∠∠HOG+∠DOE+∠EOF=180°∠∠1+∠2+∠HOG+∠DOE+∠EOF=360°∠∠1+∠2=180°∠∠1=131°∠∠2=180°﹣131°=49°故选:A.【点睛】本题考查折叠的性质、三角形内角和解题的关键是掌握折叠的性质、三角形内角和.17.如图a是长方形纸带∠DEF=25° 将纸带沿EF折叠成图b 再沿BF折叠成图c 则图c中的∠CFE的度数是____________°.【答案】105°【解析】【详解】由图a知∠EFC=155°.图b中∠EFC=155° 则∠GFC=∠EFC-∠EFG=155°-25°=130°.图c中∠GFC=130° 则∠CFE=130°-25°=105°.故答案为105°.点睛:在长方形的折叠问题中因为有平行线和角平分线所以存在一个基本的图形等腰三角形即图b中的等腰∠CEF其中CE=CF这个等腰三角形是解决本题的关键所在.18.如图1 ∠ABC中沿∠BAC的平分线AB1折叠剪掉重叠部分;将余下部分沿∠B1A1C的平分线A1B2折叠剪掉重叠部分;…;将余下部分沿∠B n A n C的平分线A n B n+1折叠点B n与点C重合无论折叠多少次只要最后一次恰好重合我们就称∠BAC是∠ABC的好角.(1)如图2 在∠ABC中∠B>∠C 若经过两次折叠∠BAC是∠ABC的好角则∠B与∠C的等量关系是_______;(2)如果一个三角形的最小角是20° 则此三角形的最大角为______时该三角形的三个角均是此三角形的好角.【答案】 B 2C ∠∠= 140°、120°或80°【解析】【分析】(1)根据折叠性质可得∠A 1B 1B 2=∠C ∠AA 1B 1=∠B 由三角形外角性质可得∠AA 1B 1=2∠C 根据等量代换可得∠B=2∠C ;(2)先求出经过三次折叠 ∠BAC 是△ABC 的好角时 ∠B 与∠C 的等量关系为∠B=3∠C 进而可得经过n 次折叠 ∠BAC 是△ABC 的好角时∠B 与∠C 的等量关系为∠B=n∠C 因为最小角是20º 是△ABC 的好角 根据好角定义 设另两角分别为20mº 4mn° 由题意得20m+20mn+20=180° 所以m(n+1)=8 再根据m 、n 都是正整数可得m 与n+1是8的整数因子 从而可以求得结果.【详解】(1)根据折叠性质得∠B=∠AA 1B 1 ∠A 1B 1B 2=∠C∠∠AA 1B 1=∠A 1B 1B 2+∠C∠∠B=2∠C故答案为∠B=2∠C(2)如图:∠根据折叠的性质知 ∠B=∠AA 1B 1 ∠C=∠A 2B 2C ∠A 1B 1C=∠A 1A 2B 2∠根据三角形的外角定理知 ∠A 1A 2B 2=∠C+∠A 2B 2C=2∠C ;∠根据四边形的外角定理知 ∠BAC+∠B+∠AA 1B 1-∠A 1B 1C=∠BAC+2∠B -2∠C=180°根据三角形ABC 的内角和定理知 ∠BAC+∠B+∠C=180°∠∠B=3∠C ;∠当∠B=2∠C 时 ∠BAC 是△ABC 的好角;当∠B=3∠C 时 ∠BAC 是△ABC 的好角;故若经过n 次折叠∠BAC 是△ABC 的好角 则∠B 与∠C (不妨设∠B >∠C )之间的等量关系为∠B=n∠C ; ∠最小角为20°∠设另两个角为20m°和20mn°∠20°+20m°+20mn°=180° 即m(1+n)=8∠m 、n 为整数∠m=1 1+n=8;或m=2 1+n=4;或m=4 1+n=2.解得:m=1 n=7;m=2 n=3 m=4 n=1∠另两个角为20°、140°或40°、120°或80°、80°∠此三角形最大角为140°、120°或80°时 三个角均是此三角形的好角.故答案为140°、120°或80°【点睛】本题考查了翻折变换(折叠问题).充分利用三角形内角和定理、三角形外角定理以及折叠的性质是解题关键.19.直线MN 与直线PQ 垂直相交于O 点A 在射线OP 上运动 点B 在射线OM 上运动 连接AB .(1)如图1 已知AC BC 分别是BAP ∠和ABM ∠角的平分线①点A B 在运动的过程中 ACB ∠的大小是否发生变化?若发生变化 请说明理由;若不发生变化 试求出ACB ∠的大小.②如图2 将ABC ∆沿直线AB 折叠 若点C 落在直线PQ 上 记作点C ' 则ABO ∠=_______︒;如图3 将ABC ∆沿直线AB 折叠 若点C 落在直线MN 上 记作点C '' 则ABO ∠=________︒.(2)如图4 延长BA 至G 已知BAO ∠ OAG ∠的角平分线与BOQ ∠的角平分线交其延长线交于E F 在AEF ∆中 如果有一个角是另一个角的32倍 求ABO ∠的度数. 【答案】(1)∠ACB 的大小不会发生变化 ∠ACB =45°;(2)30 60;(3)60°或72°.【解析】【分析】(1)①由直线MN 与直线PQ 垂直相交于O 得到∠AOB=90° 根据三角形的外角的性质得到∠PAB+∠ABM=270° 根据角平分线的定义得到∠BAC=12∠PAB ∠ABC=12∠ABM 于是得到结论;②图2中 由于将∠ABC 沿直线AB 折叠 若点C 落在直线PQ 上 得到∠CAB=∠BAQ 由角平分线的定义得到∠PAC=∠CAB 根据三角形的内角和即可得到结论;图3中根据将∠ABC沿直线AB折叠若点C落在直线MN上得到∠ABC=∠ABN 由于BC平分∠ABM 得到∠ABC=∠MBC 于是得到结论;(2)由∠BAO与∠BOQ的角平分线相交于E可知∠EAO=12∠BAO ∠EOQ=12∠BOQ 进而得出∠E的度数由AE、AF分别是∠BAO和∠OAG的角平分线可知∠EAF=90° 在∠AEF中由一个角是另一个角的32倍分情况进行分类讨论即可解答.【详解】(1)①∠ACB的大小不变∠直线MN与直线PQ垂直相交于O∠∠AOB=90°∠∠OAB+∠OBA=90°∠∠PAB+∠ABM=270°∠AC、BC分别是∠BAP和∠ABM角的平分线∠∠BAC=12∠PAB ∠ABC=12∠ABM∠∠BAC+∠ABC=12(∠PAB+∠ABM)=135°∠∠ACB=45°;②∠图2中将∠ABC沿直线AB折叠若点C落在直线PQ上∠∠CAB=∠BAQ∠AC平分∠PAB∠∠PAC=∠CAB∠∠PAC=∠CAB=∠BAO=60°∠∠AOB=90°∠∠ABO=30°∠图3中将∠ABC沿直线AB折叠若点C落在直线MN上∠∠ABC=∠ABN∠BC平分∠ABM∠∠ABC=∠MBC∠∠MBC=∠ABC=∠ABN∠∠ABO=60°故答案为:30 60;(2)∠∠BAO与∠BOQ的角平分线相交于E∠∠EAO=12∠BAO ∠EOQ=12∠BOQ∠∠E=∠EOQ-∠EAO=12(∠BOQ-∠BAO)=12∠ABO∠AE、AF分别是∠BAO和∠OAG的角平分线∠∠EAF=90°.在∠AEF中∠有一个角是另一个角的32倍故有:①∠EAF=32∠E ∠E=60° ∠ABO=120°(不合题意舍去);②∠EAF=32∠F ∠E=30° ∠ABO=60°;③∠F=32∠E ∠E=36° ∠ABO=72°;④∠E=32∠F ∠E=54° ∠ABO=108°(不合题意舍去);.∠∠ABO为60°或72°.【点睛】本题主要考查的就是角平分线的性质以及三角形内角和定理的应用.解决这个问题的关键就是要能根据角平分线的性质将外角的度数与三角形的内角联系起来然后再根据内角和定理进行求解.同学们在解答这种问题的时候一定要注意外角与内角之间的联系不能只关注某一部分.在需要分类讨论的时候一定要注意分类讨论的思想.。
三角形折叠问题总结

三角形折叠问题总结
三角形折叠问题是指将一个平面三角形折叠成一个四面体的问题,这个问题可以通过解析几何、向量运算、线性代数等多种数学方法进行求解。
下面是对该问题的总结:
1. 折叠前后的三角形具有相似性质。
2. 折叠后的四面体底面积等于原三角形的面积。
3. 折叠后的四面体体积可以通过向量叉积计算。
4. 折叠后的四面体的高可以通过点到平面距离公式计算。
5. 折叠后的四面体的底面中心、重心、外心、垂心的坐标可以通过向量运算计算。
6. 折叠后的四面体底面与侧面、侧面之间的夹角可以通过余弦定理和向量运算计算。
7. 通过三维软件制作三维模型,可以更加直观地看到折叠前后的变化。
8. 该问题的应用包括三角形的展开、折纸问题、人工智能中的空间感知等。
总之,三角形折叠问题是一个基础但重要的数学问题,通过掌
握相关的数学知识和方法,可以深入了解三维空间中的几何性质,对于相关领域的研究和应用有很大的帮助。
折叠问题中的角度运算
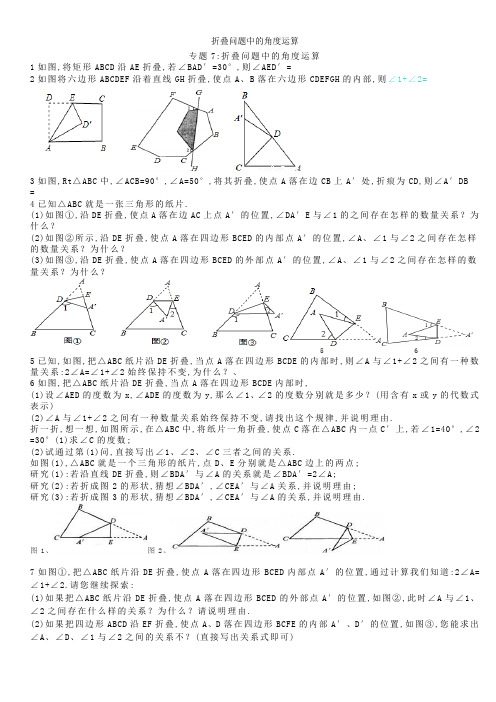
专题7:折叠问题中的角度运算1如图,将矩形ABCD沿AE折叠,若∠BAD′=30°,则∠AED′=2如图将六边形ABCDEF沿着直线GH折叠,使点A、B落在六边形CDEFGH的内部,则∠1+∠2=3如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=4已知△ABC就是一张三角形的纸片.(1)如图①,沿DE折叠,使点A落在边AC上点A′的位置,∠DA′E与∠1的之间存在怎样的数量关系?为什么?(2)如图②所示,沿DE折叠,使点A落在四边形BCED的内部点A′的位置,∠A、∠1与∠2之间存在怎样的数量关系?为什么?(3)如图③,沿DE折叠,使点A落在四边形BCED的外部点A′的位置,∠A、∠1与∠2之间存在怎样的数量关系?为什么?5 65已知,如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的内部时,则∠A与∠1+∠2之间有一种数量关系:2∠A=∠1+∠2始终保持不变,为什么?、6如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,(1)设∠AED的度数为x,∠ADE的度数为y,那么∠1、∠2的度数分别就是多少?(用含有x或y的代数式表示)(2)∠A与∠1+∠2之间有一种数量关系始终保持不变,请找出这个规律,并说明理由.折一折,想一想,如图所示,在△ABC中,将纸片一角折叠,使点C落在△ABC内一点C′上,若∠1=40°,∠2 =30°(1)求∠C的度数;(2)试通过第(1)问,直接写出∠1、∠2、∠C三者之间的关系.如图(1),△ABC就是一个三角形的纸片,点D、E分别就是△ABC边上的两点;研究(1):若沿直线DE折叠,则∠BDA′与∠A的关系就是∠BDA′=2∠A;研究(2):若折成图2的形状,猜想∠BDA′,∠CEA′与∠A关系,并说明理由;研究(3):若折成图3的形状,猜想∠BDA′,∠CEA′与∠A的关系,并说明理由.图1、图2、7如图①,把△ABC纸片沿DE折叠,使点A落在四边形BCED内部点A′的位置,通过计算我们知道:2∠A=∠1+∠2.请您继续探索:(1)如果把△ABC纸片沿DE折叠,使点A落在四边形BCED的外部点A′的位置,如图②,此时∠A与∠1、∠2之间存在什么样的关系?为什么?请说明理由.(2)如果把四边形ABCD沿EF折叠,使点A、D落在四边形BCFE的内部A′、D′的位置,如图③,您能求出∠A、∠D、∠1与∠2之间的关系不?(直接写出关系式即可)8三角形纸片ABC中,∠A=55°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内(如图),则∠1+∠2的度数为度.9如图,已知四边形ABCD,∠C=72°,∠D=81°.沿EF折叠四边形,使点A、B分别落在四边形内部的点A′、B′处,求∠1+∠2的大小.10、如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=22°,则∠BDC等于( )11、将五边形纸片ABCDE按如图方式折叠,折痕为AF,点E、D分别落在E′、D′,已知∠AFC=76°,则∠CFD′等于12如图,在平面内,把矩形ABCD沿EF对折,若∠1=50°,则∠AEF等于13如图,把△ABC沿线段DE折叠,使点A落在点F处,BC∥DE;若∠B=50°,则∠BDF的度数为1 1如图,把一张长方形纸片ABCD,沿EF折叠后,ED′与BC的交点为G,点D,C分别落在D′,C′的位置上.若∠EFG=55°,则∠1等于14将一条两边沿互相平行的纸带按如图折叠.设∠1=x°,则∠α的度数为( )15将长方形ABCD沿折痕EF折叠,使CD落在GH的位置,若∠FGH=55°,则∠HEF=( )16如图,一个宽度相等的纸条按如图所示方法折叠一下,则∠1=( )17如图,D、E分别为△ABC的边AB、AC上的点,DE∥BC,将△ABC沿线段DE折叠,使点A落在BC上的点F处,若∠B=55°,则∠BDF的度数为( )18如图所示,将一张长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置上,ED′的延长线与BC的交点为G.若∠EFG=80°,则∠BFC′的度数为( )19如图a就是长方形纸带,∠DEF=24°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数( )20如图,三角形纸片ABC,AB=10cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为( )21如图,将长方形ABCD沿对角线BD折叠,使点C恰好落在如图C′的位置,若∠DBC=15°,则∠ABC′=( )22一张长方形纸条折成如图的形状,如果∠1=130°,∠2=( )23如图:将一张长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,ED′的延长线与BC交于点G.若∠EFG=55°,则∠1=( )24如图,已知长方形ABCD,我们按如下步骤操作可以得到一个特定角:(1)以点A所在直线为折痕,折叠纸片,使点B落在AD上,折痕与BC交于E;(2)将纸片展平后,再一次折叠纸片,以E所在直线为折痕,使点A落在BC上,折痕EF交AD于F,则∠AEF的度数25如图,将纸片△ABC沿着DE折叠压平,且∠1+∠2=72°,则∠A=( )26如图,把△ABC纸片沿DE折叠,当点A落在四边形BCED的外部时,则∠A与∠1与∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,您发现的规律就是( )27如图,三角形纸片ABC,AB=10cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为( )28一个宽度相等纸条,按如图所示的方式折叠一下,已知∠3=120°,则∠1的度数为( )29如图,把一张长方形纸条折叠后,若∠AOB′=70°,则∠OGC的度数为( )30如图,∠A=60°,∠B=70°,将纸片的一角折叠,使点C落在△ABC内,若∠2=80°,则∠1的度数为( )31如图(1)就是长方形纸带,∠DEF=α,将纸带沿EF折叠成图(2),再沿BF折叠成图(3),则图(3)中的∠CFE的度数就是( )32如图,生活中,将一个宽度相等的纸条按右图所示折叠一下,如果∠1=140°,那么∠2的度数为( )33如图,四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B =( )34如图,一张长方形纸条沿AB折叠,如果∠1=124°,那么∠2的度数就是( )35如图,把长方形ABCD沿EF对折后使两部分重合,若∠AEF=110°,则∠1=( )36如图,一张三角形纸片△ABC,沿DE折叠使得顶点C落在边AB上,若DE∥AB,∠A=45°,则∠ADC的度数就是( ) 37如图所示,把一个三角形纸片ABC顶角向内折叠3次之后,3个顶点不重合,那么图中∠1+∠2+∠3+∠4+∠5+∠6的度数与就是( )38如图,将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处,则∠1+∠2的度数为( )39如图,正方形纸片ABCD的边长为8,将其沿EF折叠,则图中①②③④四个三角形的周长之与为( )40如图,将五边形ABCDE沿AE对折到如图的位置,其中∠AEC=72°,则∠CED′=( )41如图,在△ABC中,∠A=35°,在平面内沿直线DE将△ABC折叠后,量得∠BDA′=110°,那么∠CEA′的度数为( ) 42如图,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB=65°,则∠AED′等于( )43如图,已知△ABC中,∠BAC=140°,现将△ABC进行折叠,使顶点B、C均与顶点A重合,求∠DAE的度数.。
三角形角度问题带参考答案
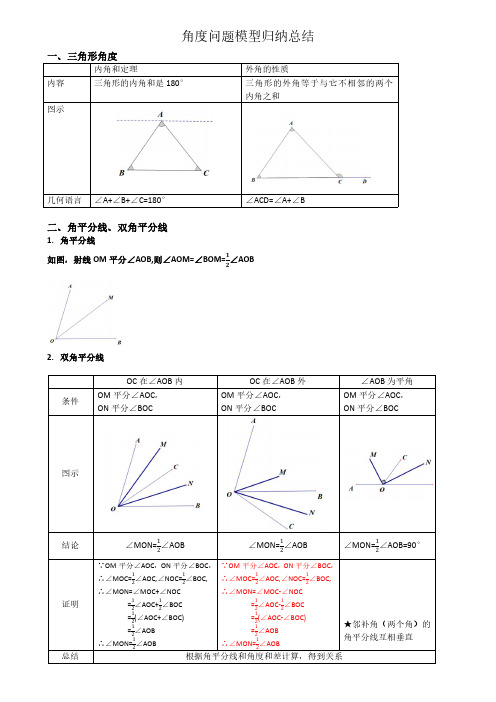
条件
OC 在∠AOB 内 OM 平分∠AOC, ON 平分∠BOC
OC 在∠AOB 外 OM 平分∠AOC, ON 平分∠BOC
∠AOB 为平角 OM 平分∠AOC, ON 平分∠BOC
图示
结论 证明 总结
∠MON=12∠AOB
∠MON=12∠AOB
∠MON=12∠AOB=90°
∵OM 平分∠AOC,ON 平分∠BOC, ∵OM 平分∠AOC,ON 平分∠BOC,
∵∠D+∠E=180°+∠A, ∠P=90°+ 12∠A,
∴∠D+∠E=2∠P
五、常见模型+双角平分线
条件
8 字形+ AP 平分∠BAC, CP 平分∠DCB
飞镖+ AP 平分∠BAD, CP 平分∠BCD
小鱼+ AP 平分∠EAD, CP 平分∠DCF
图示
结论
∠P= 12(∠B+∠D)
∠P= 12(∠B+∠D)
∠2+∠BEB'=180°, ∴∠1+∠BDB'+∠2+∠BEB'=360°
又 ∵ ∠ B+ ∠ B’+ ∠ BDB+ ∠ BEB'=360°,∠B=∠B’ ∴∠1+∠2=2∠B
如图, ∵∠1=∠B+∠3,
∠3=∠B’+∠2, ∠B=∠B’ ∴∠1=2∠B+∠2 ∴∠1-∠2=2∠B
如图, ∵∠2=∠B+∠3,
★邻补角(两个角)的 角平分线互相垂直
根据角平分线和角度和差计算,得到关系
三、三角形的双角平分线
条件
两内 △ABC,BP 平分∠ABC, CP 平分∠ACB
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题:三角形折叠问题中的角度运算
活动一:
如图,Rt △ABC 中,∠ACB=90°,∠A=50°,将其折叠,使点A 落在边CB 上A ′处,折痕为CD ,则∠A ′DB=( )
活动二:
已知△ABC 是一张三角形的纸片.
(1)如图①,沿DE 折叠,使点A 落在边AC 上点A ′的位置,∠DA ′E 与∠1的之间存在怎样的数量关系?为什么?
(2)如图②所示,沿DE 折叠,使点A 落在四边形BCED 的内部点A ′的位置,∠A 、∠1与∠2之间存在怎样的数量关系?为什么?
(3)如图③,沿DE 折叠,使点A 落在四边形BCED 的外部点A ′的位置,∠A 、∠1与∠2之间存在怎样的数量关系?为什么?
(4)如图4,沿DE 折叠,使点A 落在四边形BCED 的外部,∠A 、∠1与∠2之间存在怎样的数量关系?为什么?
图4
活动三:
1、三角形纸片ABC中,∠A=55°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内(如图),则∠1+∠2的度数为()度.
2、如上图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=22°,则∠BDC等于()
3、如图所示,把一个三角形纸片ABC顶角向内折叠3次之后,3个顶点不重合,那么图中∠1+∠2+∠3+∠4+∠5+∠6的度数是()
4、如上图,将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处,则∠1+∠2的度数为()
5、如图,已知△ABC中,∠BAC=140°,现将△ABC进行折叠,使顶点
B、C均与顶点A重合,求∠DAE的度数.
6、将一条两边沿互相平行的纸带按如图折叠.设∠1=20°,则∠α的度数为()
7、如图,一个宽度相等的纸条按如图所示方法折叠一下,则∠1=()
8、如图,把△ABC沿线段DE折叠,使点A落在点F处,
BC∥DE;若∠B=50°,则∠BDF的度数为()。
