小学三年级奥数 12巧求周长
【小学奥数】巧求周长

一、基本概念①周长:封闭图形一周的长度就是这个图形的周长. ②面积:物体的表面或封闭图形的大小,叫做它们的面积.二、基本公式:①长方形的周长2=⨯(长+宽),面积=长⨯宽.②正方形的周长4=⨯边长,正方形的面积=边长⨯边长.三、常用方法:(1)对于基本的长方形和正方形图形,可以直接用公式求出它们的周长和面积,对于一些不规则的比较复杂的几何图形,我们可以采用转化的数学思想方法割补成基本图形,利用长方形、正方形周长及面积计算的公式求解.(2)转化是一种重要的数学思想方法,在转化过程中要抓住“变”与“不变”两个部分.转化后的图形虽然形状变了,但其周长和面积不应该改变,所以在求解过程中不能遗漏掉某些线段的长度或某部分图形的面积.转化的目标是将复杂的图形转化为周长或面积可求的图形.(3)寻求正确有效的解题思路,意味着寻找一条摆脱困境、绕过障碍的途径.因此,我们在解决数学问题时,思考的着重点就是要把所需解决的问题转化为已经能够解决的问题.也就是说,在直接求解不容易或很难找到解题途径的问题时,我们往往转化问题的形式,从侧面或反面寻找突破口,知道最终把它转化成一个或若干个能解决的问题.这种解决问题的思想在数学中叫“化归”,它是数学思维中重要的思想和方法.(4)在几何中,有许多图形是由一些基本图形组合、拼凑而成的.这样的图形我们称为不规则图形.不规则图形的面积往往无法直接应用公式计算.那么,不规则图形的面积怎样去计算呢?对称、旋转、平移这几种几何变换就是解决这类面积问题的手段.四、几个重要的解题思想 (1)平移在平面图形的计算中,常常要将一个平面图形移动到平面上的另一个位置进行计算.其中,将图形沿一个固定方向的移动叫做平移,一个图形经过平行移动不改变其形状与大小,所以图形面积是保持不变的.利知识点拨4-2-2.巧求周长用图形的平移,可以使面积计算问题的解法简捷明快,颇有新意.(2)割补割补法在我国古代叫“出入相补原理”,我国古代魏晋时期著名的数学家刘徽在《九章算术注》中就明确地提出“出入相补,各从其类”的出入相补原理.这个原理的内容是几何图形经过分、合、移、补所拼凑成的新图形,它的面积不变.(3)旋转在平面图形的割补中,有时要将一个图形绕定点旋转到一个新的位置,产生一种新的图形结构,图形在转动过程中形状大小不发生改变.利用这种新的图形结构可以帮我们解决面积的计算问题.(4)对称平面图形中有许多简单漂亮的图形都是轴对称图形.轴对称图形沿对称轴折叠,轴两侧可以完全重合.也就是说,如果一个图形是轴对称图形,那么对称轴平分这个图形的面积.熟悉轴对称图形这个性质,对面积计算会有很大帮助.(5)代换在几何计算中,对有关数量进行适当的等量代换也是解决问题的已知技巧.小结:本讲主要通过求一些不规则图形的周长,体会一种转化思想,重点在于把不规则图形转化为规则图形的方法,包括平移、旋转、割补、差不变原理,通过这些方法的学习,让学生体会求周长的技巧,提高学生的观察能力、动手操作能力、综合运用能力.例题精讲模块一、图形的周长和面积——割补法【例 1】求图中所有线段的总长(单位:厘米)D【例 2】如图所示,点B是线段AD的中点,由A、B、C、D四个点所构成的所有线段的长度均为整数,若这些线段的长度之积为10500,则线段AB的长度是。
小学奥数习题版三年级几何巧求周长教师版
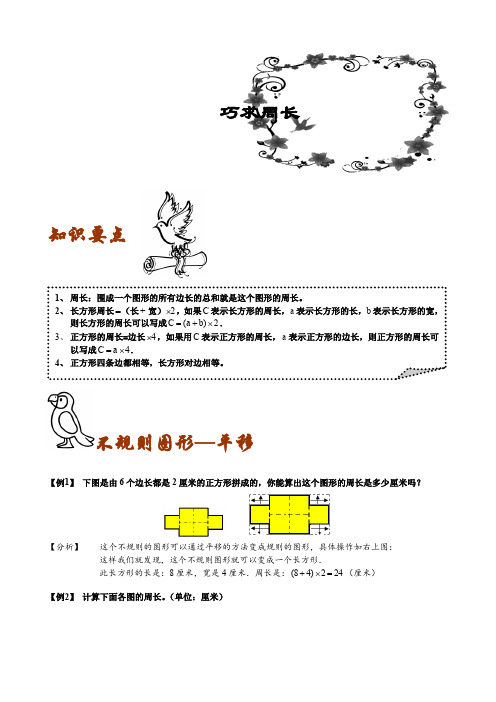
知识要点不规则图形—平移【例1】下图是由6个边长都是2厘米的正方形拼成的,你能算出这个图形的周长是多少厘米吗?【分析】这个不规则的图形可以通过平移的方法变成规则的图形,具体操作如右上图:这样我们就发现,这个不规则图形就可以变成一个长方形.此长方形的长是:8厘米,宽是4厘米.周长是:(84)224+⨯=(厘米)【例2】计算下面各图的周长。
(单位:厘米)巧求周长51015381053【分析】 (1)周长是:35216+⨯=()(厘米)(2)周长是:10823242+⨯+⨯=()(厘米) (3)周长是:⨯⨯(10+15)2+52=60(厘米)【例3】 求下列图形的周长.(单位:米)10040404040408040302013【分析】 对于不规则的图形计算周长,我们一般可以通过平移,把不规则的图形转换成长方形或正方形来进行计算.⑴这个不规则图形通过平移,可以转化成求一个长方形的周长4+条40米线段;列式: (100403)2440600+⨯⨯+⨯=(米)⑵这个不规则图形通过平移,可以转化成求一个长方形的周长2+条30米线段;列式: (8040)2302300+⨯+⨯=(米)⑶这个不规则图形通过平移,可以转化成求一个正方形的周长;列式:13452⨯=(米)【例4】 计算下面各图的周长(单位:厘米)11432852049【分析】 (1)周长是:20524466+⨯+⨯=()(厘米) (2)周长是:8322226+⨯+⨯=()(厘米)(3)周长是: 911124440+++⨯+⨯=()(厘米)【例5】 (第七届小机灵杯复赛第8题)下面两张图中,周长比较大的是 。
(在横线上填写表示图名的字母)【分析】通过移动线条图A 可以变形为长为14宽为10的长方形,而图B 可以变成长为14宽为10的长方形再加6条小线段,因此可知这两张图中,周长比较大的是图B 。
【例6】 (第一届小机灵杯第7题)把边长分别是10厘米、9厘米、8厘米和7厘米的4个正方形按从大到小的顺序排成一行(如图),排成的图形周长是( )厘米。
最新小学三年级奥数 12巧求周长

小学三年级奥数12巧求周长本教程共30讲第12讲巧求周长我们知道:这两个计算公式看起来十分简单,但用途却十分广泛。
用它们可以解决许多直角多边形(所有的角都是直角的多边形)的周长问题。
这是因为直角多边形总可以分割成若干个正方形或长方形。
例如,下面的图形都可以分割成若干个正方形或长方形,当然分割的方法不是唯一的。
由此,可以演变出许多只涉及正方形、长方形周长计算公式的题目。
例1一个苗圃园(如左下图),周边和中间有一些路供人行走(图中线段表示“路”),几个小朋友在里面观赏时发现:从A处出发,在速度一样的情况下,只要是按“向右”、“向上”方向走,几个人分头走不同的路线,总会同时达到B处。
你知道其中的道理吗?分析与解:如右上图所示,将各个交点标上字母。
由A处到B处,按“向右”、“向上”方向走,只有下面六条路线:(1)A→C→D→E→B;(2)A→C→O→E→B;(3)A→C→O→F→B;(4)A→H→G→F→B;(5)A→H→O→E→B;(6)A→H→O→F→B。
因为A→C与H→O,G→F的路程一样长,所以可以把它们都换成A→C;同理,将O→E,F→B都换成C→D;将A→H,C→O都换成D→E;将H →G,O→F都换成E→B。
这样换过之后,就得到六条路线的长度都与第(1)条路线相同,而第(1)条路线的长“AD+DB”就是长方形的“长+宽”,也就是说,每条路线的长度都是“长+宽”。
路程、速度都相同,当然到达B处的时间就相同了。
例2计算下列图形的周长(单位:厘米)。
解:(1)将图中右上缺角处的线段分别向上、向右平行移动到虚线处(见左下图),这样正好移补成一个正方形,所以它的周长为25×4=100(厘米)。
(2)与(1)类似,可以移补成一个长方形,周长为(10+15)×2=50(厘米)。
例3求下面两个图形的周长(单位:厘米)。
解:(1)与例2类似,可以移补成一个长(15+10+15)厘米、宽(12+20)厘米的长方形,所以周长为(15+10+15)×2+(12+20)×2=144(厘米)。
三年级奥数巧求周长

第 1 页三年级奥数:巧求周长(A) 年级 班 姓名 一、填空 米.第1题 第2题 第3题 第4题 2.求图“十〞“十〞间周长是 厘米. 3.求图“凹〞形周长是 .〔单位:厘米〕“土山〞两个字,每个正方形边长是3厘米,这两个字周长分别是 、 厘米.“5〞字,长方形长4厘米,宽2厘米,“5〞字周长是 厘米.第5题 第6题第7题米. 7.求图7周长是 .单位:厘米8.下列图是一个公园平面图,A 是公园大门.问:小明从A 门进公园,不重复地沿道路走公园一圈,他走了多少米第8题 第9题 第10题50501 3 5 211 1 1 1 123 34 4 360240A 15 4050 4第 2 页 9是某建立物设计图,如下图(单位:米)现根据需要在它周围绕电线一圈,试求需电线多少米10.用15个边长2厘米小正方形摆成如下列图形状,求图形周长是多少厘米二、解答题11.一个正方形被分成了5个相等长方形.每个长方形周长都是40厘米,求正方形周长是多少厘米如下图.ABCD 边长为4cm,每边被四等分.求图中所有正方形周长与.5厘米、4厘米、3厘米与2厘米4个正方(如图),排成图形周长是多少厘米 14.将一张边长为12厘米正方形纸对折,再将对折后纸沿它竖直中线(得到三个矩形纸片,其中两个较小矩一、填空题:厘米.. b =50米,c =30米,g =10米,这座楼房平面周长是 米. 4.,如果这个图形面积是400那么它周长是 厘米. 5.下列图“E 〞字周长是 厘米.厘米)bc 35第 3 页 “T 〞字形,它周长是 厘米.“环球游戏探险隧道〞平面图,一儿童沿隧道周游一周,他走了多少米 8下列图是由10个边长为3厘米小正方形组成.每个小正方形顶点恰在另一个正方形中心,且边相互平行,求这个图形周长. 9.把一块长20厘米,宽12厘米长方形纸按右下列图所示方法一层、二层、三层摆下去,共要摆十层,摆好后图形周长是 厘米. 10.下列图是一个零件平面图,图中每一条最短线段均长5厘米.零件长35厘米,高30厘米,这个零件周长是多少厘米二、解答题 “干〞字形图形.两横均由长6厘米,宽1厘米长方形构成,中间一竖是由长6厘米,宽2厘米长方形构成,求出“干〞字图形周长是多少厘米 cm 7cm 正方形网格(如图)中,所有正方形周长与是多少cm BD 对折得到一几何图形,试求图形阴影局部周长.14.如图,在长方形ABCD 中,EFGHAF =10厘米,HC =7厘米,那么长方形ABCD 周长是 厘米35厘30AE F A BD EF G H 6050 402 单位:3 31 12 3 6 1 1。
三年级奥数经典课题――巧求周长和面积

巧求周长和面积-授课学案学生姓名:授课教师:班主任:科目:三年级奥数上课时间: 2012 年月日时—时跟踪上次授课情况上次授课回顾○完全掌握○基本掌握○部分掌握○没有掌握作业完成情况○全部完成○基本完成○部分完成○没有完成本次授课内容授课标题巧求周长和面积学习目标重点难点例题与方法例1.有一块长8分米,宽4分米的长方形纸板与两块边长4分米的正方形拼也一个正方形。
拼成的正方形的周长是多少分米?例2.两个大小相同的正方形拼成一个长方形后,周长比原来的两个正方形周长的和减少6厘米。
原来一个正方形的周长是多少厘米?例3.求图3和图4的周长和面积。
(单位:米)图3 图4例4.图7是一座厂房的平面图,求这座厂房平面图的周长。
例5.图9是个多边形,图中每个角都是直角,它的周长是多少?例6.一个正方形被分成3个大小、形状完全不一样的长方形(如图10),每个小长方形的周长都是24厘米,求这个正方形的周长。
图10例7.图11是由四个一样大的长方形和一个周长是4分米的小正方形拼成的一个边长是11分米的大正方形。
每个长方形的长和宽各是多少?周长是多少?图例8.一根铁丝长12厘米,能围成几种长和宽都是整厘米数的长方形,每咱长方形的长和宽各是几厘米?围成的正方形的边长是几厘米?例9. 有9个小长方形,它们的长和宽分别相等,用这9个小长方形拼成的大长方形(如图)的面积是30平方厘米,求这个大长方形的周长。
练习与思考1.把一个长10厘米,宽5厘米的长方形,分成两个大小一样的正方形,每个正方形的周长是多少?2.用一个长8厘米,宽4厘米的长方形与7个边长4厘米的正方形,拼成一个大正方形。
拼成的大正方形的周长是多少?3.图14是一座楼房的平面图,这座楼房平面图的周长是多少米?4.有两个相同的长方形,长7厘米,宽3厘米,把它们按图(16)的样子重叠在一起,这个图形的周长是多少厘米?5.一块长方形布,周长是18米,长比宽多1米,这块布的长是几厘米?宽是几米?6.用4个一样大的长方形和一个小正方形,拼成一个边长是16分米的大正方形(如图18),每个长方形的周长是多少?例题与方法例1.一块长方形土地,长是宽的2倍,中间有一座雕塑,雕塑的底面是一个正方形,周围是草坪(如图1),草坪的面积是多项式少平方米?例2.图2是由6个相等的三角形拼成的图形,求这个图形的面积。
小学三年级《巧求周长》奥数教案

师:同学们,我们都学过周长了是吗?生:是。
师:那什么叫做周长呢?生:绕封闭图形一周的长度我们叫周长。
师:很好。
看来同学们是真正用心在学习,记忆力也非常好。
那现在我们看到例题一的第一个图形。
这个图形我们知道所有线段的长度吗?生:不知道。
师:对,但是我们能不能用已知的线段长来求出图形的周长呢?生:……师:我们都学过图形的平移,对不对?生:对。
师:那我们能不能把这道题中的某一条或者某几条线段进行平移,得到一个我们能立刻算出周长的图形呢?同学们想想看,移移看。
生:可以!师:哦,来说说看。
生:这里有三层,我们把下面两层的宽度向上移到和最上层同样高的地方,把每层的高度向右移到和最左侧高度一致的地方。
师:大家听清楚了吗?生:没有。
师:好的,那老师老帮助这位同学把图形的平移画出来。
(通过PPT的演示)现在大家清楚怎么移动了吗?生:清楚了。
师:好的,那同学们请看,现在我们看到的图形是什么?生:是长方形。
师:对,我们知道长方形的长了吗?生:知道,是120厘米。
师:没错,那我们知道长方形的宽了吗?生:不知道,但是我们能把它算出来。
师:那我们怎么算呢?生:12+24+48=84(厘米)。
师:非常好。
那我们现在周长是不是可以算了?生:没错。
师:周长是?生:(120+84)×2=408(厘米)。
师:非常棒!师:解决了第一小题,我们来看一看第二小题。
这道题目能不能跟第一小题一样,我们进行平移?生:可以。
师:那请同学们先试试看。
把尝试的结果告诉老师。
生:可以平移,但是有线段多出来。
师:哦,多出来,哪条线段多出来了?生:是10厘米的,多了两条。
师:那我们算周长的时候该怎么办呢?生:把多出来的也加进去。
师:非常好,我们不能落下每一条线段。
所以最后的答案是?生:(50+35)×2+10×2=190(厘米)师:非常棒,看来同学们掌握的都很不错,观察的也很仔细。
那么我们就开始做练习,熟能生巧,我们不仅要会做,还要做得快、做得正确。
小学奥数题目-三年级-几何类-巧求周长

巧求周长视频描述把长76厘米的铁丝围成一个长方形,围成的图形有一处接头,而接头处要重合2厘米。
如果需要使长比宽多15厘米,长和宽各是多少厘米?1.1.一个长方形鸡舍,一面靠墙,靠墙的边长为20米,其余三边用篱笆围起来。
已知篱笆长40米,请问这个鸡舍的宽是多少米?2.2.一根绳子长78厘米,围成一个长12厘米,宽9厘米的长方形,余下的围成一个正方形。
不考虑接头处的重合的话,这个正方形的边长是多少厘米?3.3.一个长方形的周长是正方形的2倍,正方形的边长与长方形的宽都为15厘米。
长方形的长是多少厘米?1.1.一张边长为4厘米的正方形纸板,从四个角上各裁去一个边长为1厘米的正方形,所剩部分的周长是多少厘米?2.2.如图所示,该多边形的任意相邻两条边都互相垂直,请求出这个多边形的周长。
(单位:厘米)3.3.如图是一个楼梯的侧面图。
已知每步台阶宽25厘米,高15厘米。
问这个楼梯侧面的周长是多少厘米?视频描述现在手上有一张长方形的纸,长是23厘米,宽是14厘米,先剪下一个最大的正方形,再从余下的纸片中,再剪下一个最大的正方形。
最后余下的长方形周长是多少?1.1.妈妈要在一块长3米,宽2米的花布上剪下一块最大的正方形花布做桌布,请问这块剪下来的正方形花布的周长是多少?2.2.有一块长方形的玻璃,从长边截去20厘米宽的一块后,剩下的玻璃正好是块正方形,它的周长是160厘米。
原来长方形玻璃的周长是多少?3.3.如下图,现有一张长方形纸条,从这张纸条中剪下一个正方形(图中的阴影部分)。
已知这个长方形纸条的原来的周长为38厘米,剪掉正方形后,剩下的小长方形的宽为5厘米。
求纸条原先的长和宽。
(多个数字答案用空格键隔开)视频描述1.1.用3个周长是12厘米的正方形拼成一个长方形(见图)。
求所拼成的长方形的周长.2.2.用15个边长2厘米的小正方形摆成如下图的形状,求图形周长是多少厘米?3.3.把周长分别是20厘米、16厘米、12厘米和8厘米的4个正方形按从大到小的顺序排成一行(如图),排成的图形周长是多少厘米?视频描述1.1.一条河流把一块长方形的田地分成甲、乙两块,如下图所示。
小学奥数 巧求周长 精选例题练习习题(含知识点拨)

4-2-2.巧求周长知识点拨一、基本概念①周长:封闭图形一周的长度就是这个图形的周长.②面积:物体的表面或封闭图形的大小,叫做它们的面积.二、基本公式:①长方形的周长2(长宽),面积长宽.②正方形的周长4边长,正方形的面积边长边长.三、常用方法:(1)对于基本的长方形和正方形图形,可以直接用公式求出它们的周长和面积,对于一些不规则的比较复杂的几何图形,我们可以采用转化的数学思想方法割补成基本图形,利用长方形、正方形周长及面积计算的公式求解.(2)转化是一种重要的数学思想方法,在转化过程中要抓住“变”与“不变”两个部分.转化后的图形虽然形状变了,但其周长和面积不应该改变,所以在求解过程中不能遗漏掉某些线段的长度或某部分图形的面积.转化的目标是将复杂的图形转化为周长或面积可求的图形.(3)寻求正确有效的解题思路,意味着寻找一条摆脱困境、绕过障碍的途径.因此,我们在解决数学问题时,思考的着重点就是要把所需解决的问题转化为已经能够解决的问题.也就是说,在直接求解不容易或很难找到解题途径的问题时,我们往往转化问题的形式,从侧面或反面寻找突破口,知道最终把它转化成一个或若干个能解决的问题.这种解决问题的思想在数学中叫“化归”,它是数学思维中重要的思想和方法.(4)在几何中,有许多图形是由一些基本图形组合、拼凑而成的.这样的图形我们称为不规则图形.不规则图形的面积往往无法直接应用公式计算.那么,不规则图形的面积怎样去计算呢?对称、旋转、平移这几种几何变换就是解决这类面积问题的手段.四、几个重要的解题思想(1)平移在平面图形的计算中,常常要将一个平面图形移动到平面上的另一个位置进行计算.其中,将图形沿一个固定方向的移动叫做平移,一个图形经过平行移动不改变其形状与大小,所以图形面积是保持不变的.利用图形的平移,可以使面积计算问题的解法简捷明快,颇有新意.(2)割补割补法在我国古代叫“出入相补原理”,我国古代魏晋时期著名的数学家刘徽在《九章算术注》中就明确地提出“出入相补,各从其类”的出入相补原理.这个原理的内容是几何图形经过分、合、移、补所拼凑成的新图形,它的面积不变.(3)旋转在平面图形的割补中,有时要将一个图形绕定点旋转到一个新的位置,产生一种新的图形结构,图形在转动过程中形状大小不发生改变.利用这种新的图形结构可以帮我们解决面积的计算问题.(4)对称平面图形中有许多简单漂亮的图形都是轴对称图形.轴对称图形沿对称轴折叠,轴两侧可以完全重合.也就是说,如果一个图形是轴对称图形,那么对称轴平分这个图形的面积.熟悉轴对称图形这个性质,对面积计算会有很大帮助.(5)代换在几何计算中,对有关数量进行适当的等量代换也是解决问题的已知技巧.小结:本讲主要通过求一些不规则图形的周长,体会一种转化思想,重点在于把不规则图形转化为规则图形的方法,包括平移、旋转、割补、差不变原理,通过这些方法的学习,让学生体会求周长的技巧,提高学生的观察能力、动手操作能力、综合运用能力.例题精讲模块一、图形的周长和面积——割补法【例1】求图中所有线段的总长(单位:厘米)4312A B C D E【例2】如图所示,点B是线段AD的中点,由A、B、C、D四个点所构成的所有线段的长度均为整数,若这些线段的长度之积为10500,则线段AB的长度是。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学三年级奥数12巧求周长
本教程共30讲
第12讲巧求周长
我们知道:
这两个计算公式看起来十分简单,但用途却十分广泛。
用它们可以解决许多直角多边形(所有的角都是直角的多边形)的周长问题。
这是因为直角多边形总可以分割成若干个正方形或长方形。
例如,下面的图形都可以分割成若干个正方形或长方形,当然分割的方法不是唯一的。
由此,可以演变出许多只涉及正方形、长方形周长计算公式的题目。
例1一个苗圃园(如左下图),周边和中间有一些路供人行走(图中线段表示“路”),几个小朋友在里面观赏时发现:从A处出发,在速度一样的情况下,只要是按“向右”、“向上”方向走,几个人分头走不同的路线,总会同时达到B处。
你知道其中的道理吗?
分析与解:如右上图所示,将各个交点标上字母。
由A处到B处,按“向右”、“向上”方向走,只有下面六条路线:
(1)A→C→D→E→B;
(2)A→C→O→E→B;
(3)A→C→O→F→B;
(4)A→H→G→F→B;
(5)A→H→O→E→B;
(6)A→H→O→F→B。
因为A→C与H→O,G→F的路程一样长,所以可以把它们都换成A→C;同理,将O→E,F→B都换成C→D;将A→H,C→O都换成D→E;将H →G,O→F都换成E→B。
这样换过之后,就得到六条路线的长度都与第(1)条路线相同,而第(1)条路线的长“AD+DB”就是长方形的“长+宽”,也就是说,每条路线的长度都是“长+宽”。
路程、速度都相同,当然到达B处的时间就相同了。
例2计算下列图形的周长(单位:厘米)。
解:(1)将图中右上缺角处的线段分别向上、向右平行移动到虚线处(见左下图),这样正好移补成一个正方形,所以它的周长为25×4=100(厘米)。
(2)与(1)类似,可以移补成一个长方形,周长为
(10+15)×2=50(厘米)。
例3求下面两个图形的周长(单位:厘米)。
解:(1)与例2类似,可以移补成一个长(15+10+15)厘米、宽(12+20)厘米的长方形,所以周长为
(15+10+15)×2+(12+20)×2=144(厘米)。
(2)设想先把长20厘米的线段向上平移到两条长15厘米的线段中间,构成一个长60厘米,宽(15+20+15)厘米的长方形,此时,还有两条长35厘米的竖线段。
所以周长为
60×2+(15+20+15)×2+35×2=290(厘米)。
例4在一张纸上画出由四个边长为3厘米的正方形拼凑或组合成的图形(重叠的线段只算画一次)。
显然,这个图形有多种多样的画法,下列各图是其中的一部分画法。
在所有的这些画法中,
(1)哪种画法画出的线段总长最长?有多长?
(2)哪种画法画出的线段总长最短?有多长?
分析与解:画的线段重叠部分越少,画的线段就越长。
反之,重叠部分越多,画的线段就越短。
因此,类似图1那样画的线条最长,共画了
3×4×4=48(厘米)。
右图画的线条最短,共画了
(3+3)×6=36(厘米)。
例5下图是一个方形螺线。
已知两相邻平行线之间的距离均为1厘米,求螺线的总长度。
分析与解:如左下图所示,按箭头方向转动虚线部分,于是得到了三个边长分别为3,5,7厘米的正方形和中间一个三边图形(见右下图)。
所以螺线总长度为
(3+5+7)×4+1×3=63(厘米)。
练习12
1.试求左下图的周长(单位:厘米)。
2.上页右下图是由边长为1厘米的11个正方形堆成的“土”字图形。
试求出其周长。
3.右图是某小学教学楼的平面示意图,设计者在图上只标明了三条线段的长度(单位:米)。
请你算出它的周长。
4.下图是由七个长5厘米、宽3厘米的相同长方形经过竖放、横放而成的图形。
求这个图形的周长。
5.下面两图中的小方格的大小相同。
图(1)的周长为48厘米,图(2)的周长等于多少?
6.如右图所示,一个正方形被分成了三个相同的长方形。
如果其中一个长方形的周长是16米,那么这个正方形的周长是多少米?
答案与提示练习12
1.50厘米。
2.24厘米。
3.188米。
解:(28+16+50)×2=188(米)。
4.76厘米。
解:7个长方形的周长之和,减去图中重叠(虚线)部分,
(5+3)×2×7-3×2×6=76(厘米)。
5.60厘米。
提示:每个小方格的边长为3厘米。
6.24米。
解:三个长方形的周长等于正方形的8个边长,即等于正方形的两个周长,故正方形的周长为16×3÷2=24(米)。
