第四章 进排气管内非定常流的数值分析
喷管内非定常气体流动-轴对称与UDF
ZONES
→ SPECIFY BOUNDARY TYPES
第 7 步:输出网格并保存文件 1、 输出网格文件 操作: File → Export → Mesh...
2、 保存 GAMBIT 文件并退出 GAMBIT 操作: File → Exit
4
二、利用FLUENT 进行喷管内流动的仿真计算
准备工作:启动 FLUENT 的 2d 求解器。 第 1 步:与网格相关的操作 1、 读入网格文件 操作: File → Read → Case... 2、 网格检查 操作: Grid → Check 3、设置长度单位为 mm 操作: Grid → Scale... 4、显示网格 操作: Display → Grid… 5、 通过中心轴进行对称反射 操作: Display →Views...
6
第 4 步:设置流体属性 操作: Define → Materials...,打开流体属性设置对话框如图 2-2-27 所示。 1、选择可压缩的理想气体
第 5 步:设置边界条件 操作: Define → Boundary Conditions...,打开边界类型设置对话框如图。 1、 设置喷管的入口边界条件
操作:GEOMETRY
2
→ EDGE
→ CREAT EDGE
2、利用圆角功能对 D 点处的角倒成圆弧
操 作 : GEOMETRY
→ EDGE
→CREAT EDGE
_
操作结果如图 2-2-8 所示,直线 CD 和 DE 的 交点处已经变成圆弧线。
3、由边线创建面
操作:GEOMETRY
→ FACES
→ FORM FACE
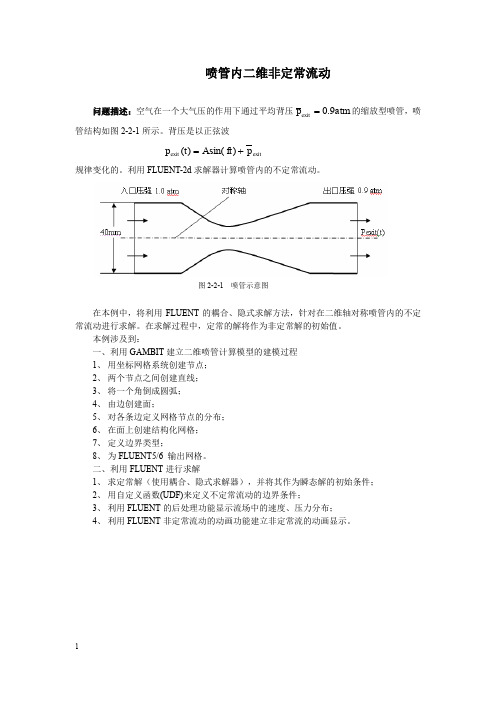
喷管示意图
在本例中,将利用 FLUENT 的耦合、隐式求解方法,针对在二维轴对称喷管内的不定 常流动进行求解。在求解过程中,定常的解将作为非定常解的初始值。 本例涉及到: 一、利用 GAMBIT 建立二维喷管计算模型的建模过程 1、 用坐标网格系统创建节点; 2、 两个节点之间创建直线; 3、 将一个角倒成圆弧; 4、 由边创建面; 5、 对各条边定义网格节点的分布; 6、 在面上创建结构化网格; 7、 定义边界类型; 8、 为 FLUENT5/6 输出网格。 二、利用 FLUENT 进行求解 1、 求定常解(使用耦合、隐式求解器),并将其作为瞬态解的初始条件; 2、 用自定义函数(UDF)来定义不定常流动的边界条件; 3、 利用 FLUENT 的后处理功能显示流场中的速度、压力分布; 4、 利用 FLUENT 非定常流动的动画功能建立非定常流的动画显示。
关于涡轮级内非定常流场的数值研究

关于涡轮级内非定常流场的数值研究1 引言在叶轮机内由于动静叶的相对运动使得叶栅内流动具有很强的非定常性,尾迹与势流的交替干扰引起压力场随时间周期性的变化。
动静干涉不仅影响叶轮机械的工作性能,而且也会因为产生非定常的气动力而影响叶轮机械的疲劳寿命,因此研究动静干涉对于提高叶片的寿命和可靠性具有重要意义并且引起了越来越多的关注。
不少学者对转静干涉对叶轮机械性能的影响进行了研究,近些年随着实验测量手段的进步和粘性流场数值方法的发展,研究者对叶列间干扰有了进一步的研究和认识。
当前研究较多的是上游叶片的尾迹和下游叶片的势扰动对叶片非定常表面压力和气动力的周期性影响[1-2] 。
Denos[3] , Valenti[4]和Miller[5,6]对涡轮中尾迹与叶片的干扰进行了实验研究。
黄伟光等人采用数值方法研究了涡轮在非定常条件下的叶片气动力[7]。
王英锋等人对上游叶片尾迹对转子叶片非定常表面压力频谱特性影响进行了研究[8]。
本文对涡轮级内的动静相干非定常流场进行了数值模拟,主要研究了动静部件受非定常的影响效应,探讨了离涡轮级内非定常相干的机理。
2 数值计算方法2.1 基本控制方程及数值算法流场的计算采用了UNSTREST 程序,该程序是基于薄边界层近似的N-S 方程的流场求解代码。
采用了二阶精度显式的SCREE 格式,其仅需要非常小的人工粘性,可以在非常低的马赫数下运行,也可以在跨音速甚至超音速马赫数下求解。
在非定常计算中引入了隐式的双时间步方法。
表面剪切应力通过物面上第一个网格点上的特定Y+ 值和速度值来计算。
2.2 边界条件计算中给定了整个级的进出口条件。
在静子的进口边界处给定了总温、总压和气流角;在转子的出口边界上给定了静压,并使用了径向平衡。
上下游延伸部分的周向边界采用周期性边界条件。
对于固体壁面,取不可渗透、无滑移及绝热壁面边界条件,以确保通过与固体边界重合的网格面的质量流量、动量通量及能量通量为零。
内燃波转子非定常流动和燃烧特性分析

J u n .2 0 1 3
内燃 波转 子 非 定 常 流 动 和 燃 烧 特 性 分 析
巩 二磊 李 建 中 韩 启 祥 王 家 骅
( 南 京航 空 航 天 大 学 能 源 与 动 力 学 院 ,南 京 , 2 1 0 0 1 6 )
摘要 : 为 研 究 内燃 波 转 子 内非 定 常 流动 和 燃 烧 特 性 , 在 分 析 内燃 波 转 子 的 结 构 和 工 作 特 点 的基 础 上 , 建 立 了 内燃 波转 子 简化 二 维模 型 。 采 用 数值 模 拟 的 方 法 , 研 究 内燃 波 转 子 内非 定 常 流 动 过 程 中预 压 缩 作 用 对 混 气 总 压 和 温
a n d t h e g a s d i s t r i b u t i o n a s we l l a s t h e f u e l — a i r i n t e r f a c e s h a p e d i s t o r t i o n a r e s t u d i e d .F i n a l l y ,t h e c o n— r
3 2 , 总温提 高了 1 O . 4 ; 混 气 与 空 气接 触 面 的扭 曲 变形 程 度 受到 内燃 波 转 子 作 用 时序 和 通 道 内 的 轴 向 速 度 分 布影 响; 热 射 流 成 功 点 燃 通 道 内 可燃 混 气 , 实 现 了转 子 通 道 内可 燃 混 气 的爆 震 燃 烧 , 爆 震 波 峰 值 压 力 约2 MP a , 爆 震 波传 播 速 度 在 2 6 0 0 ~2 8 0 0 m/ s范 围 内。 关键词 : 内燃 波 转 子 ;非 定 常 流 动 ; 等 容 燃 烧 ;爆 震 ; 数 值 模 拟 中图 分 类 号 : V 2 3 5 . 2 2 文献标志码 : A 文章编 号: 1 0 0 5 - 2 6 1 5 ( 2 0 1 3 ) 0 3 — 0 3 0 9 - 0 7
旋流排气管的一维非定常流动计算

A bs r c Un t a wilf w dey a p a s i we a h ne y I hi p r ie d lnso  ̄ t a t s e dy s r o wi l p e r n po r m c i r . n t s pa e o [— i e i n l l n
。 ^ 卢 r o
等熵 膨胀 到参考 J 力 的 m 基 f 、 Re n i ma n小变 量 Re n [ ma n不变鼍 啦)体径 向擘面 翦 力 1 2 定容 比热
S
, 、 J
截 面绕轴 线 的 均 旋转速 鹰
n
遵
温度
气体 的旋 流流 动存 在 于发动 机 的旋流 排气 管
维普资讯
第 2 卷第 1期 3 2 0 年 1月 02
工 程热Βιβλιοθήκη 物理 学报
V0 3 l2
o1
J OURNAL OF ENGI NEERI NG HERM OPHYS CS T I
Jan 2O0 2
旋流排气管的一维非定常流动计算
C A LC U LATI oN oF oN E— I EN SI D M oN A L N ST EA D Y U SW I E R
FLoW N W I L EX H A U ST A N I I S R M FoLD S
DENG n - a GU n — h a CHEN J— al Ka g Y o Ho g Z o g iQu i
e ha s n nio d fa f l c ide . u bo ha g d dis l ngne x u ti a f lso 【 一yl ) n r t r c r e e e e i .Thec m pa io fl e s e r s u e o rs n o l a urd p e s r l t a e nd n r c sa um e ia 1 ho ha hem o e asg o c u a y i un t a w ilf w r dito rc lda. s ws t tt a d lh o d a c r c n se dy s r o p e c i n l i wile ha s na f ds i s r x u ti ni 1 ol
定常与非定常流动

定常流动流体(气体、液体)流动时,若流体中任何一点的压力,速度和密度等物理量都不随时间变化,则这种流动就称为定常流动;反之,只要压力,速度和密度中任意一个物理量随时间而变化,液体就是作非定常流动或者说液体作时变流动。
所以,定常流动时,管中流体每单位时间流过的体积(体积流量)qV为常量,流体每单位体积的质量(密度)ρ也是常量。
非定常流动流体的流动状态随时间改变的流动。
若流动状态不随时间而变化,则为定常流动。
流体通常的流动几乎都是非定常的。
分类按流动随时间变化的速率,非定常流动可分为三类:①流场变化速率极慢的流动:流场中任意一点的平均速度随时间逐渐增加或减小,在这种情况下可以忽略加速度效应,这种流动又称为准定常流动。
水库的排灌过程就属于准定常流动。
可认为准定常流动在每一瞬间都服从定常流动的方程,时间效应只是以参量形式表现出来。
②流场变化速率很快的流动:在这种情况下须考虑加速度效应。
活塞式水泵或真空泵所造成的流动,飞行器和船舶操纵问题中所考虑的流动都属这一类。
这类流动和定常流动有本质上的差别。
例如,用伯努利方程(见伯努利定理)描述这类流动,就须增加一个与加速度有关的项,成为:,式中为理想流体沿流线的速度分布;A和B表示同一流线上的两个点;P 为压强;为密度;g为重力加速度;z为重力方向上的坐标;ds为流线上的长度元。
③流场变化速率极快的流动:在这种情况下流体的弹性力显得十分重要,例如瞬间关闭水管的阀门。
阀门突然关闭时,整个流场中流体不可能立即完全静止下来,速度和压强的变化以压力波(或激波)的形式从阀门向上游传播,产生很大的振动和声响,即所谓水击现象。
这种现象不仅发生在水流中,也发生在其他任何流体中。
在空气中的核爆炸也会发生类似现象。
除上述三类流动外,某些状态反复出现的流动也被认为是一种非定常流动。
典型的例子是流场各点的平均速度和压强随时间作周期性波动的流动,即所谓脉动流,这种流动存在于汽轮机、活塞泵和压气机的进出口管道中。
第4章一维定常可压缩管内流动分析

三个界限压强p1, p2, p3
2021/2/24
第4章一维定常可压缩管内
中国民航大学航空工程学院发动机系
p3 p2 p1
29
pb p1 p p
➢ 完全膨胀 ➢ 设计状态
气体动力学(Aerodynamics)
Ⅳ区
pb p
p1 p
➢ 管外有膨胀波 ➢ 未完全膨胀(欠膨胀)
2021/2/24
第4章一维定常可压缩管内
1845-1913
2021/2/24
第中4国章民一航大维学定航空常工可程学压院缩发动管机内系 流动分析
26
气体动力学(Aerodynamics)
拉瓦尔喷管面积比 e
➢最小截面称为喉部,用 p *
t
脚标t表示;出口脚标e
T*
t
Pb
e
设计状态:V Ma , Mat=1, Mae>1
Kpt*q T (t*t)A t Kpe *qT (e*e)A eKp*q T (*)A
➢特征一:一维——垂直于管道轴线的每个截面上的流动参数
保持均匀一致
➢特征二:定常——流动不随时间变化 ➢特征二:可压缩——流动速度快,气体压缩性影响显著;对
于超声速流动,可能会出现激波或膨胀波
2021/2/24
第4章一维定常可压缩管内
中国民航大学航空工程学院发动机系
2
气体动力学(Aerodynamics)
中国民航大学航空工程学院发动机系
M a>1 10
气体动力学(Aerodynamics)
截面积变化对气流参数的影响
➢管道截面积的变化,对亚音速气流和超音速气流有相
反的影响
➢V 1 dA V 1Ma2 A
汽车排气系统的声学性能及流场特性的数值分析研究的开题报告

汽车排气系统的声学性能及流场特性的数值分析研究的开题报告摘要:汽车排气系统的声学性能和流场特性一直是研究的热点之一。
本文将使用计算流体力学(CFD)方法对汽车排气系统的声学性能和流场特性进行数值分析研究。
首先,将建立汽车排气系统的几何模型,然后使用CFD软件进行数值模拟,分析汽车排气系统内部的气流分布、压力分布、温度分布、声压级等参数。
最后,将通过与实验结果的对比来验证数值模拟结果的准确性和可靠性。
关键词:汽车排气系统;声学性能;流场特性;计算流体力学;数值分析一、研究背景和意义近年来,汽车行业的快速发展使得人们对于汽车排气系统的声学性能和流场特性的研究越来越重视。
汽车排气系统的声学性能和流场特性不仅对于排放控制、节能减排等方面有着重要的作用,同时也会直接影响到汽车的性能指标和驾驶舒适度。
因此,对汽车排气系统的声学性能和流场特性进行深入研究,不仅有助于改善汽车排气系统的工作效率和性能指标,还能提高汽车的安全性和舒适性,从而为汽车产业的可持续发展做出贡献。
二、研究内容和方法本文将采用计算流体力学(CFD)方法对汽车排气系统的声学性能和流场特性进行数值分析研究。
具体而言,将分以下几个方面展开研究:1、建立汽车排气系统的几何模型,包括排气管、中段消声器、尾气消声器等组成部分。
2、使用CFD软件对汽车排气系统进行数值模拟,分析汽车排气系统内部的气流分布、压力分布、温度分布、声压级等参数。
3、通过参数的变化来分析汽车排气系统的声学特性和流场特性,并优化排气系统的结构、材料和参数等方面的设计,以提高汽车排气系统的性能指标和工作效率。
三、研究进展和计划目前,本文已经完成了对汽车排气系统的几何模型的建立,并开始进行基于CFD 方法的数值模拟研究。
计划在接下来的研究中,将进行如下工作:1、采用声学仿真方法,对汽车排气系统在不同工况下的噪声特性进行数值模拟,并与实验结果进行对比验证。
2、通过对汽车排气系统内部气流分布的数值模拟,分析气流的流速、压力、温度等参数,以及气流中的湍流特性,为排气系统的优化设计提供依据。
离心式压气机模型级内非定常流动的数值试验

收稿日期:2001-02-12;修订日期:2001-05-23基金项目:国家自然科学基金资助项目(59876028)作者简介:刘立军(1970-),男,西安交通大学能源与动力工程学院博士生.第17卷第1期2002年1月航空动力学报Journal of Aerospace PowerVoi.17No.1!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!Jan.2002文章编号:1000-8055(2002)01-058-07离心式压气机模型级内非定常流动的数值试验刘立军,徐忠,张玮(西安交通大学能源与动力工程学院,陕西西安710049)摘要:应用同位网格下的压力校正算法和滑移网格技术,在贴体曲线坐标系下,对离心式压气机模型级内部由于叶轮与叶片扩压器相互作用引起的三维非定常湍流流场进行了数值模拟。
计算结果表明,在设计工况下,由于叶轮与叶片扩压器的相互作用引起的非定常干涉流动,对整级内部流动有非定常影响。
速度场的非定常特性主要表现在叶轮与叶片扩压器间的径向间隙范围内和扩压器的入口处,在叶轮和扩压器叶道内部衰减很快。
而压力脉动同时向流道的上下游传播,在叶轮和扩压器内部流动仍具有显著的压力非定常脉动。
计算结果还模拟了扩压器入口处运动涡系与扩压器叶片的相互作用及其周期性衍灭过程。
关键词:非定常流动;离心压气机;数值试验;叶轮/扩压器相互作用中图分类号:0356文献标识码:ANumerical Experiment of the Unsteady Flow in a Centrifugal Compressor Stage Model Dueto Impeller /Diffuser InteractionLIU Li-jun ,XU Zhong ,ZHANG Wei(Xi ’an Jiaotong University ,Xi ’an 710049,China )Abstract :Using the technigue of coiiocated grid scheme and siiding mesh ,coupied with standard k-!turbuience modei ,the computation of the unsteady fiow in a centrifugai compressor stage modei due to im-peiier /diffuser interaction is performed by a pressure-based aigorithm under the generai curviiinear coordi-nate system.The computation resuits show that ,the impeiier /diffuser interaction has unsteady effect on the whoie fiow fieid of the stage.The unsteady component of the veiocity is marked in the gap between the im-peiier and diffuser ,whiie vanishes guickiy in the biade channeis of the impeiier and diffuser.However ,the pressure unsteadiness due to the impeiier /diffuser interaction remains obviousiy throughout the biade chan-neis.The resuits simuiate the impingement of the fiow from the impeiier on the diffuser biades adjacent downstream ,and ,the transportation of the vortex series at the diffuser iniet and its interaction with the dif-fuser biades ,which may resuit in noise.Key words :unsteady fiows ;centrifugai compressor ;numericai simuiation ;impeiier /diffuser interaction!前言在叶轮机械内部,由于动/静叶片排之间的相对运动,流场不仅在空间上极不均匀,而且在时间上表现为强非定常流动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 正是基于这一原因,包括本书在内的有关内燃机 数值模拟书籍都对特征线原理和解法进行了详细 的介绍。
4.1 非定常一维流动的基本方程
一、非定常一维不等熵流动
取控制容积 ABCD,根据上 述假定,就可从 质量守恒定律 动量定理和 能量守恒定律 出发,来推导管 内不定常非等熵 流动的基本方程
1.连续方程
质量守恒定律: 单位时间内纯流入控制体质量等于该控制体内质量增量
u dF Fdx uF dx u dx F dx x x dx t 流入 流出流量 增量
这组方程的特点是: 1.一阶偏微分方程组 2.非线性 (系数中含未知函数) 3.系数中不含偏导数, 一阶拟线性偏微分方程组 4.双曲线型偏微分方程组, 可用特征线求解 对于等截面非定常一维等熵流动,S=常数,没有摩擦与 传热(q=0,G=0) 连续方程
u u 0 t x x
3.能量方程
热力学第一定律: dt 时间微元体内总能量变化率=控制表面净流入焓+控制表面传热率
u 2 u 2 p cvT cvT Fdx Fdx dx qFdx t 2 x 2
p
p
a2
)
将以上四式代入连续方程和动量方程,得 连续方程
2 a 2 a u u a 0 (4.1.39) 1 t 1 x x 动量方程 2a a u u u 0 (4.1.40) 1 x t x
4.2 特征线法的基本概念
特征线定义: 从物理观点来看 特征线是物理扰动的传播路径,马赫线是超声流 场中特征线 从数学观点来看, 沿特征线能将偏微分方程换成全微分方程,穿过 特征线时,物理参数的偏导可以不连续(不能唯 一确定),而物理参数本身却保持连续。 利用这一特性可以用来寻求特征线
下面用一柯西问题的例子,进一步说明特征线的概念
u u dF u 0 t x x F dx (4.1.2)
2.动量方程
作用在控制面上的外力应等于控制容积内动量的总变化率, 作用在微元体轴向上的外力有 (1)截面 AB,CD 上压力差所产生外力
p dF pF pF p dx F dx dx x dx x
4.1 非定常一维流动的基本方程
进排气管内流动一般作一维流动处理 计算时假定 (1)管轴向几何尺寸比径向的大得多,轴向 流动效应比径向的大得多,可以认为每一截 面上流动参数是均匀的,仅随轴向坐标和时 间变化,准一维流动 (2)管壁刚性,截面积变化缓慢 (3)用一维模型模拟摩擦、传热 (4)管内流体为完全气体,不计重力
• 20世纪50年代海勒(Haller)和詹尼(Jenny)将特征线 图解法应用于内燃机中,可较精确模拟管道中实际情况, 并据以改进和优化设计,但仍因计算工作量过大而难以推 广应用。直到20世纪60年代电子计算机广泛推广应用。 • 20世纪60年代以来,英国曼切斯特大学的本森(R. S. Benson)教授及其工作组长期致力于内燃机进排气及增 压系统的非定常流研究和特征线模拟计算工作,70年代开 发了UMIST程序,可用于24缸以下机型。1982年,他的 同事以本森的名义出版《内燃机的热力学与空气动力学》, 系统总结了以特征线法为基础的这一领域的研究和计算成 果 • 前后30年1960-1990年代初,特征线法一直在内燃机一维 非定常流研究和工业应用中处于主导支配地位,期间德国 赛福尔特教授1978年完成了Promo模拟计算程序,国内清 华大学80年代初引进UMIST程序移植到微机上MK-14程序。
代入能量方程
2 dp d d p a d a2 1q uG 0 q uGdt dt dt 1
热力学第二定律有
1 1 p p dp a 2d Tds dc T pd d 1 2 d 1
第四章 进、排气管内非定常流的数值分析 4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8 非定常一维流动的基本方程 特征线法的基本概念 特征线方程和相容性方程 特征线方程的数值解法 边界条件概述 排气阀的边界条件 涡轮边界条件 分支管接头的边界条件
概述
• 内燃机的进、排气过程决定了气缸充气量的多少、 多缸机各缸换气的均匀性,是决定内燃机性能优 劣的关键因素之一,所以内燃机中对进排气非定 常流动特性的研究很有必要。 • 流体力学中早已阐明了非定常流场中压力波传播 原理,并推导了计算流场状态参数的偏微分基本 方程组。 • 1885年黎曼(Riemann)提出求解双曲型偏微分 方程的特征线原理与解法之后,非定常流的工业 应用研究才得以开始。
1 p 2 1 a p x 1 a x
(因为 a
2
对上式先取对数再求偏导
1 2 1 a 1 2 1 a , , x 1 a x t 1 a t 1 p p 2 1 a 2a a 又有 x 1 a x 1 x
沿
K0
bt0
x
u u b 0 dx t x 沿特征线 b方程 解不能唯一确定 dt du u dt u dx t x
D
4F
W —流体内摩擦系数 2 1 2 u
根据牛顿第二定律“作用力=质量加速度”的关系可写出:
2.动量方程(续)
pF dF u 2 u u u dx p dx f D dx Fdx u x dx 2 u x t
展开整理后可得到动量方程
4.2 特征线法的基本概念(续)
一阶拟线性偏微分方程
a ( x, t , u ) u u b ( x, t , u ) c ( x, t , u ) t x
含有 x,t 两个方向的偏导数,求解 u( x, t ) 困难。 若在 x,t 平面上找到一个方向, 沿此方向将偏微分方程 常微分方程,求解容易 简单例子——柯西问题
ds q uG dt T
(4.1.31)
二、非定常一维等熵流动
u u dF u 0 t x x F dx u u 1 p u G 0 t x x p 2 p u 1q uG 0 u a x x t t
理想气体
由
R 1 p cv cv T 1 1
声速方程
p p a a
2
2
以及动量、连续方程得
p 2 p u 1q uG 0 u a x x t t
– 特征线法逐渐被求解方便、精度更高、速度更快的直接求解偏微 分方程组的有限差分法和有限体积法所取代, – 一维向考虑介质真实的粘性、传热和湍流等无形特点,特别是多 管接头还使用了多维模型; – 过渡过程的动态模拟及非定常流的反馈控制等新领域。
• 尽管模拟计算已由特征线法转为直接针对偏微分 方程的更精确的有限差分法,但特征线法原理及 解法在一维非定常流研究中仍具有重要而不可取 代的作用。
u u 1 p u G 0 t x x
(4.1.10)
du u u dx dt t x dt
4 f u2 u 其中 G D 2 u
G的物理意义:单位流体质量分配到沿x 方向的比摩擦力。
1 f u 2 D W Ddx 4 f u2 u 2 G 1 2 Fdx D 2 u D 4
u u 1 p u 0 动量方程 t x x p p 2 能量方程 u 0 u a x x t t
ቤተ መጻሕፍቲ ባይዱ
p p dp a2 d s
等熵条件下,能量方程为音速方程,自动满足 p,ρ可由热力学公式由a表示,只有两个独立参数a,u。
二、非定常一维等熵流动(续)
等熵条件
d
p
const
状态方程
p
T const
利用上述公式可将p,ρ用a来表示
κ 2κ 1 dp 1 dT 2 da p T κ 1 a κ 1 p 1 T 1 a p T a 0 0 0 0
(4.1.22)
4.熵方程(129页)
考察流体质点通过控制表面时的熵值变化
沿轨迹线
dx udt dp d p p p p dx dt u dt x t x t dx dt u dt x t x t
(2)作用在管壁上的正压力在轴向上的分力 dF pds sin p dF p dx dx (3)管壁上的摩擦力 u 2 u W dS cos W Ddx f D dx 2 u
其中
W —管壁上的剪应力(单位面积上的摩擦力)
——当量直径; f
• 以特征线法为基础的内燃机一维非定常气流的研究,主要 集中于两个方面: – 一是进行循环模拟计算,用以指导进气、排气、增压 系统及整机的实验、设计,改善和提高内燃机的综合 性能; – 二是利用压力波传播特性,开发和创建新型的装置和 系统,比如,利用压力波传输能量的脉冲增压系统、 调谐增压系统以及将排气压力波能量直接送到新鲜充 气中的气波增压装置,这些都是在充分掌握非定常流 中压力波传播原理之后的创新之作。 • 近一二十年来,这一领域的研究工作发展趋势:
a 1, b const,c 0
