同济大学朱慈勉-结构力学第9章-弯矩分配法
结构力学-力矩分配法

•
3、转动刚度S:
• 表示杆端对转动的抵抗能力。 在数值上= 仅使杆端发生单位转动时需在杆端施加 的力矩。AB 杆A 端的转动刚度SAB与AB 杆的线刚度 i(材料的性质、横截面 的形 状和尺寸、杆长)及远端支承有关,而 与近端支承无关。当远端是不同支承时, 等截面杆的转动刚度如下:
转动刚度
在确定杆端转动刚度时:近端看位移(是否为单位位移)
远端看支承(远端支承不同,转动刚度不同)。
下列那种情况的杆端弯矩MAB=SAB
MAB
MAB
θ MAB
1
√ ① ②
1
MAB
1
③④
1
Δ
转动刚度SAB=4i是( )
A
i
B
A
i
√ √ B ①
③
A
i
B
④
A
i
4i>SAB>3i
√B ②
A
i⑤ B
i
返回
二、基本运算
AA1155kkNN↓↓↓↓44↓↓i00↓↓=kk↓↓1NN↓↓↓↓//mm↓↓↓↓ DD
MA 10
80
mAB
M=15 i=2
mAD mAC CC
MM图图((kkNN..mm))
22mm
22mm
44mm
A
C
D
AD
AC
CA
DA
3/9
2/9
- 80
15
10
-10 返回
- 65
10
- 10
三、多结点力矩分配法
⑶为了取消结点C的刚臂,放松结点C,在结点C加上 (-(MC+ M传)),如图d,为了使BCD部分只有一个角位 移,结点B再锁住,按基本运算进行力矩分配和传递。结 点C处于暂时的平衡。
结构力学第9章__力矩分配法(新)

9-2 单结点的力矩分配——基本运算
①求固端弯矩; ②将会交于结点的固端弯矩之和按分配系数分配给每一个杆端。 ③各杆按各自的传递系数向远端传递。 ④将固端弯矩和分配(或传递的弯矩)相加,得杆端最后弯矩。
9-2 单结点的力矩分配——基本运算
例题
12kN/m
i
6m
16kN
2i
3m
3m
0.4 0.6
固端弯矩 -36
第9章 渐进法及超静定力的影响线 9-1 力矩分配法的基本概念 9-2 单结点的力矩分配法 9-3 多结点的力矩分配法 9-4 计算结果的校核
9-1力矩分配法的基本概念
M
4
2 i12 1
i14
i13
3
4i12Δ1
2i12Δ1
i13Δ1 i13Δ1
3i14Δ1
M12 4i121 M13 i131 M14 3i141
M
1 M21 2 M12 M31 M13 M41 0 M14
9-1力矩分配法的基本概念
1 转动刚度:梁端发生单位转角产生的弯矩。
M ik Sik 1
4iik 远端为固定端
S ik
3iik iik
远端为铰支端 远端为平行支链杆
0 远端为自由端
2 分配系数:与转动刚度成正比
ik
96 64 → 32
-23.6 ← -47.3 -47.3 → -23.6 14.2 9.4 → 4.7
-1.2 ← 0.7 0.5 →
-2.3 -2.3 → -1.2 0.3
-0.1 -0.2
200.9 -200.9
237.3 -237.3 87.7
200.9
237.3
87.7
(完整版)完整的结构力学答案-同济大学朱慈勉
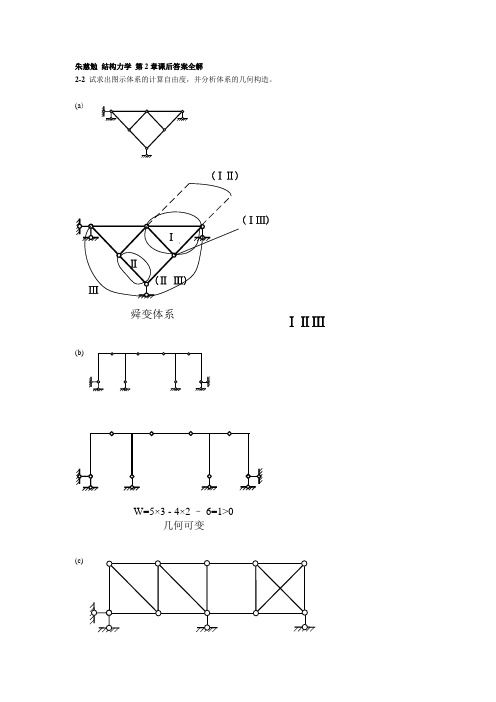
朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a )(ⅠⅡ)(ⅠⅢ)舜变体系ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)W=3×3 - 2×2 – 4=1>0可变体系2-3 试分析图示体系的几何构造。
(a)(ⅡⅢ)Ⅲ几何不变2-4 试分析图示体系的几何构造。
(a)几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系(ⅠⅢ)(ⅡⅢ)几何不变(d)Ⅲ(ⅠⅢ)有一个多余约束的几何不变体(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系(f)(ⅠⅢ)(ⅡⅢ)无多余约束内部几何不变(h)二元体W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)Ⅲ(ⅡⅢ)(ⅠⅢ)同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)2P F a 2P F a4P F Q34P F 2P F(b)aaaa a2m6m2m4m2m2020Q10/326/310(c)18060(d)3m2m2m3m3m4m3m2m2m2mA2m 2m2m2m7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)242018616MQ18(b)4kN ·m 3m3m6m1k N /m2kN A CBD6m10kN3m3m 40kN ·mABC D30303011010QM 210(c)45MQ(d)3m3m 6m6m2m 2m444444/32MQN(e)4481``(f)4m4m2m3m4m222220M3-4 试找出下列各弯矩图形的错误之处,并加以改正。
(a)F P(b)(c)(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F 两铰的位置。
同济大学朱慈勉-结构力学-第10章-结构动..习题答案

同济大学朱慈勉 结构力学 第10章 结构动..习题答案10-1 试说明动力荷载与移动荷载的区别。
移动荷载是否可能产生动力效应10-2 试说明冲击荷载与突加荷载之间的区别。
为何在作厂房动力分析时,吊车水平制动力可视作突加荷载10-3 什么是体系的动力自由度它与几何构造分析中体系的自由度之间有何区别如何确定体系的 动力自由度10-4 将无限自由度的振动问题转化为有限自由度有哪些方法它们分别采用何种坐标 10-5 试确定图示各体系的动力自由度,忽略弹性杆自身的质量。
(a)(b)EI 1=∞EImyϕ分布质量的刚度为无穷大,由广义坐标法可知,体系仅有两个振动自由度y ,ϕ。
(c)](d)在集中质量处施加刚性链杆以限制质量运动体系。
有四个自由度。
10-6 建立单自由度体系的运动方程有哪些主要方法它们的基本原理是什么 10-7 单自由度体系当动力荷载不作用在质量上时,应如何建立运动方程10-8 图示结构横梁具有无限刚性和均布质量m ,B 处有一弹性支座(刚度系数为k ),C 处有一阻尼器(阻尼系数为c ),梁上受三角形分布动力荷载作用,试用不同的方法建立体系的运动方程。
解:1)刚度法该体系仅有一个自由度。
可设A 截面转角a 为坐标顺时针为正,此时作用于分布质量m 上的惯性力呈三角形分布。
其端部集度为..ml a 。
取A 点隔离体,A 结点力矩为:....3121233I M ml a l l mal =⨯⨯⨯= |由动力荷载引起的力矩为:()()2121233t t q l l q l ⋅⋅= 由弹性恢复力所引起的弯矩为:.2133la k l c al ⋅⋅+ 根据A 结点力矩平衡条件0I p s M M M ++=可得:()3 (322)1393t q l ka m al l c al ++=整理得:()...33t q ka c a m a l l l++= 2)力法.cα解:取AC 杆转角为坐标,设在平衡位置附近发生虚位移α。
同济大学朱慈勉-结构力学第9章-弯矩分配法
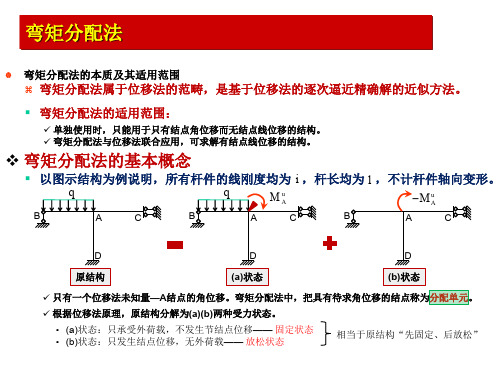
• 弯矩分配法中,结点转动在远端产生的弯矩可通过近端弯矩乘以传递系数得到。
• 远端为固定支座:CAB 1 2
A 1 i
A SAB 4i
M BA 2i B
• 远端为铰支座: CAB 0
A 1 i
A SAB 3i
M BA 0 B
• 远端为定向滑动支座:CAB 1
A 1 i
i2
4m
C
4m
3m 2m
B
A
C
BA AB AC AD CA
0.3 0.4 0.3
60
48
0 3.6 4.8 3.6 2.4
【解】 ⑴计算分配系数:
SAB 2 3 6, SAC 2 4 8, SAD 1.5 46 6
AB
6 20
0.3,
AC
8 20
•
M
u A
M
g AB
M
g AC
M
g AD
1 ql2 8
2019/12/5
q
q
M
u A
B
A
C
B
A
C
B
M
u A
A
C
D 原结构
D (a)固定状态
D (b)放松状态
放松状态内力分析
放松状态就是原结构承受结点不平衡力矩的反向力矩(相当于解除约束)。 放松状态的内力可借助转动刚度、分配系数、传递系数等概念计算。
相当于原结构“先固定、后放松”
q
q
M
u A
B
A
C
B
A
C
B
朱明zhubob结构力学9-2_1弯矩分配法

AB
SAB
SAB SAE SAD
SAC
4i 4i 4i i 3i
1 3
,
AE
4i 12i
1 3
,
AD
i 12i
1 12
,
AC
3i 12i
1 4
⑵计算固端弯矩(查表7-1): 0.035ql 2 0.179ql 2
M
F AB
MBFA
ql2 12
,
0.048ql 2 0.096ql 2 0.073ql 2 0.083ql 2 0.083ql 2
SAB M S
A
MAC SAC A iACA
SAC M S
A
MAD SAD A 3iADA SAD M S
近端弯矩:
远端弯矩:A
MAB 4iABA MAC iACA MAD 3iADA
MBA 2iABA MCA iACA
§9-2 弯矩分配法 9-2-1 基本概念
⒈ 名词解释 ⑴ 转动刚度S: 表示杆端对转动的抵抗能力。
远端固定: S 4i
远端简支:S 3i
远端滑动: S i
远端自由:S 0
§9-2 弯矩分配法
9-2-1 基本概念
⒈ 名词解释
⑴ 转动刚度S: 表示杆端对转动的抵抗能力。
⑵ 分配系数μ :
发生, 适合于用弯矩分配法。
S 15i
⑴各杆转动刚度: O
SOA k l l 3i, SOB 3i,
SOC 0, SOD 4i, SOE 0, SOF 0, SOG 4i, SOH i
建筑力学-弯矩分配法

THANKS
感谢观看
简化假设
弯矩分配法基于一些简化假设,如各杆件的线刚度相等,实际情况 可能并非如此。
无法处理复杂边界条件
对于具有复杂边界条件的结构,弯矩分配法可能无法给出准确的结 果。
弯矩分配法的改进方法
1 2
扩展应用范围
研究如何将弯矩分配法应用于不同类型的梁和结 构。
考虑非线性因素
在弯矩分配法中考虑非线性因素,如材料非线性 和几何非线性,以提高计算精度。
与有限元法的比较
弯矩分配法适用于线性静力分析,而有限元法则更适用于复 杂的非线性问题和动力分析。在某些情况下,将弯矩分配法 和有限元法结合使用可以更好地解决复杂的结构问题。
04
弯矩分配法的局限性与改进方法
弯矩分配法的局限性
仅适用于连续梁
弯矩分配法最初是为连续梁设计的,对于其他类型的梁(如简支 梁、悬臂梁等)可能不适用。
高层建筑结构分析
高层建筑结构复杂,弯矩分配法可以 帮助设计者更好地分析各楼层之间的 相互作用,优化楼层布局和结构形式, 提高建筑的抗震性能。
弯矩分配法在结构设计中的优化作用
01 02
结构形式优化
弯矩分配法可以帮助设计者根据实际受力情况,优化结构形式,选择合 理的梁、柱等构件的截面尺寸和连接方式,提高结构的承载能力和稳定 性。
建筑力学-弯矩分配法
• 引言 • 弯矩分配法的基本原理 • 弯矩分配法的实际应用 • 弯矩分配法的局限性与改进方法 • 结论
01
引言
弯矩分配法的定义
01
弯矩分配法是一种计算超静定结 构内力的方法,通过将结构中的 弯矩进行分配,使结构达到静力 平衡状态。
02
弯矩分配法的基本原理是将结构 中的各个杆件按照其刚度进行弯 矩的分配,刚度越大,分配到的 弯矩越大。
结构力学 课件 力矩分配法

SAB
1
2 传递系数C
传递系数: 一单跨超静定梁的一端(A端)单位转角时,发生于远 端(B端)的弯矩与近端(A端)的弯矩之比。
如: 当远端(B端)固定,C AB
M
BA
SAB
1 2 S AB
MBA
A B
图(a)
1
C 当远端(B端)铰支 , AB
M
SAB
A
B
BA
0
SAB
A
1
图(b)
S AB
(1)设想在结点B增加一个附加刚臂,得到位 移法基本结构。阻止其转动如图(g)所示。 查表容易得到各单跨超静定梁的杆 端弯矩。则附加刚臂的约束力矩由 结点B的平衡条件得
M
B
Fp
A
q
B C
图(f)
MB
A
Fp
B
q
C
图(g)
M
F BA
M
F BC
MB MBAF -MB
A B C
附加刚臂的约束力矩MB 是原结构 上所没有的,它反映了基本结构汇 交于B结点的各杆B端弯矩所不能平 衡的差额。我们称之为B结点的不 平衡力矩。
MBCF
图(h)
(2)原结构在结点B本来没有转动约束,即不存在不平衡力矩MB ,因 此,为了与实际情况相符,必须消除人为引入的附加刚臂,即使MB 0,这就相当于在 MB的基础上再施加上一个(- MB )如图(h)所示。
此时梁将产生新的杆端弯矩M´BA 、 M´BC (分配弯矩),在远端将产生新 的杆端弯矩M´AB 、 M´CB 、(传递弯 矩)。 (3)原结构在荷载的作用下的实际杆端弯 矩应为图(g) 和图(h)两种情况的叠加。 下面举例说明力矩分配法的解题过 程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相当于原结构“先固定、后放松”
q
q
M
u A
B
A
C
B
A
C
B
M
u A
A
C
D 原结构
D (a)固定状态
D (b)放松状态
固定状态内力分析
弯矩分配法是一种数值算法,正负号规定非常重要!
固定状态下,由荷载引起的杆端弯矩称为固端弯矩。正负号规定:绕杆端顺时针为正。
• 固端弯矩根据第7章位移法表7-1计算,其本质就是位移法Mp图的计算。
转动刚度:AB杆件A端(又称近端)发生单位转角时,A端产生的弯矩值,称为AB杆A端的转动刚度, 记为 S AB 。
• 转动刚度不仅与杆件的弯曲线刚度 i EI l 有关,而且与杆件另一端(又称远端)的支承条件有关。 • 远端为固定支座:SAB 4i • 远端为铰支座: SAB 3i • 远端为定向滑动支座: SAB i
A
M
u A
D (b)放松状态
M
f AD
A结点力矩
得,
A
M
u A
SAB SAC SAD
从而,
M
f AB
S AB S Aj
M
u A
AB
M
u A
称为力矩分配系数,表示杆件刚度在结点刚度中占的比例。
每个分配单元上,力矩分配系数之和恒等于1,即 1。
A 1 i
A SAB 4i
M BA 2i B
A 1 i
A SAB 3i
M BA 0 B
A 1 i
A SAB i
M BA i B
2019/5/17
放松状态内力分析
传递系数:AB杆件仅A端发生转角时,B端弯矩与A端弯矩之比,称为从A到B的弯矩传递系数,记为 CAB 。
• 分配系数: AB 3 8; AC 1 8; AD 1 2
•
M
u A
M
g AB
M
g AC
M
g AD
1 ql2 8
2019/5/17
q
q
M
u A
B
A
C
B
A
C
B
M
u A
A
C
D 原结构
D (a)固定状态
D (b)放松状态
放松状态内力分析
放松状态就是原结构承受结点不平衡力矩的反向力矩(相当于解除约束)。 放松状态的内力可借助转动刚度、分配系数、传递系数等概念计算。
固定状态,计算固端弯矩和结点不平衡力矩。
• •
固端弯矩
M
g AB
1 8
ql 2 ,
结点不平衡力弯矩
M
u A
M
g BA
0;
M
g AB
M
g AC
M
g AC
M
g AD
0,
M
g CA
1 ql2 8
0;
放松状态,计算分配力矩和传递力矩。
M
g AD
0,
M
g DA
0;
• 杆件转动刚度: SAB 3i; SAC i; SAD 4i
•
M
g AB
1 ql2, 8
M
g BA
0;
M
g AC
0,
M
g CA
0;
M
g AD
0,
M
g DA
0;
结点附加刚臂上的约束力矩称为结点不平衡力矩。正负号规定:顺时针为正。
• 结点不平衡力矩的计算:根据固端弯矩,利用结点力矩平衡条件计算。 • 在上述正负号规定条件下,结点不平衡力矩就是与该结点相连的所有杆件该端固端弯矩的代数和。
• 分配系数:CAB 3 8; CAC 1 8; CAD 1 2
•
近端分配力矩:
M
f AB
3 64
ql 2 ;
M
f AC
1 64
ql 2 ;
M
f AD
1 16
ql 2
•
远端传递力矩:M来自c BA 0;
M
c CA
1 64
ql 2 ;
M
c DA
1 32
ql 2
杆端最终弯矩=固端弯矩+分配力矩+传递力矩
q
q
M
u A
M
u A
B
A
C
B
A
C
B
A
C
D
D
D
原结构
(a)状态
(b)状态
只有一个位移法未知量—A结点的角位移。弯矩分配法中,把具有待求角位移的结点称为分配单元。
根据位移法原理,原结构分解为(a)(b)两种受力状态。
• (a)状态:只承受外荷载,不发生节结点位移—— 固定状态 • (b)状态:只发生结点位移,无外荷载—— 放松状态
弯矩分配法
弯矩分配法的本质及其适用范围
弯矩分配法属于位移法的范畴,是基于位移法的逐次逼近精确解的近似方法。
弯矩分配法的适用范围:
单独使用时,只能用于只有结点角位移而无结点线位移的结构。 弯矩分配法与位移法联合应用,可求解有结点线位移的结构。
弯矩分配法的基本概念
以图示结构为例说明,所有杆件的线刚度均为 i ,杆长均为 l ,不计杆件轴向变形。
2019/5/17
q
结点 B
A
C D 备注
B
A
C
杆端 BA AB AC AD CA DA
38 18 12
D 原结构
计算过程小结
Mg
分配 传递
M终
18 0 3 64 1 64 1 16 1 64 1 32 0 5 64 1 64 1 16 1 64 1 32
ql 2
分配力矩下划 线,以示与传 递力矩区分
固定状态,计算固端弯矩和结点不平衡力矩。
• •
固端弯矩
M
g AB
1 8
ql 2 ,
结点不平衡力弯矩
M
u A
M
g BA
0;
M
g AB
M
g AC
M
g AC
M
g AD
0,
M
g CA
1 ql2 8
0;
放松状态,计算分配力矩和传递力矩。
M
g AD
0,
M
g DA
0;
• 杆件转动刚度: SAB 3i; SAC i; SAD 4i
A SAB i
M BA i B
放松状态内力(分配系数)
B
M
u A
A
C
M
f AB
M
u A
A
M
f AC
A结点力矩平衡方程:
M
f AB
M
f AC
M
f AD
M
u A
而,M
f AB
S AB A;
M
f AC
SAC A;
M
f AD
SAD A
所以,
SAB SAC SAD
• 弯矩分配法中,结点转动在远端产生的弯矩可通过近端弯矩乘以传递系数得到。
• 远端为固定支座:CAB 1 2
A 1 i
A SAB 4i
M BA 2i B
• 远端为铰支座: CAB 0
A 1 i
A SAB 3i
M BA 0 B
• 远端为定向滑动支座:CAB 1
A 1 i
物W理h含y?义:结点力矩平衡
M
f AC
S AC S Aj
M
u A
AC
M
u A
M
f AD
S AD S Aj
M
u A
AD
M
u A
2019/5/17
q
q
M
u A
B
A
C
B
A
C
B
M
u A
A
C
D 原结构
D (a)固定状态
D (b)放松状态
计算过程小结
