统计学计算题复习
统计学试题库计算题部分
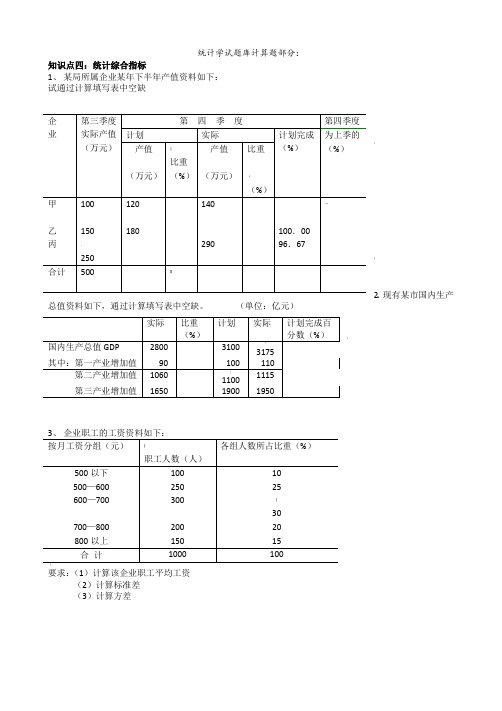
统计学试题库计算题部分:知识点四:统计综合指标1、 某局所属企业某年下半年产值资料如下: 试通过计算填写表中空缺:;2、现有某市国内生产总值资料如下,通过计算填写表中空缺。
(单位:亿元):要求:(1)计算该企业职工平均工资(2)计算标准差 (3)计算方差(2)比较哪个企业职工平均年龄更具代表性'、(7、甲、乙两企业工人有关资料如下:~要求:(1)比较哪个企业职工工资偏高(2)比较哪个企业职工平均工资更具代表性?10、甲、乙两钢铁生产企业某月上旬的钢材供货量资料如下:试比较甲、乙两企业该月上旬钢材供货的均衡性【11、某校甲、乙两班学生的统计学原理考试成绩分组情况如下:…要求:(1)计算各班学生的平均成绩(2)通过计算说明哪个班学生平均成绩的代表性强\求平均利润率。
问哪一个公司招员考试的成绩比较整齐(用标准差)!知识点五:时间数列及动态分析:试计算该市“九五”时期国民生产总值的年均递增率|(2)预测2004年存款余额将达到多少4、1997—2002年某企业职工人数和非生产人数资料如下:人员占全部职工人数的平均比重|要求:根据上述资料计算该企业这种产品第一季度单位产品成本(2)计算上半年平均计划完成程度,(2)计算四年平均工业增加值占国内生产总值的比重^^(2)用最小平方法配合直线趋势方程)年的销售额。
|知识点六:统计指数'(2)编制产量总指数、计算由于产量变动而增减的产值(3)编制出厂价格总指数,计算由于价格变动而增减的产值(2)计算销售量总指数(3)对总销售额的变动进行因素分析—(2)三种商品价格及销售量的综合变动指数(3)由于价格提高和销售量的增加各使销售额增加多少[(2)物价总指数(3)由于物价变动所引起的总产值的增加或减少额5、&(2)销售量总指数以及由于销售量变动对销售额的影响(8、[.8、某商店出售三种商品,资料如下:试计算价格总指数Array@~'11、某工业企业生产甲、乙两种产品,基期和报告期的产量、单位产品成本和出厂价格资料如下: 试计算:(1)以单位成本为同度量因素的产量总指数;(2)单位成本总指数;(3)对总成本进行两因素分析。
统计学计算题整理

:典型计算题一1、某地区销售某种商品的价格和销售量资料如下:根据资料计算三种规格商品的平均销售价格。
解:36==∑∑ffxx (元)点评: 第一,此题给出销售单价和销售量资料,即给出了计算平均指标的分母资料,所以需采用算术平均数计算平均价格。
第二,所给资料是组距数列,因此需计算出组中值.采用加权算术平均数计算平均价格。
第三,此题所给的是比重权数,因此需采用以比重形式表示的加权算术平均数公式计算。
2、某企业1992年产值计划是1991年的105%,1992年实际产值是1991的的116%,问1992年产值计划完成程度是多少?解:%110%105%116===计划相对数实际相对数计划完成程度.即1992年计划完成程度为110%,超额完成计划10%.点评:此题中的计划任务和实际完成都是“含基数”百分数,所以可以直接代入基本公式计算.3、某企业1992年单位成本计划是1991年的95%,实际单位成本是1991年的90%,问1992年单位成本计划完成程度是多少?解: 计划完成程度%74.94%95%90==计划相对数实际相对数。
即92年单位成本计划完成程度是94。
74%,超额完成计划5.26%。
点评:本题是“含基数”的相对数,直接套用公式计算计划完成程度。
4、某企业1992年产值计划比91年增长5%,实际增长16%,问1992年产值计划完成程度是多少?解:计划完成程度%110%51%161=++=点评:这是“不含基数"的相对数计算计划完成程度,应先将“不含基数”的相对数还原成“含基数”的相对数,才能进行计算。
5、某企业1992年单位成本计划比1991年降低5%,实际降低10%,问1992年单位成本降低计划完成程度是多少?解:计划完成程度%74.94%51%101=--=点评:这是“不含基数”的相对数计算计划完成程度,应先将“不含基数”的相对数还原成“含基数”的相对数,才能进行计算。
6、某企业产值计划完成103%,比上期增长5%,问产值计划规定比上期增加多少? 解:103%=105%÷(1+x ) x=1.9%即产值计划规定比上期增加1。
《统计学》复习题及答案

《统计学》复习题一、单选题1.某城市进行工业企业未安装设备普查,个体是( B )A.工业企业全部未安装设备 B.工业企业每一台未安装设备C.每个工业企业的未安装设备 D.每一个工业企业2.工业企业的设备数,产品产值是( A )A.连续变量 B.离散变量C.前者是连续变量,后者是离散变量 D.前者是离散变量,后者是连续变量3.对某班学生按年龄分成16-18岁、19—21岁、22-24岁三组,则24岁是( A )A。
最大值 B。
组中值 C. 第三组的上限 D。
第三组的组中值4.一个组的上限与下限之差称为( D )A。
组中值B。
组数 C. 全距 D. 组距5.连续变量数列中,其末组为开口组,下限是1000,相邻组的组中值为975,则末组的组中值为( D )A. 987。
5B. 1000 C。
1025 D. 10506. 在建筑业设备普查中,每个建筑企业是( B )A. 调查对象B. 填报单位C. 调查单位 D。
调查项目7.向上累计次数表示截止到某一组为止( A )A.上限以下的累计次数 B.下限以上的累计次数C.各组分布的次数 D.各组分布的频率8。
一组样本数据为3、3、1、5、13、12、11、9、7.这组数据的中位数是( D )A.3 B。
13 C.7。
1 D.7 9。
算术平均数、众数和中位数之间的数量关系决定于总体次数的分布状况.在对称的钟形分布中( A )A。
算术平均数=中位数=众数 B。
算术平均数〉中位数>众数C。
算术平均数<中位数<众数 D。
中位数>算术平均数。
>众数10.用不考虑顺序的不重复抽样方法,从8个人中抽选3个人,所得样本可能数目的公式为( B )A. B. C. D.11.某同学的英语成绩为80分,则“成绩”是( A )A.品质标志 B.数量标志 C.标志值 D.数量指标12.了解某地区工业企业职工的情况,下列哪个是统计指标( C )A.该地区每名职工的工资额 B.该地区职工的文化程度C.该地区职工的工资总额 D.该地区职工从事的工种13.对于统计分组设计,下列哪种说法是错误的( B )A。
统计学期末复习资料_计算题

五、计算题(要求写出公式、列出计算步骤) 1. 某产品资料如下:要求按以下三种方法计算产品的平均收购价格:(1) 不加权的平均数;(2)加权算术平均数;(3)调和平均数 解:不加权05.139.005.12.1=++=x (元/斤)加权02.140003000200040009.0300005.120002.1=++⨯+⨯+⨯==∑∑fxf x (元/斤)加权调和02.19.0360005.131502.1240036000315024001=++++==∑∑m xm x (元/斤)2. 某公司所属三个企业生产同种产品,2004年实际产量、计划完成情况及产品优质品率资料如下:要求计算:(1)该公司产量计划完成百分比; (2)该公司的实际优质品率。
解:1)以实际产值为m,完成计划百分比为x,该公司产量计划完成百分比:%95.9320.5325008.02501.11502.1100250150100==++++==∑∑x m m x2)以实际优质品率为x,以实际产量为f,该公司的实际优质品率:%8.9650048425015010098.025096.015095.0100==++⨯+⨯+⨯==∑∑fxfx3. 某企业有50名工人,其月产值(万元)如下:要求:(1)根据上述资料将50名工人按产值分7组编制组距为10万元的等组距数列;(2)按上述分组编制向上累计的累计频数和累计频率数列;(3)并以第三组为例说明累计频数和累计频率的含义。
解:(1)根据上述资料将50名工人按产值分7组编制组距为10万元的等组距数列;(2)按上述分组编制向上累计的累计频数和累计频率数列;(3)并以第三组为例说明累计频数和累计频率的含义。
第三组数据说明在50名工人中,月产值在105以下的有30人,占总数的60%4. 南宁化工厂2008年现有生产工人600人。
现用不重复抽样抽出40人调查其年产值(万元)如下:(1)将40个工人按产值分组,编制组距为10万元的等组距数列,并列出向上累计频数和累计频率。
《统计学》复习题

《统计学》复习题一、判断题(每空1分,共10分)1.所有的统计指标都是变量。
()2.统计所研究的对象就是社会经济现象的数量方面。
()3.将收集到得的数据分组,组数越多,丧失的信息越多。
4.绝对数随着总体范围的扩大而增加。
()5.总体单位总量和总体标志总量是不能转化的。
()6.水平法和累计法的选择依据是计划指标。
()7.相关系数是测定变量之间相关密切程度的唯一方法。
( )8.A产品产量与单位成本的相关系数是-0.88,B产品单位成本与利润率的相关系数是-0.94,因此A比B的相关程度高。
( )9、工人的工资(元)与劳动生产率(千元)的回归方程为y=10+70x,这意味着如果劳动生产率每增加1000元,则工人工资平均增加80元。
( )10.时间数列就是将一系列统计指标按时间先后顺序排列。
( )二、选择题(每小题2分,共30分)1.某城市进行工业企业未安装设备普查,总体单位是()。
A.工业企业全部未安装设备B.企业每一台未安装设备C.每个工业企业的未安装设备D.每一个工业企业2.工业企业的设备台数、产品产值是()。
A.连续变量B.离散变量C.前者是连续变量D.前者是离散变量3.对某地区工业企业职工情况进行研究,统计总体是()。
A.每个工业企业B.该地区全部工业企业C.每个工业企业的全部职工D.该地区全部工业企业的全部职工4.通过调查大庆.胜利等几大主要油田来了解我国石油生产的基本情况,这种调查方式属于()。
A.随机调查B.典型调查C.重点调查D.抽样调查5.抽样调查与重点调查的主要区别是()。
A.容量不同B.组织方式不同C.灵活程度不同D.取调查单位的方法不同6.我国目前收集统计资料的主要形式是()。
A.全面调查B.普查C.抽样调查D.统计报表7.社会经济统计中最基本的统计指标是()。
A .总量指标 B.相对指标 C.平均指标 D.变异指标8.总量指标按其说明总体内容的不同,可分为()。
A.时期指标和时点指标B.总体单位总量指标和标志总量指标C. 总体数量指标和质量指标D. 实物指标和价值指标9.用有名数表现的相对指标是()。
统计学原理计算题复习(六种题型重点)

第三章:编制次数分配数列1.根据所给资料分组并计算出各组的频数和频率,编制次数分布表;根据整理表计算算术平均数。
例题:某单位40名职工业务考核成绩分别为: 68 89 88 84 86 87 75 73 72 68 75 82 97 58 81 54 79 76 95 76 71 60 90 65 76 72 76 85 89 92 64 57 83 81 78 77 72 61 70 81单位规定:60分以下为不及格,60─70分为及格,70─80分为中,80─90分为良,90─100分为优。
要求:(1)将参加考试的职工按考核成绩分为不及格、及格、中、良、优五组并编制一张考核成绩次数分配表;(2)指出分组标志及类型及采用的分组方法;(3)根据考核成绩次数分配表计算本单位职工业务考核平均成绩; (4)分析本单位职工业务考核情况。
解答:(1)该企业职工考核成绩次数分配表:成 绩(分) 职工人数(人) 频率(%)不及格(60以下) 3 7.5 及格 (60-70) 6 15 中 (70-80) 15 37.5 良 (80-90) 12 30 优 (90-100) 4 10 合 计 40100(2)此题分组标志是按“成绩”分组,其标志类型是“数量标志”; 分组方法是“变量分组中的组距式分组的等距分组,而且是开口式分组”;(3)根据考核成绩次数分配表计算本单位职工业务考核平均成绩。
(4)分析本单位职工考核情况。
本单位的考核成绩的分布呈两头小,中间大的“钟形分布”(即正态分布),不及格和优秀的职工人数较少,分别占总数的7.5%和10%,本单位大部分职工的考核成绩集中在70-90分之间,占了本单位的为67.5%,说明该单位的考核成绩总体良好。
)(774095485127515656553分=⨯+⨯+⨯+⨯+⨯==∑∑f xf x第四章:计算加权算术平均数、加权调和平均数(已知某年某月甲、乙两农贸市场A 、B 、C 三种农产品价格和成交量、成交额资料,试比较哪一个市场农产品的平均价格 较高?并说明原因。
统计学原理复习题

期末复习题一、判断题(把正确的符号“√”或错误的符号“×”填写在题后的括号中。
)1.社会经济统计的研究对象是社会经济现象总体的各个方面。
(×)2.在全国工业普查中,全国企业数是统计总体,每个工业企业是总体单位。
(×)3.总体单位是标志的承担者,标志是依附于单位的。
(√)4.在全国工业普查中,全国工业企业数是统计总体,每个工业企业是总体单位。
(×)5.全面调查和非全面调查是根据调查结果所得的资料是否全面来划分的(×)。
6.调查单位和填报单位在任何情况下都不可能一致。
(×)7.对全同各大型钢铁生产基地的生产情况进行调查,以掌握全国钢铁生产的基本情况。
这种调查属于非全面调查。
(√)8.统计分组的关键问题是确定组距和组数(√)9.总体单位总量和总体标志总量是固定不变的,不能互相变换。
(×) 10.相对指标都是用无名数形式表现出来的。
()11.国民收入中积累额与消费额之比为1:3,这是一个比较相对指标。
(×)12.抽样推断是利用样本资料对总体的数量特征进行估计的一种统计分析方法,因此不可避免的会产生误差,这种误差的大小是不能进行控制的。
(×)13.从全部总体单位中按照随机原则抽取部分单位组成样本,只可能组成一个样本。
(×) 14.在抽样推断中,作为推断的总体和作为观察对象的样本都是确定的、唯一的。
(×) 15.抽样估计置信度就是表明抽样指标和总体指标的误差不超过一定范围的概率保证程度。
(√) 16.在其它条件不变的情况下,提高抽样估计的可靠程度,可以提高抽样估计的精确度。
(×) 17.施肥量与收获率是正相关关系。
(×) 18.计算相关系数的两个变量都是随机变量(√) 19.利用一个回归方程,两个变量可以互相推算(×) 20.数量指标作为同度量因素,时期一般固定在基期(×)。
统计学期末复习计算题汇总

3—5
5—7 7—9 合计
30
40 30 100
4
6 8 -
120
0 120 240
3—5
5—7 7—9 合计
40
40 20 100
4
6 8 -
1.024
0.064 1.152 2.24
σ
甲
=
(x - x) f f
2
2
=
240 = 1.55 100
f σ乙 = (x - x) Σf = 2.24 = 1.5
年份 2008 2009 2010 2011
工业总产值(万元)
增长量(万元) 发展速度(%)
(
─ ─
)
(
5000 (
) (
( ) 106
) (
) ( (
)
) )
增长速度(%)
增长1%的绝对值(万元)
─
─
(
800
) (
(
)
) (
4
)
2.某企业历年工业总产值资料如下表,试填上表中所缺 的各种动态分析指标,并计算该企业工业总产值平均每 年的发展速度。 年 份 2008 2009 2010 ( 2011
9.某企业两个生产班组,各有100名工人,它们生产某 种产品的日产量资料如下表,计算有关指标,比较哪 个班组平均日产量的代表性强。
甲班组 日产量 工人数 (件) f 3—5 5—7 7—9 合计 30 40 30 100 组中值 xf x 4 6 8 — 120 240 240 600 日产量 (件) 3—5 5—7 7—9 合计 乙班组 x 生产工人 f
比重% Σf
x
f Σf
4 6 8 —
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
K
x1 f1 x2 f2 xK f1 f2 fK
fK
xi fi
i1 K
fi
k i1
x
x1 f1 x2 f2 xk fk f1 f2 fk
xi fi
i 1 n
fi
i1
• 公X式中: 为均值; f为相应频数;Xi为第i个单位的变量值。
高校教育精品PPT
9
加权平均数的计算方法 案例分析 4.11
(Sample Variance and Standard Deviation)
方差的计算公式
未分组数据:
n
(xi x)2
s 2 i1 n 1
注意:
样本方差用自 由度n-1去除!
未标分组准数差据的:计算公式
n
(xi x)2
s i1 n 1
组距分组数据:
组距分组数据:
k
(Mi x)2 fi
s 2 i1 n 1
46 29.5 2.0
31.5
高校教育精品PPT
3
中位数 (位置的确定)
奇数个数的数据:中位数位置 n 1 2
偶数个数的数据:中位数位置 n , n 1 22
高校教育精品PPT
4
中位数的确定(分组数据)
• 根据位置公式确定中位数所在的组
• 采用下列近似公式计算:
Me
L
N 2
S m1 fm
N
N
• 样本均值
n
x
x1 x2
xn
xi
i 1
n
n
• 式中:X,μ为均值; N(n)为总体(样本)单位总数;
Xi为第i个单位的变量值。
高校教育精品PPT
7
算术平均数的计算方法 案例分析 4.10
某售货小组5个人,某天的销售额分别为520 元、600元、480元、750元、440元,则
平均每人日销售额为:
频数 5 7 12 18 22 16 10 8
Koala Sightings
25
Line 1
20
Line 2
15
Frequency
Line 3
10
5
0 10 – 14 15 – 19 20 – 24 25 – 29 30 – 34 35 – 39 40 – 44 45 – 49
பைடு நூலகம்
Number of koalas seen in a day
8
合计
50
(人) 3 10 42 50
—
Me
L
N 2
Sm1 i
fm
50 10
Me
400
2 32
600 400 493.75件
高校教育精品PPT
6
简单平均数 (Simple Mean)
• 设一组数据为:X1 ,X2 ,… ,Xn
适用于总体资料未经分组整理、尚为原始n 资料的情况
• 总体均值 x1 x2 xN i1 xi
例:根据某电脑公司在各市场上销售量的分
组数据,计算电脑销售量的均值。
按销售量分组(台)
140~150 150~160 160~170 170~180 180~190 190~200 200~210 210~220 220~230 230~240
合计
组中值(Mi)
145 155 165 175 185 195 205 215 225 235
• 某企业某日工人的日产量资料如下:
日产量(件)
X
工人人数(人)
f
10
70
11
100
12
380
13
150
14
100
合计
800
计算该企业该日高校全教育部精品工PPT人的平均日产量。 10
加权平均数的计算方法 案例分析 4.11
k
x
xi fi
i 1 n
fi
10 70 ... 14100 70 ... 100
9710 800
12.1375
i 1
• 若上述资料为分组数列,则应取各组的组中值作为该
组的代表值用于计算;此时求得的算术平均数只是其
真值的近似值。
高校教育精品PPT
11
简单平均数与加权平均数 (Simple Mean / Weighted Mean)
设一组数据为: x1 ,x2 ,… ,xn
各组的组中值为: M1 ,M2 ,… ,Mk
X X 520 600 480 750 440 1395 元
n
5
高校教育精品PPT
8
加权平均数 (Weighted Mean)
• 设一组数据为: x1 ,x2 ,… ,xn • 相应的频数为: f1 ,f2 ,… ,fk
适用于总体资料经过分组整理形成变量数列的情况
• 总体均值
• 样本均值 (未分组)
众数的确定 (分组数据)
频数
直方图
众数=25
30
25
20
15
10
5
0 0-<10 10-<20 20-<30 30-<40 40-<50 50-<60 60-<70 70-<80 年龄
高校教育精品PPT
1
众数的确定 (分组数据)
组距 10 – 14 15 – 19 20 – 24 25 – 29 30 – 34 35 – 39 40 – 44 45 – 49
—
市场个数(fi)
4 9 16 27 20 17 10 8 4 5
∑fi= 120
Mi fi
580 1395 2640 4725 3700 3315 2050 1720
900 1175
∑Mi fi =22200
k
X i1 高Mn校i教f育i 精品2P2P1T22000 185(台)
13
样本方差和标准差
相应的频数为: f1 , f2 ,… ,fk n
简单平均数
x
x1 x2
xn
xi
i1
n
n
加权平均数 (分组数据)
k
x
M1
f1 f1
M2 f2 Mk f2 fk
fk
Mi fi
i 1
n
Mi 表示各组的变量值(分组数列的组中值); fi 高表校示教各育精组品变PP量T 值出现的频数(即权数)。12
k
(Mi x)2 fi
s i1 n 1
高校教育精品PPT
14
样本标准差 例题分析 4.18
按销售量分组
i
• L –中位数组的真实组下限的值
• N –整组数据的总数量
• Sm-1 –中位数组为止以上的累积频数
• fm –中位数组的频数
•
i –组距的个数 高校教育精品PPT
5
: 某车间50名工人月产量的资料如下
月产量(件) 工人人数(人) 向上累计次数
200以下
3
200~400
7
400~600
32
600以上
高校教育精品PPT
2
众数为31.5
众数的确定 (分组数据)
Mo L d1 i
△
d1 d2
• L—众数组的真实下限值
• d1—众数组频数-众数组前一组频数
• d2—众数组频数-众数组后一组频数
• i — 每组数据的组距个数
thus : L 29.5, d1 22 18 4, d2 22 16 6,i 5 Mo 29.5 4 (5)
