江西省2015年高考数学理科押题卷及标准答案
江西省2015年高考数学理科押题卷及标准答案

江西省2015年高考数学理科押题卷及标准答案————————————————————————————————作者:————————————————————————————————日期:泄露天机——2015年江西省高考押题 精粹数学理科本卷共60题,三种题型:选择题、填空题和解答题。
选择题36小题,填空题8小题,解答题18小题。
一、选择题(36个小题)1. 已知全集{}1,2,3,4,5U =, 集合{}3,4,5M =, {}1,2,5N =, 则集合{}1,2可以表示为( )A .M N IB .()I U M N ðC .()U M N I ðD .()()U UM N I 痧答案:B解析:有元素1,2的是,U M N ð,分析选项则只有B 符合。
2. 集合 {}{}{}1,2,3,4,5,1,2,3,|,A B C z z xy x A y B ====∈∈且,则集合C 中的元素个数为( )A .3B .4C .11D .12 答案:C解析:{1,2,3,4,5,6,8,9,10,12,15}C =,故选C 。
3. 设集合{}1,0,1,2,3A =-,{}220B x x x =->,则A B ⋂=( )A .{}3B .{}2,3C .{}1,3-D .{}0,1,2 答案:C解析:集合{}{}22020B x x x x x x =->=><或,{}1,3A B ⋂=-。
4. 若(1)z i i +=(其中i 为虚数单位),则||z 等于( )A .1 B. 32 C. 22D. 12答案:C 解析:化简得i z 2121+=,则||z =22,故选C 。
5. 若复数iia 213++(i R a ,∈为虚数单位)是纯虚数,则实数a 的值为( )A. 6-B. 2-C. 4D. 6答案: A 解析:3(3)(12)63212(12)(12)55a i a i i a a i i i i ++-+-==+++-,所以6320,0,655a aa +-=≠∴=-。
2015年高考理科数学押题密卷(全国新课标II卷)

(5)2(A ) 8+ 2 .5 (B ) 6+ 2 5 (C ) 8+ 2 3(D ) 6+ 2 32015年高考理科数学押题密卷(全国新课标II 卷)2015年高考绝密押题,仅限 VIP 会员学校使用,版权所有,严禁转载或商业传播, 违者必究; 说明:一、 本试卷分为第 I 卷和第n 卷•第I 卷为选择题;第n 卷为非选择题,分为必考和选 考两部分.二、 答题前请仔细阅读答题卡上的 注意事项”,按照 注意事项”的规定答题. 做选择题时,每小题选出答案后,用铅笔把答题卡上对应题目的标号涂黑•如需改 用橡皮将答案擦干净后,再涂其他答案.考试结束后,将本试卷与原答题卡一并交回. 选择题:本大题共 12小题,每小题5分, 有且只有一项符合题目要求.动, 四、共60分,在每小题给出的四个选项中,(1) 已知集合 A = {x |x 2— 5x + 6W 0}, B= {x ||2 x — 1| > 3},则集合 A n B =(3) (A ) {x |2 w x < 3} (C ) {x |2 v x w 3} 1 — i 1 + i (1 + i)汁 (1 —厂 (A )— 1(B ) 1-1^宀曰.—b 满足 | a | = | b | = 2,(A ) 4 (B ) 6等比数列 {a n }的前n 项和为S n , (A ) 7(B ) 8(B) (D ) {x |2 w x v 3}{x | — 1 v x v 3}(D ) i60 , a •( a + b )等于(D ) 4 + 2、.:3且4a 1,2a 2,a 3成等差数 列,若 a 1=1,则 S 4 为 (D) 15空间几何体的三视图如图所示,则该几何体 的表面积为 (C )— ia 与b 的夹角为 (C ) 2+ ;'3(C ) 161正视图侧视图一 2 ------- ' 俯视图(6) (x 2—二)的展开式中的常数项为x(11)某方便面厂为了促销, 制作了 3种不同的精美卡片,每袋方便面随机装入一张卡片,集齐3种卡片可获奖,现购买该方便面 5袋,能获奖的概率为(12) 给出下列命题:1_ 1 0 2 O)log 05 3 23 (一). ; ②函数 f (x) log q x 2si n x 有 5 个零点; 3x 4 x5㊂函数f (x) =ln的图像以(5,)为对称中心;x 6 1212曾已知a 、b 、m n 、x 、y 均为正数,且 a * b ,若a 、m b 、x 成等差数列,a 、n 、b 、y 成等比数列,则有 n > n , x <y .其中正确命题的个数是(A ) 15(B )— 15 (C 20 (D )— 20(7) 执行右边的程序框图,则输出的(A) 5040 ( B ) 4850(C 2450(8) 2x + 4x + 3, x w 0, 已知函数f (x )=3 x ,x > 0,则方程 的实根个数为 (A ) 3 (B ) 2(C ) 1(D ) 0(9)2 2x y若双曲线孑一孑=1 (a >0,1的距离等于焦距的—,则双曲线的离心率为b >0) 一个焦点到一条渐近线(10) (B )攀(C)(D )手偶函数f (x )的定义域为R若f (x + 2)为奇函数,且f (1)=1,则 f (89) + f (90)为(A )— 2(B )— 1(C ) 0(D ) 1(A )31 81(B ) 3381 81(D )50 81(D ) 2550f (x ) + 1= 0(A) 1 个(B) 2 个(C) 3 个(D) 4 个第口卷二、填空题:本大题共4小题,每小题5分,共20分,把答案填写在题中横线上.(13) _______________________________________________________________ 由直线x = 1, y= 1 - x及曲线y= e x围成的封闭图形的面积为 ____________________________ .n n(14) __________________________________________________________________ 数列{a n}的通项公式a n= n sin — + 1,前n项和为S,则S? 015 = ____________________________________________ .x —y + 5> 0,(15) 已知x、y满足x + y >0, 若使得z = ax+ y取最大值的点(x, y)有无数个,则ax w 3,的值等于 ___________ .(16) _______________________________________________________________________ 已知圆O x2+ y2=8,点A(2 , 0),动点M在圆上,则/ OMA勺最大值为____________________ .三、解答题:本大题共70分,其中(17) — (21)题为必考题,(22), ( 23), (24)题为选考题•解答应写出文字说明、证明过程或演算步骤.(17) (本小题满分12分)已知f(x)=sin (2x ——) + 2COS2X.6(I)写出f(x)的对称中心的坐标和单增区间;(□)△ ABC三个内角A B C所对的边为a、b、c,若f (A) =0, b+ C=2.求a的最小值.(18) (本小题满分12分)某青年教师专项课题进行“学生数学成绩与物理成绩的关系”的课题研究,对于高二年级800名学生上学期期末数学和物理成绩,按优秀和不优秀分类得结果:数学和物理都优秀的有60人,数学成绩优秀但物理不优秀的有140人,物理成绩优秀但数学不优秀的有100人.(I)能否在犯错概率不超过0.001的前提下认为该校学生的数学成绩与物理成绩有关系?(n)将上述调查所得到的频率视为概率,从全体高二年级学生成绩中,有放回地随机抽取3名学生的成绩,记抽取的3个成绩中数学、物理两科成绩至少有一科优秀的次数为X,求X的分布列和期望E( X).附:P (心 k o ) 0.010 0.0050.001k o6.6357.879 10.828n ( ad — be )(a + b )( c + d )( a + e )( b +d )(A ) 1 个 (B ) 2 个 (C ) 3 个 (D ) 4 个(19) (本小题满分12分)(22)(本小题满分10分)选修4-1 :几何证明选讲如图,在△ ABC 中,/ C = 90o , BC= 8, AB= 10, 0为 BC 上一点,以O 为圆心,OB 为半径作半圆与 BC 边、AB 边分别交于点 D E 连结DE(I)若BD= 6,求线段DE 的长;(n)过点E 作半圆O 的切线,切线与AC 相交于点F ,如图,在三棱柱 ABGABG 中,已知 A 吐侧面 BBCC, BO ^2 , AB= BB = 2,Z BCC厂点E 在棱BB 上.(I)求证:CB 丄平面ABC(n)若BE =入BB ,试确定 入的值,使得二面 角ACE -C 的余弦值为專 (20)(本小题满分12分) 设抛物线y 2=4m x ( m>0)的准线与x 轴交于F , 1 焦点为F 2;以F 1、F 2为焦点,离心率 e =2 2 2/6的椭圆与抛物线的一个交点为 日一, );3 〜uuu 自F 1引直线交抛物线于 P 、Q 两个不同的点,点P 关于x 轴的对称点记为 M 设F 1P 3 uuu F 1Q.(I)求抛物线的方程和椭圆的方程; 1(n)若 [了",求|PQ 的取值范围.(21)(本小题满分12分)2 exX已知 f (x ) = e (x -a — 1)+ ax .(I)讨论f (x )的单调性;(n)若x 》0时,f (x ) + 4a >0,求正整数 a 的值.参考值:e 2~ 7.389 , e 3~ 20.086请考生在第(22), (23), (24)三题中任选一题作答,如果多做,则按所做的第题记分•作答时用2B 铅笔在答题卡上把所选题目对应的题号涂黑. ACDO证明:AF= EF.(23)(本小题满分10分)选修4-4 :坐标系与参数方程2 2x y已知椭圆c: 4 + 3 = 1,直线I: x=—3 + 寸3ty=2 3+t(t为参数)(I)写出椭圆C的参数方程及直线I的普通方程;(H)设A(1 , 0),若椭圆C上的点P满足到点A的距离与其到直线求点P的坐标.l的距离相等,(24)(本小题满分10分)选修4-5 :不等式选讲已知函数f (x) = | x —1| .(I)解不等式f(x) + f (x+ 4) >8;b(n)若| a| v 1, | b| v 1,且a* 0,求证:f (ab) > | a| f ().a所以能在犯错概率不超过0.001的前提下认为该校学生的数学成绩与物理成绩有关.理科数学参考答案2015年高考绝密押题,仅限 VIP 会员学校使用,版权所有,严禁转载或商业传播, 违者必究; 、选择题: CABDA ACBBD DC 、填空题: (13) e —亍; (14) 1007; (15)— 1; (16)4三、解答题: (17)解:(I)化简得: f (x )=cos ( 2x + 3 单增区间为: [k 23 ,k 6] (k z)(□)由(I) 知:f (A ) cos(2A3)10 cos(2 A 3)Q 0 A2A73332A 一于是: A33根据余弦定理:2ab 22c 2bc cos =43当且仅当b c1时,a 取最小值1.k 对称中心为:^,D (kz ) (18) (I) (6)分1 (9)分, b c 23bc4 3()2 12.............................. 12分因为k =800( 60X 500— 140 X100)160X 640X 200X 6002-=16.667 > 10.828 .所以能在犯错概率不超过0.001的前提下认为该校学生的数学成绩与物理成绩有关.1 所以当入=亍时,二面角ACE-C 的余弦值为專(20) 解:(n)每次抽取1名学生成绩,其中数学物理两科成绩至少一科是优秀的频率 频率视为概率,即每次抽取 为+ .由题意可知X B(3, 0.375 .将1名学生成绩,其中数学物理两科成绩至少一科是优秀的概率X0 1 23 p 125 225 135 27 512 512 旋 5123 厂),从而X 的分布列为E (X ) = np =专12分(19)解:(I)因为 BC= 2 , CC = BB = 2,/ BCC=〒,在厶BCC 中,由余弦定理,可求得 CB = 2 ,所以 GB 2+ B C = C C, CB 丄 BC 又 ABL 侧面 BCG 1,故 AB1 BC, 又CBH AB- B ,所以GB 丄平面ABC(n)由(I)知, BC BA BC 两两垂直, 以B 为空间坐标系的原点,建立如图所示的坐标系, 则 B (0 , 0, 0) , A (0 , 2, 0) , C ( 2 , 0, 0), 13A =(0, 2 , - 2),B E =(3B + 入目B = 13B + ^<5C = ( — 2 入,0 , 2 入一2),设平面ACE 的一个法向量为 m= (x , y , z),则有 m- S A = 0,即 2y — 2 z = 0 ,m i- S E = 0 , .2 入 x + (、2 ― 2 入)z = 0 ,令 z = .2 ,取 m -(宀日,1,2),分 又平面GEC 的一个法向量为 n = (0 , 1, 0), 12 =芈,解得3 5所以cos m n =吕i m i n |5分(I)由题设,得:4 9a 212②a 2由①、②解得a = 4, b = 3,2匕13y 2= 4x .Qg y 2)、M (X 1,— y 1), y 1=入y 2 ③设直线PQ 的方程为y = k (x +1),与抛物线的方程联立,得:ky 2 4y4ky 1 y 2= 44y 1 + y 2=k(21) 解:xx由◎ ◎ ◎消去y i , 得:k 21)2I PQI J k 12 I y 2y 1由方程O 得: I PQ I 、(1 ;2)16 16k1616k 4k 7化简为: I PQ I 2,代入 入:I PQ I 2(1)4216 1)216疋:那么: 2)2161 [2,1)PQ |2I PQ I (0,174亿 寸12分x 2椭圆的方程为一4易得抛物线的方程是:(H)记 P (x 1, y"、UJU uuu②(I) f (x) = e (x—a) —x+ a= (x—a)(e —1),由a >0,得:x € ( —g, 0)时,f (x ) >0, f (x )单增;x € (0 , a )时,f (x ) v 0, f (x )单减; x €(a ,+g )时,f (x ) >0, f (x )单增.所以,f (x )的增区间为(—g, 0) , (a ,+m );减区间为(0 , a ). (5)分2a(n)由(I)可知,x >0 时,f min (x ) = f ( a ) =— e + —,2a a所以 f (x ) + 4a >0,得 e — 2 — 4a w 0. (7)分2 aa a令 g ( a ) = e — — 4a,贝U g (a ) = e — a —4;令 h ( a ) = e a — a — 4,贝U h (a ) = e a — 1 >0,所以 h ( a )在(0,+g )上是增函数, 又 h (1) = e — 5v 0, h (2) = e 2— 6>0,所以 a °€ (1 , 2)使得 h (a 。
2015高考数学真题精准预测密卷 理科(含答案)

2015 高考数学真题精准预测密卷 (理科)
(考试时间 120 分钟 满分 150 分) 本试卷分为选择题(共 40 分)和非选择题(共 110 分)两部分
注意事项:
1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号 填写在答题卡上. 2.选择题每小题选出答案后,用 2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如 需改动,用橡皮擦干净后,再选涂其他答案.答案不能答在试卷上. 3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须填写在答题卡各题目指定区域内 相应位置上; 如需改动, 先划掉原来的答案, 然后再写上新的答案; 不准使用铅笔和涂改液. 不 按以上要求作答的答案无效. 4.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.
①曲线 C 关于原点对称; ③曲线 C 围成的面积大于 上述命题中, 真命题的序号为 A.①②③
②曲线 C 关于直线 y x 对称 ④曲线 C 围成的面积小于 ( C.①④ D.①③ )
B.①②④
18、若直线 y kx 1 与曲线 y x ( ).
1 1 x 有四个不同交点,则实数 k 的取值范围是 x x
c
.
0 x , 2sin x, 7、若 f x 2 则方程 f x 1 的所有解之和等于 x 0, x ,
.
8 、 若 数 列
lim a1 a2 an n2
an
为 等 差 数 列 , 且 .
a1 1, a2 a3 a4 21
, 则
n
9、 设 等 比 数 列 an 的 公 比 为 q , 前 n 项 和 为 Sn , 若 Sn 1 , Sn , Sn 2 成 等 差 数 列 , 则
年江西省高考押题精粹数学试题及答案(理)

2015年江西省高考押题(理)本卷共60题,三种题型:选择题、填空题和解答题。
选择题36小题,填空题8小题,解答题18小题。
一、选择题(36个小题)1. 已知全集, 集合, , 则集合可以表示为( ) A . B . C . D . 【答案】B【解析】有元素1,2的是,分析选项则只有B 符合。
2. 集合 ,则集合C 中的元素个数为( )A .3B .4C .11D .12 【答案】C【解析】,故选C 。
3. 设集合,,则=( )A .B .C .D . 【答案】C【解析】集合,。
4. 若(其中为虚数单位),则等于( )A .1 B. C. D.【答案】C{}1,2,3,4,5U ={}3,4,5M ={}1,2,5N ={}1,2MN ()U M N ð()U MN ð()()U U M N 痧,U M N ð{}{}{}1,2,3,4,5,1,2,3,|,A B C z z xy x A y B ====∈∈且{1,2,3,4,5,6,8,9,10,12,15}C ={}1,0,1,2,3A =-{}220B x x x =->A B ⋂{}3{}2,3{}1,3-{}0,1,2{}{}22020B x x x x x x =->=><或{}1,3A B ⋂=-(1)z i i +=i ||z12【解析】化简得,则,故选C 。
5. 若复数(为虚数单位)是纯虚数,则实数的值为( ) A. B. C.D.【答案】A 【解析】,所以。
6. 复数在复平面内对应的点位于( ) A .第一象限 B .第二象限C .第三象限D .第四象限【答案】D【解析】根据复数的运算可知,所以复数的坐标为,所以正确选项为D 。
7. 已知向量,若,则( )A. B .C .D .【答案】B【解析】,。
8. 已知为的边的中点,所在平面内有一个点,满足,则的值为()i z 2121+=||z iia 213++i R a ,∈a 6-2-463(3)(12)63212(12)(12)55a i a i i a a i i i i ++-+-==+++-6320,0,655a aa +-=≠∴=-21ii -()()22121215521i i i i i i +==---21,55⎛⎫- ⎪⎝⎭()()1,1,2,2m n λλ=+=+()()m n m n +⊥-=λ4-3-2--1(23,3),(1,1)m n m n λ+=+-=--()()()(),23130,3λλ+⊥-∴+⨯--=∴=-m n m n D ABC ∆BC ABC ∆P PA PB PC =+||||PD ADA .B .C .D .【答案】C【解析】如图,四边形是平行四边形,D 为边BC 的中点,所以D 为边的中点,的值为1。
(泄露天机)江西省高考数学押题精粹试题 理

泄露天机——2015年江西省高考押题 精粹数学理科本卷共60题,三种题型:选择题、填空题和解答题。
选择题36小题,填空题8小题,解答题18小题。
一、选择题(36个小题)1. 已知全集错误!未找到引用源。
, 集合错误!未找到引用源。
, 错误!未找到引用源。
, 则集合错误!未找到引用源。
可以表示为( )A .错误!未找到引用源。
B .错误!未找到引用源。
C .错误!未找到引用源。
D .错误!未找到引用源。
答案:B解析:有元素1,2的是错误!未找到引用源。
,分析选项则只有B 符合。
2. 集合 错误!未找到引用源。
,则集合C 中的元素个数为( ) A .3 B .4 C .11 D .12 答案:C解析:错误!未找到引用源。
,故选C 。
3. 设集合错误!未找到引用源。
,错误!未找到引用源。
,则错误!未找到引用源。
=( ) A .错误!未找到引用源。
B .错误!未找到引用源。
C .错误!未找到引用源。
D .错误!未找到引用源。
答案:C解析:集合错误!未找到引用源。
,错误!未找到引用源。
4. 若错误!未找到引用源。
(其中错误!未找到引用源。
为虚数单位),则错误!未找到引用源。
等于( )A .1 B. 错误!未找到引用源。
C. 错误!未找到引用源。
D. 错误!未找到引用源。
答案:C解析:化简得错误!未找到引用源。
,则错误!未找到引用源。
=错误!未找到引用源。
,故选C 。
5. 若复数i ia 213++(i R a ,∈为虚数单位)是纯虚数,则实数a 的值为( )A. 6-B. 2-C. 4D.6答案:A解析:错误!未找到引用源。
,所以错误!未找到引用源。
6. 复数错误!未找到引用源。
在复平面内对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 答案:D 解析:根据复数的运算可知错误!未找到引用源。
,所以复数的坐标为错误!未找到引用源。
,所以正确选项为D 。
7. 已知向量错误!未找到引用源。
2015年高考数学(理)押题试卷及答案(word版可打印)

2015年高考理科数学押题试卷及答案(word 版可打印)第I 卷(共60分)一、选择题:本大题共12小题。
每小题5分,共60分.在每小题给出的四个选项中。
只有一项是 符合题目要求的.1.已知集合(){}{}2lg 4,3,0=x A x y x B y y x A B ==-==⋂>时, A.{}02x x << B.{}2x x 1<< C.{}12x x ≤≤ D.∅2.若复数12a ii--是纯虚数,则实数a 的值为A.2-B.12-C.2D.25-3.如图给出的是计算11112462014+++⋅⋅⋅的值的程序框图,其中判断框内应填入的是A.2014i ≤B.2014i >C.1007i ≤D.1007i >4.已知随机变量X 服从正态分布()()3,1,150.6826N P X ≤≤=且则()5=P X >A.0.1588B.0.1587C.0.1586D.0.15855.已知命题:ap x≥“a=1是x >0,x+ 2 的充分必要条件”;命题2000:q ∃∈“x R,x +x -2>0”.下列命题正确的是 A.命题“p q ∧”是真命题 B.命题“()p q ⌝∧”是真命题 C.命题“()p q ∧⌝”是真命题 D.命题“()()p q ⌝∧⌝”是真命题6.已知{}n a 是首项为1的等比数列,{}361n n n S a n S a ⎧⎫=⎨⎬⎩⎭是的前项和,且9S ,则数列的前5项和为 A.1558或 B.31516或 C.3116D.1587.或实数x y ,满足不等式组330,230,210,x y x y z x y x y +-≥⎧⎪--≤=+⎨⎪-+≥⎩则的最大值为A.307B.14C.9D. 138.设函数()cos xf x x x=+的图象为9.某运动会某项目参赛领导小组要从甲、乙、丙、丁、戊五名志愿者中选派四人分别从事翻译、导游、礼仪、司机四项不同工作,若其中甲、乙只能从事前三项工作,其余三人均能从事这四项工作,则不同的选派方案共有 A.18种 B.36种 C.48种 D.72种10.已知,A ,B ,C ,D ,E 是函数()sin 2y x πωϕωϕ⎛⎫=+ ⎪⎝⎭>0,0<<一个周期内图象上的五个点,如图所示,,06A π⎛⎫- ⎪⎝⎭,B 为y 轴上的点,C 为图象上的最低点,E 为该函数图象的一个对称中心,B 与D 关于点E 对称,CD 在x 轴上的投影为,,12πωϕ则的值为A.2,6πωϕ== B.2,3πωϕ== C. 1,23πωϕ== D. 1,212πωϕ==11.设双曲线的一个焦点为F ,虚轴的一个端点为B ,如果直线FB与该双曲线的一条渐近线垂直,那么此双曲线的离心率为12.定义域内R 的偶函数()()()(),21f x x R f x f x f ∀∈+=-满足对有,且当[]()22,321218x f x x x ∈=-+-时,,若函数()()()log 10,a y f x x =-++∞在上至少有三个零点,则a 的取值范围是A.⎛ ⎝⎭B. ⎛ ⎝⎭C. ⎛ ⎝⎭D. ⎛ ⎝⎭第II 卷(非选择题 共90分)二、填空题:本大题共4小题,每小题4分,共16分。
2015年江西省高考适应性测试理科数学word版含答案
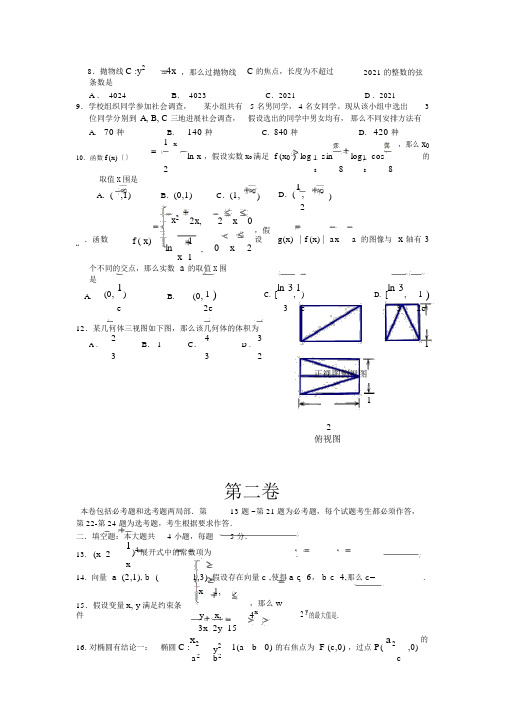
...8.抛物线C :y 2 4x ,那么过抛物线 C 的焦点,长度为不超过2021 的整数的弦条数是A . 4024B . 4023C .2021D .20219.学校组织同学参加社会调查, 某小组共有 5 名男同学, 4 名女同学。
现从该小组中选出3位同学分别到 A, B, C 三地进展社会调查, 假设选出的同学中男女均有, 那么不同安排方法有A. 70 种B.140 种C. 840 种D. 420 种1 xln x ,假设实数x 0满足 f (x 0 ) log 1 sinlog 1 cos ,那么 x 0的10.函数f (x)〔〕28888取值X 围是A .( ,1)B .(0,1)C .(1,)D .(1,)2x 2 2x,2 x 0x.函数f ( x)1,假设g(x) | f (x) | ax a 的图像与 轴有 311ln0 x2,x 1个不同的交点,那么实数 a 的取值X 围是A.(0, 1)B.(0, 1 )C. [ln 3,1) D. [ln 3,1 )e2e3e32e12.某几何体三视图如下图,那么该几何体的体积为2B . 1C .4 31A .3D .32正视图侧视图12 俯视图第二卷本卷包括必考题和选考题两局部.第 13 题 ~第 21 题为必考题,每个试题考生都必须作答,第 22-第 24 题为选考题,考生根据要求作答.二.填空题:本大题共 4 小题,每题5 分.13. (x 21)4展开式中的常数项为.x,假设存在向量c ,使得a c 6, b c 4,那么c =14. 向量 a (2,1), b (1,3) .x1,15.假设变量x, y 满足约束条件y x,,那么 w4x2 y 的最大值是.3x 2y 1516. 对椭圆有结论一: 椭圆C :x 2y 2 1(a b 0) 的右焦点为 F (c,0) ,过点 P( a 2,0)的a 2b 2c直线 l 交椭圆于 M , N 两点,点 M关于x 轴的对称点为M ',那么直线M ' N过点F。
江西省南昌市2015届高三第二次模拟考试数学理科试题有答案(扫描版)

2015 年 高 三 测 试 卷数学(理科)参考答案及评分标准一、选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的.二、填空题:本大题共4小题,每小题5分.13.214.13π 15.1316.2212x y -= 三、解答题:解答应写出文字说明,证明过程或演算步骤.17.解:(Ⅰ)由点,C B 的坐标可以得到34AOC π∠=,23AOB π∠=,…………………2分 所以cos cos()COB AOC AOB ∠=∠+∠1()2222=-⨯--4=-;……6分 (Ⅱ)因为c =23AOB π∠=,所以3C π=,所以2sin sin a b A B ===,………8分所以22sin 2sin()3a b A A π+=+-2sin()6A π=+,2(0)3A π<<,……………………11分 所以当3A π=时,a b +最大,最大值是12分18.解:(Ⅰ)该校运动会开幕日共有13种选择,其中运动会期间至少两天空气质量优良的选择有:1日,2日,3日,5日,9日,10日,12日,所以运动会期间至少两天空气质量优良的概率是2713P =.…………………………………6分(Ⅱ)随机变量ξ所有可能取值有:0,1,2,3;………………………………………………7分(0)P ξ==113,(1)P ξ==613,(2)P ξ==613,(3)P ξ==113,……………………9分所以随机变量ξ的分布列是:随机变量ξ的数学期望是1661012313131313E ξ=⨯+⨯+⨯+⨯=2113.……………………12分 19.(Ⅰ)证明:在梯形ABCD 中,因为2AD DC CB ===,4AB =,4212cos 22CBA -∠==,所以60,ABC ∠=︒由余弦定理求得AC=90ACB ∠=︒即BC⊥又因为平面AEFC ⊥平面ABCD ,所以BC ⊥平面所以BC AG ⊥,………………………………………3分 在矩形AEFC 中,tan 1AE AGE EG ∠==,4AGE π∴∠=tan 1CF CGF GF ∠==,4CGF π∠=,所以2CGF AGE π∠+∠=,即AG CG ⊥,所以AG ⊥平面BCG ;……………………………………………………………………………6分(Ⅱ)FC AC ⊥,平面AEFC ⊥平面ABCD ,所以FC ⊥平面ABCD , 以点C 为原点,,,CA CB CF 所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系, 则)(0,0,0),(0,2,0),1,0)C A B D-,G ,…………………………8分平面BCG 的法向量(3,0,GA =,设平面GCD 的法向量(,,)n x y z =,则0n CG n CD ⎧⋅=⎪⎨⋅=⎪⎩,从而00x z y +=⎧⎪-=,令1x =则(1,3,1)n =-,…………………………………………………………………………10分 所以cos ,n GA <>==,…………………………………………………11分 而二面角D —GCB 为钝角, 故所求二面角的余弦值为.………………………………………………………………12分 20.解:(Ⅰ)当l 垂直于OD 时||AB 最小,因为||OD =2r ==,…………………………………2分因为圆1C 222:(0)x y r r +=>的一条直径是椭圆2C 的长轴,所以2a =,又点D 在椭圆22222:1(0)x y C a b a b +=>>上,所以291414b b+=⇒=, 所以圆1C 的方程为224x y +=,椭圆2C 的方程为22143x y +=;………………………5分 (Ⅱ)椭圆2C 的右焦点F 的坐标是(1,0),当直线m 垂直于x 轴时,||PQ = ||4MN =,四边形PMQN 的面积S =当直线m 垂直于y 轴时,||4PQ =,||3MN =,四边形PMQN 的面积6S =,…………6分……………………10分当直线m 不垂直于坐标轴时,设n 的方程为(1)y k x =-(0)k ≠,此时直线m 的方程为1(1)y x k=--, 圆心O 到直线m的距离为:d =,所以||PQ ==,…………8分 将直线n 的方程代入椭圆2C 的方程得到:()22224384120k x k x k +-+-=,||MN =所以:四边形PMQN 的面积1||||2S PQ MN =⋅===∈,综上:四边形PMQN的面积的取值范围是.…………………………………………12分21.解:(Ⅰ)21221'()22x ax f x x a x x-+=+-=(0)x >,记2()221g x x ax =-+………1分 (一)当0a ≤时,因为0x >,所以()10g x >>,函数()f x 在(0,)+∞上单调递增;……2分(二)当0a <≤时,因为24(2)0a =-≤△,所以()0g x ≥,函数()f x 在(0,)+∞上单调递增;…………………………………………………………………………………………………3分(三)当a >0()0x g x >⎧⎨>,解得x∈,所以函数()f x 在区间上单调递减,在区间(0,),()2a a +∞上单调递增.…………………………5分(Ⅱ)由(1)知道当(1a ∈时,函数()f x 在区间(0,1]上单调递增, 所以(0,1]x ∈时,函数()f x的最大值是(1)22f a =-,对任意的a ∈,都存在0(0,1]x ∈使得不等式20()ln()f x a m a a +>-成立,等价于对任意的(1a ∈,不等式222ln ()a a m a a -+>-都成立,……………………………………6分即对任意的(1a ∈,不等式2ln (2)20a ma m a +-++>都成立, 记2()ln (2)2h a ama m a =+-++,则(1)0h =,1(21)(1)'()2(2)a ma h a ma m a a --=+-+=,因为(1a ∈,所以210a a->, 当1m ≥时,对任意(1a ∈,10ma ->,所以'()0h a >,即()h a 在区间上单调递增,()(1)0h a h >=成立;…………………………………………………………………………9分 当1m <时,存在0(1a ∈使得当0(1,)a a ∈时,10ma -<,'()0h a <,()h a 单调递减,从而()(1)0h a h <=,所以(1a ∈时,()0h a >不能恒成立.综上:实数m 的取值范围是[1,)+∞.……………………………………………………………12分 22.解:AF 是圆的切线,且18,15AF BC ==,∴由切割线定理得到2218(15)12AF FB FC FB FB FB =⋅⇒=⋅+⇒=,…………………3分 ,AB AD ABD ADB =∴∠=∠,则,//FAB ABD AF BD ∠=∠∴,…………………………………………………………………6分 又//AD FC ,∴四边形ADBF 为平行四边形.12,,18AD FB ACF ADB F ACAF ==∠=∠=∠∴==,//,18AE ADAD FC AE BC∴=-,解得8AE =。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
泄露天机——2015年江西省高考押题 精粹数学理科本卷共60题,三种题型:选择题、填空题和解答题。
选择题36小题,填空题8小题,解答题18小题。
一、选择题(36个小题)1. 已知全集{}1,2,3,4,5U =, 集合{}3,4,5M =, {}1,2,5N =, 则集合{}1,2可以表示为( ) A .MN B .()U M N C .()U MN D .()()U U M N答案:B解析:有元素1,2的是,UM N ,分析选项则只有B 符合。
2. 集合 {}{}{}1,2,3,4,5,1,2,3,|,A B C z z xy x A y B ====∈∈且,则集合C 中的元素个数为( )A .3B .4C .11D .12 答案:C解析:{1,2,3,4,5,6,8,9,10,12,15}C =,故选C 。
3. 设集合{}1,0,1,2,3A =-,{}220B x x x =->,则A B ⋂=( )A .{}3B .{}2,3C .{}1,3-D .{}0,1,2 答案:C解析:集合{}{}22020B x x x x x x =->=><或,{}1,3A B ⋂=-。
4. 若(1)z i i +=(其中i 为虚数单位),则||z 等于( )A .1 3 C. 22D. 12答案:C 解析:化简得i z 2121+=,则||z =22,故选C 。
5. 若复数iia 213++(i R a ,∈为虚数单位)是纯虚数,则实数a 的值为( )A. 6-B. 2-C. 4D. 6答案:A 解析:3(3)(12)63212(12)(12)55a i a i i a a i i i i ++-+-==+++-,所以6320,0,655a aa +-=≠∴=-。
6. 复数21ii -在复平面内对应的点位于( ) A .第一象限 B .第二象限C .第三象限D .第四象限答案:D解析:根据复数的运算可知()()22121215521i i i i i i +==---,所以复数的坐标为21,55⎛⎫- ⎪⎝⎭,所以正确选项为D 。
7. 已知向量()()1,1,2,2m n λλ=+=+,若()()m n m n +⊥-,则=λ( )A. 4- B .3-C .2-D .-1答案:B解析:(23,3),(1,1)m n m n λ+=+-=--,()()()(),23130,3λλ+⊥-∴+⨯--=∴=-m n m n 。
8. 已知D 为ABC ∆的边BC 的中点,ABC ∆所在平面内有一个点P ,满足PA PB PC =+,则||||PD AD 的值为( ) DABCPA .12B .13C .1D .2答案:C解析:如图,四边形PBAC 是平行四边形,D 为边BC 的中点,所以D 为边PA 的中点,||||PD AD 的值为1。
9.ΔABC 中,120BAC ∠=,AB=2,AC=1,D 是边BC 上的一点(包括端点),则•的取值范围是( )A . [1,2]B .[0,1]C .[0,2]D . [﹣5,2]答案:D解析:∵D 是边BC 上的一点(包括端点),∴可设(1)(01)λλλ=+-≤≤AD AB AC120∠=BAC ,2=AB ,1=AC ,211201∴=⨯⨯=-AB AC COS22,(1)()(21)(1)(21)417 2.01(72)52λλλλλλλλλλλ⎡⎤∴=+--⎣⎦=--+-=---+-=-+≤≤⎡⎤∴-+∈-⎣⎦AD BC AB AC AC AB AB AC AB AC∴AD BC 的取值范围是,52⎡⎤-⎣⎦。
10.已知命题p :x R ∃∈,20x ->,命题q :x R ∀∈,x x <,则下列说法中正确的是( )A .命题p q ∨是假命题B .命题p q ∧是真命题C .命题()p q ∧⌝是真命题D .命题()p q ∨⌝是假命题 答案:C解析:命题p 为真命题.对命题q ,当14x =时,1124x x =>=,故为假命题,q ⌝为真命题.所以C 正确。
11.命题“x R ∃∈,2210x x -+<”的否定是( )A .x R ∃∈,2210x x -+≥B .x R ∃∈,2210x x -+>C .x R ∀∈,2210x x -+≥D .x R ∀∈,2210x x -+< 答案:C解析:命题“x R ∃∈,2210x x -+<” 是特称命题,则它的否定是全称命题,即x R ∀∈2210x x -+≥。
12.命题p :关于x 的方程20()-+=∈x x x m m R 有三个实数根;命题q :01≤<m ;则命题p 成立时命题q 成立的( )A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分又不必要条件答案:B解析:由方程(2),0 20(2)(2),-≥⎧-+=⇒=-=⎨+<⎩x x xx x x m m x xx x x,易知函数()f x是R上的奇函数,由()f x的图像可知,函数()f x在[)0,+∞上的最大值是1,根据图像的对称性知函数()f x在(),0-∞上的最小值为-1,又函数()f x的图像与x轴有3个交点,那么原方程有3个实数根的充要条件是()1,1-,而[)()0,11,1⊆-/,所以选择B。
13.若某几何体的三视图如右图所示,则此几何体的体积等于()A.30B.12 C.24D.4答案:C解析:由三视图可知,原几何体是一个三棱柱被截去了一个小三棱锥得到的,如图111345(34)324232V=⨯⨯⨯-⨯⨯⨯=,故选C。
14.某几何体的三视图如图所示,图中三个正方形边长均为2,则该几何体的体积为()A.38B.82π- C.43π D.283π-答案:D解析:由三视图可知此几何体是:棱长为2 的正方体挖去了一个圆锥而形成的新几何体,43233正视图侧视图俯视图3243其体积为3212212833ππ-⨯⨯⨯=-,故选 D 。
15.某几何体的三视图如图所示,则该几何体的体积为( ) A .43 B .52 C .73 D .53答案:A解析:该几何体是下面是一个三棱柱,上面是一个有一个侧面垂直于底面的三棱锥。
其体积为11141211212323⎛⎫⎛⎫⨯⨯⨯+⨯⨯⨯⨯=⎪ ⎪⎝⎭⎝⎭。
16.已知0a >,,x y 满足约束条件13(3)x x y y a x ≥⎧⎪+≤⎨⎪≥-⎩,若2z x y =+的最小值为1,则a =( )A .14 B .12C .1D .2答案:B解析:依题意可以画出不等式表示的图形,当过点()1,2a -时取最小值,即2-2a =1,a =12。
17.已知110220x x y x y ≥⎧⎪-+≥⎨⎪--≤⎩,若ax y +的最小值是2,则a =( )A .1B .2C .3D .4答案:B解析:由已知得线性可行域如图所示,则z ax y =+的最小值为2,若2a >-,则(1,0)为最小值最优解,∴2a =,若2a ≤-,则(3,4)为最小值最优解,不合题意,故选B 。
18.已知不等式组240,30,0-+≥⎧⎪+-≤⎨⎪≥⎩x y x y y 构成平面区域Ω(其中x ,y 是变量)。
若目标函数6(0)z ax y a =+>的最小值为-6,则实数a 的值为( ) A .32 B .6 C .3 D .12 答案:C解析:不等式组240,30,0-+≥⎧⎪+-≤⎨⎪≥⎩x y x y y 表示的平面区域如图阴影部分所示,因为0a >,故06a -<。
可知6z ax y =+在C 点处取得最小值,联立240,0x y y -+=⎧⎨=⎩解得2,0,x y =-⎧⎨=⎩即(2,0)C -,故6260a -=-+⨯,解得3a =。
19. 如图给出的是计算11112462014++++的值的程序框图,其中判断框内应填入的是( )A .2013≤i ?B .2015≤i ?C .2017≤i ?D .2019≤i ? 答案:B解析:由程序知道,2,4,6,2014i =都应该满足条件,2016=i 不满足条件,故应该选择B 。
20.执行如图所示的程序框图,则输出的结果是( ) A. 14 B. 15C. 16D. 17答案:C解析:由程序框图可知,从1n =到15n =得到3S <-,因此将输出 16n =. 故选C 。
21. 执行如图所示的程序框图,若输入n 的值为22,则输出的s 的值为( ) A.232 B.211 C. 210 D. 191开始0,1S n ==输出n 结束3?S <-21log 2n S S n +=++否是1n n =+答案:B解析:第一次运行时,1,2S i ==;第二次运行时,11,3S i =+=;第三次运行时,112,4S i =++=;第四次运行时,1123,5S i =+++=; 第五次运行时,11234,6S i =++++=;…,以此类推,直到112341920,22S i =+++++++=…,程序才刚好不满足i n <,故输出()2011202112S =+⨯+=.故选B 。
22. 已知x 、y 取值如下表:x 0 1 4 5 6 y1.3m3m5.67.4画散点图分析可知:y 与x 线性相关,且求得回归方程为ˆ1y x =+,则m 的值(精确到0.1)为( ) A.1.5B.1.6C.1.7D.1.8答案:C解析:将 3.2x =代入回归方程为ˆ1yx =+可得 4.2y =,则4 6.7m =,解得 1.675m =,即精确到0.1后m 的值为1.7. 故选C 。
23. 如图是2013年某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和众数依次为( ) A.85,84B.84,85C.86,84D.84,867 8 994 4 6 4 7 3答案:A解析:去掉一个最高分和一个最低分后,所剩数据为84,84,86,84,87,平均数为8484868487855++++=,众数为84. 故选A 。
24. 学校为了解学生在课外读物方面的支出情况,抽取了n 个同学进行调查,结果显示这些同学的支出都在[)10,50(单 位:元),其中支出在[)30,50(单位:元)的同学有67人,其频率分布直方图如图所示,则n 的值为( )A .100B .120C .130D .390 答案:A解析:支出在[)30,50的同学的频率为1(0.010.023)100.67-+⨯=,671000.67n ==。
