第2章 matlab数值计算功能共84页文档
合集下载
第2章 MATLAB 数值计算功能
3 线性等分向量的生成
●功能函数为linspace，
●其调用格式有两种：
一是 linspace(x1,x2,n) % 把 [x1，x2] 分为n-1等分； 二是 linspace(x1,x2) % 把 [x1，x2] 分为100-1等分。
4 对数等分向量的生成
●功能函数为logspace，
●其调用格式有两种：
第2章 MATLAB 数值计算功能
2.1 MATLAB的数据类型 主要包括五种数据类型: ●数字 ●字符串 ●矩阵(数组) ●单元型数据 ●结构型数据
2.1.1 变量与常量
(1)变量 特点：不要求事先说明，不要求指 定变量类型(根据赋值和操作来确 定变量类型)。若变量已存在，将 由新值代旧值，新类型代替旧类 型。 遵循的规则： ●变量区分大小写; ●变量名长度不超过31位，之 后字符被忽略;
A = [1,2,3; 4,5,6; 7,8,9] A= 1 4 7 2 5 8 3 6 9 a=[1 2 456 7 8 9] a= 1 4 7 3 2 5 8 3 6 9
2 创建M文件输入大矩阵； 3 直接从数据获取系统得到。
1 矩阵的加和减 c=a+b
a=[1 2 3;2 3 4; 3 4 5]; c= 2 3 4 4 5 6 6 7 8
8 矩阵的指数运算 exp（A）和 expm(A) expm1(A) expm2(A) expm3(A) 注意：有m表示矩阵运算，无m表示元素 运算；expm的计算结果与expm1相 同，几个函数的计算是有差别的，但 差别很小。 9 矩阵的对数运算 log（b） 和 logm（b） 10 矩阵的开方运算 sqrt（b）和 sqrtm（b） 注意：有m表示矩阵运算，无m表示元素 运算
第2章-MATLAB数值计算.
>> a=[1 2;3 4;5 6] a= 1 2 3 4 5 6 >> a(3,3) ??? Index exceeds matrix dimensions >> a(3,3)=9 a= 1 2 0 3 4 0 5 6 9
%提取a(3,3)的值 %给a(3,3) 赋值
（2）单下标方式。矩阵元素也可以用“单下标”标志，就是先把矩阵的所有 列按先左后右的次序连接成“一维长列”，然后对元素位置进行编号。以mn的矩 阵A为例，若元素A(i,j)则对应的“单下标”为s=(j1) mi。矩阵A的元素下标如 图2.2所示。
2．子矩阵块的产生方式 MATLAB利用矩阵下标可以产生子矩阵。对于a(i,j)，如果i和j是向量而不是标 量，则将获得指定矩阵的子矩阵块。子矩阵是从对应矩阵中取出一部分元素构成 的，如图2.3所示，分别用全下标和单下标方式取子矩阵。
（1）用全下标方式。矩阵A如图2.3所示，使用以下几种方式都可以构成子矩 阵。 ① a([1 3],[2 3])：取行数为1、3，列数为2、3的元素构成子矩阵。 ans = 2 0 6 9 ② a(1:3,2:3)：取行数为1～3，列数为2～3的元素构成子矩阵，“1:3”表示1、 2、3行下标。 ans = 2 0 4 0 6 9
3.5000
4.0000
%空矩阵
%两行向量构成矩阵
（2）使用linspace和logspace函数生成向量。 ① linspace用来生成线性等分向量。与“from:step:to”方式不同的是，它直接 给出元素的个数从而得出各个元素的值。 语法： linspace(a,b,n) 说明：a、b、n 3个参数分别表示开始值、结束值和元素个数。生成从a到b之 间线性分布的n个元素的行向量，n如果省略则默认值为100。 ② logspace用来生成对数等分向量，它和linspace一样直接给出元素的个数从 而得出各个元素的值。在画Bode图等应用中，需要使用logspace命令生成对数等间 隔的数据。 语法： logspace (a,b,n) 说明：a、b、n 3个参数分别表示开始值、结束值和数据个数，n如果省略则默 认值为50。生成从10a到10b之间按对数等分的n个元素的行向量。
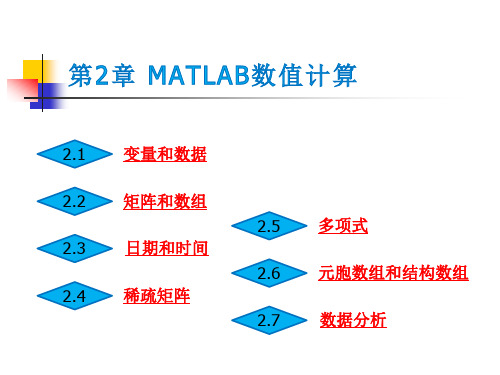
%提取a(3,3)的值 %给a(3,3) 赋值
（2）单下标方式。矩阵元素也可以用“单下标”标志，就是先把矩阵的所有 列按先左后右的次序连接成“一维长列”，然后对元素位置进行编号。以mn的矩 阵A为例，若元素A(i,j)则对应的“单下标”为s=(j1) mi。矩阵A的元素下标如 图2.2所示。
2．子矩阵块的产生方式 MATLAB利用矩阵下标可以产生子矩阵。对于a(i,j)，如果i和j是向量而不是标 量，则将获得指定矩阵的子矩阵块。子矩阵是从对应矩阵中取出一部分元素构成 的，如图2.3所示，分别用全下标和单下标方式取子矩阵。
（1）用全下标方式。矩阵A如图2.3所示，使用以下几种方式都可以构成子矩 阵。 ① a([1 3],[2 3])：取行数为1、3，列数为2、3的元素构成子矩阵。 ans = 2 0 6 9 ② a(1:3,2:3)：取行数为1～3，列数为2～3的元素构成子矩阵，“1:3”表示1、 2、3行下标。 ans = 2 0 4 0 6 9
3.5000
4.0000
%空矩阵
%两行向量构成矩阵
（2）使用linspace和logspace函数生成向量。 ① linspace用来生成线性等分向量。与“from:step:to”方式不同的是，它直接 给出元素的个数从而得出各个元素的值。 语法： linspace(a,b,n) 说明：a、b、n 3个参数分别表示开始值、结束值和元素个数。生成从a到b之 间线性分布的n个元素的行向量，n如果省略则默认值为100。 ② logspace用来生成对数等分向量，它和linspace一样直接给出元素的个数从 而得出各个元素的值。在画Bode图等应用中，需要使用logspace命令生成对数等间 隔的数据。 语法： logspace (a,b,n) 说明：a、b、n 3个参数分别表示开始值、结束值和数据个数，n如果省略则默 认值为50。生成从10a到10b之间按对数等分的n个元素的行向量。
第二章matlab02数值运算功能1
范 例 3.1416 3.1416e+000
3.14159265358979
format long
15 位数字表示
format long e
15位科学记数表示
format rat 分数近似 format bank 两位小数
3.1415926535897 93e+000 355/113 3.14
MATLAB命令 format hex format +
realmax-系统所能表示的最大正实数： 系统所能表示的最大正实数： 系统所能表示的最大正实数 1.797693134862316e+308 realmin-系统所能表示的最小正实数： 系统所能表示的最小正实数： 系统所能表示的最小正实数 2.225073858507201e-308
7.变量查询和清除函数（变量操作） 变量查询和清除函数（变量操作）
可用load指令调用已生成的 指令调用已生成的mat文件 可用 指令调用已生成的 文件
load data
load data a b
即可恢复保 存过的所有 变量
load filename variables的使用说明 的使用说明
• 将以前用 将以前用save命令保存的变量 命令保存的变量variables从磁 命令保存的变量 从磁 盘文件中调入MATLAB工作空间。 工作空间。 盘文件中调入 工作空间 • 用load 命令调入的变量，其名称为用 命令调入的变量，其名称为用save命 命 令保存时的名称，取值也一样。 令保存时的名称，取值也一样。 • Variables所表示的变量列表中，不能用逗 所表示的变量列表中， 所表示的变量列表中 号，各个不同的变量之间只能用空格来分隔。 各个不同的变量之间只能用空格来分隔。 空格来分隔 • 未列出 未列出variables时，表示将磁盘文件中的 时 所有变量都调入工作空间。 所有变量都调入工作空间。
第2章 MATLAB的基本数值计算
d=[-1;0;2];f=pi*d f = -3.1416 0 6.2832
(4)矩阵除法 运算包括正斜杠和反斜杠两种。 左除： A\B=A－1B, A为方矩阵 右除： A/B=AB－1，B为方矩阵
矩阵的左除（\）
对于矩阵A和B，A\B表示矩阵A左除矩阵B，其计算 结果与A的逆与B相乘相似。 但MATLAB所用的算法不同。事实上，A\B是方程 AX=B的解，当方程是欠定或超定时，A\B对应的是 最小二乘解。
第2章 MATLAB的语言的主要构成
§2-1 数值和变量
§2-1 数值和变量
一、数据类型 MATLAB的数据类型主要有：数值型、 字符串型、元胞型、结构型等，其中数值 型有双精度型、单精度型和整数类。
§2-1 数值和变量
二、数值
MATLAB的数值采用十进制表示，可用带小 数点的形式直接表示，也可用科学计数法， eps为相对精度位数，数值的表示范围 为 10309 ～ 10
(5)数据的保存与获取
把matlab工作空间中一些有用的数据长 久保存下来的方法是生成mat数据文件。 save —— 将工作空间中所有的变量 存到matlab.mat文件中。 默认文件名
save data——将工作空间中所有的变量存到
data.mat文件中。
save data a b ——将工作空间中a和b变量存
返回
%A为实数阵 %B为虚数阵
(2)矩阵转置 >> A=[1 2 3;4 5 6] A=
1 2 3 4 5 6
>>A'
ans= 1 4 2 5 3 6
(3)矩阵的乘法（＊） 两个矩阵A、B能进行乘法运算的前提是A的列数要 与B的行数相等。若A为m×n的矩阵， B为n×p的 矩阵，则所得结果为一个m×p的矩阵。(克莱姆
matlab第2章 数值计算
i或j
虚数单位，表示 1 =0.0000 + 1.0000i
NaN或nan
表示不定数，非数值型，如0/0
realmin realmax
可用的最小正实数值，最小浮点数，21022 =2.2251e-308
可用的最大正实数值最大浮点数， 21022=4.4942e+307
2.1.2 变量与基本函数
1．变量
B=[1 3 6 8 10 13. 17 19 21]; save xyz A B
首页
这样就将数组A、B保存在文件名为xyz的数据文件，即xyz.mat文件。
3．利用Workspace菜单保存数组
若Workspace内存变量中已有数组A、B，可使用菜单栏 中的“File”→“Save Workspace As”对话框来进行操 作。
>> x(2)=0
x=
2 0 3 16 1 27 39 4 48
>> x(a)=10
x=
2 0 3 10 1 10 10
4
10 。 首页
2.2.4 数组排序及维数
1．数组排序
格式
sort(x)
%将数组x中的元素按升序排列
sort(x,'ascend') %将数组x中的元素按升序排列
sort(x,'descend') %将数组x中的元素按降序排列
含义
a+b a.*b a./b a.\b a.^k
对应元素相加
a-b 对应元素相减
对应元素相乘
a的元素被b的 对应元素相除 b的元素被a的 对应元素相除 a的每个元素的og(a)
标量k与b中每 一个元素相乘
标量k被b中每 一个元素相除
第二章matlab02数值运算功能2
a*b ans = 25 55 85 a.*b 37 85 133 46 109 172 ans = 2 4 49 8 15 72 18 3应元素间的商 给出a,b对应元素间的商 对应元素间的商. a.\b=b./a a./b=b.\a — 都是 的元素除以 的对应元素 都是a的元素除以 的元素除以b的对应元素 a.\b=b./a — 都是 的元素除以 的对应元素 都是b的元素除以 的元素除以a的对应元素
2.4.3矩阵的关系和逻辑运算 矩阵的关系和逻辑运算
1.矩阵的关系运算符：<, >, <=, >=, = =, ~= 矩阵的关系运算符： 矩阵的关系运算符 • 矩阵之间的每个元素进行比较，运算结果 矩阵之间的每个元素进行比较， 为与原矩阵大小一样的由0 为与原矩阵大小一样的由0和1组成的矩阵 注意：1=<a<=2错误 注意： 错误 例: 1<＝a<=2正确 ＝ 正确
• •
§2.4 矩阵的运算
矩阵的数学运算 矩阵的点(数组 运算 矩阵的点 数组)运算 数组 矩阵的关系和逻辑运算
2.4.1矩阵的数学运算 矩阵的数学运算
矩阵运算符 含义 A’ 矩阵转置 A+B 矩阵相加 A-B 矩阵相减 A*B 矩阵相乘 A/B 矩阵相除（右除） 矩阵相除（右除） B\A 矩阵相除（左除） 矩阵相除（左除） A^n A阵的 n次幂 阵的 次幂
x X = y z
10 B = 5 −1
要解上述的联立方程式， 要解上述的联立方程式，可利用矩阵左除 \ 做运 时要求A、 的行数相等 相等。 算，即：X=A\B， 左除时要求 、B的行数相等。 ， 左除时要求
如果将原方程式改写成 X*A=B，且令 X, A 和 B ， 分别为
2.4.3矩阵的关系和逻辑运算 矩阵的关系和逻辑运算
1.矩阵的关系运算符：<, >, <=, >=, = =, ~= 矩阵的关系运算符： 矩阵的关系运算符 • 矩阵之间的每个元素进行比较，运算结果 矩阵之间的每个元素进行比较， 为与原矩阵大小一样的由0 为与原矩阵大小一样的由0和1组成的矩阵 注意：1=<a<=2错误 注意： 错误 例: 1<＝a<=2正确 ＝ 正确
• •
§2.4 矩阵的运算
矩阵的数学运算 矩阵的点(数组 运算 矩阵的点 数组)运算 数组 矩阵的关系和逻辑运算
2.4.1矩阵的数学运算 矩阵的数学运算
矩阵运算符 含义 A’ 矩阵转置 A+B 矩阵相加 A-B 矩阵相减 A*B 矩阵相乘 A/B 矩阵相除（右除） 矩阵相除（右除） B\A 矩阵相除（左除） 矩阵相除（左除） A^n A阵的 n次幂 阵的 次幂
x X = y z
10 B = 5 −1
要解上述的联立方程式， 要解上述的联立方程式，可利用矩阵左除 \ 做运 时要求A、 的行数相等 相等。 算，即：X=A\B， 左除时要求 、B的行数相等。 ， 左除时要求
如果将原方程式改写成 X*A=B，且令 X, A 和 B ， 分别为
第二章Matlab数值计算
第⼆章Matlab数值计算第⼆章 MATLAB 数值运算学习⽬标：掌握矩阵的构造和运算⽅法，能够使⽤常⽤的⼏种函数进⾏简单的问题求解。
本章重点难点：利⽤Matlab 软件学习数据的操作，包括矩阵的⽣成、数组运算数据分析和统计分析函数、矩阵运算多项式运算、代数⽅程求解、函数的极值问题求解、函数的微积分问题求解、数据插值运算。
MATLAB ⽀持线性代数所定义的全部矩阵运算。
⽤户可通过MATLAB ⽅便的处理线性代数的运算，可以很容易完成原来复杂、费时的运算⼯作。
作为MATLAB 本⾝，它最初的⽬的也是为了解决矩阵问题⽽开发的，甚⾄连英⽂名称都是matrix （矩阵）和laboratory （实验室）两个英⽂单词缩写的组合。
了解了这⼀点，对MATLAB 将矩阵作为基本的操作对象的做法就很容易理解了。
实际上，通过⼀定的转化⽅法，都可以将⼀般的数学计算转化成相应的矩阵运算来处理。
例如，前⾯讲到的标量就可以看作是只有⼀⾏⼀列的矩阵，列向量是只有⼀列的矩阵，⾏向量是只有⼀⾏的矩阵。
矩阵是MATLAB 的基本运算单元，该单元是定义在复数域上的，系统会根据⽤户的输⼊⾃动设置，运算期间会⾃动调整矩阵的维数，事先不需要⽤户定义矩阵的维数。
2.1 变量及其赋值2.1.1 基本概念在MATLAB 中，经常使⽤到标量、向量、矩阵和数组，其定义分别如下： 1)标量：是指11?的矩阵,即只含有⼀个数的矩阵。
2)向量：是指n ?1或1?n 的矩阵，即只有⼀⾏或⼀列的矩阵。
3)矩阵：是⼀个矩形的数组，即⼆维数组，其中向量和标量都是矩阵的特例，00?矩阵为空矩阵（[ ]）。
4)数组：是指n 维的数组，为矩阵的延伸，其中矩阵和向量都是数组的特例。
2.1.2 基本运算使⽤matlab 进⾏数学式的计算就像⽤计算器进⾏数字运算⼀样简便。
在MATLAB 下进⾏基本数学运算，只需将运算式直接打⼊系统提⽰符号（>>）之后，并按⼊Enter 键即可，这是命令⾏⽅式。
MATLAB课件第二章 MATLAB语言的数值计算
2.1.3 变量精度
在matlab中,变量的精度问题不需要设 定,一律使用双精度,但是我们可以通过 format命令或者更改preferences中的 Numericformat项来更改数据的显示格式. 命令格式为:format short
2.1.4 永久变量
Matlab语言设置了一些永久变量 eps,pi,Inf,NaN,i,j,nargin,nargout, realmax,realmin (1)这些变量不能被clear清除; (2)这些变量不响应who和whos; (3)nargin,nargout为函数变量; (4)pi,i,j,realmax,realmin为机器常数变 量; (5)Inf 为无穷变量,NaN为非数变量.
2、矩阵乘（）运算规则：
A矩阵的列数必须等于B矩阵的行数；
标量可与任何矩阵相乘。
除算） .^ 点乘方（用于矩阵点运算） ./ 点除（用于矩阵点运算） kron 张量积 ‘ 矩阵转置 inv 矩阵求逆 fliplr 矩阵左右翻转 flipud 矩阵上下翻转 rot90 矩阵逆时针方向旋转90度
线性代数方程组的表达式为AX = B或者 XA = B，由于矩阵维数的不同，方程组解 的形式也不同，设解向量X为n×1维的，系 数矩阵A的维数为m×n维的，系数矩阵B 的维数为n×1维的；那么方程组的解可以 分为以下三类： m=n，为恰定方程，可求得唯一解； m>n，为超定方程，求最小二乘解，多 于一组解； m<n，为欠定方程，解无实际意义，解 中至多有m个非零元素。
例2.27 已知矩阵a，求特征多项式与特征根。
3、多项式计算 我们可以利用polyval函数来计算出多项 式在指定点处的值，例如：
4、卷积和反卷积（多项式乘法与除法） 例如：求a(x)=x^3+2x^2+3x+4和 b(x)=x^3+4x^2+9x+16的乘积c(x);
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2、由函数创建和修改矩阵：
MATLAB提供用于创建某些特殊矩阵的函数
A=[ ] 创建空矩阵 注意空矩阵与零矩阵的差别
常用创建矩阵函数
zeros(m,n) 元素全为零的mn阶矩阵 ones(m,n) 元素全为 1 的mn矩阵 rand(m,n) 元素为在[0，1]上均匀分布的mn随机矩阵 randn(m,n) 元素为标准正态分布的mn随机矩阵
3.续行标志（…） 当一条语句或矩阵太长，一行显示不下时，可用
续行标志…，另起一行继续完成该条语句的书写。
2.1.3 矩阵及其元素的赋值
矩阵是 MATLAB 进行数据处理的基本单元，MATLAB 的大部分运算都是在矩阵的意义上进行的，矩阵运算也 是 MATLAB 最重要的运算。赋值就是把数赋予代表常 量或变量的标识符。 MATLAB中的变量或常量都代表 矩阵，标量应看作是1×1阶的矩阵。
t=初值：增量：终值
其中 “增量”是可以省略的，省略时，默认的增量步 长为1。增量也可以是负值，但此时，初值应该大于终 值。
例如：x=1:5; y=0:pi/4用函数linspace和logspace创建向量：
linspace 函数，创建指定长度的等距向量 t=linspace(初值d1，终值d2，点数n）
>> C(:,:,3)=ones(2,3)*3
C(:,:,1) =
111
111
C(:,:,2) = 222 222
同样的方法还可以创建4维… 等更高维的数组。
C(:,:,3) =
333
333
3. 由ones、zeros等函数直接创建
2.1.4 向量的生成
在MATLAB中数组可以看成是行向量，即只有一行或 一列的矩阵。前面介绍的所有矩阵的建立和保存的方 法，对向量同样适用，这里不再重复。同时，介绍 matlab中创建向量的特殊命令。 1.利用冒号“：”创建等差数列：
00 00 A(:,:,2) = 00 01
>> B(2,5,:)=1:3 B(:,:,1) =
00000 00001 B(:,:,2) = 00000 00002 B(:,:,3) = 00000 00003
2.由若干个同样大小的低维数组合成
>> C=ones(2,3);
>> C(:,:,2)=ones(2,3)*2;
意义为：在线性空间上，行矢量的值从d1到d2，数 据个数n，缺省时n为100。
例：k=linspace(-pi,pi,4) logspace 函数，创建对数等距的向量
y=logspace(d1,d2) y=logspace(d1,d2,N) 意义为：从10的d1次幂到d2次幂之间按等比级数等分 为N个点，N缺省时，默认为50。
2.1.2、 MATLAB 的语句
1.百分号（注释符）% 与其它程序语言一样，为了方便其他人及日
后自己对程序的阅读，增加程序的可读性，需要 在MATLAB文件中加入注释。注释行必须以%号 开始，执行文件时，%号后面的语句不予执行。 2.逗号和分号
在赋值语句中，逗号（空格）用在同一行中各 元素之间，分号用在行与行之间。多条语句放在一 行，用逗号分开表示要求显示结果，由分号分开表 示不要求显示结果。
例如输入语句
显示的结果为：
a=[1 2 3;4 5 6;7 8 9]
a= 123 456 789
矩阵里的元素也可以用表达式代替，例如输入
X=[-1.3,sqrt(3),(1+2+3)/5*4]
显示结果
矩阵里的元素还可以是
X=
复数，复数用内定变量
-1.3000 1.7321 4.8000 i，j表示
矩阵的创建可以通过以下几种形式： （1）直接列出元素形式； （2）通过语句和函数产生； （3）从外部文件装入； （4）建立在M文件中。
1、直接输入矩阵：
对于较小的简单矩阵，从键盘上直接输入矩阵时最常 用、最方便和最好的数值矩阵创建方法。创建矩阵的 基本原则： •矩阵的所有元素必须放在方括号“[ ]”内； •矩阵元素之间必须用逗号“，”或空格隔开； •矩阵行与行之间用分号“；”或回车符隔开； •矩阵元素可以是数字或任何不含未定义变量的表达式。
2.1 变量及其赋值
2.1.1变量
像任何其他计算机语言一样，MATLAB 也是使用变量 来保存信息的。变量由变量名表示，变量的命名应遵 循如下规则：
1．变量名必须以字母开头；由字母、数字和下划线 混合组成；不允许使用空格、标点符号；
2．变量名的字符长度不应超过31个（对于6.x版本）； 3. MATLAB严格区分大小写字母，因此，A和a是不同 的变量。 4．关键字（如 if，while 等）不能作为变量名。
MATLAB的内定变量见表2 - 1
永久变量
• eps — 容差变量，定义为1.0到最近浮点数的
距离,在 pc机上= 2-52 • pi — 圆周率的近似值3.1415926 • inf或Inf — 表示正无大,定义为1/0 • NaN — 非数，它产生于0× ，0/0，/ 等 运算
• i，j — 虚数单位 • ans — 对于未赋值运算结果，自动赋给ans
例如：有文本文件mydata.txt，将后缀改为.dat，在命 令窗口输入：
load mydata.dat %把文件中的内容调入到工作空间中 mydata %显示变量mydata
4、利用M文件中的函数生成矩阵
高维矩阵的创建（简单了解）
1.通过全下标元素赋值方式
>> A=zeros(2,2) A=
00 00 >> A(2,2,2)=1 A(:,:,1) =
以上命令可以只有一个参数，生成的是方阵
eye(n) 单位矩阵, nn阶的方阵 magic(n) 魔方矩阵，其特点是元素由1到n2的自然数 组成，每行、每列及两对角线上的元素之和均等于 (n3+n)/2
3、从外部数据文件调入矩阵：
在MATLAB中，还可以从外部文件读入数据生成矩阵。 这些文件可以是存储Matlab已经生成的矩阵二进制文 件，也可以是包含数值数据的文本文件。在文本文件 中，数据必须排成一个矩阵表，数据之间用用空格分 隔，每行包含矩阵的一行。保存文件时，文件名后缀 为.dat
2.1.5 矩阵的下标
创建了矩阵之后，若要调用矩阵里的元素，就要了解 单个元素标志和寻访的3种方式： 1.“全下标”标志